The ADMM algorithm for audio signal recovery and performance modification with the dual Douglas-Rachford dynamical system

1.   Introduction

The graphs considered in this paper are finite, undirected and simple. Let $G$ be a graph with vertex set $V(G)$ and edge set $E(G)$. For any $X\subseteq V(G)$, denote by $G[X]$ the subgraph of $G$ induced by $X$. For any $u, v\in V(G)$, denote by $d_G(u, v)$ the distance from $u$ to $v$ in $G$ as well as $d_G(v)$, $N_{G}(v)$ and $N_{G}[v]$ the degree, open neighborhood and closed neighborhood in $G$, respectively. Furthermore, for any $U\subseteq V(G)$, the open and closed neighbourhood of $U$ are defined as $N_G(U) = \bigcup\nolimits_{v\in U}N_G(v)$ and $N_G[U] = N_G(U)\cup U$, respectively. Two graphs $G$ and $H$ are disjoint if they have no vertices in common and no vertex of $G$ is adjacent to any vertex of $H$. The union of graphs $G$ and $H$ is the graph $G\cup H$ with $V(G\cup H) = V(G)\cup V(H)$ and $E(G\cup H) = E(G)\cup E(H)$.

A set $S \subseteq V(G)$ is called a $2$-packing of graph $G$ if $d_{G}(x, y) > 2$ for every pair of distinct vertices $x, y \in S$. A set $D\subseteq V(G)$ is called a dominating set of $G$ if every vertex of $G$ is either in $D$ or adjacent to a vertex of $D$. The domination number $\gamma(G)$ is the cardinality of a minimum dominating set of $G$. We denote by $\underline{MDS}(G)$ the set of all the minimum dominating sets. That is, $\underline{MDS}(G) = \{D \mid D$ is a minimum dominating set of $G\}$.

Remark. We use the symbol $\underline{MDS}$ but not $MDS$, because $MDS(G)$ has been defined to be the set of all the minimal dominating set of a graph $G$ in the textbook ^[14].

1.1.   Vertex-critical graphs and strong $l$-vertex-set-critical graphs

Definition 1.1. A vertex $v\in V(G)$ is called a critical vertex of $G$ if $\gamma(G-v) = \gamma(G)-1$.

Observation 1.2. For any $v\in V(G)$,

Definition 1.3. A graph $G$ is called vertex-critical if every vertex of $G$ is critical.

The research on vertex-critical graphs was conducted in ^[4]. Afterwards, authors studied on its diameter ^[9], connectivity ^[1], existence of perfect matching ^[1,2,16] and factor critical property ^[2,22,23]. Interested reads could consider the existence of irregular dominating set on vertex-critical graphs ^[7,18].

Furthermore, based on the right and the left of Formula (1.1), Brigham et al. ^[5] and Phillips et al. ^[21] extended the notion of vertex-critical graphs by introducing $(\gamma, k)$-critical graphs and $(\gamma, t)$-critical graphs, respectively.

Definition 1.4. ^[5] A graph $G$ is called $(\gamma, k)$-critical if $\gamma(G-S) < \gamma(G)$ for every $S\subseteq V(G)$ with $|S| = k$.

Definition 1.5. ^[21] A graph $G$ is called $(\gamma, t)$-critical if $\gamma(G-S) = \gamma(G)-t$ for every 2-packing $S$ of $G$ with $|S| = t$.

In Definition 1.4, if $k = 2$, then $G$ is called domination bicritical. For more information of $(\gamma, k)$-critical or domination bicritical graphs, readers are suggested to refer to ^{[8,10,11,17,19,20]}.

Now, again based on the left of Formula (1.1), we introduce the definition of strong critical vertex-set to extend the notion of critical vertex in the following Definition 1.1$^\prime$. (It is easy to get that a strong critical vertex-set of $G$ is also a $2$-packing of $G$.) To compare Observation 1.2 and Definition 1.3, we give Observation 1.2$^\prime$ and Definition 1.3$^\prime$, and then we introduce Definition 1.6 with a remark.

Definition 1.1$^\prime$. ^[25] A set $S\subseteq V(G)$ is called a strong critical vertex-set (or just st-critical vertex-set for short) of $G$ if $\gamma(G-S) = \gamma(G)-|S|$.

Observation 1.2$^\prime$. For any $S\subseteq V(G)$, $\gamma(G-S) = \gamma(G)-|S| \; \Leftrightarrow \; \gamma(G-S)\leq\gamma(G)-|S|$.

Definition 1.3$^\prime$. A graph $G$ is called strong $l$-vertex-set-critical if $V(G)$ can be partitioned into $l$ non-empty strong critical vertex-sets of $G$.

Definition 1.6. Let $S_1, S_2, \ldots, S_l$ be non-empty strong critical vertex-sets of $G$. If $\{S_1, S_2, \ldots, \; S_l\}$ is a partition of $V(G)$, then we call $\{S_1, S_2, \ldots, S_l\}$ or ${S_1\cup S_2\cup\cdots\cup S_l}$ as a strong critical vertex-set partition of $G$.

Lemma 1.7. ^[25] A subset of an st-critical vertex-set of $G$ is still an st-critical vertex-set of $G$.

Remark. Let $S_1 = S_{1}^{1}\cup S_1^{2}$ with $S_1^{1}, S_1^{2}\neq \emptyset$. According to Definition 1.6 and Lemma 1.7, if $S_1\cup \; S_2\cup\cdots\cup S_l$ is an st-critical vertex-set partition of $G$, then ${S_1^{1}\cup S_1^{2}\cup S_2\cup\cdots\cup S_l}$ is also an st-critical vertex-set partition of $G$. Thus, in general, if $G$ is a strong $l$-vertex-set-critical graph, then it may also be a strong $j$-vertex-set-critical graph for any $l\leq j\leq |V(G)|$.

1.2.   On strong critical vertex-set and two-colored $\gamma$-set

When we talk about st-critical vertex-sets, we would like to mention another related notion---Two-colored $\gamma$-set. The present authors think that both of them are important on the problem of building family of graphs that make the equality hold in Vizing's Conjecture ^[15,25].

Definition 1.8. ^[15] Let $D\in \underline{MDS}(G)$. $D$ is called a two-colored $\gamma$-set of $G$ if $D$ partitions as $D = D_1 \cup D_2$ such that $V(G)-N_G[D_1] = D_2$ and $V(G)-N_G[D_2] = D_1$.

In Definition 1.8, since $V(G)-N_G[D_1] = D_2$, we can deduce that $D_1\in \underline{MDS}(G-D_2)$. So $\gamma(G-D_2) = |D_1| = |D|-|D_2| = \gamma(G)-|D_2|$, which implies that $D_2$ is an st-critical vertex-set of $G$, and so is $D_1$ symmetrically. Because two-colored $\gamma$-set is not the motif of this paper, we just introduce a proposition and a conjecture about it below.

Proposition 1.9. ^[15] If $G$ is a generalized comb and $H$ has a two-colored $\gamma$-set, then $\gamma(G \square H) = \gamma(G)\gamma(H)$.

Conjecture 1.10. ^[13] If $G$ is a connected bipartite graph such that $V(G)$ can be partitioned into two-colored $\gamma$-sets, then $G$ is the $4$-cycle or $G$ can be obtained from $K_{2t, 2t}$ by removing the edges of $t$ vertex-disjoint $4$-cycles.

In Proposition 1.9, "$\square$" represents the cartesian product and a nontrivial connected graph $G$ is called a generalized comb if each vertex of degree greater than one is adjacent to exactly one 1-degree-vertex of $G$. Conjecture 1.10 tries to give a necessary condition for a connected bipartite graph whose vertex set can be partitioned into two-colored $\gamma$-sets. Note that if a graph can be partitioned into $k$ two-colored $\gamma$-sets, then it can partitioned into $2k$ domination critical vertex-sets.

At last, we sketch the coming two sections. To extend the previous concept---Vertex coalescence, we introduce the concept of vertex-set coalescence and give two theorems about it in Section 2, which are fundamental results of strong $l$-vertex-set-critical graphs. Let $\mathscr{C}_l = \{G\mid G$ is a strong $l$-vertex-set-critical connected graph$\}$. We will obtain that $\mathscr{C}_l\neq\emptyset$ if and only if $l\notin\{2, 3, 5\}$ in Section 3.

2.   Vertex coalescence and vertex-set coalescence

Brigham et al. ^[4] studied on the vertex-critical graphs, and listed the following Theorems 2.2 and 2.3 without proofs because they thought the proofs are cumbersome but straightforward. In order to state these two theorems, we have to introduce the notion of vertex coalescence first. (Readers who want to know the concept of edge coalescence can refer to ^[12].)

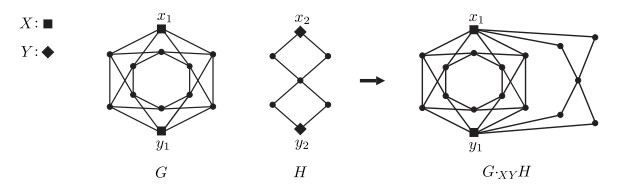
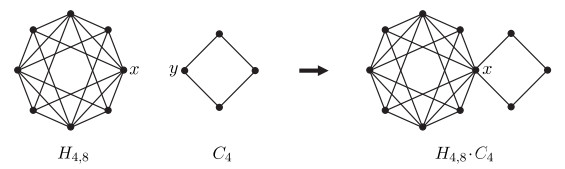
Definition 2.1. ^[4,15] Let $G$ and $H$ be two disjoint graphs with $x\in V(G)$ and $y\in V(H)$. The vertex coalescence $G\cdot_{xy}H$ (or just $G\cdot H$ if $x$ and $y$ are arbitrary) of $G$ and $H$ via $x$ and $y$, is the graph obtained from the union of $G$ and $H$ by identifying $x$ with $y$. (Refer to Figure 1.)

Agreement. In this section, when identifying $x$ with $y$, we choose $x$ but $y$ to represent the identified vertex in the resulting graph.

Theorem 2.2. ^[4] Let $G$ and $H$ be two disjoint graphs, and let $G\cdot H$ be any vertex coalescence of $G$ and $H$. Then $\gamma(G)+\gamma(H)-1\leq\gamma(G\cdot H)\leq\gamma(G)+\gamma(H)$. Furthermore, if both $G$ and $H$ are vertex-critical or $G\cdot H$ is vertex-critical, then $\gamma(G\cdot H) = \gamma(G)+\gamma(H)-1$.

Theorem 2.3. ^[4] The graph $G\cdot H$ is vertex-critical if and only if both $G$ and $H$ are vertex-critical.

To compare Brigham's results, we give the corresponding results on strong $l$-vertex-set-critical graphs one to one (see Definition 2.1$^\prime$, Theorems 2.2$^\prime$ and 2.3$^\prime$). For the mathematical rigor, we are going to prove them without the supporting of Theorems 2.2 and 2.3, where in fact, our proofs include the derivation of Brigham's results. Before this, we need to introduce the definition of "compatible" and two lemmas.

Definition 2.4. Let $G$ be a graph with $x, y\in V(G)$. $x$ and $y$ are called compatible in $G$ if there exists $D_0\in \underline{MDS}(G)$ such that $\{x, y\}\subseteq D_0$, and incompatible in $G$ if $|\{x, y\}\cap D| < 2$ for any $D\in \underline{MDS}(G)$.

Lemma 2.5. ^[6] Let $G$ be a graph with $x, y\in V(G)$, and $G^{\prime}$ be the graph obtained from $G$ by identifying the two vertices $x$ and $y$. Then $\gamma(G^{\prime}) < \gamma(G)$ if and only if $x$ and $y$ are compatible or at least one of $x$ and $y$ is critical in $G$.

Lemma 2.6. Let $J$ be a graph with $x, y\in V(J)$, and $J^{\prime}$ be the graph obtained from $J$ by identifying the two vertices $x$ and $y$. Then $\gamma(J)-1\leq \gamma(J^{\prime})\leq \gamma(J)$ with the second equality holds if and only if $x$ and $y$ are incompatible and neither $x$ nor $y$ is critical in $J$.

Proof. Let $D^{\prime}\in \underline{MDS}(J^{\prime})$. Then $D^{\prime}\cup\{y\}$ is a dominating set of $J$, and so $\gamma(J)\leq|D^{\prime}\cup\{y\}|\leq\gamma(J^{\prime})+1$, which implies that $\gamma(J)-1\leq\gamma(J^{\prime})$. Let $D\in \underline{MDS}(J)$ and

Then $D_0^{\prime}$ is a dominating set of $J^{\prime}$, and so $\gamma(J^{\prime})\leq|D_0^{\prime}|\leq|D| = \gamma(J)$.

Now, since $\gamma(J^{\prime})\leq \gamma(J)$, it follows from the contrapositive of Lemma 2.5 that $\gamma(J^{\prime}) = \gamma(J)$ if and only if $x$ and $y$ are incompatible and neither $x$ nor $y$ is critical in $J$. □

Definition 2.1$^\prime$. Let $G$ and $H$ be two disjoint graphs with $\emptyset\neq X\subseteq V(G)$, $\emptyset\neq Y\subseteq V(H)$ and $|X| = |Y|$. Let $X = \{x_1, x_2, \ldots, x_m\}$ and $Y = \{y_1, y_2, \ldots, y_m\}$. The vertex-set coalescence $G\cdot_{XY}H$ of $G$ and $H$ via $X$ and $Y$, is the graph obtained from the union of $G$ and $H$ by identifying $x_i$ with $y_i$ for every $1\leq i\leq m$. (Refer to Figure 2.)

Theorem 2.2$^\prime$. Let $G$ and $H$ be two disjoint graphs with $\emptyset\neq X\subseteq V(G)$, $\emptyset\neq Y\subseteq V(H)$ and $|X| = |Y|$. Let $G^{\circ}$ and $H^{\circ}$ be the subgraphs of $G\cdot_{XY}\negthinspace H$ induced by $V(G)$ and $V(H-Y)\cup X$, respectively. Then

(a) $\gamma(G)+\gamma(H)-|X|\leq\gamma(G\cdot_{XY}\negthinspace H)\leq\gamma(G)+\gamma(H)$. Furthermore, the first equality holds if $X$ is an st-critical vertex-set of $G$ or there exists $\widetilde{D}_{G}\in \underline{MDS}(G)$ and $\widetilde{D}_{H}\in \underline{MDS}(H)$ such that $X\subseteq \widetilde{D}_{G}$ and $Y\subseteq \widetilde{D}_{H}$; the second equality holds only if ${D}_{G^\circ}\cap {D}_{H^\circ} = \emptyset$ for any ${D}_{G^\circ}\in \underline{MDS}(G^\circ)$ and ${D}_{H^\circ}\in \underline{MDS}(H^\circ)$.

(b) $X$ and $Y$ are st-critical vertex-sets of $G$ and $H$ respectively if and only if $X$ is an st-critical vertex-set of $G\cdot_{XY}\negthinspace H$;

(c) if $X$ is an st-critical vertex-set of $G\cdot_{XY}\negthinspace H$, then $\gamma(G\cdot_{XY}\negthinspace H) = \gamma(G)+\gamma(H)-|X|$.

Proof. (a) Firstly, let $D^{\prime}\in \underline{MDS}(G\cdot_{XY}H)$, $B_1$ and $B_2$ be the subsets of $X$ which can not be dominated by $D^{\prime}\cap V(G^\circ)$ and $D^{\prime}\cap V(H^\circ)$ in $G$ and $H$, respectively. Then $\big(D^{\prime}\cap V(G^\circ)\big)\cup B_1$ and $\big(D^{\prime}\cap V(H^\circ)\big)\cup B_2$ are dominating sets of $G$ and $H$, respectively. Since $D^{\prime}\in \underline{MDS}(G\cdot_{XY}H)$, it follows that the vertices of $X$ not dominated by $D^{\prime}\cap V(G^\circ)$ in $G$ must be dominated by $D^{\prime}\cap V(H^\circ)$ in $H$, and the converse is also true. Thus $B_1\cap B_2 = \emptyset$. Now, we have $\gamma(G)+\gamma(H)\leq|\big(D^{\prime}\cap V(G^\circ)\big)\cup B_1|+|\big(D^{\prime}\cap V(H^\circ)\big)\cup B_2| = |D^{\prime}|+|D^{\prime}\cap X|+|B_1|+|B_2|\leq\gamma(G\cdot_{XY}H)+|X|$, which implies that $\gamma(G)+\gamma(H)-|X|\leq\gamma(G\cdot_{XY}\negthinspace H)$. Secondly, let $D_{G^{\circ}}\in\underline{MDS}(G^{\circ})$ and $D_{H^{\circ}}\in\underline{MDS}(H^{\circ})$. Since $G$ and $H$ are spanning subgraphs of $G^{\circ}$ and $H^{\circ}$ respectively, it follows that $\gamma(G\cdot_{XY}\negmedspace H)\leq|D_{G^{\circ}}\cup D_{H^{\circ}}|\leq\gamma(G^\circ)+\gamma(H^\circ)\leq\gamma(G)+\gamma(H)$.

Furthermore, if $X$ is an st-critical vertex-set of $G$, then $\gamma(G\cdot_{XY}\negthinspace H)\leq\gamma(G^\circ-X)+\gamma(H^\circ)\leq\gamma(G-X)+\gamma(H) = \gamma(G)-|X|+\gamma(H)$, which implies that $\gamma(G\cdot_{XY}\negthinspace H) = \gamma(G)+\gamma(H)-|X|$; if there exists $\widetilde{D}_{G}\in \underline{MDS}(G)$ and $\widetilde{D}_{H}\in \underline{MDS}(H)$ such that $X\subseteq \widetilde{D}_{G}$ and $Y\subseteq \widetilde{D}_{H}$, then $\gamma(G\cdot_{XY}\negthinspace H)\leq|(\widetilde{D}_{G}-X)\cup\widetilde{D}_{H}| = |\widetilde{D}_{G}|-|X|+|\widetilde{D}_{H}| = \gamma(G)+\gamma(H)-|X|$, which also implies that $\gamma(G\cdot_{XY}\negthinspace H) = \gamma(G)+\gamma(H)-|X|$. Meanwhile, if $\gamma(G\cdot_{XY}\negthinspace H) = \gamma(G)+\gamma(H)$, then from $\gamma(G\cdot_{XY}\negthinspace H)\leq |D_{G^\circ}\cup D_{H^\circ}| = |D_{G^\circ}|+|D_{H^\circ}|-|D_{G^\circ}\cap D_{H^\circ}|\leq\gamma(G^\circ)+\gamma(H^\circ)-0\leq\gamma(G)+\gamma(H)$, we obtain that ${D}_{G^\circ}\cap {D}_{H^\circ} = \emptyset$.

(b) ($\Rightarrow$) Let $D_G^{-}\in \underline{MDS}(G-X)$ and $D_H^{-}\in \underline{MDS}(G-Y)$. Then $D_G^{-} \cup D_H^{-}$ is a dominating set of $G\cdot_{XY}H-X$. So $\gamma(G\cdot_{XY}H-X)\leq|D_G^{-} \cup D_H^{-}| = \gamma(G)-|X|+\gamma(H)-|Y| = \gamma(G)+\gamma(H)-2|X|$. By Item (a), we have $\gamma(G)+\gamma(H)-2|X|\leq\gamma(G\cdot_{XY}H)-|X|$. By Observation 1.2$^\prime$, $X$ is an st-critical vertex-set of $G\cdot_{XY}\negthinspace H$.

($\Leftarrow$) We are going to prove the sufficiency by induction on $|X|$. When $|X| = 1$, we let $X = \{x\}$, $Y = \{y\}$ and $J = G\cup H$. If $\gamma(G\cdot_{xy}H) = \gamma(G)+\gamma(H)$, then by Lemma 2.6, neither $x$ nor $y$ is critical in $J$. Thus $\gamma(G)+\gamma(H)-1 = \gamma(G\cdot_{xy}H)-1 = \gamma(G\cdot_{xy}H-x) = \gamma(G-x)+\gamma(H-y)\geq\gamma(G)+\gamma(H)$, a contradiction. So we have $\gamma(G\cdot_{xy}H) = \gamma(G)+\gamma(H)-1$ by Item (a). Thus $\gamma(G)-1+\gamma(H)-1 = \gamma(G\cdot_{xy}H)-1 = \gamma(G\cdot_{xy}H-x) = \gamma(G-x)+\gamma(H-y)\geq\gamma(G)-1+\gamma(H)-1$, from which we have $\gamma(G-x) = \gamma(G)-1$ and $\gamma(H-y) = \gamma(H)-1$, and so the sufficiency holds.

Suppose that the sufficiency holds when $|X| = n$ ($n\geq1$). We consider the case when $|X| = n+1$ below. Let $x \in X$, $y\in Y$, $X_0 = X-\{x\}$, $Y_0 = Y-\{y\}$, $J = G\cdot_{X_0Y_0}H$ and $J^{\prime} = G\cdot_{XY}H$. Let $D_1\in \underline{MDS}(G- \; X)$, $D_2\in \underline{MDS}(H-Y)$ and $D^{\prime} = D_1\cup X \cup D_2$. Since $X$ is an st-critical vertex-set of $J^{\prime}$, it follows that $D^{\prime}\in \underline{MDS}(J^{\prime})$. Also, $D^{\prime}$ is a dominating set of $J-y$. So $\gamma(J-y)\leq|D^{\prime}| = \gamma(J^{\prime})$. By Definition 1.1 and Lemma 2.6, we have

from which we know $\gamma(J-y)\geq\gamma(J^{\prime})$. Thus $\gamma(J-y) = \gamma(J^{\prime})$. Therefore $\gamma\big((J-y)-X\big) = \gamma(G-X)+\gamma(H-Y) = \gamma(J^{\prime}-X) = \gamma(J^{\prime})-|X| = \gamma(J-y)-|X|$, which implies that $X$ is, and so $X_0$ is, an st-critical vertex-set of $J-y$. Since $\gamma\big((J^{\prime}-X_0)-x\big) = \gamma(J^{\prime}-X) = \gamma(J^{\prime})-|X| = \gamma\big((J^{\prime})-|X_0|\big)-|\{x\}| = \gamma(J^{\prime}-X_0)-1$, we have $x$ is a critical vertex of $J^{\prime}-X_0$. Note that $J-y = G\cdot_{X_0Y_0}(H-y)$ and $J^{\prime}-X_0 = (G-X_0)\cdot_{xy}(H-Y_0)$. By the inductive hypothesis, we have that $X_0$ is an st-critical vertex-set of $G$ and $x$ is a critical vertex of $G-X_0$. Hence $\gamma(G-X) = \gamma\big((G-X_0)-x\big) = \gamma(G-X_0)-1 = \gamma(G)-|X_0|-1 = \gamma(G)-|X|$. That is to say, $X$ is an st-critical vertex-set of $G$. Symmetrically, one can prove that $Y$ is an st-critical vertex-set of $H$. Thus the result is true when $|X| = n+1$. Item (b) follows.

(c) It is an immediate result of Items (b) and (a). □

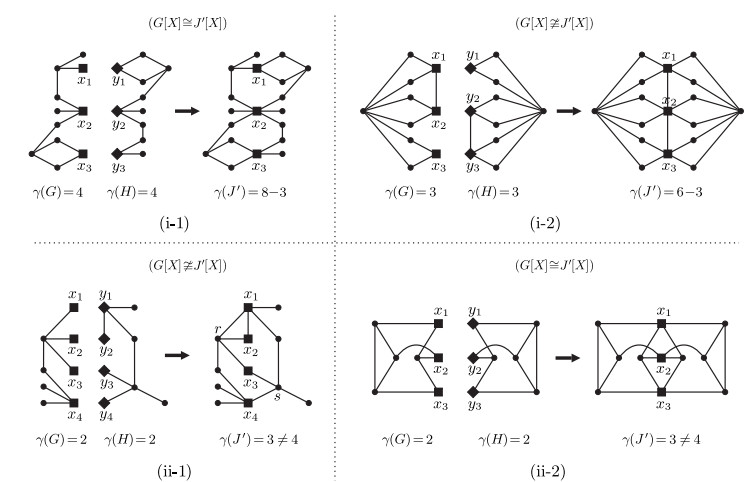
Remark for Theorem 2.2$^\prime$(a). Let $J^\prime = G\cdot_{XY}\negthinspace H$. In this item, we give a sufficient condition for $\gamma(G)+\gamma(H)-|X| = \gamma(J^\prime)$ and a necessary condition for $\gamma(J^\prime) = \gamma(G)+\gamma(H)$. However, neither of them is sufficient and necessary condition. Here, we give the counter examples.

(I) As shown in Figure 3(i-1) and (i-2), we have $\gamma(G)+\gamma(H)-|X| = \gamma(J^\prime)$, but $X$ is not an st-critical vertex-set of $G$ and $X\nsubseteq {D}_{G}$ for any ${D}_{G}\in \underline{MDS}(G)$.

(II) As shown in Figure 3(ii-1), we have $\{r, x_4\}$ and $\{s, x_1\}$ are unique minimum dominating sets of $G^\circ$ and $H^\circ$ respectively, and $\{r, x_4\}\cap \{s, x_1\} = \emptyset$, but $\gamma(J^\prime)\neq\gamma(G)+\gamma(H)$; and in (ii-2), we have ${D}_{G^\circ}\cap {D}_{H^\circ} = \emptyset$ for any ${D}_{G^\circ}\in \underline{MDS}(G^\circ)$ and ${D}_{H^\circ}\in \underline{MDS}(H^\circ)$ (because $X\cap D_{G^\circ} = \emptyset$ for any $D_{G^\circ}\in \; \underline{MDS}(G^\circ)$), but $\gamma(J^\prime)\neq\gamma(G)+\gamma(H)$.

Theorem 2.3$^\prime$. Let $G$ and $H$ be two disjoint graphs. Let $\emptyset\neq X_i\subseteq V(G)$ for $i = 1, 2, \ldots, k$ and $\emptyset\neq Y_j\subseteq V(H)$ for $j = 1, 2, \ldots, l$ with $|X_1| = |Y_1|$. Then $\{X_1, X_2, \ldots, X_k\}$ and $\{Y_1, Y_2, \cdots, Y_l\}$ are st-critical vertex-set partitions of $G$ and $H$ respectively if and only if $\{X_1, X_2, \ldots, X_k, Y_2, \; Y_3, \ldots, Y_l\}$ is an st-critical vertex-set partition of $G._{X_1Y_1}H$.

Proof. Let $\mathbb{X} = \{X_1, X_2, \ldots, X_k\}$, $\mathbb{Y} = \{Y_1, Y_2, \cdots, Y_l\}$ and $\mathbb{X}.\mathbb{Y} = \{X_1, X_2, \ldots, X_k, Y_2, Y_3, \; \ldots, Y_l\}$.

$(\Rightarrow)$ Clearly, $\mathbb{X}.\mathbb{Y}$ is a partition of $V(G\cdot_{X_1Y_1}\negmedspace H)$. For any $S\in \mathbb{X}.\mathbb{Y}$, we have $S\in \mathbb{X}$ or $S\in\mathbb{Y}$. If $S\in \mathbb{X}$, then by Theorem 2.2$^\prime$(c), we have $\gamma(G\cdot_{X_1Y_1}\negmedspace{H}-S)\leq\gamma(G-S)+\gamma(H-Y_1) = \gamma(G)-|S|+\gamma(H)-|X_1| = \gamma(G\cdot_{X_1Y_1}\negmedspace H)-|S|$. Similarly, we can also prove that $\gamma(G\cdot_{X_1Y_1}\negmedspace H-S)\leq \gamma(G\cdot_{X_1Y_1}\negmedspace H)-|S|$ if $S\in \mathbb{Y}$. The necessity follows.

$(\Leftarrow)$ Clearly, $\mathbb{X}$ and $\mathbb{Y}$ are partitions of $V(G)$ and $V(H)$, respectively. Firstly, by Theorem 2.2$^\prime$ (b), $X_1$ and $Y_1$ are st-critical vertex-sets of $G$ and $H$, respectively. Secondly, for any $S\in \mathbb{X}-\{X_1\}$, we let $\dot{D}^{-}\in \underline{MDS}(G\cdot_{X_1Y_1}\negmedspace{H}-S)$, $L = X_1-(X_1\cap \dot{D}^{-})$ and $L_G$ be the subset of $L$ that can be dominated by $\dot{D}^{-}\cap V(G)$ in $G\cdot_{X_1Y_1}\negmedspace{H}$. Let $H^{\circ}$ be the subgraph of $G\cdot_{X_1Y_1}\negmedspace H$ induced by $V(H-Y_1)\cup X_1$. Then $\dot{D}^{-}\cap V(G)$ and $\dot{D}^{-}\cap V(H^\circ)$ are dominating sets of $(G-S)-(L-L_G)$ and $H^\circ-L_G$, respectively. So

By the forth equality, we have $\gamma(G-S) = \gamma(G)-|S|$. Thirdly, for any $S\in \mathbb{Y}-\{Y_1\}$, we can similarly prove that $\gamma(H-S) = \gamma(H)-|S|$. From these three observations, the sufficiency follows. □

3.   Existence of strong $l$-vertex-set-critical graphs with fixed $l$

In this section, we write $d_G(\ast) = d(\ast)$, $N_G(\ast) = N(\ast)$, $N_G[\ast] = N[\ast]$ and $D^{-}_G = D^{-}$, as well as $C_4\cdot C_4 = (C_4)^2$, $C_4\cdot C_4\cdot C_4 = (C_4)^3$ and so on for belief.

Lemma 3.1. ^[25] An st-critical vertex-set of a graph $G$ is a $2$-packing of $G$.

Lemma 3.2. ^[24] If $d(u) = 1$ and $v\in N(u)$, then $v$ is not a critical vertex of $G$. (This implies that a vertex-critical graph has no vertices of degree one.)

Lemma 3.3. ^[25] Let $S$ be an st-critical vertex-set of $G$. If $D^{-}\in \underline{MDS}(G-S)$, then $|D^{-}| = \gamma(G)-|S|$ and $D^{-}\cap N(S) = \emptyset$.

Lemma 3.4. Let $S$ be an st-critical vertex-set of $G$ and $w\in V(G-S)$.

(a) If $z\in N(w)\cap S$, then there exists $v_0\in N(w)-\{z\}$ such that $N(v_0)\cap S = \emptyset$.

(b) Let $uvwz$ be a path or a cycle in $G \; ($i.e. $u = z$ is possible$)$. If $u, z\in S$, then $d(w) > 2$.

(c) Let $X = N(w)$. If $2\leq|X|\leq3$ and $N(x)\cap S\neq\emptyset$ for every $x\in X$, then $|N(X)\cap S| = 1$.

(d) Let $uvwyz$ be a trail in $G$. If $u, z\in S$ and $d(w) = 2$, then $u = z$.

Proof. (a) Suppose to the contrary that $N(v)\cap S\neq\emptyset$ for every $v\in N(w)-\{z\}$. Then $N[w]-\{z\}\subseteq N(S)$. By Lemma 3.3, there exists $D^{-}\in \underline{MDS}(G-S)$ such that $D^{-}\cap(N[w]-\{z\}) = \emptyset$. However, we see that $D^{-}$ can not dominate $w$ in $G-S$, a contradiction.

(b) It is an immediate result of Item (a).

(c) Suppose to the contrary that $|N(X)\cap S|\neq1$. By Lemma 3.1, we have $|N(X)\cap S|\leq|X|$. This implies $|N(X)\cap S| = 2$ or $3$. Let $\{r, s\}\subseteq N(X)\cap S$. Then $N(r)\cap N(s) = \emptyset$. So we must have that at least one of $r$ and $s$, say $r$, is adjacent to only one element of $X$. Thus we may suppose that $\{r\} = N(x^{\prime})\cap S$, where $x^{\prime}\in X$. Note that $N(x)\cap S\neq\emptyset$ for every $x\in X$ implies $X\subseteq N(S)$. By Lemma 3.3, there exists $D^{-}\in \underline{MDS}(G-S)$ such that $D^{-}\cap X = \emptyset$ and $|D^{-}|+|S| = \gamma(G)$. In order to dominate $w$ in $G-S$, we have $w\in D^{-}$. However, $(D^{-}-\{w\})\cup (S-\{r\})\cup\{x^{\prime}\}$ is a dominating set of $G$ with cardinality $\gamma(G)-1$, a contradiction.

(d) It is an immediate result of Item (c). □

Theorem 3.5. There exists a connected graph $G$ such that $V(G)$ can be partitioned into $l$ strong critical vertex-sets if and only if $l\notin\{2, 3, 5\}$.

Proof. $(\Leftarrow)$ Let $k\in \mathbb{Z}^+$ and $H_{4, 8}$ be the (Harary) graph as shown in Figure 1. Based on the fact that $\mathbb{Z}^+-\{2, 3, 5\} = \{1\}\cup\{3k\mid k\geq2\}\cup\{3k+1\mid k\geq1\}\cup\{3k+2\mid k\geq2\}$, we let

Noting that $V(C_4)$ and $V(H_{4, 8})$ can be partitioned into 4 and 8 st-critical vertex-sets respectively, we can recursively deduce that $V\big((C_4)^{k}\big)$ and $V\big(H_{4, 8} \cdot (C_4)^{k-2}\big)$ can be partitioned into $3k+1$ ($k\geq1$) and $3k+2$ ($k\geq2$) st-critical vertex-sets respectively by Theorem 2.3$^{\prime}$. Also, note that $V\big((C_4)^{2}\big)$ can be partitioned into 6 st-critical vertex-sets. So $V\big((C_4)^{k}\big)$ can be partitioned into $3k$ ($k\geq2$) st-critical vertex-sets. The sufficiency follows.

$(\Rightarrow)$ Suppose to the contrary that $l\in\{2, 3, 5\}$. If $l = 2$, then by Lemma 3.1, we get that $d(h) = 1$ for every $h\in V(G)$, which implies that $G\cong K_2$, contradicting the fact that $K_2$ is not a vertex-critical graph. If $l = 3$, then by Lemmas 3.2 and 3.1, we deduce that $d(h) = 2$ for every $h\in V(G)$, which implies that $G$ is a cycle. However, one can check that this is impossible. (According to the two well-known facts that $\gamma(C_n) = \lceil\frac{n}{3}\rceil$ and $\gamma(P_n) = \lceil\frac{n}{3}\rceil$, we can easily deduce that a cycle of order at least 4 can not own an st-critical vertex-set of cardinality $2$.)

If $l = 5$, then we let $V(G) = S_1\cup S_2\cup S_3\cup S_4\cup S_5$ be an st-critical vertex-set partition of $G$. By Lemmas 3.2 and 3.1, we have that $2\leq d(g)\leq 4$ for every $g\in V(G)$.

Claim 1. Let $\{j, k, l, m, n\} = \{1, 2, 3, 4, 5\}$. If $N(s_n) = \{s_j, s_k, s_l\}$, where $s_i\in S_i$ for every $i\in\{j, k, l, n\}$, then $|N(\{s_j, s_k, s_l\})\cap S_m| = 1$.

For convenience, suppose without loss of generality that $(j, k, l, m, n) = (1, 2, 3, 4, 5)$. We use reduction to absurdity. Assume that $|N(\{s_1, s_2, s_3\})\cap S_4|\neq1$. Then since

by the contrapositive of Lemma 3.4(c), at least one of $s_1$, $s_2$ and $s_3$, say $s_1$, satisfies $N(s_1)\cap S_4 = \emptyset$. Thus $N(s_1)-\{s_5\}\subseteq S_2\cup S_3$. To combine this with Lemma 3.4(b), we must have $d(s_1)\neq 2$, which implies that $d(s_1) = 3$. So $N(s_1)\cap S_2\neq\emptyset$ and $N(s_1)\cap S_3\neq\emptyset$.

Since $s_1\in N(s_5)\cap S_1$, by Lemma 3.4(a), one of $N(s_2)\cap S_1$ and $N(s_3)\cap S_1$, say $N(s_2)\cap S_1$, is empty set. By Lemma 3.1, we have $(N(s_2)-\{s_5\})\cap (S_2\cup S_5) = \emptyset$. Since $s_3\in N(s_5)$ and $N(s_1)\cap S_3\neq\emptyset$, by Lemma 3.4(a), we obtain that $N(s_2)\cap S_3 = \emptyset$. So by Lemma 3.2, we have $N(s_2)\cap S_4\neq\emptyset$. Let $N(s_2)\cap S_4 = \{s_4\}$. Then

So we have $N(s_4)\cap S_5 = \emptyset$ by the contrapositive of Lemma 3.4(b). Thus $N(s_4)-\{s_2\}\subseteq S_1\cup S_3$. Since $d(s_2) = 2$, we have $s_4s_3\in E(G)$ or $s_4s_1\in E(G)$ by Lemma 3.4(d). However, we have supposed that $N(s_1)\cap S_4 = \emptyset$ in the third sentence of the first paragraph. Thus, only $s_4s_3\in E(G)$ holds, which implies that

So by Lemma 3.4(b), we have

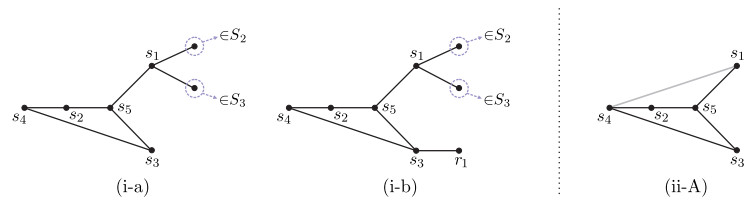
Now, if $N(s_3)\cap S_1 = \emptyset$, then $s_1$ is a cut-vertex of $G$ (refer to Figure 4(i-a)). Thus by Theorem 2.3, $G[\{s_1, s_2, s_3, s_4, s_5\}]$ is vertex-critical. However, one can check that it is not true. If $N(s_3)\cap S_1\neq \emptyset$, let $N(s_3)\cap S_1 = \{r_1\}$. ($r_1 = s_1$ is possible.) Then $\{r_1\}\cup\{s_1\}$ is a vertex-cut of $G$ (refer to Figure 4 (i-b)). By Lemmas 3.2 and 1.7 and Theorem 2.3$^\prime$, $G[\{s_1, s_2, s_3, s_4, s_5, r_1\}]$ is vertex-critical, which is also not true.

Claim 2. $d(g)\neq3$ for every $g\in V(G)$.

Without loss of generality, suppose to the contrary that there exists $s_5\in S_5$ such that $N(s_5) = \{s_1, s_2, s_3\}$, where $s_i\in S_i$, $i = 1, 2, 3$. By Claim 1, we can let

Case A. At least two of $s_1$, $s_2$ and $s_3$, say $s_2$ and $s_3$, have degree $2$ in $G$.

Then, by Lemma 3.4(b), we obtain that $N(s_2)\cap S_1 = \emptyset$ and $N(s_3)\cap S_1 = \emptyset$, as well as $N(s_2)\cap S_3 = \emptyset$ and $N(s_3)\cap S_2 = \emptyset$. So we must have $N(s_2)\cap S_4\neq\emptyset$ and $N(s_3)\cap S_4\neq\emptyset$ because $d(s_2) = d(s_3) = 2$. By (3.1), we have $N(s_2)\cap S_4 = \{s_4\} = N(s_3)\cap S_4$. Again by Lemma 3.4(b), we have $N(s_4)\cap S_5 = \emptyset$.

If $N(s_4)\cap S_1\neq \emptyset$, then by Lemma 3.4(d), we have $N(s_4)\cap S_1 = \{s_1\}$. From this, we see that either $G = G[\{s_1, s_2, s_3, s_4, s_5\}]$, or $s_1$ is a cut-vertex of $G$ (no matter $N(s_4)\cap S_1 = \emptyset$ or not). Altogether, we have $G[\{s_1, s_2, s_3, s_4, s_5\}]$ is vertex-critical by Theorem 2.3. This is not true (refer to Figure 4(ii-A).)

Case B. At most one of $s_1$, $s_2$ and $s_3$, say $s_1$, has degree $2$ in $G$.

Then $d(s_2), d(s_3)\geq3$. Since $s_1\in N(s_5)$, by Lemma 3.4(a), at least one of $N(s_2)\cap S_1 = \emptyset$ and $N(s_3)\cap S_1 = \emptyset$, say $N(s_2)\cap S_1 = \emptyset$, holds. So $N(s_2)\subseteq S_3\cup S_4\cup S_5$, and thus $d(s_2) = 3$. This implies that $N(s_2)\cap S_4\neq\emptyset$ and $N(s_2)\cap S_3\neq\emptyset$. From the former, we get $N(s_2)\cap S_4 = \{s_4\}$ while by the latter we can let $N(s_2)\cap S_3 = \{r_3\}$. ($r_3 = s_3$ is possible.) Since $s_3\in N(s_5)$, we get

by Lemma 3.4(a). There are two subcases.

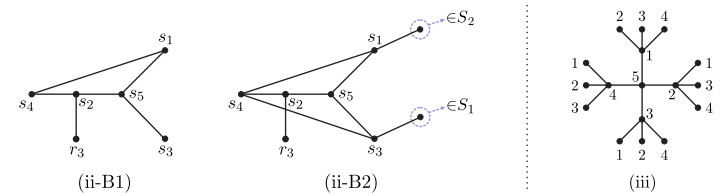
When $N(s_1)\cap S_2 = \emptyset$, we have $N(s_1)\cap S_4\neq\emptyset$ since $d(s_1)\geq2$. By (3.1), we have $N(s_1)\cap S_4 = \{s_4\}$. So $N(s_1) = \{s_4, s_5\}$. Thus by Lemma 3.4(b), we have $N(s_4)\cap S_5 = \emptyset$. Since $r_3\in N(s_2)$, we get $N(s_4)\cap S_3 = \emptyset$ by Lemma 3.4(a), and so $N(s_4) = \{s_1, s_2\}$. Now, we see that $\{r_3\}\cup \{s_3\}$ is a vertex-cut of $G$. (Refer to Figure 5(ii-B1).) By Theorem 2.3$^\prime$, $G[\{s_1, s_2, s_3, s_4, s_5, r_3\}]$ is vertex-critical, which is not true.

When $N(s_1)\cap S_2\neq\emptyset$, by (3.2) and Lemma 3.4(b), we have $N(s_1)\cap S_4\neq\emptyset$, which implies that $N(s_1)\cap S_4 = \{s_4\}$. Since $s_2\in N(s_5)$, we have $N(s_3)\cap S_2 = \emptyset$ by Lemma 3.4(a). So $d(s_3) = 3$, and thus $N(s_3)\cap S_1\neq\emptyset$ and $N(s_3)\cap S_4\neq\emptyset$. By (3.1), we have $N(s_3)\cap S_4 = \{s_4\}$. (Refer to Figure 5(ii-B2).) Now, we have $r_3\in N(s_2)$, $N(s_4)\cap S_3 = \{s_3\}$ and $N(s_5)\cap S_3 = \{s_3\}$. However, according to Lemma 3.4(a), this is impossible.

Claim 3. $d(g)\neq4$ for every $g\in V(G)$.

Without loss of generality, suppose to the contrary that there exists some $s_5\in S_5$ such that $N(s_5) = \{s_1, s_2, s_3, s_4\}$, where $s_i\in S_i$, $i = 1, 2, 3, 4$. For every $1\leq i\leq 4$, by Lemma 3.4(b) and Claim 2, we have $d(s_i)\neq2$ and $d(s_i)\neq3$, which implies that $d(s_i) = 4$. (Refer to Figure 5(iii).) However, by Lemma 3.4(a), this is impossible.

Now, by Claims 2 and 3, we get that $d_H(g) = 2$ for every $g\in V(G)$, which implies that $G$ is a cycle, a contradiction. The necessity follows. □

4.   Conclusions

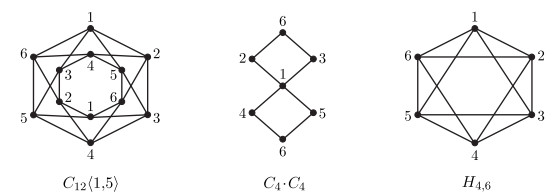
In ^[25], the authors got the following Proposition 4.1, which tells us that$\mathscr{C}_4 = \{C_4\}$, where $\mathscr{C}_4$ was defined in the last paragraph of Section 1. It is easy to see that the circulant graph $C_{12}\langle1, 5\rangle$, the vertex coalescence $C_4\cdot C_4$ and the Harary graph $H_{4, 6}$ (see Figure 6) belong to $\mathscr{C}_6$. Referring to Proposition 4.1, we want to know whether $\mathscr{C}_6$ is a finite set. So we present Problem 4.2.

Proposition 4.1. ^[25] Let $H$ be a connected graph. Then $V(H)$ can be partitioned into $4$ strong critical vertex-sets if and only if $H\cong C_4$.

Problem 4.2. Give a constructive characterization of the connected graphs $G$ such that $V(G)$ can be partitioned into $6$ strong critical vertex-sets of $G$.

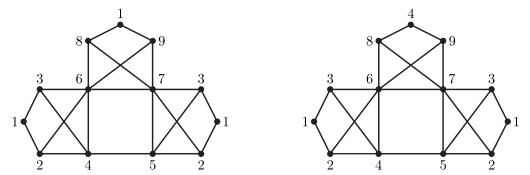
It is known that each graph has a degree sequence, but a given sequence may not be a degree sequence of any simple graph. For instance, the sequence (7, 6, 5, 4, 3, 3, 2) cannot become a degree sequence of a simple graph (see ^[3], Ex. 1.5.6). If $V(G) = S_1\cup S_2\cup\cdots\cup S_l$ is a strong critical vertex-set partition of a graph $G$, then we call the sequence $(|S_1|, |S_2|, \ldots, |S_l|)$ a strong critical vertex-set sequence of $G$. It is noteworthy that even a connected graph may own different strong critical vertex-set sequences. For example, both (3, 2, 2, 1, 1, 1, 1, 1, 1) and (2, 2, 2, 2, 1, 1, 1, 1, 1) are strong critical vertex-set sequences of the graph depicted in Figure 7. Also, for connected graphs, it follows from Theorem 3.5 that the strong critical vertex-set sequence (1, 1, 1, 1) exists but (1, 1, 1, 1, 2) does not exist.

Problem 4.3. What kinds of strong critical vertex-set sequences do exist$?$ Or to be concrete about it, if $(|S_1|, |S_2|, \ldots, |S_l|)$ is a strong critical vertex-set sequence of a connected graph $G$, then what are the relations of $|S_1|, |S_2|, \ldots, |S_l|$, $l$ and $\gamma(G)$$?$

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

(1) Thank Professor D. F. Rall for his suggestion on the definition of strong critical vertex-set, and e-mailing the article (ref. ^[21]) to us!

(2) Funding Information:

(i) National Natural Science Foundation of China (No. 12061047);

(ii) National Natural Science Foundation of Fujian Province (No. 2022J05199);

(iii) Jiangxi Provincial Natural Science Foundation (No. 20212BAB201027);

(iv) Scientific Research Project Funding Plan of Jianghan University (No. 2022XKZX11).

7.   Conflict of interest

The authors declare that they have no conflicts of interest in this work.