Chaotic behavior and construction of a variety of wave structures related to a new form of generalized q-Deformed sinh-Gordon model using couple of integration norms

1.   Introduction

Nonlinear partial differential equations (NLPDEs) demonstrate the foundation for the mathematical representation of complicated physical phenomena. These days, analysis of the NLPDEs is being accomplished in many nonlinear fields, including physics, chemical kinematics, meteorology, plasma dynamics, chemistry, propagation of shallow water waves, condensed matter physics, mathematical fluid dynamics, and geochemistry ^[1,2]. An increasing amount of attention is being paid to research involving soliton wave solutions for NLPDEs. Solitons, also known as permanent-form shallow-water waves, are a unique class of long waves that are non-dispersive and move in the form of packets at a constant speed. Due to their reliability and utility in physics applications, the behavior of solitons has drawn the attention of mathematicians, physicists, and engineers. The soliton develops as a solution to NLPDEs ^[3,4,5].

GDSGE incorporates the q-deformation parameter to accommodate non-commutative or quantum group effects ^[6]. It is a variation of the well-known sinh-Gordon equation. The proposed equation has opened up new possibilities for modelling asymmetric physical systems. This work is part of a series we're working on at the moment. This deformation parameter introduces another level of complexity to the system and affects how solutions and soliton structures behave. The objective of this work is to conduct a thorough analysis of the GDSGE, emphasizing its mathematical characteristics and physical applications. The analysis consists of the determination of exact solutions, investigation of soliton dynamics, and detailed study of the impact of the q-deformation element on the behavior of the equation. There hasn't been enough research done on these equations using the q-calculus.

Many effective techniques for solving NLPDEs have been developed in recent years, some of them are Hirota's direct method ^[7], Jacobi elliptic analysis ^[8], the physics-informed neural network (PINN) method ^[9], a sine-cosine technique ^[10], extended direct algebraic approach, functional variable method, sub-equation approach, extended trial technique, a new auxiliary equation approach, generalized Bernoulli sub-ODE, and numerous others ^{[11,12,13,14,15,16]}. In this research work, we conduct a thorough investigation of this nonlinear equation using two different but complementary approaches: the sine-Gordon expansion technique ^[17,18,19], and the Sardar sub-equation method. Expanding upon the sub-equation approach, the Sardar sub-equation method has shown itself to be an efficient analytical approach for extracting precise informations for nonlinear equations ^[20,21,22]. With the use of this technique, one may systematically untangle the dynamics suggested by the GDSGE and get insight into how soliton structures and wave patterns are affected by the q-deformation parameter. To enhance our comprehension of the equation, we present the sine-Gordon expansion approach in addition to the SSEM. This approach, which is based on the well-known sine-Gordon equation, offers an alternate viewpoint on the GDSGE dynamics, especially when considering the implications of q-deformation. This study tries to acquire exact solutions and understand complex behaviors affected by the q-deformation parameter by applying the SGEM in conjunction with the SSEM. The results not only advance the theoretical knowledge of NLPDEs but also shed light on the special characteristics developed by the interaction of quantum group deformations and non-commutative effects. This thorough investigation establishes a solid foundation for solving equations including quantum effects and advances our understanding of nonlinear phenomena and mathematical physics.

The governing equation has been investigated for the very first time in this article via Sardar sub-equation method and sine-Gordon expansion approaches. The employed approaches have the ability of extracting full spectrum of solutions that includes bright, dark, Kink solitons and anti-Kink solutions, singular solitons and periodic solutions. The Sardar sub-equation method is an efficient approach and easily applicable on nonlinear evolution equations. It obeys certain constraint conditions that results in providing variety of solitary wave solutions. The main advantage of SSEM is that it yields the bright and dark soliton solutions that have strong physical importance and extensively applied in soliton theory. On the other hand, the sine-Gordon expansion approach is equivalently important. It is very helpful for finding soliton solutions along with complexitons. Both the applied approaches are new, reliable and efficiently applied on NLEEs.

In the past few years, extensive research has been conducted on chaos theory across various scientific fields such as mathematics, physics, and others, as evidenced by multiple sources ^[23]. In the realm of literature, numerous scholars have explored the phenomenon of chaotic behavior in various nonlinear models. Among these model are Schrödinger equation ^[24], Sakovich equation ^[25], system of shallow equations ^[26], and Ginzburg-Landau model ^[27].

The article is structured as follows: This paper is divided into nine sections: governing model is described in Section 2. Section 3 is about detailed explanation of Sardar sub-equation method. Section 4 gives the applications of the Sardar sub-equation method. Section 5 analysis the sine-Gordon expansion method. The applications of the sine-Gordon expansion method is carried out Section 6. Results and discussion of obtained solutions is explained in Section 7. Dynamical analysis of the governing model is discussed in section 8. Finally, concluding points are presented in Section 9.

2.   Governing equation

Both the system's and the solution's symmetry are broken when the q-deformed function ^[28,29], first proposed by Arai in the nineteenth century, is included into the dynamical system. Furthermore, not enough research has been done using the q-calculus to study these equations. Nonetheless, new papers on the subject have been published. Q-calculus is an area of research with several applications. The theory of relativity, special functions, and mathematical physics are only a few of the fields in which the q-calculus has been developed and applied ^[30,31,32]. The conformal time derivative generalized q-deformation yields the one-dimensional sinh-Gordon equation, also referred to as the Eleuch equation ^[33]. Such model has been solved with various techniques such as using the $\frac{G'}{G}$ expansion methodology and finite element method, the three-dimensional conformal time derivative of the generalised q-deformed sinh-Gordon equation is studied ^[34]. The generalized q-deformed sinh-Gordon equation is solved analytically with Kudryashov's new generalized version in ^[35]. A proposed model is investigated using the Lie symmetry method in ^[36]. In ^[37], the $\frac{G'}{G^2}$ expansion methodology, phase portraits and bifurcation behaviors are carried out for the GDSGE model and many more. In addition, our group studied the solutions of the q-deformed sinh-Gordon equation in several papers ^[38,39].

In this presented article, we have considered $\epsilon = -1$ which is different as compared to the articles already published. The following is a novel form of GDSGE:

In this article we discuss its special case: When $\epsilon = -1$, $\gamma = 1$ and $p = 1$,

In this study we discuss Eq (2.2), we proceed with the following assumptions:

And we also introduce a novel variables for Eq (2.2)

By utilizing traveling wave solution in Eq (2.2), the transformed ODE is given as

where $v(x, t) = \psi (\xi)$ and $\psi(\xi) = \frac{1}{h(\xi)}$.

3.   Analysis of the SSEM

The detail description of the proposed technique "SSEM" is given in this section.

Step 1: Consider the following structure showcase the NLEE for

The traveling wave transformation $F(x, t) = U(\xi)$, where $\xi = k x- w t$ is used for converting Eq (3.1) into the following structure:

Step 2: The solution of Eq (3.2) has the following form:

here, $q _{i}\; (i = 0, 1, 2, 3, ..., N)$ are unknown constants to be resolved. Considering following auxiliary equation:

here, $r$, $a$ and $b$ are constants and Eq (3.4) presents solution as

Case 1: If $a \; > \; 0$ and $r = 0$, then,

Case 2: If $a \; < \; 0$, $b > 0$, and $r = 0$, then,

Case 3: If $a \; < \; 0$, $b > 0$ and $r = \frac{a^2}{4b}$, then,

Case 4: If $a \; > \; 0$, $b > 0$ and $r = \frac{a^2}{4b}$, then,

$\text{sec}_{mn}(\xi)$, $\tanh_{mn}(\xi)$, $\tan_{mn}(\xi)$, $\cot_{mn}(\xi)$ etc. are generalized trigonometric and hyperbolic functions with parameters $m$ and $n$. Upon $m = n = 1$, they become known trigonometric and hyperbolic functions.

Step 3: $N$ is determined by homogeneous balance approach.

Step 4: A polynomial in $V^{i}$ can be achieved by inserting Eq (3.3) into Eq (3.2). Associating every terms of similar power and relating them to zero to get algebraic equations. We obtain the values of unknowns by solving the obtained system.

4.   Applications of the Sardar sub-equation method

In this section, we obtain new closed form solutions with the application of the Sardar sub-equation method to GDSGE. Considering the ODE Eq (2.5). The assumed solution via Sardar sub-equation method takes the form

where $q_{0}$ and $q_{1}$ are constants to be determined. Next, using Eq (4.1) into Eq (2.1), and employing the proposed method. Distinctive kind of solutions are obtained.

Set 1:

and

Set 2:

Utilizing values of parameters given by Set 1, for the solution of the proposed model Eq (2.1) becomes

Case 1: If $a \; > \; 0$, and $r = 0$, then,

Case 2: If $a \; < \; 0$, $b > 0$, and $r = 0$, then,

Utilizing values of parameters given by Set 2, for the solution of the proposed model Eq (2.1) becomes

Case 3: If $a \; < \; 0$, $b > 0$ and $r = \frac{a^2}{4b}$, then,

Case 4: If $a \; > \; 0$, $b > 0$ and $r = \frac{a^2}{4b}$, then,

5.   Analysis of the SGEM

This section is based on providing the description of SGEM. First of all the traveling wave transformation $F(x, t) = q(\xi), \xi = x-w t$ is used to convert the sine-Gordon equation

into

The above second order ODE is converted into first order ODE by once integrating it and taking the constant of integration to be zero as

Assume that $\frac{q}{2} = l$ and $m = \sqrt{\frac{u^{2}}{1-w^{2}}} = 1$, the above equation becomes

Equation (5.4) possesses the following solutions:

Assumed solution of Eq (5.2) can takes the form

Using Eqs (5.5) and (5.6), the above equation becomes

Inserting Eq (5.8) into ODE. Construct system of equations by equating powers of $\sin(l)\cos(l)$ to zero. The values $A_{0}$, $A_{i}$, $B_{i}$ can be determined by solving the obtained system of equations.

6.   Applications of the sine-Gordon expansion method

This section is devoted to obtain new closed form solutions with the application of the sine-Gordon expansion method to the proposed model. According to SGEM, the solution of Eq (2.5) becomes

Using the solution procedure as in explained Section 5, the values of unknowns $A_{0}$, $A_{1}$, $B_{1}$ are calculated, as

Set 3:

Solutions corresponding to Set 3 have been obtained as

Set 4:

Solutions corresponding to Set 3 have been obtained as

7.   Results and discussion

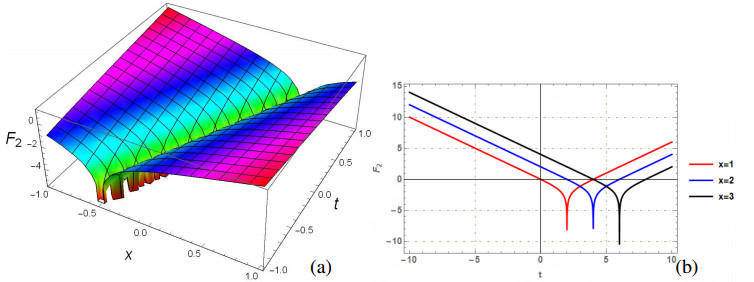
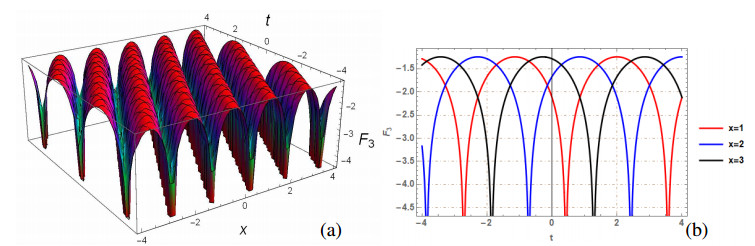
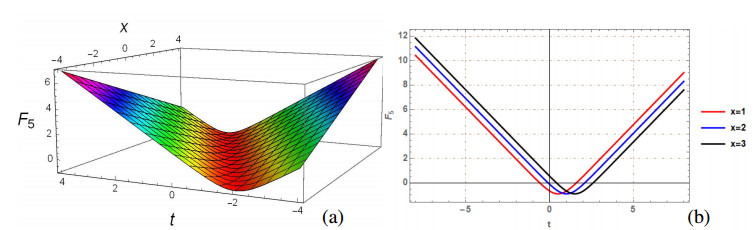
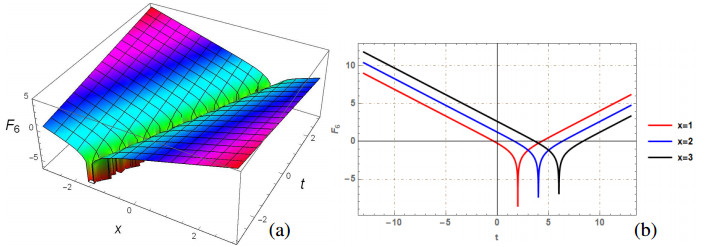
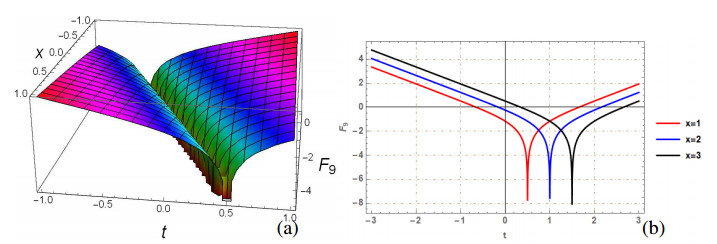
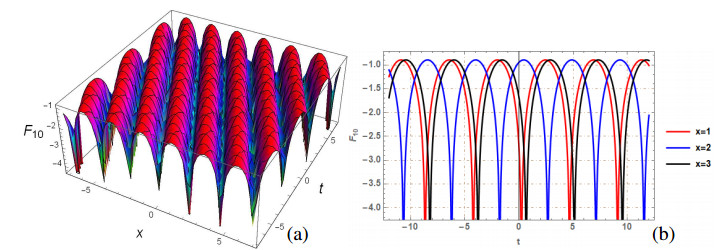
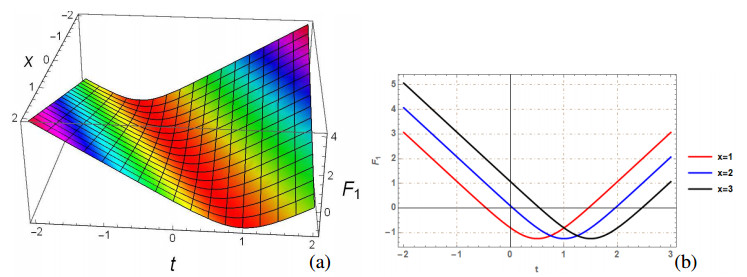
The generalized q-deformed sinh Gordon equation (GDSGE) is the significant nonlinear PDE that has great importance and applications in mathematics and physics. This paper is devoted to investigate the mathematical and physical properties of proposed model, by finding solutions using two analytical approaches: SSEM and SGEM. The proposed methods extract a wide range of solitons, including bright, singular, dark, combination dark-singular, combined dark-bright, and periodic singular solitons. The fundamental property of Soliton solutions is that they maintain their shape and energy while propagating over large distances and transfer data through an optical fiber without losing an information. To understand the physical behavior, few of the obtained solutions are plotted. The 2D and 3D visualizations are generated, by taking precise values for parameters, using mathematical software, Mathematica 12. Each figure include two subgraphs in which (a) and (b) depict 3D and 2D graph, respectively. Few obtained solutions such as $F_1(x, t), F_2(x, t), F_3(x, t), F_5(x, t), F_6(x, t), F_9(x, t), F_{10}(x)$ and $F_{15}(x, t)$ are plotted by selecting suitable values of arbitrary parameters satisfying the constraint conditions of suggested methods. Figures 1–7 are the graphical visualization of solutions obtained by SSEM while Figure 8 is graphical view of $F_{15}(x, t)$ acquired by SGEM. On comparing our finding with ^[34,35,36], it has been found that the results obtained in this paper using suggested methods are new and have not been reported earlier in literature.

Figure 1 depicts the graphical illustration of $F_1(x, t)$ by taking values of parameters as $m = n = a = k = 1$, $w = 2$ and $q = 0.5$. Figure 1(a) represents the 3D surface plot and Figure 1(b) depicts the line plot of $F_1(x, t)$. Figure 2 depicts the graphical illustration of $F_2(x, t)$ by taking values of parameters as $m = n = a = w = 1$, $k = 2$ and $q = 0.5$. Figure 2(a) represents the 3D surface plot and Figure 2(b) depicts the line plot of $F_2(x, t)$. Figure 3 depicts the graphical illustration of periodic solution $F_3(x, t)$ by taking values of parameters as $m = n = w = 1$, $a = -1$, $k = 2$ and $q = 0.5$. Figure 3(a) represents the 3D surface plot and Figure 3(b) depicts the line plot of $F_3(x, t)$. Figure 4 depicts the graphical illustration of $F_5(x, t)$ by taking values of parameters as $m = n = k = 1$, $a = -1$, $w = 2$ and $q = 0.5$. Figure 4(a) represents the 3D surface plot and Figure 4(b) depicts the line plot of $F_5(x, t)$. Figure 5 depicts the graphical illustration of singular soliton solution $F_6(x, t)$ by taking values of parameters as $m = n = w = 1$, $a = -1 \; k = 2$ and $q = 0.5$. Figure 6 depicts the graphical illustration of singular soliton solution $F_9(x, t)$ by taking values of parameters as $m = n = k = b = 1$, $a = -1 \; w = 2$ and $q = 0.5$. Figure 7 depicts the graphical illustration of periodic solution $F_{10}(x, t)$ by taking values of parameters as $m = n = w = 1$, $a = -1 \; k = 2$ and $q = 0.5$. Figure 8 depicts the graphical illustration of bright soliton $F_{15}(x, t)$ by taking values of parameters as $w = 2$, $k = 1$ and $q = 0.2$.

8.   Dynamical analysis

In this portion, we are interested to analyze the dynamic nature of Eq (2.2). We obtain the following planar system by allowing $h^{\prime} = y$,

which is not a Hamiltonian system. The chain rule can be used to rewrite (8.1),

where $\sigma_1 = \frac{q}{\kappa^2-\omega^2}$, $\sigma_2 = \frac{2\delta-1}{\kappa^2-\omega^2}$. Next, we present the solution of (8.2):

where $c$ is the constant of integration, we obtain

which is Hamiltonian. The potential energy for Eq (8.4) is

by taking the derivative of (8.5); after some modifications, we have

By applying the taylor expansion of $\ln(h)$ around $y = 0$, ignoring higher terms, yields

where $\rho_{1} = -2(c+3\sigma_2)$, $\rho_{2} = 2(3\sigma_1+2\sigma_2)$. Hence, the required planar system is

In this study, our focus is on analyzing the chaotic nature of a dynamical system. In the upcoming subsection, we will delve into the examination of the suggested model's periodic, quasi-periodic, and chaotic behaviors.

8.1.   Chaotic phenomena

In this section, we will explore the chaotic patterns displayed by Eq (2.2). While previous research, as documented in ^[36], has extensively examined the chaotic phenomena associated with Eq (2.1), the chaotic behavior of Eq (2.2) remains unexplored in the existing literature. To explore these patterns, we intend to introduce a external $\theta_0 \cos(\Lambda\xi)$ into the system (8.8). Here, $\theta_0$ represents the intensity, and $\Lambda$ denotes the frequency of this perturbed term. Consequently, the modified system can be expressed as follows:

where $\mathcal{F} = \Lambda\xi$. The quasi-periodic and chaotic characteristics have been examined of the system (8.9) utilizing various tools, including 3D and 2D phase plots, and time plots. Various random values for physical parameters are tested to discern the dynamical behaviors of the disturbed system. We will explore the implications of altering both $\theta_0$ and $\Lambda$, with the remaining parameters held constant as $\rho_1 = -3.5$, and $\rho_2 = -1$.

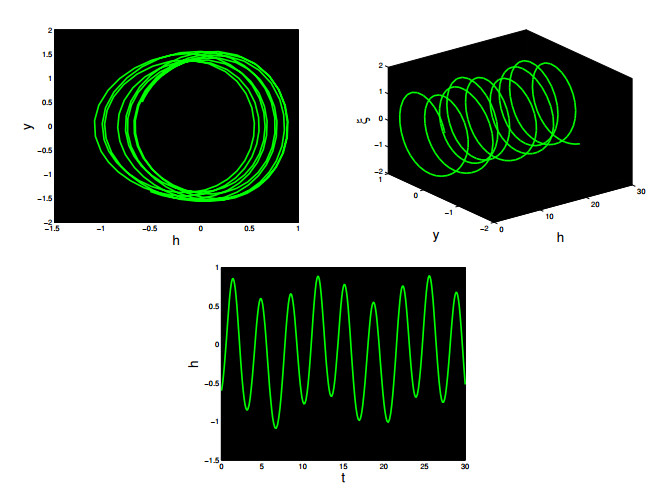
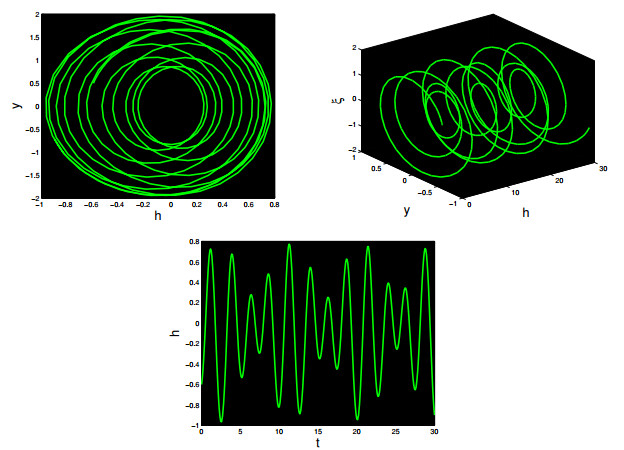
$\bullet$ Figure 9 presents phase plots and time series graphs for $\theta_0 = 0.6$ and $\Lambda = 0.5$. In this instance, where both the intensity and frequency of the external force are minimal, the system (8.9) demonstrates periodic behavior.

$\bullet$ Figure 10 displays the 3D plot, 2D plot, and time analysis graph while incrementing the intensity with $\theta_0 = 1.6$ and frequency $\Lambda = 2.5$. It is observed that the disturbed system (8.9) with modifications demonstrates quasi-periodic characteristic.

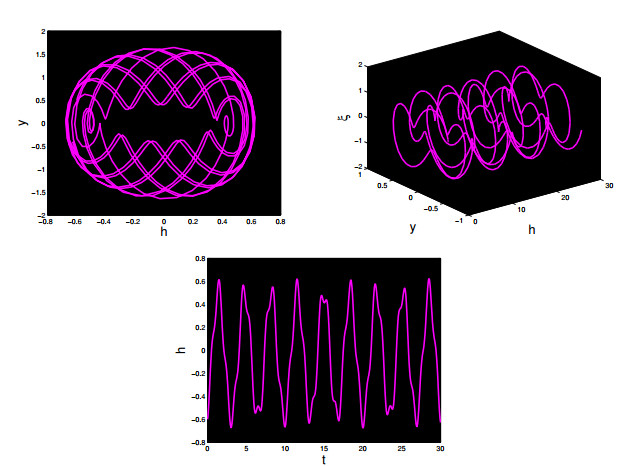
$\bullet$ In Figure 11, we depict 3D and 2D phase images, and perform time analysis for specific parameter values: $\theta_0 = 3.6$, and $\Lambda = 2\pi$. The observed results indicate that variations in these parameters lead to the manifestation of a quasi-periodic chaotic pattern in system (8.9).

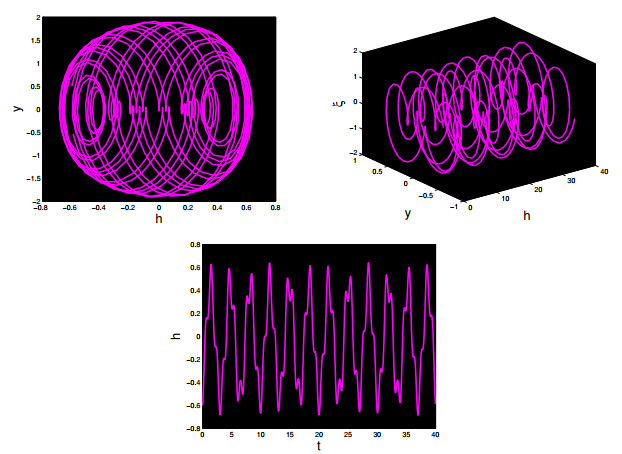
$\bullet$ Figure 12 illustrates the examination of changing amplitude and frequency when $\theta_0 = 5.6$, and $\Lambda = 2\pi$. The results indicate the manifestation of chaotic phenomena in the modified system.

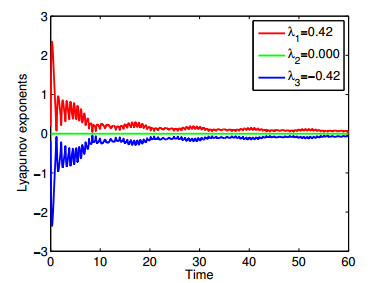
Representation of system (8.9) through Lyapunov exponent is explored in Figure 13.

9.   Conclusions

The proposed model "GDSGE" is a nonlinear partial differential equation that demonstrates the propagation of optical solitons in the framework of quantum deformations. In this paper, we have applied two effective and powerful methods to obtain exact solutions for this equation. We have produced a variety of solutions, including singular, periodic, combination, bright, and dark solitons, and visually demonstrated their characteristics in Section 7. We additionally compared our outcomes with certain current approaches and displayed the strengths as well as efficiency of the Sardar sub-equation method followed by the sine-Gordon expansion method. It has been observed that the SSEM yields more general and distinct solutions compared to the SGEM, while the latter can yield some elegant and simple solutions that the former is unable to produce. We additionally noticed that the deformation parameter $q$ performs an essential part in the structure, amplitude, and frequency that characterize the soliton solutions and that the soliton solutions demonstrate a few fascinating characteristics, such as the presence of a critical value of $q$ that divides two different structures of soliton propagation, and an appearance of new types of solutions, like as $q$-breathers and $q$-periodic solutions. GDSGE has prospective uses in many fields of physics, including quantum gravity, quantum field theory, as well as quantum optics, and the exact solutions generated in this paper may be advantageous in subsequent scientific and mathematical investigations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R157), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This study was supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445). The authors are thankful to the Deanship of Graduate Studies and Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program.

Conflict of interest

The authors declare that they have no conflicts of interest.