Pattern formation of a volume-filling chemotaxis model with a bistable source

1.   Introduction

In the 1970s, Keller and Segel ^[1,2] studied the morphogenetic development of many species of cellular slime mold (Acrasiales), and proposed the first chemotaxis model which is called the Keller-Seger model. Since then, a vast number of results ^[3,4] have been developed for the Keller-Segel models. Considering the size of the individual organism or cell, Hillen and Painter ^[5,6] proposed classical chemotaxis models with a volume-filling effect. Then, in ^[7], they summarized the derivation and variations of the original Keller-Segel models, outlined mathematical approaches for determining global existence, and showed the instability conditions. Wang and Hillen proved that solutions exist globally in time and stay bounded for a very general class of volume-filling models in ^[8]. The related mathematical model with volume-filling effect can be written as

where $u(x, t)$ and $v(x, t)$ are cell density and the chemical concentration at location $x$ and time $t$, respectively. $d_1 > 0$ and $d_2 > 0$ represent the cell and chemical diffusion coefficients, respectively. $\chi u (1-u) \nabla v$ denotes the chemotaxis flux under a volume constraint, where 1 is defined as crowding capacity and $\chi > 0$ is called the chemotaxis coefficient. $\alpha u-\beta v$ with $\alpha, \beta > 0$ stands for the dynamic term of the chemical substances, $\alpha u$ implies that the chemical is secreted by cells themselves, $\beta v$ is the degradation of the chemicals, and $g(u)$ is the cell kinetics term. It is classified into three cases by Mimura and Tsujikawa in ^[4]. (i) If $g(0) = 0$ and $g(u) < 0$ for any $u > 0$, it implies that the cells become extinct. (ii) If $g(0) = g(1) = 0$ and $g(u) > 0$ for $0 < u < 1$, the cell growth can be described by the logistic model. (iii) If $g(0) = g(\theta) = g(K) = 0$ for some $0 < K < 1$, $g(u) < 0$ for $0 < u < \theta$, and $g(u) > 0$ for $\theta < u < K$, it belongs to the bistable type.

For model (1.1) with a logistic source term, many important conclusions have been drawn in the last decade. Jiang and Zhang ^[9] studied the convergence of the steady state solutions of a chemotaxis model with a volume-filling effect. Ou and Yuan ^[10] established the existence of a traveling wavefront of a volume-filling model. Ma, Ou, and Wang ^[11] derived the conditions of the existence and stability of stationary solutions for a volume-filling model. Wang and Xu ^[12] obtained the existence of patterns by a bifurcation method. Ma and Wang ^[13,14] established the global existence of classical solutions and global bifurcation for another chemotaxis model with a volume-filling effect. Ma et al. ^[15] investigated the emerging process and the shape of patterns for a reaction diffusion chemotaxis model with a volume-filling effect. Han et al. ^[16] investigated the asymptotic expressions of stationary patterns and amplitude equations near the bifurcation point for a volume-filling chemotaxis model. Ma, Gao, and Carretero-Gonzalez ^[17] obtained the analytical expressions of stationary patterns formation for a volume-filling chemotaxis model with a logistic growth on a two-dimensional domain.

In the present paper, we investigate the pattern formation for the following volume-filling model with a bistable source:

where $\Omega$ is a bounded domain in $\mathbb{R}^{N}(N\le3)$ with smooth boundary $\partial \Omega$, and $\nu$ is the outward unit normal vector on $\partial \Omega$. $\mu$ is the intrinsic growth rate of the cell, $K$ represents the carrying capacity with $0 < K < 1$, and $\theta$ denotes a critical threshold of the cell density, $\theta > 0$, below which the cell becomes extinct. The homogeneous Neumann boundary conditions indicate that model (1.2) is self-contained with zero flux across the boundary. The initial data $u_0(x)$ and $v_0(x)$ are non-negative smooth functions.

This paper is organized as follows. In Section 2, we discuss the stability of equilibria of model (1.2) by local stability analysis. It is shown that the self-diffusion cannot induce spatial inhomogeneous patterns. In Section 3, sufficient conditions of destabilization are given for the steady state solution by local stability analysis. Section 4 is devoted to acquiring the process of pattern formation by weakly nonlinear analysis. We first derive the Stuart-Landau equations to capture the evolution of the amplitude of the first admissible unstable mode both in the case of supercritical and subcritical bifurcation, obtain an asymptotic expression for the stationary pattern, and show the coexisting phenomenon by the bifurcation diagram in the subcritical case. Then we acquire the competitive mechanism of the double unstable mode case. All these are verified by numerical simulation. In Section 5, the conclusion is summarized. Finally, for the completeness of the calculation process, some specific calculations are given in the two appendices at the end of this paper.

2.   Linearization analysis for the semi-linear model

The local model corresponding to (1.2) can be written in the form

Obviously, (2.1) has three equilibria: the trivial equilibrium $E_0 = (0, 0)$, and two non-trivial equilibria $E_\theta = (\theta, \theta \alpha/\beta)$ and $E_K = (K, K \alpha/\beta)$. In the phase plane, $E_0$, $E_\theta$, and $E_K$ are collinear. The Jacobian matrices of (2.1) at $E_0$, $E_\theta$, and $E_K$ are denoted as follows, respectively:

Based on the accord Jacobian matrices at the equilibria, for the given non-negative coefficients $\mu, \alpha, \beta$, and $K$, the model (2.1) has the following conclusions that hold:

Theorem 2.1. (i) If $\theta \le 0$, then the trivial equilibrium $E_0$ is unstable and the positive equilibrium $E_K$ is stable; (ii) if $0 < \theta < K$, then the trivial equilibrium $E_0$ and the positive equilibrium $E_K$ are stable, and another positive equilibrium $E_\theta$ is unstable.

In model (2.1), $E_0$ is the saddle point if $\theta \le 0$, so cells continue to grow away from $E_0$. $E_\theta$ is the saddle point if $0 < \theta < K$, so cells continue to grow away from $E_\theta$ toward $E_K$ only when cell density $u > \theta$, and when $u < \theta$, cell density continues to decrease away from $E_\theta$ toward $E_0$ until extinction. Since $E_\theta$ is unstable and plays the role of a separator between two stable equilibria $E_0$ and $E_K$, in the latter part, we are only concerned with $E_K$ and $E_0$ when $0 < \theta < K$ holds.

The model (2.1) reflects the dynamic properties of the cell growth and changes in chemical concentrations, without considering diffusion effects. In model (1.2), let $\chi = 0$, and we get a semi-linear model as follows:

In order to discuss model (2.3) by local stability analysis, some properties about the negative Laplace operator $-\Delta$ are given. Let $X = H^1(\Omega, \mathbb{R}^2)$ be a Sobolev space, and $\varphi (x)\in X$ be one nontrivial solution to $-\Delta \varphi = \mu _i \varphi$, $x\in \Omega$, with the homogeneous Neumann boundary condition, where

are its eigenvalues. $E(\mu_i)$ is the eigenspace corresponding to $\mu_i$ in $H^1(\Omega, \mathbb{R}^2)$, and its orthonormal basis is $\{\varphi_{ij}|j = 1, 2, \cdots, \text{dimE}(\mu_i)\}$.

In particular, if $\Omega = (0, l) \subset \mathbb{R}$, then

Combining (2.4) with (2.5) and (2.6), the equilibrium $E_K$ is transformed to the origin by the transformations $\tilde{u} = u-K$ and $\tilde{v} = v-K \alpha/\beta$. For convenience, we still denote $\tilde{u}$ and $\tilde{v}$ by $u$ and $v$, respectively. The linearized system of (2.3) at $E_K$ is

So, the characteristic equation of the model (2.7) is

where

If $K > \theta$, then $\text{Tr}(\mathcal{L}(\mu _i)) < 0$ for all $i = 0, 1, 2, \cdots$ and $\text{Det}(\mathcal{L}(\mu _i)) > 0$. A similar result appears for the trivial equilibrium $E_0$. Then we omit the details and summarize the results:

Theorem 2.2. The positive equilibrium $E_K$ and the trivial equilibrium $E_0$ of model (2.3) are asymptotically stable.

Remark 2.1. Theorem 2.2 implies that self-diffusion does not have a destabilization effect. Moreover, since $\text{Tr}(\mathcal{L}(\mu _i))\neq 0$, Hopf bifurcation cannot appear for model (2.3).

The following section will mainly discuss the effect of chemotaxis coefficient $\chi$ at equilibrium $E_K$ in the chemotaxis model.

3.   Turing instability in the chemotaxis model

In this section, we discuss chemotaxis-driven Turing instability of model (1.2). The linearized problem of (1.2) at $E_K$ is

where

According to the properties of the negative Laplace operator $-\Delta$, model (3.1) has solutions in the form of

where $\textbf{k}$ is the wave vector with wave number $k = |\textbf{k}|$ and $\lambda$ is the temporal growth rate depending on $k^2$. Substituting this into (3.1), we have the dispersion relation

where

Notice that characteristic equation (3.2) has two solutions:

From the local stability theory, the chemotaxis coefficient $\chi$ is solved as

and (3.5) holds if and only if

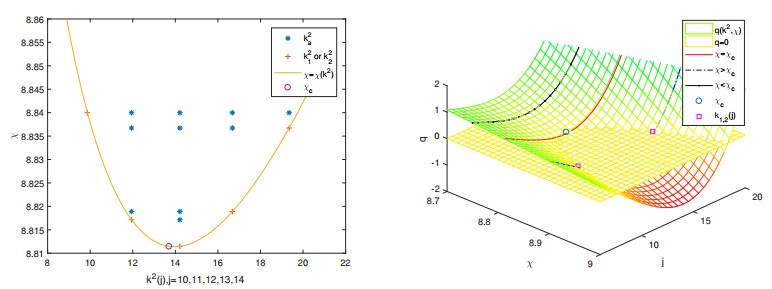
Here, $\chi_c$ is called the critical value for chemotaxis and $k_c$ is the critical value for the wave number. If $\chi\leq\chi _c$, for all $k > 0$, then $p^{^2}(k^2)-4q(k^2)\leq 0$ and the eigenvalues of (3.2) satisfy $\text{Re}(\lambda)\leq 0$, and therefore, the equilibrium $E_K$ is locally stable. If $\chi > \chi _c$, then there exists modes $k^2$ such that (3.2) has two real eigenvalues with different signs, which leads $\text{Re}(\lambda) > 0$ to destabilization.

Especially, if $q(k^2) = 0$, then

and the equal sign holds if and only if (3.6) holds.

Based on the above analysis, we obtain the following results.

Theorem 3.1. Let $K, \alpha, \beta, \mu, \theta, d_1$, and $d_2$ be fixed. If $\chi = \chi_c$, the equilibrium $E_K$ of model (1.2) is neutrally stable. If $\chi > \chi_c$ and there exists modes $k^2$ such that

then the equilibrium $E_K$ destabilizes in the case $q(k^2) < 0$ and $q(k_i^2) = 0, \; i = 1, \; 2$, with

Now we discuss the case at stable equilibrium $E_0$. The corresponding linearized operator is given by

Referring to the deducing process of (3.2), (3.3), and (3.4), we have the following results:

Theorem 3.2. The equilibrium $E_0$ of model (1.2) is always locally stable, where $K, \alpha, \beta, \mu, \theta, d_1$, and $d_2$ are fixed. In this case, chemotaxis diffusion does not induce a pattern.

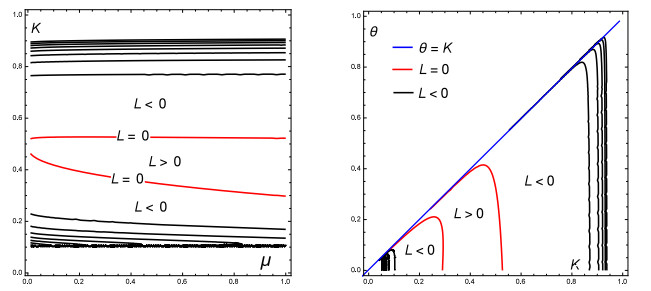
Remark 3.1. Let $\Omega = (0, l)$, and wave number $k = \frac{ \pi j}{l}, j = 1, 2, \cdots$ for model (1.2). For $\chi\geq\chi_c$, define $K_{\chi} = \{ k = \frac{\pi j}{l} |k_1^2 < k^2 < k_2^2, \; j\in \mathbb{N}_+\}$ to be admissible wave number sets. When $\chi$ is sufficiently greater than $\chi_c$, then $K_{\chi}\neq ø$. Substituting $k\in K_{\chi}$ into (3.7), we can define $S_\chi$ to be a set of all admissible bifurcation values, where

and $\chi_m$ is the smallest admissible bifurcation value, $\chi_m\geq\chi_c$. The equal sign holds if and only if there exists $j_0\in \mathbb{N}_+$ such that $\pi j_0/l = k_c$ holds. In this case, $k_c$ is admissible, and then $k_c \in K_{\chi}$. On the other hand, $S_{\chi} = Ø$ and $K_{\chi} = Ø$ when $\chi < \chi_c$.

Remark 3.2. Suppose $\chi > \chi_c$, and if at least one mode $k^2$ is admissible for the domain $\Omega$ and zero-Neumann boundary conditions, then a spatial pattern appears.

Remark 3.3. Since $p(k^2)\neq 0$, Hopf bifurcation cannot appear at the positive equilibrium $E_K$ of model (1.2).

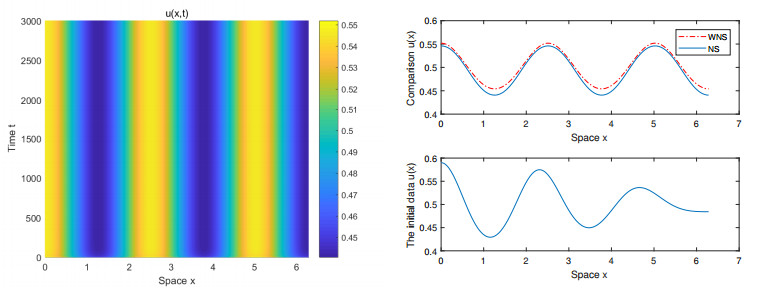
Relations of mode $k^2(j)$, wave number $k(j)$, and the coefficient of chemotaxis $\chi$ are shown in Figure 1. It notes the admissible wave numbers and bifurcation values, critical wave number $k_c$, and bifurcation value $\chi_c$, as well as borderline curve $\chi = \chi(k^2)$, and surface $q = q(k^2, \chi)$.

The linear stability analysis mainly discusses the behavior of the model near the equilibrium. In the following sections, we will discuss how the model may appear to have new behaviors when it leaves the equilibrium and loses stability.

4.   A stationary pattern for the chemotaxis model

In this section, we will discuss the pattern solution of model (1.2) when the chemotaxis coefficient $\chi$ exceeds the critical value $\chi_c$ by weakly nonlinear analysis. The amplitude equations of the spatiotemporal patterns are established using a multiple-scale perturbation approach, and the asymptotic expressions for the stationary patterns are determined by analyzing the amplitude equations. For simplicity, let $\Omega = (0, l)\subset \mathbb{R}$.

4.1.   Multiple-scale analysis

Given the linear transformations $U = u-K, \; V = v-K\beta/\theta$, and $W = (U, V)^T$, model (1.2) is rewritten as follows:

where

We expand $\chi$, $W$, and $t$ as follows:

where $W_i = (U_i, V_i)^T$, $T_i$, $i = 1, 2, \cdots$ represent different time scales, $\chi_a$ is the bifurcation value, and $\varepsilon$ is a control parameter that implies the distance from $\chi$ to the bifurcation point $\chi_a$.

Substituting (4.2) into (4.1), collecting terms at each order in $\varepsilon$, and comparing the coefficients of terms $\varepsilon, \; \varepsilon^2, \; \varepsilon^3, \; \varepsilon^4$, and $\varepsilon^5$ on both sides of the equation, we get a sequence of coefficient equations.

where $F = (F_1, F_2)^T, \; G = (G_1, G_2)^T, \; H = (H_1, H_2)^T$, and $P = (P_1, P_2)^T$.

and

The explicit expression of $H, P$ and all the detailed calculations are given in Appendix I.

4.2.   A stationary pattern under small perturbations

Since Eqs (4.3)–(4.7) satisfy the Neumann boundary conditions, let $k_a\in K_{\chi}$ and $\chi_a \in S_{\chi}$ be the first admissible wave number and the smallest admissible bifurcation value, respectively, so we consider the solution of (4.3) as the following:

where $M = \frac{\beta+d_2 k_a^2}{\alpha}$, $\rho \in \mathrm{Ker}(\mathcal{L}({\chi_a}))$, and $A$ is the amplitude function depending only on the time scales $T_i, \; i = 1, 2, \cdots$.

Substituting $W_1$ into $F(W_1)$, leads to

Let $L^*$ be the adjoint operator of $\mathcal{L}({\chi_a})$. A fundamental solution of $L^* w^* = 0$ is given as follows:

According to the Fredholm theorem, the solvability condition of (4.4) is

and then we obtain

Since $A$ is the amplitude of the slow change in the time scales $T_1, \; T_2, \cdots$, but the solution of (4.10) increases rapidly with $T_1$, then we take $\chi_1 = 0$ and $T_1 = 0$, so that $\frac{\partial A}{\partial T_1} = 0$, and it implies independence between solutions and time scales $T_1$. From this, the solution of (4.4) can be represented in the form

By substituting (4.11) into (4.4), the following expression is obtained:

Combining (4.8), (4.11), and (4.5), noting $\chi_1 = 0, \; T_1 = 0, \; \frac{\partial W}{\partial T_1} = 0$, and $\frac{\partial W}{\partial T_3} = 0$, then $G$ is rewritten as follows:

where

By the Fredholm solvability condition $\int_0^l G\cdot w^* \, dx = 0, \; l = \frac{j \pi }{k_a}, \; j \in \mathbb{N}_+$, and the cubic Stuart-Landau equation of amplitude $A$ is obtained as follows:

where

Obviously, $\sigma > 0$, and we obtain the following result.

Theorem 4.1. Let $\mu, \alpha, \beta, \theta, K, d_1$, and $d_2$ be fixed. If $L > 0$, then (4.12) is supercritical. If $L < 0$, then (4.12) is subcritical.

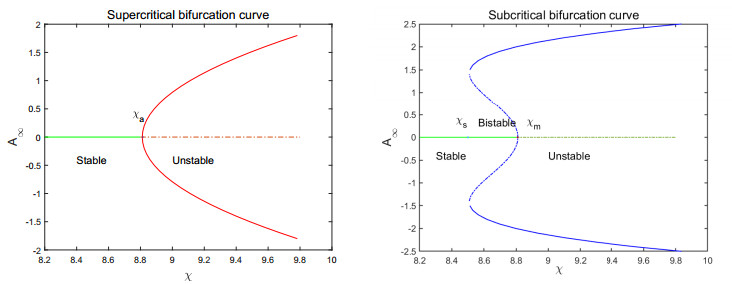
Due to the complexity of the $L$ expression, it is very difficult to analyze its positivity or negativity in the parameter space. Figure 2 gives supercritical and subcritical bifurcation diagrams on the phase planes ($\mu, K$) and ($\theta, K$), respectively, for a given parameter. In the following, we respectively derive asymptotic expressions about the evolution of the spatiotemporal pattern for the supercritical and subcritical cases.

4.2.1.   The supercritical case

Since $\frac{\partial W_1}{\partial T_1} = 0$, the amplitude $A$ in (4.12) only depends on time scale $T_2$. Considering the cubic Stuart-Landau equation (4.12) subject to initial data $A(0) = A_0$, we have

Substituting $A(T_2)$, (4.8), and (4.11) into (4.2), one can express the spatiotemporal pattern $W(t, x)$ at $O(\varepsilon^3)$ as follows:

It is easy to verify that the unique positive equilibrium $\sqrt{\sigma/L}$ is asymptotically stable when $\sigma > 0$ and $L > 0$:

Base on the above analysis, we get the following conclusion.

Remark 4.1. Consider model (1.2) in $\Omega = (0, l)$ and parameters ($\mu, \alpha, \beta, \theta, K, d_1$, $d_2$) are fixed. Assume $\chi > \chi_c$ and there is only one admissible wave number $k_a\in K_{\chi}$ when the control parameter $\varepsilon^2 = (\chi-\chi_a)/\chi_a$ is small enough. If $L$ is positive, then we have the second-order asymptotic expression of the stationary pattern near the equilibrium $E_K$ as follows:

Remark 4.2. Substituting $\sigma, L$, and $\chi_2 = (\chi-\chi_a)/\varepsilon^2$ into $\sqrt{\sigma/L} = A_{\infty}$, we have the supercritical bifurcation curve as follows:

Its bifurcation diagram is shown in the red curve on the left of Figure 3.

Example 4.3. We choose coefficients in model (1.2) as follows:

It is easy to obtain the positive equilibrium $E_K = (0.5, 0.5)$, the chemotaxis critical value $\chi_c = 6.28033 \notin S_\chi$, and critical wave number $k_c = 2.84304\notin K_{\chi}$. Set $\chi = 6.29603$ and $\chi = 6.3413$, the corresponding control parameters are $\varepsilon = 0.05$ and $\varepsilon = 0.1$, respectively, the conditions of Theorem 3.1 holds, and $E_K$ destabilizes. Further, we take the bifurcation value $\chi_a = 6.28954$ and the first admissible wave number $k_a = 3$, and then $\chi_2 = \frac{\chi-\chi_a}{\varepsilon^2}$, $\sigma > 0$, and $L > 0$, so Example 4.3 belongs the supercritical case. The corresponding second-order asymptotic expression of the stationary pattern is given as follows:

To illustrate the correctness of the asymptotic expression, we give numerical solutions for Example 4.3. In Figure 4, we have a comparison between the numerical solution and the weakly nonlinear asymptotic solution of Example 4.3. Of these, the absolute deviation ($|$WNS-NS$|$) is approximately less than 1.5%.

4.2.2.   The subcritical case

If $L < 0$, the unique equilibrium $A = 0$ of the cubic Stuart-Landau equation (4.12) is unstable. The amplitude equation lacks a saturation term to limit the amplitude development, so a higher-order perturbation term should be introduced for analysis.

Therefore, we push the weakly nonlinear expansion to $O(\varepsilon^5)$, and get the quintic Stuart-Landau equation for the amplitude as follows:

where

and $\sigma$ and $L$ are given in (4.13). $W_3$, $W_4$, $\tilde{\sigma}, \; \tilde{L}$, and $\tilde{Q}$ are deduced at the same time. The detailed calculations are given by (A.3), (A.6), and (A.9) in Appendix I.

Substituting $W_1, \; W_2, \; W_3, \; W_4$, and $A(t)$ into Eq (4.2), we obtain the explicit approximation of the spatiotemporal pattern $W(x, t)$ at $O(\varepsilon^5)$:

where all coefficients are expressed in Appendix I.

In this subcritical case, since $\bar{\sigma} > 0$ and $\bar{L} > 0$, when $\bar{Q} < 0$, it is easy to prove that quintic Stuart-Landau equation (4.16) has a globally asymptotically stable solution:

By substituting $A_{\infty}$ into (4.18), the fourth-order weakly nonlinear asymptotic expression of the stationary pattern is given:

Example 4.4. Choose coefficients in model (1.2) as follows:

Then, $E_K = (0.6, 0.6)$, $\chi_c = 8.81140452\notin S_{\chi}$, $k_c = 1.18921 \notin K_{\chi}$, and $\chi_m = 8.81148148$. We take $\chi_a = 8.81714876$, $k_a = 1.2$, $\chi = 8.89951$, and $\varepsilon = 0.1$. All conditions of Theorem 3.1 are satisfied, and the positive equilibrium $E_K$ is unstable. Further $\bar{\sigma} = 2.39871$, $\bar{L} = -8.75287$, and $\bar{Q} = -2.16447$. Eq (4.16) has a stable equilibrium $A_{\infty} = 2.07401$, so this case is the subcritical. One can reduce the Example 4.4 to the form of (4.18).

By solving for $\chi(A_{\infty})$ from (4.19), the subcritical bifurcation curve can be written in the form:

The right of Figure 3 illustrates that there exist two extreme points $\chi_m$ and $\chi_s$, where $\chi_m$ is the root of $\chi(A_{\infty}) = 0$ and $\chi_s$ is the root of $\bar{L}^2-4\bar{\sigma}\bar{Q} = 0$. According to the calculation, we have

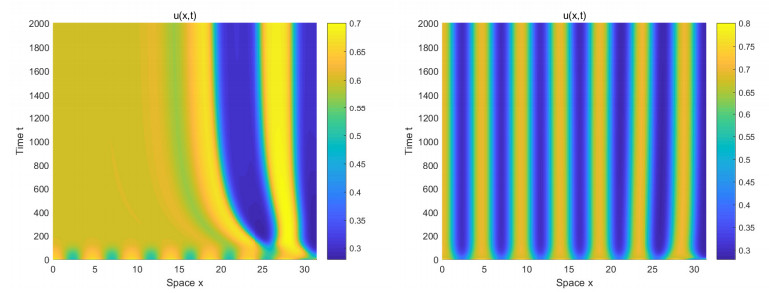
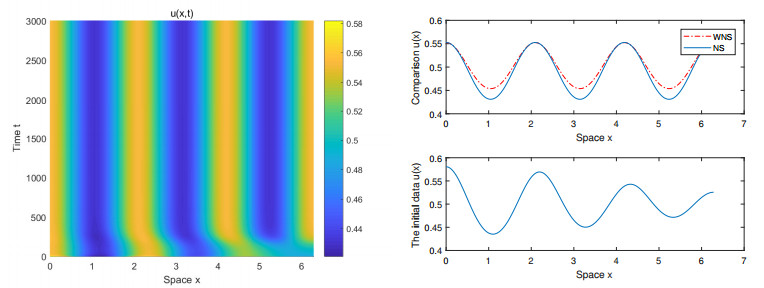
In the example, there are two stable branches coexisting at $\chi\in (\chi_s, \chi_m)$, which are called bistability. The two essential ingredients for bistable behavior are nonlinearity and feedback ^[18]. Suppose that $\chi$ is increased from some value less than $\chi_s$. For any given small amplitude perturbation around $E_K$, the steady state remains until $\chi = \chi_m$, where the $E_K$ loses stability. Namely, while $\chi_m$ is exceeded, the solution jumps to the stable equilibrium with large amplitude. By the same method, for the stable branch with larger amplitude, the jump exists at $\chi = \chi_s$. In this way, a bistable interval is given, as depicted in Figure 3. The solution around equilibrium sensitively depends on the initial conditions. We respectively take initial perturbations of different amplitudes $A = 0.1$ and $A = 0.2$ at $\chi = 8.735059 \in (\chi_s, \chi_m)$, which induce different patterns. The left of Figure 5 shows a critical case of the uniform equilibrium rapidly turning to the spatiotemporal pattern at a given small amplitude initial perturbation. The right of Figure 5 shows that stationary pattern $W$ expressed by (4.18) is reached at a given initial perturbation of large amplitude. According to the analysis, we have the following result.

4.3.   A stationary pattern for large perturbations

Previously, we discussed the stationary pattern of model (1.2) when the equilibrium $E_K$ loses stability if given bifurcation parameter $\chi > \chi_c$, and $\chi$ deviates $\chi_a$ small enough to have a unique unstable mode $k_a\in K_{\chi}$, i.e., control parameter $\varepsilon$ is small enough. In this section, we derive how the unstable modes interact and how to determine the shape of the stationary pattern while $\varepsilon$ is large enough to have two unstable modes for model (1.2) with $\Omega = (0, l)$. According to Theorem 3.1 and Remark 3.1, we have the following conclusion.

Theorem 4.2. Set $\chi_{m_i} \in S_{\chi}, \; i = 1, 2, 3, \cdots$, and $\chi_c \leq \chi_m = \chi_{m_1} < \chi_{m_2} < \chi_{m_3} < \cdots$. If $\chi > \chi_{m_2}$, then there exist at least two unstable modes for given chemotaxis coefficient $\chi$.

Proof. By the definition of $S_{\chi}$, since $\chi_m \in S_{\chi}$, then there exists a $j_1 \in \mathbb{N}_+$ such that

Similarly, for $\chi_{m_2} \in S_{\chi}$, there exists a $j_2 \in \mathbb{N}_+$ such that

So if $\chi > \chi_{m_2}$, wave numbers $k_{j_1}$ and $k_{j_2}$ are in sets $K_{\chi}$, i.e., $q(k^2_{j_1}, \chi) < 0$ and $q(k^2_{j_2}, \chi) < 0$. This implies that $k^2_{j_1}$ and $k^2_{j_2}$ are unstable modes of $\chi$. □

Based on the above analysis, we investigate the competitive law between unstable modes $k^2_{1}$ and $k^2_{2}$ by deriving their amplitude equations. Then we set the solution of (4.3) in the following form:

where $A_i$'s only depending temporal variable is the amplitude of modes $k^2_{i}$ with $i = 1, 2$ and

Substituting (4.21) into (4.4) and (4.5), and combining with the Fredholm theorem, we obtain the following ODE model of the amplitude:

where the explicit expressions of $\tau_i, \; L_i$, and $Q_i$, $i = 1, 2$, are presented in Appendix II. Obviously, $\tau_i > 0, \; i = 1, 2$. Under the conditions $L_i > 0, \; i = 1, 2$ and

Model (4.22) has four non-negative equilibria in the first quadrant:

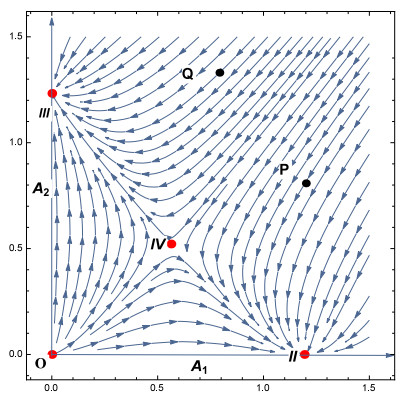
By linearization analysis, we know that $E_1$ is an unstable node, $E_2$ and $E_3$ are stable nodes, and $E_4$ is a saddle point. These points divide the first quadrant of the phase plane of the amplitude $A_1, \; A_2$ into four regions when (4.23) holds. Outgoing trajectories in these areas point to one of two. So we have $A_{1\infty} = \sqrt{\frac{\tau_1}{L_1}}$ and $A_{2\infty} = \sqrt{\frac{\tau_2}{L_2}}$. Let $W_2 = (U_2, V_2)^T$, and $U_2$ and $V_2$ satisfy

where the coefficients are given in Appendix II (B.2). Therefore, the second-order stationary pattern with amplitude $(A_{1\infty}, A_{2\infty})$ for the double unstable modes is as follows:

Example 4.5. The coefficients of the given model (1.2) are chosen the same as in Example 4.3 except $\varepsilon = 0.04$.

According to Theorem 4.2, we have $\chi_{m_1} = 6.28193$ with $j_{m_1} = 6$, $\chi_{m_2} = 6.28954$ with $j_{m_2} = 5$, and $\chi_{m_3} = 6.30463$. Set $\chi = 6.29961 > \chi_{m_2}$. So two unstable modes $k^2_1 = 2.5^2$ and $k^2_2 = 3^2$ are obtained. According to the formulas given by Appendix II (B.1)–(B.3), we have

and the four non-negative equilibria are $E_1 \; (0, 0)$, $E_2\; (1.19319, 0)$, $E_3\; (0, 1.23366)$, $E_4\; (0.563221, 0.521921)$. Their stability is consistent with the above analysis. Then, $A_{1\infty} = 1.19319$ and $A_{2\infty} = 1.23366$. If we take the initial data $(1.2, 0.8)$, which corresponds to the $P$ point in Figure 6, and its trajectory is attracted to the equilibrium $E_2\; (A_{1\infty}, 0)$. The stationary pattern, the detailed comparison between the numerical solution of model (1.2), and weakly nonlinear solution (4.25) are presented in Figure 7. While the trajectory of the initial point $Q = (0.6, 1.2)$ is attracted to the equilibrium $E_3\; (0, A_{2\infty})$, and corresponds to the stationary pattern, the comparison between the numerical solution of model (1.2) and the weakly nonlinear solution (4.25) are presented in Figure 8.

When the bifurcation parameter $\chi$ is far enough away from the critical value $\chi_c$, there exists a competition among two unstable modes. If we perturb the equilibrium $E_K$ by different initial data, different stationary patterns are induced. However, after a long period of evolution, one of the unstable modes will be reduced to extinction, and another will perform a critical role in the competition of unstable modes.

5.   Concluding remarks

The mechanism of the emerging process in the pattern formation has been systematically analyzed for the model (1.2) in this paper. It has been verified that some chemotaxis flux can induce pattern formation, while self-diffusion does not. The dynamics of model (1.2) is similar to the logistic model ^[16] if $\theta \le 0$, where the model develops a Turing pattern when the chemotaxis coefficient $\chi > \chi_c$. Whereas if $0 < \theta < K$, two stable constant steady state solutions, $E_0$ and $E_K$, are separated. When the cell density $u < \theta$, $E_0$ is attractive and chemotaxis cannot induce a Turing pattern, so the cells tend to extinction. When $u > \theta$, a Turing pattern occurs in the model as the chemotaxis coefficient increases until $\chi > \chi_c$. Decreasing the threshold $\theta$ of cell density and increasing the chemotaxis coefficient are important methods to keep the cells growing and to induce a Turing pattern, respectively.

Acknowledgments

The author would like to thank the associate editor and the anonymous reviewer for their valuable comments and suggestions, which have led to a significant improvement of the whole manuscript.

Conflict of interest

The author declares no conflict of interest.

A.   Appendix I. The single unstable mode case

This appendix aims to give the parts omitted in the derivation of the Stuart-Landau equation and spatiotemporal pattern from the previous sections. According to the derivation of the $F, G$ (4.7) in Section 4, we obtain the expressions of $H$ and $P$ as follows:

According to the quintic Stuart-Landau equation (4.12), we can display the solutions of Eq (4.6) as follows:

By substituting $W_1, \; W_2$, and $W_3$ into (4.6), and comparing the coefficients on both sides, the coefficient of the equation is obtained and solved as follows:

Combining $W_1, \; W_2, \; W_3$, (4.12), and (4.6), taking $\chi_1 = 0$ and $\frac{\partial W_1}{\partial T_1} = 0$, we have

where

According to the solvability conditions, we have $\int_{0}^{l} H\cdot w^*dx = 0, l = j \pi/k_a, \; j\in \mathbb{N}_+$, and

Since the solution of the above equation cannot predict the evolution of the amplitude, we take $T_3 = 0$ and $\chi_3 = 0$.

Furthermore, the solution of Eq (4.7) can be written in the form:

Substituting $W_1, \; W_2, \; W_3, \; W_4$, and (4.12) into (4.7), taking $\chi_1 = \chi_3 = 0$, $T_1 = T_3 = 0$, $\frac{\partial W}{\partial T_1} = 0$, and $\frac{\partial W}{\partial T_3} = 0$, and combining the solvability condition$\int_{0}^{l}H\cdot w^{*}dx = 0$, we have

and

where

Since $T_i = \varepsilon^i t$, the derivative of amplitude is given by

where $T_1 = 0$ and $T_3 = 0$. So we obtain

where

Let $T = \varepsilon^2t$, and then $dT = \varepsilon^2dt$. So we obtain the amplitude equation (4.16).

B.   Appendix II. The double unstable mode case

In this section, the derivation of double unstable mode case is given. Let $k_1^2$ and $k_2^2$ be unstable modes of model (1.2). We presume that $w^*$ is a fundamental solution of $L^* w^* = 0$, where $L^*$ is the adjoint operator of $\mathcal {L}({\chi_c})$.

where

Substituting (4.21) into $F = (F_1, F_2)^T$, we have

So we assume that Eq (4.4) has solutions as in (4.24). Substituting $W_1$, $W_2$, and (4.24) into (4.4), combining the solvability condition for (4.4), i.e., $\int_{0}^{l} F\cdot w^* dx = 0$, and setting $\chi = 0$ and $T_1 = 0$, then we obtain (4.24) and its coefficients as follows:

By substituting $W_1$ and $W_2$ into $G = (G_1, G_2)^T$, and combining the solvability condition for (4.5), i.e., $\int_{0}^{l} F\cdot w^* dx = 0, l = 2\pi/k_i, i = 1, 2$, (4.25) is given. Since the expressions are too long, we omit it and just give the integral result, i.e., the amplitude equations of the double unstable modes (4.22). The coefficients of the equation are as follows: