On generalized discrete Ricker map

1.   Introduction

In recent decades, the study of nonlinear dynamics in population models has made significant progress, unveiling complex behaviors such as chaos and bifurcations. ^[11] demonstrated that even simple mathematical models, including population dynamics, can lead to highly complex dynamics, sometimes resulting in chaotic behavior in seemingly straightforward systems. Similarly, the pioneering work of ^[14] laid the foundation for understanding stock-recruitment relationships in fisheries, with the Ricker map emerging as a central tool in discrete population modeling.

The investigation of stability in population models has continued to evolve. ^[1,12] contributed to this by analyzing global stability, shedding light on how various conditions can either stabilize or destabilize population dynamics. This line of inquiry was further advanced by ^[19], who explored global stability in various population models, reinforcing the importance of stability analysis in ecological studies. More recently, ^[2] revisited the stability and instability in one-dimensional population models, broadening our understanding of discrete-time dynamics.

The Ricker map has frequently been employed in predator-prey models, serving as a cornerstone for research into complex population dynamics. Particularly, Ricker-type predator-prey models have been extensively studied in the context of bifurcations and chaotic behavior. ^[9,10] conducted detailed bifurcation analyses within these models, revealing intricate predator-prey interactions across various parameter regimes. Their work underscores how different parameter settings can significantly influence population persistence and the stability of predator-prey relationships ^[5,8,9].

Beyond ecological studies, mathematicians like ^[4,15] have deepened our understanding of nonlinear dynamics and chaos, providing a theoretical framework applicable to both biological and physical systems. Works such as ^[17,18] offer comprehensive introductions to nonlinear dynamical systems and chaos, providing valuable insights into the behavior of both discrete and continuous systems.

Building on foundational concepts in population dynamics, ^[3,6,7] expanded the study of stability, bifurcation, and chaos to piecewise and discrete systems, demonstrating their wide applicability across various fields. Radwan et al. extended this understanding by investigating generalized discrete logistic maps, providing additional insights into the complexity of long-term population dynamics ^[13].

The study of Ricker-type models has seen significant advancements and generalizations. In particular, ^[16] generalized the conventional Ricker map by introducing an arbitrary power to the population variable $x$, resulting in the following form:

Building upon Stewart's work, we further extend the Ricker map (1.1) by introducing an additional parameter to increase its generality. The new generalized Ricker map with arbitrary powers is given by:

where $\alpha$, $\beta$, and $r$ are positive parameters. This extension allows for a more flexible analysis of population dynamics under various conditions.

In the subsequent sections, we investigate the behavior and properties of the proposed generalized Ricker map. Section 2 focuses on the existence and stability of equilibria, offering both theoretical and numerical insights. Section 3 provides bifurcation analyses and numerical simulations, exploring how parameter changes affect the system's dynamics. Finally, Section 4 concludes with a summary of the findings and a comparison of the results, discussing the broader implications of the generalized Ricker map in population dynamics.

2.   Fixed points: existence and stability

The following passage sets the foundation for our inquiry into the existence and stability of equilibria within the generalized Ricker map represented by Eq (1.2):

where $x \geq 0$, $\alpha > 0$, $\beta > 0$, and $r > 0$. Our investigation is structured around the parameter $\alpha$, which guides our analysis into two distinct cases: the first case where $\alpha > 1$, and the second where $0 < \alpha \leq 1$.

2.1.   Case 1. $\alpha > 1$

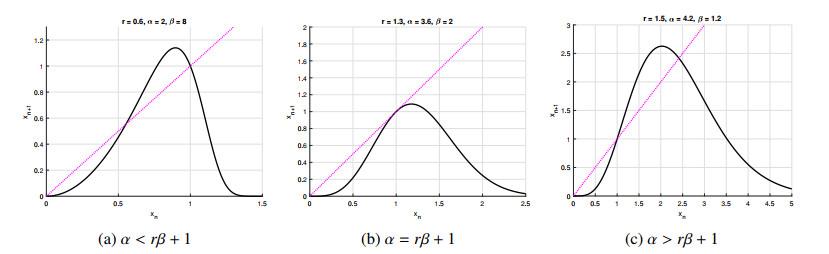
The function $f$ may exhibit either one or two positive fixed points, contingent upon the number of intersections between its graph and $y = x$. In Figure 1, the graph of $f$ for two distinct cases is illustrated. In Figure 1(a,c), there are two positive equilibria, while in Figure 1(b), there is only one positive fixed point. The next theorem will provide us with the conditions to distinguish between these different cases.

Theorem 1. For the difference Eq (1.2) with $\alpha > 1$, the following statements are true:

(ⅰ) If $\alpha = r \beta +1$, the Eq (1.2) has two equilibria $0$ and one positive equilibrium point $\bar{x} = 1$;

(ⅱ) If $\alpha \neq r \beta +1$, the Eq (1.2) has three equilibria $0$ and two positive equilibria $\bar{x} = 1$ and $\tilde{x}$.

Proof. To establish the validity of the theorem, we delve into the solutions of the equation:

It is evident that $x = 0$ and $x = 1$ satisfy Eq (2.2). To explore further positive solutions, we introduce the functions:

and

The roots of $h(x)$ coincide with the fixed points of $f(x)$.

The derivative of $h(x)$ is:

which equals zero when $x = \sqrt[\beta]{\frac{\alpha-1}{r \beta}}$.

Given that

for $\alpha >1$. Now, at $x = \sqrt[\beta]{\frac{\alpha-1}{r \beta}}$, function $h$ has a minimum. For $x \in (0, \sqrt[\beta]{\frac{\alpha-1}{r \beta}})$, $r \beta x^{\beta}-\alpha+1 < 0$, making $h$ decreasing on $(0, \sqrt[\beta]{\frac{\alpha-1}{r \beta}})$. Conversely, for $x \in (\sqrt[\beta]{\frac{\alpha-1}{r \beta}}, \infty)$, $r \beta x^{\beta}-\alpha+1>0$, indicating $h$ increases on $(\sqrt[\beta]{\frac{\alpha-1}{r \beta}}, \infty)$. Hence, at $x = \sqrt[\beta]{\frac{\alpha-1}{r \beta}}$, there is a global minimum of $h$. Notably, $h(0) = 1$ and $\lim_{x\to\infty} h(x) = 1$. If $h(\sqrt[\beta]{\frac{\alpha-1}{r \beta}}) = 0$, then $h(x)>0$ for all $x\neq \sqrt[\beta]{\frac{\alpha-1}{r \beta}}$, indicating $h$ possesses one zero only at $x = 1$. This condition holds true when

which is equivalent to $\alpha = r \beta +1$. When $\alpha = r \beta +1$ holds, it implies that $h(x)$ equals zero at $x = \sqrt[\beta]{\frac{\alpha-1}{r \beta}} = 1$, thereby completing the proof of part (ⅰ).

A similar argument demonstrates that $h\left(\sqrt[\beta]{\frac{\alpha-1}{r \beta}}\right) < 0$ when $\alpha \neq r \beta +1$. It's noteworthy that $0 < \tilde{x} < \sqrt[\beta]{\frac{\alpha-1}{r \beta}} < 1$ when $\alpha < r \beta +1$. Conversely, $0 < 1 < \sqrt[\beta]{\frac{\alpha-1}{r \beta}} < \tilde{x}$ when $\alpha > r \beta +1$. □

After defining the equilibria of Eq (1.2), the subsequent focus lies in determining their local asymptotic stability. This entails analyzing the behavior of the system in the vicinity of each equilibrium point to discern whether small disturbances lead to a return to equilibrium over time.

Theorem 2. Consider the difference Eq (1.2) with $\alpha > 1$, $\beta > 0$, and $r > 0$. It can be deduced that

(ⅰ) The equilibrium at $0$ is locally asymptotically stable;

(ⅱ) The equilibrium at $1$ is locally asymptotically stable when $\frac{\alpha-1}{\beta} < r < \frac{\alpha+1}{\beta}$;

(ⅲ) The equilibrium at $\tilde{x}$ is locally asymptotically stable when $1 < \sqrt[\beta]{\frac{\alpha-1}{r \beta}} < \tilde{x} < \sqrt[\beta]{\frac{\alpha+1}{r \beta}}$;

Proof. Starting with Eq (2.1), we express the derivative $f'(x)$ as follows:

Upon evaluation, we find that $f'(0) = 0 < 1$, indicating the local asymptotic stability of the equilibrium at $0$. This concludes the proof of part (ⅰ).

For part (ⅱ), we examine $f'(1) = \alpha-r \beta$. The condition $-1 < f'(1) < 1$ holds if and only if $\frac{\alpha-1}{\beta} < r < \frac{\alpha+1}{\beta}$.

Turning to part (ⅲ), let us analyze $f'(\tilde{x}) = (\alpha-r \beta \tilde{x}^\beta)\tilde{x}^{(\alpha-1)} \mathrm{e}^{r(1-\tilde{x}^\beta)}$, with the constraint $\tilde{x}^{(\alpha-1)} \mathrm{e}^{r(1-\tilde{x}^\beta)} = 1$. This yields $f'(\tilde{x}) = \alpha-r \beta \tilde{x}^\beta$.

Now, the condition $-1 < f'(\tilde{x}) < 1$ translates to $\sqrt[\beta]{\frac{\alpha-1}{r \beta}} < \tilde{x} < \sqrt[\beta]{\frac{\alpha+1}{r \beta}}$. However, this condition cannot hold when $0 < \tilde{x} < 1$.

To clarify this, note that $\tilde{x}$ and $1$ are roots of the function $h(x)$ in Eq (2.3). Moreover, this function has a global minimum value at $\sqrt[\beta]{\frac{\alpha-1}{r \beta}}$. Therefore, if this minimum value falls within the interval $(0, 1)$, for $\tilde{x}$ to be stable, it should satisfy the inequality $\sqrt[\beta]{\frac{\alpha-1}{r \beta}} < \tilde{x} < 1$. However, such a scenario contradicts the nature of the function $h(x)$, which is increasing on the interval $(\sqrt[\beta]{\frac{\alpha-1}{r \beta}}, \infty)$. As a result, the stability condition for $\tilde{x}$ can be satisfied when $1 < \sqrt[\beta]{\frac{\alpha-1}{r \beta}} < \tilde{x} < \sqrt[\beta]{\frac{\alpha+1}{r \beta}}$. □

From this theorem, it is evident that the equilibrium point $x = 1$ may lose its stability via a fold bifurcation when the slope of the tangent at this point is $1$. This occurs when $\alpha = r\beta + 1$. On the other hand, a period-doubling bifurcation can arise when the slope of the tangent is $-1$, which happens when $\alpha = r\beta - 1$.

As for the other positive equilibrium point, the potential bifurcation at this point is a period-doubling bifurcation, occurring at $\tilde{x} = \sqrt[\beta]{\frac{\alpha+1}{r\beta}}$.

Two Lemmas will now be introduced, playing a pivotal role in the analysis of the basin of attraction encompassing equilibrium points within the difference equation referenced as (1.2).

Lemma 1. The function $f(x) = x^\alpha \mathrm{e}^{r (1-x^\beta)}$ is increasing on $(0, \sqrt[\beta]{\frac{\alpha}{r \beta}})$ and decreasing on $(\sqrt[\beta]{\frac{\alpha}{r \beta}}, \infty)$.

Proof. By computing the derivative of $f(x)$:

The sign of $f'(x)$ is determined by the sign of $\alpha - r \beta x^\beta$. □

Lemma 2. Consider the difference equation defined by (1.2) with $r \beta +1 > \alpha > 1$. Under these conditions, there exists $\hat{x} \neq \tilde{x}$ such that $f(\hat{x}) = \tilde{x}$.

Proof. The function $f(x) = x^\alpha e^{r(1-x^\beta)}$ achieves a global maximum at $x = \sqrt[\beta]{\frac{\alpha}{r \beta}}$, where $f(\sqrt[\beta]{\frac{\alpha}{r \beta}}) > \tilde{x}$. This is due to the fact that $f$ is increasing on the interval $(0, \sqrt[\beta]{\frac{\alpha}{r \beta}})$ as demonstrated in Lemma 1. Furthermore, $f$ decreases on $(\sqrt[\beta]{\frac{\alpha}{r \beta}}, \infty)$, and $\lim _{x \rightarrow \infty} f(x) = 0$. Consequently, by the intermediate value theorem, there must exist $\hat{x}$ in the interval $(\sqrt[\beta]{\frac{\alpha}{r \beta}}, \infty)$ such that $f(\hat{x}) = \tilde{x}$. □

Theorem 3. Let $\alpha > 1$ and $r \beta + 1 > \alpha$. Consider the difference equation defined by (1.2). Suppose there exists $\hat{x} \neq \tilde{x}$ such that $f(\hat{x}) = \tilde{x}$. Then the basin of attraction of the equilibrium at $0$ is the set $[0, \tilde{x}) \cup (\hat{x}, \infty)$.

Proof. Let $x_0 \in [0, \tilde{x})$. We establish by induction that $\{x_n\}$ remains within $[0, \tilde{x})$. For $n = 0$, this holds since $x_0 \in [0, \tilde{x})$. Assuming it holds for $n = k$ ($0 \leq x_k < \tilde{x}$), we have to prove that $0 \leq x_{k+1} < \tilde{x}$, as a result of that, we obtain $\{x_n\} \in [0, \tilde{x})$ for all integers $n$. Given that $f(x)$ is increasing on the interval $\left(0, \sqrt[\beta]{\frac{\alpha}{r \beta}}\right)$ according to Lemma $(1)$, and both $0$ and $\tilde{x}$ are equilibrium points, we can establish the following inequality: $f(0) \leq f(x_k) < f(\tilde{x})$, which is equivalent to $0 \leq x_{k+1} < \tilde{x}$. Furthermore, since $f(x) < x$ on the interval $\left(0, \tilde{x}\right)$, it follows that $x_{n+1} = f(x_n) < x_n$, indicating that the sequence ${x_n}$ is decreasing. As a consequence, since the sequence ${x_n}$ is both bounded and decreasing, it is guaranteed to converge. Thus,

and

As the only solution to $x = x^\alpha e^{r(1-x^\beta)}$ in $[0, \tilde{x})$ is $x = 0$, $\{x_n\}$ converges to $0$ if $x_0 \in[0, \tilde{x})$.

For $\hat{x} < x_0 < \infty$, as $f(x)$ is decreasing on $(\hat{x}, \infty)$, we have $\lim _{x \rightarrow \infty} f(x) = 0 < f\left(x_0\right) < f(\hat{x}) = \tilde{x}$. This implies $0 < x_1 < \tilde{x}$, as previously shown to converge to $0$. □

Theorem 4. Consider the difference Eq (1.2), where $\alpha > 1$ and $\frac{\alpha-1}{\beta} < r < \frac{\alpha+1}{\beta}$. Let $\hat{x} \neq \tilde{x}$ satisfy $f(\hat{x}) = \tilde{x}$. Then the basin of attraction of the positive equilibrium $\bar{x}$ is the interval $(\tilde{x}, \hat{x})$.

Proof. Let $\alpha > r \beta$. In this scenario, according to Lemma (1), the global maximum of the function $f(x)$ exceeds $1$. We proceed by dissecting the interval $(\tilde{x}, \hat{x})$ into four sub-intervals to scrutinize the behavior of the sequence $\{x_n\}$ within each subdivision.

Case 1. $\tilde{x} < x_0 \leq 1$: We aim to demonstrate that if $x_0 \in (\tilde{x}, 1]$, then $\{x_n\}$ converges to $1$. We employ an inductive argument akin to the proof of Theorem $(2.3)$. Suppose $x_0 \in (\tilde{x}, 1]$. We establish, by induction, that $\{x_n\}$ remains within the interval $(\tilde{x}, 1]$. The case $n = 0$ is trivial since $x_0 \in (\tilde{x}, 1]$. Assume the statement holds for $n = k$, where $k$ is a positive integer, i.e., $\tilde{x} < x_k \leq 1$. Given that $f(x)$ is increasing on $(0, \sqrt[\beta]{\frac{\alpha}{r \beta}})$ by Lemma $(1)$, we have $f(\tilde{x}) < f(x_k) \leq f(1)$, implying $\tilde{x} < x_{k+1} \leq 1$. This proves $\{x_n\} \in (\tilde{x}, 1]$ for all integers $n$. Additionally, since $f(x) > x$ on $(\tilde{x}, 1]$, we deduce $x_{n+1} = f(x_n) > x_n$, rendering $\{x_n\}$ an increasing sequence. As $\{x_n\}$ is both bounded and increasing, it converges. Hence,

and

Given that the sole solution to $x = x^\alpha e^{r(1-x^\beta)}$ in $(\tilde{x}, 1]$ is $x = 1$, $\{x_n\}$ converges to $1$ if $x_0 \in (\tilde{x}, 1]$.

Case 2. $1 \leq x_0 < \sqrt[\beta]{\frac{\alpha}{r \beta}}$: The proof parallels Case 1.

Case 3. $\sqrt[\beta]{\frac{\alpha}{r \beta}} < x_0 \leq x^{\star}$ with $f(x^{\star}) = 1$:

This aligns with Case 2.

Case 4. $x^{\star} \leq x_0 < \hat{x}$:

Thus, we revert to Case 1.

When $\alpha \leq r \beta$, the proof can be obtained in a similar approach. □

2.2.   Case 2. $0 < \alpha \leq 1$

Theorem 5. Consider the difference Eq (1.2) with parameters satisfying $0 < \alpha \leq 1$, $\beta > 0$, and $r > 0$. This equation possesses two equilibria: one at $0$ and another at the positive value of 1.

Proof. The equilibrium points of the difference Eq (1.2) correspond to the solutions of the following equation:

Hence, the solutions to $f(x) = x$ are $x = 0$, and the solutions to $1-x^{(\alpha-1)} e^{r(1-x^\beta)} = 0$. Since $x \neq 0$,

Define $g(x) = x^{(1-\alpha)} - e^{r(1-x^\beta)}$. We find that $g(0) = -e^r < 0$, $g(1) = 0$, and $\lim_{x \rightarrow \infty} g(x) = \infty$. According to the intermediate value theorem, since $g(x)$ is continuous and real-valued, it must intersect the line $x = 0$ at least once on the interval $(0, \infty)$. Therefore, the Eq (1.2) possesses at least one positive equilibrium. Notice that $g'(x) = (1-\alpha) x^{-\alpha} + r \beta x^{(\beta-1)}e^{r(1-x^\beta)}$. Since $0 < \alpha \leq 1$, $g'(x) > 0$ for all $x \in (0, \infty)$, and $g(x)$ is strictly increasing on $(0, \infty)$. Consequently, the Eq (1.2) has exactly one positive equilibrium at $x = 1$. □

Theorem 6. Consider the difference Eq (1.2), where $0 < \alpha \leq 1$, $\beta > 0$, and $r > 0$. Then the following statements are true:

(ⅰ) The equilibrium at $0$ is unstable.

(ⅱ) If $0 \leq r \beta -1 < \alpha < r \beta +1$, then the positive equilibrium at 1 is locally asymptotically stable.

Proof. Part (ⅰ): We compute

For $0 < \alpha < 1$, $f^{\prime}(0)$ is undefined. However, $\lim _{x \rightarrow 0+}\left|f^{\prime}(x)\right| = \infty > 1$, indicating that the equilibrium at 0 is unstable.

When $\alpha = 1$, $f^{\prime}(0) = e^r > 1$ for $r > 0$, hence the equilibrium at 0 is again unstable.

Part (ⅱ):

□

The following theorem sheds light on the dynamics of populations by examining the difference Eq (1.2). This equation serves as a representation of a population model under specific conditions: $0 < \alpha \leq 1$, $\beta > 0$, and $r > 0$. Capturing the intricate interplay between growth parameters and environmental factors, it reflects dynamic behaviors pertinent to population dynamics. Through a thorough analysis of its properties, we can effectively assess its suitability for modeling population phenomena.

Theorem 7. The difference Eq (1.2) represents a population model when $0 < \alpha \leq 1$, $\beta > 0$, and $r > 0$.

Proof. According to the definition of a population model presented in ^[1], the model $x_{t+1} = f(x_t)$ represents a population model when it satisfies the following conditions:

(1) The function $f$ is a continuous function.

(2) $f(0) = 0$.

(3) The model has a unique positive equilibrium point $f(\bar{x}) = \bar{x}$.

(4) $f(x) > x$ for $0 < x < \bar{x}$ and $f(x) < x$ for $x > \bar{x}$.

(5) If $f(x)$ has a maximum $x_M$ in $(0, \bar{x})$, then $f(x)$ is monotonically decreasing for $x < x_M$.

It is evident that the model $x_{n+1} = f(x_n) = x_{n}^{\alpha}\mathrm{e}^{r \left(1-x_{n}^{\beta}\right)}$ satisfies all the above conditions. □

Theorem 8. The equilibrium point $1$ of the difference Eq (1.2), when $0 < \alpha \leq 1$, $\beta > 0$, and $r > 0$, under the condition $0 \leq r \beta -1 < \alpha < r \beta +1$, is globally stable.

Proof. The global stability of the equilibrium point is established by invoking Theorem 1 part (a) from Cull's study ^[1]. Initially, it is noted that the equilibrium point remains globally stable when the difference equation (1.2) does not exhibit a maximum point within the interval $(0, 1)$, a condition satisfied when $\alpha > r \beta$.

Assuming the presence of a maximum point $x_M = \sqrt[\beta]{\frac{\alpha}{r \beta}}$ within $(0, 1)$, Theorem 2 part (a1) in Cull's work ^[1] is invoked. This theorem implies that establishing global stability necessitates demonstrating that $f(x) = x^{\alpha} \mathrm{e}^{r(1-x^\beta)}$ maintains consistent concavity within the interval $(x_M, x)$. Concavity is investigated by ascertaining the second derivative and establishing its sign within $(x_M, x)$.

The second derivative of $f(x)$ is expressed as:

The roots of $f''(x)$ coincide with those of the following equation:

These roots are expressed as:

It is demonstrated that the roots (2.7) lie outside the interval $(x_M, 1)$ through proof by contradiction.

Assuming:

This last inequality is invalid for positive parameter values. Similarly, the same approach reveals that the other root cannot reside in the interval $(x_M, 1)$. Thus, the function maintains its concavity within the specified interval, establishing the theorem. □

3.   Bifurcation analysis and numerical simulations

In this section, we embark on a comprehensive exploration of potential bifurcations inherent in our discrete difference Eq (1.2). Initially, guided by Theorem (2.1), we observe the occurrence of a fold bifurcation, where a pair of equilibrium points collide and subsequently vanish as the parameter undergoes variation. This collision event reduces the equilibrium count to two, but as the parameter evolves further, a new pair of equilibrium points emerges, restoring the equilibrium count to three. This phenomenon is visually represented in Figure 1, where the diagonal $y = x$ tangentially intersects the function $f(x) = x^\alpha \mathrm{e}^{r (1-x^\beta)}$, precisely occurring when $\alpha = r \beta + 1$.

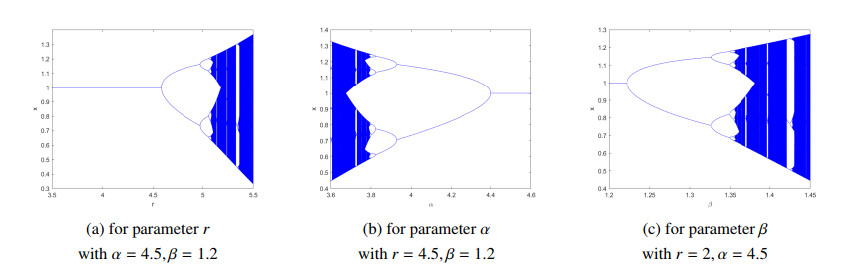
From Theorem 2, we further analyze the behavior of the equilibrium point $x = 1$ under different parameter regimes. When $\alpha < r \beta + 1$, the slope of the tangent at $x = 1$ can reach $-1$, leading to a period-doubling bifurcation. Figure 2 presents a bifurcation diagram, illustrating how parameter variations $r$, $\alpha$, and $\beta$ induce transitions from stable equilibria to periodic orbits and chaotic dynamics. The diagram clearly shows how the equilibrium point $x = 1$ transitions from stability to a period-2 orbit, followed by higher-order periodic orbits, ultimately culminating in chaos, a characteristic feature of nonlinear dynamical systems.

Additionally, a period-doubling bifurcation may also occur at the other positive equilibrium point, $\tilde{x}$. A similar approach can be applied to analyze the system's behavior near this equilibrium point, analogous to the analysis we will conduct for equilibrium point 1.

3.1.   Bifurcation Diagrams (Figure 2)

Figure 2 offers a detailed view of the system's bifurcation structure as $r$ increases. Initially, the system remains stable at the equilibrium point, but as $r$ approaches a critical value, a period-doubling bifurcation occurs. This leads to a cascade of period-doubling bifurcations, progressing through period-4, period-8, and eventually chaotic behavior. The bifurcation diagram is a crucial tool that highlights how the system's qualitative dynamics shift as parameters vary, confirming theoretical predictions of period-doubling and chaos.

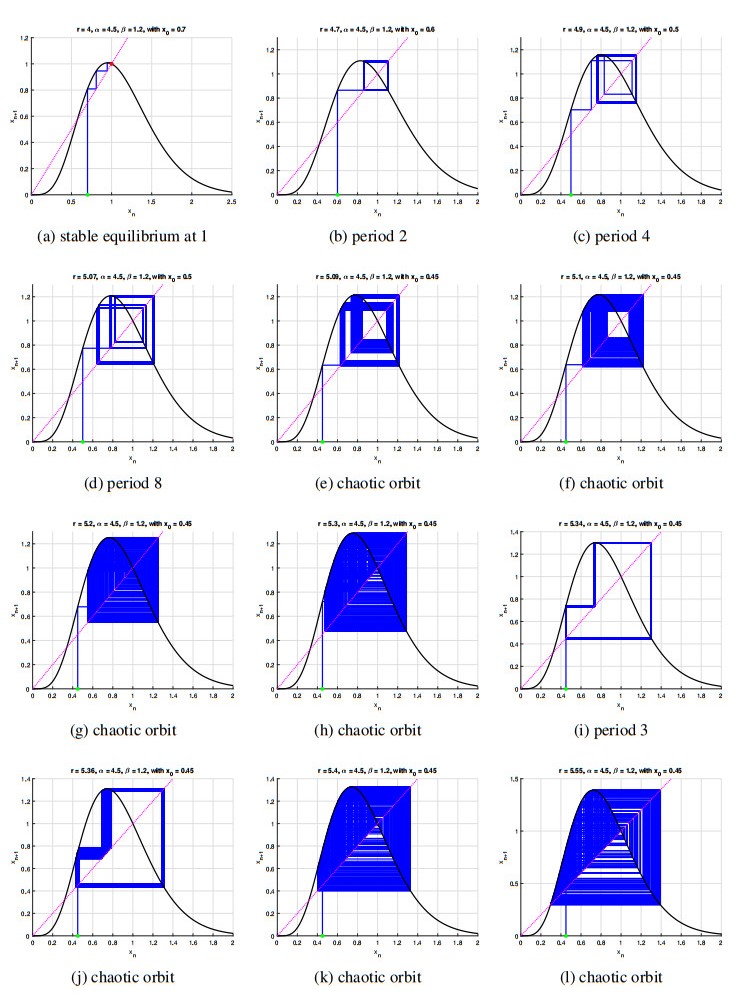
3.2.   Cobweb Diagrams (Figure 3)

The cobweb diagrams in Figure 3 provide further insight into the iterative behavior of the system, particularly the transition from stability to chaos as $r$ increases. As shown, the stable equilibrium at $r = 4$ transitions through a series of period-doubling bifurcations as $r$ increases, eventually leading to chaotic behavior beyond $r = 5.07$. These diagrams offer a step-by-step visual demonstration of how the system's dynamics unfold, with particular emphasis on the parameter sensitivity and cascading bifurcations.

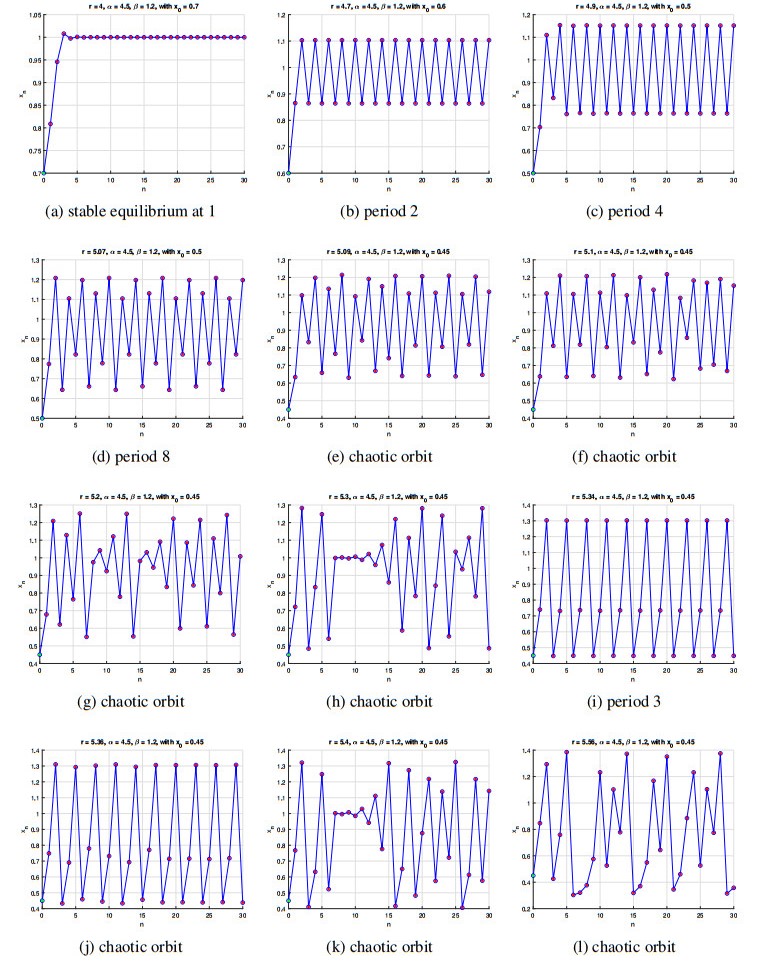
3.3.   Time Series (Figure 4)

Figure 4 presents time series diagrams for the same parameter values as the bifurcation and cobweb diagrams, providing a temporal perspective on the system's behavior. The time series reinforce the bifurcation and cobweb findings by showing how the state variable $x_n$ evolves over time. For smaller $r$, the system remains stable, but as $r$ increases, periodic and chaotic oscillations emerge, clearly linking the time-domain behavior to the bifurcation phenomena discussed earlier.

3.4.   Interpretation and Link to Theoretical Results

The numerical simulations across Figures 2–4, combined with the theoretical insights, offer a robust understanding of the system's dynamics. The fold bifurcation observed early in the analysis is followed by a series of period-doubling bifurcations, eventually leading to chaos, a result that aligns well with the predictions from Theorem (2.1). By using these diagrams as analytical tools, rather than mere illustrations, we highlight the critical role of parameter variation in controlling system stability and behavior. This comprehensive exploration of bifurcations not only confirms the theoretical framework but also deepens our understanding of the system's complex dynamics.

4.   Conclusions

In conclusion, the generalized discrete Ricker map introduced in this paper extends the conventional Ricker map by incorporating additional parameters, enhancing its versatility and applicability across various fields. Through a comprehensive analysis of equilibria, stability conditions, and bifurcation diagrams, we have illuminated the intricate dynamics of the generalized Ricker map, showcasing its behavior across different parameter regimes.

Our investigation revealed that the map's behavior is highly contingent upon the values of parameters $\alpha$, $\beta$, and $r$, with distinct stability properties emerging under varying parameter combinations. The existence of multiple equilibria and their respective stability conditions underscore the rich dynamical landscape of the generalized Ricker map, aligning with findings in the literature while also introducing novel dynamics not previously explored in similar models.

Furthermore, our exploration of basins of attraction elucidated the regions of phase space where trajectories converge to specific equilibria, providing crucial insights into the long-term behavior of the system. This analysis not only enhances understanding of transient and asymptotic dynamics but also resonates with prior studies on basin behavior, establishing a connection between our findings and established theories in dynamical systems.

By comparing our results with previous studies that examine bifurcation structures and chaotic dynamics in related models, we highlight the unique contributions of the generalized Ricker map. Our results reveal new bifurcation scenarios and parameter interactions, enriching the existing body of knowledge and suggesting implications for modeling complex systems.

Moving forward, future research endeavors may investigate extensions and refinements of the generalized Ricker map, delving deeper into its chaotic properties, exploring higher-dimensional analogues, and examining its applications in emerging fields such as network dynamics and machine learning. Additionally, comparing our findings with those involving the Allee effect and other related phenomena could further enhance the understanding of its dynamics.

In summary, the generalized discrete Ricker map stands as a testament to the enduring relevance and utility of iterated maps in modeling complex systems, offering a rich tapestry of dynamical phenomena ripe for exploration and discovery. By situating our findings within the broader context of existing literature, we not only highlight the contributions made by this study but also lay the groundwork for future research.

Author contributions

M. Y. Hamada: Investigation, Writing-original draft, Validation, Writing-review and editing; H. El-Metwally: Conceptualization, Methodology, Investigation, Supervision; Ibraheem M. Alsulami: Writing-original draft, Writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgements

We would like to thank the editor and the anonymous referees for their valuable comments and helpful suggestions, which have led to a great improvement of the initial version.

Conflict of interest

The authors declare that they have no conflict of interests regarding the publication of this paper.