Exact Jacobi elliptic solutions of some models for the interaction of long and short waves

1.   Introduction

The interaction between predators and prey is one of the most critical topics in biomathematics literature. Consequently, several ecologists, mathematicians, and biologists have studied the dynamical behavior of the predator-prey system, which describes the relationship between prey and predator. Lotka ^[1] and Voltera ^[2] established the Lotka-Volterra predator-prey system, a basic population model. Numerous scholars have modified this model over the years to provide a more realistic explanation and enhance comprehension since it ignores many real-world scenarios and complexity. Several ecological concepts, including functional response, refuge, harvesting, fear, and the Allee effect, have been added to the predator-prey system to provide a more realistic description ^[3,4,5,6,7].

In population dynamics, the functional response is one of the most important characteristics of all interactions between predators and prey. The functional response is proportional to the prey density. It indicates how much prey each predator consumes. In 1965, Holling ^[8] proposed three kinds of functional responses. Later, researchers such as Crowley-Martin ^[9] and Beddington-DeAngelis ^[10,11] provided various functional responses. After that, several researchers looked at models that were developed on interactions between predators and prey, including various kinds of functional responses ^{[12,13,14,15,16,17]}.

In recent years, it has been widely accepted that the Allee effect significantly impacts population dynamics and may enrich them. Allee ^[18] was the first to describe this phenomenon. The Allee effect is a biological phenomenon that describes the relationship between population size or density and growth rate. Generally, it happens when a species' population has a very low density, making reproduction and survival difficult. The Allee effect is classified into two categories based on the strength of density dependency at low densities: the strong Allee effect and the weak Allee effect ^[19]. Several works in the literature explore this impact in various population models ^{[20,21,22,23,24,25]} and find that it may significantly influence system dynamics.

We consider the following class of predator-prey interaction with the strong Allee effect ^[26]:

where $x(t)$ and $y(t)$ are the densities of prey and predator populations at time $t$ with the initial conditions $x(0)\geq 0, \; y(0) \geq 0$, $r$ is the rate of growth of $x(t)$, and $k$ is the carrying capacity of prey. The per capita conversion rate from prey to predator is described by $\frac{bx}{1+bhx}$, which is supposed to be the usual Holling type Ⅱ functional response form, $\lambda$ represents the conversion efficiency, $A$ is the strong Allee effect parameter, and it meets $0 < A < k$. All of the parameters are positive. Let $\bar{t} = krt, \ \bar{x} = \frac{x}{k}$, and $\bar{y} = \frac{b}{r}y$, and dropping the bars, the system (1.1) becomes

where $\alpha = \frac{A}{k}, \ \omega = \frac{\lambda b}{r}, \ \sigma = \frac{d_1}{kr}, \ \eta = bhk$.

Mathematical models can be expressed as either continuous-time models or discrete-time models. In recent years, many authors have significantly contributed to discrete models. The reasons are that, when there are no overlapping generations in a population, discrete-time models governed by difference equations are much more suitable than continuous ones, and moreover, discrete models provide more effective results for numerical simulations. Many species, like monocarpic plants and semelparous animals, have different generations that don't mix with each other, and births happen at predictable times during mating seasons. Difference equations or discrete-time mappings are used to describe their interactions. The dynamical characteristics of discrete dynamical systems are rich and complicated. Studies on the nonlinear dynamics of continuous-time predator-prey systems have a long history. There are a significant number of papers on the local and global stability of fixed points, bifurcation analysis, limit cycles, permanence, extinction, the Allee effect, and so on in the literature ^{[20,27,28,29]}. On the other hand, studies on those discrete-time predator-prey systems have attracted much attention over the past three decades. Most of these works have focused on the existence and stability of fixed points, the Allee effect on their dynamics, resonance and bifurcation analysis, and complex and chaotic behaviors. These discrete-time predator-prey models were usually obtained from their continuous-time counterparts by utilizing the forward Euler scheme with an integral step size that was either varying or fixed ^{[30,31,32,33]}. It is observed that discrete-time models exhibit complex dynamics depending on the integral step size. It motivates us to study the discrete counterpart of the system (1.2) by using the forward Euler scheme.

The qualitative behavior of the continuous system (1.2) has recently been explored in ^[26]. We study the discrete analog of the system (1.2) to investigate the complex dynamical character of such predator-prey interactions. To discretize, we use the following Euler's approximation to the system (1.2):

where $\delta$ is the step size.

This paper's primary contributions are as follows:

● The existence and topological classification of fixed points are discussed.

● At the interior fixed point, we investigate period-doubling (PD) and Neimark-Sacker (NS) bifurcation by using $\delta$ as bifurcation parameter.

● About the interior fixed points, the direction and existence conditions for both kinds of bifurcations are investigated.

● To control chaos in the system, a hybrid control strategy is used.

● Numerical simulations are performed to illustrate that a discrete system has rich dynamics due to integral step size $\delta$.

The rest of the paper is structured as follows: We study fixed points' existence and topological classification in Section 2. We then investigate the local bifurcation phenomenon at the interior fixed point in Section 3. A hybrid control method is used for controlling chaos and bifurcations in Section 4. Some numerical examples are provided to support and illustrate the theoretical discussion in Section 5. Finally, we conclude our analysis in Section 6.

2.   Fixed points and stability analysis

In this section, we discuss the existence of fixed points for the system (1.3) and then study the stability of the fixed points by using the characteristic polynomial or the eigenvalues of the Jacobian matrix evaluated at the fixed points. Let us now provide some important information. Let us consider the two-dimensional discrete dynamical system of the following form:

where $f:I\times J \to I$ and $g:I\times J \to J$ are continuously differentiable functions and $I, \; J$ are some intervals of real numbers. Furthermore, a solution $\{(x_n, y_n)\}_{n = 0}^{\infty}$ of system (2.1) is uniquely determined by initial conditions $(x_0, y_0)\in I\times J$. A fixed point of system (2.1) is a point $(\bar{x}, \bar{y})$ that satisfies

Let $(\bar{x}, \bar{y})$ be a fixed point of the map $F(x, y) = (f(x, y), g(x, y))$, where $f$ and $g$ are continuously differentiable functions at $(\bar{x}, \bar{y})$. The linearized system of (2.1) about the fixed point $(\bar{x}, \bar{y})$ is given by $X_{n+1} = JX_n$, where $X_n = \begin{bmatrix} x_n \\ y_n \end{bmatrix}$ and $J$ is the Jacobian matrix of system (2.1) about the fixed point $(\bar{x}, \bar{y})$.

The following results are helpful in examining the stability of the fixed points.

Lemma 2.1. ^[34] Let $F(\theta) = \theta^2+A_1 \theta+A_0$ be the characteristic equation of the Jacobian matrix at $(\bar{x}, \bar{y})$ and $\theta_1, \theta_2$ are solutions of $F(\theta) = 0$, then $(\bar{x}, \bar{y})$ is a

(1) sink iff $|\theta_1| < 1$ and $|\theta_2| < 1$,

(2) source iff $|\theta_1| > 1$ and $|\theta_2| > 1$,

(3) saddle point iff $|\theta_1| < 1$ and $|\theta_2| > 1$ (or $|\theta_1| > 1$ and $|\theta_2| < 1$),

(4) non-hyperbolic point iff either $|\theta_1| = 1$ or $|\theta_2| = 1$.

Lemma 2.2. ^[34] Let $F(\theta) = \theta^2+A_1\theta+A_0$. Assume that $F(1) > 0$. If $\theta_1$ and $\theta_2$ are two roots of $F(\theta) = 0$, then,

(1) $|\theta_1| < 1$ and $|\theta_2| < 1$ iff $F(-1) > 0$ and $A_0 < 1$,

(2) $|\theta_1| < 1$ and $|\theta_2| > 1$ (or $|\theta_1| > 1$ and $|\theta_2| < 1$) iff $F(-1) < 0$,

(3) $|\theta_1| > 1$ and $|\theta_2| > 1$ iff $F(-1) > 0$ and $A_0 > 1$,

(4) $\theta_1 = -1$ and $|\theta_2|\neq 1$ iff $F(-1) = 0$ and $A_1 \neq 0, 2$,

(5) $\theta_1, \theta_2 \in \mathbb{C}$ and $|\theta_{1, 2}| = 1$ iff $A_1^2-4A_0 < 0$ and $A_0 = 1$.

2.1.   Existence of fixed points

The fixed points of the system (1.3) can be obtained by algebraically solving the following system of equations:

It is found that system (1.3) has four fixed points $E_0(0, 0), \ E_1(1, 0), \ E_2(\alpha, 0)$ and $E^*(-\frac{\sigma }{\eta \sigma -\omega }, -\frac{k (\sigma +\eta \sigma -\omega) (\sigma +\alpha \eta \sigma -\alpha \omega)}{(\eta \sigma -\omega)^2})$. The trivial fixed point $E_0$ and boundary fixed points $E_1$ and $E_2$ always exist. The interior fixed point exists iff $\frac{\alpha \omega}{1+\alpha \eta} < \sigma < \frac{\omega}{1+\eta}$.

2.2.   Stability of fixed points

The stability of the fixed points can be established by calculating the eigenvalues $\theta$ of the Jacobian matrix $J$ corresponding to each fixed point. The Jacobian matrix for system (1.3) is

Proposition 2.3. The trivial fixed point $E_0(0, 0)$ is a

(1) sink if $\sigma < \frac{2}{\delta}$ and one of the requirements listed below is satisfied:

(a) $\delta \leq 2$,

(b) $\delta > 2, \ 0 < \alpha < \frac{2}{\delta}$,

(2) saddle point if one of the requirements listed below is satisfied:

(a) $\delta > 2, \ \frac{2}{\delta} < \alpha < 1$, and $0 < \sigma < \frac{2}{\delta}$,

(b) $\delta \leq 2$ and $\sigma > \frac{2}{\delta}$,

(c) $\delta > 2, \ 0 < \alpha < \frac{2}{\delta}$, and $\sigma > \frac{2}{\delta}$,

(3) source if $\delta > 2, \ \frac{2}{\delta} < \alpha < 1$, and $\sigma > \frac{2}{\delta}$,

(4) non-hyperbolic point if one of the requirements listed below is satisfied:

(a) $\delta > 2$ and $\alpha = \frac{2}{\delta}$,

(b) $\sigma = \frac{2}{\delta}$.

Proof. The Jacobian matrix computed at $E_0$ is

The eigenvalues of $J(E_0)$ are $\theta_1 = 1-\alpha \delta$ and $\theta_2 = 1-\delta \sigma$. One can easily check that

and

It is clear that if $\alpha = \frac{2}{\delta}$ or $\sigma = \frac{2}{\delta}$, then one of the eigenvalues of $J(E_0)$ is $-1$. As a result, there is the potential for PD bifurcation to take place if the parameters are allowed to change in a close neighborhood of $\Gamma_{01}$ or $\Gamma_{02}$, where

Proposition 2.4. The boundary fixed point $E_1(1, 0)$ is a

(1) sink if $\frac{\omega}{1+\eta} < \sigma < \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$ and one of the requirements listed below is satisfied:

(a) $\delta \leq 2$,

(b) $\delta > 2, \ \frac{-2+\delta}{\delta} < \alpha < 1$,

(2) saddle point if one of the requirements listed below is satisfied:

(a) $\delta > 2, \ \alpha < \frac{-2+\delta}{\delta}$, and $\frac{\omega}{1+\eta} < \sigma < \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$,

(b) $\delta \leq 2$ and $\sigma < \frac{\omega}{1+\eta}$,

(c) $\delta \leq 2$ and $\sigma > \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$,

(d) $\delta > 2, \ \frac{-2+\delta}{\delta} < \alpha < 1$, and $\sigma < \frac{\omega}{1+\eta}$,

(e) $\delta > 2, \ \frac{-2+\delta}{\delta} < \alpha < 1$, and $\sigma > \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$,

(3) source if $\delta > 2, \ \alpha < \frac{-2+\delta}{\delta}$, and one of the requirements listed below is satisfied:

(a) $\sigma < \frac{\omega}{1+\eta}$,

(b) $\sigma > \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$,

(4) non-hyperbolic point if one of the requirements listed below is satisfied:

(a) $\delta > 2$ and $\alpha = \frac{-2+\delta}{\delta}$,

(b) $\sigma = \frac{\omega}{1+\eta}$,

(c) $\sigma = \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$.

Proof. The Jacobian matrix computed at $E_1$ is given by

The eigenvalues of $J(E_1)$ are $\theta_1 = 1+(-1+\alpha) \delta$ and $\theta_2 = 1-\delta \sigma +\frac{\delta \omega }{1+\eta }$. One can easily check that

and

It is clear that if $\alpha = \frac{-2+\delta}{\delta}$ or $\sigma = \frac{2(1+\eta)+\delta \omega}{\delta (1+\eta)}$, then one of the eigenvalues of $J(E_1)$ is $-1$. As a result, there is the potential for PD bifurcation to take place if the parameters are allowed to change in a close neighborhood of $\Gamma_{11}$ or $\Gamma_{12}$, where

Moreover, if $\sigma = \frac{\omega}{1+\eta}$, then one of the eigenvalues of $J(E_1)$ is $1$. As a result, a transcritical bifurcation may take place if the parameters are allowed to fluctuate within a close neighborhood of $\Gamma_{13}$, where

Proposition 2.5. The boundary fixed point $E_2(\alpha, 0)$ is

(1) never a sink,

(2) a saddle point if $\frac{\alpha \omega}{1+\alpha \eta} < \sigma < \frac{2(1+\alpha \eta)+\alpha \delta \omega}{\delta(1+\alpha \eta)}$,

(3) a source if one of the requirements listed below is satisfied:

(a) $\sigma < \frac{\alpha \omega}{1+\alpha \eta}$,

(b) $\sigma > \frac{2(1+\alpha \eta)+\alpha \delta \omega}{\delta(1+\alpha \eta)}$,

(4) a non-hyperbolic point if one of the requirements listed below is satisfied:

(a) $\sigma = \frac{\alpha \omega}{1+\alpha \eta}$,

(b) $\sigma = \frac{2(1+\alpha \eta)+\alpha \delta \omega}{\delta(1+\alpha \eta)}$.

Proof. The Jacobian matrix computed at $E_2$ is given by

The eigenvalues of $J(E_2)$ are $\theta_1 = 1+(1-\alpha)\alpha \delta$ and $\theta_2 = 1-\delta \sigma +\frac{\alpha \delta \omega }{1+\alpha \eta }$. One can easily check that $\theta_1 > 1$ and

It is clear that if $\sigma = \frac{\alpha \omega}{1+\alpha \eta}$, then one of the eigenvalues of $J(E_2)$ is $1$. As a result, a transcritical bifurcation may take place if the parameters are allowed to fluctuate within a close neighborhood of $\Gamma_{21}$, where

Moreover, if $\sigma = \frac{2(1+\alpha \eta)+\alpha \delta \omega}{\delta(1+\alpha \eta)}$, then one of the eigenvalues of $J(E_2)$ is $-1$. As a result, a PD bifurcation may take place if the parameters are allowed to fluctuate within a close neighborhood of $\Gamma_{22}$, where

Next, we investigate the local dynamics of the system (1.3) about $E^*(-\frac{\sigma }{\eta \sigma -\omega }, -\frac{k (\sigma +\eta \sigma -\omega) (\sigma +\alpha \eta \sigma -\alpha \omega)}{(\eta \sigma -\omega)^2})$ by using Lemma 2.2. The Jacobian matrix of the system (1.3) at $E^*$ is given by

Thus, the characteristic polynomial of $J(E^*)$ is

where

Since $\frac{\alpha \omega}{1+\alpha \eta} < \sigma < \frac{\omega}{1+\eta}$, therefore $T > 0$. By simple computations, we obtain

Thus, we can conclude with the following result.

Proposition 2.6.

The following holds true for the unique positive fixed point $E^*$ of system (1.3):

(1) $E^*$ is a sink if $S > 0$ and if one of the requirements listed below is satisfied:

(a) $S^2-4T \geq 0$, and $\delta < \frac{S-\sqrt{S^2-4T}}{T}$,

(b) $S^2-4T < 0$ and $\delta < \frac{S}{T}$,

(2) $E^*$ is a saddle point if $S > 0, \ S^2-4T > 0$, and $\frac{S-\sqrt{S^2-4T}}{T} < \delta < \frac{S+\sqrt{S^2-4T}}{T}$,

(3) $E^*$ is a source if one of the requirements listed below is satisfied:

(a) $S \leq 0$,

(b) $S > 0, \ S^2-4T > 0$, and $\delta > \frac{S+\sqrt{S^2-4T}}{T}$,

(c) $S > 0, \ S^2-4T \leq 0$, and $\delta > \frac{S}{T}$,

(4) $E^*$ is a non-hyperbolic point if $S > 0$ and one of the requirements listed below is satisfied:

(a) $S^2-4T > 0$ and $\delta = \frac{S\pm\sqrt{S^2-4T}}{T}$,

(b) $S^2-4T = 0$ and $\delta = \frac{S-\sqrt{S^2-4T}}{T}$,

(c) $S^2-4T < 0$ and $\delta = \frac{S}{T}$.

It is clear that if $\delta = \frac{S\pm\sqrt{S^2-4T}}{T}$, then one of the eigenvalues of $J(E^*)$ is $-1$. As a result, there is the potential for PD bifurcation to take place if the parameters are allowed to change in a close neighborhood of $\Gamma_{1}$ or $\Gamma_{2}$, where

Furthermore, if $\delta = \frac{S}{T}$, the eigenvalues of $J(E^*)$ are unit-modulus complex. Thus, the system experiences NS bifurcation if the parameters are varied in a close neighborhood of $\Gamma_{3}$, where

3.   Bifurcation analysis

The PD and NS bifurcations of system (1.3) around the interior fixed point $E^*(-\frac{\sigma }{\eta \sigma -\omega }, -\frac{k (\sigma +\eta \sigma -\omega) (\sigma +\alpha \eta \sigma -\alpha \omega)}{(\eta \sigma -\omega)^2})$ are discussed in this section. We began by investigating the PD bifurcation at $E^*$ when parameters vary in a small neighborhood of $\Gamma_1$. Similar investigations can be done for $\Gamma_2$. We consider the following set:

Giving a perturbation $\epsilon$ (where $|\epsilon|\lll 1$) of the bifurcation parameter $\delta_1$ to the system (1.3), we have

Assuming that $u_n = x_n+\frac{\sigma }{\eta \sigma -\omega }, \ v_n = y_n+\frac{k (\sigma +\eta \sigma -\omega) (\sigma +\alpha \eta \sigma -\alpha \omega)}{(\eta \sigma -\omega)^2}$, after substituting the value of $\delta_1$ the system (3.1) is reduced to the following form:

where

We diagonalize system (3.2) by considering the following transformation:

Under this transformation, the system (3.2) becomes

where

Next, we assume that $W^C(0, 0, 0)$ is the center manifold for (3.4) computed at $(0, 0)$ within a small neighborhood of $\epsilon = 0$. Consequently, $W^C(0, 0, 0)$ can be estimated as follows:

where

The system (3.4) restricted to the center manifold is

Now for PD bifurcation, we require that the following two quantities $l_1$ and $l_2$ are non-zero, where

As a consequence of the above study, we reach the following conclusion:

Theorem 3.1. Suppose that $(\delta, \alpha, k, \omega, \eta, \sigma)\in \Upsilon_{1}$. The model (1.3) undergoes PD bifurcation at interior fixed point $E^*$ if $l_1$ and $l_2$ defined in (3.6) and (3.7) are nonzero and $\delta$ differs in a small neighborhood of $\delta_1 = \frac{S+\sqrt{S^2-4T}}{T}$. Moreover, if $\ l_2 > 0$ (respectively $l_2 < 0$), then the period-2 orbits that bifurcate from $E^*$ are stable (respectively, unstable).

Next, we investigated the NS bifurcation around the interior fixed point $E^*$ of the system (1.3). We consider the following set:

Giving a perturbation $\epsilon$ (where $|\epsilon|\lll 1$) of the bifurcation parameter $\delta_2$ to the system (1.3), we have

Assuming that $u_n = x_n+\frac{\sigma }{\eta \sigma -\omega }, \ v_n = y_n+\frac{k (\sigma +\eta \sigma -\omega) (\sigma +\alpha \eta \sigma -\alpha \omega)}{(\eta \sigma -\omega)^2}$, after substituting the value of $\delta_2$, the system (3.8) is reduced to the following form:

where

Let

be the characteristic equation of the Jacobian matrix of the system (3.9) evaluated at $(0, 0)$, where

Because $(\delta_2, \alpha, k, \omega, \eta, \sigma) \in \Upsilon_{2}, \ |\theta_{1, 2}| = 1$ such that $\theta_{1, 2}$ are solutions of (3.10), it follows that

We then obtain $|\theta_{1, 2}| = \sqrt{q(\theta)}$, and

Further, we need that when $\epsilon = 0, \; \theta_{1, 2}^i \neq 1$ for $i = 1, 2, 3, 4,$ which is equivalent to $p(0) \neq -2, 0, 1, 2$. Since $(\delta_2, \alpha, k, \omega, \eta, \sigma) \in \Upsilon_{2}$, it follows that

Next we assume that $p(0)\neq 0, 1$, that is,

The canonical form of (3.9) at $\epsilon = 0$ can be obtained by using the following transformation:

Under the transformation (3.13), the system (3.9) becomes

where

To examine the direction of the NS bifurcation, we consider the first Lyapunov exponent derived as follows:

where

Thus, we can obtain the following theorem based on the above analysis:

Theorem 3.2. If the condition (3.12) holds and $L$ defined in (3.15) is nonzero, then system (1.3) passes through NS bifurcation at the interior fixed point $E^*$ provided the parameter $\delta$ changes its value in a small vicinity of $\delta_2 = \frac{S}{T}$. Moreover, if $L < 0$ (respectively, $L > 0$) then the NS bifurcation of system (1.3) at $\delta = \delta_2$ is supercritical (subcritical) and there exists a unique closed invariant curve bifurcation from $E^*$ for $\delta = \delta_2$, which is attracting (repelling).

4.   Chaos control

It is desirable, in dynamical systems, to optimize the system according to certain performance requirements and to minimize chaos. Nearly all disciplines of applied research and engineering make extensive use of chaos control techniques. In the case of mathematical biology, bifurcations and unstable fluctuations have long been viewed as negative events, since they are destructive for the breeding of the biological population. As the order to regulate chaos under the impact of period-doubling and Neimark-Sacker bifurcations, one may develop a controller that can adjust the bifurcation features for a given nonlinear dynamical system and in a consequence certain desired dynamical properties can be acquired. To control the chaos in the system (1.3), we use the hybrid control technique ^[35] for controlling chaos through both forms of bifurcation effects. We consider the controlled system shown below to correspond to the system (1.3):

where $0 < \rho < 1$. The fixed points of the controlled system (4.1) and the uncontrolled system (1.3) are identical. At its interior fixed point $E^*$, the Jacobian matrix of the controlled system (4.1) is

The trace $T$ and determinant $D$ of $J(E^*)$ are

and

The Jury condition states that the fixed point $E ^*$ of system (4.1) is stable if and only if the following is true:

5.   Numerical simulation

In this section, several numerical simulations and calculations are performed to support the analytical findings' validity. Using $\delta$ as the bifurcation parameter for system (1.3) about interior fixed point $E^*$, we perform numerical simulations to confirm the previously obtained results. The parameter values were taken from the ^[26]. We used MATLAB for the calculations and graphic drawings.

5.1.   Neimark-Sacker bifurcation

Considering the parameter values as

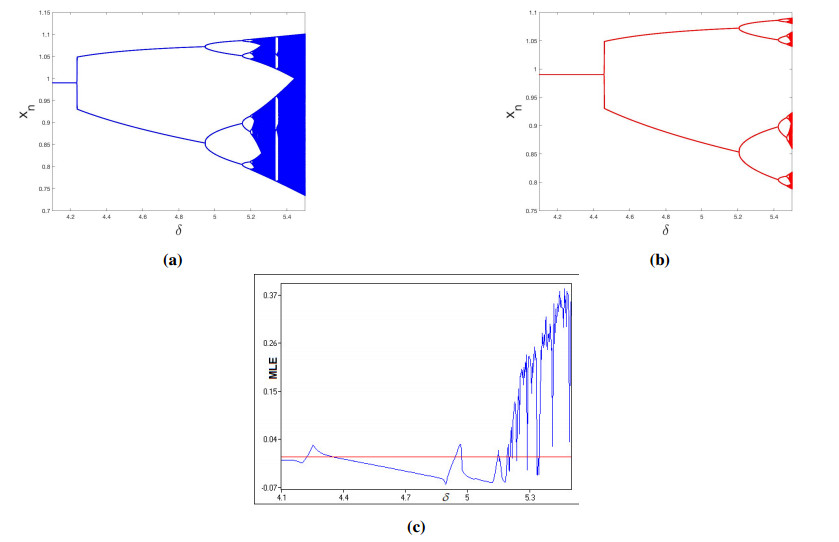
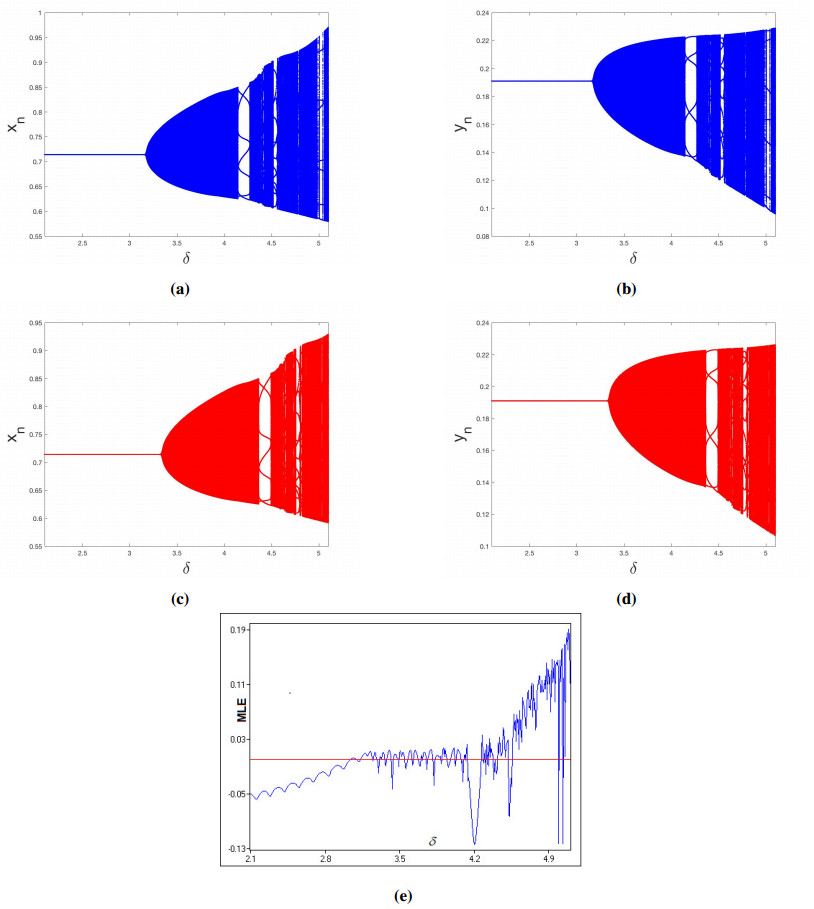
with initial conditions $x_0 = 0.7, \; y_0 = 0.2$, the NS bifurcation value is computed as $\delta_2 = 3.1746$ and the interior fixed point of system (1.3) has been evaluated as $E^* = (0.714286, 0.19102)$. The eigenvalues of $J(E^*)$ are $\theta_{1, 2} = 0.740849\pm 0.671672i$ with $|\theta_{1, 2}| = 1$. It verifies that the system (1.3) undergoes NS bifurcation at $E^*$. Furthermore, the value of the first Lyapunov exponent is calculated as $L = -14.2754$. As a result, the NS bifurcation is supercritical, demonstrating the accuracy of Theorem 3.2. Figure 1a, b depict bifurcation figures for prey and predator for $\delta \in [2.1, 5.1]$. Moreover, to confirm the chaotic behavior of system (1.3) maximum Lyapunov exponents (MLE) are shown in Figure 1e.

The fixed point $E^*$ is a sink for these parameter values iff $\delta < 3.1746$. Figure 2 depicts phase portraits of the system (1.3) for different values of $\delta$. The figures show that the fixed point $E^*$ is a sink for $\delta < 3.1746$ but becomes unstable at $\delta\approx 3.1746$, where the system (1.3) experiences NS bifurcation. A smooth invariant curve appears for $\delta\geq 3.1746$, increasing its radius as $\delta$ increases. By increasing the value of $\delta$, the invariant curve disappears suddenly, and some periodic orbit appears, and then again, we have an invariant curve in place of a periodic orbit. It leads to the appearance of a strange chaotic attractor for large values of $\delta$.

For the controlled system (4.1), we consider the same parameter values with $\rho = 0.95$. The stability condition (4.3) for these values is $0 < \delta < 3.34169$. The bifurcation diagram for the controlled system depicts that NS bifurcation has been delayed. See Figure 1c, d. The controlled system is experiencing NS bifurcation when $\delta$ passes through $\delta_2 = 3.34169$. The NS bifurcation can be delayed for a wider range of $\delta$ by using small values of the control parameter $\rho$.

5.2.   Period-doubling bifurcation

Considering the parameter values as

with the initial conditions $x_0 = 0.95, \; y_0 = 0.01$ for system (1.3). The PD bifurcation value is computed as $\delta_0 = \frac{S-\sqrt{S^2-4T}}{T} = 4.23443$ and the interior fixed point has been computed as $E^* = (0.990099, 0.00630821)$. The eigenvalues of $J(E^*)$ are $\lambda_1 = -1, \lambda_2 = 0.986766$, confirming that system (1.3) undergoes PD bifurcation at $E^*$ as the bifurcation parameter $\delta$ passes through $\delta_0 = 4.23443$. See Figure 3a. Moreover, to confirm the chaotic behavior of the system (1.3), maximum Lyapunov exponents (MLE) are shown in Figure 3c. For controlled system (4.1), we consider the same parameter values with $\rho = 0.95$. The stability condition (4.3) for these values is $0 < \delta < 4.4573$. The bifurcation diagram for the controlled system shows that PD bifurcation has been delayed. See Figure 3b. The controlled system is experiencing PD bifurcation when $\delta$ passes through $\delta_0 = 4.4573$. The PD bifurcation can be delayed for a wider range of $\delta$ by using small values of the control parameter $\rho$.

5.3.   Time series plots with and without Allee effect

This section shows that the Allee effect can cause the solutions of a system to take much longer to reach a stable fixed point. Considering the parameter values as

with initial conditions $x_0 = 0.7, \; y_0 = 0.2$, the interior fixed point of system (1.3) is computed as $E^* = (0.724286, 0.19102)$. The time series plots for prey and predator populations are presented in Figure 4a, b.

If we consider the system (1.2) without the Allee effect, then the following discrete-time system is obtained:

The time series plots for prey and predator populations are presented in Figure 4c, d.

By considering the same parameter values and initial conditions, the interior fixed point of system (5.1) is computed as $(0.198556, 1.2208)$. Comparing interior fixed points, it is found that the prey population is increased and the predator population is decreased when we use the Allee effect. Moreover, the time series plots reveal that the system with the Allee effect requires much more time to attain fixed point.

6.   Conclusions

This paper examined a discrete predator-prey model with a strong Allee effect on prey. We obtained the discrete system (1.3) by applying the forward Euler scheme to the system (1.2), which was proposed in ^[26]. The discrete system (1.3) has the same fixed points as its corresponding continuous system (1.2). However, the dynamic behaviors of systems (1.2) and (1.3) are quite different. Local stability analysis of fixed points is discussed. Also, we carry out an examination of local bifurcations at the interior fixed point in detail. It is shown that system (1.3) experiences PD and NS bifurcation. In system (1.2), the trivial fixed point $(0, 0)$ is always stable, but in the system (1.3), it has complex dynamics. Moreover, the topological classification of fixed points of the system (1.3) depends on step size $\delta$. Our numerical simulations show that PD and NS bifurcations occur when a large step size is considered in Euler's method. However, the dynamics of the system (1.2) do not depend on $\delta$. Therefore, we have good reasons to believe that the dynamic behavior of the system (1.3) is richer than that of the system (1.2). Moreover, a hybrid control technique is used to control the chaotic behavior of the system (1.3). Consequently, both forms of bifurcation can be controlled over a wide range of control parameters. Finally, numerical simulations are performed to describe the theoretical analysis discussed in the form of bifurcation diagrams, phase portraits, and time series plots. It is shown that the system with the Allee effect requires much more time to reach a fixed point.

Conflict of interest

The authors declare no conflicts of interest.