An almost second order uniformly convergent method for a two-parameter singularly perturbed problem with a discontinuous convection coefficient and source term

1.   Introduction

Endogenous hemoglobin-derived peptides (hemorphins) have been shown to exhibit pharmacological potential related to their numerous biological activities [1],[2]. Hemorphins are promising therapeutic agents and biomarkers in oncology, nephrology and vascular medicine and can be efficiently applied in inflammation and for mood regulation [3]–[8]. The detailed characterization of hemorphins' interaction mechanisms with biomembranes provides useful data in view of increasing expectations towards peptides in the prevention and treatment of various diseases and conditions [9]. The application of lipid vesicles as drug carriers motivates the investigation of their physical properties, dynamics, and stability in the presence of medicinal substances for vectorization. The bending rigidity, which characterizes the deformability of lipid bilayers, is relevant to the flow properties of vesicles in blood circulation. Thus, the investigation of membrane mechanical properties is of practical importance regarding biomedical applications of liposomes.

Quantitative characterization of valorphin association with LUVs could allow the determination of peptides partitioning between the aqueous solution and the lipid membrane [10]. Also, a thermodynamic description of the binding process would provide better insight into the mechanism of these interactions [11] and make a valuable impact on the investigation of peptide effects on the structural, mechanical and electrical properties of lipid membranes. Isothermal titration calorimetry (ITC) is a technique capable of measuring directly the binding energetics of biological processes and to generate information concerning the nature of interactions. In the present study it is considered as a suitable approach to confirm and thermodynamically characterize the binding of valorphin to phosphatidylcholine membranes [12].

2.   Materials and methods

2.1.   Materials

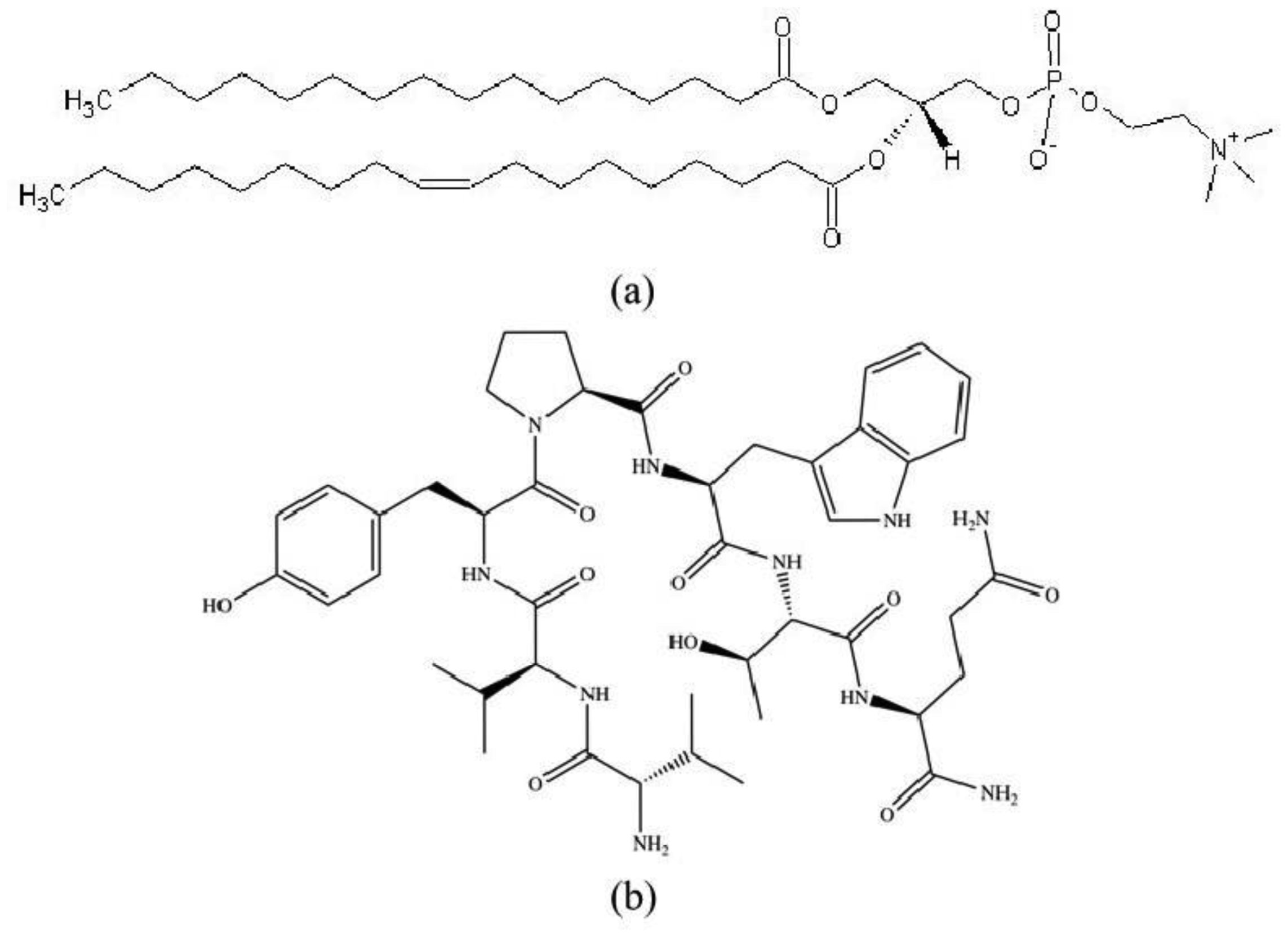
The synthetic lipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine, POPC (Avanti Polar Lipids Inc. (AL, USA) was used for the preparation of model membranes. Bidistilled water (pH 5.5) was produced in a quartz distiller. Chloroform and methanol for lipid solutions were purchased analytical grade from Sigma-Aldrich (Germany). Polydimethylsiloxane (PDMS) was supplied by Dow Corning (Germany). VV-hemorphin-5 was obtained by solid phase synthesis as described previously [13]. Structural formulas of the peptide and phosphatidylcholine used in the study are shown in Figure 1 as drawn by ACD Labs (ACD Inc., Canada) and PerkinElmer ChemDraw Professional 16.0, CambridgeSoft (MA, USA).

2.2.   Methods

2.2.1.   Large unilamellar vesicles (LUV)

LUVs were obtained by extrusion [14]. LUV suspensions were prepared from POPC dissolved in chloroform/methanol (1: 1 v/v). The solvent was completely removed from the samples after evaporation under a stream of oxygen-free dry nitrogen followed by desiccation under vacuum overnight. Lipid depositions were then hydrated with filtered (220 nm) bidistilled water to a lipid concentration of 1.3 mmol/L. The samples were vortexed for 1 min, then left in a sonication bath for 5 min. The multilamellar vesicles thus obtained were subsequently extruded with a LipoFast small-volume extruder equipped with polycarbonate filters (Avestin, Ottawa, Canada) by performing 11 extrusions through 800 nm, followed by 21 extrusions through 100 nm filters. LUV samples were studied the same day after equilibration for 20 min at 22 ± 1 °C.

2.2.2.   Giant unilamellar vesicles (GUV)

Valorphin-containing quasispherical giant unilamellar vesicles (GUV) were produced by electroformation [15] on indium tin oxide (ITO)-coated glass plates separated by a polydimethylsiloxane (PDMS, Dow Corning, Germany) spacer following the procedure reported in [16]. Lipid depositions were formed by the uniform spreading of 50 µL of POPC-valorphin solution with the total concentration of 1 g/L in chloroform-methanol (9: 1 volume parts) on the ITO-coated side of each electrode. After the complete evaporation of the organic solvents under vacuum, the electroformation chamber (4 mL) was filled in with bidistilled water, thus achieving the final lipid concentration of 33 µM. Subsequently, AC electric field with a frequency of 10 Hz and 3 V peak-to-peak voltage was applied to the ITO-electrodes for a couple of hours in order to obtain a high yield of nearly spherical fluctuating GUVs appropriate for analysis of thermal fluctuations of their shape according to [17].

2.2.3.   Analysis of thermal shape fluctuations (ATSF) of GUVs

The analysis of thermal shape fluctuations (ATSF) [18],[19] of GUVs observed by phase-contrast microscopy allows for the calculation of the modulus of bending elasticity, k_c, of lipid membranes. The measurement of membrane bending rigidity is based on Legendre analysis of the autocorrelation function ξ(γ, t) of the vesicle contour radius ρ(φ,t)=R0[1+u(φ,t)] at a moment t and angular direction φ. R₀ denotes the radius of a sphere having the same volume as the volume of the studied vesicle, and u(φ, t) stands for the normalized function of contour radius fluctuations [18],[20]. The coefficients Bn(σ−,kc) in the Legendre polynomials, P_n(cos γ), presentation of ξ(γ, t) are related to the bending constant k_c, and the reduced membrane tension σ−=σR02/kc by the expression [17],[18],[20],[21]:

Here n ≥ 2, k_B is the Boltzmann constant and T is the absolute temperature. The real mechanical tension of the bilayer σ=ks(ΔS/S0) depends on the membrane stretching deformation ΔS/S₀ and its stretching modulus k_s [22].

ATSF performed on visibly fluctuating quasispherical GUVs with diameters larger than 10 µm, exploits algorithms for quality control of the recorded vesicles as discussed in [17]. Thus, alterations of the calculated k_c value by systematic artifacts (volume and surface changes during measurements, non-quasisphericity, blurred contours, membrane defects, etc.) are eliminated.

Observation chambers of two parallel glass slides, separated by a 0.5 mm-thick (CoverWell®) spacer (Sigma-Aldrich Inc., USA) were used containing ~400 µL of GUV suspension freshly prepared. GUVs' shape fluctuations were observed under Axiovert 100 (Zeiss, Germany) inverted microscope operating in phase contrast and equipped with an oil-immersed objective Zeiss N-Achroplan (Ph3, 100x, NA 1.25). The stroboscopic sample illumination, synchronized with the camera, makes it accessible for the acquisition and analysis of fast fluctuation modes [23]. The image record and processing were carried out through a CCD camera (C3077, Hamamatsu Photonics, Japan) connected to a frame grabber board (DT3155, Data Translation, USA, 768x576 8-bit pixels; 0.106 µm/pix) mounted in a computer for digitization and analysis.

2.2.4.   Isothermal titration calorimetry (ITC)

The association of VV-hemorphin-5 to phosphatidylcholine membranes is assessed by high-sensitivity titration calorimetry [24],[25] The heat flow resulting from the peptide-lipid interaction was measured using a low-volume NanoITC calorimeter (TA Instruments, Lindon, UT, USA) with a reaction cell of 190 µL and 50 µL syringe. Prior to use, the device is electrically calibrated at 25 °C with both the sample and reference cells filled with distilled water.

We studied LUV suspensions prepared from POPC and bidistilled water following the procedure described above. The binding behavior of VV-hemorphin-5 was assessed in the concentration range between 1.75 and 3.5 µmol/L. All samples were tempered (25 °C) and thoroughly degassed under vacuum (84 kPa, 20 min with stirring) to prevent air bubble formation. In a series of measurements, 300 µL of peptide solutions were titrated with LUV suspensions. Aliquots of 2 µL were injected in 25 steps with a 300 s interval and a stirring speed of 250 rpm at 25 °C. The blank experiment, accounting for the heat of vesicle dilution in a pure solvent, is performed at the same conditions. Heat rate changes, detected during the interactions, were submitted to the calorimeter software for calculation of injection heats (ITCRun software) and thermodynamic parameters of binding (NanoAnalyze software, TA Instruments, Lindon, UT, USA), respectively.

3.   Results and discussion

Isothermal titration calorimetry (ITC) was applied to probe the association of VV-hemorphin-5 to phosphatidylcholine membranes. Thermodynamic parameters of valorphin-membrane interactions were studied for model systems comprised of POPC vesicle suspensions and diluted (3.5 µmol/L) valorphin aqueous solutions. The heat of LUV dilution in hemorphin solutions was measured in multiple injection modes. The inner panels in Figure 2 represent the heat flow during the ITC experiments in which 2 µL aliquots of lipid vesicles (1.3 mmol/L lipid concentration) were repeatedly injected into the sample cell containing valorphin solution. The detected peaks were exothermic for all investigated peptide concentrations and indicated that binding interactions were accompanied by the release of heat from the system. In the course of titration, the heat flow decreased because of the free peptide depletion in the calorimeter cell but even at the end of titration peaks did not diminish completely to the baseline. This was attributed to the dilution heat of LUVs since the injection heats after about 10 aliquots were comparable to those measured in the blank experiment. Therefore, the signals were corrected by the average area of dilution peaks before the evaluation of reaction enthalpies and binding isotherms [26]. The calorimetric data were analyzed using the NanoAnalyze software provided with the instrument.

Thermodynamic characterization of the studied interactions required applying of a theoretical model consistent with the experimental results. In our case the model for one set of binding sites the most satisfactorily fitted the data. It assumed the existence of N independent and thermodynamically identical binding sites on lipid vesicles. Interaction of VV-hemorphin-5 with these sites is an equilibrium process dependent on the unbound peptide concentration and free lipids from LUVs external monolayers [26],[27]. As thoroughly discussed by Seelig [28] peptide-membrane interactions represent partitioning and/or adsorption rather than the specific binding between peptide and lipid molecules.

Partitioning of the amphiphilic VV-hemorphin-5 between the bulk solution and the hydrophobic core or interface of LUVs is quantified by the equilibrium constant [29],[30]:

where ΔG⁰/N_A stands for the standard free energy of peptide transfer from the bulk phase into the membrane [30]; N_A is Avogadro's number, and R = N_Ak_B (k_B being Boltzmann's constant) is the gas constant; Cpb represents the bound peptide molar concentration; Cpf denotes the free (unbound) peptide molar concentration and CLtot is the total lipid molar concentration, all of them referring to the volume of the sample. The free energy change, ΔG⁰, which is associated with the transfer of the peptide from the bulk aqueous phase into the lipid membrane, involves contributions of different origin accounting for the sоlvation, perturbation of lipid molecules and immobilization of the peptide in the membrane environment as thoroughly discussed in [30]. The relation expressed by Eq 2 is relevant only to small enough peptide concentrations in the membrane as well as in the water solution. We considered valorphin association to LUVs following the binding isotherm approach [24]. During ITC measurement, the equilibrium between the peptide solution in the cuvette and the lipid molecules from the external monolayer of liposomes injected, is characterized by the partition coefficient by Kp=Cpb/[Cpf(NCLtot−Cpb)], where N stands for the number of bound peptide molecules at saturation of the binding sites [31]. Тhe equilibrium constant can also be expressed in terms of the fraction of binding sites engaged by peptide Φ=Cpb/NCLtot and acquires the form Kp=Φ/[(1−Φ)Cpf]. As far as the number N of binding sites reflects the number of peptides that fully saturate the accessible lipids, the unbound peptide concentration is related to the total concentration of peptide molecules in the sample through the expression Cpf=Cptot−NΦCLtot.

From the last two relations the fraction Φ can be presented as a function of the lipid concentration. The heat release ΔQ=CLtotVΔΦΔH per injection in the cell with volume V is related to the molar enthalpy of the association process, ΔH, and the change of the bound peptide fraction, ΔΦ. The extended expression given in (3), where Cl(i) stands for the total lipid concentration at the i-th titration step, suggests that at the end of i-th injection Q(i) can be calculated for the set of parameters N, K_p and ΔH.

As far as the ITC experiment measures the heat change Q(i) – Q(i – 1) is measured, ΔQ(i) for the i-th injection is given by Eq 4. The expression is corrected for the displaced volume dV_i at the i-th titration step.

Nonlinear regression analysis of experimental data with Eqs 3 and 4 was performed. The iterative procedure of ΔQ(i) fitting with an initial guess of the adjustable parameters K_p, N, and ΔH, compared the results with the respective injection heats. The procedure continued up to 10⁶ cycles. Consequently, the Gibbs free energyΔG=−RTlnKp and the entropy gain ΔS=(ΔH−ΔG)/T were calculated using K_p, N, and ΔH values acquired from the fitting procedure (Table 1).

ITC measurements were performed at three different valorphin concentrations as shown in Table 1. The peptide concentration range was chosen not to exceed valorphin concentrations applied in nociceptive screening in vivo [13].

Peptide-membrane interactions possess exothermic nature and suggest an association by van der Waals forces, intra- and/or intermolecular hydrogen bonds. Since ITC only generates information for the overall enthalpy they cannot be distinguished. The heat release during the experiment indicates the transfer of the system to formation of associates between the peptides and lipid bilayers.

An inverse relationship was observed between the strength of peptide-to-lipid binding and peptide concentrations in solution, possibly due to the steric hindrance between molecules. The calculated Gibbs free energy ΔG was negative in the range of investigated valorphin concentrations and verified the spontaneous peptide-membrane association via partitioning and adsorption. Both enthalpy and entropy terms had a favorable impact on Gibbs free energy with a more pronounced effect of entropy (Table 1). Usually, the entropy increase is attributed to hydrophobic interactions, desolvation of molecular surfaces and conformational changes of the interacting species [28].

The exothermic nature of membrane-peptide interaction (Figure 2) is related to the partitioning and/or adsorption phenomena, which are more energetically favorable than the existence of free monomers in solution. The most significant reaction enthalpy was measured in the most diluted valorphin solutions. Gibbs free energy, calculated from the partition coefficient K_p is negative for all the investigated interactions. As far as the lowest peptide concentration ΔH and TΔS contribute almost equally to the Gibbs free energy (with a slight predominance of TΔS) the process is not exceptionally driven by entropy, in contrast to the other valorphin concentrations studied. The number of binding sites N accounts for the number of peptide molecules bound to each lipid at saturation. We obtained N = 0.1 the highest Cptot= 3.5 µmol/L studied, while for more diluted valorphin solutions its value was higher.

The effect of valorphin on the membrane mechanical properties was assessed by measuring the bending rigidity of POPC bilayers containing various concentrations of the opioid peptide. Several hundred frames were acquired once per second for every studied GUV [18]. Taking into account that the time lapse between two adjacent images was 1 s, we performed a correlation test of each image sequence. Consequently, only vesicles with a correlation time of the second fluctuation mode, n = 2 in Eq 1 [32],[33], lower than half a second, τ₂ ≤ 0.5 s were used for the calculation of the membrane bending modulus. The values of the bending modulus reported here, represent the weighted average of k_c with standard deviations, calculated over the vesicles, meeting all requirements for goodness [17] as shown in Table 2 and Figure 3 (black closed circles). At P/L ~ 0.035 mol% we report a considerable increase (~40%) of the bending constant testifying to more rigid lipid bilayers in the presence of valorphin. As it has been established theoretically and experimentally [22],[34]–[40] the bending elasticity of lipid membranes is related to structural parameters of the bilayer such as chemical composition, phase state, thickness, lipid packing, unsaturation of the aliphatic chains, surface charge, etc. It has been revealed that the interaction of amphipathic peptide molecules with lipid bilayers may significantly change the membrane bending rigidity. The effect of amphiphilic peptides such as alamethicin, magainin, melittin and other antimicrobial peptides on the mechanical properties of lipid bilayers has been reported in previous studies of ours and other authors [41]–[45]. Most of them lead to membrane softening as a result of the lateral perturbation of lipid molecules in the bilayer by the presence of adsorbed peptide molecules inducing spontaneous curvature and membrane thinning [46]. In the case of valorphin studied here, an interesting non-monotonic behavior of the membrane bending elasticity is reported as a function of the peptide concentration. The above finding suggests that the origin of membrane stiffening may be related to changes in the membrane thickness and/or packing density of the bilayer in the presence of 0.035 mol% of valorphin. For example, similar stiffening has been reported previously for polymer-grafted [47] or cholesterol-containing bilayers [48],[49]. A previous study on native gramicidin/phosphatidylcholine interactions has revealed a biphasic change in membrane behavior at a critical peptide-to-lipid molar ratio [50]. In the case of the highly hydrophobic long-chain gramicidin the observations have been related to the condensing effect of the polypeptide on the surrounding lipid molecules with a local maximum of the densely packed area around a critical molar concentration. In this densely packed area, an ordered arrangement of gramicidin dimers have been obtained together with a disordered arrangement of gramicidin monomers in the fluid membrane regions. In our study we correlate results from mechanical and calorimetric measurements, both yielding similar non-monotonic dependence on valorphin concentration (Figure 3). Since data on valorphin conformation in the phosphatidylcholine membrane from experiments or molecular dynamic simulations are not available, only assumptions can be made about the molecular mechanisms involved. In order to explore the molecular mechanisms leading to the observed non-monotonic behavior of k_c with the peptide concentration, further investigations need to be performed such as circular dichroism spectroscopy for characterization of valorphin conformation and aggregation.

Thermodynamic parameters of valorphin interaction with POPC membranes were studied at peptide bulk concentrations up to Cptot = 3.5 µmol/L. We obtained a non-monotonic dependence of the number of binding sites as a function of VV-hemorphin-5 bulk concentration in agreement with the bending elasticity behaviour reported in Table 2. The strongest association of valorphin was measured at Cptot = 2.6 µmol/L, which corresponds to P/L ~ 0.8 mol% peptide-to-lipid molar ratio in the sample. This finding correlates with the alteration of the bending elasticity measured for POPC bilayers as a function of VV-hemorphin-5 molar content in the cell (Table 2).

The higher strength of valorphin-membrane interactions obtained from the calorimetric measurements at total peptide concentration P/L ~ 0.8 mol% is coherent with the stronger effect of VV-hemorphin-5 on POPC membrane elasticity revealed by thermal shape fluctuation analysis of GUVs. Figure 3 displays the membrane bending modulus, k_c, together with the data for the strength of peptide binding to the bilayer in terms of N. Qualitatively the pictures of k_c and N dependence on P/L are similar in the covered peptide concentration range but their maxima are shifted, most probably for methodological reasons. Noteworthy features of the studied vesicle suspensions are the different characteristic curvatures and tensions of LUVs and GUVs, which might affect valorphin association to membranes. Nevertheless, as discussed in [51] the lipid packing in LUVs is close to planar membranes. Therefore, this type of unilamellar vesicle is preferred to compare with results acquired on GUVs. The observed valorphin effects on membrane bending and affinity are presented as functions of the total peptide-to-lipid molar ratio in the sample P/L. The total lipid concentration in GUV experiments CLtot= 33 µM is considerably lower than in LUV samples CLtot= 1.3 mM thus leading to much lower bound peptide content in GUVs compared to LUVs. The two methods applied here required different experimental conditions, which led to considerable differences in the total lipid concentrations for the studied P/L range. Hence, the samples prepared for ATSF measurements contained at least ten-fold lower POPC and valorphin total concentrations compared to suspensions studied by ITC. Тhe partitioning of VV-hemorphin-5 between the bulk solution and the bilayer therefore results in different bound, Cpb, and free, Cpf, peptide concentrations in the two experiments, which supposedly is the origin of the maxima's shift in Figure 3.

Limited solubility and concentration-dependent conformation of valorphin in water have not been systematically investigated yet. VV-hemorphin-5 is a heptapeptide consisting of hydrophobic non-polar and hydrophilic polar amino acids as shown in Figure 1b. The presence of nonpolar valine, proline and tryptophan in the structure usually involves peptides in hydrophobic-effect-based interactions, while the polar threonine, tyrosine and glutamine residues participate in hydrogen bonding to water and lipid molecules, which is important in the mechanisms of peptide interaction with membranes. The non-polar residues contribute mainly to the detected entropy change of the system. From general considerations, apart from hydrophobic interactions, they are also supposed to be engaged in van der Waals interactions that decrease the enthalpy. Another source of enthalpy decrease is the possibility of hydrogen bond formation between the hydroxyl groups in the side chains of tyrosine and threonine and water molecules solvating LUV surfaces. Formation of intramolecular hydrogen bonds between skeletal amino and carbonyl groups of the peptide is also possible since they stabilize the conformation of a peptide chain. Tyrosine is the only ionizable amino acid in valorphin structure. It behaves as a very weak acid but at pH 5.5 is fully protonated. At the same pH, the N-terminus of glutamine is positively charged and can be electrostatically attracted by the lipid phosphate group. The membrane stiffening at very low valorphin concentrations indicates a peptide-induced increase of the lipid packing density and thickening until a ‘critical’ total peptide concentration is achieved, above which membrane softening is measured. The observed phenomena may be due to a concentration-dependent valorphin aggregation changing the peptide-membrane interaction above this ‘threshold’ valorphin concentration. This assumption may underlie further investigations by structural methods on valorphin-phosphatidylcholine membranes. The latter is intended to be performed as an objective of a future study. In further investigations of molecular mechanisms of valorphin/POPC interactions the application of a number of experimental techniques such as circular dichroism spectroscopy, and in silico methods may be considered. The answer to the question regarding the origin of the effect may be found by correlating the obtained results on the number of binding sites and membrane stiffening with circular dichroism measurements and numerical simulations of the peptide conformation and aggregation in solution and in the membrane environment.

4.   Conclusions

The results reported above contribute to the physicochemical description of valorphin-containing lipid bilayers. The bending modulus of POPC membranes was measured in a wide range of VV-hemorpin-5 concentrations revealing a considerable increase in its value at a given valorphin concentration. Similar behavior was obtained for the strength of valorphin interaction with the bilayer quantified by the number of binding sites considering partitioning and/or adsorption rather than the specific binding between peptide and lipid molecules. Future efforts to study the conformation of the opioid peptide as a function of its concentration in the bulk solution would provide useful insight regarding the concentration-related valorphin effect on the membrane mechanics.

Knowledge attained on the interplay between the endogenous hemoglobin-derived heptapeptide VV-hemorphin-5 with phosphatidylcholine bilayers may be useful in the development of various applications of lipid membrane systems in pharmacology and biomedicine. The determination of material parameters of lipid bilayers in the presence of peptide and protein molecules is relevant also to characterization of mechanical properties of cell membranes, which are highly dynamic, fluid structures, made functional by complex lipid–lipid, lipid–protein and protein–protein interactions.