Incorporating stochastic volatility and long memory into geometric Brownian motion model to forecast performance of Standard and Poor's 500 index

1.   Introduction

In the financial world, the market index of any country reveals the level of financial stability and economic progress. In the USA, the most standout index amongst recognized lists is Standard and Poor's 500 (S&P 500). The S&P 500 is the main stock market indicator of major public companies in the US, where 500 of the top market leaders are included in it. These market leaders reflect the level of aggregate conduct among its business sectors. Therefore, forecasting of the performance of S&P 500 is a crucial issue because it assists in making correct decisions. For this purpose, there were various models presented in literature to forecast future market performance such as the jump diffusion process, random walk process, Brownian motion (BM) process, geometric Brownian motion (GBM) and geometric fractional Brownian motion (GFBM). This work focuses on GBM and GFBM models.

GBM and GFBM models are special cases of stochastic differential equations (SDE). In general, SDE models have wide applications in financial environment, especially in predicting and modeling financial products. For some examples, GBM models together with the famous Black-Scholes model obtained a closed-form solution for the European option pricing problem ^[1], SDE with stochastic volatility is used to overcome the smile effect such as in the Heston model ^[2] and Hull-White model ^[3], models dealing with crises where the impact of a financial crunch is represented by an additional term in the stochastic part of the stochastic differential equation such as in ^[4,5], jump-diffusion models where the asset prices, dynamics are assumed to be driven by a continuous part represented by the Brownian motion and a jump part usually described by a compounded Poisson process as in ^[6].

In the work that follows, we will investigate SV models perturbed by Brownian motion (BM) and fractional Brownian motion (FBM) because the SV models have good features which permit them to provide more details on the empirical characteristics of the joint time-series behavior of option prices, stocks and index prices which cannot be captured by limited models. Furthermore, by incorporating FBM into an SV model, the behaviors of real markets can be depicted more accurately since these models show memory, or dependency ^[7]. Indeed, this work is only considering stochastic volatility and long memory, but there are other issues that affect indexes, like those discussed in works ^[8,9,10,11].

This paper is comprised of four main sections. Section 1 contains a brief introduction. Next, Section 2 provides the models of GBM and GFBM under study. Section 3 validates the models under study through investigation on forecasting index prices of S&P 500. Finally, Section 4 concludes the study.

2.   Materials and methods

2.1.   GBM and GFBM models

Bachelier in ^[12] is one of the first scholars who used BM for predicting financial assets. In the modern era, Ross in ^[13] also utilized the BM process directly to model stock price. However, this direct employment of BM faced heavy criticism because the BM process permits the price to be negative where the stock prices are assumed to follow a normal random variable. To deal with this situation, a non-negative variation of BM named geometric Brownian motion (GBM) was employed to recover the shortness of the BM in financial applications. GBM showed that it can describe the real situation better. Therefore, it was widely utilized in many applications of financial mathematics, such as index price, mortgage insurance, the Black-Scholes model, option pricing and exchange rates.

Definition I ^[14]. A stochastic process ${S}_{t}$ is said to follow a GBM if the following stochastic differential equation (SDE) is satisfied:

where ${W}_{t}$is a Brownian motion and $\mu$ and $\sigma$ are drift and volatility respectively. The solution of Eq (1) is of the form

where ${s}_{0}$ represents an initial value.

Despite the evolution of this approach, numerous researchers such as ^{[15,16,17,18,19,20,21,22,23]}, observed the appearance of memory in the time series data which is controlled by this model. This implies the next step by proposing a model of GBM that can incorporate the properties of long memory. Fractional Brownian motion (FBM) is one of models that were offered to deal with this issue.

Definition II ^[24]. The fractional Brownian motion (FBM), {${B}_{H}\left(t\right)$}, with Hurst parameter $H\in \left(\mathrm{0, 1}\right)$ is a centered Gaussian process whose paths are continuous with probability 1 and its distribution is defined by the covariance structure:

FBM represents a continuous Gaussian process with independent increments. The correlation between the increments of FBM fluctuates consistently with it self-similarity parameter which is called the Hurst parameter ($H$ index). The Hurst parameter was used to capture the correlation dynamics of data and consequently yield better results in forecasting. There are three different types of memory dependency which were detected according to the value of $H$. If $0.5 < H < 1$, this means existence of long memory dependence, if $0 < H < 0.5$, this means short memory dependence, while when $H = 0.5$ there is no memory dependence.

If FBM is substituted in GBM instead of BM, this gives a model called geometric fractional Brownian motion (GFBM). GFBM is an evolution version of GBM which incorporates memory properties.

Definition III ^[25]. A stochastic process $S$_t is said to follow a GFBM if the following stochastic differential equation (SDE) is satisfied:

where ${B}_{H}\left(t\right)$ represents a FBM and $\mu$ and $\text{σ}$ represent mean (drift) and volatility respectively. The solution of Eq (3) is of the form

where ${s}_{0}$ represent an arbitrary initial value.

The volatility ($\sigma)$ in Definitions Ⅰ and Ⅲ is assumed to be constant. It can be considered as the historical volatility and is computed by several formulas as in Table 1.

To simplify the derivation and computations of the models in Definitions Ⅰ and Ⅲ, the volatility $\sigma$ was assumed to be constant. However, several empirical studies claimed that the assumption of constant volatility is not enough to describe the real situation accurately ^[15,26,27]. As an alternative, many efforts investigated using stochastic volatility (SV) in GBM instead of constant volatility such as ^{[28,29,30,31,32,33,34,35,36]}. In an attempt to develop a model that can describe and demonstrate real financial circumstances more accurately, Alhagyan in ^{[7,37,38,39,40]} extended existing works by incorporating stochastic volatility into GFBM instead of constant volatility.

In a SV model, $\sigma$ (constant volatility) in Eqs (1) and (3) are replaced by $\sigma \left({Y}_{t}\right)$ which is a function of a stochastic process ${Y}_{t}$ (${Y}_{t}$ is the solution of an SDE that is driven by different noise).

Table 2 shows some different SDE models that describe ${Y}_{t}$ in different forms. This work focuses on an SV model that follows the fractional Ornstein-Uhlenbeck (FOU) process.

Definition IV ^[7]. A stochastic process $S$_t is said to follow a GFBM perturbed by stochastic volatility if it satisfies the following SDE:

where ${Y}_{t}$ is a stochastic process, $\mu$is mean (drift), ${B}_{{H}_{1}}\left(t\right)$ is a (FBM) with Hurst index ${H}_{1}$ and $\sigma \left({Y}_{t}\right)$ is a deterministic function.

Let the dynamics of volatility ${Y}_{t}$ be described by FOU process which is the solution of the following SDE

where $\alpha, {\beta }_{}$ and$m$ all are constant parameters and represent mean reverting of volatility, volatility of volatility, and mean of volatility, respectively. ${B}_{{H}_{2}}\left(t\right)$ is another FBM which is independent from ${B}_{{H}_{1}}\left(t\right)$.

The deterministic function $\sigma \left({Y}_{t}\right)$ has many formulas in literature. This work chooses three formulas: $\sigma \left({Y}_{t}\right) = {Y}_{t}$, $\sigma \left({Y}_{t}\right) = \sqrt{{Y}_{t}}$ and $\sigma \left({Y}_{t}\right) = {e}^{{Y}_{t}}$.

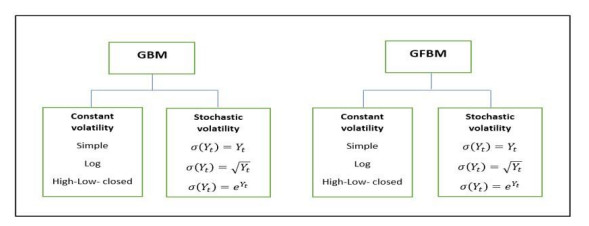
This research forecasts values of closing prices of the S&P 500 in an aim to make a comparative study of the performance between 12 models; 6 models of GBM and 6 models of GFBM with volatility formulations available in Table 1 and FOU in Table 2 as illustrated in Table 3. Figure 1 shows the models under study.

2.2.   Forecasting the performance of S&P 500

2.2.1.   Description of data

The data is accessible online at http://finance.yahoo.com. The total daily observations of data is 252 beginning from 2^nd Jan. 2015 to 31^st Dec. 2015. This period was chosen because the Hurst parameter is $H > 0.5$, which means the existence of long memory. The return series is considered in logarithm (i.e., ${r}_{n} = \mathrm{l}\mathrm{n}({s}_{n}/{s}_{n-1}$)) to control data with high volatility. Figures 2 and 3 show the closing prices and its return series.

2.2.2.   Forecasting and evaluation

According to the data of the S&P 500 in 2015, all parameters involved in the models under study were computed by using Mathematica 10 software (See Table 4). Next, all these parameters were utilized to compute the values of constant volatilities according to the formulas given in Table 1 and stochastic volatilities according to three deterministic functions mentioned earlier (see Table 5).

The parameters in Table 4 were utilized to forecast closing prices of the first three months of 2016. The forecasted closing prices values were computed using six models of GBM and six models of GFBM as mentioned above (see Figure 1).

To evaluate the forecasting methods, two measures of error were used; mean square error (MSE) and mean absolute percentage error (MAPE) were applied as follows:

where ${F}_{i}$ and ${Y}_{i}$ represent the forecasted price and the actual price at day i, respectively, while $n$ is the total number of forecasting days.

Lawrence in ^[41] determined intervals to judge the accuracy of the forecast methods by using MAPE as illustrated in Table 6.

3.   Results

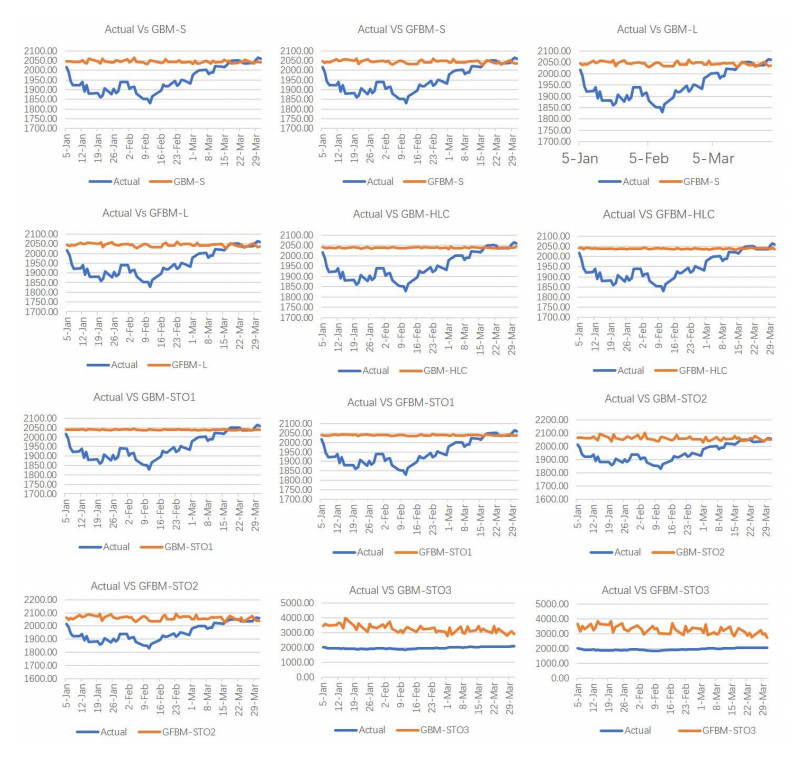
The forecasted prices of twelve models in addition to actual prices of S&P 500 are shown in Appendix 1 and the accuracy levels of all models are listed in Tables 7 and 8.

The findings reveal that GFBM-STO1 ranked first in terms of accuracy with the smallest values of MSE and MAPE. This result was achieved based on the two sources of memory ${H}_{1}$ and ${H}_{2}$ which were incorporated in GFBM-STO1 as well as the stochastic volatility assumption under the deterministic function $\sigma \left({Y}_{t}\right) = {Y}_{t}$ that obeys the FOU process. In contrast, GBM-STO3 and GFBM-STO3 ranked last with huge values of MSE and MAPE. There are some differences between ranks of accuracy in Tables 7 and 8. These differences do not have much effect on the results because the MSE values are close together and the MAPE values are close together too.

The huge gap between the ten models with high accuracy from one side and GBM-STO3 and GFBM-STO3 on the other side can be justified by the large difference between the values of stochastic volatilities as shown in Table 5. Therefore, large volatility means large fluctuation.

Appendix 1 shows almost close values of forecasting values based on all models except GBM-STO3 and GFBM-STO3. Tables 8 indicates that the forecasting using GBM or GFBM models have high accuracy since MAPE < 10%.

These findings suggest that models with long memory are more suitable in empirical analysis. This result agrees with many studies, such as ^{[16,20,21,22,23,37]}. Figure 4 illustrates the comparison between the actual closing prices versus the forecasted closing prices computed by the twelve methods under study.

4.   Conclusions

Index price reflects the performance of economic growth and financial stability. Therefore, understanding the future direction of index prices is one of the top priorities of investors. For this goal, numerous scholars in literature have proposed numerous models. GBM and GFBM models are two of the most important. In literature, there are two main assumptions with respect to volatility: a constant assumption and a stochastic assumption upon financial environments. Moreover, there are many ways to compute constant volatility and many considerations of the deterministic function in the case of stochastic volatility.

The present study has dealt study with three formulas of computing constant volatility including simple, log and high-low-closed. Furthermore, three deterministic functions of stochastic processes including identity $\sigma \left({Y}_{t}\right) = {Y}_{t}$, square root $\sigma \left({Y}_{t}\right) = \sqrt{{Y}_{t}}$ and exponential $\sigma \left({Y}_{t}\right) = {e}^{{Y}_{t}}$.

In fact, this study has examined the effect of incorporating stochastic volatility and memory into the classical GBM model through forecasting index prices of the S&P 500. The results showed that performance of GFBM-STO1 is the best due to having the smallest values of MSE and MAPE. This empirical result has proved the direct positive affection of merging stochastic volatility and memory into GBM models which may use as a tool to forecast the index prices. These findings are consistent with many empirical studies such as ^{[7,16,20,21,22,23,37]}. Generally, the results exhibited that the models with exponential deterministic functions (GBM-STO3 and GFBM-STO3) cannot be used in forecasting index prices since the MSE and MAPE are very large. Meanwhile, the rest of models have high accuracy (MAPE$\le$10%) and thus, can be used in a real financial environment.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF2/PSAU/2022/01/21160).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix 1