A mathematical model study on plant root pest management

1.   Introduction

At the beginning of the 21st century, due to a stronger resistance of pests against pesticides, drugless biologic pest management became increasingly significant for agriculture. Generally, pests damage three parts of plants: the top layer, middle layer and roots. Pest management currently focuses more on the upper and middle parts of plants, yet less attention has been given to plant roots. In addition, the soil around plant roots is full of abundant beneficial microbes, and these microbes are vital for the growth of crops. However, there are also pests consuming these beneficial microbes, and more beneficial microbes are consumed once the number of pests increases, thus causing a reduction in grain yields. To eliminate pests, using chemicals, e.g., pesticides, was once an effective method that was largely used previously, but pesticides kill beneficial microbes in the soil as well, and it may result in serious pollution in the soil ^[1].

Pest control is a complex question that has always been a research object of ecologists and mathematicians. To better maintain the ecological security of crops, pesticides are less considered for pest management as long as the harm of insect pests to crops can remain within an appropriate range. Once the pest number reaches a threshold value (also known as the economic threshold (EI), artificial intervention will be applied, spraying pesticides to kill pests ^[2,3,4]. Since the theory of semi-continuous dynamic systems was proposed and applied to pest control ^[5], it has received attention from relevant scholars ^{[6,7,8,9,10,11,12,13,14,15,16,17,18]}. Achievements in the management of plant root pests are few at present, only see ^[19], which considers the following state feedback control model of plant root pest management

where $x(t)$ and $y(t)$ represent the density of microorganisms and pests in soil at time $t$, respectively. $r > 0$ is the growth rate, $\omega > 0$ is the growth coefficient of microbial population density under an unsaturated state; $\alpha$ and $\alpha_1$ are positive numbers. $\beta > 0$ stands for the mortality of pests. $0 < a < 1$ is the rate of microorganisms killed by the pesticide; and $0 < b < 1$ is the rate of pests killed by the pesticide. $y^*$ indicates the critical value of the pest population. In this paper, the conditions for the existence and orbital asymptotic stability of the one-periodic solution of the model (1.1) are obtained. To better protect the beneficial microorganisms in the plant root soil, it is necessary to eliminate pests to the maximum extent possible while reducing soil pollution and promoting the growth of crops. Therefore, considering that the living environment of beneficial microbial populations in the soil has been destroyed to varying degrees. In general, it follows a non-linear growth rate $g(x) = a-bx^\alpha-cx^{2\alpha}$^[20], where $a >$ is the growth rate and $\alpha > 0$ is a positive number. In ^[21], cheng et al also considered that the relative growth rate of prey population $g(x)$ is nonlinear, that is, $g(x) = a-bx^m$ for $a > 0, b > 0$ and $0 < m < 1$. Inspired by ^[20,21], this paper considers that the growth rate of beneficial microorganisms in soil is nonlinear, that is, $g(x) = r(1-\frac{\sqrt{x}}{k})$, see (1.2) for the biological significance represented by its specific parameters. Therefore, encouraged by ^[19,20,21], in view of the problem of plant root pest management, this paper proposes the following plant root pest management model.

where $x(t)$ and $y(t)$ are the density of beneficial microorganisms in the soil and the density of pests in the soil, respectively; $r$ is the growth rate; $k$ represents the capacity of beneficial microorganisms in the natural environment; $m$ is the unsaturated coefficient; $w$ is the growth coefficient of microbial population density under an unsaturated state; $b$ is the predation rate of pest populations on microbial populations; $a$ represents the natural mortality of pest populations; $c$ is the number of newly born pests; $\frac{bx}{m+wx}$ represents the function of pest predation on microorganisms; $h$ indicates the critical value of the pest population; $0 < \alpha < 1$ is the rate of microorganisms killed by the pesticide; and $0 < \beta < 1$ is the rate of pests killed by the pesticide, all parameters of model (1.2) are positive numbers according to the actual meaning of parameters representing biology. However, readers want to know more about the theory and application of the existence of periodic solutions to nonlinear differential equations, here are some good references for readers ^[22,23,24] and references therein. For mathematical simplicity, we non-dimensionalize the system (1.2) with the following scaling

and then system (1.2) becomes the form

where $a_1 = \frac{m}{w} > 0$, $a_2 = \frac{2akm}{rw} > 0$, and $a_3 = \frac{2k(cb-aw)}{rw}$, and to ensure the existence of the equilibria of model (1.3), we supposed $cb-aw > 0$, then $a_3 > 0$. As long as the population behaviour in model (1.3) is understood, the population behaviour in model (1.2) is then clear. According to the actual biological significance of the population, this paper discusses the population behaviour in model (1.3) is limited to the region ${\mathbb{R}}^2_{+} = \{(x, y)|x \geq 0, y \geq 0 \}$.

This paper is organized as follows. In the next section, we give some preliminary results. In Section 3, we discuss the properties of the continuous dynamics of the system (1.3). Section 4 is devoted to the study of existence and stability of order 1 periodic solutions for system (1.3). We give a brief conclusion in Section 5.

2.   Preliminary results

In this section, we first give some definitions and lemmas for the later proofs.

Definition 2.1. ^[5,25] Considers the following state impulse differential equations

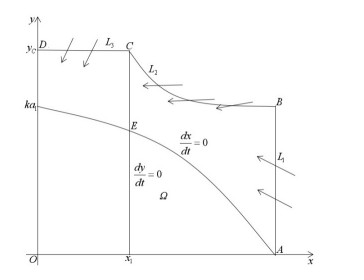
The solution mapping of system (2.1) is called as the semi-continuous dynamical system. Marked as $(\Omega, f, \varphi, M)$. We specify that the initial point $p$ of the mapping system cannot be on the impulse set. $p \in \Omega = {\mathbb{R}}^2_{+}-M\{x, y\}$, $\varphi$ is continuously mapped. $\varphi(M) = N$, here $M\{x, y\}$ and $N\{x, y\}$ are the straight line or curve on a plane. ${\mathbb{R}}^2_+ = \{(x, y)\in {\mathbb{R}}^2:x\geq 0, y\geq 0\}$, $M\{x, y\}$ is pulse sets, $N\{x, y\}$ is a phase set.

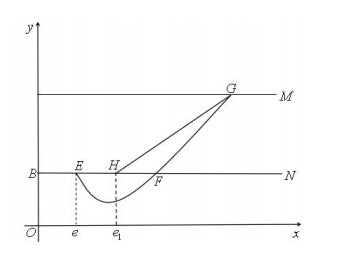
Definition 2.2. ^[5,25] If in phase set $N$, $\exists p \in N$ and $\exists T_1$, satisfy that $f(p, T_1) = q_1\in M\{x, y\}$, and the impulse map $\varphi(q_1) = \varphi(f(p, T_1)) = p\in N\{x, y\}$, then $f(p, T_1)$ is called the periodic solution of order one. Its phase is marked as $T_1$ and is shown in Figure 1.

Definition 2.3. ^[5,25] In pulse system (1.3), supposes that $M = \{(x, y)\in {\mathbb{R}}^2_+\mid y = h, x\geq0\}$ is a pulse set, and $\varphi$ is marked as the pulse function. It is specifically $\varphi:(x, h)\in M \rightarrow ((1-\alpha)x, (1-\beta)h)\in {\mathbb{R}}^2_+$, the phase set is $N = \varphi(M) = \{(x, y)\in {\mathbb{R}}^2_+\mid x\geq0, \ y = (1-\beta)h\}$, and $M$ and $N$ are both straight lines, as shown in Figure 2. Suppose that $B$ is the intersection point of the phase set $N$ and axis $y$, and $e$ is the distance from point $E$ to point $B$ in phase set $N$. A trajectory starts from point $B$ of set $E$ and intersects with the pulse set at point $G$. After pulse mapping, point $G$ has its phase point $H$ at phase set $N$, and the distance is $e_1$. $H$ is defined as the successor point of point $E$, and the successor function of point $E$ is $G(E) = e_1-e$.

Lemma 2.1. ^[5,25] Successor function $G(E)$ is continuous.

Lemma 2.2. ^[5,25] Supposes continuous dynamic $(X, \Pi)$, if there are two points $A$ and $B$ in the phase set $N$ such that $G(A) \cdot F(B) < 0$, then there must exist a point $E\in N$ between $A$ and $B$ such that $G(E) = 0.$

Lemma 2.3. ^[5,25] As a sufficient and necessary condition for $G(B) = 0$ is that the trajectory through point $B$ is a periodic solution of order 1 of system (1.3).

Lemma 2.4. ^[26] upposes the $T-$periodic solution of the system below $x = \psi(t), y = \phi(t)$ is asymptotically stable

If multiplier $\mu_2$ satisfies $|\mu_2| < 1$, where

and $P, \ Q, \ { } \frac{\partial \alpha_1}{\partial x}, \ { } \frac{\partial \alpha_1}{\partial y}, \ { } \frac{\partial \beta_1}{\partial x}, \ { } \frac{\partial \beta_1}{\partial y}, \ { } \frac{\partial \Phi}{\partial x}, \ { } \frac{\partial \Phi}{\partial y}$ have solution $q$ in point $(\psi(\tau_k), \phi(\tau_k)), \ P_+ = P(\psi(\tau^+_k), \phi(\tau^+_k)), \ Q_+ = Q(\psi(\tau^+_k), \phi(\tau^+_k))$.

3.   Analysis of continuous system dynamic behaviour

When $\alpha = \beta = 0$, system (1.3) can be transformed to the continuous dynamic system function below

Its equilibria are $O(0, 0)$ and $A(k, 0)$. when $x < k$, there is also a unique positive equilibrium point $E(x_1, y_1)$ that can be obtained, and $x_1 = \sqrt{\frac{a_2}{a_3}}, \ y_1 = (k-x_1)(x^2_1+a_1)$, thus $0 < x_1 < k$. Next, we analyze the stability of the equilibrium point. Assuming that $P(x, y)\triangleq x(k-x)(x^2+a_1)-xy, \ Q(x, y)\triangleq y(-a_2+a_3x^2)$, thus ${ } \frac{\partial P}{\partial x} = (k-2x)(x^2+a_1)+2x^2(k-x)-y, \ { } \frac{\partial P}{\partial y} = -x, \ { } \frac{\partial Q}{\partial x} = 2a_3xy, \ { } \frac{\partial Q}{\partial y} = -a_2+a_3x^2$.

Lemma 3.1. When $k^2 < 3a_1$, system (1.3) has no limit cycle in ${\mathbb{R}}^2_+ = \{(x, y)|x\geq 0, y\geq 0\}$.

Proof. Supposing Dulac function $B(x, y) = \frac{1}{xy}$, then

Thus we obtain ${ } \frac{\partial (BP)}{\partial x}+{ } \frac{\partial (BQ)}{\partial y} = -\frac{1}{y}(3x^2-2kx+a_1) < 0$. when $k^2 < 3a_1$, system (1.3) has no limit cycle in ${\mathbb{R}}^2_+ = \{(x, y)|x\geq 0, y\geq 0\}$. The proof is completed.

Lemma 3.2. System (1.3) is all bounded with the positive half trajectory in ${\mathbb{R}}^2_+ = \{(x, y)|x\geq 0, y\geq 0\}$.

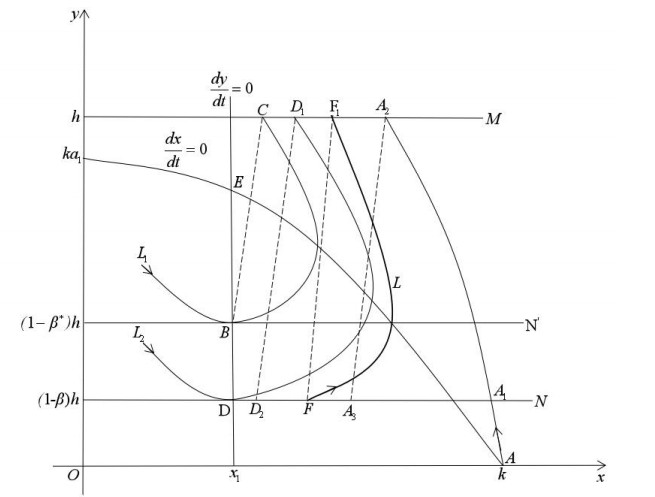
Proof. Assuming a straight line $L_1 = x-k = 0$ through point $A(k, 0)$, then for system (1.3), there is $\frac{dL_1}{dt}|_{L_1 = 0} = -ky < 0$, when trajectory meet line $L_1$, it passes through the line from right to left, as shown in Figure 3. Then, we assumed that a curve $L_2 = \ln y+x-M = 0$ intersected isoclinic line $\frac{dy}{dt} = 0$ at point $C$ and intersected straight line $L_1$ at point $B(k, y_B), \ y_B > y_1$. When $x_1\leq x\leq k$, supposing $f(x) = -a_2+a_3x^2+x(k-x)(x^2+a_1) > 0$, as long as $M$ is sufficiently large, then $\frac{dL_2}{dt}\mid_{L_2 = 0} = f(x)-xe^{M-x} < 0$, when trajectory meets curve $L_2$, it all passes through the curve from up to down. In addition, drawing a line $L_3 = y-y_C = 0$ through point $C$ of the curve, line $L_3$ intersects with the $y-$axis at point $D$. When $0 < x < x_1, \ \frac{dL_3}{dt}\mid_{L_3 = 0} = y_C(-a_2+a_3x^2) < 0$, and when trajectory meets line $L_3$, it passes the line from top to bottom. Lines $x = 0$ and $y = 0$ are both the trajectory of system (1.3). Since the boundary equilibria $O(0, 0)$ and $A(k, 0)$ are saddle points, the $x-$axis, $y-$axis, line $L_1$, line $L_2$, and line $L_3$ surround domain $\Omega$ and construct its outer boundary, as shown in Figure 3. The positive half trajectory of system (1.3) in ${\mathbb{R}}^2_+ = \{(x, y)|x\geq 0, y\geq 0\}$ finally pass into domain $\Omega$. Then we complete the proof.

Lemma 3.3. (i) Equilibria $O(0, 0)$ and $A(k, 0)$ are saddle points. (ii) When $k^2 < 3a_1$, the unique positive equilibrium point $E(x_1, y_1)$ is stable, and it is locally asymptotically stable.

Proof. (ⅰ) can be simply obtained. Therefore, only (ⅱ) needs to be verified. For $E(x_1, y_1)$, the characteristic root at equilibria is

Thus, the characteristic function $\lambda^2+m_1\lambda+m_2 = 0$, where $m_1 = x_1(3x^2_1-2kx_1+a_1) = x_1g(x_1), \ g(x_1) = 3x^2_1-2kx_1+a_1, \ m_2 = 2a_3x^2_1y_1 > 0$, When $k^2 < 3a_1$, $g(x_1) = 0$ has no real root for $x_1$. If $g(x_1) > 0$, then $m_1 > 0$. It is easy to know that all eigenvalues have negative real parts. Therefore, the unique positive equilibrium point is locally asymptotically stable. The proof is ended.

The following conclusions can be drawn from Lemma 3.1–3.3.

Theorem 3.1. When $k^2 < 3a_1$, the unique positive equilibria $E(x_1, y_1)$ of system (1.3) are globally asymptotically stable on ${\mathbb{R}}^2_+$.

4.   Existence and stability of order 1 periodic solutions for system (1.3)

When $k^2 < 3a_1$, system (1.3) has its unique positive equilibria $E(x_1, y_1)$, which is also globally asymptotically stable on ${\mathbb{R}}^2_+$, considering the existence of order 1 periodic solutions of this system. In pulse system (1.3), supposing $M = \{(x, y)\in {\mathbb{R}}^2_+|y = h, \ x\geq0\}$ to be a pulse set, then $\varphi$ is a pulse function, specifically, $\varphi:(x, h)\in M\rightarrow ((1-\alpha)x, (1-\beta)h)\in {\mathbb{R}}^2_+$. $N = \varphi(M) = \{(x, y)|x\geq0, \ y = (1-\beta)h\}$ is the phase set. Based on the relationship of the phase set, pulse set and equilibria, this paper mainly discusses the existence and stability of order 1 periodic solutions in both situations, i.e., $0 < (1-\beta)h < y_1 < h$ and $0 < (1-\beta)h < h < y_1$.

4.1.   Existence and stability of order 1 periodic solutions of system (1.3) for $0 < (1-\beta)h < h < y_1$

Theorem 4.1. When $k^2 < 3a_1$ and $\forall \alpha^*, \alpha\in(0, 1)$, regardless of the changes in $\alpha^*, \alpha$, system (1.3) has a unique order 1 periodic solution.

Proof. To verify Theorem 4.1, 3 conditions need to be considered regarding the different values of $\alpha^*, \alpha$.

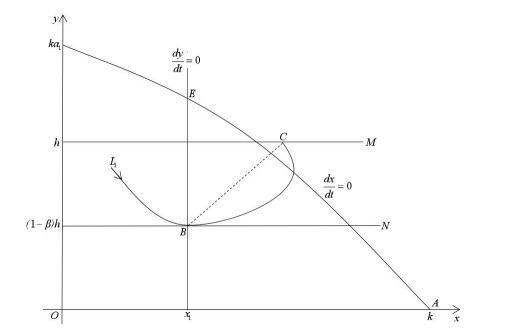
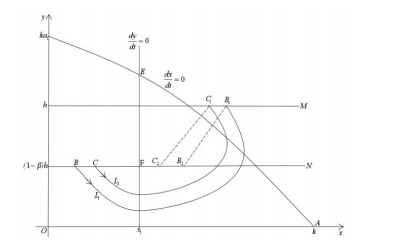
Case Ⅰ: When $0 < \alpha = \alpha^* < 1$, supposing phase set $N$ has intersection point $B(x_1, (1-\beta)h)$ with isoclinic line $\frac{dy}{dt} = 0$. Therefore, there must be a trajectory $L_1$ tangent with phase set at point $B$, and trajectory $L_1$ also intersects with pulse set $M$ at a point, marked as $C(x_C, h)$. Pulse function $\varphi(x, \alpha) = (1-\alpha)x$ is a monotonic function, monotonically increased by $x$ and monotonically decreased by $\alpha$. According to the direction of trajectory, when $x_C > x_1$, there must be $\alpha^*\in(0, 1)$, making $\varphi(x_C, \alpha^*) = (1-\alpha^*)x_C = x_B$. In other words, the phase point of $C$ after impulse is exactly point $B$. Therefore, the subsequent function of $B$ becomes $G(B) = 0$. Based on Lemma 2.3, system (1.3) has an order 1 periodic solution when $0 < \alpha = \alpha^* < 1$, as shown below in Figure 4.

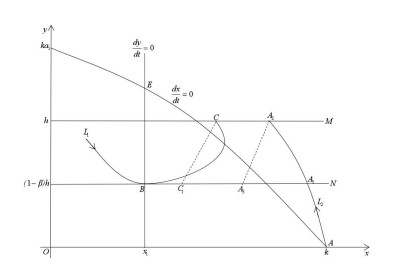
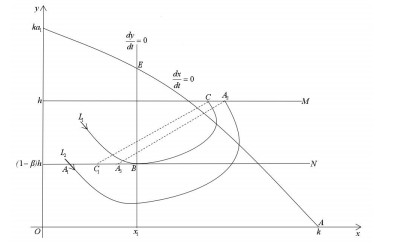
Case Ⅱ: When $0 < \alpha < \alpha^* < 1$, supposing phase set $N$ intersects with isoclinic line $\frac{dy}{dt} = 0$ at point $B(x_1, (1-\beta)h)$, then there must be a trajectory $L_1$ tangent with phase set at point $B$, and trajectory $L_1$ also intersects with pulse set $M$ at a point, marked as $C(x_C, h)$. Pulse function $\varphi(x, \alpha) = (1-\alpha)x$ is a monotonic function, monotonically increased by $x$ and monotonically decreased by $\alpha$. $\varphi(x_C, \alpha^*) = (1-\alpha^*)x_C = x_B, \ \varphi(x_C, \alpha) = (1-\alpha)x_C = x_{C_1}$. Thus, $x_{C_1} > x_B$, and the subsequent function of $B$ is $G(B) = x_{C_1}-x_B > 0$. Because point $A$ is the saddle point, there is necessarily but only one separatrix $L_2$ across point $A_1$ in the phase set. After impulse action occurs, the phase point of phase set $N$ is $A_3$. By analysing the direction of trajectory, if $(1-\alpha)x_{A_2} < x_{A_2} < x_{A_1}$, then $(1-\alpha)x_{A_2} = x_{A_3} < x_{A_1}$, and the subsequent function of $A_1$ goes to $G(A_1) = x_{A_3}-x_{A_1} < 0$. According to Lemma 2.2, there must be a point between $B$ and $A_1$ in phase set $N$, marked as point $F$, and its subsequent function is $G(F) = 0$. Based on Lemma 2.3, when $0 < \alpha < \alpha^* < 1$, system (1.3) has an order 1 periodic solution, as shown below in Figure 5.

Case Ⅲ: When $0 < \alpha^* < \alpha < 1$, supposing phase set $N$ intersects with isoclinic line $\frac{dy}{dt} = 0$ at point $B(x_1, (1-\beta)h)$, then there must be a trajectory $L_1$ tangent with phase set at point $B$, and trajectory $L_1$ also intersects with pulse set $M$ at a point, marked as $C(x_C, h)$. Pulse function $\varphi(x, \alpha) = (1-\alpha)x$ is a monotonic function, monotonically increased by $x$ and monotonically decreased by $\alpha$. $\varphi(x_C, \alpha^*) = (1-\alpha^*)x_C = x_B, \ \varphi(x_C, \alpha) = (1-\alpha)x_C = x_{C_1}$. Thus, $x_{C_1} < x_B$, and the subsequent function of $B$ is $G(B) = x_{C_1}-x_B < 0$. Drawing a line $L_2$ across phase set $N$ and pulse set $M$ at points $A_1$ and $A_2$, respectively, after impulse action occurs, the phase point of phase set $N$ is $A_3$. According to the direction of the trajectory and disjunction of the trajectory, $x_c < x_{A_2}$. In addition, by $\varphi(x, \alpha) = (1-\alpha)x$, gained $(1-\alpha)x_C = x_{C_1} < (1-\alpha)x_{A_2} = x_{A_3}$. Hence, point $A_3$ is on the right side of $C_1$, and the subsequent function is $G(A_1) = x_{A_3}-x_{A_1} > 0$. According to Lemma 2.2, there must be a point between $B$ and $A_1$ in phase set $N$, marked as point $F$, and its subsequent function is $G(F) = 0$. Based on Lemma 2.3, when $0 < \alpha^* < \alpha < 1$, system (1.3) has on order 1 periodic solution, as shown below in Figure 6.

The uniqueness of order 1 periodic solutions of system (1.3) is discussed as follows.

Assuming two points $B$ and $C$ in phased set $N$, suppose that $x_B < x_C < x_F$. Thus, there must be a trajectory $L_1$ across to point $B$, intersecting the point $B_1$ at the pulse set. After impulse action, the phase point in the phase set is $B_2$, which is also the subsequent point of $B$. Furthermore, there must be another trajectory $L_2$ across point $C$ at the phase set, intersecting $C_1$ at the pulse set. After impulse action, the phase point in the phase set is $C_2$, which is also the subsequent point of $C$. Due to the direction and disjointedness of the trajectory, there must be $x_{C_1} < x_{B_1}$, and because function $\varphi(x, \alpha) = (1-\alpha)x$ is monotone, $\varphi(x_{C_1}, \alpha) = (1-\alpha)x_{C_1} = x_{C_2}, \ \varphi(x_{B_1}, \alpha) = (1-\alpha)x_{B_1} = x_{B_2}$, so $x_{B_2} > x_{C_2}$ for the subsequent functions $G(B)$ and $G(C)$, $G(C)-G(B) = (x_{C_2}-x_C)-(x_{B_2}-x_B) = (x_{C_2}-x_{B_2})-(x_C-x_B) < 0$, which indicates that subsequent functions are monotonically decreasing in phase set $N$. With the above analysis, understanding that there must be a point $H$ in phase set $N$ that satisfies $G(H) = 0$, the uniqueness can be verified, as shown in Figure 7. On the whole, when $k^2 < 3a_1$, $\alpha^*, \alpha\in(0, 1)$, disregarding how the parameters of $\alpha^*, \alpha$ change, system (1.3) has its unique order 1 periodic solution.

The proof is ended.

Theorem 4.2. When $k^2 < 3a_1$ and $-2 < \frac{a_3\psi^2_0(\alpha^2-2\alpha)}{-a_2+a_3\psi^2_0} < 0$, the trajectory $\Gamma$ across point $(\psi_0, h)$ for order 1 periodic solution of system (1.3) is asymptotically stable.

Proof.

thus, we can obtain

where

where $k^2 < 3a_1, \ 3\psi^2(t)-2k\psi(t)+a_1 > 0, \ \exp\bigg\{-\int_{0}^{T}\psi(t)(3\psi^2(t)-2k\psi(t)+a_1)dt\bigg\}\leq 1$. Bringing $\Delta_1$ into $\mu_2$, then, we have

When $k^2 < 3a_1$ and $-2 < \frac{a_3\psi^2_0(\alpha^2-2\alpha)}{-a_2+a_3\psi^2_0} < 0$, there is $|\mu_2| < 1$, according to Lemma 2.4, the trajectory $\Gamma$ across point $(\psi_0, h)$ for order 1 periodic solution of system (1.3) is asymptotically stable. The proof is completed.

4.2.   Existence and stability of order 1 periodic solutions of system (1.3) for $0 < (1-\beta)h < y_1 < h$

Theorem 4.3. When $k^2 < 3a_1$ and $\forall \beta^*, \beta\in(0, 1)$, , whatever the $\beta^*, \beta$ change.

$(i)$ If $0 < \beta = \beta^* < 1$, then system (1.3) has an order 1 periodic solution;

$(ii)$ If $0 < \beta < \beta^* < 1$, then the trajectory of system (1.3) is going to $E(x_1, y_1)$;

$(iii)$ If $0 < \beta^* < \beta < 1$, then system (1.3) has an order 1 periodic solution.

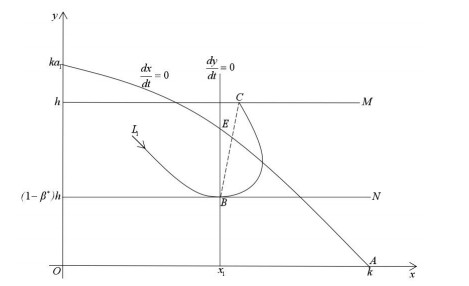
Proof. $(i)$ If $0 < \beta = \beta^* < 1$, see Figure 8. For system (1.3), drawing a trajectory $L_1$ through isoclinic line $\frac{dy}{dt} = 0$ and letting it be tangent to phase set $N$ at point $B(x_B, y_B)$. Point $B$ is the intersection of isoclinic line $\frac{dy}{dt} = 0$, trajectory $L_1$ and phase set. Trajectory $L_1$ intersects with pulse set $M$ at point $C$. Due to pulse function $y_B = \varphi(\beta, h) = (1-\beta)h, \ x_B = \varphi(x_C, \alpha) = (1-\alpha)x_C$. If $h$ is fixed, $y_B$ is a decreasing function. Thus, the location of $x_B$ depends on the location of $y_B$. Therefore, $\beta^*, \alpha^*\in(0, 1)$ satisfies $y_B = (1-\beta^*)h$ and $x_B = (1-\alpha^*)x_C$. When trajectory $L_1$ reaches point $C$ in pulse set $M$, impulse action occurs, and point $B$ is exactly the subsequent point. Therefore, if $0 < \beta = \beta^* < 1$, trajectory $L_1$ constructs an order 1 periodic solution for system (1.3) with $\widehat{BC}$ and $\widehat{CB}$, i.e., according to Lemma 2.3, there must be $G(B) = 0$.

$(ii)$ when $0 < \beta < \beta^* < 1$, straight line $y = (1-\beta)h$ is located above line $y = (1-\beta^*)h$, as shown in Figure 9. The trajectory (e.g., $L_2$) starting from the initial value is probably both intersected and non-intersected with line $y = (1-\beta)h$. If trajectory $L_2$ does not intersect with $y = (1-\beta)h$, no impulse occurs. However, because the positive $E(x_1, y_1)$ equilibria have globally asymptotic stability, the trajectory tends to further approach positive equilibria $E(x_1, y_1)$. If the trajectory intersects with line $y = (1-\beta)h$ and the interaction is point $F$, after impulse, it turns back to phase set $N$. Finally, after several impulses, the trajectory must enter the left side of other trajectories (e.g., $L_1$) because the positive equilibria $E(x_1, y_1)$ are globally asymptotic stable, and finally, the trajectory tends to positive equilibria $E(x_1, y_1)$. Therefore, when $0 < \beta < \beta^* < 1$, the trajectory of system (1.3) is going to $E(x_1, y_1)$.

$(iii)$ If $0 < \beta^* < \beta < 1$, see Figure 10. Straight line $y = (1-\beta)h$ is located below line $y = (1-\beta^*)h$, and it indicates that if $\beta = \beta^*$, an order 1 periodic solution for system (1.3) exists. Drawing a trajectory $L_2$ under $L_1$ across the intersection point $D$ of phase set $N$ and isoclinic line $\frac{dy}{dt} = 0$, it intersects with pulse set $M$ at point $D_1$, based on direction and disjointedness of the trajectory, point $D_1$ must be at the right side of point $C$. After impulse action, it reaches to point $D_2$ at phase set. Here $D_2$ is the subsequent point of $D$. Considering the pulse function $\varphi(x, \alpha) = (1-\alpha)x$ and the direction of trajectory, point $D_2$ must be at the right side of $D$. Therefore, the subsequent function of $D$ is $G(D) = x_{D_2}-x_D > 0$. Drawing a trajectory $L_3$, intersected phase set $N$ at point $A_1$ and intersected pulse set $M$ at point $A_2$, after impulse action, the trajectory $L_3$ reaches the point $A_3$ at phase set $N$, and $A_3$ is the subsequent point of $A_1$. According to the direction and trend of trajectory, point $A_3$ must be on the left side of $A_1$. Therefore $x_{A_3} < x_{A_1}$, and the subsequent function $G(A_1) = x_{A_3}-x_{A_1} < 0$. According to Lemma 2.2, there must be a point $F$ between point $D$ and $A_1$, which makes subsequent function $G(F) = 0$. In addition, by Lemma 2.3, when $0 < \beta^* < \beta < 1$, an order 1 periodic solution for system (1.3) exists. The proof is thereby complete.

Theorem 4.4. When $k^2 < 3a_1$ and $0 < \beta^*\leq \beta < 1$, an order 1 periodic solution for system (1.3) exists, the order 1 periodic solution is unique and its trajectory is asymptotically stable.

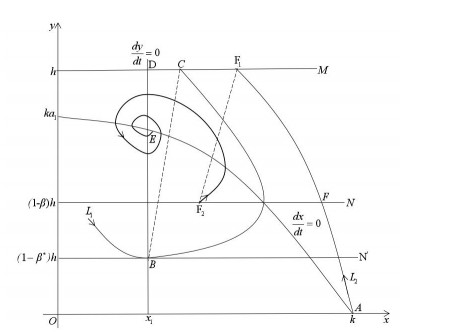
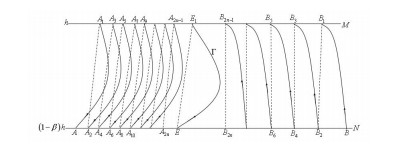
Proof. First, uniqueness is verified as follows, as shown in Figure 11. Furthermore, based on the analysis above, the trajectory passes through point $A$ in the phase set and intersects with pulse set $M$ at $A_1$. After impulse mapping of $A_1$, it is mapped to the phase set at point $A_2$. Clearly, the subsequent point of $A$ is $A_2$. In addition, the trajectory, which starts from $A_2$, passes through point $A_3$ at the pulse set. After the same process, it is mapped to the phase set at $A_4$. Therefore, $A_4$ is the subsequent point of $A_2$. Reasoning this with the same procedures, two sequences can be obtained as follows

Likewise, the other two can be obtained if assuming the trajectory starts from point $B$

The sequences $\{A_{2n-1}\}$ and $\{A_{2n}\}$ monotonically increase; in contrast, $\{B_{2n-1}\}$ and $\{B_{2n}\}$ monotonically decrease. According to Figure 11, $\overline{A_1B_1}$ maps to $\overline{AB}$. Hence, $(x_{A_{2n-1}}, x_{B_{2n-1}})\subset (x_{A_{2n}}, x_{B_{2n}})$. Thus, $\mathop {\lim }\limits_{n \to \infty }d(x_{A_{2n}}, x_{B_{2n}}) = 0$, and $\mathop {\lim }\limits_{n \to \infty }x_{A_{2n}} = x_E = \mathop {\lim }\limits_{n \to \infty }x_{B_{2n}}$, where system (1.3) has an order 1 periodic solution.

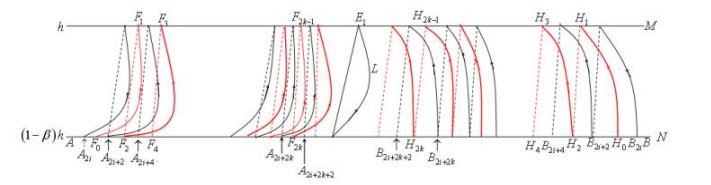
secondly, we verify the trajectory stability of the order 1 periodic solution. Drawing two random points $F_0, H_0$ infinite near $E$. These two points satisfy $x_A < x_{F_0} < x_E < x_{H_0} < x_B$, as shown in Figure 12. There is a positive integer $i$, allowing $x_{A_{2i}} < x_{F_0} < x_{A_{2i+2}} < < x_E < x_{B_{2i+2}} < x_{H_0} < x_{B_{2i}}$.

The trajectory that starts from $F_0$ intersects point $F_1$ of pulse set $M$. After impulse, the phase point turns to $F_2$. Because of the disjointedness of the trajectory, point $F_2$ is located between $A_{2i+2}$ and $A_{2i+4}$. By the monotonicity of sequence $\{x_{A_{2n}}\}$, thus $x_{A_{2i+2}} < F_2 < x_{A_{2i+4}}$. Similarly, the subsequent point of $F_2$ is $F_4$, and $x_{A_{2i+4}} < F_4 < x_{A_{2i+6}}$. By applying the same processes above, a new sequence $\{F_{2k}\}$ can be obtained, i.e., $\{F_{2k}\}\subset \overline{AB}, \ k = 0, 1, 2, \cdots$, which also satisfies the requirements below.

$(I)$ $F_{2k}$ is located between $A_{2i+2k}$ and $A_{2i+2k+2}$.

$(II)$ $x_{A_{2i+2k}} < x_{F_{2k}} < x_{A_{2i+2k+2}}$.

In addition, the trajectory that starts from $H_0$ intersects point $H_1$ of pulse set $M$. After impulse, the phase point turns to $H_2$. Because of the disjointedness of the trajectory, point $H_2$ is located between $B_{2i+2}$ and $B_{2i+4}$. By the monotonicity of sequence $\{x_{A_{2n}}\}$, thus $x_{B_{2i+2}} < H_2 < x_{B_{2i+4}}$. Similarly, the subsequent point of $H_2$ is $H_4$, and $x_{B_{2i+4}} < H_4 < x_{B_{2i+6}}$. By applying the same processes above, a new sequence $\{H_{2k}\}$ can be obtained, i.e., $\{H_{2k}\}\subset \overline{AB}, \ k = 0, 1, 2, \cdots$, which also satisfies the requirements below.

$(a)$ $H_{2k}$ is located between $B_{2i+2k}$ and $B_{2i+2k+2}$.

$(b)$ $x_{B_{2i+2k}} < x_{H_{2k}} < x_{B_{2i+2k+2}}$.

So, we have $\mathop {\lim }\limits_{k \to \infty }x_{F_{2k}} = \mathop {\lim }\limits_{k \to \infty }x_{A_{2i+2k}} = \mathop {\lim }\limits_{k \to \infty }x_{H_{2k}} = \mathop {\lim }\limits_{k \to \infty }x_{B_{2i+2k}} = x_E$, due to the arbitrariness of $F_0, H_0$, when $k^2 < 3a_1$ and $0 < \beta^*\leq \beta < 1$, the trajectory of the order 1 periodic solution for system (1.3) is asymptotically stable. This completes the proof.

4.3.   Discussion

If the unique positive equilibrium is globally asymptotically stable, that means the two populations remain dynamically stable for a considerably long period and will not become extinct due to slight changes in the environment or man-made changes in the environment. The existence of an order 1 periodic solution for the two populations means that the two populations maintain periodic stability. However, in a certain period, if a sudden growth of one group occurs, it has in fact a huge impact to the growth of another, leading the growth of species deviates from the stable periodic orbit. While, according to the situation observed, we can implement the state pulse control on the increasing species at this moment, so that the growth of two species can return to the stable periodic orbit. Due to the uniqueness of the periodic orbit, an implement pulse behavior on the population is necessary. The point is to implement pulse behavior when the population deviates too far from the orbit within a fixed period, to make the population return to a stable period and maintain a dynamic balance among the populations. In addition, as certain parameter conditions are satisfied, there is a unique asymptotic stability of periodic orbit, which means that the dynamic stability between populations can be maintained for a long time, it is also beneficial to remain growth of two species steady.

5.   Conclusions

In this paper, a mathematical model of pest control based on plant roots was systematically studied. First, the existence and stability of system equilibria under an impulse-free state were analysed. Furthermore, considering that positive equilibria of the system exist, a sufficient condition for the existence of order 1 periodic solutions was obtained by controlling the impulse parameters $\alpha, \beta$. Finally, by applying theorems (e.g., geometric theory of differential equations, successive function method, interval set theorem in mathematical analysis, and squeeze criterion), this study gained that the system has a unique order 1 periodic solution $\Gamma$ when several conditions are satisfied, and the trajectory of this order 1 periodic solution $\Gamma$ is asymptotically stable. By analysing the model with the theory of semi-continuous dynamic systems, the condition of a stabilizing order 1 periodic solution can be obtained. Furthermore, in real practice, a pulse control strategy can be implemented regarding the model and number of pests, i.e., only when the number of pests exceeds the threshold value are artificial means needed to control pests. This is not only to keep pests at an appropriate amount but is also beneficial to maintain the balance of the ecochain.

Acknowledgments

The authors would like to thank the anonymous referees and the editor for very helpful suggestions and comments which led to improvements of our original paper. Research partially supported by the Guangxi Natural Science Foundation under Grant (No. 2016GXNSFAA380102), Innovation Project of Guangxi Graduate Education (No. JGY2019174), and Guangxi Young and middle-aged Teachers Basic Ability Improvement Project (No. 2022KY0428).

Conflict of interest

All the authors affirmed that they have no conflicts of interest.