The dynamics and harvesting strategies of a predator-prey system with Allee effect on prey

1.   Introduction

The driving mechanism of predator-prey systems has consistently been a focal point in ecology, biomathematics and evolutionary biology ^[1,2,3]. The Allee effect in population ecology describes a phenomenon where a population's growth rate declines when its density falls below a specific threshold. The Allee effect was first proposed by an American ecologist called Allee in the early 20th century. In nature, many species have been reported to have the Allee effect, such as insects ^[4], plants ^[5], marine invertebrates ^[6], mammals ^[7] and so on. Many theoretical studies show that the Allee effect has potential value in the study of small population dynamics ^{[8,9,10,11,12]}, so it is more practical to consider the population model with the Allee effect. The Allee effect can be expressed in different forms in predator-prey systems:

(ⅰ) Population density threshold ^[13,14]:

where $N$ is the density of the species, $b$ is the highest per capita fertility of this species and $A_{1}$ is the Allee effect constant of this species. In population density threshold, when $A_{1}$ tends to 0, that is, under the influence of the weak Allee effect, we have $f = b$. When $A_{1}$ tends to infinity, that is, under the influence of the strong Allee effect, the population tends to go extinct more easily. The more significant the $A_{1}$, the stronger the Allee effect. When the population density is below a certain threshold, the survival and reproduction ability of the population will be affected.

(ⅱ) Breeding threshold ^[15]:

where $\varepsilon$ represents the Allee effect. When the population density is below a certain threshold, the reproduction rate of the population will decrease, resulting in the decrease of the population.

(ⅲ) Pairing threshold ^{[16,17,18,19]}:

where $\mu$ represents the Allee effect. When the population density is below a certain threshold, the pairing between individuals will be affected, resulting in a decrease in reproduction rate.

The Allee effect, described in these three expressions, has been thoroughly investigated. Wang et al. ^[20] studied the behavior of a reaction-diffusion predator-prey systems, with a strong Allee effect in the prey population. The authors demonstrated that the Allee effect significantly enhances the spatiotemporal complexity of the system. Hamada et al. ^[21] explored the influence of a weak Allee effect on the stability of a discrete-time predator-prey system, using mathematical analysis and numerical simulations. Rana et al. ^[22] explored a predator-prey system with Allee effects in both populations, conducting analyses for non-spatial and spatial models, and identifying conditions for instability and bifurcations. Zu and Mimura ^[23] studied the impact of the Allee effect on Rosenzweig-MacArthur predator-prey system with Holling type Ⅱ functional response. The model is as follows:

where $N(t)$ is used to represent the density of the prey at time $t$ and $P(t)$ is the density of the predator. Moreover, $d_{i}$ are the per capita death rates of the prey and predator respectively, $\alpha$ denotes the strength of intra-competition of the prey, $s$ denotes the effective search rate, $h_{1}$ denotes the handling time of the predator, and $c_{1}$ denotes the conversion efficiency of the ingested prey into new predator. The authors found that the Allee effect of prey species increases the extinction risk of both predator and prey. Our model for this paper is based on this model.

In natural ecosystems, human interventions like harvesting can disrupt predator-prey systems. Therefore, it is crucial to consider the impact of harvesting effects when studying and managing these ecological dynamics. Dunne et al. ^[24] investigated the significant effects of food network structure in biodiversity loss, including secondary and 'cascade' extinctions. Ghosh et al. ^[25] considered an alternative harvesting function form to study MSTY and optimal tax policy. The harvesting function plays a crucial role in promoting system stability and preserving ecosystem equilibrium under specific conditions. Moreover, it enhances our ability to predict predator behavior. The most commonly used in a biological system is the proportional harvesting function ^{[26,27,28,29]}, which is expressed as $H(x, E) = qEx$, where $q$ represents the coefficient of harvesting and $E$ is the harvesting effort.

The combined effects of harvesting and the Allee effect on the dynamics of predator-prey systems have gained increasing attention in both theoretical and empirical studies ^[30,31]. Wu et al.^[32] investigated the complex dynamical problems of a diffusive predator-prey system subject to strong Allee effects and threshold harvesting. They found that introducing strong Allee effects and harvesting efforts increased the spatiotemporal complexity of the system. Yu et al.^[33] studied a Gauss predator-prey system with the Allee effect and Holling type Ⅲ functional response and also considered the impact of predator competition and artificial fishing on predator-prey systems. They found that the model has multiple positive periodic solutions. Gupta and Yadav ^[34] researched a food-web model of these species in the presence of the multiplicative Allee effect and harvesting, and then observed that this makes the model more complex in the form of multiple coexisting steady states.

Studying harvesting items in predator-prey systems is crucial. Without considering harvesting efforts, our understanding remains limited, and real ecosystem dynamics are not accurately represented. Harvesting directly impacts predator and prey populations, shedding light on the true nature of these interactions. Additionally, it aids in validating and refining ecological models, underscoring the importance of investigating harvesting items. Hence, gaining insights into the impact of harvesting strategies on predator-prey dynamics, especially in the context of Allee effects, becomes imperative. Moreover, the linear harvesting function is often easier to analyze, making them invaluable for understanding the influence of harvesting in predator-prey systems with the Allee effect. Hence, this paper primarily focuses on an in-depth examination of the proportional harvesting function and the Allee effect.

Based on the previous studies and models, we add a harvesting function to the system (1.1), and finally, the predator-prey model is as follows:

where $e_{i}(i = 1, 2)$ are the harvesting efforts and $q_{i}(i = 1, 2)$ are the catch ability coefficients of the prey and predator, respectively. Due to biological considerations, $N(0) = N_{ 0} > 0, P(0) = P_{ 0} > 0$. To reduce variables and reduce operations, we perform the following transformation:

for simplicity, we still use variabes $x$, $y$, $t$ instead of $N$, $P$, $\tau$. Then we obtain system (1.3)

where

where $A$ is the recalculation intensity of the Allee effect, $m_{1}$ is the recalculation mortality of the prey, and $m_{2}$ is the recalculation mortality of the predator. $x(0) = x_{0} > 0, y(0) = y_{0} > 0$. All parameters are positive constants.

This paper is organized as follows. In section 2, we demonstrate the uniform boundedness of the system (1.3) in $R_{+}^{2}$. In section 3, we study the existence and stability of equilibrium points of the system. In section 4, we study the Hopf bifurcation of the system (1.3). In section 5, we give a comprehensive analysis of the harvesting strategy of the system (1.3), including MSY, MSTY and the optimal economic profit of the system (1.3). Conclusions are presented in section 6.

2.   Positivity and boundedness

In this section, we demonstrate that the solutions of system (1.3) are positive and bounded using the techniques used in ^[35]. When the system satisfies positive initial conditions, it ensures the local existence and positivity of solutions, allowing both prey and predator populations to fluctuate within a defined range while remaining bounded.

Theorem 1. The solutions of the system (1.3) starting from $x_0 > 0, y_0 > 0$ are positive for all $t\geq0$ and uniformly bounded.

Proof. From system (1.3), the solutions can be written as

for all $t > 0$. Therefore, the solutions are positive.

Now we prove the boundedness of the system (1.3). Define the function

Integrating $\Psi$ with respect to $t$, we get

Then

Applying the theory of differential inequality ^[36], we know that

As $t$$\rightarrow$ $\infty$, we can see that the limit of the right-hand side is $W/(m_{2}+E_{2})$, so $\Psi(t)$ is bounded, and all solutions of the system (1.3) are bounded in the interior of $R_{+}^{2}$.

3.   Existence and stability of equilibria

3.1.   Existence of equilibria

The equilibria of the system are the intersection points of the prey isocline on which $\dot{x} = 0$ and the predator isocline on which $\dot{y} = 0$. We find that there are at most four equilibrium points in the system (1.3), which are one trivial equilibrium point ($S_{0}$), two axial equilibrium points ($S_{1}$, $S_{2}$) and one interior equilibrium point ($S^{*}$), where

Obviously, we can find that $S_{0}$ always exists. The form of $S_{i}(i = 1, 2)$ can be given from the following equation

where, if it exists, the form would be

where

We can easily prove that $x_{i} > 0$ if $\Delta > 0$; that is to say, $S_{i}(i = 1, 2)$ always exists if the following condition is satisfied

Then, we study the existence of the interior equilibrium point denoted by $S^{*}(x^{*}, y^{*})$, where

If $S^{*}$ exists, the following conditions should be satisfied

3.2.   Stability of equilibria

The Jacobian matrix for the system (1.3) takes the following form

3.2.1.   Stability of $S_{0}(0, 0)$

Theorem 2. $S_{0}$ is always locally asymptotically stable.

Proof. The Jacobian matrix about $S_{0}$ is given by

It is easy to find that, at $S_{0}$, the Jacobian matrix $J_{S_{0}}$ has two eigenvalues given by $\lambda_{1} = -m_{1}-E_{1} < 0$ and $\lambda_{2} = -m_{2}-E_{2} < 0$. We can know that $S_{0}$ is a locally asymptotically stable point, which indicates that when the density of the prey or predator lies in the attraction region of $S_{0}$, they will become extinct.

3.2.2.   Stability of $S_{i}(x_{i}, 0)(i=1, 2)$

The Jacobian matrix about $J_{S_{i}}(i = 1, 2)$ is given by

The two eigenvalues are given by

and we have proved that $\lambda_{1} > 0$ at $x_{1}$ and $\lambda_{1} < 0$ at $x_{2}$. Then, $S_{1}$ is a saddle point if $\lambda_{2} < 0$, which is

and is a unstable point if $E_{2} < \eta_{1}$.

$S_{2}$ is a saddle point if $\lambda_{2} > 0$, which is

and is a stable point if $E_{2} > \eta_{2}$. Then, we have the following theorem:

Theorem 3. (ⅰ) $S_{1}$ is a saddle point if $E_{2} > \eta_{1}$, and is an unstable point if $0 < E_{2} < \eta_{1}$.

(ⅱ) $S_{2}$ is a stable point if $0 < E_{2} < \eta_{2}$, and is a saddle point if $E_{2} > \eta_{2}$.

3.2.3.   Stability of $S^{*}(x^{*}, y^{*})$

Theorem 4. $S^{*}$ is locally asymptotically stable if $\varphi < 0$, and is unstable if $\varphi > 0$, where

Proof. The Jacobian matrix about $S^{*}$ is given by

The trace (Tr$[J_{S^{*}}]$) and the determinant ($\rm {Det}$$[J_{S^{*}}]$) of Jacobian matrix $J_{S^{*}}$ at $S^{*}$ are given by

and the characteristic equation is given by $\lambda^{2}-\mathrm{Tr}[J_{S^{*}}]\lambda+\mathrm{Det}[J_{S^{*}}] = 0$. Then, we have

Therefore, when $\mathrm{Tr}[J_{S^{*}}] < 0$, $S^{*}$ is locally asymptotically stable, or it is unstable.

Theorem 5. Assume that $S^{*}$ of the system (1.3) is locally asymptotically stable in $R_{+}^{2}$. Then, it is globally asymptotically stable if $E_{1} > \mathrm{max}\bigg\{{\frac{h(1-A)-1}{h}-m_{1}, \frac{1-A}{Ah+1}-m_{1}}\bigg\}$.

Proof. Now we prove that there is no periodic orbit in $R_{+}^{2}$. Take a Dulac function

and

then we have

which is negative in the first quadrant if the following condition holds:

3.3.   Numerical simulations

3.3.1.   Existence and stability of equilibria

In this section, we perform numerical simulations to make analytical studies more complete. We take the parameters of the system (1.3) as

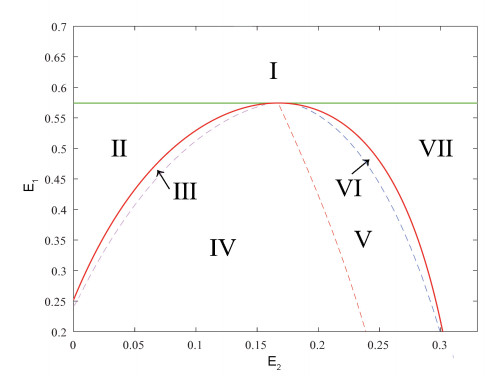
Based on analysis of the existence and stability of equilibrium points of the system (1.3), we give the partition diagram of the existence and stability of equilibria (see Figure 1).

We get that five lines $(l_{i}, i = 1, 2, 3, 4, 5)$ divide the positive quadrant of the $E_{1}E_{2}$-plane into seven regions, named Ⅰ-Ⅶ. The boundary between Ⅱ and Ⅲ, Ⅵ and Ⅶ is the line $l_{1}$, the boundary between Ⅲ and Ⅳ is the line $l_{2}$, the boundary between Ⅳ and Ⅴ is the line $l_{3}$, the boundary between Ⅴ and Ⅵ is the line $l_{4}$ and the boundary between Ⅰ and other regions is the line $l_{5}$, where

The existence and stability of equilibrium points are shown in Table 1.

Then, we can give examples of each region (see Table 2). The corresponding solutions of the system in region Ⅰ and region Ⅵ are presented in Figures 2 and 3.

Through the analysis and simulations of equilibrium points in region Ⅵ, we have identified two stable equilibrium points. The system's stability depends on the initial population densities. Under the combined influence of the Allee and harvesting effects, when the initial population densities of both species are high, the predator population faces extinction. Conversely, when the initial densities are low, coexistence of the predator and prey populations is possible.

In terms of biology, coexistence is observed with harvesting efforts in regions Ⅴ and Ⅵ, but both species go extinct when efforts are in region Ⅰ. This highlights the importance of controlling harvesting intensity to maintain the coexistence of both prey and predator populations.

3.3.2.   The impact of the harvesting

In the following, we study the effect of the harvesting effect on the predator-prey systems. Under the same parameter values given in (3.11) and the same initial conditions as Figure 3, the paths of the prey and predator species of system (1.1) are given in Figure 4.

Simulation results indicate that populations in system (1.1) tend towards $(0, 0)$, indicating the extinction of both prey and predator. Without the influence of harvesting efforts, the system remains unstable, and predator-prey coexistence is unattainable regardless of initial population densities. Comparing system (1.1) to system (1.3), we observe that low-density populations, which could not coexist, achieve coexistence under the influence of harvesting. Conversely, at high population densities, the prey, which could not survive, persists due to harvesting efforts, while the predator goes extinct.

Limit cycles represent periodic fluctuations in population numbers over time within a system. In real-world ecological systems, these periodic fluctuations play a critical role in establishing a dynamical equilibrium between prey and predator, preventing the unchecked growth or extinction of populations. We can numerically simulate the limit cycles of the system by choosing the following parameters

In this case, $S^{*}(0.1452, 0.6746)$ is unstable, and a limit cycle appears in the system (1.3) with periodic behavior. This is shown in Figure 5.

In order to further study the effect of the harvesting items on the system, we investigate the sensitivity of predator populations in system (1.1) and system (1.3) to parameters (Figure 6). In the process of controlling variables, the parameters are given as

We investigate dynamic changes in the predator population by altering parameters in the prey-predator dynamics. In Figure 6, the blue line illustrates equilibrium point changes as each variable increases by 20$%$, while the green line shows changes when each variable decreases by 20$%$, with the original values represented by the black line. Without harvesting, variables $A$, $c$, $m_{1}$ and $m_{2}$ exert a substantial influence on the predator population. A 20$%$ increase in $A$, $c$, $h$ and $m_{1}$ leads to a decrease in predator numbers, while an increase in $m_{2}$ results in higher predator numbers. The decline in $m_{2}$ is attributed to a significant decrease in the predator population. Under the influence of harvesting, variables $c$, $E_{1}$ and $E_{2}$ have a pronounced impact on predator numbers. An increase in $c$ negatively affects predator populations, posing a threat to their existence. The presence of harvesting efforts $(E_{1}, E_{2})$ mitigates the influence of the Allee effect. Notably, the number of predators varies with the level of harvesting effort. An increase in conversion rate $c$ can significantly disrupt ecosystem stability, potentially disturbing the ecological balance.

3.3.3.   The impact of the Allee effect

In system (1.1), it becomes evident that when the interior equilibrium point is unstable, the Allee effect on the prey species is more pronounced. Conversely, when the interior equilibrium point is stable, the Allee effect on the prey species has a weaker influence. Furthermore, as the intensity of the Allee effect increases, the region of stable coexistence between predator and prey contracts. The coexistence of prey and predator populations hinges on their initial placement within this stable region; otherwise, they risk extinction.

To further investigate the influence of the Allee effect on the system, we vary its strength using two different values of $A$, specifically $0.003$ and $0.1$. Then we conduct numerical simulations utilizing parameter (3.11), as depicted in Figure 7.

In the system (1.3), the coexistence of predator and prey is contingent upon the stability of the interior equilibrium point; otherwise, both populations may face extinction. In essence, when the Allee effect is particularly strong, prey populations tend to decrease over time, elevating the risk of extinction. However, an intriguing phenomenon arises when the initial populations of predators and prey differ significantly: the predator population gradually overtakes that of the prey, eventually resulting in a state of coexistence.

4.   Hopf bifurcation

In nature, under the influence of human interference-harvesting, the predator-prey systems tends to produce oscillatory behavior and may also have limited cycles. Due to a cyclic nature, the populations in the system may exhibit periodic fluctuations, periodic crashes, or outbreak events. The Hopf bifurcation marks the transition from a stable state to a periodic oscillation state, which is of great significance to the long-term stability of an ecosystem. By controlling the intensity of harvest, we can avoid such crashes and then maintain the stable survival of the population system. In the following, we will analyze Hopf bifurcation. Through the preceding analysis, $S^{*}$ may lose its stability through Hopf bifurcation under certain parameter restrictions. Consider $E_{2}$ as the bifurcation parameter. Then, according to the definition of Hopf birfurcation, we have Tr$[J_{S^{*}}] = 0$ and Det$[J_{S^{*}}] > 0$. Then, from

We draw that the bifurcation threshold is a positive root of $\mathrm{Tr}[J_{S^{*}}] = 0$ and the bifurcation parameter is given by $E_{2} = E_{2}^{H}$, which satisfies $\mathrm{Det}[J_{S^{*}}]\big|_{E_{2} = E_{2}^{H}} > 0$.

Assume that the parameters satisfy the conditions for the existence of equilibrium point $S^{*}$. Then $S^{*}$ changes its stablity through Hopf bifurcation threshold $E_{2}\equiv E_{2}^{H}$ such that $\mathrm{Tr}[J_{s^{*}}]\big|_{E_{2} = E_{2}^{H}} = 0$. Obviously, at $E_{2} = E_{2}^{H}$, let $\omega^{2}(E_{2}^{H})$ denote $\mathrm{Det}(E_{2}^{H})$ and $S^{*}$ have eigenvalues $\lambda_{1, 2}(E_{2}^{H}) = \pm i\omega(E_{2}^{H})$. We use the normal form theorem ^[36] for analysis. We get that

where $g_{1} = E_{2}h-c+hm_{2}$, $g_{2} = E_{2}+m_{2}+Ac-AE_{2}h-Ahm_{2}$.

Then, we compute the first Lyapunov coefficient ^[37]. Fixing the parameter $E_{2}$ at its critical value $E_{2}^{H}$, $S^{*}$ at $E_{2} = E_{2}^{H}$ has the coordinates $\bigg{(}x_{1}^{H}\big|_{E_{2} = E_{2}^{H}}, y_{1}^{H}\big|_{E_{2} = E_{2}^{H}}\bigg{)}$. Translating the origin of the coordinates at this equilibrium point by the change of variables

and then expanding in Taylor series, we have

where $\mu_{10}, \mu_{01}, \nu_{10}, \nu_{01}$ are the elements of Jacobian matrix evaluated at the equilibrium point $S^{*}$ and $E_{2} = E_{2}^{H}$. Since we have

The coefficients $\mu_{ij}$ and $\nu_{ij}$ are determined by

and

and $W(x_{h}, y_{h})$ and $T(x_{h}, y_{h})$ are power series in $(x_{h}, y_{h})$ with terms $x_{h}^{i}y_{h}^{j}$ satisfying $i+j\geq4$.

The first Lyapunov number $l_{1}$ ^[38], which is used to determine the stability of limit cycle around the Hopf bifurcation, is given by

Furthermore, the first Lyapunov number in system (1.3) is given by the following form

where

If $l_{1} < 0$, the Hopf bifurcation is supercritical, which means that $S^{H}$ would lose stability. If $l_{1} > 0$, the Hopf bifurcation is subcritical.

Next, we analyze the Hopf bifurcation curve via the MATLAB toolbox matcont. Take the following parameters

Then, we can find that the following equation (4.2) satisfies the transversal condition of Hopf bifurcation

The Hopf bifurcation threshold for $E^{*}_{2}$ is $0.050001754$. In the MATLAB Command Window, there is a bifurcation point detected: a Hopf point (labeled by H) around $S^{*}(0.238099, 0.943511)$ (Figure 8 (a)(b)). The first Lyapunov coefficient is $-0.4663762.$ In this occasion, the Hopf bifurcation is supercritical, and a stable limit cycle may bifurcate there, which means that when the population sizes reach specific values, they fluctuate around them without infinitely increasing or decreasing. This periodic regulation helps maintain relatively balanced population sizes and prevents one population from growing or declining indefinitely. Further, we give the phase portraits of the limit cycle to observe the change of limit cycle with bifurcation parameters (Figure 8 (c)).

5.   Harvesting strategy research

5.1.   Yield analysis

Yield analysis is one of the key methods to study the sustainable utilization of resources in predator-prey systems. The maximum sustainable yield (MSY) is the maximum fishery output that humans can get on the basis of protecting the ecological environment. Under the premise of ensuring the sustainable survival of all populations in the system, harvesting all populations and achieving the maximum yield is called the maximum sustainable total yield (MSTY) ^[39,40]. First, we investigate if, for system (1.3), MSTY exists. The yield function at $S^{*}$ is

If MSTY exists, the optimal harvesting efforts $E_{1}$ and $E_{2}$ are the solution of $\partial Y/\partial E_{1} = 0$ and $\partial Y/\partial E_{2} = 0$ and the Hessian matrix is negative definite. The Hessian matrix of $Y$ is

We know that the $H$ matrix is negative definite if, and only if, the odd-order orderings of $H$ are all less than 0 and the even-order orderings of $H$ are all greater than 0. Because $Y$ is linear with respect to $E_{1}$, and $\triangle_{1} = \partial^{2}Y/\partial E_{1}^{2} = 0$, the sufficient condition for $Y$ to maximize $(E_{1}, E_{2})$ is not satisfied.

In the following, we will discuss whether there is MSTY of the system when the harvesting effort on the prey and the predator is the same. The yield function of the equilibrium state is

There are two possible cases for MSTY, which we illustrate with examples:

(ⅰ) MSTY exists when both species can continue to survive. Take the parameter values A = 0.001, $m_{1} = 0.15$, $m_{2} = 0.25$, h = 4.5, c = 13. The simulations of changes of yield and equilibrium values with varying effort is shown in Figure 9. It can be seen that when the yield function reaches its maximum value, the prey and predator of the system can coexist, and at this point, $S^{*} = (0.1531, 0.3504)$, $(E^{*}, G^{*}) = (0.5123, 0.2527)$. Further, $\mathrm{Tr}[J_{S^{*}}] = -0.0185 < 0$, which means the interior equilibrium is stable. Therefore, the system can produce MSTY. From the simulation, we find that the number of prey and predator is monotonous with the harvesting effort.

(ⅱ) There is no MSTY. Take the parameter values A = 0.005, $m_{1} = 0.125$, $m_{2} = 0.4$, h = 5, c = 7. From Figure 9, we get that when yield reaches its maximum, predator species go to extinction. This is the harvesting of a single species. When the human harvesting of predators gradually increased, the number of predators gradually decreased, and eventually led to the extinction of the predator population.

Next, we examine the influence of each parameter change on the system yield $Y(E_{1}, E_{2})$. Model simulations before parameter manipulations are shown in the black line for comparison. When a particular parameter increases by 20$%$, the yield changes are marked with orange lines, and vice versa with pink lines. In the process of controlling variables, the parameters are given as

By changing the parameters in the yield function, the following radar map of the yield change is obtained. (see Figure 10)

From the simulations, we can observe that when each variable is increased by 20$%$, the yield will drop to varying degrees, indicating that excessive population harvesting will reduce the population number and economic benefits. Meanwhile, when it is decreased by 20$%$, the yield will have a different performance. For example, when $E_{1}$ decreases by 20$%$, the yield increases. Therefore, making sustainable yield larger is to achieve the maximum economic benefits to ensure sustainable development rather than blindly improving benefits through a large amount of fishing.

Next, we examine whether the system exhibits MSY using the methods described in the paper ^[41]. First, we consider harvesting only the prey, and system (1.3) becomes

The system has the coexisting equilibrium point $S_{E_{1}}(x_{E_{1}}, y_{E_{1}})$, where

The yield at $S_{E_{1}}$ is $Y_{E_{1}} = m_{2}E_{1}/(c-hm_{2})$. Clearly, as the harvesting effort intensifies, the equilibrium prey biomass remains constant, while the predator biomass declines. In this scenario, the yield increases with effort and exhibits no maximum point. Consequently, when the effort surpasses a critical threshold, the predator species faces extinction. Therefore, pursuing prey species harvesting at the maximum level is not a sustainable fishing strategy, implying that MSY cannot be attained.

Then, we consider harvesting only the predator, and system (1.3) becomes

At this time, the coexisting equilibrium point is $S_{E_{2}}(x_{E_{2}}, y_{E_{2}})$, where

and the yield from the predator species is

We use numerical simulations to find MSY. Take the parameter values A = 0.003, $m_{1} = 0.25$, $m_{2} = 0.55$, h = 3, c = 7.7. The coexisting equilibrium of the system becomes (0.6538, 0.2735). The simulations of changes of yield and equilibrium values with varying effort are shown in Figure 11(a). Therefore, MSY exists when the predator species is harvested. It can be verified that, in this scenario, the coexistence equilibrium point of the system is stable, allowing both species to persist continuously (see Figure 11(b)).

5.2.   Optimal harvesting problem

We will discuss the optimal harvesting strategy of the system (1.3). $E_{1}$ and $E_{2}$ are selected as control variables, and then the control system is as follows:

where $E_{i}(t)\; (i = 1, 2)$ are the harvesting efforts of the prey and predator, respectively, which satisfy

where $\alpha_{i}, \beta_{i}\; (i = 1, 2)$ are positive constants. The objective function is given by

where $\delta$ is the continuous annual discount rate. $p_{1}$ and $p_{2}$ represent the selling prices of the two populations, respectively. $c_{1}$ and $c_{2}$ represent the fishing costs of the two populations, respectively.

On the premise of ensuring the sustainable development of the system population, the control $E_{i}\; (i = 1, 2)$ is in $U$, so that the solution of the system through the initial value $(x_{0}, y_{0})$ makes the performance index $J$ reach the maximum value, that is, the optimal control $(E_{1}^{\mathrm{opt}}, E_{2}^{\mathrm{opt}})$ satisfies

We use the maximum principle to get the optimal solution, and the Hamiltonian function $H$ is

where $\lambda_{i}(t)$ (i = 1, 2) are adjoint variables, related to $x$ and $y$ respectively, which can be determined by the following conditions

and satisfy the transversal conditions

Then, we can calculate that

Meanwhile, we have

with control $E_{i}^{b}(t)\; (i = 1, 2)$ satisfying

The control that depends on the switch function $\delta_{i}(t)\; (i = 1, 2)$ to switch between the minimum and maximum values is a Bang-Bang control ^[42]. However, when $\delta_{i}(t) = 0\; (i = 1, 2)$, the Hamiltonian function $H$ does not depend on the control variable $E_{i}(t)\; (i = 1, 2)$, so the optimal control cannot be determined, and therefore a singular case exists. If condition $\alpha_{i} < E_{i}^{s} < \beta_{i}\; (i = 1, 2)$ is satisfied, the optimal harvesting strategy is as follows

Singular control occurs at $\sigma_{i}(t) = 0(i = 1, 2)$, that is

It can be obtained from the above equation

Further, we need to consider the following equation

Then, we can get the singular solution $(x^{s}, y^{s})$ from (5.9), which is the optimal equilibrium state of the system, also denoted as $(x^{\mathrm{opt}}, y^{\mathrm{opt}})$ ^[43,44]. The singular control is

Before solving the optimal control problem of the system (5.5), let us discuss the following problem first. In order to make the system reach the optimal equilibrium state as soon as possible, we give the following two schemes for comparison.

(ⅰ) Plan 1: We adopt the method of combining Bang-Bang control and singular control, and the control scheme is shown as follows

where $T^{\mathrm{opt}}$ represents the time to reach the optimal equilibrium state.

(ⅱ) Plan 2: The system is always harvested using singular control $(E_{1}^{s}, E_{2}^{s})$.

First we select the appropriate parameters

Then we give the domain of control according to the existence and stability of the interior equilibrium point ($S^{*}$)

The optimal equilibrium state is $(x^{\rm{opt}}, y^{\rm{opt}}) = (0.52, 0.21)$, the singular control is $(E_{1}^{s}, E_{2}^{s}) = (0.0879, 0.0061)$. The optimal yield is $0.047$. We choose $t = 10$ as the time period, and find that Plan 1 only needs the maximum harvesting intensity in a short period of time, and will be transformed into the optimal harvesting intensity. Plan 2 always maintains the optimal harvesting intensity. Figure 12 shows the effect of Plans $1$ and $2$.

We can obviously find that Plan 1 takes less time to reach the optimal equilibrium state than Plan 2. Therefore, Plan 1 is the best scheme to control the equilibrium state.

The impact of human harvesting on economic benefits is profound. People aim to maximize the species harvesting through rational strategies to optimize economic gains. In predator-prey systems, preserving population equilibrium and ensuring sustainable resource utilization are of utmost importance. Overfishing or irrational harvesting practices can deplete prey populations, disrupt predator-prey dynamics and lead to ecosystem collapse. Hence, it is imperative to formulate relevant optimal control problems that can provide a scientific basis for real-world scenarios. In the following, we address the following optimal control problems, denoted as (Q1) and (Q2):

We use the method of control parametrization to solve the optimal control problem $\rm{(Q1)}$ and $\rm{(Q2)}$ with the help of the MISER $3$ toolbox of MATLAB. The results are shown in Figure 13.

For problem (Q1), we choose a final time $t_{f}$ of $20$, initial value $(x_{0}, y_{0})$ of (1.2, 1) and control constraints $U$ of (5.11). Then, we get $J_{\rm{max}} = 14.926$. In this problem, we want to find a harvesting strategy that maximizes the amount of prey harvested while minimizing the cost of harvesting to achieve maximum economic profit.

For problem (Q2), we choose a final time $t_{f}$ of $10$, initial value $(x_{0}, y_{0})$ of (1, 1) and control constraints $U$ of (5.11). Then, we get $J_{\rm{max}} = 0.25$. By solving this optimization problem, we can find the best harvesting strategy to optimize the system and maximize the economic benefit.

These two issues highlight the important role and impact of human harvesting in predator-prey systems and raise the challenge of balancing economic efficiency with sustainability.

6.   Conclusions

In this paper, with the Allee effect and harvesting effort at the center, the dynamics of the predator-prey system are researched. We verify that the solutions of system (1.3) are positive and uniformly bounded (see Theorem 1). The local stabilities of the equilibrium points of (1.3) have been investigated. The conditions for the Hopf bifurcation in system (1.3) have been discussed (see Theorem 5). We verify the results by numerical simulations.

Further, we give a simple comparison of systems with and without harvesting effort (system (1.1) and system (1.3)) to study the effects of harvesting terms. In addition, we find that the sensitivity of the predator population to different parameters is different, especially when the predator population is harvested, and it is susceptible to the influence of $c$ (see Figure 6). Both theoretical and numerical results show that, in the predator-prey systems (1.3), the harvesting effort weakens the Allee effect and makes it easier for the system to reach a coexistence state. However, the coexistence of prey and predator also depends on their initial population densities within the prey population, which are influenced by the harvesting effort. We can determine whether the system is stable or oscillating periodically by controlling the threshold of the harvesting effort and the initial value of the system (see Figures 3–5).

Through our study of the Allee effect, we have found that the strength of the Allee effect is determined by the parameter $A$. When the Allee effect is robust, populations tend towards extinction, resulting in a reduced stable range for both prey and predators. Interestingly, substantial disparities in the initial populations of predators and prey can trigger dynamical changes in the sizes of both populations over time.

When it comes to MSY and MSTY, we explore four distinct scenarios: different harvesting efforts, uniform harvesting efforts, exclusive prey harvesting and exclusive predator harvesting. In our investigations, we identify MSTY in the case of uniform harvesting efforts, which maintained system population stability. Furthermore, we determine that MSY could be achieved through predator harvesting, also resulting in a stable system population.

It is a combination of Bang-Bang control and singular control to achieve the optimal equilibrium state (see Figure 12). In addition, we establish objective optimization, and problem (Q1) finds the best harvesting strategy to maximize economic benefits while problem (Q2) finds the best harvesting strategy under the condition that the termination state is the optimal equilibrium state and the economic benefits are maximized, which has guiding significance for realistic harvesting. These results are shown in Figure 13.

In natural ecosystems, populations can be vulnerable to substantial Allee effects, which may drive species towards extinction. Human intervention through harvesting can mitigate these effects, increasing the likelihood of population coexistence. This approach plays a crucial role in maintaining stable population densities over the long term and reducing the risk of extinction. In the realm of fisheries, responsible fishing practices play a crucial role in promoting sustainable stock growth and fostering the development of the fishing industry.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 12301637); the Science and Technology Planning Projects of Wenzhou (Grant No. N20220002) and the Natural Science Foundation of Wenzhou University of Technology (Grant No. ky202213).

Conflict of interest

All authors declare no conflicts of interest in this paper.