On a SEIR-type model of COVID-19 using piecewise and stochastic differential operators undertaking management strategies

1.   Introduction

The deadly COVID-19 disease broke out at the tail end of 2019 in Wuhan, a prominent Chinese metropolis. The aforementioned disease has rapidly spread around the world. By the end of March 2020, the World Health Organization (WHO) proclaimed it a global pandemic ^[30,68,72]. Globally, more than six million deaths linked to COVID-19 have been recorded. Infected individuals in the same queue number from 600 to 700. People's health, the way of life and the situation of the economy have all been significantly disturbed. To find the best cure for the aforementioned illness, experts and researchers are working around the clock ^[69]. The COVID-19 is a persistent major health problem and concern with a global focus. Breakout poses a new type of worldwide threat, regardless of the fact that there are major gaps in our knowledge of COVID-19 epidemiology, transmission dynamics, research techniques and management. For instance, several US states and other countries around the world adopted lockdown and reopening procedures. Hence, various management strategies have been used to control the epidemic's development.

Technology has advanced epidemiology to the point where several infectious diseases are now examined for treatment, control, curing and other outcomes ^[52]. It should be mentioned that the study of many diseases also heavily incorporates mathematical biology. As a result, over the past several decades, there has been a tremendous advancement in the mathematical modeling of infectious diseases ^[58,63] and mathematical modeling has become more common in research. In order to successfully control a variety of diseases, such as those listed in citations ^[35,36], secure public health approaches are developed with the help of mathematical models. The dynamic behaviour of infections can be studied using these mathematical models, as well as spatiotemporal patterns, academics have studied COVID-19 from a variety of angles during the past three years, with the help of mathematical models. To create effective methods for managing this illness, researchers in this field are taking a range of approaches (several recent studies are included as ^[9,21,28,70]). A mathematical model was recently used to examine the effects of vaccinations in nursing homes ^[37]. Researchers ^[46] examined mathematical modeling and practical COVID-19 epidemic intervention approaches. It is worth mentioning that the area devoted to model COVID-19 using various analysis and tools to investigate the transmission dynamics of the said disease has attracted very well in the last three years. For instance, global stability and cost-effectiveness analysis of COVID-19 with impact of the environment by using data from Ghana has been studied ^[5]. In the same way, authors ^[6] have studied optimal control and comprehensive cost-effectiveness analysis for COVID-19. Proceeding with the same process, sensitivity and optimal control analysis have been performed ^[7,8] for COVID-19 mathematical models. Different numerical results have been presented there. Moreover, authors ^[61] have studied the role of asymptomatic infections in the COVID-19 epidemic via complex networks and stability analysis. Also, authors ^[31] have used stochastic concepts along with environmental white noise to investigate a COVID-19 mathematical model. Researchers ^[64] have used mathematical models for forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan. In all the mentioned studies researchers have used classical or stochastic type models for their study.

As far as we are aware, the concept of the classical derivative has been intensively investigated in the subject of epidemiology. As we know, the classical differential operators have local nature and a number of inherited, long-term and short-term memory processes. To better comprehend the aforementioned process, fractional calculus has therefore attracted a lot more interest in recent years. It has grown in popularity as a result of the dynamic properties that have shown a variety of uses in practical contexts, including biological and physical processes ^[64]. Like normal calculus, fractional calculus has a lengthy history ^[47]. Several authors have explored the topic from various perspectives ^[48,49,62] and it has been found that it has numerous applications in science and technology ^[50,55]. The fractional order derivative has a higher degree of freedom ^[24] due to its non-locality. Therefore, in the mathematical modeling of infectious diseases, the aforementioned derivative might be preferred to the standard order derivative. In the past, a number of authors have produced insightful work, such as the existence theory of solutions to fractional differential equations ^[4] and qualitative findings ^[51,59], respectively. In order to investigate fractional order differential and integral equations (FODIEs) for approximate or analytical results, a variety of tools and methods have been developed (such as the fractional visco-elasticity model in ^[2], the fractional calculus in mechanical system modeling ^[1] and the fractional model for creep/recovery testing of asphalt mixtures ^[22].

It is authenticating that the area devoted to fractional order epidemiological models has been extensively considered in the last two decades. Researchers have investigated numerous diseases including dengue infection, malaria disease, TB, HBV and HCV, AIDS, cancer and so on. Researchers have extended classical susceptible, infected and recovered (SIR), susceptible, exposed, infected and recovered (SEIR), susceptible, exposed, infected, asymptomatic and recovered (SEIAR) type models to fractional orders ^[23]. For recent work in fractional orders models of infectious diseases, we refer to ^[3,25]. In addition, problems devoted to describe some physical phenomenons have also been well investigated using the concept of fractional order derivatives ^[57,60].

The majority of real-world issues are unpredictable to some extent, which traditional mathematical models are unable to account for. The idea of stochastic mathematical differential equations has been put forth and used extensively in recent decades, with remarkable outcomes. Other issues, however, demonstrate non-locality tendencies instead of randomness, including long-range dependence, fractal processes, power law processes and crossover behaviors, suggesting that physical occurrences exhibit a variety of behaviors. A class of fractional derivatives was proposed to overcome these problems. However, these operators still do a poor job of describing crossover behavior. The idea of short memory with a real or complex order derivative was developed to characterize the aforementioned behavior for the first time. The piecewise idea has been proved to be more powerful than the stated, despite the fact that fractional derivatives have extended memory capability ^[66]. Various concepts including fractal-fractional derivative, fractional order derivative with singular and non-singular kernels and various additional derivative operator have been defined recently to look at the crossover qualities and important work on nonlocal operators and their applications ^[13,29,40] refers to fractional dynamics of cellulose degradation, ^[10] refers to existence and uniqueness with applications to epidemiology and ^[12] refers to local and nonlocal operators. The crossover dynamical behavior has not been addressed, despite the fact that stochastic equation considerations lead to more realistic conclusions ^[11]. This behavior is seen in a lot of real-world process models, including heat flow, fluid flow, and many complex advection problems ^[71]. In fractional calculus, the timing of crossovers cannot be determined using the exponential or Mittag-Leffler mappings because the typical fractional order derivative fails to accurately describe crossover behavior that is common in real-world problems. The phenomena such as earthquakes, pendulum motion, the current economic instability in less developed nations, etc are few examples have crossover behavior. This crossover behavior is exemplified by piecewise equations with fractional order derivatives. Through the analysis of numerous models, certain crucial elements in this regard have recently been discovered ^[16]. Along with several applications, the authors created classical and global piecewise derivatives. As shown in papers ^{[19,38,39,43,45,67]}, a number of infectious illness models have lately been studied using non-singular and power-law type operators.

With the aforementioned significance in mind, we planned to concentrate on these fundamental issues in our work by using a model motivated from ^[56] that has been specially tailored to reflect the dynamics of said disease as well as the curbs of human response to it. A usual SEIR model that allows for lengthy incubation, we first recreated the epidemic dynamics within a single community with a particular social pattern. Here, using piecewise derivative, we formulated our model by including birth rate and natural death rate in the model investigated as

where $^{PCC}_0\mathbf{D}_t^\mathrm{r}$ stands for piecewise Caputo derivative, which can be described for any function say $y$ as

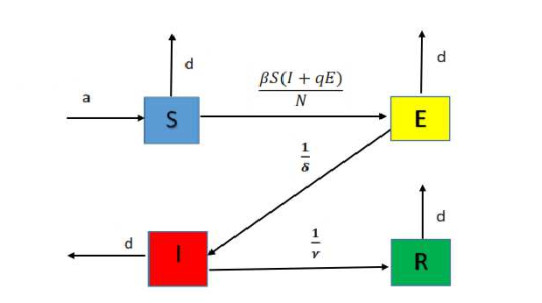
where $_0 \mathbf{D}_t^\mathrm{r}$ represents the usual Caputo fractional order derivative. The flow chart of our model is given in Figure 1 and the parameters are described in Table 1.

The birth rate is $a$, and the carrier can either be infected or exposed. The fractions $\frac{SI}{N}$ and $\frac{SE}{N}$ indicate the probability of a random contact between a susceptible person and an infected person, and the probability of a contact between a susceptible person and an exposed person respectively. The scaling factor $q$ in the model is used for the rate of interaction with an exposed person, which results in a different likelihood of transmission than contact with an infected person. Following the transition state, individuals may contract an infectious class at a rate determined by $\frac{1}{\delta}$. The same way, $\frac{1}{\gamma}$ represents the rate at which people pass away or recover from an infection.

It is notable that such dynamical concerns are given some unique perspectives by existence theory with piecewise derivatives of fractional orders. The hypothesis suggests that such physical problems can be resolved. In recent years, a variety of numerical techniques have proven to be particularly successful for classical fractional order systems ^[32]. For instance, the Range-Kutta method was used to address a number of fractional order problems ^[18], and the authors ^[44] also took use of a groundbreaking parameter estimate method, according to researchers. Problems of fractional order were solved by a novel numerical method in ^[33], and in ^[27] studied a fractional order system by using the finite difference approach. For a different set of non-integer order problems, improved finite-difference techniques were also used ^[17,42,65]. We used actual data of Japan for infected, recovered cases whose sources have listed as ^[73,74,75] and a numerical approach to elaborate the numerical analysis of the model under consideration at various fractional orders. In fact, it was stated that the memory rate was highlighted by the order of the time derivative, and the memory function was the kernel of the fractional-order derivative ^[14]. The boundedness were established for the existence of solution and feasible region was determined. The existence and uniqueness of approximation solutions were then investigated for the aforementioned model using the Banach and Schauder fixed point theorems. In addition, the results devoted to Hyers-Ulam stability were also derived. The concerned stability was investigated about the best approximate or exact solution. For the existence theory, we used research from Arzelá-Ascoli ^[41] and the Schauder fixed point theorem ^[15].

It is remarkable that in the actual world, everything is susceptible to chance, including people and animal movement. Stochastic models are used to mathematically interpret this effect. Mathematical models have been investigated by using the afore said concepts. It is worth mentioning that there are significant applications in modeling real world process by using stochastic calculus. Hence, due to this fact, researchers have recently investigated COVID-19 mathematical models by using the aforementioned area. The said differential equations have been increasingly used to model other infectious disease as well. Here we referenced to articles ^[20,34,54]. Motivated from the said importance of stochastic calculus, we attempted to simulate the proposed model (1.1) under the stochastic white noise as

where $\mathbf{b}_i$ denotes Brownian motion with $\mathbf{b}_i(0) = 0.$ Further, $\rho_i > 0,$ for $i = 1, 2, 3, 4$ and denotes the intensity of white noise. Here, it should be kept in mind that we simulated our model (1.2) using the numerical scheme developed in ^[53].

This manuscript is arranged as follows: A substantial introduction to our work is contained in Part one, and crucial results that we need for this work are given in Section two. We established the existence theory for a rough solution to the proposed model using the fixed point theory in Section three. Section four discusses the numerical approach for a rough solution to the suggested model. Section five is devoted to illustrating our conclusions. Finally, Section six offers a brief summary and explanation of the numerical outcomes.

2.   Elementary results

Recollecting some basic results as follows:

Definition 2.1. ^[16] If $\varpi$ is a differentiable function with $\mathrm{r} > 0$, then the piecewise integral is described by considering $\mathbb{I} = [0, T], \ \mathbb{I}_1 = [0, t_1], \ \mathbb{I}_2 = (t_1, T]$ as

where $^{PC}_{0}\mathbf{I}_{t}$ stands for classical integration in $\mathbb{I}_1$ and represents Riemann-Liouville integration in $\mathbb{I}_2.$

Definition 2.2. ^[16] Let $0 < \mathrm{r}\leq 1$, and if $\varpi \in C(\mathbb{I})$ is differentiable, then the classical and fractional order piecewise derivative is defined as

Lemma 2.3. ^[16] Let $\varpi\in L(\mathbb{I})\cap C(\mathbb{I})$ and $\psi\in L(\mathbb{I})$, then the solution of the given problem

is derived as

2.1.   Some fundamental results about the model (1.1)

For (1.1), we derived some axillary results. The feasible region is given in Remark 2.4.

Remark 2.4. Let ${N}$ be the total papulation at any time $t$, we have

Applying the piecewise derivative defined in (2.1) w.r.t '$t$' from model (1.1), we get

which on taking Laplace transform and using $t\rightarrow \infty$ yields

Hence, the feasible region is described as

2.2.   Equilibrium points and basic reproduction number

Putting left hand sides of model (1.1) equal to zero and solving the equations, the disease free equilibrium is obtained as follows ^[32]. From the first two equations of (1.1), one has

and on solving at disease free equilibrium state when $I^0 = 0$, we have ${S}^0 = \frac{a}{d}, \ E^{0} = 0, \ R^0 = 0.$ Hence, local equilibrium is given by

In the same line, we can also compute the endemic equilibria as

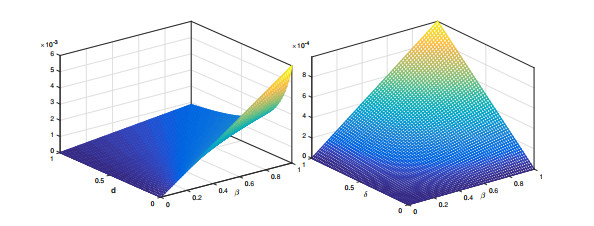
In addition, the fundamental reproductive number can be computed as $\mathscr{R}_0 = \frac{\beta q\delta}{1+\delta d}.$ Clearly, if $\mathscr{R}_0 < 1$, the local equilibrium point will be locally asymptotically stable. Further, the 3D profile of the said number is given in the following Figure 2.

3.   Existence theory

Here, we developed sufficient results for the qualitative theory of existence and uniqueness using the fixed point approach. Assume that $\mathbb{F}: \mathbb{I}\times \mathbf{R}\rightarrow \mathbf{R}$ is a nonlinear continuous function. In view of Lemma 2.3, the solution of

is given as

where

Let $\infty > t_2\geq t > t_1 > 0$ with Banach space defined as $\mathbb{H} = {C}(\mathbb{I})\times {C}(\mathbb{I})\times {C}(\mathbb{I})\times{C}(\mathbb{I})$ under the norm

These hypotheses hold for further results.

(C1) If $L_ \mathbb{F} > 0$ is real number and $\varpi, \ \bar{\varpi}\in \mathbb{H},$ then

(C2) For real values $C_ \mathbb{F} > 0$ and $M_ \mathbb{F} > 0,$ we have

Theorem 3.1. Under the hypotheses $(C1)$ and $(C2)$, if there exists a closed bounded subset $\mathscr{B} = \{\varpi\in \mathbb{H}:\ \|\varpi\|\leq {R}_{1, 2}, \ {R_{1, 2}} > 0\}$ of $\mathbb{H},$ where

then (3.1) has at least one solution. Consequently, (1.1) has at least one solution.

Proof. Considering $\mathscr{B}\subset \mathbb{H}$ is closed and bounded, such that

If $\mathbb{Q}: \mathscr{B} \rightarrow \mathscr{B}$, then the operator is defined as

For $\varpi\in \mathscr{B}$ we have

where for $t\in \mathbb{I}_2$, we put $|(t_1-\ell)^\mathrm{r}-(t_2-\ell)^\mathrm{r}|\leq T^\mathrm{r}.$ Hence, we have that $\| \mathbb{Q}(\varpi)\|\leq R_{1, 2}$ which yields that $\mathbb{Q}(\mathscr{B})\subset \mathscr{B}$. Thus, $\mathbb{Q}$ maps bounded set to bounded and $\mathbb{Q}$ is bounded operator. Since $\mathbb{F}$ is continuous function, $\mathbb{Q}$ is also continuous operator. Next, for complete continuity, consider $t_m < t_n \in \mathbb{I}_1$, then

From (3.5), we see that $t_m\rightarrow t_n$, then

Also $\mathbb{Q}$ is bounded operator. So,

Hence, $\mathbb{Q}$ is equi-continuous in this case. In addition, take $t_m < t_n \in \mathbb{I}_2$ and consider

Further from (3.6), we see that

Additionally, $\mathbb{Q}$ is bounded over $\mathbb{I}_2$ so it is uniformly continuous. Hence,

Therefore, $\mathbb{Q}$ is equi-continuous in the $\mathbb{I}_2$ interval and $\mathbb{Q}$ is equi-continuous mapping over $\mathbb{I}_1\cup \mathbb{I}_2$. Thus $\mathbb{Q}$ is a relatively compact operator. By using the Arzelá-Ascoli theorem stated in ^[41], operator $\mathbb{Q}$ is completely continuous. In view of the Schauder's fixed point theorem ^[15], (3.1) has at least one solution, meaning that (1.1) has at least one solution. □

Theorem 3.2. Inview of Hypothesis $(C1)$, and if $\max\bigg\{{T}L_ \mathbb{F}, \frac{T^\mathrm{r}}{\Gamma(\mathrm{r}+1)}L_ \mathbb{F}\bigg\} < 1$ holds, then (1.1) has a unique solution.

Proof. Let $\mathbb{Q}: \mathbb{H}\rightarrow \mathbb{H}$ be the mapping defined as

Let $\varpi, \ \bar{\varpi} \in \mathbb{H},$ then over $\mathbb{I}_1$, one has

From (3.7), we have

By the same fashion for $t\in \mathbb{I}_2$, we have

From (3.9), we have

Hence, from (3.8) and (3.10), we see that $\mathbb{Q}$ is a contraction operator and (3.1) has a unique solution. Consequently, (1.1) has a unique solution. □

Remark 3.3. Let there exist a non-decreasing function $\varsigma\in C[0, T]$, such that

$(i)$ $|\varsigma(t)|\leq \varepsilon, \ t\in \mathbb{I}.$

In addition, the solution of the problem

is given as

In view of (i), we have from (3.12) that

and

Theorem 3.4. Under the hypothesis $(C_1)$, and Remark 3.3, the solution of problem (3.1) is Hyers-Ulam stable if $\max\bigg\{L_ \mathbb{F} t_1, \frac{\varepsilon t_1 L_ \mathbb{F}}{\Gamma{(\mathrm{r+1})}}\bigg\} < 1.$

Proof. Let $\varpi$ be any solution of (3.1), for which we have a unique solution $\widehat{\varpi}$. Then for $t\in \mathbb{I}_1$ we have

which further yields that

In the same way, if $t\in \mathbb{I}_2,$ repeating the same process, one has

Hence, from (3.15) and (3.16), we have that the solution is Hyers-Ulam stable. Consequently, the solution of (1.1) is Hyers-Ulam stable. □

4.   Numerical scheme

For numerical presentation of (1.1), we constructed a numerical method for the two sub-intervals of $\mathbb{I}$. The numerical scheme for the piecewise problem is like an integer order numerical scheme as established in ^[14] by using $\varpi = (S, E, I, R)$ as

where $h = t_{n+1}-t_n,$ and

In the same way, we established for other compartments as given by

and for the last class as

5.   Numerical simulation

In this section, we present the numerical simulation in Figures 3–11 using the obtained scheme under classical and piecewise derivative concepts. We divided the whole interval into two sub-intervals and checked the first interval for integer order derivative while the second interval was tested on different fractional orders in the sense of the Caputo derivative by using the data given in Table 2.

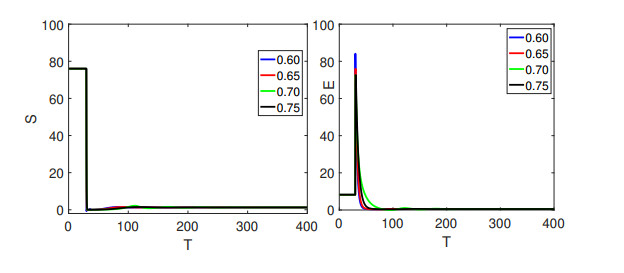
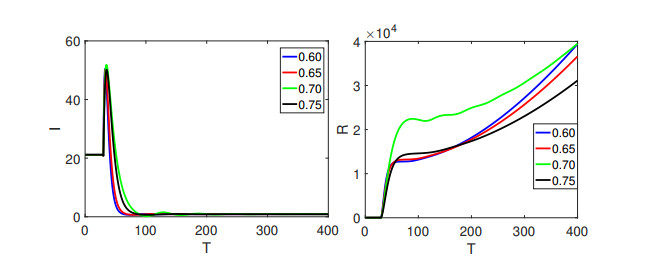
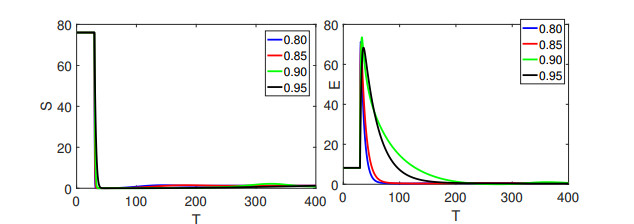
Figure 3 expressed the susceptible and exposed populations which declined, and then became stable as the remaining classes increased on both intervals as presented in Figure 4. The single curve was for the first interval and it showed integer order classical behavior from $[0, t_1] = [0, 50]$, while the four different curves showed the global order derivative behavior on $(t_1, t_2] = (500, 400].$ Here, we have considered the first set of fractional orders values in $(0, 0.75]$.

Here, we considered another set of fractional orders values in $(0.75, 0.95]$. Figure 5 contains the graphical presentations of susceptible, and exposed classes while in Figure 6 presents the dynamical behaviors of infected and recovered classes respectively corresponding to given fractional orders.

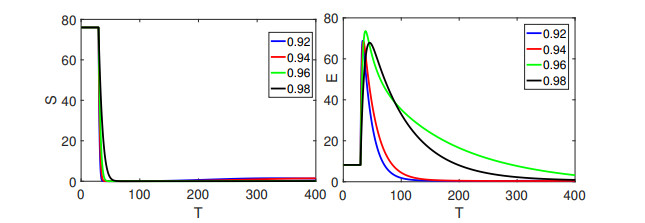
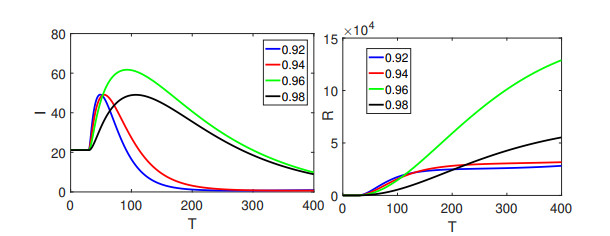
Furthermore, Figures 7 and 8 show the dynamical behaviors of different classes of the proposed model by considering another set of fractional orders values in $(0.90, 1]$. The crossover behaviors in dynamics of different classes can be observed clearly at $t_1 = 50$.

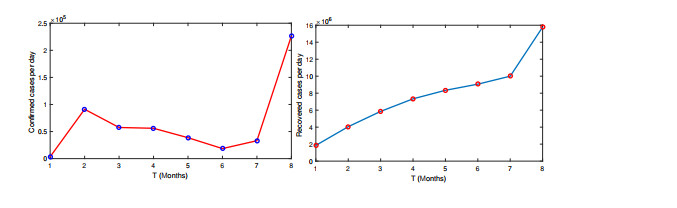
From Figures 3–8 we have observed the crossover behavior at the given points. The numerical simulation of all four compartments has been shown for three sets of different fractional orders. The bending effects are also shown on $t_1$ describing the piecewise derivative dynamics. Since the population of the infected class is decreasing, as a result the recovered class population is rising. Here, we have presented the real data fit for the recorded values of confirmed infected and recovered cases per day in Japan from January 2022 to August 2022 in Figure 9.

5.1.   Stochastic analysis

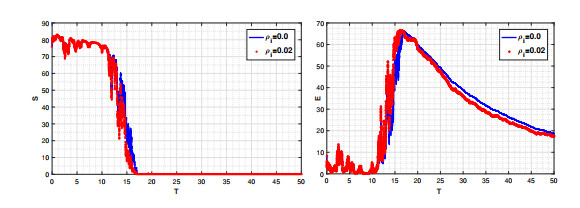
Here, we considered the same numerical values given in Table 2 to simulated the aforesaid considered model under the stochastic concepts described in (1.2). We simulate (1.2) corresponding to two different values of white noise. Figures 10 and 11 show, the dynamics of $S, E$ and $I, R$ of the proposed model using stochastic concepts. Here, we have taken the fractional order as one and simulated the results against two distinct values of white noise, $\rho_i = 0, 0.02$ for $i = 1, 2, 3, 4$. In addition to keeping in mind the importance of stochastic calculus, we have also attempted to simulate the proposed model under the mentioned concept in Figures 10 and 11, respectively. The concerned behavior due to stochastic is more realistic than the usual or traditional fractional derivatives. The crossover properties of both stochastic and fractional orders can be handled by our suggested investigation.

6.   Conclusions

In the presented research work, we have established a model under the concept of piecewise equations with the fractional order Caputo derivative. By using Schauder and Banach's fixed point theory, we have established the existence theory of solution to the proposed model and a numerical scheme has been established by using the modified Euler method. The results have been presented by using real data graphically for various fractional orders. Additionally, concerned results have been demonstrated and compared with real data in the case of reported infected individuals. Since many real-world problems are subject to abrupt changes in their state of rest or uniform motion which is also called crossover behavior traditional derivatives of either classical or fractional form cannot demonstrate this effect properly. The mentioned effect can be excellently explained by using piecewise equations with fractional order derivatives. Further, fractional order derivatives are more flexible and keep a greater degree of freedom. In the future, such a type of analysis can be extended to more complex dynamical problems involving Mittag-Leffler and fractal-fractional type derivatives. In addition, the aforesaid model will be investigated under the stochastic fractional order differential equations using non-singular differential operators.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RG23124).

Conflict of interest

The authors declare that they have no conflict of interest.