Properties of solutions for fractional-order linear system with differential equations

1.   Introduction

A fractional-order system means a system described by a fractional differential equation or fractional integral equation or by a system of such equations. A fractional differential equation is an equation which contains fractional derivative. There are many forms of fractional derivatives, such as Riemann-Liouville, Grünwald-Letnikov, Caputo and Caputo-Fabrizio fractional derivatives, one can refer to ^[1]. Fractional differential equations have been applied in various fields, and have been studied in the literature, for example, Lin and Xu studied the time-fractional diffusion equation using finite difference/spectral approximations in ^[2]; Zhuang et al. ^[3] considered the numerical methods for the variable-order fractional advection diffusion equation with a nonlinear source term; Properties of a new fractional derivative without singular kernel was studied by Losada and Nieto in ^[4]; Fardi and Khan considered the finite difference-spectral method for fractal mobile/immobiletransport model based on Caputo-Fabrizio derivative^[5]; Solution of a fractional logistic ordinary differential equation was obtained by Nieto in ^[6]. It has been found that the behavior of many physical systems can be properly described by using the fractional-order system theory. Generally speaking, the exact solutions of fractional differential equations are difficulty solved by some analytic methods. However, for some special fractional differential equations, we can still obtain their analytical solutions, such as fractional-order linear system involving Caputo-Fabrizio fractional derivative. Caputo-Fabrizio fractional derivative was proposed by Caputo and Fabrizio ^[7]. Algahtani ^[8] represented the model by Allen-Cahn with both derivatives (Atangana-Baleanu and Caputo-Fabrizio) in order to see their difference in a real world problem. Akman et al. ^[9] computed Caputo-Fabrizio derivatives of some known functions both theoretically and numerically. Baleanu et al. constructed a fractional order model of 2019 coronavirus disease transmission using Caputo-Fabrizio derivative in ^[10], and proposed a new fractional model for human liver involving Caputo-Fabrizio derivative with the exponential kernel in ^[11]. Aydogan et al. ^[12] investigated a new version of the mathematical model of Rabies disease by using the fractional Caputo-Fabrizio derivative. Additional researches on Caputo-Fabrizio fractional derivative can be found in ^{[13,14,15,16,17,18]}, among others. There are many results about autonomous system, one can refer to ^{[19,20,21,22]}. Also, the fractional-order system has been studied by many scholars ^[23,24,25].

In this paper, we consider the Caputo-Fabrizio fractional-order real linear system. The main goal of this paper is to obtain the analytical solutions of fractional-order linear system, where the fractional derivative is in the Caputo-Fabrizio sense. The system is of the form

where $0 < \alpha < 1$, $X(t) = [x(t), y(t)]'$ and $A = \left(\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array} \right).$ The fractional derivative $\mathcal{D}^{\alpha}_{t}x(t)$ is Caputo-Fabrizio fractional derivative of order $\alpha$, defined as (one can see ^[4])

In ^[4], we know that $M{(\alpha)} = \frac{2}{2-\alpha}$. Thus, we have (one can see ^[7])

For Caputo-Fabrizio fractional derivative, the corresponding fractional integral of a function $x(t)$ is

where $x_{0} = x(0)$ is the initial condition. By (1.4), if $x_{0}\neq0$ and $x(t) = x_{0}e^{-\frac{\alpha}{1-\alpha}t}$, then we can obtain that $\mathcal{I}^{\alpha}_{t}x(t) = 0$. Hence the kernel of the operator $\mathcal{I}^{\alpha}_{t}$ is the one-dimensional subspace generated by $e^{-\frac{\alpha}{1-\alpha}t}$. This is quite different to the case of the usual fractional where $I^{\alpha}_{t}x(t) = 0$ implies that $x(t) = 0$. Thus, we have

where $c$ is an arbitrary constant. The behavior of classical fractional derivative (Rieman-Liouville or Caputo) is similar to the classical integer order derivative in the sense that it satisfies that the derivative of the integral is the same function. However, for the new Caputo-Fabrizio derivative, we have

Let $x(t)$ be the solution of (1.5), by (1.5) and (1.6), then $x(t)$ is the solution of (1.6) with a kernel $e^{-\frac{\alpha}{1-\alpha}t}$.

This paper is organized as follows. In Section 2, we solove the Caputo-Fabrizio fractional-order real linear system and obtain the analytical solutions which coincides with the solutions of classical linear system when $\alpha\rightarrow1^{-}$. In Section 3, we plot the solutions of system (1.1) under given conditions at different values of $\alpha$.

2.   Solutions of fractional-order linear system

In this section, we consider fractional-order real linear system (1.1) under the assumption that $det(A)\neq0$. According to the theoretical knowledge of linear algebra, if $A$ is a nonsingular matrix, then there exists a nonsingular matrix $T$ such that $B = T^{-1}AT$ and $X(t) = T\widetilde{X}(t)$, where $B$ is a Jordan normal form and $\widetilde{X}(t) = [u(t), v(t)]'$. The corresponding characteristic polynomial of $A$ is

which has zeros $\lambda = \frac{1}{2}(p-\sqrt{p^{2}-4q})$ and $\mu = \frac{1}{2}(p+\sqrt{p^{2}-4q})$. Thus, the system (1.1) will become

where $B$ is one of the following normal forms:

Here $\lambda, \mu, \eta$ and $\gamma$ are real numbers with $\mu\neq0$ and $\gamma > 0$. If $\lambda = \mu\neq 0$, then it will become a special case of $\mathcal{L}(\lambda, \mu)$. The above three cases are denoted by $\mathcal{L}$ for left, $\mathcal{M}$ for middle and $\mathcal{R}$ for right, respectively. Therefore, we need to consider the case one by one.

If $A = \mathcal{L}(\lambda, \mu)$, then system (1.1) will become as follows

Observe that for $\alpha = 1$, system (2.3) is recovered to the classical linear system as follows

which has the solutions $x(t) = c_{1}e^{\lambda t}$ and $y(t) = c_{2}e^{\mu t}$.

The analytical solutions of system (2.3) can be obtained by the following theorem.

Theorem 2.1. Let $x_{0}$ and $y_{0}$ be the initial conditions of system (2.3). Then the solutions of system (2.3) are $x(t) = c_{1}e^{\frac{\lambda\alpha}{1-\lambda+\lambda\alpha}t}$ and $y(t) = c_{2}e^{\frac{\mu\alpha}{1-\mu+\mu\alpha}t}$, where $c_{1} = x_{0}$ and $c_{2} = y_{0}$.

Proof. If $x(t)$ and $y(t)$ are the solutions of (2.3), by (1.4) and (1.5), interating we get

Taking the first derivative both sides of (2.5), we get

By (2.6), for $1-\lambda+\lambda\alpha\neq0$ and $1-\mu+\mu\alpha\neq0$, the analytical solutions of the system (2.3) with $0 < \alpha < 1$ are given by

where $c_{1} = x_{0}$ and $c_{2} = y_{0}$ are real constants. This proves the theorem.

If $A = \mathcal{M}(\lambda)$, then system (1.1) will become as follows

Observe that for $\alpha = 1$, system (2.8) is recovered to the classical linear system as follows

which has the solutions $x(t) = c_{1}e^{\lambda t}$ and $y(t) = (c_{1}t+c_{2})e^{\lambda t}$.

The analytical solutions of system (2.8) can be obtained by the following theorem.

Theorem 2.2. Let $x_{0}$ and $y_{0}$ be the initial conditions of system (2.8). Then the solutions of system (2.8) are $x(t) = c_{1}e^{\frac{\lambda\alpha}{1-\lambda+\lambda\alpha}t}$ and $y(t) = \Big(\frac{c_{1}\alpha}{(1-\lambda+\lambda\alpha)^{2}}t+c_{2}\Big)e^{\frac{\lambda\alpha}{1-\lambda+\lambda\alpha}t}$, where $c_{1} = x_{0}$ and $c_{2} = y_{0}$.

Proof. If $x(t)$ and $y(t)$ are the solutions of (2.8), by (1.4) and (1.5), interating we get

Taking the first derivative both sides of (2.10), we get

By (2.11), for $1-\lambda+\lambda\alpha\neq0$, the analytical solutions of the system (2.8) with $0 < \alpha < 1$ are given by

where $c_{1} = x_{0}$ and $c_{2} = y_{0}$ are real constants. This proves the theorem.

Similarly, if $A = \mathcal{R}(\eta, \gamma)$, then system (1.1) will become as follows

Observe that for $\alpha = 1$, system (2.13) is recovered to the classical linear system as follows

which has the solutions $x(t) = c_{1}e^{\eta t}\cos(-\gamma t+c_{2})$ and $y(t) = c_{1}e^{\eta t}\sin(-\gamma t+c_{2})$. Where $c_{1}, c_{2}$ satisfy that $x_{0} = c_{1}\cos c_{2}$ and $y_{0} = c_{1}\sin c_{2}$.

The analytical solutions of system (2.13) can be obtained by the following theorem.

Theorem 2.3. Let $x_{0}$ and $y_{0}$ be the initial conditions of system (2.13). Then the solutions of system (2.13) are $x(t) = c_{1}e^{\eta_{1}t}\cos(-\gamma_{1}t+c_{2})$ and $y(t) = c_{1}e^{\eta_{1}t}\sin(-\gamma_{1}t+c_{2})$, where $\eta_{1} = \frac{\eta\alpha-(\alpha-\alpha^{2})(\eta^{2}+\gamma^{2})}{(1-\eta+\eta\alpha)^{2}+(\gamma-\gamma\alpha)^{2}}$ and $\gamma_{1} = \frac{\gamma\alpha}{(1-\eta+\eta\alpha)^{2}+(\gamma-\gamma\alpha)^{2}}$, and $c_{1}, c_{2}$ satisfy that $x_{0} = c_{1}\cos c_{2}$ and $y_{0} = c_{1}\sin c_{2}$.

Proof. If $x(t)$ and $y(t)$ are the solutions of (2.13), by (1.4) and (1.5), interating we get

Taking the first derivative both sides of (2.15), we get

By (2.16), we get

where $\eta_{1} = \frac{\eta\alpha-(\alpha-\alpha^{2})(\eta^{2}+\gamma^{2})} {(1-\eta+\eta\alpha)^{2}+(\gamma-\gamma\alpha)^{2}}$ and $\gamma_{1} = \frac{\gamma\alpha} {(1-\eta+\eta\alpha)^{2}+(\gamma-\gamma\alpha)^{2}}$.

The system (2.17) can be solved explicitly by introducing polar coordinates $x = \rho \cos\theta$ and $y = \rho \sin\theta$, as follows. First note that

It follows that

thus, the solutions of system (2.18) may be expressed in the form

where $c_{1} = \rho(0)$ and $c_{2} = \theta(0)$.

By (2.19), the solutions of system (2.13) may be expressed in the form

This proves the theorem.

3.   Computational results and discussion

In this section, we plot the solutions of system (1.1) under given conditions at different values of $\alpha$. We consider the following three cases, that are $A = \mathcal{L}(\lambda, \mu)$, $A = \mathcal{M}(\lambda)$ and $A = \mathcal{R}(\eta, \gamma)$.

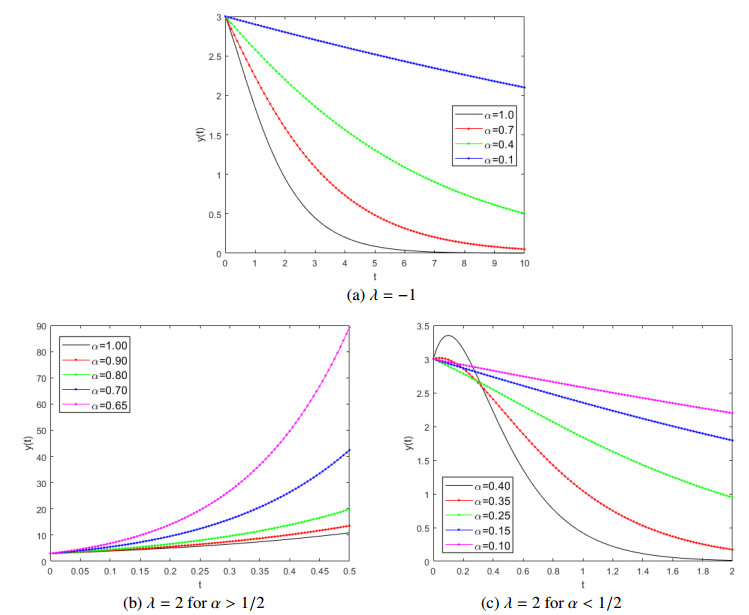
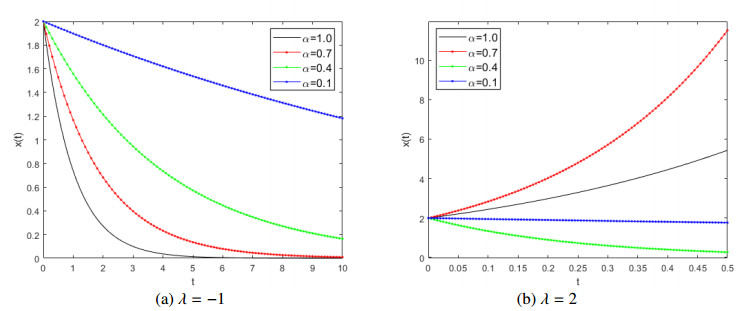
For $A = \mathcal{L}(\lambda, \mu)$. If $\lambda = -1$ or $\lambda = 2$, then the solutions $x(t)$ of system (2.3) for different $\alpha$ are shown in Figure 1 (similarly, the solutions of $y(t)$ can be obtained for given $\mu$). For $\lambda = -1$, the results are shown in Figure 1 (a), which shows that $x(t)\rightarrow 0$ as $t\rightarrow +\infty$ and the speed of $x(t)$ approaching zero gradually becomes faster with the increase of $\alpha$. For $\lambda = 2$, by Theorem 2.1, we know that $\alpha\neq1/2$, and $\alpha = 1/2$ is the demarcation line, the results are shown in Figure 1 (b). If $\alpha > 1/2$, then $x(t)$ is increasing with the evolution of time and the speed increase of $x(t)$ becomes faster with the decrease of $\alpha$. If $\alpha < 1/2$, then $x(t)$ is decreasing with the evolution of time and the speed decrease of $x(t)$ becomes faster with the increase of $\alpha$.

For $A = \mathcal{M}(\lambda)$. If $\lambda = -1$ or $\lambda = 2$, then the solutions $y(t)$ of system (2.8) for different $\alpha$ are shown in Figure 2 ($x(t)$ can be obtained as in system (2.3)). For $\lambda = -1$, the results are shown in Figure 2k (a), which shows that $x(t)\rightarrow 0$ as $t\rightarrow +\infty$ and the speed of $x(t)$ approaching zero gradually becomes faster with the increase of $\alpha$. For $\lambda = 2$, by Theorem 2.2, we know that $\alpha\neq1/2$, and $\alpha = 1/2$ is the demarcation line. If $\alpha > 1/2$, then $x(t)$ is increasing with the evolution of time and the speed increase of $x(t)$ becomes faster with the decrease of $\alpha$, the result is shown in Figure 2 (b). Figure 2 (c) shows the results for $\lambda = 2$ and $\alpha < 1/2$, on the whole, $x(t)$ is decreasing with the evolution of time and the speed decrease of $x(t)$ becomes faster with the increase of $\alpha$. However, a special phenomenon will occur in this case, that is $x(t)$ will increase firstly and then decrease when $\alpha$ reaches a critical value, in particular, this phenomenon is more obvious when $\alpha\rightarrow 0.5$.

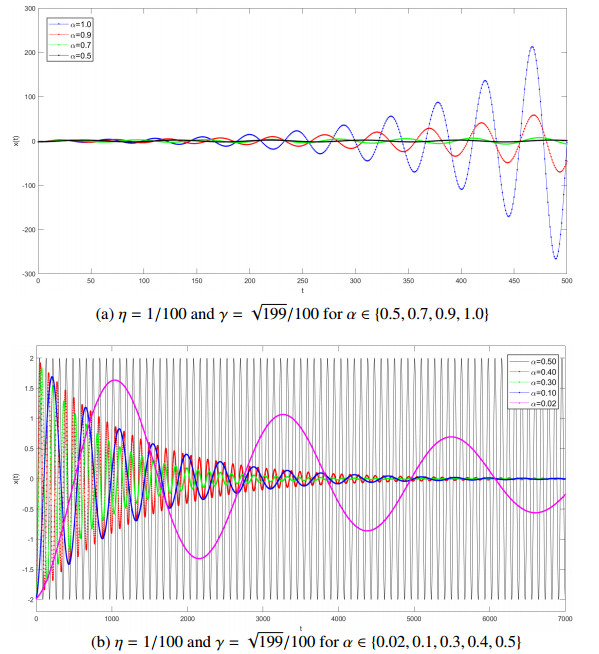
For $A = \mathcal{R}(\eta, \gamma)$. If $\eta = 1/100$, $\gamma = \sqrt{199}/100$ and $c_{1} = \rho(0) = 2$, $c_{2} = \theta(0) = 3$, then the solutions $x(t)$ of system (2.13) are shown in Figure 3 (similarly, the Figure of $y(t)$ can be obtained). By Theorem 2.3, we know that $x(t) = 2\cos(-\sqrt{199}t/199+3)$ when $\alpha = 1/2$. If $\alpha > 1/2$, then $x(t)$ behaves an oscillating phenomenon and the amplitude becomes wide with the evolution of the time (Figure 3k (a)). If $\alpha < 1/2$, then $x(t)$ behaves an oscillating phenomenon and tends to zero with the evolution of the time. In particular, the speed of $x(t)$ approaching zero will firstly increase with the decrease of $\alpha$. When $\alpha$ reaches a critical value, the speed of $x(t)$ approaching zero will slow down with the decrease of $\alpha$ (Figure 3 (b)).

4.   Conclusions

In this paper, we study the analytical solutions for fractional-order linear system involving Caputo-Fabrizio fractional derivative. This problem is a natural generalization of the classical linear system. Compared with classical linear system, the solutions of fractional-order linear system have richer behaviors and abnormal phenomena for different $\alpha$. From the examples, we can find that the results of this paper can be applied not only to fractional order linear system when $0 < \alpha < 1$, but also to classical linear systems as $\alpha = 1$, which means that the classical linear system is the limit form of fractional system. In the future, fractional-order nonlinear system can also be studied.

Acknowledgments

We are very grateful to both referees for their carefully reading the paper and most valuable comments and suggestions.

The paper is supported by the Natural Science Foundation of Xinjiang Uygur Autonomous Region of China (No. 2022D01E13), the National Natural Science Foundation of China (No. 11861068, No. 11761071), Guizhou Key Laboratory of Big Data Statistical Analysis, China (No. [2019]5103) and the Scientific research foundation for Outstanding young teachers of Xinjiang Normal University, China (No. XJNU202112).

Conflict of interest

This work does not have any conflict of interest.