1.
Introduction
The idea of statistical convergence was given by Zygmund [39] in the first edition of his monograph published in Warsaw in 1935. Later on, Fast [10] introduced the statistical convergence of number sequences in terms of the density of subsets of N (see also [32,33,36]). The concept of statistical convergence has been developed and enriched with deep and beautiful results by many authors [8,9,13,14,16,19,21,25,37].
The strongly Cesàro convergence for real numbers was introduced by Hardy-Littlewood [15] and Fekete [11] in connection with the convergence of Fourier series. For a wider perspective, the reader is referred to the most recent monographs [5,7], and also to [38] for some historical notes.
In [2], by means of a new concept of density of a subset of natural numbers that relies on modulus functions, it is defined the non-matrix concept of f-statistical convergence. It was observed that f-statistical convergence implies statistical convergence. However, a statistically convergent sequence need not be f-statistically convergent for every unbounded modulus f. Following this line, in [22] the authors proved that if f is a compatible modulus function, the above statement is provided, that is, a sequence which is statistically convergent is also f-statistically convergent.
Ruckle [31] and Maddox [24] have introduced and discussed some properties of sequence spaces defined by means of a modulus function. For a wider perspective on modulus functions, one may refer to [1,3,4,6,20,23,26,30] and many others.
Very basic finite difference formulas in numerical analysis serve to approximate the derivative of a real-valued function via a null positive sequence, such as Newton's difference quotient, which determines the slope of a secant line of the graph of the function, and the symmetric difference quotient, which determines the slope of a cord of the graph of the function. In [29], the authors defined and studied sequential secant and sequential cord derivatives of real-valued functions. Later, in [28] the author introduced the notions of Cesàro and statistical derivative obtaining some basic results.
Very recently, in the past few years, a series of works [17,18,34,35] on different versions of statistical probability convergence, such as statistical deferred Nörlund summability, deferred Cesàro statistical probability convergence, deferred weighted statistical probability convergence, and statistical probability convergence via the deferred Nörlund mean, have been appearing with interesting applications to Korovkin-type approximation theorems, enriching the literature of statistical convergence.
The purpose of this paper is to introduce, investigate, and explore the concepts of f-statistical continuity, f-statistical derivative, and f-strongly Cesàro derivative for real-valued functions.
2.
Materials and methods
This section compiles, into several subsections, all the necessary tools and techniques that we will rely on throughout the Results section.
2.1. Modulus functions
The notion of modulus function was introduced by Nakano [27]. A modulus f is a function from [0,∞) to [0,∞) that satisfies the following conditions:
1) f(x)=0 if and only if x=0,
2) f(x+y)≤f(x)+f(y) for x,y≥0,
3) f is increasing,
4) f is continuous from the right at 0.
It follows that f must be continuous everywhere on [0,∞), and f(xr)≥1rf(x) for all x∈R+ and all r∈N. Notice that a modulus f may be bounded or unbounded. For example, f(x)=xx+1 is bounded, whereas f(x)=xp, for 0<p<1, is unbounded.
A modulus function f is compatible [22] if for any ε>0 there exists ˜ε>0 and n0=n0(ε) such that f(n˜ε)f(n)<ε for all n≥n0. Examples [22] of compatible modulus functions are f(x)=x+log(x+1) and f(x)=x+xx+1. Examples of non-compatible modulus functions are f(x)=log(x+1) and f(x)=W(x), where W is the W-Lambert function restricted to R+.
2.2. f-Density of subsets of N
Let f be a modulus function. The f-density of a subset A⊆N is defined as
if the limit exists. The notion of f-density was introduced in [2]. When f is the identity, we obtain the classical version of density [12] of subsets of N. Notice that df is increasing, that is, df(A)≤df(B) whenever A⊆B {and df(A),df(B) exist}. Since df(N)=1, we have that 0≤df(A)≤1 for all A⊆N for which df(A) exists. Also, df is subadditive, that is, df(A∪B)≤df(A)+df(B) for all A,B⊆N for which df(A),df(B) exist. An example displayed in [2] shows that df is not additive even for disjoint pairs of subsets of N. Finally, if df(A)=0, then df(N∖A)=1. In [2,Example 2.1], it is shown that the converse to the previous proposition does not hold, that is, df(A)=1 does not necessarily mean df(N∖A)=0.
The following lemma, which can be found in [2], will be very useful in the upcoming Results Section.
Lemma 2.1. If H is a infinite subset of N, then there exists an unbounded modulus function f such that df(H)=1.
2.3. f-Statistical convergence
A real-valued sequence (xn)n∈N is said to be f-statistically convergent to x0∈R if for every ε>0, the set {n∈N:|xn−x0|≥ε} has natural f-density zero, in other words,
In this case we write f− st limnxn=x0. The notion of f-statistical convergence was introduced in [2]. When f is the identity, we obtain the classical definition of statistical convergence [10,39].
Remark 2.2. If (xn)n∈N is convergent to x0, then for every ε>0 there exists n0∈N with |xn−x0|<ε for all n≥n0, which assures that
if f is unbounded, meaning then that (xn)n∈N is f-statistically convergent to x0. Conversely, if (xn)n∈N is not convergent to x0, then there exists ε>0 such that H:={k∈N:|xk−x0|≥ε} is infinite. By Lemma 2.1, there exists an unbounded modulus function f with df(H)=1, meaning that (xn)n∈N is not f-statistically convergent to x0.
Remark 2.2 can be summarized into:
Remark 2.3. If (xn)n∈N is f-statistically convergent to x0 with f not necessarily unbounded, then for every ε>0 and every r∈N, there exists nr∈N such that
for all n≥nr, that is,
for all n≥nr, which implies, in view that f is increasing, that
for all n≥nr, yielding stlimnxn=x0. Conversely, suppose that (xn)n∈N is statistically convergent to x0 and take any compatible modulus functions f. Take any δ>0. Fix an arbitrary ε>0. Since f is compatible, there exists ˜ε>0 and n0=n0(ε)∈N such that f(n˜ε)f(n)<ε for all n≥n0. Since stlimnxn=x0, there exists r0=r0(ε)∈N such that if n≥r0, then |{k≤n:|xk−x0|≥δ}|≤n˜ε. Using the increasing monotonicity of f, we obtain
for all n≥max{n0,r0}. Thus, (xn)n∈N is f-statistically convergent to x0.
Remark 2.3 can be summarized into:
The previous two remarks are just standard arguments from [2].
2.4. Discrete derivative
Let λ be a real function, that is, real valued and of real variable. Let (xk)k∈N be a real-valued sequence such that xk≠0 for all n∈N and limk→∞xk=0 (such sequences will be called proper null sequences). Newton's difference quotient determines the slope of a secant line to the graph of λ:
On the other hand, making use of positive null sequences, that is, proper null sequences of positive terms, the symmetric difference quotient determines the slope of a cord of the graph of λ:
2.5. Statistical derivative
In [28], the notion of statistical derivative was defined as follows. A real function λ:R→R has a statistical derivative λ0∈R at a point x0∈R provided that the sequence (λ(x0+xk)−λ(x0)xk)k∈N is statistically convergent to λ0 whenever (xk)k∈N is a proper null sequence. In other words, for every ε>0
holds whenever limk→∞xk=0 and xk≠0 for each k∈N.
2.6. Strongly Cesàro convergence and derivative
A real-valued sequence (xn)n∈N is said to be Cesàro convergent [11,15,38] to the number x0∈R if limn→∞1nn∑k=1xk=x0, and it is said to be strongly Cesàro convergent to x0 if limn→∞1nn∑k=1|xk−x0|=0.
Recall [28,Definition 2.3] that a real function λ:R→R is said to have a (strongly) Cesàro derivative λ0∈R at a point x0∈R provided that the sequence (λ(x0+xk)−λ(x0)xk)k∈N is (strongly) Cesàro convergent to λ0 whenever (xk)k∈N is a proper null sequence. In other words,
holds whenever limk→∞xk=0 and xk≠0 for each k∈N.
3.
Results
Here we will state and prove all the original results of this manuscript. Like the previous one, this section will also be divided into several subsections.
3.1. f-Statistical continuity
In this subsection, we introduce the notion of f-statistical continuity for real-valued functions.
Definition 3.1. Let f be a modulus function. A real function λ:R→R is said to be f-statistically continuous at x0∈R provided that, whenever a real-valued sequence (xn)n∈N is f-statistically convergent to x0, then the sequence (λ(xn))n∈N is f-statistically convergent to λ(x0).
In other words, f− st limnxn=x0⇒f− st limnλ(xn)=λ(x0). Our first result shows that continuous functions are f-statistically continuous as well.
Theorem 3.2. Let f be a modulus function. If λ:R→R is continuous at a point x0∈R and (xn)n∈N⊆R satisfies f - st limnxn=x0, then f - st limnλ(xn)=λ(x0).
Proof. Let ε>0. From the continuity of λ, for every ε>0 there exists δ>0 such that
Thus, we have the following statement
In particular, we obtain that {k≤n:|λ(xk)−λ(x0)|≥ε}⊆{k≤n:|xk−x0|≥δ}. Hence, by assumption we have
This means that λ(xn) is f-statistically convergent to λ(x0).
Notice that, by relying on Remark 2.2, we can actually obtain the converse to Theorem 3.2.
Corollary 3.3. Let λ:R→R be a real function. Let x0∈R. Then λ is continuous at x0 if and only if λ is f-statistically continuous at x0 for every unbounded modulus function f.
Proof.
⇒ This implication is a direct consequence of Theorem 3.2.
⇐ Let (xn)n∈N⊆R be a sequence converging to x0. For any unbounded modulus function f, by bearing in mind Remark 2.2, we have that (xn)n∈N is f-statistically convergent to x0. By hypothesis, (λ(xn))n∈N is f-statistically convergent to λ(x0). Finally, the arbitrariness of the unbounded modulus function f together with Remark 2.2 allow to deduce that (λ(xn))n∈N is convergent to λ(x0). This shows the continuity of λ at x0.
To finalize this subsection, if we keep in mind Remark 2.3, we immediately deduce the following corollary.
Corollary 3.4. Let f be a compatible modulus function. Let λ:R→R be a real function. Let x0∈R. Then λ is statistically continuous at x0 if and only if λ is f-statistically continuous at x0.
Proof.
⇒ Let (xn)n∈N⊆R be a sequence f-statistically converging to x0. Remark 2.3 assures that (xn)n∈N is statistically convergent to x0. By hypothesis, (λ(xn))n∈N is statistically convergent to λ(x0). Finally, Remark 2.3 allows to deduce that (λ(xn))n∈N is f-statistically convergent to λ(x0). This shows the f-statistical continuity of λ at x0.
⇐ Let (xn)n∈N⊆R be a sequence statistically converging to x0. By Remark 2.3, we have that (xn)n∈N is f-statistically convergent to x0. By hypothesis, (λ(xn))n∈N is f-statistically convergent to λ(x0). Finally, in view of Remark 2.2, we deduce that (λ(xn))n∈N is statistically convergent to λ(x0). This shows the statistical continuity of λ at x0.
3.2. f-Statistical derivative
Our next step is to provide the definition of f-statistical derivative. Then we will establish some relationships between the classical derivative and the f-statistical derivative.
Definition 3.5. Let f be a modulus function. A real function λ:R→R has a f-statistical derivative λ0∈R at a point x0∈R provided that the sequence (λ(x0+xk)−λ(x0)xk)k∈N is f-statistically convergent to λ0 whenever (xk)k∈N is a proper null sequence. In other words, for every ε>0
holds whenever limk→∞xk=0 and xk≠0 for each k∈N.
Since every convergent sequence is trivially f-statistically convergent for f unbounded in view of Remark 2.2, it is obvious that if a real function has a derivative, then it has the same f-statistical derivative for every unbounded modulus function f. For the converse of this statement to hold, we need to make use of Lemma 2.1.
Theorem 3.6. If λ:R→R has a f-statistical derivative λ0∈R at a point x0∈R for every unbounded modulus function f, then it has the same derivative λ0 at x0.
Proof. Suppose on the contrary that λ0 is not the derivative of λ at x0. We can then find ε>0 and a proper null sequence (xk)k∈N in such a way that the set
is infinite. By Lemma 2.1, we can found a modulus function f with df(H)=1. Since λ0 is a f-statistical derivative of λ at the point x0, the fact that df(H)=1 contradicts Eq (3.1).
As a consequence of Remark 2.2 and the previous theorem, we immediately obtain the following corollary.
Corollary 3.7. Let λ:R→R be a real function. Let x0∈R and λ0∈R. The following conditions are equivalent:
1) λ0 is the derivative of λ at x0.
2) λ0 is the f-statistical derivative of λ at x0 for every unbounded modulus function f.
Next, the relation between the f-statistical derivative and the statistical derivative of a real function is presented. Notice that every f-statistically convergent sequence (for f bounded or unbounded) is statistically convergent. Therefore, it is clear that if a real function has a f-statistical derivative at a certain point (for f bounded or unbounded), then it has the same statistical derivative at the same point. For the converse of the previous sentence to remain true, we need to consider compatible modulus functions.
Theorem 3.8. If λ:R→R has a statistical derivative λ0∈R at a point x0∈R, then it has the same f-statistical derivative at the same point for every compatible modulus function f.
Proof. Take f any compatible modulus functions. Fix an arbitrary real-valued sequence (xk)k∈N with limk→∞xk=0 and xk≠0 for each k∈N. We have to show that (λ(x0+xk)−λ(x0)xk)k∈N is f-statistically convergent to λ0. Indeed, take any δ>0. We will prove that
So, fix an arbitrary ε>0. Since f is compatible, there exists ˜ε>0 and n0=n0(ε)∈N such that f(n˜ε)f(n)<ε for all n≥n0. By hypothesis, λ0 is a statistical derivative for λ at x0, thus, there exists r0=r0(ε)∈N such that if n≥r0, then
Using the increasing monotonicity of f, we obtain
for all n≥max{n0,r0}. Hence, the proof is complete.
To finalize this subsection, if we keep in mind Remark 2.3 together with the previous theorem, we immediately deduce the following corollary.
Corollary 3.9. Let f be a compatible modulus function. Let λ:R→R be a real function. Let x0∈R and λ0∈R. The following conditions are equivalent:
1) λ0 is the statistical derivative of λ at x0.
2) λ0 is the f-statistical derivative of λ at x0.
3.3. f-Strongly Cesàro derivative
This subsection is devoted to introduce the notion of f-strongly Cesàro derivative and to relate it with the strongly Cesàro derivative and the f-statistical derivative.
Definition 3.10. Let f be a modulus function. A real function λ:R→R is said to have a f-strongly Cesàro derivative λ0∈R at a point x0∈R if
holds whenever limk→∞xk=0 and xk≠0 for each k∈N.
The following proposition justifies the use of unbounded modulus functions in order for the concept of f-strongly Cesàro derivative not to become trivial.
Proposition 3.11. Let f be a bounded modulus function. Let λ:R→R be a real function. Let x0∈R. Then λ has a f-strongly Cesàro derivative at x0 if and only if λ(x)=ax+b for some a,b∈R.
Proof. Indeed, if λ(x)=ax+b for some a,b∈R, then the f-strongly Cesàro derivative at x0 of the function λ is a. Conversely, let λ0∈R be a f-strongly Cesàro derivative for f at x0. Suppose that there exist a proper null sequence (xk)k∈N and k0∈N satisfying
Then
for every n∈N, contradicting (3.2). As a consequence, for every proper null sequence (xk)k∈N and every k∈N
that is, λ(x0+xk)=λ0xk+λ(x0). Since every x∈R∖{x0} can be written as x=x0+x1 with x1 being the first term of a proper null sequence (xk)k∈N, it is easy to understand that λ(x)=λ0x+(λ(x0)−λ0x0) for all x∈R. Hence, we simply take a:=λ0 and b:=λ(x0)−λ0x0.
In the upcoming theorem, we will show that the f-strongly Cesàro derivative implies the strongly Cesàro derivative and the f-statistical derivative.
Theorem 3.12. Let f be a modulus function. If λ:R→R has a f-strongly Cesàro derivative λ0∈R at a point x0∈R, then λ0 is also a strongly Cesàro derivative and a f-statistical derivative for λ at x0.
Proof. We will itemize the proof for clarification and presentation purposes.
● We will prove first that λ0 is a strongly Cesàro derivative for λ at x0. Fix an arbitrary proper null sequence (xk)k∈N. We have to show that the sequence (λ(x0+xk)−λ(x0)xk)k∈N is strongly Cesàro convergent to λ0, that is,
By hypothesis, λ0 is a f-strongly Cesàro derivative for λ at x0, therefore, for all r∈N there exists nr∈N such that
for all n≥nr. Basic properties of modulus functions yield
for all n≥nr. Since f is increasing, we obtain
for all n≥nr, meaning that λ has a strongly Cesàro derivative λ0 at the point x0.
● Second, let us show that λ0 is also a f-statistical derivative for λ at x0. Fix an arbitrary proper null sequence (xk)k∈N. We have to show that the sequence (λ(x0+xk)−λ(x0)xk)k∈N is f-statistically convergent to λ0, that is, for each r∈N
Indeed, fix an arbitrary r∈N. For every n∈N, denote
For every n∈N, we have
If both sides of the above inequality are divided by f(n) and taking the limit as n→∞, we obtain the following inequality
Since λ0 is a f-strongly Cesàro derivative for λ at x0, the left side of (3.3) is zero, hence
meaning that λ0 is also a f-statistical derivative for λ at the point x0.
We will conclude this manuscript with the converse to Theorem 3.12, which can be obtained under not so restrictive conditions.
Definition 3.13. A real function λ:R→R is said to be rate-of-change bounded at a point x0∈R provided that (λ(x0+xk)−λ(x0)xk)k∈N is bounded for every proper null sequence (xk)k∈N.
Notice that rate-of-change bounded functions must be continuous. However, continuity is not a sufficient condition to be rate-of-change bounded.
Example 3.14. The real function
is continuous at 0 but not rate-of-change bounded at 0.
Locally Lipschitz functions are nontrivial examples of rate-of-change bounded functions, as shown in the next result. Recall that a real function λ:R→R is locally Lipschitz at a point x0∈R provided that there exists a neighborhood U of x0 and a positive constant M>0 satisfying that |λ(x)−λ(x0)|≤M|x−x0| for all x∈U.
Proposition 3.15. Let λ:R→R be a real function. Let x0∈R. Then λ is rate-of-change bounded at x0 if and only if λ is locally Lipschitz at x0.
Proof.
⇒ Suppose that λ is rate-of-change bounded at x0. Assume on the contrary that λ is not locally Lipschitz at x0. Then, for every k∈N, we can find ak∈(x0−1k,x0+1k) such that
We will reach a contradiction by constructing a proper null sequence (xk)k∈N such that (λ(x0+xk)−λ(x0)xk)k∈N is unbounded. For every k∈N, define xk:=ak−x0. It is clear that (xk)k∈N converges to 0. Also, notice that (xk)k∈N is proper because Eq (3.4) forces ak≠x0 for all k∈N. Finally, for every k∈N, we have
meaning that (λ(x0+xk)−λ(x0)xk)k∈N is unbounded.
⇐ Suppose that λ is locally Lipschitz at x0. Consider a neighborhood U of x0 and a positive constant M>0 satisfying that |λ(x)−λ(x0)|≤M|x−x0| for all x∈U. Let us prove that λ is rate-of-change bounded at x0. Pick any proper null sequence (xk)k∈N. We may assume without any loss of generality that x0+xk∈U for all k∈N. Then |λ(x0+xk)−λ(x0)|≤M|(x0+xk)−x0|=M|xk| for all k∈N, meaning that |λ(x0+xk)−λ(x0)xk|≤M for each k∈N. The arbitrariness of (xk)k∈N shows that λ is rate-of-change bounded at x0.
Like we mentioned earlier, a direct consequence of Proposition 3.15 is that rate-of-change bounded functions are continuous.
Theorem 3.16. Let f be a compatible modulus function. Let λ:R→R be a real function. Then:
1) If λ has a f-statistical derivative λ0∈R at a point x0∈R and is rate-of-change bounded at x0, then λ0 is also a f-strongly Cesàro derivative for λ at x0.
2) If λ has a strongly Cesàro derivative λ0∈R at a point x0∈R, then λ0 is also a f-strongly Cesàro derivative at x0.
Proof. We will prove both items.
1) Fix an arbitrary proper null sequence (xk)k∈N. We have to prove that
By hypothesis, (λ(x0+xk)−λ(x0)xk)k∈N is bounded, meaning that there exists M>0 satisfying that |λ(x0+xk)−λ(x0)xk−λ0|≤M for each k∈N. Take any ε>0. Since f is compatible, there exists ˜ε>0 and n0=n0(ε)∈N such that f(n˜ε)f(n)<ε for all n≥n0. For every n∈N, denote
and Gn the complementary of Hn in {1,…,n}. Therefore, for every n∈N, we obtain the following inequalities:
By dividing by f(n), we conclude, for every n≥n0, that
Finally, taking the limit as n→∞ and by bearing in mind the arbitrariness of ε>0 and that λ0 is a f-statistical derivative for λ at x0, we obtain the desired result that
2) Fix an arbitrary real-valued sequence (xk)k∈N with limk→∞xk=0 and xk≠0 for each k∈N. Again, we have to prove that
Fix an arbitrary ε>0. Since f is compatible, there exists ˜ε>0 and n0=n0(ε)∈N such that f(n˜ε)f(n)<ε for all n≥n0. By hypothesis, λ0 is a strongly Cesàro derivative for λ at x0, thus, there exists r0=r0(ε)∈N such that if n≥r0, then
Using the increasing monotonicity of f, we obtain
for all n≥max{n0,r0}. Hence, the proof is complete.
By combining together Theorem 3.12 and 3.16, we obtain the following final corollary.
Corollary 3.17. Let f be a compatible modulus function. Let λ:R→R be a real function which is rate-of-change bounded at a point x0∈R. Let λ0∈R. The following conditions are equivalent:
1) λ0 is the f-strongly Cesàro derivative for λ at x0.
2) λ0 is the f-statistical derivative for λ at x0.
3) λ0 is the strongly Cesàro derivative for λ at x0.
4.
Conclusions
Unbounded modulus functions allow that, for real functions, the notions of continuity/derivative and f-statistical continuity/derivative be equivalent (Corollary 3.3 and 3.7). Compatible modulus functions allow that, for real functions, the notions of statistical continuity/derivative and f-statistical continuity/derivative be equivalent (Corollary 3.4 and 3.9). Finally, compatible modulus functions make possible that, for real functions satisfying good continuity properties, such as locally Lipschitz conditions, the novel concepts of f-strongly Cesàro derivative and f-statistical derivative be both equivalent to the previously known concept of strongly Cesàro derivative (Corollary 3.17).
Acknowledgments
The second author has been partially supported by Research Grant PGC-101514-B-I00 awarded by the Ministry of Science, Innovation and Universities of Spain. This work has also been co-financed by the 2014-2020 ERDF Operational Programme and by the Department of Economy, Knowledge, Business and University of the Regional Government of Andalusia, under Project Reference FEDER-UCA18-105867. The APC has been paid by the Department of Mathematics of the University of Cadiz.
Conflict of interest
The authors declare that there is no conflicts of interest.









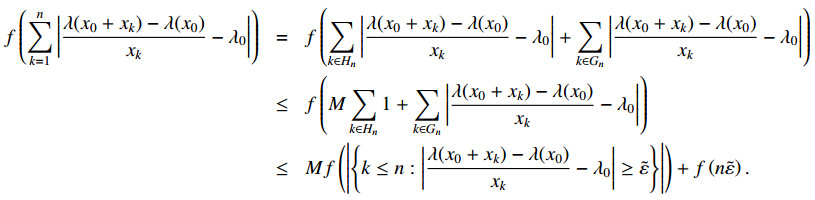
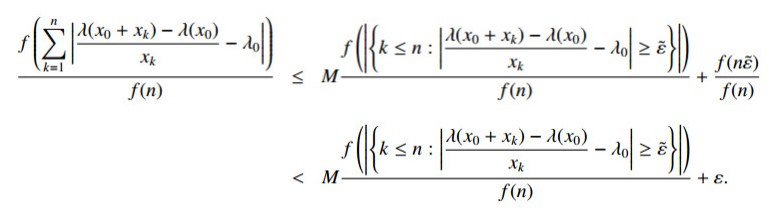




 DownLoad:
DownLoad: