1.
Introduction
Mathematical modeling helps to develop a scientific understanding, quantify the current knowledge of a system, and test the impact of changes in a system. It is used in natural sciences and engineering disciplines. So, the mathematical modeling has been attracting the attention of many authors [1,2,3,4].
Worldwide energy consumption is increasing by around 2.1 percent annually on average [5]. 84 percent of the fuels produced are produced with Fossil fuels, Coal and Natural Gas. Increasing electricity consumption increases CO2 emissions and increases global warming.
According to 2020 Eurostat data in [6], 26 percent of energy consumption in Europe in 2018 was at homes. 14.1 percent of the total electricity consumption was used for white goods and lighting. The rate of use of dishwashers in Europe is over 44 percent. Dishwashers are among the white goods with a high potential to become widespread. Using a dishwasher provides 50 percent water savings and 28 percent energy savings compared to hand washing [7,8]. The annual energy consumption of dishwashers in Europe reached 31TWH/year in 2015. Efficiency increases in dishwashers have an important place in preventing the global water and energy crisis.
In the studies about the dishwasher, the factors affecting the efficiency are determined. One of them is to wash with an intermittent water jet instead of applying a conventional continuous water jet from the lower spray arm [9]. Also, the author has investigate the lower energy consumption and the increase in washing performance depending on the operation case. In [10], Tsouknidas and Zhang have presented the relationships among water pressure, rotational speed, and washing performance using motor-controlled spray arm. The nozzles on the standard spray arm are fixed angled. Since these fixed angle nozzles provide rotation, the rotation speed of the spray arm is directly related to the angle of the nozzles. When higher pressure is applied to increase the washing performance, the rotation speed increases, but when the speed increases, the washing performance decreases and energy consumption increases. Since nozzle angle, water pressure, rotational speed are determined according to the priority of maintaining the washing performance in the conventional spray arm, then energy consumption and water consumption remain in the background. The new spray arm design provides a great improvement in energy and water consumption as it stretches conventional design criteria [10].
Arçelik company has developed a spray arm that sweep the inside of the dishwashers in all four corners. When the spray arm is viewed as a projection, since it sweep a square profile, it can send water vertically to every region. In this way, it can exhibit lower energy, water pressure, sound level and higher washing performance. This new system is called as CornerWash spray arm. In this study, we have obtained a mathematical model of the new spray arm motion. The path followed by the new spray arm corresponds to the spherical timelike helix motion in Minkowski 3−space. We examine the new spray arm motion as a two-dimensional projection, we can see that it makes a hypocycloid motion.
2.
Basic notions in the Minkowski 3−space
Minkowski 3−space is defined with the following inner product
for the vectors u=(u0,u1,u2) and v=(v0,v1,v2) in the scalar space R31. The exterior product in R31 is defined by
where {ei,i=0,1,2} is canonical bases of R31 [11]. In Minkowski 3−space, vectors and curves have casual characters and they are called spacelike, timelike, or lightlike respect to their casual characters. If the observer is moving less than the speed of light along the curve, then the curve is called a timelike curve; if it is moving at a speed of light called a lightlike curve; and if it is moving faster than the speed of light called a spacelike curve. Similarly, the norm of the vector in Minkowski 3−space is equal to −1, 0, or 1. Then, it is called a timelike, a lightlike, or a spacelike, respectively. Also, the spheres are defined as follows in Minkowski 3−space:
The curve x is a non-null curve with the arc length parameter s in the Minkowski 3−space. The Frenet frame apparatus of the curve x are {t(s),n(s),b(s),ϰ(s),τ(s)}, where n(s), b(s) are unit normal and binormal vector field of the curve x, respectively. The derivatives of the Frenet vectors are given in terms of themselves as follows:
where εi (i=0,1,2) is shown signum functions of the Frenet vectors t(s), n(s), and b(s), respectively. Also, the cross product of these vectors is given as b=t×n, −ε1t=n×b, and −ε0n=b×t.
Helix curve is one of the important curves in science and nature. The applications of helices are encountered in many applied fields. In differential geometry, a helix is defined as a geometric curve with a non-vanishing constant curvature and a non-vanishing constant torsion. Another definition is that the tangent makes a constant angle with a fixed straight line (the axis of the general helix). Also, slant helix is defined that the normal makes a constant angle with a fixed straight line. In [12], the authors have given parametric representations of the slant helices on de Sitter 2−space and hyperbolic 2−space.
3.
Motion of dishwasher spray arm with spherical timelike helix
In this section, we have examined the geometrical movements of the conventional and new dishwasher spray arms. We give the relationships between the motions of dishwasher spray arms and helices.
Theorem 1. The unit speed curve x lies on de Sitter 2−space with radius r if and only if the curvatures of the curve x are saisfied the equation ε1κ2(s)+ε2[1τ(s)(1κ(s))′]2=r2.
Proof. If the curve x(s) lies on the de Sitter 2−space with radius r and center a, then g(x(s)−a,x(s)−a)=r2 is satisfied. From the last equation, we calculate the followings g(x(s)−a,t(s))=0, g(x(s)−a,n(s))=−ε0κ(s), and g(x(s)−a,b(s))=−ε0τ(s)(1κ(s))′. The position vector of the curve x(s) is expressed by x(s)−a=a1(s)t(s)+a2(s)n(s)+a3(s)b(s). By using these equations, we obtain a1(s)=0, a2(s)=−ε0ε1κ(s), and a3(s)=−ε0ε2τ(s)(1κ(s))′. If these equations are replaced in g(x(s)−a,x(s)−a)=r2, the desired result is obtained.
Assume that the equation ε1κ2(s)+ε2τ(s)(1κ(s))′=r2 is provided. The following curve α is defined as α(s)=x(s)+ε0ε1Rn(s)+ε0ε2TR′b(s) where T=1/τ(s) and R=1/κ(s). Now, we take the derivative of α(s), we hold α′(s)=0 and so α is a constant. The radius of the pseudo sphere is calculated as g(x(s)−α,x(s)−α)=r2. This demonstrates that x(s) lies on the de Sitter 2−space with radius r.
Theorem 2. Let x(s):I⊂R→R31 be spherical timelike helix on the de Sitter 2−space. The parametric representation of the spherical timelike helix is
for m∈R∖[−1,1].
Proof. The first derivative of the curve x(s) is obtained ˙x(s)=sins√m2−1{1,sin(√m2−1sm)m,−cos(√m2−1sm)m}, and g(˙x(s),˙x(s))=−sin2sm2. Since the norm of the vector ˙x(s) is not equal to ∓1, then the curve x(s) is not a unit speed curve. The tangent vector field t(s) of the curve x with an arbitrary parameter s is calculated by
so, we get ˙x(s)=sinsmt(s). The second derivative of the curve x(s) is found
To find the binormal vector field b(s)=˙x(s)רx(s)‖˙x(s)רx(s)‖, we calculate
and the norm ‖˙x(s)רx(s)‖=sin2sm3. Thus, we get
The normal vector field of the timelike curve x(s) is
with the curvature κ(s)=1sins and the torsion τ(s)=msins. Since the ratio of the curvatures is m=constant, then the curve x is a helix. Since g(x(s),x(s))=1 is satisfied, then the curve lies on the de Sitter space S21.
The natural equation of the curve is the equation that characterizes the curve independent of the choice of coordinates. It is said to be intrinsic because it is invariant under transformations that preserve length and angle. The study of natural equations began with the following problem: given the curvature and torsion of one parameter, find the space curve for two functions. We will now consider the natural equations of spherical helix on the de Sitter 2−space projects on a plane perpendicular to its axis.
Theorem 3. The projection of the spherical timelike helix on a plane perpendicular to its axis is the plane curve with the natural equations
where R(s)=1κ(s).
Proof. A space curve x(s) lies on the de Sitter 2−space with radius r if and only if the condition ε1κ2(s)+ε2[1τ(s)(1κ(s))′]2=r2 is satisfied. This condition with considering the equation κ(s)=ε1τ(s)tanθ give the following ODE after elimination of τ(s)
where the parameter θ is showen the angle between the tangent vector of the helix and its axis. Integrated for R, and by suitable choice of the additive constant in s, gives the desired results. The projection of the spherical timelike helix on a plane perpendicular to their axis is |−ε1R2±r2|=cot2θs2. This type of curves is discussed for Euclidean 2−sphere in [13].
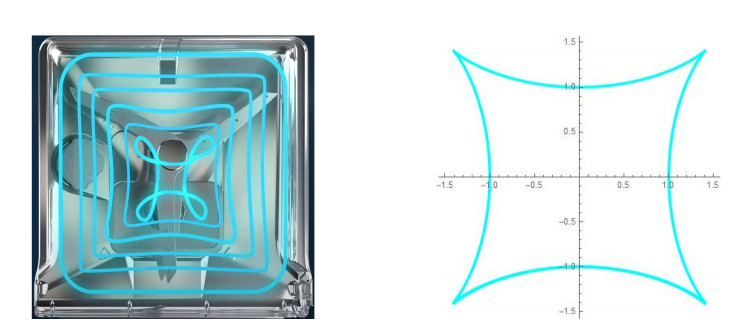
Corollary 1. The spherical timelike helix x(s) on the de Sitter 2−space projects on a plane perpendicular to its axis in an arc of hypocycloid.
Proof. The natural equation of the projection on yz−plane perpendicular to its axis of the spherical timelike helix x(s) is obtained the following equation cot2θs2+R2(s)=1. From the last equation, we obtain cotθ=m. Since m>1, projection of the curve x(s) on a plane perpendicular to its axis is an hypocycloid.
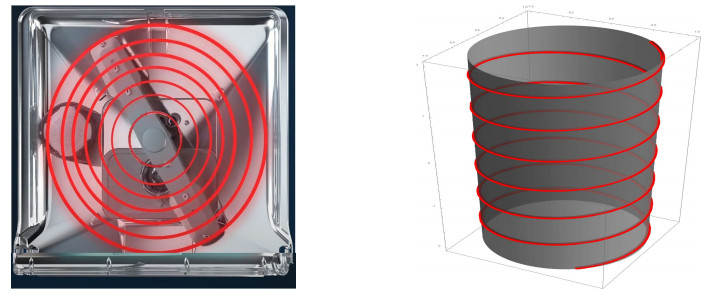
The conventional dishwasher spray arm, simply, is in the form of a rotating line at its midpoint. When viewed from the top of the machine, dishwashers have a square area, while conventional spray arm sweep a circular area in a square structure. This structure geometrically corresponds to a circular cylinder. When the movement of the water coming out of the nozzles is examined depending on time, it makes a cylindrical helix movement with the parametric representation α(s)=(coss,sins,ks) where k is constant (red curve in Figure 1 right). Therefore, the spray arm creates regions where the water cannot reach vertically. For water to reach these areas, it is necessary to make angled nozzles on the conventional spray arm. When the water comes at an angle to the area where outside the projection of the conventional spray arm, it loses some of the force required to clean it due to the angled exit. To reduce this loss of force, water must be sprayed with greater pressure from the angled nozzle. So, the pump must be more powerful and consume more energy for high pressure. Also, the amount of water must be higher in order to remove the dirt. For these reasons, the conventional spray arm increases energy and water consumption, while reducing washing performance. As the water coming out of the spray arm with the angled nozzle hits the inner walls of the dishwasher, it also increases the amount of noise.
New designed spray arm called the CornerWash by Arçelik in Figure 2, since it sweeps projectively the square area of the dishwasher, it is not necessary to use an angled nozzle. Therefore, the water coming out of the nozzle with a lower pressure will be able to provide the necessary force in every region to clean the dishes. Moreover, as the force on the dishes increases, the amount of water to be consumed decreases and the washing performance increases. It is possible to use a smaller pump, thus reducing energy consumption. Since the water does not hit the side walls directly, the operating noise level of the dishwasher is reduced.
The movement of CornerWash begins with the rotation of the orange arm around the red dot on the axis of rotation. The axis of rotation of the three-armed spray arm is off-axis on the orange lever. The axis of rotation of the three-armed spray arm moves on the white circle. Thus, the nozzles on the three-armed spray arm make hypocycloid movement in Figure 3.
When the movement of CornerWash is examined geometrically, the path of the water coming out of the nozzle on the new spray arm projectively draws a hypocycloid. When the time-dependent variation of this motion in 3-dimensional space is examined, we find that it corresponds to the timelike helix with
lying on the de Sitter 2−space in Figure 4 for m=1.155 (right). The projection on yz−plane perpendicular to its axis of the spherical timelike helix x(s) is obtained cot2θs2+sin2s=1. From the last equation, we calculate cotθ=1.155. Since cotθ>1, this equation gives a hypocycloid.
Note: CornerWash images are provided from the website: https://www.youtube.com/watch?v=8ertBCEdhlU.
4.
Conclusions
In this article, the authors created a geometric model of the water flow of a CornerWash arm design used in dishwashers. This design improves the washing performance and sound level while providing efficiency increase in the water and energy consumed by the dishwashers. The study is important because it includes the geometric interpretation of a movement that has an application. Since it can be used as an infrastructure for Fluid Dynamics, it will help scientists doing similar work.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: