Cospectral graphs for the normalized Laplacian

1.   Introduction

Let $G$ be a simple connected graph with vertex set $V(G) = \{v_1, v_2, \ldots, v_n\}$ and edge $E(G)$. Let $d(v)$ denote the degree of vertex $v$ of $G$ and $D(G) = diag(d(v_{1}), d(v_{2}), \ldots, d(v_{n}))$ the diagonal matrix of vertex degrees. The adjacency matrix of $G$ is defined to be the $n\times n$ matrix $A(G) = (a_{ij})$, where $a_{ij} = 1$ if $v_{i}$ and $v_{j}$ are adjacent and $a_{ij} = 0$ otherwise. The normalized Laplacian matrix is defined to be $\mathcal{L}(G) = D(G)^{-1/2}(D(G)-A(G))D(G)^{-1/2}$ (with the convention that if the degree of $v$ is 0 then $d(v)^{-1/2} = 0$) by Chung ^[7]. So its entries are defined by

The normalized Laplacian characteristic polynomial of a graph is the characteristic polynomial of its normalized Laplacian matrix. Denote by $\Phi(B; x) = \det(xI-B)$ the characteristic polynomial of the square matrix $B$. Hence $\Phi(\mathcal{L}(G); x) = \det(xI-\mathcal{L}(G))$ is the normalized Laplacian characteristic polynomial of a graph $G$.

Spectral graph theory examines relationships between the structure of a graph and the eigenvalues (or spectrum) of a matrix associated with that graph. Different matrices are able to give different information, but all the common matrices have limitations. This is because there are graphs which have the same spectrum for a certain matrix but different structure–such graphs are called cospectral with respect to that matrix ^[4].

Cospectral graphs for the adjacency matrix (see for example ^{[8,10,11,12,13]}) and the Laplacian matrix (see for example, ^[12,17,19]) have been studied extensively, particularly for graphs with few vertices. But little is also known about cospectral graphs with respect to the normalized Laplacian since the normalized Laplacian is a rather new tool which has rather recently (mid 1990's) been popularized by Chung ^[7]. One of the original motivations for defining the normalized Laplacian was to be able to deal more naturally with non-regular graphs. In some situations the normalized Laplacian is a more natural tool that works better than the adjacency matrix or Laplacian matrix. In particular, when dealing with random walks, the normalized Laplacian is a natural choice. This is because $D(G)^{-1}A(G)$ is the transition matrix of a Markov chain which has the same eigenvalues as $I-\mathcal{L}(G)$. Previously, the only cospectral graphs with respect to normalized Laplacian were bipartite (complete bipartite graphs ^[19] and bipartite graphs found by "unfolding" a small bipartite graph in two ways ^[3]). Some recent studies on cospectral graphs were carried out in ^{[1,2,5,6,14,15,16,18]}.

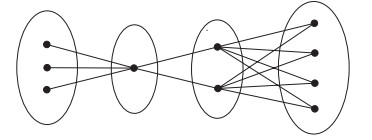
In this paper, a particular class of graphs are constructed as follows. Let $G(a_1, a_2, \ldots, a_k)$ be a simple graph with vertex set $V(G) = V_1\cup V_2\cup \cdots \cup V_k$ and edge set $E(G) = \{(u, v)|u\in V_i, v\in V_{i+1}, i = 1, 2, \ldots, k-1\}$, where $|V_i| = a_i > 0$ for $1\leq i\leq k$ and $V_i\cap V_j = \emptyset$ for $i\neq j$. The graph $G(3, 1, 2, 4)$ is illustrated in Figure 1.

Given two positive integers $k$ and $n$, and $k-2$ positive rational numbers $t_2, t_3, \ldots, t_{\lceil k/2\rceil}$ and $t_2', t_3', \ldots, t_{\lfloor k/2\rfloor}'$, let $\Lambda$ be the set of the positive integer solutions $(a_1, a_2, \ldots, a_k)$ of the following equations:

It is not difficult to show that $\Lambda = \{(a_1, a_2, \ldots, a_k)\in N\times N\times \cdots\times N = :N^k|(1+t_2+t_3+\cdots+t_{\lceil k/2\rceil})a_1$$+(1+t_2'+t_3'+\cdots+t_{\lfloor k/2\rfloor}')a_2 = n; a_{2i-1}$$= t_{i}a_1, a_{2j} = t_j'a_2, i = 2, 3, \ldots, \lceil k/2\rceil, j = 2, 3, \ldots, \lfloor k/2\rfloor\}$, where $N$ is the set of positive integers. Define $\Upsilon(n; k)_t^{t'} = \{G(a_1, a_2, \ldots, a_k)|(a_1, a_2, \ldots, a_k)\in \Lambda\}$, where $t = (t_2, t_3, \ldots, t_{\lceil k/2\rceil}), t' = (t_2', t_3', \ldots, t_{\lfloor k/2\rfloor}')$.

Example 1.1. If $n = 20, k = 5$, and $t_2 = t_3 = \frac{1}{2}$ and $t_2' = \frac{1}{3}$, then the set of positive integer solutions $(a_1, a_2)$ of the Eq $(1+\frac{1}{2}+\frac{1}{2})a_1+(1+\frac{1}{3})a_2 = 20$ is $\{(2, 12), (4, 9), (6, 6), (8, 3)\}$. Hence

and

In this paper, we prove that all graphs in $\Upsilon(n; k)_t^{t'}$ are cospectral with respect to the normalized Laplacian if it is not an empty set.

2.   Main results

Given $2n-1$ real numbers $a_1, a_2, \ldots, a_n, b_1, b_2, \ldots, b_{n-1}$, define $\mathcal {T}_{a_1, a_2, \ldots, a_n}^{b_1, b_2, \ldots, b_{n-1}}$ to be the set of tridigonal matrices $Q = (q_{ij})_{n\times n}$ with form of

where $x_iy_i = b_i, i = 1, 2, \ldots, n-1$.

Lemma 2.1. Keeping the above notation, then, for arbitrary two matrices $Q_{1}, Q_{2}\in \mathcal{T}_{a_1, a_2, \ldots, a_n}^{b_1, b_2, \ldots, b_{n-1}},$ we have$\Phi(Q_{1};x) = \Phi(Q_{2};x)$. That is, all matrices in $\mathcal{T}_{a_1, a_2, \ldots, a_n}^{b_1, b_2, \ldots, b_{n-1}}$ are cospectral.

Proof. We prove the lemma by induction on $n$. if $n$ = 2, then matrix

Note that

So, for arbitrary $Q_{1}, Q_{2}\in \mathcal T_{a_1, a_2}^{b_1},$ $\Phi(Q_{1};x) = \Phi(Q_{2};x)$.

Now we assume that $n > 2$. Let

Hence,

where $Q_{n-1}$ and $Q_{n-2}$ are the matrices obtained from $Q_n$ by deleting the first row and column and first two rows and columns, respectively. Obviously, $Q_{n-1}\in \mathcal T_{a_2, a_3, \ldots, a_n}^{b_2, b_3, \ldots, b_{n-1}}$ and $Q_{n-2}\in \mathcal T_{a_3, \ldots, a_n}^{b_3, \ldots, b_{n-1}}$. By induction, all matrices in $T_{a_2, a_3, \ldots, a_n}^{b_2, b_3, \ldots, b_{n-1}}$ (resp. $T_{a_3, a_4, \ldots, a_n}^{b_3, b_4, \ldots, b_{n-1}}$) are cospectral. Hence, by Eq (1), it is not difficult to see that all matrices in $\mathcal {T}_{a_1, a_2, \ldots, a_n}^{b_1, b_2, \ldots, b_{n-1}}$ are cospectral. The lemma has thus been proved.

Now we use a similar method to that in ^[9] to prove the following theorem.

Theorem 2.2. The characteristic polynomial of normalized Laplacian matrix ofgraph $G(a_{1}, a_{2}, \ldots, a_{k})$ with $\sum_{i = 1}^{k}a_{i} = n$is

where $M = (m_{ij})_{k\times k}$ is the tridigonal matrix satisfying$m_{ij} = 1$ if $i = j$ and $m_{ij} = -a_{j}/\sqrt{d_{i}d_{j}}$ if $i = j-1$or $i = j+1$, and $m_{ij} = 0$ otherwise, $d_1 = a_2, d_2 = a_1+a_3, d_3 = a_2+a_4, \ldots, d_{k-1} = a_{k-2}+a_k, d_k = a_{k-1}$.

Proof. Note that if vertices $v$ and $w$ are in the same part of $G(a_{1}, a_{2}, \ldots, a_{k})$, the transpose of the row vector $\beta_{i}$ whose coordinates on $v$, $w$ and elsewhere are respectively $1$, $-1$ and $0$ is an eigenvector for the eigenvalue 1 of the normalized Laplacian matrix $\mathcal{L}(G(a_{1}, a_{2}, \ldots, a_{k}))$, and there are $a_{i}-1$ eigenvectors for the eigenvalue 1 $(1\leq i\leq k)$. So we can find $\sum_{i = 1}^{k}(a_i-1) = n-k$ linearly independent eigenvectors of matrix $\mathcal{L}(G(a_{1}, a_{2}, \ldots, a_{k}))$ which generate a linear subspace $U$ of dimension $n-k$. Now we choose an orthogonal basis of the orthogonal complement of $U$. It is constituted by the transposes of $k$ row vectors $\gamma_{i}$ $(1\leq i\leq k)$, where $\gamma_{i}$ is the vector whose coordinates on vertices $v\in V_{i}$ are $1$ and elsewhere are $0$, that is, $\gamma_{i} = (0, \ldots, 0, \overbrace{1, \ldots, 1}^{a_{i}}, 0, \ldots, 0)$. It is easy to find that $\mathcal{L}(G(a_{1}, a_{2}, \ldots, a_{k}))(\gamma_{1}^{T}, \gamma_{2}^{T}, \ldots, \gamma_k^{T}) = (\gamma_{1}^{T}, \gamma_{2}^{T}, \ldots, \gamma_{k}^{T}) M$, where $M = (m_{ij})$ is a $k\times k$ matrix such that $m_{ij} = 1$ if $i = j$, $m_{ij} = -a_{j}/\sqrt{d_{i}d_{j}}$ if $i = j-1$ or $i = j+1$, $m_{ij} = 0$ otherwise. Hence Eq (2) holds.

Theorem 2.3. Given two positive integers $k$ and $n$, and $k-2$ positive rationalnumbers $t_2, t_3, \ldots, t_{\lceil k/2\rceil}$ and$t_2', t_3', \ldots, t_{\lfloor k/2\rfloor}'$, then all graphs in$\Upsilon(n; k)_t^{t'}$ are cospectral with respect to the normalized Laplacianif it is not an empty set.

Proof. We only need to consider the case $|\Upsilon(n; k)_t^{t'}|\geq 2$. Let $G(a_1, a_2, \ldots, a_k)$ and $G(b_1, b_2, \ldots, b_k)$ be two graphs in $\Upsilon(n; k)_t^{t'}$. Then, by Theorem 2.2,

and

where $M_1 = (m_{ij})_{k\times k}$ and $M_2 = (m_{ij}')_{k\times k}$ are two tridigonal matrices satisfying $m_{ij} = m_{ij}' = 1$ if $i = j$ and $m_{ij} = -a_{j}/\sqrt{d_{i}d_{j}}$ and $m_{ij}' = -b_{j}/\sqrt{d_{i}'d_{j}'}$ if $i = j-1$ or $i = j+1$, and $m_{ij} = m_{ij}' = 0$ otherwise, $d_1 = a_2, d_2 = a_1+a_3, d_3 = a_2+a_4, \ldots, d_{k-1} = a_{k-2}+a_k, d_k = a_{k-1}$, and $d_1' = b_2, d_2' = b_1+b_3, d_3' = b_2+b_4, \ldots, d_{k-1}' = b_{k-2}+b_k, d_k' = b_{k-1}$. Hence we need to show that $\Phi(M_1;x) = \Phi(M_2;x)$.

Note that $(a_{1}, a_{2}, \ldots, a_{k})$ and $(b_{1}, b_{2}, \ldots, b_{k})$ are two solutions of the following equations:

It is not difficult to show that tridigonal matrices $M_1$ and $M_2$ satisfy $m_{i, i+1}m_{i+1, i} = m_{i, i+1}'m_{i+1, i}'$ for $i = 1, 2, \cdots, k-1$. For example,

and so on. By Lemma 2.1, $M_1$ and $M_2$ are cospectral. Hence the theorem has been proved.

3.   Examples

In this section, by using Theorem 2.3, we give some examples of cospectral graphs with respect to the normalized Laplacian.

Note that the graphs with form of $G(a_1, a_2)$ or $G(b_1, b_2, b_3)$ are complete bipartite graphs. Using Theorem 2.2, it is not difficult to see that, if $a_1+a_2 = n$ and $b_1+b_2+b_3 = n$, then

Hence we have the following.

Corollary 3.1 (^[19]). All complete bipartite graphs with $n$ vertices are cospectral withrespect to the normalized Laplacian.

By Theorems 2.2 and 2.3, four graphs $G(2, 12, 1, 4, 1), G(4, 9, 2, 3, 2), G(6, 6, 3, 2, 3)$, and $G(8, 3, 4, 1, 4)$ in Example 1.1 are cospectral with respect to the normalized Laplacian. Their normalized Laplacian characteristic polynomial is

Example 3.2. It is not difficult to show that

By Theorems 2.2 and 2.3, all six graphs in $\Upsilon(24;4)_{1}^{1}$ are cospectral with respect to the normalized Laplacian. Their normalized Laplacian characteristic polynomial is

Example 3.3. It is not difficult to show that

By Theorem 2.3, all nine graphs in $\Upsilon(60;5)_{2, 3}^{2}$ are cospectral with respect to the normalized Laplacian.

4.   Conclusions

In this paper, we construct a class of graph $\Upsilon(n; k)_t^{t'}$, and proved that all graphs in $\Upsilon(n; k)_t^{t'}$ are cospectral graphs with respect to the normalized Laplacian. We also give some examples to verify our results.

Acknowledgments

We are grateful to the anonymous referees for many friendly and helpful revising suggestions that greatly improved the presentation of the paper. The second author was supported by NSFC Grant (No. 11701324), the Natural Science Foundation of Fujian Province, China (No. 2021J05185) and the Program for Outstanding Young Scientific Research Talents in Fujian Province University.

Conflict of interest

There is no conflict interest for this paper.