Synchronizations of fuzzy cellular neural networks with proportional time-delay

1.   Introduction

Tuberculosis (TB) is a chronic infectious disease caused by Mycobacterium tuberculosis, which has brought serious hazards to human health. Usually, it can be transmitted through respiratory tract, digestive tract, skin, urogenital tract, placenta, etc., of which respiratory tract is the main way of TB transmission ^[1]. Healthy (or susceptible) individuals could be infected through inhaling the droplet nucleus which are expelled into the atmosphere when an actively infectious TB person coughs, speaks or sneezes^[2]. In general, not all infected individuals will rapidly progress the active TB cases. About 5% of the newly infected would develop TB directly (fast progression) but most newly infected individuals remain as latently infected carriers for their entire lives^[3,4,5], and they are considered at highest risk of developing active TB cases during the first two years of infection, during which approximately 5% of persons eventually develop active TB cases (slow progression) ^[6]. The incubation period of infected individuals may vary from one year to several years due to their own immune system and the virulence of Mycobacterium tuberculosis^[2]. With currently-recommended treatments (a 4–6 months course of anti-TB drugs), about 85% of people could be cured. Regimens of 1–6 months are available to treat TB infection ^[2]. However, either inadequate regimen treatment or insufficient treatment duration (because of patents' poor compliance) would result in the endogenous reactivation of Mycobacterium tuberculosis, i.e., the relapse after treatment occurs^[3,7]. In 2021, based on the estimation of the World Health Organization, there would be about 10.6 million new TB patients and approximately 1.6 million people deaths from TB, and the incidence of morbidity and mortality are 134 and 17 (per 100, 000 population per year) in the world, respectively. Among the 30 countries with high burden of TB in the world, China ranks the third (7.4%), behind India (28%) and Indonesia (9.2%). In China, the estimated number of new TB patients is 7.8 million and the estimated TB incidence is 55 (per 100, 000 population per year) ^[2].

Mathematical models have been used extensively in studying the transmission dynamics of infectious diseases and could help us to formulate control strategies ^{[8,9,10,11,12,13,14,15,16]}. The pioneer work about the TB transmission model proposed by Waaler in 1962 ^[17] could shed light on how to describe the transmission of TB. Blower et al. ^[5] established a detailed model to reflect the intrinsic transmission dynamics of Mycobacterium tuberculosis. This model captures the temporal dynamics of five groups: susceptible individuals $(X)$, latently infected individuals (that is, individuals who have been infected with Mycobacterium tuberculosis but have no clinical illness and hence are non-infectious) $(L)$, infectious TB cases (a case would transmit the infection to others) $(T_i)$, non-infectious TB cases (these cases maybe spontaneously cured and move into the recovered non-infectious state) $(T_n)$ and recovered cases (that is, an individual in the recovered state may either relapse and develop TB again or may never relapse and die of other cause) $(R)$. The corresponding model is given by

This model separately assessed the TB transmission risks of the fast and slow processes, and enabled us to understand the dynamics of TB and design some disease control strategies. After that, there have been many studies on the mathematical modeling of TB transmission ^{[18,19,20,21,22]}. For instance, Xu et al. ^[18] studied the TB transmission model with fast-slow progression, age related latency and infection, proving that the global dynamics of this model is completely determined by the basic reproduction number. Liao et al. ^[19] established a deterministic TB transmission model to study the potential impact of the recurrence and reinfection on TB spread. And a probabilistic risk model was developed to assess the TB infection risk of diseases occurring in Taiwan. A dynamical TB transmission model with fast-slow progression and relapse was addressed to estimate the contribution percentages of drug-sensitive and drug-resistant Mycobacterium tuberculosis infections in Xinjiang^[20]. Wu et al. ^[21] fitted an age-structured TB model in Hong Kong between $1968$ and $2008$ and used the model to quantify the proportion of annual cases due to recent transmission versus endogenous reactivation of latent infection. Weerasuriya et al. ^[22] established a TB model incorporating relapse and drug-resistance under different vaccine strategies and found that targeting TB vaccination by age may be a more economical method.

However, uncertainty and random phenomena are ubiquitous in the transmission process of infectious diseases. Hence, it is more realistic to investigate the dynamical behaviors of infectious disease models incorporating stochastic variability. Stochastic variability usually includes the variability associated with the environment (such as conditions related to terrestrial or aquatic settings, referred to as environmental variability) and the one associated with individual dynamics (such as transmission, recovery, births or deaths, referred to as demographic random effects)^[23]. Due to the variability associated with individual dynamics during the spread of infectious diseases, the population of each compartment may change at every time. Therefore, the continuous-time Markov chain model (CTMC) is used to characterize this random variability and approximately estimate the disease extinction or outbreak probability and expected epidemic duration of infectious diseases. Thus it could provide the basis and guidance for the prevention and control of infectious diseases^[24]. Jacquez et al. ^[25] studied a continuous-time stochastic SI (Susceptible-Infectoius) epidemic model with recruitment and death. West and Thompson^[26] analyzed continuous-time and discrete-time stochastic SI models and compared the difference between them and the deterministic model. Allen et al. compared the dynamical behaviors of deterministic and stochastic discrete-time SIS (Susceptible-Infectoius-Susceptible) and SIR (Susceptible-Infectoius-Recovered) and obtained the probability distribution and quasi stationary distribution of the infectious in ^[27]. Fatimatuzzahroh et al. ^[28] established a CTMC model for TB transmission incorporating isolation measures and analyzed the impact of isolation measures at different levels on the expected epidemic duration of the disease.

Inspired from the above work, in this paper, we formulate the stochastic CTMC model with fast-slow progression and relapse to explore the impact of stochastic variability associated with individual dynamics on TB transmission. By using the multitype Galton-Waston branching process, we obtain the extinction threshold and the extinction probability of the CTMC model. In numerical simulations, we estimate the probability of the disease extinction and outbreak and expected epidemic duration of the disease and compare the differences between the dynamical behaviors of this stochastic model and those of the deterministic one.

This paper is organized as follows. In Section 2, a deterministic TB model with fast-slow progression and relapse is introduced. In Section 3, a CTMC model is developed based on the deterministic model using the infinitesimal transition probabilities. In Section 4, we use the multitype Galton-Watson branching process to obtain the stochastic threshold for disease extinction and the approximate extinction probability. Numerical simulations are provided to demonstrate our analytical results in Section 5. A brief discussion is given in Section 6.

2.   Deterministic model

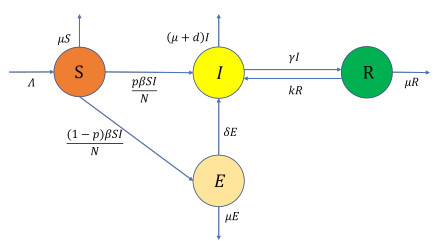
Model (1), proposed by Blower et al. in ^[5], is a classic TB dynamical transmission model. This model was established on the assumption that only a certain fraction of cases are assumed to be infectious and a case may be spontaneously cure (i.e., without treatment) and move into the recovered non-infectious state (so he/she is non-infectious case), that is, there is a non-infectious compartment $T_n$ considered in model (1). However, there are relevant clinical and experimental data indicating that non-infectious is uncommon in immunocompetent individuals ^[29]. Therefore, on basis of model (1), in this paper, we amalgamate the infectious and non-infectious compartments into single one, that is, the total population $N$ is divided into four sub-populations: $S$ (susceptible), $E$ (latently infected, that is, individuals who have been infected with Mycobacterium tuberculosis but have no clinical illness and hence are non-infectious), $I$ (infectious) and $R$ (recovered, that is, an individual in the recovered state may either relapse and develop TB again or may never relapse and die of other cause). The total population has the common natural death rate denoted by $\mu$. Recruitment to the susceptible population occurs at a constant rate $\Lambda$. The susceptible individuals may acquire the infection by contacting infectious individuals at a rate $\frac{\beta SI}{N}$, where $\beta$ is the probability of successful infection for a susceptible individual after contacting with an infected individual per unit time. A proportion $p$ of the newly infected to develop the infectious $I$ directly (fast-progression) and a proportion $(1 - p)$ of the newly infected to enter the class $E$ (slow-progression). Latently infected individuals would either slowly develop TB at an average rate $\delta$ due to endogenous reactivation (several years after infection) or they would die of other causes at an average rate $\mu$ before developing TB. Most active TB patients could be effectively cured by a regimen treatment with recovery rate $\gamma$ and move into the recovered class $R$. The rest of TB patients would die due to TB with a mortality rate $d$. Some recovered individuals may either relapse due to endogenous reactivation and develop the actively infectious TB patients again with the rate $k$ or may never relapse and die of other cause.

Based on the above description, a flowchart for the transmission of TB can be proposed in Figure 1. According to this flowchart, we can establish a TB dynamical transmission model with fast-slow progression and relapse as follows.

where $N = S+E+I+R.$ The detailed descriptions of parameters are provided in Table 1.

The basic reproduction number, $\mathcal{R}_0$, is defined as the number of secondary infections that one infective would produce in a completely susceptible population over the entire period of infectiousness ^[30]. We compute the basic reproduction number for model (2) by using the next generation matrix approach^[30]. The rates of appearance of new infections and transition of individuals are given by

respectively. Then, the new incidence and transition matrices are

respectively. Hence, by calculating $FV^{-1}$, we obtain

Thus, the basic reproduction number $\mathcal{R}_0$ of model (2) is

where $\rho$ denotes the spectral radius of $FV^{-1}.$ Applying Theorem 2 in ^[30], we establish the following result:

Theorem 1. The disease-free equilibrium $E_0 = (\frac{\Lambda}{\mu}, 0, 0, 0)$ of model (2) is locally asymptotically stable if $\mathcal{R}_0 < 1$ and unstable if $\mathcal{R}_0 > 1$.

Theorem 1 shows that when the basic reproduction number $\mathcal{R}_0 < 1$, the disease in model (2) will die out. Otherwise, the disease in model (2) will be prevalent when $\mathcal{R}_0 > 1$.

3.   Stochastic model

Deterministic models have already done well in exploring transmission dynamics of infectious diseases from a theoretical perspective. It could help us to know whether the disease is prevalent or not for long-term infection relying on the basic reproduction number or threshold. However, when there are few infected individuals, deterministic models could not capture the uncertainty and variability that is inherent in real-life epidemics due to demographics or the environment, which is significant when the initial number of infected individuals is small ^[27]. In particular, if one infectious individual is introduced in a completely susceptible population, there is a probability that an infectious individual could die or recover before transmitting the infection to a sufficient number of susceptible population ^[31,32]. Therefore, it is important to consider a stochastic model to capture the variability associated with individual dynamic (e.g., birth or death, transmission, recovery), i.e., demographic variability ^[23]. Since models with demographic variability describe a discrete movement of individuals between epidemiological classes and not average rate, the number in these stochastic models are integers and not continuously changing values ^[31,33]. Therefore, in this paper, based on the assumptions of deterministic TB model (2), we develop a CTMC TB model because the random variables corresponding to the deterministic state variables are discrete and time is continuous. Moreover, inspired by the CTMC models discussed in ^[28,34], we also consider the random effects of individual birth and death processes (i.e., demographic variability).

For simplicity, we use the same notation for the random variables and parameters as used in the deterministic model (2). Let $S(t)$, $E(t)$, $I(t)$ and $R(t)$ be the discrete random variables for the number of the susceptible, latently infected, infectious and recovered at time $t\in[0, +\infty),$ respectively. Here, $S(t)$, $E(t)$, $I(t)$ and $R(t)$ take values in the finite state space $\{0, 1, 2, 3, \cdots, G\},$ where $G$ is the maximum size of the number of total population. For the CTMC model, the transition from one state to another state may occur at any time $t$. All possible state transitions and their corresponding rates for the CTMC model are presented in Table 2.

The stochastic process $\{{\boldsymbol{Z(t)}} = (S(t), \; E(t), \; I(t), \; R(t), t\in[0, +\infty))\}$ is a multivariate process with a joint probability function ^[35,36]

and it is time-homogeneous and satisfies the Markov property stating that the future state of the process at time $(t+\Delta t)$ only depends on the current state of the process at time $t$ ^[31,35]. Hence,

Owing to the Markov assumption, the time to the next event is exponentially distributed ^{[31,35,37,38]}. It is assumed that $\Delta t$ is sufficiently small such that the transition probabilities of the process are within the interval $[0, 1]$ ^[27,35,39] and at most one event takes place during the time interval $[t, t+\Delta t]$ ^[31,40]. Using the notation in ^[35], we have the infinitesimal transition probabilities for the stochastic process ${\boldsymbol{Z}}(t) = (S(t), E(t), I(t), R(t))$ from state $(s, e, i, r)$ at time $t$ to a new state $(s+j_s, e+j_e, i+j_i, r+j_r)$ at time $(t+\Delta t)$ is

and are defined by

where $Q = \Lambda +\mu s+\frac{\beta si}{N}+(\mu+\delta)e+(\mu+d+\gamma)i+(\mu+k)r.$

Applying the Markov property to the stochastic process and the infinitesimal transition probabilities given in Eq (3), we can express the state probabilities at time $(t +\Delta t)$ in terms of the state probabilities at time $t$ ^[41]. Thus, the state probabilities $P_{(s, e, i, r)}(t)$ satisfy the following difference equation

To investigate the time evolution of $P_{(s, e, i, r)},$ we rearrange the terms of Eq (4) and then take the limit as $\Delta t\rightarrow0.$ Then, the following forward Kolmogorov differential equation is derived

4.   Stochastic threshold for disease extinction

Similar to the basic reproduction number $\mathcal{R}_0$ in deterministic models, there exists a threshold in stochastic models which could provide important information about disease extinction and outbreak. If a disease emerges from one infectious group with $\mathcal{R}_0 > 1$ and if $i$ infectious individuals are introduced into a whole susceptible population, then the probability of major disease outbreak is $1-\left(1/\mathcal{R}_0\right)^i$ ^[42]. However, this result does not hold if the infection emerges from multiple infectious groups. For multiple infectious groups, stochastic threshold for disease extinction and outbreak depends not only on the number of individuals in each group but also on the probability of disease extinction for each group. The multitype Galton-Watson branching processes is used to approximate the probability of disease extinction and outbreak. In this section, we first present a general theory of multitype Galton-Watson branching process and then apply it to our stochastic TB model in order to obtain the approximation of the disease extinction and a major outbreak.

4.1.   The multitype Galton-Watson branching process

The multitype Galton-Watson branching process theory addresses questions about extinction and survival in ecology and evolutionary biology ^[42]. In the theory of Galton-Watson branching process, individuals' behaviors are categorised into a finite number of types and each individual's behavior is independent of the other. An individual of a given type could provide offsprings of all possible types, and individuals of the same type have the same offspring distribution. Some of theory of continuous-time, multitype Galton-Watson branching process that relates to probability of ultimate extinction are briefly summarized as follows.

Definition 1. ^[31,42] A multitype Galton-Watson branching process $\{{\boldsymbol{Y}}(t)\}^{\infty}_{t = 0}$ is a collection of vector random variables ${\boldsymbol{Y}}(t)$, where each vector consists of $k$ different types, ${\boldsymbol{Y}}(t) = (y_1(t), y_2(t), \cdots, y_k (t))$ and each random variable $y_i(t)$ has $k$ associated offspring random variables for the number of offsprings of type $j = 1, 2, \cdots, k$ from a parent of type $i$.

The multitype Galton-Watson branching process is applied only to the infectious groups and assumes that susceptible populations are at the disease-free equilibrium ^[43]. Since the multitype Galton-Watson branching process is linear near the disease-free equilibrium, it is homogeneous in time and births (i.e., new infections) and deaths or recovery are independent. Hence, the offspring probability generating functions for the birth and death of infected individuals could be defined. These probability generating functions are then used to approximate the probability of disease extinction or a major outbreak ^[31,43].

Let $\{X_{ji}\}_{j = 1}^n$ be the offspring random variables for type $i$ ($i\in{0, 1, 2, \cdots, n}$) so that $X_{ji}$ be the number of offspring of type $j$ generated by infectious individuals of type $i$. Let the probability that an individual of type $i$ gives birth to $u_j$ individuals of type $j$ be

Thus, the offspring probability generating function for individual of type $i$ given that $y_i(0) = 1$ and $y_j(0) = 0$, $j\neq i$, $f_i:[0, 1]^n\to[0, 1]$ is

There is always a fixed point at $f_i(1, 1, \cdots, 1) = 1$, $f_i(0, 0, \cdots, 0)$ denotes the probability of extinction for $y_i$ given that $y_i(0) = 1$ and $y_j(0) = 0$ for all other types ^[37,42,44].

The expectation matrix of the offspring probability generating functions is defined as $M = [m_{ji}]$, which is an $n \times n$, nonnegative and irreducible matrix, and the element $m_{ji}$ represents the expected number of offsprings of individuals of type $j$ produced by one infective individual of type $i$. $m_{ji}$ is calculated from Eq (6) by differentiating the probability generating functions $f_i$ with respect to $x_j$ and then evaluating all the ${\bf{x}}$ variables at ${\bf{1}}$, that is,

The spectral radius of the expectation matrix $M$, i.e., $\rho(M)$, determines the probability of disease extinction or persistence by the multitype Galton-Watson branching process ^[31]. Thus, if $\rho(M) \leq1$ (sub-critical and critical cases), the probability of disease extinction is $1$ as $t \to\infty$, but when $\rho(M) > 1$ (supercritical case), there is a positive probability that disease may persist ^[31,45]. The criteria for the probability of disease extinction or persistence are summarized in Theorem 2 ^{[31,37,42,43,44]}.

Theorem 2. Let the initial sizes for each type of the infected ${\boldsymbol{Y}}(t) = (y_1(t), y_2(t), \cdots, y_k(t))$ be ${\boldsymbol{Y}}(0) = (y_1(0), y_2(0), \cdots, y_k(0))$. Suppose the generating functions $f_i(x_1, x_2, \cdots, x_k)\; (i = 1, 2, \cdots, k)$ for the infective of type $i$ $(y_i(t))$ are nonlinear functions of $x_j\; (j = 1, 2, \cdots, k)$ with $f_i(0, 0, \cdots, 0) > 0$. Also, suppose that the expectation matrix $M = [m_{ji}]$ of the offspring probability generating functions is an $n \times n$, nonnegative and irreducible matrix. Let $\rho(M)$ be the spectral radius of $M$.

(ⅰ) If $\rho(M) < 1$ or $\rho(M) = 1$ (subcritical and critical cases, respectively), then the probability of ultimate extinction for the infected ${\boldsymbol{Y}}(t)$ is one, that is

(ⅱ) If $\rho(M) > 1$ (supercritical case), then the probability of ultimate extinction for the infected ${\boldsymbol{Y}}(t)$ is less than one, that is

where $(x_1, x_2, \cdots, x_k)$ is the unique fixed point of the offspring probability generating function, $f_i(x_1, x_2, \cdots, x_k)=x_i$ and $0 < x_i < 1$ $(i=1, 2, \cdots, k)$, and the value of $x_i$ is the probability of ultimate extinction for infectives of type $i$. Furthermore, the probability of outbreak for the disease is approximately reached

Moreover, Allen and van den Driessche^[43] proved that the deterministic and stochastic thresholds for disease extinction, $\mathcal{R}_0 > 1$ and $\rho(M)$, respectively, satisfy the following relationship

4.2.   Application of the multitype Galton-Watson branching process to TB model

In our CTMC model, a susceptible individual would be infected by effectively contacting an active TB patient, thus becoming the infectious or latently infected individual with fast-slow progression. A latently infected individual may further progress to the infectious due to endogenous activation of Mycobacterium tuberculosis. Infectious individuals would be cured with a regimen treatment of no less than six months and eventually enter to the recovered. However, individuals who had recovered may also lose their immunity after a period of time and become the infectious (i.e., relapse). Thus, the number of infected individuals during the early stages of TB transmission could be approximated by a three-type Galton-Watson branching process. That is, we define the offspring probability generating functions for three classes: the latent infected $E$, the infectious $I$ and the recovered $R$.

If initially there is a single latently infected individual but no infectious individuals and recovered individuals (i.e., $E(0) = 1$, $I(0) = 0$ and $R(0) = 0$), then the offspring probability generating function for $E$ by using Eq (6) is given by

with $x_i\in[0, 1]$ for $i = 1, 2, 3$. Here, the term $\delta/(\delta+\mu)$ stands for the probability that a latently infected individual successfully progressed the infectious in his/her lifespan, while the term $\mu/(\delta+\mu)$ is the probability that a latently infected individual may die before becoming infectious individual which results in zero latently infected and infectious individuals.

Similarly, when there is a single infectious individual but no the latent infected and recovered individuals at the beginning, that is $I(0) = 1$, $E(0) = 0$ and $R(0) = 0$, the offspring probability generating function for $I$ is given by

with $x_i\in[0, 1]$ for $i = 1, 2, 3$. Here, the term $(1-p)\beta/(\beta+d+\gamma+\mu)$ is the probability that a susceptible individual is successfully infected by an infectious individual and then becomes the latently infected one with slow progression. The term $p\beta/(\beta+d+\gamma+\mu)$ is the probability that a susceptible individual is successfully infected by an infectious individual and then becomes the actively infectious individual with fast progression. The term $\gamma/(\beta+d+\gamma+\mu)$ is the probability that the infectious individual may recover resulting in zero infectious individual and one recovered individual. The term $(d+\mu)/(\beta+d+\gamma+\mu)$ is the probability that the infectious individual may die before transmitting the infection to a susceptible individual leading to zero infectious individual.

If there is a single recovered individual, without the latent infected and infectious individuals at the beginning (i.e., $R(0) = 1$, $E(0) = 0$ and $I(0) = 0$), then the offspring probability generating function for $R$ is given by

with $x_i\in[0, 1]$ for $i = 1, 2, 3$. Here, the term $k/(k+\mu)$ represents the probability that a recovered individual may relapse resulting in an infectious individual and zero recovered individual. The term $\mu/(k+\mu)$ is the probability that the recovered individual may die before relapsing which results in zero recovered individual.

Then, the expectation matrix of the branching process is a $3\times3$ matrix which is determined by using Eq (7), the offspring probability generating Eq (9–11) and evaluated at ${\bf{x}} = (x_1, x_2, x_3) = {\bf{1}}.$ Thus, the expectation matrix $M$ of the offspring probability generating functions is given by

The elements of the first column for the expectation matrix $M$ separately represent the expected number of the latently infected, the infectious and the recovered, generated by a latently infected individual. Likewise, the elements of the second column of $M$ are the expected number of the latently infected, the infectious and the recovered, respectively, generated by a actively infectious individual. And the elements of the third column of $M$ are the expected number of the latently infected, the infectious and the recovered, respectively, generated by a recovered individual.

The threshold for disease extinction or persistence for the CTMC model is the spectral radius of expectation matrix $M$, $\rho(M)$, which is given by

where $a = \delta+\mu, b = \beta+d+\gamma+\mu, c = \mu+k.$ It could easily be verified that Eq (8) holds.

For the supercritical branching process, i.e., $\rho(M) > 1$ and $\mathcal{R}_0 > 1$, there exists a fixed point, $(x_1, x_2, x_3)\in(0, 1)^3$ of the offspring probability generating Eq (9–11), which is used to write the explicit expression for the probability of disease extinction ^[31,42,43]. Let $f_i(x_1, x_2, x_3) = x_i$ for $i = 1, 2, 3.$ Thus, we obtain the following system of equations:

Solving system (12) for $x_1, x_2$ and $x_3$, we obtain

Because $\mathcal{R}_0 = \frac{\beta(\delta+\mu p)(\mu+k)}{(\delta+\mu)(dk+d\mu+\gamma\mu+k\mu+\mu^2)}$, we rewrite $x_2 = \frac{1}{\mathcal{R}_0}$, so $x_1 = \frac{\delta}{(\delta+\mu)\mathcal{R}_0} +\frac{\mu}{\delta+\mu}$ and $x_3 = \frac{k}{(\mu+k)\mathcal{R}_0}+\frac{\mu}{\mu+k}.$ The expression for $x_1$ is the sum of two probabilities: (ⅰ) the probability of a successful progression from one latently infected individual to the infectious $\delta/(\delta+\mu)$ times the probability there are no secondary infections $1/\mathcal{R}_0$ plus (ⅱ) the probability of no successful infections $\mu/(\mu+\delta)$, that is, natural death for the latently infected individual. Similarly, $x_2$ is the probability that there are no secondary infections $1/\mathcal{R}_0$. The value of $x_3$ is the sum of two probabilities: (ⅰ) the probability of a successful relapse from one recovered individual to the infectious $k/(\mu+k)$ times the probability there are no secondary infections $1/\mathcal{R}_0$ plus (ⅱ) the probability of no successful infections $\mu/(\mu+k)$, that is, natural death for the recovered individual.

Therefore, given that the initial numbers of latently infected, infectious and recovered are separately $E(0), I(0)$ and $R(0)$, the probability of extinction for TB is approximated to be ^{[23,35,40,42]}

Moreover, the probability of the outbreak or persistence of disease will be approximated to $1-P_0.$

5.   Numerical simulations

By using numerical simulation, we calculate the probability of disease extinction or outbreak and expected epidemic duration for CTMC model, and compare the differences of dynamical behaviors for deterministic model (2) and CTMC model. The time unit is day.

We set the effective transmission rate of the infectious TB is $\beta = 5.0000\times10^{-3}$ ^[28]. We assume that $\Lambda = 1/(3\times365) = 9.1324\times10^{-4}.$ Because people diagnosed as a TB patient requires about $6$ months to $20$ months treatment regimens ^[2], then we set $\gamma = 1/365 = 2.7397\times10^{-3},$ and TB-related mortality rate is about $6%$ ^[5], so we set $d = 0.06/365 = 1.6438\times10^{-4}$. Since the average lifetime of people in China is $76.34$ years ^[46], that is, $\mu = 1/(76.34\times365) = 3.5888\times10^{-5}$. Moreover, during the first two years of infection, only around $5%$ of these latently infected individuals would progress the infectious^[6]. Hence, we choose $p = 0.05.$ It takes an average of $15$ years for the latently infected to progress the infectious, and about $2.4%$ of the recovered would relapse and become the infectious again^[47]. Then, we select $\delta = 1/(15\times365) = 1.8265\times10^{-4}$ and $k = 0.024/365 = 6.5753\times10^{-5}.$

Under these values of parameters, we obtain that the fixed point of the offspring probability generating functions is $(x_1, x_2, x_3)\approx(0.3955, 0.2767, 0.5321)$. The basic reproduction number of deterministic model (2) is $\mathcal{R}_0\approx3.6141$ and the stochastic threshold of CTMC model is $\rho(M)\approx1.243$. In the following, the multitype Galton-Waston branching process is applied to obtain the probability of disease extinction $P_0$.

5.1.   Probability of disease extinction

We calculate the probability of disease extinction $P_0$ under different initial conditions. As shown in Table 3, the probability of disease extinction is highest $(P_0\approx0.5321)$ when there is a single recovered individual (i.e., $S(0) = 100$, $E(0) = 0$, $I(0) = 0,$ $R(0) = 1),$ the probability of disease prevalence $(1-P_0\approx0.4679)$ is the lowest. Moreover, $P_0$ is smaller $(P_0\approx0.0582)$ if the disease is introduced by one latently infected individual, one infectious individual and one recovered individual. In particular, when the number of all three infected groups increases, $P_0$ decreases $(P_0\approx0.0034)$, that is, the probability of disease outbreak is very high $(1-P_0\approx0.9966)$ if all three infected groups are present at the onset of the epidemic process.

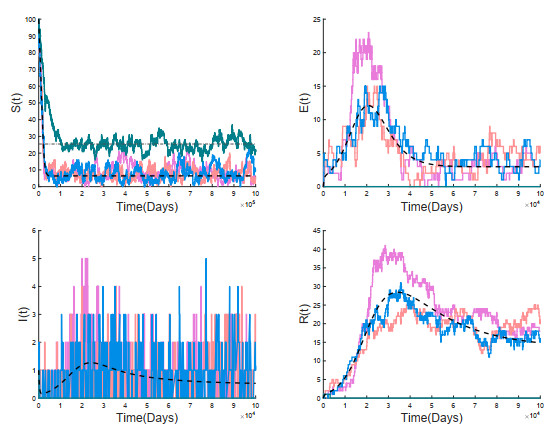
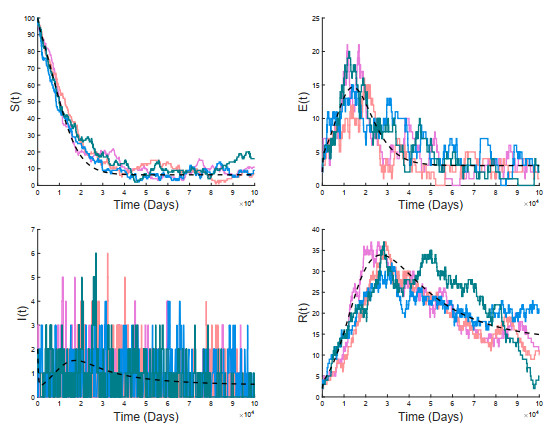
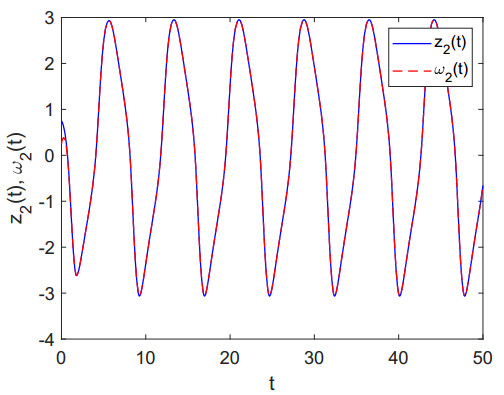
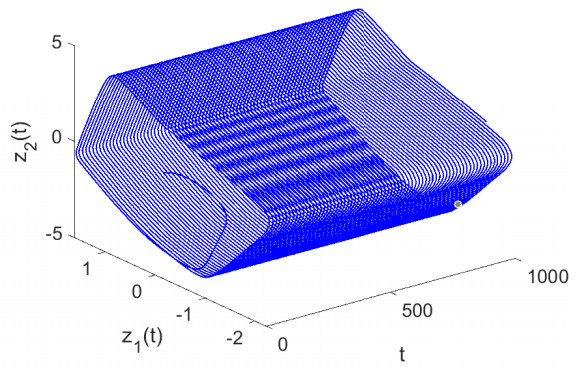
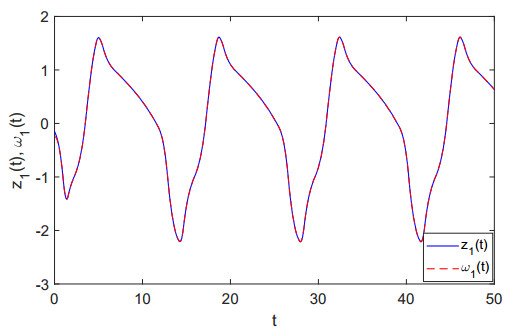
Moreover, we plot the trajectories of the solutions for deterministic model (2) and CTMC model with different initial conditions, respectively. As shown in Figures 2 and 3, the disease is persistent for deterministic model $\mathcal{R}_0\approx3.6141 > 1$ whereas the disease could be extinct (Figure 2) or prevalent (Figure 3) for CTMC model when $\rho(M)\approx 1.243 > 1$, depending on the initial value of three infected groups. This indicates that the dynamical behaviors of CTMC model would be highly dependent on the initial conditions, whereas those of deterministic model would be not affected by the initial conditions.

5.2.   Expected epidemic duration

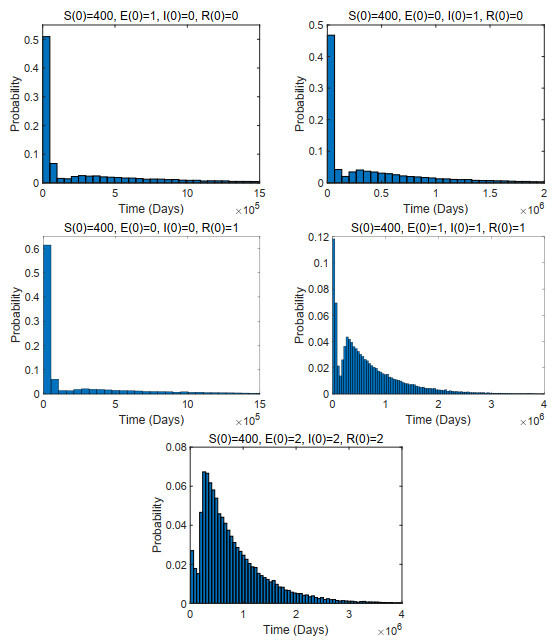
The other difference between stochastic and deterministic models is that stochastic models could estimate the expected epidemic duration of the disease $(T)$, that is, the time until the number of infectious individuals asymptotically approaches zero. The length of $T$ depends on the initial number of infected classes, the population size and the value of $\mathcal{R}_0$ ^[37,39]. In Table 4, the expected epidemic duration $T$ of the disease for CTMC model is estimated under the different initial conditions, based on 50, 000 sample paths and $95$th percentile of end times as indicators of expected epidemic duration.

It could be seen from Table 4 that $T$ is the longest $(1.7040 \times 10^6)$ when the disease is only introduced by an infectious individual, compared with those values of $T$ when the disease is only introduced by one latently infected individual and one recovered individual. This may be due to the fact that it takes a long time for a latently infected individual to progress the actively TB patient (about 10–15 years). In addition, if the disease is introduced by all three infectious classes $(E(0) = I(0) = R(0) = 1$ or $E(0) = I(0) = R(0) = 2),$ then the expected epidemic duration $T$ is the longest $(T = 2.0070\times10^6$ or $2.1532\times10^6).$ Figure 4 shows the approximate probability distribution of expected epidemic duration when the disease is introduced by a latently infected individual, an infectious individual, a recovered individual and all infected groups. The mass of probability distribution in Figure 4 that make up the early disease extinctions corresponds to the probability of disease extinction as predicted by the multitype Galton-Watson branching process (see Table 4).

6.   Discussion

Considering the demographic variation that occurs in the TB transmission (the changes related to individual dynamics, such as births, deaths, infection, recovery and relapse etc.), in this paper, a stochastic CTMC model with fast-slow progression and relapse was established. By using multitype Galton-Watson branching process, the stochastic threshold $\rho(M)$ of this model and the probability of disease extinction and outbreak were obtained. General speaking, the disease would become extinct for deterministic model and stochastic model both for when $\mathcal{R}_0 < 1$ and $\rho(M) < 1.$ However, the disease would be persistent for deterministic model if $\mathcal{R}_0 > 1$, whereas there is a possibility of disease extinction for the stochastic model if $\rho(M) > 1$. Numerical simulations were performed not only to support our analytical results but also to obtain the probability of extinction and expected epidemic duration when the disease was introduced by different initial conditions. Figures 2 and 3 indicated that when $\mathcal{R}_0 > 1$ and $\rho(M) > 1,$ the disease of the deterministic model would be prevalent while the disease for stochastic model might be extinct with a certain probability, depending on the initial value of infectious classes. The factor which causes this difference might be the demographic stochasticity that is inherent in the stochastic models, which is one of the major asymptotic differences between deterministic and stochastic models^[23,39].

In addition, the random fluctuation in the infectious compartment $I$ is strongest, followed by the random fluctuation in latently infected compartment $E$, and the random fluctuations in the recovered compartment $R$ is weakest (see Figures 2 and 3), which indicates that the susceptible should minimize the contacts with TB patients as much as possible and some latently infected individuals should be detected as early as possible so that the spread of TB could be effectively prevented.

There are also other interesting questions deserving our further exploration. Although we put our model in the context of a biological question, we determine parameter from some related literature in our numerical simulations. If we can calibrate the transmission rate $\beta$ of our stochastic CTMC model by using actual reported TB cases in China, for example, similar to the references [48,49], it would make progress on the biological question by way of numerical simulations. Then, the conclusions obtained in our paper would be more convincing. In addition, relevant reports indicated that Bacillus Calmette-Guerin vaccine has been introduced in the national immunization program in more than 80% of countries worldwide ^[2]. Therefore, we could further establish a stochastic SVEIR model to assess the effect of vaccination on TB transmission. Moreover, most TB patients could be cured after receiving regular treatments, but those patients might eventually develop into drug-resistant TB patients due to unreasonable or nonstandard treatment ^[2,20]. Therefore, we could further investigate a stochastic CTMC model of drug-resistant TB transmission ^[50]. Last but not least, air temperature, relative humidity and the other climatic factors may affect the Mycobacterium tuberculosis transmission. Hence, it is important to establish a stochastic CTMC model in order to explore the effects of seasonal variation on TB transmission dynamic ^[51].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Grants No. 12061079, 12101529, 12371504) and Project of Top-notch Talents of Technological Youth of Xinjiang (Grant No. 2022TSYCCX0108).

Conflict of interest

The authors declare there is no conflicts of interest.