Planar graphs without $\{4, 6, 8\}$-cycles are 3-choosable

1.   Introduction

All graphs considered in this paper are simple and finite. Let $G$ be a planar graph, and let $V(G)$, $E(G)$ and $F(G)$ be sets of vertices, edges and faces of $G$, respectively. Let $f$ be a face in $F(G)$, we write $f = [v_{1}v_{2}\cdots v_{k}]$ when the vertices incident with $f$ are in a cyclic order $v_{1}, v_{2}, \cdots, v_{k}$. Let $|C|$ ($|P|$) be the number of edges incident with the cycle $C$ (the path $P$). A $k$-path $P$ is a path with $|P| = k$. Let a $k$-vertex ($k^{-}$-vertex, $k^{+}$-vertex) be a vertex with degree $k$ (at most $k$, at least $k$). The notations will be same for cycles and faces. A triangle is a 3-cycle in $G$. An edge or a vertex is triangular when it is incident with a triangle. Let $Ext(C)$ (or $Int(C)$) be induced by the vertices outside (or inside) of $C$. Let $\overline{Ext}(C) = C\bigcup Ext(C)$ and $\overline{Int}(C) = C\bigcup Int(C)$. If $Ext(C)\neq \emptyset$ and $Int(C)\neq \emptyset$, then $C$ is separating.

A proper $k$-coloring of $G$ is a function $f:V (G) \rightarrow [k]$ such that $f(u) \neq f(v)$ whenever $uv \in E(G)$. The chromatic number of $G$ is the smallest $k$ such that $G$ is proper $k$-colorable, denoted by $\chi(G)$. On the 3-colorability of planar graphs, Grötzsch ^[1] proved that every planar graph without triangles is 3-colorable. In 1976, Steinberg ^[2] conjectured that planar graphs without $\{4, 5\}$-cycles are 3-colorable. Borodin et al. ^[3] proved that every planar graph without cycles of lengths 4 to 7 is 3-colorable. Wang and Chen ^[4] proved that every planar graph without $\{4, 6, 8\}$-cycles is 3-colorable. Choi, Yu and Zhang ^[5] proved that planar graphs with girth at least 5 are (3, 4)-colorable. Li and Zhang ^[6] proved that every planar graph with minimum degree at least 2 and girth at least 8 has an $RE$-$m$-coloring for each integer $m\geq4$.

List coloring was introduced by Vizing ^[7] and independently by Erdős, Rubin and Taylor ^[8]. A list assignment $L$ of $G$ is a mapping that assigns to each $v$ in $G$ a list of available colors $L(v)$. An $L$-coloring of $G$ is a function $f : V(G)\rightarrow \bigcup_{v \in V(G)}L(v)$ such that $f(v)\in L(v)$ for every $v \in V(G)$ and $f(u)\neq f(v)$ whenever $uv \in E(G)$. A graph $G$ is $k$-choosable if $G$ is $L$-colorable for each $L$ with $|L(v)|\geq k$. The choice number of $G$ is the smallest $k$ such that $G$ is $k$-choosable, denoted by $\chi_{l}(G)$. Thomassen ^[9] proved that every planar graph without $\{3, 4\}$-cycles is 3-choosable. Dvo${\rm{\hat r}}$ák ^[10] showed that every planar graph with the distance of $\{3, 4\}$-cycles from each other at least 26 is 3-choosable.

The method of identification of vertices can be used for ordinary coloring since all vertices have the same color set. But for list coloring, it is impossible to use the method since different vertices may have different color lists. To overcome this difficulty, Dvořák and Postle ^[11] introduced DP-coloring. Here we give some definitions.

Definition 1. Let $L$ be a list assignment for a simple graph $G$. Let $\mathcal{L}(v) = \{v\}\times L(v)$ for each vertex $v$ in $G$. Let $M_{uv}$ be a matching between $\mathcal{L}(u)$ and $\mathcal{L}(v)$ for each edge $uv$ in $G$. Let $\mathcal{M} = \bigcup_{uv\in E(G)}M_{uv}$ be a matching assignment for $G$. For each $v\in V(G)$, if $L(v) = [k]$, then the matching assignment is a $k$-matching assignment. A cover of $G$ is a graph $\mathcal{G}_{L, \mathcal{M}}$ which satisfies the following two conditions:

(1) The set of vertices of $\mathcal{G}_{L, \mathcal{M}}$ is the disjoint union of $\mathcal{L}(v)$ for all $v\in V(G)$;

(2) The set of edges of $\mathcal{G}_{L, \mathcal{M}}$ is $\mathcal{M}$.

Note that for each $v$ in $G$, $\mathcal{G}_{L, \mathcal{M}}[\mathcal{L}(v)]$ is an independent set.

Definition 2. Let $\mathcal{G}_{L, \mathcal{M}}$ be a cover of a simple graph $G$. If $\mathcal{G}_{L, \mathcal{M}}$ has an independent set $\mathcal{I}$ such that for each $v$ in $G$, $|\mathcal{I} \bigcap \mathcal{L}(v) | = 1$, then $G$ is $\mathcal{M}$-colorable. If $G$ is $\mathcal{M}$-colorable for each $k$-matching assignment $\mathcal{M}$, then $G$ is DP-$k$-colorable. The DP-chromatic number of $G$, denoted by $\chi_{DP}(G)$, is the smallest $k$ such that $G$ is DP-$k$-colorable.

Let $W = v_{1} v_{2} \cdots v_{m}$ be a closed walk with length $m$ in $G$. Let $\mathcal{M}$ be a $k$-matching assignment on $W$. If $l_{1}, l_{1}'\in L(v_{1})$ and $l_{i}\in L(v_{i})$ for $i = 2, \cdots, m$ such that $(v_{i}, l_{i})(v_{i+1}, l_{i+1})$ is an edge in $M_{v_{i}v_{i+1}}$ for $i = 1, \cdots, m-1$, and $(v_{m}, l_{m})(v_{1}, l_{1}')$ is an edge in $M_{v_{m}v_{1}}$ with $l_{1}'\neq l_{1}$, then $\mathcal{M}$ is inconsistent on $W$. Otherwise, $\mathcal{M}$ is consistent on $W$.

Dvořák and Postle ^[11] showed that planar graphs without cycles of lengths 4 to 8 are 3-choosable and noticed that $\chi_{DP}(G) \leq 3$ if $G$ is a planar graph with girth at least 5. Liu and Li ^[12] proved that every planar graph without adjacent cycles of length at most 8 is 3-choosable. Bernshteyn et al. ^{[13,14,15,16,17]} gave some other results of DP-coloring. Liu et al. ^[18,19,20] showed some sufficient conditions for planar graphs to be DP-3-colorable, and ^[21,22,23] showed some sufficient conditions for planar graphs to be DP-4-colorable. In this paper, we prove the following result, which extends the results of Dvořák and Postle ^[11] and Wang and Chen ^[4].

Theorem 1. Planar graphs without $\{4, 6, 8\}$-cycles are 3-choosable.

Let $\mathcal{G}$ be a set of planar graphs with no 4-, 6- or 8-cycle. We will prove the following result stronger than Theorem 1.

Theorem 2. Let $G\in\mathcal{G}$, and let $\mathcal{M}$ be a 3-matching assignment for $G$ such that $\mathcal{M}$ is consistent on every closed walk with length 3. Let $S$ be a subset of $V(G)$ such that either $|S|\leq 1$, or $S$ consists of all vertices on the outer face of $G$, then

($\rm{i}$) $G$ is $\mathcal{M}$-colorable, and

($\rm{ii}$) Let $D$ be the boundary cycle of the outer face of $G$. If $|D|\leq12$, then for every $\mathcal{M}$-coloring $\phi_{0}$ of $S$, $G$ has an $\mathcal{M}$-coloring $\phi$ whose restriction to $S$ is $\phi_{0}$.

Let $\mathcal{M}$ be a $k$-matching assignment. If $|E(M_{uv})| = k$, then $uv$ is full in $\mathcal{M}$. If for every $(u, c_{1})(v, c_{2}) \in E(M_{uv})$, $c_{1} = c_{2}$, then $uv$ is straight in $\mathcal{M}$.

Lemma 3. ^[11] Let $\mathcal{M}$ be a $k$-matching assignment for a simple graph $G$. Let $J$ be a subgraph of $G$. For every cycle $C$ in $J$, if all edges of $C$ are full and $\mathcal{M}$ is consistent on $C$, then we obtain a $k$-matching assignment $\mathcal{M}'$ from $\mathcal{M}$ by renaming $L(u)$ for $u\in J$ such that every edge in $J$ is straight in $\mathcal{M}'$.

2.   Proof of Theorem 2

Assume that Theorem 2 fails. If $G$ is a planar graph with girth at least 5, then by Reference ^[11] it is DP-3-colorable, so $G$ is $\mathcal{M}$-colorable and ($\rm{i}$) holds. If $G$ has a 3-cycle $C$ such that its $\mathcal{M}$-coloring cannot be extended either to $Int(C)$ or to $Ext(C)$, then there exists a counterexample to Statement ($\rm{ii}$). Let $G$ be a minimal counterexample, such that

Subject to (a),

Subject to (a) and (b),

Lemma 4. If $v\notin S$, then $v$ is a $3^{+}$-vertex.

Proof. Let $v$ be a 2$^{-}$-vertex in $G-S$. By condition (a), $\phi_{0}$ can be extend to $G-\{v\}$. Since $v$ has at most two neighbors, we can color $v$ such that $(v, \phi(v))(u, \phi(u))\not \in E(M_{uv})$ for each neighbor $u$ of $v$. Therefore, $G$ is $\mathcal{M}$-colorable, a contradiction.

Lemma 5. Let $C$ be a $12^{-}$-cycle in $G$. If $C$ has a chord $e$, then $|C| = 10, 11$ or 12 and either $e$ is triangular, or $e$ divides $C$ into a 5-cycle and a 7-cycle when $C$ is a 10-cycle, or $e$ divides $C$ into a 5-cycle and a 9-cycle when $C$ is a 12-cycle, or $e$ divides $C$ into two 7-cycles when $C$ is a 12-cycle.

Furthermore, if $C$ has two chords, then the two chords divide $C$ into two triangles and a 9-cycle when $C$ is an 11-cycle, or the two chords divide $C$ into two triangles and a 10-cycle when $C$ is a 12-cycle. If $C$ has three chords, then $C$ is a 12-cycle and the three chords divide $C$ into three triangles and a 9-cycle.

Proof. Since $G\in\mathcal{G}$, $G$ has no 4-, 6- or 8-cycle. If $C$ is a $9^{-}$-cycle, then $C$ has no chord.

If $C$ has one chord, then $|C| = 10, 11$ or 12. If $C$ is a 10-cycle and has a chord $e$ that is not triangular, then $e$ divides $C$ into a 5-cycle and a 7-cycle. If $C$ is an 11-cycle then $C$ has only one triangular chord. If $C$ is a 12-cycle and has a chord $e$ that is not triangular, then $e$ divides $C$ into a 5-cycle and a 9-cycle, or two 7-cycles. If $C$ has two chords $e_{1}$ and $e_{2}$, then $|C| = 11$ or 12. If $C$ is an 11-cycle, then $e_{1}$ and $e_{2}$ divide $C$ into two triangles and a 9-cycle. If $C$ is a 12-cycle, then $e_{1}$ and $e_{2}$ divide $C$ into two triangles and a 10-cycle. If $C$ has three chords, then $C$ is a 12-cycle and the three chords divide $C$ into three triangles and a 9-cycle.

Lemma 6. $G$ is 2-connected.

Proof. First, $G$ is connected by the condition (a),

Next, if $v$ is a cut-vertex of $G$ and $G = G_{1}\bigcup G_{2}$ such that $V(G_{1})\bigcap V(G_{2}) = \{v\}$. If $v \in S$, then by the condition (a), $G_{1}$ and $G_{2}$ have an $\mathcal{M}$-coloring extending $\phi_{0}$. Thus, $G$ has an $\mathcal{M}$-coloring extending $\phi_{0}$, a contradiction. If $v\not \in S$, w.l.o.g., let $S\subset V(G_{1})$. Then by the condition (a), $G_{1}$ has an $\mathcal{M}$-coloring $\phi_{1}$ extending $\phi_{0}$, and $G_{2}$ has an $\mathcal{M}$-coloring $\phi_{2}$ extending $\phi_{1}(v)$. Thus, $\phi_{1}$ and $\phi_{2}$ together give an extension of $\phi_{0}$ to $G$, a contradiction.

Lemma 7. $G$ has no separating 12$^{-}$-cycle.

Proof. Suppose that $C$ is a separating $12^{-}$-cycle in $G$. Then $\overline{Ext}(C)$ has an $\mathcal{M}$-coloring $\phi_{1}$ extending $\phi_{0}$. Then the restriction of $\phi_{1}$ to $C$ can be extended to $\phi_{2}$ of $Int(C)$. Thus, $\phi_{1}$ and $\phi_{2}$ together give a coloring of $G$ that extends $\phi_{0}$, a contradiction.

By Lemma 5 and Lemma 7, all 9$^{-}$-cycles of $G$ are facial.

Lemma 8. If $|S|\leq 1$, then $G$ is $\mathcal{M}$-colorable. So we still need to consider the case of $S = V(D)$.

Proof. Suppose that $|S|\leq 1$. If $S = \emptyset$, then we can include an arbitrary vertex of $G$ in $S$, and thus without loss of generality, we can assume that $S = \{v\}$ for some vertex $v\in V(G)$. If $v$ is on a $12^{-}$-cycle, then by Lemma 7, $v$ is on a $12^{-}$-face $f_{1}$ whose boundary cycle is induced in $G$. Now let $G$ be embedded in a plane such that $f_{1}$ is the outer face of the embedding. Let $S_{1} = V(f_{1})$. We choose an $\mathcal{M}$-coloring $\phi_{1}$ for $S_{1}$, then $|E(G)|-|E(G[S_{1}])| < |E(G)|-|E(G[S])|$ and $G$ has an $\mathcal{M}$-coloring extending $\phi_{1}$ by the condition (b). This implies that $G$ has an $\mathcal{M}$-coloring that extends $\phi_{0}$.

If every cycle incident with $v$ is a $13^{+}$-cycle, then $G$ has a $13^{+}$-face $f_{2}$ incident with $v$. Let $v _{1}, v _{2}\in V(f_{2})$ be adjacent to $v$. Let $G\bigcup \{v_{1}v_{2}\} = G'$, then $f_{3} = [v_{1}v_{2}v]$ is a 3-face. Let $G'$ be embedded in a plane such that $f_{3}$ is the outer face of the embedding. Let $S_{2} = \{v_{1}, v_{2}, v\}$ and $\mathcal{M}^{'}$ be obtained from $\mathcal{M}$ with $M_{v_{1}v_{2}}$ is edgeless. We choose an $\mathcal{M}^{'}$-coloring $\phi_{2}$ for $S_{2}$, then $|E(G')|-|E(G'[S_{2}])| < |E(G)|-|E(G[S])|$ and $G'$ has an $\mathcal{M}^{'}$-coloring extending $\phi_{2}$ by the condition (b). This implies that $G$ has an $\mathcal{M}$-coloring that extends $\phi_{0}$. So we still need to consider the case of $S = V(D)$.

Lemma 9. $D$ has no chord.

Proof. Suppose otherwise that $D$ is divided by a chord into two cycles $D_{1}$ and $D_{2}$, where $|D_{1}|\leq |D_{2}|$. Since $|D|\leq12$, $|D_{1}|+|D_{2}| = |D|+2\leq14$. Then we have $3\leq|D_{1}|\leq |D_{2}|\leq11$. By Lemma 7, both $D_{1}$ and $D_{2}$ are not separating. This implies that $V(G) = V(D)$ and $G$ has been $\mathcal{M}$-colorable, a contradiction.

$P$ is a dividing path of $C$ if its two end-vertices are in $V(C)$ and all other vertices of $P$ are in $Int(C)$.

Lemma 10. If $P$ is a dividing path of $D$, then $D$ is divided by $P$ into two cycles $D_{1}$ and $D_{2}$.

(1) If $|P| = 2$, then one of $\{D_{1}, D_{2}\}$ is a 3-cycle;

(2) if $|P| = 3$, then one of $\{D_{1}, D_{2}\}$ is a 5-cycle;

(3) if $|P| = 4$, then one of $\{D_{1}, D_{2}\}$ is a 5- or 7-cycle;

(4) if $|P| = 5$, then one of $\{D_{1}, D_{2}\}$ is a 9$^{-}$-cycle.

Proof. (1) Let $P = uvw$ and $|D_{1}|, |D_{2}|\geq5$. $v$ has a neighbor $v'$ not in $V(P)$ by Lemma 4. W.l.o.g., let $|D_{1}|\leq |D_{2}|$. Since $|D|\leq12$, $|D_{1}|+|D_{2}| = |D|+2\times|P|\leq12+2\times|P| = 16$. Then we have $5\leq|D_{1}| < 8$ and $5\leq |D_{2}|\leq11$. Since $|D_{1}|$ and $|D_{2}|$ are not separating by Lemma 7, $vv'$ is a chord of $D_{1}$ or $D_{2}$. Since $5\leq|D_{1}| < 8$, $D_{1}$ has no chord by Lemma 5. Then $vv'$ is a chord of $D_{2}$ and $|D_{2}|\geq10$. Since $G$ has no 6-cycle, if $|D_{2}| = 10$, then $|D_{1}| = 5$ and $vv'$ splits $D_{2}$ into a triangle and a 9-cycle, or a 5-cycle and a 7-cycle. This implies that $G$ contains a 6-cycle or an 8-cycle, a contradiction. If $|D_{2}| = 11$, then $|D_{1}| = 5$ and $vv'$ splits $D_{2}$ into a triangle and a 10-cycle. This implies that $G$ contains a 6-cycle, a contradiction.

(2) Let $P = uvwx$ and $|D_{1}|, |D_{2}|\geq7$. W.l.o.g., let $|D_{1}|\leq |D_{2}|$. Since $|D|\leq12$, $|D_{1}|+|D_{2}| = |D|+2\times|P|\leq12+2\times|P| = 18$. Then we have $7\leq|D_{1}|\leq 9$ and $7\leq |D_{2}|\leq11$. If two nonconsecutive vertices of $P$ are connected by an edge $e$, then a part of $P$ together with $e$ can form a cycle $C$. Since $G$ has no 4-cycle, $|C| = 3$. W.l.o.g., let $e = uw$ and let $e$ lie inside $D_{1}$. Now $D$ is divided by the path $uwx$ into $D'$ and $D''$. By (1), one of $\{D', D''\}$ is a triangle. By Lemma 7, the triangle is not separating. Since the location of vertex $v$, $D_{1}$ is a 4-cycle, a contradiction. So $w$ ($v$) has a neighbor $w'$ ($v'$) not in $V(P)$ by Lemma 4.

Since $|D_{1}|$ and $|D_{2}|$ are not separating by Lemma 7, $vv'$ and $ww'$ are two chords of $D_{1}$ or $D_{2}$. Since $7\leq|D_{1}| < 9$, $D_{1}$ has no chord by Lemma 5. Then $vv'$ and $ww'$ are two chords of $D_{2}$. By Lemma 5, $|D_{2}| = 11$. Since $|D_{1}|+|D_{2}|\leq18$, $|D_{1}| = 7$ and the two chords split $D_{2}$ into two triangles and a 9-cycle. This implies that $G$ has an 8-cycle, a contradiction.

(3) Let $P = vwxyz$ and $|D_{1}|, |D_{2}|\geq9$. W.l.o.g., let $|D_{1}|\leq |D_{2}|$. Since $|D|\leq12$, $|D_{1}|+|D_{2}| = |D|+2\times|P|\leq12+2\times|P| = 20$. Then we have $9\leq|D_{1}|\leq 10$ and $9\leq |D_{2}|\leq11$. If two nonconsecutive vertices of $P$ are connected by an edge $e$, then a part of $P$ together with $e$ can form a cycle $C$. By Lemma 9, $D$ has no chord, so $|C|\neq5$. Since $G$ has no 4-cycle, $|C| = 3$. W.l.o.g., let $e = wy$ and let $e$ lie inside $D_{1}$. Now $D$ is divided by the path $vwyz$ into $D'$ and $D''$. By (2), one of $\{D', D''\}$ is a 5-cycle. By Lemma 7, the 5-cycle is not separating. Since the location of vertex $x$, $D_{1}$ is a 6-cycle, a contradiction. So $y$ ($w$, $x$) has a neighbor $y'$ ($w'$, $x'$) not in $V(P)$ by Lemma 4.

Since $|D_{1}|$ and $|D_{2}|$ are not separating by Lemma 7, $ww'$, $xx'$ and $yy'$ are three chords of $D_{1}$ or $D_{2}$. If $|D_{1}| = 9$, then $|D_{2}|\in\{9, 10, 11\}$. By Lemma 5, $D_{1}$ has no chord and $D_{2}$ cannot have three chords, a contradiction. If $|D_{1}| = 10$, then $|D_{2}| = 10$. By Lemma 5, both $D_{1}$ and $D_{2}$ have at most one chord respectively, a contradiction.

(4) Let $P = uvwxyz$ and $|D_{1}|, |D_{2}|\geq10$. W.l.o.g., let $|D_{1}|\leq |D_{2}|$. Since $|D|\leq12$, $|D_{1}|+|D_{2}| = |D|+2\times|P|\leq12+2\times|P| = 22$. Then we have $10\leq|D_{1}|\leq 11$ and $10\leq |D_{2}|\leq12$. If two nonconsecutive vertices of $P$ are connected by an edge $e$, then a part of $P$ together with $e$ can form a cycle $C$. Since $G$ has no 4- or 6-cycle, $|C| = \{3, 5\}$. Let $|C| = 5$. W.l.o.g., let $e = vz$ and let $e$ lie inside $D_{1}$. Then $D$ is divided by the path $uvz$ into $D'$ and $D''$. By (1), one of $\{D', D''\}$ is a triangle. By Lemma 7, the 3-cycle is not separating. Since the location of vertex $w$, $D_{1}$ is a 6-cycle, a contradiction. Let $|C| = 3$. W.l.o.g., let $e = vx$ and let $e$ lie inside $D_{1}$. Then $D$ is divided by the path $uvxyz$ into $D'$ and $D''$. By (3), one of $\{D', D''\}$ is a 5- or 7-cycle. By Lemma 7, the $7^{-}$-cycle is not separating. Since the location of vertex $w$, $D_{1}$ is a 6-cycle or an 8-cycle, a contradiction. So $x$ ($w$, $y$, $v$) has a neighbor $x'$ ($w'$, $y'$, $v'$) not in $V(P)$.

Since $|D_{1}|$ and $|D_{2}|$ are not separating by Lemma 7, $ww'$, $xx'$, $vv'$ and $yy'$ are four chords of $D_{1}$ or $D_{2}$. If $|D_{1}| = 10$, then $|D_{2}| = \{10, 11, 12\}$. Since $D_{1}$ has at most one chord by Lemma 5, $|D_{2}| = 12$ and $D_{2}$ has three chords. Then the three chords split $D_{2}$ into three triangles and a 9-cycle, this implies that $G$ has a 4-cycle, a contradiction. If $|D_{1}| = 11$, then $|D_{2}| = 11$. By Lemma 5, both $D_{1}$ and $D_{2}$ have two chords respectively, and the chords split them into two triangles and a 9-cycle respectively. Since $G$ contains no edge that connects two nonconsecutive vertices on $P$ and two chords split $D_{1}$ into two triangles and a 9-cycle, $vv'$ and $yy'$ are the two chords of $D_{1}$. But $ww'$ and $xx'$ cannot split $D_{2}$ into two triangles and a 9-cycle, a contradiction.

The following Lemma 11 and Lemma 12 about some crucial properties of the 3-matching assignment $\mathcal{M}$ are from ^[11]. Since the proof processes are similar, they are omitted here.

Lemma 11. ^[11] If $uv\in E(G)$ and $uv\not \in E(D)$, then $|E(M_{uv})|\geq 2$ in the 3-matching assignment $\mathcal{M}$. Moreover, if $uv$ is not triangular, then $uv$ is full in the 3-matching assignment $\mathcal{M}$.

Lemma 12. ^[11] Let $T = [uvw]$ be a triangle in $G$. If $u, w\not\in V(D)$ and $d(u) = d(w) = 3$, then all edges on the triangle are full in the 3-matching assignment $\mathcal{M}$.

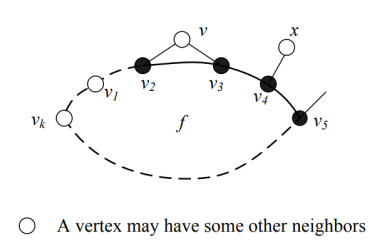
Let $f_{0}$ be the outer face of $G$, then $D$ is the boundary cycle of $f_{0}$. A vertex or an edge is internal when it is not on $D$. A 3-path $P$ is good if every $v\in V(P)$ is an internal 3-vertex and at least one end-edge of $P$ is triangular as shown in Figure 1.

Lemma 13. No face of $G$ is incident with a good 3-path.

Proof. Suppose otherwise that $G$ contains a $k$-face $f$ which is incident with a good 3-path $P$ (see Figure 1). Since $G$ has no 4-, 6- or 8-cycle, $k\geq9$. Let $f = [v_{1}v_{2}\cdots v_{k}]$ and $P = v_{2}v_{3}v_{4}v_{5}$. Let $v$, which is not on $P$, be the common neighbor of $v_{2}$ and $v_{3}$. Let $x$, which is not on $P$, be the neighbor of $v_{4}$. Since $G$ contains no 4-cycle, $x\neq v$ and $x\neq v_{1}$. We delete $\{v_{5}, v_{4}, v_{3}, v_{2}\}$ and identify $x$ and $v_{1}$. Let $G'$ be the resulting planar graph.

Suppose that two vertices of $D$ are identified, or two vertices of $D$ are connected by an edge. Then $P$ is a dividing 4- or 5-path of $D$ which has $\{x, v_{4}, v_{3}, v_{2}, v_{1}\}$. Thus $G$ contains a 9$^{-}$-cycle $C$ formed by a part of $D$ and $P'$ by Lemma 10. Since $|C|\leq9$, $C$ is facial and neither $v$ nor $v_{5}$ lie inside $C$. Since $v_{5}$ is internal, $v$ is on $C$. Now $vv_{2}$ and $vv_{3}$ are two chords of $C$, contrary to that $C$ is facial. For each $uv\in E(G')$, let $M'_{uv} = M_{uv}$ and $\mathcal{M}' = \bigcup_{uv\in E(G')}M'_{uv}$. Then the $\mathcal{M}'$-coloring of $D$ in $G'$ is $\phi_{0}$.

Suppose that an 8$^{-}$-cycle is created. Then $G-\{v_{5}\}$ contains a 12$^{-}$-cycle $C$ that contains $v_{1}v_{2}\cdots v_{4}x$. If $v$ is on $C$, then $G$ contains a 6$^{-}$-cycle adjacent to $[vv_{2}v_{3}]$, a contradiction. Thus $v$ lies inside $C$, and $C$ is separating, contradicting Lemma 7. Therefore we create no $8^{-}$-cycle. So $G'\in\mathcal{G}$ and $\mathcal{M}'$ is consistent on every closed walk of length 3.

Since $|V(G')| < |V(G)|$, then $G'$ has an $\mathcal{M}'$-coloring $\phi'$ extending $\phi_{0}$ by condition (a). Since $d(v_{2}) = d(v_{3}) = 3$, each edge of $[vv_{2}v_{3}]$ is full by Lemma 12. If $v_{5}$ is adjacent to $x$, recall $d(v_{4}) = d(v_{5}) = 3$, then each edge of $[xv_{4}v_{5}]$ is full by Lemma 12. If $v_{5}$ is not adjacent to $x$, then $v_{4}$ is not on a triangle, then by Lemma 11 and Lemma 12, all edges incident with $v_{2}$, $v_{3}$ and $v_{4}$ are full. Since $\mathcal{M}$ is consistent on each closed walk of length 3, we can rename the vertices in $\{v_{2}$, $v$, $v_{3}$, $v_{4}$, $x\}$ so that each edge in $\{v_{1}v_{2}$, $v_{2}v$, $v_{2}v_{3}$, $v_{3}v$, $v_{3}v_{4}$, $v_{4}x\}$ is straight by lemma 3. Now we keep the color of every vertex in $G'$ and give the color of the identified vertex to $v_{1}$ and $x$. We color $v_{5}$ and $v_{4}$ in the order. Since $v_{1}$ and $v_{4}$ have different colors, $v_{2}$ and $v_{3}$ can be colored. Thus, $G$ has an $\mathcal{M}$-coloring extending $\phi_{0}$, a contradiction.

A vertex is bad if it is a triangular internal vertex with degree 3. Otherwise it is good.

Lemma 14. No face of $G$ has five bad vertices which are consecutive. Furthermore, if a 9$^{+}$-face $f$ of $G$ contains a path $v_{0} v_{1}\cdots v_{5}$ and the vertices $v_{1}, \cdots, v_{4}$ are bad, then each edge in $\{v_{0}v_{1}$, $v_{2}v_{3}$, $v_{4}v_{5}\}$ is triangular.

Proof. Since $G$ has no 4-, 6- or 8-cycle, $f$ has no bad vertex when $d(f)\leq7$. Let $d(f)\geq9$. Suppose that $f$ contains five bad vertices in a path $v_{1}v_{2}\cdots v_{5}$. Since $v_{3}$ is triangular and $G$ contains no 4-cycle, we can assume that $v_{2}v_{3}$ is triangular by symmetry. Since $d(v_{3}) = 3$, $v_{3}v_{4}$ is not triangular, and thus the triangle which is incident with $v_{4}$ contains $v_{4}v_{5}$. Then $v_{2}v_{3}v_{4}v_{5}$ is a good 3-path, a contradiction.

Similarly, if a 9$^{+}$-face $f$ of $G$ contains a path $v_{0} v_{1}\cdots v_{5}$ and the vertices $v_{1}, \cdots, v_{4}$ are bad, then either each edge in $\{v_{1}v_{2}, v_{3}v_{4}\}$ or each edge in $\{v_{0}v_{1}, v_{2}v_{3}, v_{4}v_{5}\}$ is triangular. In the former case, the path $v_{1}v_{2}v_{3}v_{4}$ is a good 3-path, contrary to Lemma 13. Therefore, only the latter case remains. Then each edge in $\{v_{0}v_{1}, v_{2}v_{3}, v_{4}v_{5}\}$ is triangular.

Lemma 15. $G$ has no 5-face containing five internal 3-vertices.

Proof. Suppose otherwise that a 5-face $f$ in $G$ contains five internal 3-vertices. Let $f = [v_{1}v_{2}\cdots v_{5}]$, and let $u_{i}$ be the neighbor of $v_{i}$ not on $f$ for $1\leq i \leq 5$. Since $G$ has no 4- or 6-cycle, the vertices in $\{u_{1}, u_{2}, \cdots, u_{5}\}$ are pairwise distinct. Since $G$ has no 6- or 8-cycle, each vertex in $V(f)$ is on two $7^{+}$-faces. By Lemma 11, each edge in $\{u_{2}v_{2}, v_{2}v_{1}, v_{1}u_{1}, v_{1}v_{5}, v_{5}u_{5}\}$ is full. We can rename the vertices in $\{v_{2}, v_{1}, u_{1}, v_{5}, u_{5}\}$ so that each edge in $\{u_{2}v_{2}, v_{2}v_{1}, v_{1}u_{1}, v_{1}v_{5}, v_{5}u_{5}\}$ is straight by Lemma 3. We delete $\{v_{1}, v_{2}, \cdots, v_{5}\}$ and add an edge between $u_{2}$ and $u_{5}$. Let $G'$ be the resulting planar graph.

Assume $u_{5}, u_{2}\in V(D)$. Then the path $u_{5}v_{5}v_{1}v_{2}u_{2}$ is a dividing 4-path of $D$, and it together with a part of $D$ form a 5- or 7-cycle $C$ in $G$ by Lemma 10. Since $C$ is a 7$^{-}$-cycle, $C$ is facial. According to the location of vertices $u_{1}$ and $u_{4}$, $C$ cannot be facial, a contradiction. For each $uv\in E(G')\bigcap E(G)$, let $M'_{uv} = M_{uv}$ and let $M'_{u_{2}u_{5}}$ be a full and straight matching. Let $\mathcal{M}' = \bigcup_{uv\in E(G')}M'_{uv}$. Then the $\mathcal{M}'$-coloring of $D$ in $G'$ is $\phi_{0}$.

Suppose that an 8$^{-}$-cycle is created. Then $G-\{v_{4}, v_{3}\}$ contains an 11$^{-}$-cycle $C$ which contains $u_{2}v_{2}v_{1}v_{5}u_{5}$. Since $|C|\leq11$, no vertex in $\{u_{1}, v_{3}, v_{4}\}$ lies inside $C$ by Lemma 7. Then $u_{1}$ is on $C$ and $C$ is divided by $u_{1}v_{1}$ into two cycles $C_{1}$ and $C_{2}$ and $|C_{1}|+|C_{2}| = |C|+2\leq13$. Recall each vertex in $V(f)$ is on two $7^{+}$-faces, $|C_{1}|+|C_{2}|\geq14$, a contradiction. Therefore no $8^{-}$-cycle is created. So $G'\in\mathcal{G}$ and $\mathcal{M}'$ is consistent on every closed walk of length 3.

Since $|V(G')| < |V(G)|$, then $G'$ has an $\mathcal{M}'$-coloring $\phi'$ extending $\phi_{0}$ by condition (a). Now we keep the color of every vertex in $G'$. Since $M'_{u_{2}u_{5}}$ is full and straight, $u_{2}$ and $u_{5}$ have different colors. So at least one color of $\{u_{5}, u_{2}\}$ is different from the color of $u_{1}$. W.l.o.g., let the color of $u_{1}$ be different from $u_{2}$. Since each edge in $\{u_{2}v_{2}, v_{2}v_{1}, v_{1}u_{1}, v_{1}v_{5}, v_{5}u_{5}\}$ is straight, we give $v_{2}$ the color of $u_{1}$ and color $v_{3}$, $v_{4}$, $v_{5}$ and $v_{1}$ in the order. Thus, $G$ has an $\mathcal{M}$-coloring extending $\phi_{0}$, a contradiction.

Lemma 16. $G$ has no 7-face containing seven internal 3-vertices.

Proof. Suppose otherwise that a 7-face $f$ in $G$ contains seven internal 3-vertices. Let $f = [v_{1}v_{2}\cdots v_{7}]$, and let $u_{i}$ be the neighbor of $v_{i}$ not on $f$ for $1\leq i \leq 7$. Since $G$ has no 4-, 6- or 8-cycle, the vertices in $\{u_{1}, u_{2}, \cdots, u_{7}\}$ are pairwise distinct. By Lemma 11, each edge in $\{u_{1}v_{1}, v_{1}v_{7}, v_{7}u_{7}, v_{7}v_{6}, v_{6}u_{6}, v_{6}v_{5}, v_{5}u_{5}\}$ is full. We can rename the vertices in $\{v_{1}, v_{7}, u_{7}, v_{6}, u_{6}, v_{5}, u_{5}\}$ so that each edge in $\{u_{1}v_{1}, v_{1}v_{7}, v_{7}u_{7}, v_{7}v_{6}, v_{6}u_{6}, v_{6}v_{5}, v_{5}u_{5}\}$ is straight by Lemma 3. We delete $\{v_{1}, v_{2}, \cdots, v_{7}\}$ and add an edge between $u_{1}$ and $u_{5}$. Let $G'$ be the resulting planar graph.

Suppose $\{u_{1}, u_{5}\}\in V(D)$. Then the path $u_{1}v_{1}v_{7}v_{6}v_{5}u_{5}$ is a dividing 5-path of $D$, and it together with a part of $D$ form a 9$^{-}$-cycle $C$ in $G$ by Lemma 10. Since $C$ is a 9$^{-}$-cycle, $C$ is facial. Since $v_{2}$ is internal, $u_{6}$, $u_{7}\in V(C)$. Then $v_{6}u_{6}$ and $v_{7}u_{7}$ are two chords of $C$, contrary to that $C$ is facial. For each $uv\in E(G')\bigcap E(G)$, let $M'_{uv} = M_{uv}$ and let $M'_{u_{1}u_{5}}$ be a full and straight matching. Let $\mathcal{M}' = \bigcup_{uv\in E(G')}M'_{uv}$. Then the $\mathcal{M}'$-coloring of $D$ in $G'$ is $\phi_{0}$.

Suppose that an 8$^{-}$-cycle is created. Then $G-\{v_{4}, v_{3}, v_{2}\}$ contains a 12$^{-}$-cycle $C$ which contains $u_{1}v_{1}v_{7}v_{6}v_{5}u_{5}$. Since $|C|\leq12$, none of $v_{2}$, $v_{3}$ and $v_{4}$ lie inside $C$ by Lemma 7. It follows that both $u_{6}$ and $u_{7}$ are on $C$, then $v_{6}u_{6}$ and $v_{7}u_{7}$ are two chords of $C$. If $|C|\leq10$, then $C$ has at most one chord by Lemma 5, a contradiction. If $|C| = 11$ and $C$ has two chords, then the chords split $C$ into two triangles and a 9-cycle by Lemma 5, contrary to that the vertices in $\{u_{1}, u_{2}, \cdots, u_{7}\}$ are pairwise distinct. If $|C| = 12$ and $C$ has two chords, then the chords split $C$ into two triangles and a 10-cycle by Lemma 5, contrary to that the vertices in $\{u_{1}, u_{2}, \cdots, u_{7}\}$ are pairwise distinct. Therefore we create no $8^{-}$-cycle. So $G'\in\mathcal{G}$ and $\mathcal{M}'$ is consistent on every closed walk of length 3.

Since $|V(G')| < |V(G)|$, then $G'$ has an $\mathcal{M}'$-coloring $\phi'$ extending $\phi_{0}$ by condition (a). Now we keep the color of every vertex in $G'$. Since $M'_{u_{1}u_{5}}$ is straight, $u_{1}$ and $u_{5}$ have different colors. Since each edge in $\{u_{1}v_{1}, v_{1}v_{7}, v_{7}u_{7}, v_{7}v_{6}, v_{6}u_{6}, v_{6}v_{5}, v_{5}u_{5}\}$ is straight, if $u_{7}$ and $u_{1}$ have different colors, then color $v_{7}$ same as $u_{1}$ and color $v_{6}$, $v_{5}$, $v_{4}$, $v_{3}$, $v_{2}$, $v_{1}$ in the order. If $u_{7}$ and $u_{1}$ have the same color, then $u_{7}$ and $u_{5}$ have different colors. If $u_{6}$ and $u_{5}$ have different colors, then color $v_{6}$ same as the color of $u_{5}$ and color $v_{7}$, $v_{1}$, $v_{2}$, $v_{3}$, $v_{4}$, $v_{5}$ in the order. If $u_{6}$ and $u_{5}$ have the same color, then $u_{7}$ and $u_{6}$ have different colors, color $v_{7}$ same as $u_{6}$ and color $v_{1}$, $v_{2}$, $v_{3}$, $v_{4}$, $v_{5}$, $v_{6}$ in the order. Thus, $G$ has an $\mathcal{M}$-coloring extending $\phi_{0}$, a contradiction.

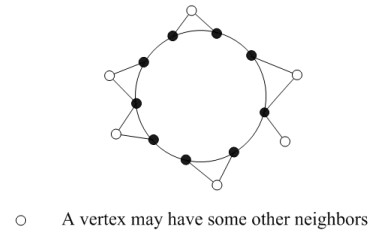
A 9-face is light if it has two internal 4-vertices and seven bad vertices. By Lemma 14, a light 9-face is adjacent to five 3-faces. So it is isomorphic to the graph in Figure 2.

Let the initial charge $\mu(x) = d(x)-4$ for $x\in V(G)\bigcup F(G)-\{f_{0}\}$, and $\mu(f_{0}) = d(f_{0})+4$.

The rules:

(R1): Let $f$ be a 3-face. If $v$ is on $f$, then $f$ receives $\frac{1}{3}$ from $v$.

(R2): Let $v$ be a 3-vertex not on $D$ and let $f$ be a face that contains $v$.

$①$ If $d(f) = 5$, then $f$ sends $\frac{1}{4}$ to $v$.

$②$ Suppose $d(f)\geq7$. If $v$ is a bad vertex, then $f$ sends $\frac{2}{3}$ to $v$. If one of the other two faces that contain $v$ is a 5-face, then $f$ sends $\frac{3}{8}$ to $v$. If all faces that contain $v$ are 7$^{+}$-faces, then $f$ sends $\frac{1}{3}$ to $v$.

(R3): Let $v$ be a 4-vertex not on $D$.

$①$ If $v$ is on two triangles, then $v$ receives $\frac{1}{3}$ from the other two faces that contain $v$.

$②$ Suppose that $v$ is on one triangle $f$. If $v$ is not on a light 9-face, then $v$ receives $\frac{1}{6}$ from the two incident $9^{+}$-faces adjacent to $f$, respectively. If $v$ is on a light 9-face $f_{1}$ adjacent to $f$, then $v$ receives $\frac{1}{6}$ from each incident face except $f$ and $f_{1}$. If $v$ is on two light 9-faces adjacent to $f$, then $v$ receives $\frac{1}{3}$ from the face incident with $v$ which is not adjacent to $f$.

(R4): The outer face $f_{0}$ sends $\frac{4}{3}$ to each vertex on $D$.

(R5): Let $v$ be a vertex on $D$ and be incident with a 5$^{+}$-face $f\neq f_{0}$.

$①$ If $v$ is a 2-vertex, then $v$ receives $\frac{2}{3}$ from $f$.

$②$ Suppose that $v$ is a 3-vertex. If $v$ is on a 3-face, then $v$ receives $\frac{1}{12}$ from $f$. If $v$ is not on a 3-face, then $f$ receives $\frac{1}{12}$ from $v$.

$③$ If $d(v)\geq4$, then $f$ receives $\frac{1}{3}$ from $v$.

After discharging, let $\mu^{*}(x)$ be the final charge.

Lemma 17. $\mu^{*}(f)\geq0$ for each $f\in F(G)$.

Proof. First suppose that all vertices on $f$ are internal. By Lemma 4, $d(v)\geq3$ for each $v\in V(f)$. Since $G$ has no 4-, 6- or 8-cycle, if $d(f) = 5$, then $f$ cannot be adjacent to a 3- or 5-face. If $d(f) = 7$, then $f$ cannot be adjacent to a 3-face.

Let $d(f) = 3$. Then $\mu^{*}(f) = \mu(f)+\frac{1}{3}\times3 = 0$ by (R1).

Let $d(f) = 5$. Since $f$ has at most four 3-vertices by Lemma 15, $\mu^{*}(f) = \mu(f)-\frac{1}{4}\times 4 = 0$ by (R2) $①$.

Let $d(f) = 7$. Since $f$ is adjacent to no 3-face, by (R2) $②$ and (R3) $②$, $f$ sends at most $\frac{3}{8}$ to each $v\in V(f)$. Therefore, $\mu^{*}(f)\geq \mu(f)-7\times \frac{3}{8} > 0$.

Let $d(f)\geq9$. Let $D(f)$ be the set of bad vertices of $f$. Let $uvw$ be a 2-path on $f$ and $A(f) = \{v:$ $v$ is good, both $u$ and $w$ are bad$\}$, $B(f) = \{v:$ $v$ is good, $u$ is bad, and $w$ is good$\}$, $C(f) = \{v:$ $v$ is good, both $u$ and $w$ are good$\}$. Then $V(f) = D(f)\bigcup C(f)\bigcup B(f)\bigcup A(f)$ and $D(f)$, $A(f)$, $B(f)$ and $C(f)$ are pairwise disjoint. Let $n_{1} = |A(f)|$, $n_{2} = |B(f)|$, $n_{3} = |C(f)|$ and $n_{4} = |D(f)|$. If $v\in D(f)$, then $f$ sends $\frac{2}{3}$ to $v$ by (R2) $②$. If $v\in A(f)$. Since $v$ is good, if $v$ is a 3-vertex, then $v$ cannot be triangular. Since $u$ and $w$ are bad and $G$ has no 6-cycle, $v$ is incident with no 5-face. By (R2) $②$, $f$ sends $\frac{1}{3}$ to $v$. If $v$ is a 4-vertex, then $f$ sends at most $\frac{1}{3}$ to $v$ by (R3) $①$ $②$. So if $v\in A(f)$, $v$ receives at most $\frac{1}{3}$ from $f$. If $v\in B(f)\bigcup C(f)$, then $f$ sends at most $\frac{3}{8}$ to $v$ by (R2) $②$ and (R3) $①$ $②$. Therefore,

Clearly, if $n_{2}\neq0$, then $n_{2}$ is even. If $n_{2} = 0$, then $n_{3} = d(f)$ or $n_{3} = 0$.

Suppose $d(f) = 9$. If $n_{1}\geq3$, then by inequality (2.1), $\mu^{*}(f)\geq0$. So we need to consider the following cases.

Case 1: $n_{1}\leq2$, $n_{2} = 0$ and $n_{3} = 0$. Then $n_{1} = 2$ by Lemma 13. Let $f = [v_{1}\cdots v_{9}]$ and every edge in $\{v_{1}v_{2}, v_{3}v_{4}, v_{4}v_{5}, v_{6}v_{7}, v_{8}v_{9}\}$ be triangular, then $A(f) = \{v_{4}, v_{8}\}$ and $D(f) = V(f)-A(f)$. If one vertex in $\{v_{4}, v_{8}\}$ is a $5^{+}$-vertex, then the $5^{+}$-vertex receives nothing from $f$ by the rules. Therefore, $\mu^{*}(f)\geq \mu(f)-7\times\frac{2}{3}-\frac{1}{3} = 0$. If $d(v_{4}) = d(v_{8}) = 4$, then $f$ is a light 9-face and sends no charge to $v_{8}$ by (R3) $②$. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times7-\frac{1}{3} = 0$.

Case 2: $n_{1} = 1$, $n_{2} = 2$ and $n_{3} = 0$. Then $A(f)\bigcup B(f)$ divides $D(f)$ into 4+2 (four consecutive bad vertices and two other consecutive bad vertices) or 3+3 (three consecutive bad vertices and three other consecutive bad vertices) on $f$ by Lemma 13.

In the former case 4+2, let $f = [v_{1}\cdots v_{9}]$, $A(f) = \{v_{1}\}$ and $B(f) = \{v_{4}, v_{5}\}$. By Lemma 14, $d(v_{1}), d(v_{5})\geq 4$. If $d(v_{1})\geq5$, then $f$ sends no charge to $v_{1}$ by the rules. Therefore, $\mu^{*}(f)\geq \mu(f)-6\times\frac{2}{3}-2\times\frac{3}{8} > 0$. Now let $d(v_{1}) = 4$. By Lemma 14, $v_{1}v_{9}$ is triangular. If $v_{1}$ is on one 3-face, then $f$ sends at most $\frac{1}{6}$ to $v_{1}$ by (R3) $②$. Therefore, $\mu^{*}(f)\geq \mu(f)-6\times\frac{2}{3}-\frac{1}{6}-2\times\frac{3}{8} > 0$. If $v_{1}$ is on two 3-faces, then $d(v_{4}), d(v_{5})\geq4$. Then by (R3) $①$, $f$ sends at most $\frac{1}{3}$ to $v_{1}$. By (R3) $①$ $②$, $f$ sends at most $\frac{1}{3}$ to $v_{4}$ and $v_{5}$, respectively. Therefore, $\mu^{*}(f)\geq d(f)-4-6\times\frac{2}{3}-3\times\frac{1}{3} = 0$.

In the latter case 3+3, let $f = [v_{1}\cdots v_{9}]$ and $A(f) = \{v_{1}\}$, then $B(f) = \{v_{5}, v_{6}\}$ and $D(f) = \{v_{2}, v_{3}, v_{4}, v_{7}, v_{8}, v_{9}\}$. By Lemma 13, at least one vertex in $\{v_{5}, v_{6}\}$ should be a 4$^{+}$-vertex. If one vertex in $\boldsymbol{\{v_{5}, v_{6}\} }$ is a 5$^{+}$-vertex, then the 5$^{+}$-vertex receives nothing from $f$ by the rules. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times6-\frac{1}{3}-\frac{3}{8} > 0$. So $d(v_{5}), d(v_{6})\leq4$. If $d(v_{5}) = d(v_{6}) = 4$, then $f$ sends at most $\frac{1}{3}$ to $v_{5}$ and $v_{6}$ by (R3) $①$ $②$, respectively. Therefore, $\mu^{*}(f)\geq \mu(f)-6\times\frac{2}{3}-3\times\frac{1}{3} = 0$. If one vertex in $\boldsymbol{ \{v_{5}, v_{6}\} }$ is a 3-vertex, then $v_{5}v_{6}$ cannot be on a 3-face since $\{v_{5}, v_{6}\}\in B(f)$. W.l.o.g., let $d(v_{5}) = 3$ and $d(v_{6}) = 4$. Since $v_{5}$ is good and all vertices in $\{v_{2}, v_{3}, v_{4}\}$ are bad, every edge in $\{v_{1}v_{2}, v_{3}v_{4}\}$ is triangular. Recall $A(f) = \{v_{1}\}$, $d(v_{1})\neq3$. If $d(v_{1})\geq5$, then $f$ sends no charge to $v_{1}$ by the rules. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times6-\frac{1}{3}-\frac{3}{8} > 0$. If $d(v_{1}) = 4$ and $v_{1}$ is on precise one 3-face, recall $v_{1}v_{2}$ is triangular, then $f$ sends at most $\frac{1}{6}$ to $v_{1}$ by (R3) $②$. Therefore, $\mu^{*}(f)\geq \mu(f)-6\times\frac{2}{3}-\frac{1}{6}-\frac{1}{3}-\frac{3}{8} > 0$. If $v_{1}$ is on two 3-face, then $v_{6}v_{7}$ is not triangular and $v_{6}$ is on at most one 3-face. If $v_{6}$ is not triangular, then $v$ receives nothing by (R3) $①$ $②$. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times6-\frac{1}{3}-\frac{3}{8} > 0$. If $v_{6}$ is on a 3-face $T$, then $T$ is not adjacent to $f$. By (R3) $②$, $f$ sends at most $\frac{1}{3}$ to $v_{6}$. Since $G$ has no 6-cycle, both $v_{4}v_{5}$ and $v_{5}v_{6}$ are not on a 5-face. Then $f$ sends at most $\frac{1}{3}$ to $v_{5}$ by (R2) $②$. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times6-\frac{1}{3}\times3 = 0$.

Case 3: $n_{1} = 0$, $n_{2} = 2$ and $n_{3}\leq2$. Since $n_{2}+n_{3}\leq4$, $f$ has at least five consecutive bad vertices, contradicting Lemma 14.

Suppose $d(f)\geq10$. If $2\times n_{1}+n_{2}\geq4$, then $\mu^{*}(f)\geq0$ by inequality (2.1). Now, we assume either $n_{1}\leq1$ and $n_{2} = 0$, or $n_{1} = 0$ and $n_{2} = 2$. If $n_{1}\leq1$ and $n_{2} = 0$, then $n_{3} = 0$ and $f$ contains at least nine consecutive bad vertices, contradicting Lemma 14. If $n_{1} = 0$ and $n_{2} = 2$, then $n_{4}\leq4$ by Lemma 14. So $n_{3}\geq4$ and $\mu^{*}(f)\geq0$ by inequality (2.1).

Next assume $f$ and $f_{0}$ have some common vertices. If $f = f_{0}$, then $\mu^{*}(f_{0})\geq d(f_{0})+4-\frac{4}{3}\times d(f_{0})\geq0$ by R5 since $d(f_{0})\leq12$. Now, let $f\neq f_{0}$. If $d(f)\leq7$, then the vertices in $V(f)\bigcap V(f_{0})$ are consecutive one by one by Lemma 5, Lemma 7 and Lemma 10. Furthermore, there is at most one 2-vertex in $V(f)$ when $f$ is a 5-face, and at most two 2-vertices in $V(f)$ when $f$ is a 7-face.

Let $d(f) = 3$. By (R1), $\mu^{*}(f) = \mu(f)+\frac{1}{3}\times3 = 0$.

Let $d(f) = 5$. If there is no 2-vertex in $V(f)$, then by (R2) $①$, $f$ sends at most $\frac{1}{4}$ to each incident internal vertex. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{1}{4}\times4 = 0$. If there is one 2-vertex in $V(f)$, then $f$ contains two 3$^{+}$-vertices of $f_{0}$. By (R5), both of the 3$^{+}$-vertices send at least $\frac{1}{12}$ to $f$. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}-2\times\frac{1}{4}+2\times\frac{1}{12} = 0$.

Let $d(f) = 7$. Since $f$ cannot be adjacent to a triangle, by (R2) $②$ and (R3) $②$, $f$ sends at most $\frac{3}{8}$ to each incident internal vertex. If $f$ and $f_{0}$ has a common $4^{+}$-vertex $v$, then $f$ receives $\frac{1}{3}$ from $v$ by (R5) $③$. Therefore, $\mu^{*}(f)\geq \mu(f)-2\times\frac{2}{3}-3\times\frac{3}{8}+\frac{1}{3} > 0$. If $f$ and $f_{0}$ has no common $4^{+}$-vertex, then $f$ and $f_{0}$ have at least two common $3$-vertices $u$ and $v$. Since $d(f) = 7$, both $u$ and $v$ are not triangular, then $f$ receives $2\times\frac{1}{12}$ from them by (R5) $②$. Since $f$ cannot be adjacent to a triangle, by (R2) $②$ and (R3) $②$, $f$ sends at most $\frac{3}{8}$ to each incident internal vertex. Therefore, $\mu^{*}(f)\geq \mu(f)-2\times\frac{2}{3}-3\times\frac{3}{8}+2\times\frac{1}{12} > 0$.

Let $d(f)\geq9$. If $f$ and $f_{0}$ have a common $4^{+}$-vertex $v$, then by (R5) $③$, $v$ sends $\frac{1}{3}$ to $f$. Therefore, $\mu^{*}(f)\geq \mu(f)-(d(f)-1)\times\frac{2}{3}+\frac{1}{3} = \frac{1}{3}(d(f)-9)\geq0$. If $f$ and $f_{0}$ has no common $4^{+}$-vertex, then $f$ and $f_{0}$ have at least two common $3$-vertices. By (R5) $②$, $f$ sends at most $\frac{1}{12}$ to the two $3$-vertices, respectively. Therefore, $\mu^{*}(f)\geq \mu(f)-\frac{2}{3}\times(d(f)-2)-2\times\frac{1}{12} = \frac{1}{6}(2d(f)-17) > 0$.

Lemma 18. $\mu^{*}(v)\geq0$ for each $v\in V(G)$.

Proof. If $v$ internal, then by Lemma 4, $d(v)\geq3$.

Let $d(v) = 3$. The lengths of the faces that contain $v$ is $\{7^{+}, 7^{+}, 7^{+}\}$, $\{3, 9^{+}, 9^{+}\}$ or $\{5, 7^{+}, 7^{+}\}$ since $G$ is in $\mathcal{G}$. By (R1) and (R2) $①$ $②$ $\mu^{*}(v)\geq0$.

Let $d(v) = 4$. the charge that $v$ receives is equal to the charge that $v$ sends out by (R1) and (R3) $①$ $②$. Therefore, $\mu^{*}(v) = \mu(v) = 0$.

If $d(v)\geq5$, then $v$ sends $\frac{1}{3}$ to each incident 3-face by (R1). Therefore, $\mu^{*}(v)\geq \mu(v)-\frac{d(v)}{2}\times\frac{1}{3} = \frac{5}{6}\times d(v)-4 > 0$.

If $v$ is not internal, then $d(v)\geq2$.

If $d(v) = 2$, then $v$ is not triangular by Lemma 9. By (R4) and (R5) $①$, $\mu^{*}(v)\geq \mu(v)+\frac{4}{3}+\frac{2}{3} = 0$.

Let $d(v) = 3$. If $v$ is triangular, then $\mu^{*}(v)\geq \mu(v)+\frac{4}{3}-\frac{1}{3}+\frac{1}{12} > 0$ by (R4) and (R5) $②$. If $v$ is not triangular, then $\mu^{*}(v)\geq \mu(v)+\frac{4}{3}-\frac{1}{12} > 0$ by (R4) and (R5) $②$.

Let $d(v)\geq4$. By (R4), $f_{0}$ sends $\frac{4}{3}$ to $v$. By (R5) $③$ and (R1), $v$ sends $\frac{1}{3}$ to each other incident face than $f_{0}$. Therefore, $\mu^{*}(v)\geq \mu(v)+\frac{4}{3}-\frac{1}{3}\times(d(v)-1) = \frac{2}{3}\times d(v)-\frac{7}{3} > 0$.

Proof of Theorem 2. Clearly, $V(G)\neq V(D)$. Let $x_{0}$ be a 3$^{+}$-vertex on $D$. From Lemma 18, $\mu^{*}(x_{0}) > 0$. Therefore, $\sum_{x\in V \bigcup F}\mu^{*}(x) > 0$ from Lemmas 17 and 18, contradicting Euler's Formula. So Theorem 2 is true.

3.   Conclusions

It is well known that the problem of deciding whether a planar graph is 3-colorable is NP-complete. This provides motivation for finding some sufficient conditions for 3-coloring of planar graphs. DP-coloring is a stronger version of list coloring.

In this paper, we prove that planar graphs without $\{4, 6, 8\}$-cycles are 3-choosable by using the technique developed in DP-coloring. We like to conclude this paper by raising the following conjecture:

Conjecture 1 Planar graphs without $\{4, 6, 8\}$-cycles are DP-3-colorable.

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and suggestions, which led to considerable improvement of the article.

The research is supported by the National Natural Science Foundation of China (No.11771443) and partially supported by the National Natural Science Foundation of China (No.12071265).

Conflict of interest

All authors declare no conflicts of interest in this paper.