Solution of the Chen-Chvátal conjecture for specific classes of metric spaces

1.   Introduction

In a metric space $M = (X, d_X)$ a line induced by two distinct points $x, x'\in X$ is defined by

A line $\mathcal{L}_{M}\{x, x'\}$ is universal whenever $\mathcal{L}_{M}\{x, x'\} = X$.

For instance, if $M = \mathbb{R}^n$ is the $n$-dimensional Euclidean space, then for any pair of points $x, x'$, the metric space obtained from line $\mathcal{L}_{\mathbb{R}^n}\{x, x'\}$, equipped with its usual metric inherited from $\mathbb{R}^n$, is isometric to the one-dimensional Euclidean space. Hence, the $n$-dimensional Euclidean space has a universal line if and only if $n = 1$. Now, if a metric space $M$ is equipped with the discrete metric^*, then $\mathcal{L}_{M}\{x, x'\} = \{x, x'\}$ for every pair of points $x, x'\in X$.

^*The discrete metric is given by $d(x, y) = 0$ if $x = y$ and $d(x, y) = 1$ otherwise.

There are metric spaces with metrics that may differ from the discrete metric yet generate the same topology. Such spaces are called discrete metric spaces ^[15], i.e., a metric space $M$ is called a discrete metric space if and only if all its subsets are open (and therefore closed) in $M$. For instance, the set $\mathbb{N}$ of positive integers, with its usual metric inherited from the one-dimensional Euclidean space $\mathbb{R}$, is a discrete metric space; every finite metric space is a discrete metric space; and the vertex set of any connected graph, equipped with the shortest path distance, is a discrete metric space.

In this context, the following conjecture was stated by Chen and Chvátal ^[7] for the case of finite metric spaces, where $\ell(M)$ denotes the number of distinct lines in $M$.

Conjecture 1.1 (The Chen-Chvátal conjecture, ^[7]). Every finite metric space $M = (X, d_X)$ with at least two points either has a universal line or $\ell(M) \ge |X|$.

The Chen-Chvátal conjecture is an attempt to generalize the de Bruijn-Erdős theorem of Euclidean geometry which asserts the following.

Theorem 1.2 (The de Bruijn-Erdős theorem of Euclidean geometry, ^[5]). Every non-collinear set of $n$ points in the plane determines at least $n$ distinct lines.

The Chen-Chvátal conjecture remains open and, as time goes by, the interest of mathematicians to solve it is increasing. Recently, Chvátal ^[9] described the main progress related to the conjecture, and pointed out twenty-nine related open problems plus three additional conjectures. By way of example, three of these results are presented below.

Although in the general context of metric spaces the distance function ranges over the nonnegative reals, it was shown by Aboulker and Kapadia ^[1] that, to prove Conjecture1.1, it is enough to consider metric spaces with integral distances. This motivates to define a $k$-metric space, with $k$ a positive integer, as a metric space in which all distances are integers and are at most $k$. Chvátal ^[8] proved the conjecture for every $2$-metric space on $n\ge 2$ points.

Theorem 1.3. ^[8] Every $2$-metric space on $n\ge 2$ points either has at least $n$ distinct lines or has a universal line.

Since the vertex set of any connected graph $G$ of diameter $D(G)$, equipped with the shortest path distance, is a $D(G)$-metric space, Conjecture 1.1 automatically becomes of interest in graph theory. Obviously, Theorem 1.3 includes the case of metric spaces induced by graphs of diameter at most two. We would emphasize that the Chen-Chvátal conjecture was also proved by Beaudou et at. ^[3] for metric spaces induced by chordal graphs.

Theorem 1.4. ^[3] Every metric space induced by a chordal graph on $n$ vertices, where $n \ge 2$, either has at least $n$ distinct lines or has a universal line.

Aboulker and Kapadia ^[1] proved the Chen-Chvátal conjecture for the case of metric spaces induced by distance-hereditary graphs.

Theorem 1.5. ^[1] Every metric space induced by a connected distance-hereditary graph on $n$ vertices, where $n \ge 2$, either has at least $n$ distinct lines or has a universal line.

After that, Aboulker et al. ^[2] proved the Chen-Chvátal conjecture for metric spaces induced by a family of graphs containing chordal graphs and distance-hereditary graphs, Schrader and Stenmans ^[16] proved the conjecture for the case of $(q, q-4)$-graphs, and Beaudou et al. ^[4] proved it for the case of bisplit graphs.

In this paper, we prove the Chen-Chvátal conjecture for some classes of metric spaces. Specifically, Section 2 is devoted to lexicographic metric spaces, Section 3 is devoted to corona metric spaces, while in Section 4 we discuss the case of Cartesian metric spaces.

2.   The class of lexicographic metric spaces

Given a metric space $M = (X, d_X)$, and a point $x\in X$, we define the nearness of $x$ to be

We define the nearness of the metric space to be

Obviously, if $M$ is the metric space induced by a simple graph $G$, then $\eta(M) = 1 = \eta(x)$ for every vertex $x$ of $G$.

Definition 2.1. ^[12] Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces such that $\eta(M) > 0$. A map $\rho: (X\times Y)\times (X\times Y)\longrightarrow \mathbb{R}$ defined by

is called a lexicographic distance, and the metric space $M\circ M^* = (X\times Y, \rho)$ is called a lexicographic metric space.

The study of lexicographic metric spaces was introduced by Rodríguez-Velázquez ^[12], where the author discussed some basic properties of these metric spaces, such as completeness, boundedness, compactness and separability. Furthermore, the author gave a formula for the metric dimension of any lexicographic metric space.

Given a metric space $M = (X, d_X)$, the image of $d_X$ will be denoted by $\operatorname{Im}(d_X)$. The diameter of a finite metric space $M = (X, d_x)$ is defined to be

and the eccentricity of a point $x\in X$ is defined to be

In this section we discuss the class of finite lexicographic metric spaces $M\circ M^*$ with the restriction on $M = (X, d_X)$ that $\eta(x) = 1$ for every $x\in X$. We first consider the case where $D(M)\le 2$.

Theorem 2.1. Let $M = (X, d_X)$ be a finite $2$-metric space such that $\eta(x) = 1$ for every $x\in X$, and let $M^* = (Y, d_Y)$ be a finite metric space. If $(0, 2)\cap \operatorname{Im}(d_Y)\subseteq \{1\}$, then either $M\circ M^*$ has a universal line or $\ell (M\circ M^*)\ge |X\times Y|$.

Proof. Notice that $|X|\ge 2$, as $\eta(x) = 1$ for every $x\in X$. We differentiate two cases for any pair $(x, y), (a, b)\in X\times Y$ of different points of $M\circ M^*$.

Case 1. $x\ne a$. In this case, $\rho((x, y), (a, b)) = d_X(x, a)\in \{1, 2\}$, as $M$ is a $2$-metric space.

Case 2. $x = a$. If $(0, 2)\cap \operatorname{Im}(d_Y)\subseteq \{1\}$, then $\rho((x, y), (a, b)) = \min\{2, d_Y(y, b)\}\in \{1, 2\}$, as $\eta(x) = 1$ for every $x\in X$.

According to the two cases above, $M\circ M^*$ is a finite $2$-metric space. Therefore, the result follows by Theorem 1.3.

To continue with our analysis, we need to prove the following lemma.

Lemma 2.2. Let $M = (X, d_X)$ be a metric space such that $\eta(M) > 0$ and let $M^* = (Y, d_Y)$ be a metric space. If $x, x', x''\in X$ are three different points of $M$ and there exist $y, y', y''\in Y$ such that $(x'', y'')\in \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$, then $\{x''\}\times Y\subseteq \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$.

Proof. Assume $(x'', y'')\in \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$, i.e.,

or

Hence, if $x, x', x''\in X$ are three different points of $M$, then for any $z\in Y$, either

or, by analogy,

Therefore, $(x'', z)\in \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$ for every $z\in Y$, as required.

We will use the term integral metric spaces to refer to $k$-metric spaces in contexts where the value of $k$ is irrelevant. Therefore, $\operatorname{Im}(d_X)\subseteq \mathbb{Z}$ for every integral metric space $M = (X, d_X)$. Next we consider the class of finite lexicographic metric spaces $M\circ M^*$ where $D(M)\ge 3$ and $\eta(x) = 1$ for every $x\in X$. In this case, the only restriction on $M^* = (Y, d_Y)$ is that $2\le |Y| < + \infty$.

Theorem 2.3. Let $M = (X, d_X)$ be a finite integral metric space such that $\eta(x) = 1$ for every $x\in X$. Let $M^* = (Y, d_Y)$ be a finite metric space with $|Y|\ge 2$. If $D(M)\ge 3$, then either $M\circ M^*$ has a universal line or $\ell (M\circ M^*)\ge |X\times Y|$.

Proof. If $D(M)\ge 3$, then $\varepsilon_M(x)\ge 2$ for every $x\in X$, as $d_X(v, x)+d_X(x, w)\ge d_X(v, w) = D(M)\ge 3$ for every pair $v, w\in X$ of antipodal points of $M$. Thus, for every point $x\in X$ we can choose one point $x'\in X$ such that $d_X(x, x')\ge 2$. We claim that the following fact holds.

Fact 1: For any $x, x'\in X$ with $d_X(x, x')\ge 2$ and $y, y'\in Y$,

In order to prove Fact 1, notice that for any $z\in Y\setminus \{y\}$,

and, since $\eta(x) = 1$,

From (2.1) and (2.2) we deduce that

and so $(x, z)\not \in \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$, which completes the proof of Fact 1.

Obviously, from Fact 1 we derive the following consequence.

Fact 2: Given $a, a', b, b'\in Y$ and $x, x'\in X$ with $d_X(x, x')\ge 2$, the following statements are equivalent.

● $\mathcal{L}_{M\circ M^*}\{(x, a), (x', a')\} = \mathcal{L}_{M\circ M^*}\{(x, b), (x', b')\}.$

● $a = b \text{ and } a' = b'.$

Now, we claim that the following fact holds.

Fact 3: If there exist $(u, v), (u', v'), (x, y), (x', y')\in X\times Y$ such that $d_X(x, x')\ge 2$, $d_X(u, u')\ge 2$ and $\mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\} = \mathcal{L}_{M\circ M^*}\{(u, v), (u', v')\}$, then $\{x, x'\} = \{u, u'\}$.

Suppose to the contrary that $x\not \in \{u, u'\}$. Under this assumption, $u, u'$ and $x$ are three different points of $M$, and since $(x, y)\in \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\} = \mathcal{L}_{M\circ M^*}\{(u, v), (u', v')\}$, by Lemma 2.2 we deduce that $\{x\}\times Y\subseteq \mathcal{L}_{M\circ M^*}\{(u, v), (u', v')\} = \mathcal{L}_{M\circ M^*}\{(x, y), (x', y')\}$, which contradicts Fact 1, as $|Y|\ge 2$. Hence, $x \in \{u, u'\}$ and analogously, $x' \in \{u, u'\}$. Thus, Fact 3 follows.

From Fact 2 we can conclude that for every $x, x'\in X$ with $d_X(x, x')\ge 2$, there exist $|Y|^2$ different lines in $M\circ M^*$ which are generated by one point in $\{x\}\times Y$ and one point in $\{x'\}\times Y$. Therefore, Fact 3 leads to

as required.

Notice that in the proof of Theorem 2.3 we have solved the problem without worrying about the existence of universal lines. In fact, the problem of investigating the properties of metric spaces $M = (X, d_X)$ having a universal line is very interesting, even if we can check that $\ell(M) \ge |X|$. Recently, Rodríguez-Velázquez ^[13] discussed the problem for the particular case of metric spaces induced by graphs.

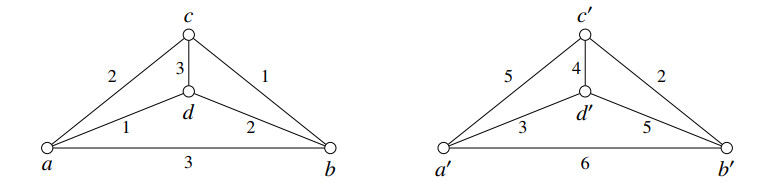
Figure 1 shows the sketch of two integral metric spaces $M = (X, d_X)$ and $M^* = (Y, d_Y)$, where $X = \{a, b, c, d\}$ and $Y = \{a', b', c', d'\}$. It is easy to check that for any $u, v\in Y$, the line $\mathcal{L}_{M\circ M^*}\{(a, u), (d, v)\} = X\times Y$ is universal. Furthermore, $D(M) = 3$ and, by the procedure described in the proof of Theorem 2.3, $\ell(M\circ M^*)\ge \frac{1}{2}|X||Y|^2 = 32 > 16 = |X||Y|$.

As mentioned above, Aboulker and Kapadia ^[1] observed that to prove the Chen-Chvátal conjecture it is enough to consider integral metric spaces. In this sense, we can say that we have solved the conjecture for any finite lexicographic metric space $M\circ M^*$ with the only restriction that $\eta(x) = 1$ for every point $x$ of $M$. We would highlight this fact in the following theorem, which is obtained from Theorems 2.1 and 2.3.

Theorem 2.4. If $M\circ M^* = (X\times Y, \rho)$ is a finite and integral lexicographic metric space, where $|Y|\ge 2$ and $\eta(x) = 1$ for every point $x\in X$, then either $M\circ M^*$ has a universal line or $\ell (M\circ M^*)\ge |X\times Y|$.

The notion of lexicographic metric space was inspired by the concept of lexicographic product graph ^[12]. The lexicographic product $G \circ H$ of two graphs $G$ and $H$ is the graph whose vertex set is $V(G \circ H) = V(G) \times V(H)$ and $(u, v)(x, y) \in E(G \circ H)$ if and only if $ux \in E(G)$ or $u = x$ and $vy \in E(H)$. For basic properties of the lexicographic product of two graphs we suggest the books ^[10,11].

A lexicographic product graph $G\circ H$ is connected if and only if $G$ is connected. We denote by $d_G$ the shortest path distance of any graph $G$. As observed in ^[12], given a connected (simple) graph $G$ and a non-necessarily connected (simple) graph $H$, the graph $G\circ H$ induces a lexicographic metric space $M\circ M^*$, which is obtained from the metric space $M$, induced by $G$, and the metric space $M^* = (V(H), d^*)$, where $d^*(y, y') = \min\{2, d_H(y, y')\}$. Notice that the distance function $d^*$ is well defined, even if $H$ is not connected, in the sense that for two vertices $y$ and $y'$ belonging to different components of $H$ we assume that $d_H(y, y') = +\infty$, and so $d^*(y, y') = \min\{2, d_H(y, y')\} = \min\{2, +\infty\} = 2$. In summary, the class of lexicographic metric spaces includes, but is not limited to, the class of metric spaces induced by lexicographic product graphs. Therefore, the following result is a particular case of Theorem 2.4.

Corollary 2.5. Every metric space induced by a lexicographic product graph $G\circ H$, where $|V(G)|\ge 2$ and $|V(H)|\ge 2$, either has at least $|V(G\circ H)|$ distinct lines or has a universal line.

3.   The class of corona metric spaces

The study of corona metric spaces was introduced by Rodríguez-Velázquez ^[14], where the author discussed some basic properties of these metric spaces, such as completeness, boundedness, compactness and separability. Furthermore, the author gave a formula for the metric dimension of any corona metric space.

Definition 3.1. ^[14] Let $M = (X, d_X)$ be a metric space with $0 < \eta(M) < +\infty$ and $\mathcal{M}$ a family of pairwise disjoint metric spaces such that there exists a bijection $f: X \longrightarrow \mathcal{M}$. Let $f(x) = M_x = (X_x, d_{X_x})$ for every $x\in X$, and

Let $d_U: U\times U\longrightarrow \mathbb{R}$ be the map defined by

The map $d_U$ is called a corona distance, and the metric space $M\odot_f \mathcal{M} = (U, d_U)$ is called a corona metric space.

One can easily check the distance function $d_U$ is well defined, i.e., $M\odot_f \mathcal{M} = (U, d_U)$ is a metric space. Notice that the requirement $\eta(M) < +\infty$ is needed, as $\inf \varnothing = +\infty$. Hence, if $|X| = 1$, then $\eta(M) = +\infty$. Therefore, the requirement $\eta(M) < +\infty$ is equivalent to $|X|\ge 2$.

As we will see below, the class of corona metric spaces includes, but is not limited to, the class of metric spaces induced by corona graphs.

Theorem 3.1. Every finite corona metric space $M\odot_f \mathcal{M} = (U, d_U)$ has a universal line or $\ell(M\odot_f \mathcal{M})\ge |U|$.

Proof. If $X = \{x, x'\}$, then for any $y\in X_x$ we have $d_U(y, x') = d_U(y, x)+d_U(x, x')$, and for any $z\in X_{x'}$ we have $d_U(z, x) = d_U(z, x')+d_U(x', x)$. Therefore, $\mathcal{L}_{M\odot_f \mathcal{M}}\{x, x'\} = X_x\cup X\cup X_{x'} = U$ is a universal line.

Now, if there exists $x\in X$ such that $|X_x| = 1$, say $X_x = \{y\}$, then for any $z\in U\setminus \{y\}$ we have $d_U(z, y) = d_U(z, x)+d_U(x, y)$. Therefore, $\mathcal{L}_{M\odot_f \mathcal{M}}\{x, y\}$ is a universal line.

From now on, assume that $|X|\ge 3$ and $|X_x|\ge 2$ for every $x\in X$. Given two different points $a, b\in U$, we define

Notice that $[x, x']\subseteq X$ for every $x, x'\in X$, and $[x, y] = \{x, y\}$ for every $x\in X$ and $y\in X_x$. Hence, for any pair of different points $x, x'\in X$, and any $a\in X_x$ and $b\in X_{x'}$,

and so

This implies that for every pair of distinct points $x, x'\in X$ there exist $|X_x||X_{x'}|$ different lines of $M\odot_f \mathcal{M}$ which are generated by one point in $X_x$ and the other one in $X_{x'}$.

Since $|X|\ge 3$, and $|X_x|\ge 2$ for every $x\in X$, we can choose three different points $u, v, w\in X$ such that $2\le |X_u| = \min\{|X_x|: \, x\in X\}$, and so

Therefore, the result follows.

Let $G$ be a connected graph, $\mathcal{H}$ a family of pairwise disjoint graphs with $|\mathcal{H}| = |V(G)|$, and $g: V(G) \longrightarrow \mathcal{H}$ a bijection. Let $g(x) = H_x$ for every $x\in V(G)$. We define the generalized corona graph $G\odot_g \mathcal{H}$ as the graph obtained from $G$, $\mathcal{H}$ and $g$, by taking one copy of $G$ and one copy of each graph in $\mathcal{H}$, and making $x$ adjacent to every vertex of $H_x$ for every $x\in V(G)$. Notice that $G\odot_g \mathcal{H}$ is connected if and only if $G$ is connected. If there exists a graph $H$ such that $g(x) = H_x$ is isomorphic to $H$ for every $x\in V(G)$, then $G\odot_g \mathcal{H}\cong G\odot H$ is a standard corona graph, as defined in 1970 by Frucht and Harary ^[6].

It is not difficult to check that if $|V(G)|\ge 2$, then the metric space induced by a generalized corona graph $G\odot_g \mathcal{H}$ is a corona metric space $M\odot_f \mathcal{M}$ constructed from $M = (X, d_X) = (V(G), d_G)$ and $f(x) = M_x = (X_x, d_{X_x})\in \mathcal{M}$ for every $x\in V(G)$, where $X_x = V(H_x)$ and $d_{X_x}(y, y') = \min\{2, d_{H_x}(y, y')\}$. As we can expect, if there exists $x\in V(G)$ such that $g(x) = H_x$ is not connected, then for two vertices $y$ and $y'$ belonging to different components of $H_x$ we assume that $d_{H_x}(y, y') = +\infty$, and so $d_{X_x}(y, y') = \min\{2, d_{H_x}(y, y')\} = \min\{2, +\infty\} = 2$.

In other words, if $G$ is a connected graph with at least two vertices, then the geodesic distance of a generalized corona graph $G\odot_g \mathcal{H}$ induces a corona distance.

Theorem 3.2. Every metric space induced by a generalized corona graph on $n$ vertices, where $n\ge 2$, either has at least $n$ distinct lines or has a universal line.

Proof. Let $G\odot_g \mathcal{H}$ be a generalized corona graph, where $G$ is connected. We first consider the cases in which $|V(G)| = 1$. If $G\cong K_1$ and $\mathcal{H} = \{H\}$, then the graph $K_1\odot_g \mathcal{H}$, which is in fact the join graph $K_1+H$, is included in the class of graphs of diameter at most two. Therefore, by Theorem 1.3, the metric space induced by $K_1\odot_g \mathcal{H}$, either has at least $|V(H)|+1$ distinct lines or has a universal line.

Now, if $|V(G)|\ge 2$ then the metric space induced by $G\odot_g \mathcal{H}$ is a corona metric space, and so the result follows by Theorem 3.1.

4.   The class of Cartesian metric spaces

It is well known that there are many ways to endow a metric on a product of two metric spaces. In general, there is no reason why an arbitrary metric on a product should have a clear relationship to the metrics of the individual spaces. Instead, if the metric on the product space preserves the metrics on the projection subspaces, then one can expect that some properties of the individual spaces can be carried over to the product space. In this section we consider a particular case of these conservative metrics.

Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. The Cartesian metric space $M\Box M^* = (X\times Y, \mu)$ is equipped with the metric,

Obviously, $M\Box M^*$ is isometric to $M^*\Box M$. Furthermore, the subspace of $M\Box M^*$ induced by $X\times \{y\}$ is isometric to $M$ for every $y\in Y$, and the subspace induced by $\{x\}\times Y$ is isometric to $M^*$ for every $x\in X$.

Given a metric space $M = (X, d_X)$ and two different points $a, b\in X$, we define

● $[a, b] = \{c\in X:\, d_X(a, b) = d_X(a, c)+d_X(c, b)\}.$

● $\langle a, b\rangle = [a, b]\setminus\{a, b\}.$

● $[\overrightarrow{a, b}] = \{c\in X:\, d_X(c, b) = d_X(c, a)+d_X(a, b)\}.$

Notice that for every $a, b\in X$, with $a\ne b$,

To ease the proof of our results, we need to establish the following four lemmas.

Lemma 4.1. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. For any $x, x'\in X$, with $x\ne x'$, and any $y\in Y$,

Proof. Let $x, x'\in X$ be two different points, let $y\in Y$ and $(a, b)\in X\times Y$. We differentiate the following cases for $x, x'$ and $a$.

Case 1. $a\in [\overrightarrow{x, x'}]$. In this case,

Hence, $(a, b)\in [\overrightarrow{(x, y), (x', y)}]$.

Case 2. $a\in [\overrightarrow{x', x}]$. By analogy to Case 1 we conclude that $(a, b)\in [\overrightarrow{(x', y), (x, y)}]$.

Case 3. $a\in \langle x, x'\rangle$. In this case,

Therefore, $(a, y) \in \langle (x, y), (x', y)\rangle$.

From Cases 1 and 2 we deduce that

while from Case 3 we deduce that

Now, we differentiate the following three cases for $(x, y), (x', y)$ and $(a, b)$.

Case 1'. $(a, b)\in [\overrightarrow{(x, y), (x', y)}]$. In this case,

Hence, $d_X(a, x') = d_X(a, x)+d_X(x, x')$, i.e., $a\in [\overrightarrow{ x, x'}]$.

Case 2'. $(a, b)\in [\overrightarrow{(x', y), (x, y)}]$. By analogy to Case 1' we conclude that $a\in [\overrightarrow{x', x}]$.

Case 3'. $(a, b) \in \langle (x, y), (x', y)\rangle$. In this case,

Therefore, $(a, b) \in \langle(x, y), (x', y)\rangle$ if and only if $b = y$ and $a\in \langle x, x'\rangle$.

According to Cases 1' and 2' we conclude that

while from Case 3' we deduce that

Therefore, the result follows.

Lemma 4.2. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. For any $x, x'\in X$ and $y, y'\in Y$ such that $x\ne x'$ and $y\ne y'$,

Proof. If $(a, b)\in [\overrightarrow{x, x'}]\times [\overrightarrow{y, y'}]$, then $d_X(a, x') = d_X(a, x)+d_X(x, x')$ and $d_Y(b, y') = d_Y(b, y)+d_Y(y, y')$. Hence,

Therefore, $(a, b)\in [\overrightarrow{(x, y), (x', y')}]$, which implies that $[\overrightarrow{x, x'}]\times [\overrightarrow{y, y'}]\subseteq [\overrightarrow{(x, y), (x', y')}]$.

Now, let $(u, v)\in X\times Y$ such that $u\not \in [\overrightarrow{x, x'}]$. In this case, $d_X(u, x') < d_X(u, x)+d_X(x, x')$. Since $d_Y(v, y')\le d_Y(v, y)+d_Y(y, y')$, we have

Hence, $(u, v)\not \in [\overrightarrow{(x, y), (x', y')}]$. Analogously, if $v\not \in [\overrightarrow{y, y'}]$, then $(u, v)\not \in [\overrightarrow{(x, y), (x', y')}]$. Therefore, $[\overrightarrow{(x, y), (x', y')}] = [\overrightarrow{x, x'}]\times [\overrightarrow{y, y'}]$.

Lemma 4.3. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. For any $x, x'\in X$ and $y, y'\in Y$ such that $x\ne x'$ and $y\ne y'$,

Proof. If $(a, b)\in [x, x']\times [y, y']$, then $d_X(x, x') = d_X(x, a)+d_X(a, x')$ and $d_Y(y, y') = d_Y(y, b)+d_Y(b, y')$. Hence,

Therefore, $(a, b)\in [(x, y), (x', y')]$, and so $[x, x']\times [y, y']\subseteq [(x, y), (x', y')].$

Now, let $(u, v)\in X\times Y$ such that $u\not \in [x, x']$. In this case, $d_X(x, x') < d_X(x, u)+d_X(u, x')$. Since $d_Y(y, y')\le d_Y(y, v)+d_Y(v, y')$, we have

Hence, from $u\not\in [x, x']$ we infer $(u, v)\not \in [(x, y), (x', y')]$. Analogously, if $v\not \in [y, y']$, then $(u, v)\not \in [(x, y), (x', y')]$. Therefore, $[(x, y), (x', y')] = [x, x'] \times [y, y']$.

From Lemmas 4.2 and 4.3 we deduce the following result.

Lemma 4.4. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. For any $x, x'\in X$ and $y, y'\in Y$ such that $x\ne x'$ and $y\ne y'$,

The following theorem provides a necessary and sufficient condition for the existence of universal lines in Cartesian metric spaces.

Theorem 4.5. If $M = (X, d_X)$ and $M^* = (Y, d_Y)$ are metric spaces with $|X|\ge 2$ and $|Y|\ge 2$, then the Cartesian metric space $M\Box M^*$ has a universal line if and only if one of the following conditions holds.

$\rm(i)$ There exist two points $x, x'\in X$ such that $\langle x, x' \rangle = \varnothing$ and $\mathcal{L}_{M}\{x, x'\}$ is universal or there exist two points $y, y'\in Y$ such that $\langle y, y' \rangle = \varnothing$ and $\mathcal{L}_{M^*}\{y, y'\}$ is universal.

$\rm(ii)$ There exist two points $x, x'\in X$ such that $[x, x'] = X$ and there exist two points $y, y'\in Y$ such that $[y, y'] = Y$.

Proof. As usual, symmetric cases will be omitted. If there exist two points $x, x'\in X$ such that $\langle x, x' \rangle = \varnothing$ and $\mathcal{L}_{M}\{x, x'\}$ is universal, then by Lemma 4.1 we have that for any $y\in Y$, $\mathcal{L}_{M\Box M^*}\{(x, y), (x', y)\} = \mathcal{L}_{M}\{x, x'\}\times Y = X\times Y.$

Now, if there exist two points $x, x'\in X$ such that $[x, x'] = X$ and there exist two points $y, y'\in Y$ such that $[y, y'] = Y$, then Lemma 4.4 leads to $\mathcal{L}_{M\Box M}\{(x, y), (x', y')\} = X\times Y$.

Conversely, assume that there exist two distinct points $(x, y), (x', y')\in X\times Y$ such that $\mathcal{L}_{M\Box M^*}\{(x, y), (x', y')\}$ is universal. We differentiate the following two cases.

Case 1. $y = y'$. In this case $x\ne x'$ and, by Lemma 4.1 we have

Therefore, $\mathcal{L}_{M}\{x, x'\} = X$ and $\langle x, x'\rangle = \varnothing$, as required.

Case 2. $x\ne x'$ and $y\ne y'$. By Lemma 4.4 we have

Now, if there exists $x_0\in [\overrightarrow{x', x}]\setminus \{x'\}$, then $(x_0, y)\not\in \mathcal{L}_{M\Box M^*}\{(x, y), (x', y')\}$, which is a contradiction. Hence, $[\overrightarrow{x', x}] = \{x'\}$ and, analogously, $[\overrightarrow{x, x'}] = \{x\}$, $[\overrightarrow{y, y'}] = \{y\}$ and $[\overrightarrow{y', y}] = \{y'\}$. Therefore, $[x, x'] = X$ and $[y, y'] = Y$, as required.

To continue the study we need to state the following lemmas.

Lemma 4.6. Let $M = (X, d_X)$ be a metric space. If there exist $a, b, u, v\in X$ such that $\{a, b\}\ne \{u, v\}$, $\langle a, b\rangle\ne \varnothing$ and $\langle u, v\rangle\ne \varnothing$, then $\mathcal{L}_{M}\{a, b\}\ne \mathcal{L}_{M}\{u, v\}$ or $\langle a, b\rangle\ne \langle u, v\rangle$.

Proof. Suppose to the contrary that $\mathcal{L}_{M}\{a, b\} = \mathcal{L}_{M}\{u, v\}$ and $\langle a, b\rangle = \langle u, v\rangle$. Under these assumptions, $u, v\in \mathcal{L}_{M}\{a, b\}$ and we can assume, without loss of generality, that $u\in [\overrightarrow{a, b}]$. Hence, for any $x\in \langle a, b\rangle = \langle u, v\rangle$,

and so

With this fact in mind, we differentiate two cases.

Case 1. $v\in [\overrightarrow{a, b}]$. In this case, for any $x\in \langle a, b\rangle = \langle u, v\rangle$,

Hence,

Thus, by (4.1) and (4.2),

which is a contradiction, as $a\ne x$.

Case 2. $v\in [\overrightarrow{b, a}]$. In this case, for any $x\in \langle a, b\rangle = \langle u, v\rangle$,

Hence,

Thus, by (4.1) and (4.3),

which is a contradiction, as $\{a, b\}\cap \langle u, v\rangle = \varnothing$ and $\{a, b\}\ne \{u, v\}$.

Lemma 4.7. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces where $|X|\ge 2$ and $|Y|\ge 2$. If there exist $a, b, u, v\in X$ such that $\{a, b\}\ne \{u, v\}$, $\langle a, b\rangle\ne \varnothing$ and $\langle u, v\rangle\ne \varnothing$, then for any $y\in Y$,

Proof. Suppose, to the contrary, that $\mathcal{L}_{M\Box M^*}\{(a, y), (b, y)\} = \mathcal{L}_{M\Box M^*}\{(u, y), (v, y)\}.$ Since $|Y|\ge 2$, Lemma 4.1 leads to $\mathcal{L}_{M}\{a, b\} = \mathcal{L}_{M}\{u, v\}$ and $\langle a, b\rangle = \langle u, v\rangle$, which contradicts Lemma 4.6. Therefore, the result follows.

The following result shows that if the number of lines of a metric space $M$ is at least the number of points, then for any finite metric space $M^*$, the number of lines of $M\Box M^*$ is at least the number of points.

Theorem 4.8. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two metric spaces. If $\ell(M)\ge |X|$ or $\ell(M^*)\ge |Y|$, then $\ell(M\Box M^*)\ge |X\times Y|$.

Proof. Assume $\ell(M)\ge |X|$. Let $y\in Y$ and $a, b, u, v\in X$ such that $\mathcal{L}_{M}\{a, b\}\ne \mathcal{L}_{M}\{u, v\}$. We differentiate the following three cases.

Case 1. $\langle a, b\rangle = \langle u, v\rangle = \varnothing$. By Lemma 4.1,

Case 2. $\langle a, b\rangle = \varnothing$ and $\langle u, v\rangle\ne \varnothing$. By Lemma 4.1,

Notice that we reach the same conclusion whether $|Y|\ge 2$ or $|Y| = 1$.

Case 3. $\langle a, b\rangle\ne \varnothing$ and $\langle u, v\rangle\ne \varnothing$. In this case Lemma 4.7 leads to

According to the three cases above, $\ell(M\Box M^*)\ge \ell(M)|Y|\ge |X||Y| = |X\times Y|$.

Next we present the case in which the metric spaces $M$ and $M^*$ are integral and for each point of these spaces there is another point at distance one.

Theorem 4.9. Let $M = (X, d_X)$ and $M^* = (Y, d_Y)$ be two finite and integral metric spaces. If $\eta(x) = 1$ for every $x\in X$ and $\eta(y) = 1$ for every $y\in Y$, then the Cartesian metric space $M\Box M^*$ has a universal line or $\ell(M\Box M^*)\ge |X\times Y|$.

Proof. If $|X| = 2$ or $|Y| = 2$, then the result follows by Theorem 4.5. From now on we assume that $|X|\ge 3$ and $|Y|\ge 3$.

We differentiate the following cases for the diameter of $M$ and $M^*$.

Case 1. $D(M)\ne 2$ and $D(M^*)\ne 2$. If $D(M) = 1$, then by Lemma 4.1, $\mathcal{L}_{M\Box M^*}\{(x, y), (x', y)\} = \{x, y\}\times Y$ for every $y\in Y$ and $x, x'\in X$ with $x\ne x'$. Hence,

Now, if $D(M)\ge 3$ and $D(M^*)\ge 3$, then for every $x\in X$ there exists $x'\in X\setminus \{x\}$ such that $\langle x, x' \rangle \ne \varnothing$, as $\eta(x) = 1$. Analogously, for every $y\in Y$ there exists $y'\in Y\setminus \{y\}$ such that $\langle y, y' \rangle \ne \varnothing$. Thus, Lemma 4.7 leads to

Case 2. $D(M) = D(M^*) = 2$. By Theorem 1.3, we have that $M$ has a universal line or $\ell(M)\ge |X|$. Likewise, $M^*$ has a universal line or $\ell(M^*)\ge |Y|$.

Let $x, x'\in X$ and $y, y'\in Y$ such that $x\ne x'$ and $y\ne y'$. Observe that if $\mathcal{L}_M\{x, x'\} = X$, then $\langle x, x'\rangle = \varnothing$ or $[x, x'] = X$, as $D(M) = 2$.

Hence, if $\mathcal{L}_M\{x, x'\} = X$ and $\langle x, x'\rangle = \varnothing$ or $\mathcal{L}_{M^*}\{y, y'\} = Y$ and $\langle y, y'\rangle = \varnothing$, then by Theorem 4.5 we conclude that $M\Box M^*$ has a universal line.

Now, if $\mathcal{L}_M\{x, x'\} = X = [x, x']$ and $\mathcal{L}_{M^*}\{y, y'\} = Y = [y, y']$, then by Lemma 4.3 we have $\mathcal{L}_{M\Box M^*}\{(x, y), (x', y')\} = X\times Y.$

Finally, if $\ell(M)\ge |X|$ or $\ell(M^*)\ge |Y|$, then Theorem 4.8 leads to $\ell(M\Box M^*)\ge |X||Y|$.

We recall that the Cartesian product of two graphs $G$ and $H$ is the graph $G\Box H$, such that $V(G\Box H) = V(G)\times V(H)$ and two vertices $(g, h), (g', h')$ are adjacent in $G\Box H$ if and only if, either $g = g'$ and $hh'\in E(H)$ or $h = h'$ and $gg'\in E(G)$. For basic properties of the Cartesian product of two graphs we suggest the books ^[10,11].

It is well known that the distance between two vertices $(g, h)$ and $(g', h')$ is given by

Hence, if $G$ and $H$ are two connected graphs, then the metric space induced by the Cartesian product graph $G\Box H$ is the Cartesian metric space $M\Box M^* = (X\times Y, \mu)$, where $X = V(G)$ is the vertex set of $G$ and $Y = V(H)$ is the vertex set of $H$. Therefore, the following result is a particular case of Theorem 4.9.

Corollary 4.10. If $G$ and $H$ are two connected graphs with at least two vertices, then the metric space induced by the Cartesian product graph $G\Box H$ has a universal line or $\ell(G\Box H)\ge |V(G)||V(H)|$.

Acknowledgments

The author would like to thank Abel Cabrera Martínez for the exchange of ideas on this subject.

Conflict of interest

The author declares no conflicts of interest in this paper.