The Hermite-Hadamard inequality for $s$-Convex functions in the third sense

1.   Introduction

With the increasing severity of the climate problem, more and more manufacturers have begun to engage in the production of low-carbon products. Such as, Gree Inn. designed the energy-efficient products ^[1], Haier produced low-carbon household appliances ^[2]. While investing in emission reduction, how to ensure the interests of firms, low-carbon decision-making becomes particularly important. In recent years, with the vigorous development of e-commerce, more and more manufacturers have also begun to build online direct sales channels. Nowadays, Gree and Haier have opened online sales channels. However, the opening of online direct sales channels by manufacturers will divert traditional offline demand, damage the interests of retailers in traditional offline channels, and produce channel conflict. As low-carbon products are gradually recognized and accepted by people, manufacturers open online direct sales channels for low-carbon products, which not only brings online/offline channel conflicts, but also changes manufacturers' carbon emission reduction decisions and channel cooperation.

In addition, with the uncertainty of demand and channel competition and cooperation, manufacturers and retailers often take a risk averse attitude in order to reasonably reduce losses. For example, Zara, a world famous fast fashion brand, not only has physical stores, but also has a wide online network. It books online orders, and its shipping is available worldwide ^[3]. With the gradual growth of development, Zara's decision-making is also affected by its risk aversion attitude. Zara designed a hyper fast supply chain at a great cost to reduce demand risk ^[4]. Therefore, the study of dual channel low-carbon supply chain (LCSC) decision-making under the background of risk aversion has significance.

In order to better understand the impact of risk aversion and dual channels on low-carbon decision-making, we need to pay attention to the degree of risk aversion of firms and consumers' channel selection preference. Based on this, this paper establishes a dual channel LCSC with one manufacturer and one retailer under risk aversion. Expected utility (EU) framework ^[5], mean variance (MV) and Conditional Value-at-Risk (CVaR) ^[6] are three commonly used risk aversion measurement methods. Although both EU approach and CVaR provide good results in dealing with the problem of newsvendors' inventory with risk aversion behavior. The MV framework also has several advantages in modeling risk aversion since it enables transforming a stochastic (probabilistic) problem to a deterministic approximation which is distribution-free in nature ^[7]. By considering manufacturer-led mode under MV framework, we summarize our main contribution as follows and unfold them in the remaining part of this paper.

First, we establish three manufacturer Stackelberg models, including single traditional offline channel, competing dual channel of online and offline, and dual channels with competition and revenue sharing. We derive the optimal emission reduction level, wholesale price and retail price for all the three models.

Second, we show that the price of low-carbon products will increase as consumers increase their low-carbon sensitivity and the firms' profits.

Third, we point out that the deepening of retailers' risk aversion promotes the increase of the manufacturer's price, while the impact of the manufacturer's risk aversion has an opposite effects. We also reflect that the arbitrage behavior of the retailer can be avoided under a certain risk aversion environment.

At last, we demonstrate that in a limited risk aversion environment, the dual channels are conducive to increasing the interests of the manufacturer, but may harm the interests of the retailer. Moreover, we reveal that the sharing of revenue by the manufacturer to the retailer helps to improve the retailer's benefit.

The remainder of the paper is organized as follows. Next section reviews the literatures. In Section 3, we introduce assumptions and notions. Section 4 analysis three models, including single channel, pure dual channel, and dual channel with revenue sharing. Section 5 shows parameter sensitivity. Section 6 investigates the firms' utilities via numerical studies. Finally, Section 7 concludes and presents future research. All technical proofs are presented in Appendix.

2.   Literature review

In this section, the literature is reviewed regarding three research streams to highlight the contributions.

2.1.   Low-carbon supply chain

Low carbon supply chain is to incorporate carbon control constraints into the traditional supply chain. Scholars have discussed LCSC from different perspectives. In terms of contract mechanism, Du et al. ^[8] proposed a scheme of carbon related price discount sharing. Peng et al. ^[9] established a revenue-sharing with subsidy on emission reduction under yield uncertainty. Han et al. ^[10] designed a joint cost and profit distribution contract for LCSC with government subsidy effect and fairness concern. In terms of optimal strategy formulation, Cong et al. ^[11] focused on impacts of green financial subsidies, low-carbon subsidies and yield uncertainty on carbon emission reduction. Zou et al. ^[12] discussed on the impact of fairness concern on the profit of supply chain with carbon quota policy. In controlling carbon emission reduction, Xia et al. ^[13] showed that how reciprocal preferences and consumers' low-carbon awareness affect supply chain's decisions. Yu et al. ^[14] investigated information sharing's effect on carbon emission reduction.

The above series of LCSC studies are carried out in the manufacturer-led supply chain, the results provide a good reference for us to deal with more complex transactions. We continue to follow the manufacturer led model for exploration, but different from previous studies, we expand the single channel to the dual channel problem, and further consider the bounded rational behavior of firms, especially the firms' risk averse behavior.

2.2.   Dual-channel supply chain

In recent years, the vigorous development of e-commerce has brought new development opportunities to low-carbon emission reduction manufacturers, the traditional supply chain is gradually transforming into a dual-channel supply chain. Scholars also begin to discuss the decision-making problem of dual-channel supply chains. Wu et al. ^[15] analyzed the online and offline low-carbon operation by considering the low-carbon awareness of online shoppers. Ghosh et al. ^[16] investigated an emissions reduction problem in a two-echelon dual-channel supply chain under consumers' low carbon preferences and cap-and-trade regulation. Che et al. ^[17] focused on different low-carbon subsidies under dual channel supply chain. These results provide a good quantitative reference for the dual channel low-carbon problem, however the direct sales channels of manufacturers will divert traditional offline demand, harm the interests of retailers in traditional offline channels, and create channel conflicts.

In order to alleviate the conflict of dual channel supply chain, some scholars began to discuss the cooperation mode of online and offline channels. As a common means of supply chain management, revenue sharing mechanism has been favored by scholars. They designed a dual channel revenue sharing mechanism for different scenarios from various perspectives, including free riding behavior^[18,19], demand disruptions scenario^[20], cap-and-trade regulatory constraints ^[21].

The design of all these mentioned dual channel revenue sharing mechanisms can better help firms obtain more profits and improve the operation efficiency of the supply chain. However, they have not considered the firms' risk aversion behavior. In contrast, we introduce risk aversion into dual channel LCSC for discussion.

2.3.   Supply chain with risk aversion

In actual traders, in the face of various uncertain factors, corporate decision-makers often hold a conservative attitude. At this time, they often show risk aversion behavior. In order to describe this psychology of firms, scholars have put forward a series of methods. Chiu and Choi ^[22] reviewed a series of literature on MV analytical models, which helped us better understand the use of MV methods in supply chain risk management. Since then, scholars have continuously improved the MV model in supply chain risk analysis from multiple backgrounds and angles, including, the channel coordination of option contracts with risk constraints ^[23], the global supply chain operation risk of aviation logistics in the era of blockchain technology ^[24], the sharing economy platforms with risk considerations ^[25] and so on. These research results show that MV method has a good quantitative reference for firms' risk aversion psychology, and provide a basis for us to use MV method for modeling.

In addition, when risk averse firms make low-carbon decisions, MV method has also received a lot of attention, and a lot of achievements have emerged. Under the framework of MV approach, Qi et al. ^[26] make the optimal operation strategies for one supplier, one manufacturer and one third-party emission-reducing contractor with carbon cap-and-trade mechanism. Bai and Meng ^[27] use the MV method to describe the decision-making problems of two competing manufacturers under the cap-and-trade regulation. However, there are few discussions about dual-channel low-carbon issues with risk aversion behavior (Bao et al. ^[28]).

In practice, the supply chain producing low-carbon products may have online and offline channels, and members have risk aversion behaviors. However, the previous literature has not adequately investigated the low-carbon strategies when these two issues are considered altogether. In summary, different from ^[28] concerning sell non-green products through online channels and green products through offline channels, we demonstrate both sales channel sell low-carbon products. Different from ^[29,30], we focus on risk aversion in a low-carbon supply chain. Different from ^[31], we discuss a dual channel. Different from ^[32,33], we investigate a low carbon strategy. The characteristics and contributions of our study are presented in Table 1.

3.   Assumptions and notions

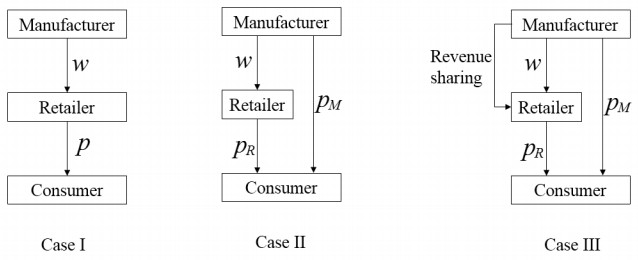
We consider a single-period supply chain consisting of a risk averse manufacturer and a risk averse retailer under random demand. In this case, the random demand consists of two parts: expected demand and demand shock. The manufacturer is a leader and produces low carbon products, she can sales through traditional retail channels or open direct sales channels. In order to reduce channel conflicts, the manufacturer will share part of the sales revenue with retailers when opening direct sales channel. Based on this, we consider three models see Figure 1, one is that there is no direct sales channel, the other is that the manufacturer has direct sales channel, and the third is that the manufacturer has direct sales channel and shares revenue with her retailer.^* We use superscripts $I$, $II$, and $III$ denote three different supply chain structures. Subscripts $M$ and $R$ denote the manufacturer and the retailer, respectively. Related notions are summarized in Table 2.

^*In life, many manufacturers have opened online sales channels, such as Zara ^[30]. Zara is also risk averse ^[4]. Therefore, our models (at lest the second model) can be used for practical sales.

For tractability, some assumptions are provided as follows.

● The sales volume of the product is equal to the market demand.

● The cost of low-carbon technologies for the manufacturer is $\frac{1}{2} ke^2$, like ^[17] and ^[34].

● The market size is 1, consumers have channel preferences, the proportion of preference for online channels is $a$, and the proportion of offline preferences is $1-a$.

● The consumer's own price sensitivity coefficient to the product is 1, and the cross price sensitivity coefficient between channels is less than the own price sensitivity coefficient, that is, b < 1.

● The wholesale price and retail price decisions are based on unit production costs, without loss of generality, we assume that production cost is 0.

● The manufacturer's retail price should be higher (at least not lower) than the wholesale price. That is, $p_M\geq w$ can prevent the retailer from exploiting loopholes and buying products only through online channel.

Noting that both the manufacturer and the retailer are risk averse, in line with Li et al. ^[35], we consider using the MV method to characterize their respective utility profits.

where $E$ is the expectation operator, and $i$ represent $M$ and $R$, respectively. Thus, $\pi_i$ is the profit function of the firm $i$, $E(\pi_i)$ is the expected profit of the firm $i$. $\lambda_i\geq 0$ is the risk aversion parameter of the firm $i$, particularly, $\lambda_i = 0$ means that the firm $i$ is risk neutral. $Var(\pi_i)$ respect the mean and variance of the profit of the firm $i$, $\sqrt{Var(\pi_i)}$ is the standard deviation of profit of the firm $i$, $U(\pi_i)$ is the mean-standard-deviation objective function of the firm $i$.

4.   Model analysis

This section considers three different models and finds the optimal strategies under the manufacturer Stackelberg (MS) models. In all three MS modes, the retailer decisions his selling price firstly, then the manufacturer decisions the wholesale price, emission reduction level and her selling price (if she open the online channel) based on the retailer's selling price, at last the retailer determines his finally selling price based on the manufacturer's decisions. ^†

^†We just consider one type of decision-making order, the more decision order types, see ^[36,37,38]. They have made a good discussion on the decision-making opportunity, and their results help firms grasp the opportunity and improve profits accurately.

4.1.   Only existence of offline sales channel

In the case of no direct sales channel, the demand equal to market size+demand shock-price dependence+low carbon dependence. That is $D^I = 1+x-p_R+te$. The manufacturer acts as the leader and sets the wholesale price $w$ and the emission reduction level $e$, simultaneously. The retailer acts as the follower and sets the retail price $p_R$. The profits of the manufacturer and the retailer are as follows, respectively.

Noting that the risk aversion attitude of the firms, we adopt the MV method, and we can obtain the firms' MV utility function as the follows.

Proposition 4.1. If $4k > t^2$, the optimal wholesale price, emission reduction level and retail price are as following, respectively.

Proposition 4.1 points out that the emission reduction cost coefficient cannot be too small, here $k > \frac{t^2}{4}$, otherwise it will cause endless investment in low-carbon technology, which is impossible in actual manufacturing.

Corollary 4.2. The $p_R^{I*} > w^{I*} > 0$ holds if i) $\lambda_R\leq\lambda_M$ and $\sigma < \frac{1}{2\lambda_M-\lambda_R}$; ii)$p_R^{I*} > w^{I*} > 0$ if $\lambda_R > \lambda_M$ and $\sigma\leq\frac{1}{3\lambda_R-2\lambda_M}$.

Corollary 4.2 reveals that both the manufacturer and the retailer can earn positive profits if and only if the demand shock fluctuation is not particularly large.

4.2.   The manufacturer opens online direct sales channel

In the case of that the direct sales channel is opened. The manufacturer not only sells through offline channel, but also sells products directly to the consumer through online channel. In addition to determining the wholesale price $w$ and carbon emission reduction level $e$, the manufacturer also need to further determine the online price $p_M$. The retailer only need to determine the offline price $p_R$. At this time, the online and offline channels are in a competitive state, and the channel market demand competes through different retail prices. Then the demand of online channel equal to online channel market scale + online channel demand risk - online price dependence + offline price dependence + low carbon dependence, i.e., $D_M^{II} = a(1+x)-p_M+bp_R+te$. The demand of offline channel equal to offline channel market scale + offline channel demand risk - offline price dependence + online price dependence + low carbon dependence, i.e., $D_R^{II} = (1-a)(1+x)-p_R+bp_M+te$.The demand in ^[28] is only affected by the retail price of a single channel, which is very different from our model. n our dual channel model, demand is influenced by the retail prices of both two channels. Thus, the profits of the manufacturer and the retailer are as follows.

Therefore, we can obtain the firms' MV utility function as the follows.

Proposition 4.3. If $b < \frac{4k-3t^2}{4k+t^2}$ and $4k > 3t^2$, the optimal wholesale price, emission reduction level, manufacturer's retail price, and retailer's retail price are as following, respectively.

where $A^{II} = 4k(1-a+ab)-(2+b)(1-2a)t^2$, $B^{II} = 4k[b^2-2-a(b+b^2-2)]-(2+b)(3a+ab-b-2)t^2$, $C^{II} = 4bk+(2+b)t^2-a(4bk-4k+3t^2+bt^2)$, $G^{II} = a(4b-3)+(1-a)t^2$, $H^{II} = 4[1-(1-b)a]k+(3a+b+ab)t^2$, and $L^{II} = 4(1-b)k-(3+b)t^2$.

Proposition 4.3 indicates that the cross price sensitivity coefficient should be smaller, otherwise it will cause a lot of interference to other channels, and even cause other channels to no longer make profits before they are closed. This is also not conducive to the development of multi-channel transactions in reality.

Proposition 4.3 also points out that the emission reduction cost coefficient should not be too small. But different from proposition 4.1, the minimum threshold of $k$ becomes larger. In other words, compared with only existence of offline channels, the simultaneous existence of online and offline channels will increase the manufacturer's investment in low-carbon, otherwise the manufacturer may not obtain the best decision.

Corollary 4.4. The retailer has no incentive to perform arbitrage if one of the following conditions satisfies. That is i) $p^{II*} > w^{II*}$ if $a\leq\frac{1}{2}$, $\lambda_R < \frac{2-3a+b-ab}{1-a+b-ab}\lambda_M$ and $\sigma > \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$; ii) $p^{II*} > w^{II*}$ if $\frac{1}{2} < a < \frac{2+b}{3+b}$, $\lambda_R > \frac{2-3a+b-ab}{1-a+b-ab}\lambda_M$ and $\sigma < \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$; iii) $p^{II*} > w^{II*}$ if $a\geq\frac{2+b}{3+b}$ and $\sigma < \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$.

Corollary 4.4 reveals that when more than half of consumers choose offline physical stores, the retailer with lower risk aversion will buy products through offline channel only when the demand fluctuation is large. When more than half of consumers choose to shop online, the retailer will use offline channel as long as the demand fluctuation is small.

Corollary 4.4 further shows that when the manufacturer opens online direct sales channel, it will damage the interests of her retailer. At this time, it is reasonable for the retailer to arbitrage by purchasing products from online channel, so the manufacturer may reduce the occurrence of her retailer arbitrage by sharing revenues to the retailer.

4.3.   The manufacturer opens online channel and shares her revenue

When a manufacturer opens a direct sales channel, in order to make up for the retailer's loss, the manufacturer shares the $\theta$ part of the sales revenue with the retailer. At this time, the manufacturer still need to determine the wholesale price $w$, carbon emission reduction level $e$ and online retail price $p_M$, while the retailer determine the offline retail price $p_R$. Online and offline channels still compete through two retail prices, and the demand remains unchanged, i.e., $D_R^{III} = D_R^{II}$ and $D_M^{III} = D_M^{II}$. Thus, the profits of the manufacturer and the retailer are as follows.

Therefore, we can obtain the firms' MV utility function as the follows.

Proposition 4.5. When sharing the revenue from the manufacturer to the retailer in dual channel supply chain, the optimal wholesale price, emission reduction level, manufacturer's retail price, and retailer's retail price are as following, respectively if $b < \frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2}$ and $k > \frac{3-2\theta}{4}t^2$.

where $A^{III} = 4k(1-a)(1-b^2\theta)+4kab(1-\theta)-(1-\theta)(2+b)(1-2a)t^2$, $B^{III} = 4k[(1+\theta)b^2+a(1-b)(2+b+b\theta)-2]-(2+b)(1-\theta)(3a+ab-b-2)t^2$, $C^{III} = (1-a)(1+b)[4k(1-b)-(1-\theta)(2+b)t^2]$, $G^{III} = 2ab\theta-ab+b-2b\theta-2a\theta+a+1$, $H^{III} = 2k(1-a)(3-b^2)+4abk+3\theta(1+b)(1-2a)t^2-(1-2a)(3+2b)t^2$, $J^{III} = 4[1-(1-b)a]k+[b+2\theta+b\theta-b^2\theta+a(3+b-5\theta-4b\theta+b^2\theta)]t^2$, $L^{III} = (1-a)(1+b)[2bk-2k+(3-\theta-b\theta)t^2]$ and $T^{III} = 4(1-b)k-(2\theta+2b\theta-3-b)t^2$.

According to Propositions 4.1, 4.3 and 4.5, we can find that $\frac{1}{4}t^2 < \frac{3-2\theta}{4}t^2 < \frac{3}{4}t^2$ and $\frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2} > \frac{4k-3t^2}{4k+t^2}$.^‡ That is, the opening of online direct sales channel has raised the minimum threshold of carbon emission reduction cost coefficient, while the introduction of revenue sharing mechanism reduces the minimum threshold of carbon emission reduction cost coefficient. Moreover, the application of revenue sharing mechanism increases the maximum threshold of cross price sensitivity coefficient. In other words, in order to maximize the utility of both sides, the opening of online channel raises the determination conditions of optimal decision-making, while the revenue sharing mechanism appropriately relaxes the decision-making conditions.

^‡Since $\frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2}-\frac{4k-3t^2}{4k+t^2} = \frac{8\theta(2k-t^2)}{[4k+(1-2\theta)t^2](4k+t^2)}$ and $k > \frac{3}{4}t^2$, then $2k-t^2 > \frac{1}{2}t^2$ and $4k+(1-2\theta)t^2 > 2t^2$. Thus $\frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2}-\frac{4k-3t^2}{4k+t^2} > 0$.

Corollary 4.6. $p^{III*} > w^{III*}$ if $\lambda_R < \frac{(2-3a+b-ab)T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]}{(1-a)(1+b)T^{III}}\lambda_M$ and $\sigma < \frac{(2a-1)T^{III}+b\theta[4(a+b-ab)k-(2a-1)t^2]}{[(2-3a+b-ab)\lambda_M-(1-a)(1+b)\lambda_R]T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]\lambda_M}$, where $T^{III} = 4(1-b)k-(2\theta+2b\theta-3-b)t^2$.

Corollary 4.6 shows that the revenue sharing mechanism still can not completely avoid retailers' arbitrage through online platform. This is in line with the fact that the retailer is profit seeking. Corollaries 4.4 and 4.6 also suggest that once the manufacturer opens online channels for sales, she has to bear the risk of arbitrage by retailers. Therefore, the manufacturer should carefully consider the simultaneous opening of online and offline channels.

5.   Sensitivity analysis on decisions

In this section, we explore the impact of low-carbon coefficient, degree of firms' risk aversion, channel preference and revenue sharing ratio on the decisions, respectively.

Theorem 5.1. In the case of ensuring that all strategies are positive values, with $t$ increases, all $e^{i*}$, $w^{i*}$, $p_R^{i*}$ and $p_M^{j*}$ increase, where $i = \{I, II, III\}$ and $j = \{II, III\}$.

Theorem 5.1 reflects that the higher the consumer's low-carbon preference coefficient, the stronger the consumer's awareness of low-carbon environmental protection, and the more inclined to buy low-carbon products, which will increase the demand for low-carbon products and increase the manufacturer's carbon emission reduction level. At the same time, the increase in the cost of abatement for manufacturers will increase the wholesale prices of low-carbon products, and retailers will also increase the retail prices of products. Therefore, the government and firms can increase consumers' awareness of low-carbon environmental protection by increasing low-carbon publicity, and guide consumers to buy low-carbon products.

In addition, Theorem 5.1 has a same conclusion that the higher consumers' low-carbon preference, the more the manufacturer is willing to cut carbon emissions compared with Proposition 1 of ^[30]. In other words, the risk aversion attitude of firms do not affect the impact of environmental friendly consumers on the low-carbon level of products.

Theorem 5.2. In the case of ensuring that all strategies are positive values, all $e^{i*}$, $w^{i*}$ and $p_M^{j*}$ increase as $\lambda_R$ increases, where $i = \{I, II, III\}$ and $j = \{II, III\}$. Under different conditions, the change of $p_R^{i*}$ with $\lambda_R$ is also different.

Theorem 5.2 shows that with the increasing risk aversion of the retailer, the retailer will adjust his retail price in time according to different situations to make profits reach the best state. At this time, the manufacturer will take this opportunity to improve the level of carbon emission reduction to improve market demand, and increase her retail price and wholesale price to make more profits.

According to Proposition 2 of ^[33], in the manufacturer-led case, the direct selling price is not affected by retailer's risk aversion and the retail price decreases with the increases in retailer's risk aversion. Combining Theorem 5.2 and ^[33], it points out that retailer's risk aversion has a different impact on online and offline retail prices under the case with and without low carbon.

Theorem 5.3. In the case of ensuring that all strategies are positive values, all $e^{i*}$, $w^{i*}$, $p_R^{i*}$ and $p_M^{j*}$ are decreasing in $\lambda_M$, where $i = \{I, II, III\}$ and $j = \{II, III\}$.

Theorem 5.3 points out that with the increasing of risk aversion of the manufacturer, the manufacturer will take a more conservative attitude. She avoids risk by reducing her retail price and wholesale price. In this case, she reduces the investment in carbon emission reduction efforts. At this time, the potential market demand will become less. Therefore, the retailer achieves the effect of attracting money by reducing his retail price.

Acoording to Corollary 2 of ^[32], the direct sale price increases in $\lambda_M$. Combining Theorem 5.3 and ^[32], it shows that with or without low-carbon strategy, the manufacturer's risk aversion attitude has brought two completely different results to the direct selling price.

Theorem 5.4. In the case of ensuring that all strategies are positive values, $w^{j*}$ and $p_R^{j*}$ all increase as $a$ decreases, while $p_M^{j*}$ is increasing in $a$, where $j = \{II, III\}$.

Theorem 5.4 reveals that the greater the proportion of consumers who prefer online direct sales channels, that is, the higher the loyalty of consumers to online channels, and the higher the price of online direct sales channels by the manufacturer. However, the lower the consumer's loyalty to offline channels, the smaller the offline demand, and the manufacturer and the retailer correspondingly lower the wholesale price and retail price of offline channels.

Theorem 5.5. In the case of ensuring that all strategies are positive values, when the manufacturer opens direct sales channels and shares her revenue, $e^{III*}$, $w^{III*}$, $p_R^{III*}$ and $p_M^{III*}$ all increase as $\theta$ decreases.

Theorem 5.5 indicates that with the increase of the revenue sharing ratio, the total profit of the manufacturer will decrease, so manufacturers will reduce their investment in carbon emission reduction. In this case, the manufacturer will reduce online direct sales price to expand the demand market for online direct sales channels, while the retailer will reduce retail price to enhance competitiveness and seize the market in order to compete with the manufacturer.

6.   Numerical studies on firms' utilities

In this section, because of the expression of the firms' utility functions of three modes are quite complex. We consider the numerical investigations to discuss the firms' utility of three modes and present new management insights. We explore the impact of low-carbon coefficient, degree of firms' risk aversion, channel preference and revenue sharing ratio, respectively. We suppose that $a = 0.5$, $b = 0.4$, $k = 1$, $t = 0.6$, $\theta = 0.3$, $\lambda_R = 0.5$, $\lambda_M = 0.6$ and $\sigma = 1$, which ensure that $4k > 3t^2$ and $4(1-b)k > (3+b)t^2$.^§

^§Because it is difficult to obtain real-life data, the data we use is only used for simulation. The assumptions of these parameters are random, as long as they meet the determination conditions of the optimal strategy. That is $4k > 3t^2$ and $4(1-b)k > (3+b)t^2$. Therefore, as long as conditions permit, the values of these parameters can be adjusted at will.

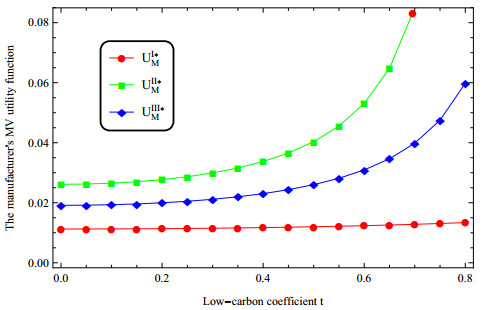
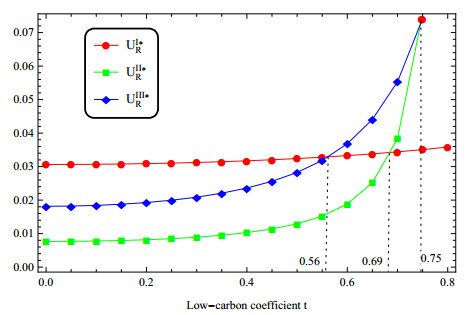
Firstly, considering the low-carbon coefficient, we change the value of $t$ and suppose the other parameters fixed. Under this condition, to obtain the optimal strategies for all three models, it holds that $t\in(0, 0.84)$. Figures 2 and 3 show that all firms' utilities are increasing in the low-carbon coefficient, that is the more consumers tend to low-carbon products, the higher the profits of firms. Figure 2 points out that $U_M^{II*} > U_M^{III*} > U_M^{I*}$, it also reflects that the opening of online channel helps the manufacturer increase revenue. Figure 3 points out that $U_R^{II*} > U_R^{I*}$ if $t > 0.69$, $U_R^{III*} > U_R^{I*}$ if $t > 0.56$, and $U_R^{III*} > U_R^{II*}$ if $t < 0.75$. It reflects that the revenue sharing mechanism is helpful to improve the revenue of the retailer.

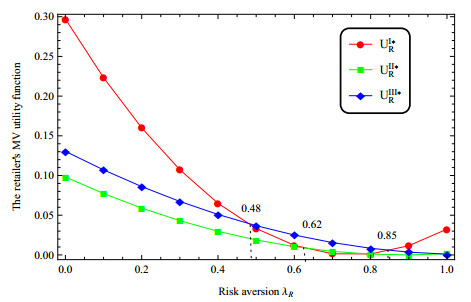
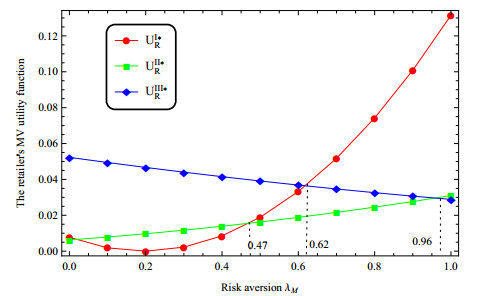
Secondly, we consider the risk aversion of the retailer, we change the value of $\lambda_R$ and suppose the other parameters fixed. Figure 4 shows that as the retailer's risk aversion degree increases, the manufacturer's risk aversion utilities of dual-channels show a upward trend, while the manufacturer's utility of single channel shows a U-shape trend. Figure 5 shows that the utilities of the retailer in dual-channels decrease as the degree of the retailer's risk aversion increases, while the retailer's utility of single channel shows a U-shape with the growth of the retailer's risk aversion. Figure 4 also points out that $U_M^{II*} > U_M^{I*}$ if $\lambda_R < 0.97$, $U_M^{III*} > U_M^{I*}$ if $\lambda_R < 0.75$, and $U_M^{III*} > U_M^{II*}$. This means that when the risk aversion degree of the retailer is limited, it is beneficial for the manufacturer to open online sales channel. In addition, according to Figures 4 and 5, in the dual channel environment, the more risk averse the retailer is, the less profit he will get and the more profit the manufacturer will make. At this time, cooperation will help the retailer improve his profit. The retailer should seize the opportunity and actively cooperate with the manufacturer's revenue sharing cooperation model. The manufacturer should take advantage of the situation to strengthen the implementation of cooperation.

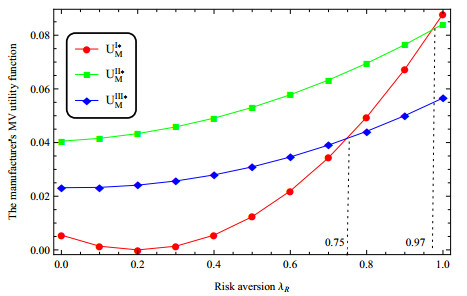
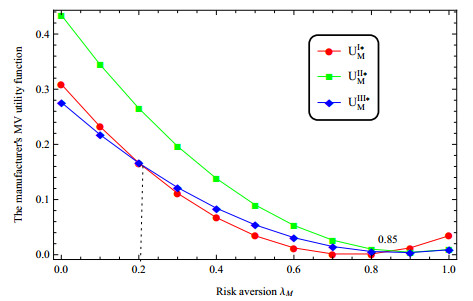
Thirdly, we consider the risk aversion of the manufacturer, we change the value of $\lambda_M$ and suppose the other parameters fixed. Figure 6 shows that as the manufacturer's risk aversion degree increases, the manufacturer's risk aversion utility shows a U-shaped trend. Figure 7 shows that the utility of a retailer under a single channel shows a U-shaped change with the change of the risk aversion coefficient. The utility of the retailer under pure dual-channel increases as the degree of risk aversion increases, and the utility of the retailer under dual-channel with revenue sharing decreases with the degree of risk aversion. Moreover, Figure 6 points out that $U_M^{II*} > U_M^{I*}$ if $\lambda_M < 0.85$, $U_M^{III*} > U_M^{I*}$ if $0.2 < \lambda_M < 0.85$, and $U_M^{III*}\geq U_M^{II*}$. This means that when the risk aversion degree of the manufacturer is limited, it is beneficial for the manufacturer to open online sales channel. In addition, according to Figures 6 and 7, under the limited risk aversion environment, the development of dual channel cooperation model will help the retailer increase profits. With the increasing risk aversion of the manufacturer, although she shared the income with the retailer, she also transferred the risk to the retailer, thus harming the interests of the retailer virtually. At this time, the retailer need to be vigilant and carefully participate in the revenue sharing cooperation of the manufacturer. The manufacturer can negotiate with her retailer to formulate a new cooperation mode, so that both sides can reach a mutually satisfactory transaction state again.

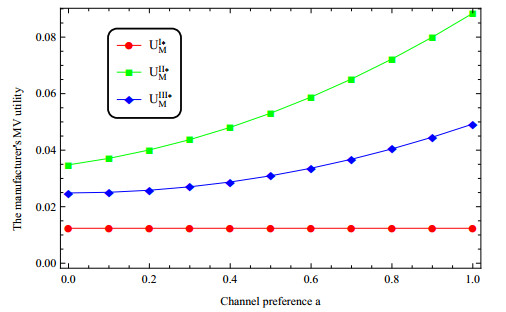
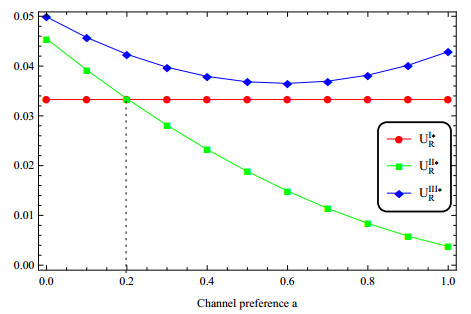
Fourthly, considering the channel preference, we change the value of $a$ and suppose the other parameters fixed. Figure 8 shows that the utility of the manufacturer increases with the increase of consumers' preference for online shopping. Figure 8 also points out that $U_M^{II*} > U_M^{III*} > U_M^{I*}$, it reflects that the opening of online channel helps the manufacturer increase revenue. Figure 9 shows that with the increase of consumers' preference for online shopping, the utility of the retailer of pure dual-channel decreases, while the retailer's utility of in dual-channel with revenue sharing shows a U-shaped change. Figure 9 points out that $U_R^{III*} > U_R^{II*}$, $U_R^{III*} > U_R^{I*}$, and $U_R^{II*} > U_R^{I*}$ if $a < 0.2$. It reflects that the revenue sharing mechanism is helpful to improve the revenue of the retailer.

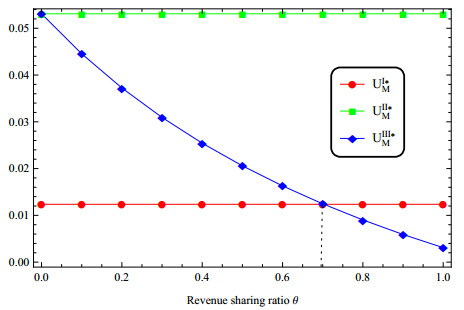
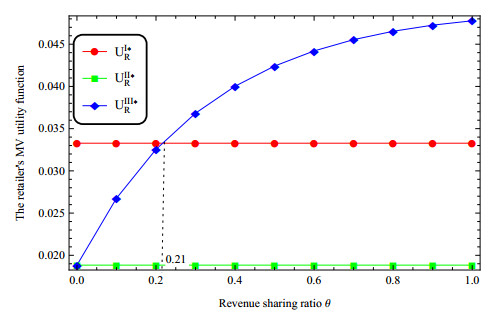
At last, considering the revenue sharing ratio, we change the value of $\theta$ and suppose the other parameters fixed. Figures 10 and 11 show that with the increase of revenue sharing ratio, the utility of the retailer increases, while the utility of the manufacturer decreases. Moreover, Figure 10 points out that $U_M^{II*} > U_M^{III*}$, $U_M^{II*} > U_M^{I*}$, and $U_M^{III*} > U_M^{I*}$ if $\theta < 0.7$. It means that the opening of online channel helps the manufacturer increase revenue. Figure 11 points out that $U_R^{II*} < U_R^{I*}$, $U_R^{III*} > U_R^{II*}$, and $U_R^{III*} > U_R^{I*}$ if $\theta > 0.2$. It reflects that the revenue sharing mechanism is helpful to improve the revenue of the retailer.

According to the previous analysis, it indicates that in a limited risk aversion environment, the opening of online direct sales channels by the manufacturer is conducive to improving the utility of the manufacturer, but it may harm the utility of the retailer. By reducing her own interests and sharing part of the revenue with the retailer, the manufacturer will help to improve the utility of the retailer under dual channels, thereby facilitating the long-term development of dual channels.

7.   Conclusions

Based on consumers' low-carbon preference and channel preference attributes, this article establishes three supply chain decision-making models. One is the manufacturer does not open online channels, the second is the manufacturer opens online channels, and the last is the manufacturer opens online channels and shares revenue with the retailer. We take the method of mean variance to characterize the risk aversion utility of the manufacturer and the retailer. The results are as follows:

First, the increased sensitivity of consumers to low-carbon products will help the manufacturer and the retailer increase the prices of low-carbon products and their profits. Second, the deepening of the retailer's risk aversion promotes the increase of the manufacturer's price, while the impact of the manufacturer's risk aversion has an opposite effects. Moreover, the arbitrage behavior of the retailer can not be completely avoided. However, as long as the conditions are sufficient, the retailer will give up arbitrage. Third, the more consumers prefer to use online channel, the selling prices of online products from the retailer and the manufacturer will rise, while the offline selling prices of the retailer will fall. As the revenue shared by the manufacturer to the retailer increases, the retail prices of products for the manufacturer and the retailer will fall. At last, in a limited risk aversion environment, dual channels can take more income to the manufacturer, while it may not be conducive to the development of the retailer. The introduction of a revenue sharing model can increase the retailer's income.

A managerial insight is that firms need to participate in the publicity of low-carbon concept, improve consumers' awareness of environmental protection, and respond to the call of low-carbon economy and sustainable development. Firms can avoid risky outcomes at the expense of lower expected profits, and can make the best decision by adopting the risk aversion attitude. Dominant manufacturers can increase product sales channels through online channel to adapt to the development trend of e-commerce. Retailers in the follow-up position should actively seek cooperation with manufacturers, strengthen the internal contact of supply chain channel, and achieve the purpose of common profit.

This study has several limitations. As competition is everywhere, and we only consider a single manufacturer and a single retailer, for further research, we can refer to ^[39] to consider the issue of dual channel supply chain network when multiple manufactures and retailers are involved. Our article only considers the carbon emission reduction level of the manufacturer, but ignores the carbon restriction rules. Therefore, in another direction, we can refer to ^[40,41] to discuss the decision-making under the cap-and-trade regulation. Moreover, different decision-making order will affect the final profit of firms, however we just discuss one stye of decisions' sequence, one direction can refer to the practices of ^[36,37,38] to investigate the influence of different decision-making timing on strategies under risk aversion. In addition, supply chain coordination has not been considered in this paper, the other interesting direction is that reference ^[42] to consider the coordination mechanisms.

Acknowledgements

This work is supported by National Natural Science Foundation of China (No.71873111; No.12002194; No.12072178), Hubei Superior and Distinctive Discipline Group of Mechatronics and Automobiles, Project (No.ZR2020QA037; No.ZR2020MA054; No.2019KJI013; No.2020KJI003) supported by Shandong Provincial Natural Science Foundation; Ministerio de Ciencia, Innovación y Universidades (No.PGC2018-097198-B-I00) and Fundación Séneca de la Región de Murcia (No.20783/PI/18).

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendixs

Proof of Proposition 4.1

Firstly, we consider the retailer's decision. Since $\frac{\partial^2 U_R^I}{\partial p_R^2} = -2$, then we can obtain that the optimal retail price for given $w$ and $e$ as the follow.

Secondly, we consider the manufacturer's decisions. Taking $p_R(w, e)$ into $U_M^I$, we can obtain that

Since the second-order derivative of $U_M^I(w, e)$ with respect to $w$ is $\frac{\partial^2 U_M^I(w, e)}{\partial w^2} = -1 < 0$. And the Hessian Matrix of $U_M^I(w, e)$ with respect to $w$ and $e$ is

Thus only $\Delta(U_M^I(w, e)) > 0$, i.e. $4k > t^2$, it holds that $U_M^I(w, e)$ is jointly concave in $w$ and $e$. Solving $\frac{\partial U_M^I(w, e)}{\partial w } = 0$ and $\frac{\partial U_M^I(w, e)}{\partial e} = 0$ simultaneously, we get $w^{I*}$ and $e^{I*}$ satisfy the Eqs (4.5) and (4.6), respectively. Taking Eqs (4.5) and (4.6) into $p_R(w, e)$, we obtain Eq (4.7).

Proof of Corollary 4.2

Noting that $w^{I*}$, $e^{I*}$ and $p_R^{I*}$ satisfy the Eqs (4.5)–(4.7), respectively. Then

To ensure that the manufacturer makes emission reduction effort, i.e., $e^{I*} > 0$. We derive that $1-(2\lambda_M-\lambda_R)\sigma > 0$, i.e. $\sigma < \frac{1}{2\lambda_M-\lambda_R}$. Under this condition, $w^{I*} > 0$ holds.

i) If $\lambda_R\leq\lambda_M$, it holds that

Since $\sigma < \frac{1}{2\lambda_M-\lambda_R}$, then $p_R^{I*}-w^{I*} > 0$.

ii) If $\lambda_R > \lambda_M$, then

Let $1+(2\lambda_M-3\lambda_R)\sigma > 0$, it holds that $\sigma < \frac{1}{3\lambda_R-2\lambda_M}$. Since $\frac{1}{3\lambda_R-2\lambda_M}-\frac{1}{2\lambda_M-\lambda_R} = \frac{4(\lambda_M-\lambda_R)}{(3\lambda_R-2\lambda_M)(2\lambda_M-\lambda_R)} < 0$, then $\sigma < \frac{1}{3\lambda_R-2\lambda_M} < \frac{1}{2\lambda_M-\lambda_R}$.

Hence $w^{I*} > 0$ and $p_R^{I*}-w^{I*} > 0$ if $\sigma < \frac{1}{3\lambda_R-2\lambda_M}$.

Proof of Proposition 4.3

Firstly, we consider the retailer's decision. Since $\frac{\partial^2 U_R^{II}}{\partial p_R^2} = -2$, then we can obtain that the optimal retailer's retail price for given $w$, $e$, and $p_M$ as the follow.

Secondly, we consider the manufacturer's decisions. Taking $p_R^{II}(w, e, p_M)$ into $U_M^{II}$, we can obtain that

Since the second-order derivative of $U_M^{II}(w, e, p_M)$ with respect to $w$ is $\frac{\partial^2 U_M^{II}(w, e, p_M)}{\partial w^2} = -1 < 0$. The second-order determinant of Hessian Matrix is

And the third-order determinant of Hessian Matrix is

Thus only $k-\frac{t^2}{4} > 0$ and $\Delta(U_M^{II}(w, e, p_M)) < 0$, i.e. $b < \frac{4k-3t^2}{4k+t^2}$ and $k > \frac{3t^2}{4}$, it holds that $U_M^{II}(w, e, p_M)$ is jointly concave in $w$, $e$ and $p_M$. Solving $\frac{\partial U_M^{II}(w, e, p_M)}{\partial w } = 0$, $\frac{\partial U_M^{II}(w, e, p_M)}{\partial e} = 0$ and $\frac{\partial U_M^{II}(w, e, p_M)}{\partial p_M} = 0$ simultaneously, we get $w^{II*}$, $e^{II*}$ and $p_M^{II*}$ satisfy the Eqs (4.12)–(4.14), respectively. Taking Eqs (4.12)–(4.14) into $p_R^{II}(w, e, p_M)$, we obtain Eq (4.15).

Proof of Corollary 4.4

Noting that $w^{II*}$ and $p_M^{II*}$ satisfy the Eqs (4.12) and (4.14), respectively. Then

i) If $a\leq\frac{1}{2}$ and $\lambda_R < \frac{(2+b-3a-ab)\lambda_M}{(1-a)(1+b)}$, it holds that $(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R > 0$. Then $\sigma > \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$ for ensuring that $p^{II*} > w^{II*}$.

ii) If $\frac{1}{2} < a < \frac{2+b}{3+b}$ and $\lambda_R > \frac{(2+b-3a-ab)\lambda_M}{(1-a)(1+b)}$, it holds that $(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R < 0$. Then $\sigma < \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$ for ensuring that $p^{II*} > w^{II*}$.

iii) If $a\geq\frac{2+b}{3+b}$, then $2+b-3a-ab < 0$, it holds that $\sigma < \frac{1-2a}{(2+b-3a-ab)\lambda_M-(1-a)(1+b)\lambda_R}$ for ensuring that $p^{II*} > w^{II*}$.

Proof of Proposition 4.5

Firstly, we consider the retailer's decision. Since $\frac{\partial^2 U_R^{III}}{\partial p_R^2} = -2$, then we can obtain that the optimal retailer's retail price for given $w$, $e$, and $p_M$ as the follow.

Secondly, we consider the manufacturer's decisions. Taking $p_R^{III}(w, e, p_M)$ into $U_M^{III}$, we can obtain that

Since the second-order derivative of $U_M^{III}(w, e, p_M)$ with respect to $w$ is $\frac{\partial^2 U_M^{III}(w, e, p_M)}{\partial w^2} = -1 < 0$. And under condition $k > \frac{3-2\theta}{4}t^2$, the second-order determinant of Hessian Matrix is

And the third-order determinant of Hessian Matrix is

Since $b < \frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2}$ and $k > \frac{3-2\theta}{4}t^2$, then it holds that $\Delta(U_M^{III}(w, e, p_M)) < 0$. Therefore, $U_M^{II}(w, e, p_M)$ is jointly concave in $w$, $e$ and $p_M$. Solving $\frac{\partial U_M^{III}(w, e, p_M)}{\partial w } = 0$, $\frac{\partial U_M^{III}(w, e, p_M)}{\partial e} = 0$ and $\frac{\partial U_M^{III}(w, e, p_M)}{\partial p_M} = 0$ simultaneously, we get $w^{III*}$, $e^{III*}$ and $p_M^{III*}$ satisfy the Eqs (4.20)–(4.22), respectively. Taking Eqs (4.20)–(4.22) into $p_R^{III}(w, e, p_M)$, we obtain Eq (4.23).

Proof of Corollary 4.6

Noting that $w^{III*}$ and $p_M^{III*}$ satisfy the Eqs (4.20) and (4.22), respectively. Then

where $T^{III} = 4(1-b)k-(2\theta+2b\theta-3-b)t^2$.

Since $T^{III} > 0$ due to $b < \frac{4k-(3-2\theta)t^2}{4k+(1-2\theta)t^2}$ and $k > \frac{3-2\theta}{4}t^2$. Then $\{[(2-3a+b-ab)\lambda_M-(1-a)(1+b)\lambda_R]T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]\lambda_M\}\sigma < 0$ if $\lambda_R < \frac{(2-3a+b-ab)T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]}{(1-a)(1+b)T^{III}}\lambda_M$. Thus $p_M^{III*}-w^{III*} > 0$ if $\lambda_R < \frac{(2-3a+b-ab)T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]}{(1-a)(1+b)T^{III}}\lambda_M$ and $\sigma < \frac{(2a-1)T^{III}+b\theta[4(a+b-ab)k-(2a-1)t^2]}{[(2-3a+b-ab)\lambda_M-(1-a)(1+b)\lambda_R]T^{III}-b\theta[T^{III}-(5a+ab-3-b)t^2]\lambda_M}$.

Proof of Theorem 5.1

Taking the first-order derivative of $w^{I*}$, $e^{I*}$, and $p_R^{I*}$ with respect to $t$, respectively. We obtain that

To ensuring that $e^{II*} > 0$, we derive that $P^{II} > 0$ and $Q^{II} > 0$, where $P^{II} = 1+a+b-ab-2\sigma\lambda_M+(1-a)(1+b)t^2\sigma\lambda_R$ and $Q^{II} = 4(1-b)k-(3+b)t^2$.

Taking the first-order derivative of $w^{II*}$, $e^{II*}$, $P_R^{II}$ and $p_M^{II*}$ with respect to $t$, respectively. We obtain that

To ensuring that $e^{III*} > 0$, we derive that $P^{III} > 0$ and $Q^{III} > 0$, where $P^{III} = 1+(a+b-ab)(1-2\theta)-2[1-(a+b-ab)\theta]\sigma\lambda_M+(1-a)(1+b)t^2\sigma\lambda_R$ and $Q^{III} = 4(1-b)k-(3+b-2\theta-2b\theta)t^2$.

Taking the first-order derivative of $w^{III*}$, $e^{III*}$, $P_R^{III}$ and $p_M^{III*}$ with respect to $t$, respectively. We obtain that

Proof of Theorem 5.2

Taking the first-order derivative of $w^{I*}$, $e^{I*}$, and $p_R^{I*}$ with respect to $\lambda_R$, respectively. We obtain that

Thus, if $t^2 > k > \frac{3}{4}t^2$, $\frac{\partial p^{I*}}{\partial \lambda_R} > 0$; if $t^2 = k$, $\frac{\partial p^{I*}}{\partial \lambda_R} = 0$; if $t^2 < k$, $\frac{\partial p^{I*}}{\partial \lambda_R} < 0$.

Since $Q^{II} = 4(1-b)k-(3+b)t^2 > 0$, then taking the first-order derivative of $w^{II*}$, $e^{II*}$, $P_R^{II}$ and $p_M^{II*}$ with respect to $\lambda_R$, respectively. We obtain that

Thus, if $\frac{3+b}{4(1-b)}t^2 > k > \frac{8+b}{8(1-b)}t^2$, $\frac{\partial p^{II*}}{\partial \lambda_R} > 0$; if $\frac{8+b}{8(1-b)}t^2 = k$, $\frac{\partial p^{II*}}{\partial \lambda_R} = 0$; if $\frac{8+b}{8(1-b)}t^2 < k$, $\frac{\partial p^{II*}}{\partial \lambda_R} < 0$.

Since $Q^{III} = 4(1-b)k-(3+b-2\theta-2b\theta)t^2 > 0$, then taking the first-order derivative of $w^{III*}$, $e^{III*}$, $P_R^{III}$ and $p_M^{III*}$ with respect to $\lambda_R$, respectively. We obtain that

Thus, if $\frac{3+b}{4(1-b)}t^2 > k > \frac{3-\theta-b\theta}{2(1-b)}t^2$, $\frac{\partial p^{III*}}{\partial \lambda_R} > 0$; if $\frac{3-\theta-b\theta}{2(1-b)}t^2 = k$, $\frac{\partial p^{III*}}{\partial \lambda_R} = 0$; if $\frac{3-\theta-b\theta}{2(1-b)}t^2 < k$, $\frac{\partial p^{III*}}{\partial \lambda_R} < 0$.

Proof of Theorem 5.3

Taking the first-order derivative of $w^{I*}$, $e^{I*}$, and $p_R^{I*}$ with respect to $\lambda_M$, respectively. We obtain that

Since $Q^{II} = 4(1-b)k-(3+b)t^2 > 0$, then taking the first-order derivative of $w^{II*}$, $e^{II*}$, $P_R^{II}$ and $p_M^{II*}$ with respect to $\lambda_M$, respectively. We obtain that

To ensuring that $p_M^{III*} > 0$ and $p_R^{III*} > 0$, we derive that $Q^{III} = 4(1-b)k-(3+b-2\theta-2b\theta)t^2 > 0$. Taking the first-order derivative of $w^{III*}$, $e^{III*}$, $P_R^{III}$ and $p_M^{III*}$ with respect to $\lambda_M$, respectively. We obtain that

Proof of Theorem 5.4

To ensuring that $p_M^{II*} > 0$ and $p_R^{II*} > 0$, we derive that $Q^{II} = 4(1-b)k-(3+b)t^2 > 0$. Taking the first-order derivative of $w^{II*}$, $P_R^{II}$ and $p_M^{II*}$ with respect to $a$, respectively. We obtain that

To ensuring that $p_M^{III*} > 0$ and $p_R^{III*} > 0$, we derive that $Q^{III} = 4(1-b)k-(3+b-2\theta-2b\theta)t^2 > 0$. Taking the first-order derivative of $w^{III*}$, $P_R^{III}$ and $p_M^{III*}$ with respect to $a$, respectively. We obtain that

where $P^{III} = [(2+b)(Q^{III}-(1-b)\theta t^2)+4(1-b)bk\theta]\sigma\lambda_M+(1+b)[Q^{III}+(1-b\theta)t^2]\sigma\lambda_R$.

where $\Psi^{III} = [Q^{III}+(3+2b-b^2)\theta t^2]\sigma\lambda_M-(1+b)[Q^{III}-(b-\theta-b\theta)t^2]\sigma\lambda_R$.

Proof of Theorem 5.5

To ensuring that $p_M^{III*} > 0$, we derive that $T^{III} > 0$ and $Q^{III} > 0$, where $T^{III} = 4k(a+b-ab)-(2a-1)t^2-[4bk+(2+b)t^2-Q^{II}]\sigma\lambda_M+(1-a)(1+b)t^2\sigma\lambda_R$, $Q^{II} = 4(1-b)k-(3+b)t^2$ and $Q^{III} = 4(1-b)k-(3+b-2\theta-2b\theta)t^2$.

Taking the first-order derivative of $e^{III*}$, $w^{III*}$, $P_R^{III}$ and $p_M^{III*}$ with respect to $\theta$, respectively. We obtain that