Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate

Mushtaq Ahmad; Muhammad Imran Asjad; Ali Akgül; Dumitru Baleanu; Mushtaq Ahmad; Muhammad Imran Asjad; Ali Akgül; Dumitru Baleanu

doi:10.3934/math.2021142

AIMS Mathematics

2021, Volume 6, Issue 3: 2344-2358. doi: 10.3934/math.2021142

Previous Article Next Article

Research article

Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate

1.
Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University Multan, Pakistan
2.
Department of Mathematics, University of Management and Technology, Lahore, Pakistan
3.
Department of Mathematics, Art and Science Faculty, Siirt University, Siirt 56100, Turkey
4.
Department of Mathematics, Cankaya University, 06530 Balgat, Ankara, Turkey
5.
Institute of Space Sciences, R76900 Magurele-Bucharest, Romania
6.
Department of Medical Research, China Medical University Taichung 40402, Taiwan

Received: 21 August 2020 Accepted: 03 December 2020 Published: 16 December 2020
MSC : 26A33, 74F10

This research article is design to elaborate the rule and significance of fractional derivative for heat transport in drilling of nanofluid. The respective nanofluid formed by the suspension of clay nanoparticles in the base fluids namely Casson fluid. The physical flow phenomenon is demonstrated with the help of partial differential equations by utilizing the respective thermophysical properties of nanoparticles. Also the geometric and thermal conditions are imposed in flow domain. In the governing equations, the partial derivative with respect to time replaced by new hybrid fractional derivative and then solved analytically for temperature and velocity field with the help of Laplace transformed. The obtained solutions for temperature and velocity are presented geometrically by Mathcad software to see the effectiveness of potent parameters. The temperature and velocity present a significant increasing trend for increasing volume fraction parameter. The obtained results for temperature as well as velocity are also compared with the existing literature and it is concluded that field variables with new hybrid fractional derivative, show more decaying trend as compare to the results with Caputo and Caputo-Fabrizio fractional derivatives.

Keywords:

Citation: Mushtaq Ahmad, Muhammad Imran Asjad, Ali Akgül, Dumitru Baleanu. Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate[J]. AIMS Mathematics, 2021, 6(3): 2344-2358. doi: 10.3934/math.2021142

Related Papers:

[1]	Taqi A. M. Shatnawi, Nadeem Abbas, Wasfi Shatanawi . Comparative study of Casson hybrid nanofluid models with induced magnetic radiative flow over a vertical permeable exponentially stretching sheet. AIMS Mathematics, 2022, 7(12): 20545-20564. doi: 10.3934/math.20221126
[2]	Ali Raza, Umair Khan, Aurang Zaib, Wajaree Weera, Ahmed M. Galal . A comparative study for fractional simulations of Casson nanofluid flow with sinusoidal and slipping boundary conditions via a fractional approach. AIMS Mathematics, 2022, 7(11): 19954-19974. doi: 10.3934/math.20221092
[3]	Umar Nazir, Abdelaziz Nasr . Utilizing the Box-Behnken method on modeling of ternary-Casson nanofluid with variable density and heat sink across a vertical jet. AIMS Mathematics, 2025, 10(4): 10093-10123. doi: 10.3934/math.2025460
[4]	Sami Ul Haq, Saeed Ullah Jan, Syed Inayat Ali Shah, Ilyas Khan, Jagdev Singh . Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach. AIMS Mathematics, 2020, 5(4): 3056-3088. doi: 10.3934/math.2020198
[5]	Nadeem Abbas, Wasfi Shatanawi, Taqi A. M. Shatnawi . Innovation of prescribe conditions for radiative Casson micropolar hybrid nanofluid flow with inclined MHD over a stretching sheet/cylinder. AIMS Mathematics, 2025, 10(2): 3561-3580. doi: 10.3934/math.2025164
[6]	Umar Nazir, Kanit Mukdasai . Combine influence of Hall effects and viscous dissipation on the motion of ethylene glycol conveying alumina, silica and titania nanoparticles using the non-Newtonian Casson model. AIMS Mathematics, 2023, 8(2): 4682-4699. doi: 10.3934/math.2023231
[7]	Fahad Alsharari, Mohamed M. Mousa . New application of MOL-PACT for simulating buoyancy convection of a copper-water nanofluid in a square enclosure containing an insulated obstacle. AIMS Mathematics, 2022, 7(11): 20292-20312. doi: 10.3934/math.20221111
[8]	Aziz Ur Rehman, Muhammad Bilal Riaz, Ilyas Khan, Abdullah Mohamed . Time fractional analysis of Casson fluid with application of novel hybrid fractional derivative operator. AIMS Mathematics, 2023, 8(4): 8185-8209. doi: 10.3934/math.2023414
[9]	Imran Siddique, Yasir Khan, Muhammad Nadeem, Jan Awrejcewicz, Muhammad Bilal . Significance of heat transfer for second-grade fuzzy hybrid nanofluid flow over a stretching/shrinking Riga wedge. AIMS Mathematics, 2023, 8(1): 295-316. doi: 10.3934/math.2023014
[10]	Yasir Khan, Sohaib Abdal, Sajjad Hussain, Imran Siddique . Numerical simulation for thermal enhancement of $H_2O$ + Ethyl Glycol base hybrid nanofluid comprising $GO + (Ag, AA7072, MoS_2)$ nano entities due to a stretched sheet. AIMS Mathematics, 2023, 8(5): 11221-11237. doi: 10.3934/math.2023568

Abstract

Nomenclature

$u-$ Velocity $[ms^{-1}]$

$U_{0}-$ Constant velocity

$s-$ Non-dimensional velocity $[ms^{-1}]$

$t-$ Time $[s]$

$\tau-$ Non-dimensional time

$y-$ Special variable $[m]$

$\xi-$ Non-dimensional special variable

$\rho_ {nf}-$ Density of nanofluid, $[kgm^{-3}]$

$\mu_{nf}-$ Dynamic viscosity of nanofluid $[kgm^{-1}s^{-1}]$

$T-$ Temperature of Nanofluid, $[K]$

$k_{f}-$ Thermal conductivity of base fluid

$k_{s}-$ Thermal conductivity of solid particle

$k_{nf}-$ Thermal conductivity of the nanofluid, $[Wm^{-2}K^{-1}]$

$\rho_{f}-$ Density base fluid, $[kgm^{-3}]$

$\rho_{s}-$ Density solid nanoparticle, $[kgm^{-3}]$

$\upsilon-$ Concentration of clay nanoparticle, $[kgm^{-3}]$

$g-$ Acceleration due to gravity, $[ms^{-2}]$

$\gamma-$ Casson fluid parameter

$\beta_{c}-$ non-dimensional Casson parameter

${\rm{Gr}}-$ Grashof number for heat transfer

$\beta-$ Volumetric thermal expansion of $[K^{-1}]$

${\rm{Pr}}-$ Prandtl number

$\phi-$ Non-dimensionless temperature

$T_{\infty}-$ Temperature at infinity, $[K]$

$T_{W}-$ Temperature at plate, $[K]$

$\alpha-$ fractional parameter

$q-$ Laplace variable

1. Introduction

Clay nanoparticles have an important rule for drilling of oil and gases because of its significant thermal conductivity. The addition of clay nanoparticles in base fluid, boosted the thermal conductivity and viscosity of nanofluid that make it capable to resist the higher temperatures. The nanofluids with clay nanoparticles fulfil the challenges to improve the thermal conductivity and improved thermal conductivity boosted the thermal execution in respective devices. Now a days this nanofluids become a potent research area of nanotechnology ^[1,2,3] and attract the researchers of physical sciences. An interesting work on free convection flow of nanofluid has presented by Asma et al. ^[4] and explained the effect of volume fraction of nanoparticles over the nanofluid flow with fractional derivative.Hussanan et al. ^[5] investigated the free convection flow of sodium Carboxymethyl Cellulose based nanofluid with Tiatania nanoparticles, with non-homogeneous thermal and mechanical conditions. Bhattad et al. ^[6] carried an a compressive review on the formation methods and performance of nanofluids in the view of applicable processes in engineering. Farhana et al. ^[7] applied the properties of nanofluids in to enhance the performance of solar collector. Some other investigations about nanofluids is have been listed in ^{[8,9,10,11,12,13,14,15]}.

Fractional calculus is the generalization classical calculus. In fractional calculus the derivative of real order are consider instead of integer order derivative and have been applied efficiently to explain the several real life problem. Several investigation are reported regarding nanofluid and ordinary fluid flows with different definitions of fractional derivatives. Imran et al. ^[16] presented a comparative study of viscous fluid flow with two definitions of fractional derivatives. Hristov ^[17] used generalized Fourier law for thermal balance for steady state conduction. Aman ^[18] discussed the nanofluid flow and obtained the numerical and analytical solutions by applying non-integer derivative. Sheikh et al. ^[19] carried out the results for free convection flow of Casson fluid with AtanganaBaleanu and Caputo-Fabrizio fractional derivatives. Azhar et al. ^[20] bring out the results for the flow of nanofluid with homogenous thermal flux by utilizing the fractional derivatives. Some more interesting studies with application of fractional derivatives are investigated in ^{[21,22,23,24,25,26,27,28,29,30]}. Atangana et al. ^[31] have presented new fractional derivatives. Thabet et al. ^[32] introduced the new class of fractional operators by taking the Discrete Mittag-Leffler Kernels. Jarad et al. ^[33] have studied On a new class of fractional operators. Atangana et al. ^[34], Akgül et al. ^[35], Mirbahar et al. ^[36], and Abro et al. ^[37] have successfully apply the fractional derivative approaches to different real life physical phenomenons. Khan et al. ^[38] investigated the heat transfer model for the flow of nanofluid formed by clay nanoparticles. Recently Baleanu ^[39] proposed the new approach of fractional operator by combining the proportional and classical diferintegrals. For more details see ^{[40,41,42,43]}.

The focal attention of this research is to extend the work ^[38] for Casson fluid and apply the new hybrid fractional derivative namely Constant Caputo fractional derivative ^[39]. According to our best knowledge there is no such result regarding Casson nanofluid formed by clay nanoparticles with constant proportional Caputo fractional derivatives established. The Casson clay nanofluid which is composed by clay nanoparticles and Casson fluid (base fluid) have supposed to flow over a vertical plate moving with constant velocity at constant surface temperature. The PDEs that governing our flow model will solved by Laplace transform technique. The established results can be applied to different engineering processes of relevant field.

2. Mathematical formulation

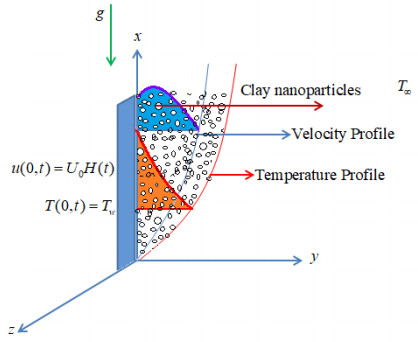
It is considered that clay nanoparticles are spread out to the incompressible Casson fluid (base fluid) and resulting clay nanofluid suppose to be flow in vicinity of a flat surface, which is situated in the xz-plane in such a way that y-axis is normal to the surface. for the time $t\leq0$ the the whole system is in rest with thermal and mechanical homogeneity. At the moment $t > 0$ suddenly the temperature of plate raises up to $T_{w}$ and the same time plate begins to move with a constant velocity $U_{0}$ . Due to this non-homogenous mechanical and thermal situation the fluid adjoining to the moving plate also start to move with the same velocity of plate. The respective convectional flow is governs by the following set of partial differential equations ^[4]:

Figure 1. Flow geometry and coordinate system.

DownLoad: Full-Size Img PowerPoint

$\begin{eqnarray} \rho_{nf}\frac{\partial u(y, t)}{\partial t} = \mu_{nf}(1+\frac{1}{\gamma})\frac{\partial ^{2}u(y, t)}{\partial y^{2}}+g(\rho\beta)_{nf}[T(y, t)-T_{\infty}], \end{eqnarray}$

(1)

$\begin{eqnarray} (\rho C_{p})_{nf}\frac{\partial T(y, t)}{\partial t} = k_{nf}\frac{\partial^{2}T(y, t)}{\partial y^{2}}, y, t > 0, \end{eqnarray}$

(2)

where the effective density of nanofluid is given by ^[44,45]

$\begin{eqnarray} \rho_{nf} = (1-\upsilon)\rho_{f}+\upsilon\rho_{s}, \end{eqnarray}$

(3)

effective dynamic viscosity define as ^[46]

$\begin{eqnarray} \mu_{nf} = \frac{\mu_{f}}{(1-\upsilon)^{2.5}}, \end{eqnarray}$

(4)

where as

$\begin{eqnarray} (\rho C_{p})_{nf} = (1-\upsilon)(\rho C_{p})_{f}+\upsilon(\rho C_{p})_{s}, \end{eqnarray}$

(5)

and

$\begin{eqnarray} \frac{k_{nf}}{k_{f}} = \frac{k_{s}+2k_{f}-2\upsilon(k_{f}-k_{s})}{k_{s}+2k_{f}+\upsilon(k_{f}-k_{s})}, \end{eqnarray}$

(6)

are the heat capacitance and effective thermal conductivity of nanofluid and $\upsilon$ is the volume fraction of clay nanoparticles. The specification of field variables at boundary are as

$\begin{eqnarray} u(y, 0) = 0, \, \, T(y, 0) = T{\infty}, \, \, y\geq 0, \end{eqnarray}$

(7)

$\begin{eqnarray} u(0, t) = U_{0}H(t), \, \, T(0, t) = T_{w}\, \, t > 0, \end{eqnarray}$

(8)

$\begin{eqnarray} u(y, t)\rightarrow 0, \, \, T(y, t)\rightarrow 0, \, {\rm{as}} \, \, y\rightarrow \infty. \end{eqnarray}$

(9)

In order to construct a shape free flow model, the following dimensionless relations are inserted in Eqs (1)–(5)

$\begin{eqnarray} && s = \frac{u}{U_{o}}, \, \, \, \xi = \frac{yU_{0}}{\nu_{f}}, \, \, \tau = \frac{t U_{0}^{2}}{\nu_{f}}, \, \phi = \frac{T-T_{\infty}}{T_{w}-T_{\infty}}, \end{eqnarray}$

(10)

and obtain the following dimensionless flow model

$\begin{eqnarray} \bigg((1-\upsilon)+\upsilon\frac{\rho_{s}}{\rho_{f}}\bigg)\frac{\partial s(\xi, \tau)}{\partial \tau} = \frac{1}{(1-\upsilon)^{2.5}}(1+\frac{1}{\gamma})\frac{\partial^{2}s(\xi, \tau)}{\partial \xi^{2}}+\bigg((1-\upsilon)+\upsilon\frac{(\rho \beta)_{s}}{(\rho \beta)_{f}}\bigg) {\rm{Gr}} \phi(\xi, \tau), \, \, \, \xi, \tau > 0, \end{eqnarray}$

(11)

$\begin{eqnarray} \bigg((1-\upsilon)+\upsilon\frac{(\rho C_{p})_{s}}{(\rho C_{p})_{f}}\bigg) {\rm{Pr}}\frac{\partial \phi(\xi, \tau)}{\partial \tau} = \frac{k_{nf}}{k_{f}}\frac{\partial^{2}\phi(\xi, \tau)}{\partial \xi^{2}}, \, \, \, \xi, \tau > 0, \end{eqnarray}$

(12)

and associated dimensionless conditions are

$\begin{eqnarray} s(\xi, 0) = 0, \, \, \phi(\xi, 0) = 0, \, \, \xi\geq 0, \end{eqnarray}$

(13)

$\begin{eqnarray} s(0, \tau) = 1, \, \, \phi(0, \tau) = 1, \, \, \tau > 0, \end{eqnarray}$

(14)

$\begin{eqnarray} s(\xi, \tau)\rightarrow 0, \, \, \phi(\xi, \tau)\rightarrow 0, \, \, {\rm{as}} \, \, \xi\rightarrow \infty, \end{eqnarray}$

(15)

where ${\rm{Gr}} = \frac{g(\beta)_{f}(T_{W}-T_{\infty})}{U_{0}^{3}}$ , ${\rm{Pr}} = \frac{\mu_{f}(C_{p})_{f}}{k_{f}}$ .

Definition 1. The constant proportional Caputo fractional derivative of order $\alpha \in (0, 1)$ is define as ^[39]

$\begin{eqnarray} ^{CPC}D^{\alpha}_{t}f(t) = \frac{1}{\Gamma(1-\alpha)}\int^{t}_{0}\bigg(k_{1}(\alpha)f(\tau)+k_{0}(\alpha)f^{'}(\tau)\bigg)(t-\tau)^{-\alpha}d\tau, \end{eqnarray}$

(16)

Definition 2. The Laplace transform of the constant proportional Caputo fractional derivative of the function $f(t)$ is define as ^[39]

$\begin{eqnarray} £\{^{CPC}D^{\alpha}_{t}f(t)\} = \bigg[\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg]q^{\alpha}\bar{f}(q)-k_{0}(\alpha)q^{\alpha-1}f(0). \end{eqnarray}$

(17)

3. Model with constant proportional Caputo derivative

After replacing ordinary time derivative with constant proportional Caputo fractional derivative $^{CPC}D^{\alpha}_{\tau}$ in Eqs (11) and (12), we obtain the following fractionalized governing equations as follows

$\begin{eqnarray} r_{1}\, ^{CPC}D^{\alpha}_{\tau} s(\xi, \tau) = r_{2}\beta_{c}\frac{\partial^{2}s(\xi, \tau)}{\partial \xi^{2}}+r_{3} {\rm{Gr}} \phi(\xi, \tau), \, \, \, \xi, \tau > 0, \end{eqnarray}$

(18)

$\begin{eqnarray} r_{4} {\rm{Pr}}^{CPC}D^{\alpha}_{\tau} \phi(\xi, \tau) = r_{5}\frac{\partial^{2}\phi(\xi, \tau)}{\partial \xi^{2}}, \, \, \, \xi, \tau > 0, \end{eqnarray}$

(19)

where $\beta_{c} = (1+\frac{1}{\gamma})$ , $r_{1} = \bigg((1-\upsilon)+\upsilon\frac{\rho_{s}}{\rho_{f}}\bigg)$ , $r_{2} = \frac{1}{(1-\upsilon)^{2.5}}$ , $r_{3} = \bigg((1-\upsilon)+\upsilon\frac{(\rho \beta)_{s}}{(\rho \beta)_{f}}\bigg)$ , $r_{4} = \bigg((1-\upsilon)+\upsilon\frac{(\rho C_{p})_{s}}{(\rho C_{p})_{f}}\bigg)$ , $r_{5} = \frac{k_{nf}}{k_{f}}$ .

4. Solution of problem

4.1. Temperature distribution

Equation (19) is transformed to following ordinary differential equation by imposing Laplace transform

$\begin{eqnarray} r_{4} {\rm{Pr}} \bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha}\bar{\phi}(\xi, q) = r_{5}\frac{\partial^{2}\bar{\phi}(\xi, q)}{\partial \xi^{2}}, \, \, \, \xi > 0, \end{eqnarray}$

(20)

where $\bar{\phi}(\xi, q)$ is the transformed image of $\phi(\xi, \tau)$ with respect to Laplace transform also satisfies the following boundary conditions

$\begin{eqnarray} \bar{\phi}(\xi, q) = \frac{1}{q}, \, \, \, {\rm{and}}\, \, \, \bar{\phi}(\xi, q)\rightarrow 0, {\rm{as}}\, \, \, \xi\rightarrow \infty. \end{eqnarray}$

(21)

The temperature field as the solution of Eq (20) subject to conditions (21) can be written as

$\begin{eqnarray} \bar{\phi}(\xi, q) = \frac{1}{s}\exp\bigg(-\xi\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha}}\bigg). \end{eqnarray}$

(22)

The exponential form of Eq (22) is so complicated that Laplace transformed cannot inverted by ordinary inversion formulae therefore it is express in summation notation as follows

$\begin{equation} \bar \phi(\xi, q) = \frac{1}{q}+\sum\limits_{a_{1} = 1}^{\infty}\sum\limits_{a_{2} = 0}^{\infty} \frac{\left(-\xi\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}\left(k_{1}(\alpha)\right)^{a_{2}}}{a_{1}!a_{2}!\left(k_{0}(\alpha)\right)^{a_{2}-\frac{a_{1}}{2}}q^{1-\frac{\alpha a_{1}}{2}+a_{2}}}\frac{\Gamma(\frac{a_{1}}{2}+1)}{\Gamma(\frac{a_{1}}{2}+1-a_{2})}. \end{equation}$

(23)

by applying the inverse Laplace transformation we have

$\begin{equation} \phi(\xi, \tau) = 1+\sum\limits_{a_{1} = 1}^{\infty}\sum\limits_{a_{2} = 0}^{\infty}\frac{\left(-\xi\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}\left(k_{1}(\alpha)\right)^{a_{2}}\tau^{-\frac{\alpha a_{1}}{2}+a_{2}}} {a_{1}!a_{2}!\left(k_{0}(\alpha)\right)^{a_{2}-\frac{a_{1}}{2}}}\frac{\Gamma(\frac{a_{1}}{2}+1)}{\Gamma(\frac{a_{1}}{2}+1-a_{2})\Gamma(1-\frac{\alpha a_{1}}{2}+a_{2})} \end{equation}$

(24)

Further, Eq (24) can be expressed in terms of more general function namely M-function ^[40],

$\begin{equation} \phi(y, \tau) = 1+\sum\limits_{a_{1} = 1}^{\infty}\frac{\left(-y\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}} {a_{1}!\left(k_{0}(\alpha)\right)^{-\frac{a_{1}}{2}}}M_{2}^{1}\left[(\frac{k_{1}(\alpha)}{k_{0}(\alpha)})\tau|_{(\frac{a_{1}}{2}+1, -1), (1-\frac{\alpha a_{1}}{2}, 1)}^{(\frac{a_{1}}{2}+1, 0)}\right] \end{equation}$

(25)

4.2. Velocity field

The Eq (18) is a partial differential equation and can be transform to ordinary differential equation by solving partial derivative with respect to time $\tau$ , with the help of integral transform namely Laplace transform as

$\begin{eqnarray} r_{1}\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha} \bar{s}(\xi, q) = r_{2}\beta_{c}\frac{\partial^{2}s(\xi, q)}{\partial \xi^{2}}+r_{3} {\rm{Gr}} \bar{\phi}(\xi, q), \, \, \, \xi > 0, \end{eqnarray}$

(26)

Equation (26) satisfies the following transformed boundary conditions

$\begin{eqnarray} \bar{s}(0, q) = 0\, \, \, {\rm{and}}\, \, \, \bar{s}(\xi, q)\rightarrow0 \, \, {\rm{as}} \, \, \xi\rightarrow \infty. \end{eqnarray}$

(27)

Solution of Eq (26) subject to condition (27) is obtain as

$\begin{eqnarray} \bar{s}(\xi, q) = \frac{1}{q} {\rm{e}}^{-\xi\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha}}} +r_{3} {\rm{Gr}}\frac{ {\rm{e}}^{-\xi\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha}}}- {\rm{e}}^{-\xi\sqrt{\frac{r_{4} {\rm{Pr}}}{r_{5}}\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha}}}} {\bigg(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\bigg)\bigg(\frac{k_{1}(\alpha)}{q}+k_{0}(\alpha)\bigg)q^{\alpha+1}}. \end{eqnarray}$

(28)

Equation (28) is also complicated and cannot be inverted by ordinary inversion formulae of Laplace transform, therefore we express it in summation form

$\begin{eqnarray} \bar{s}(\xi, q)& = &\sum\limits_{b_{1} = 0}^{\infty}\sum\limits_{b_{2} = 0}^{\infty}\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}(k_{1}(\alpha))^{b_{2}}} {b_{1}!b_{2}!(k_{0}(\alpha))^{b_{2}-\frac{b_{1}}{2}}q^{1-\frac{\alpha b_{1}}{2}+b_{2}}}\frac{\Gamma(\frac{b_{1}}{2}+1)}{\Gamma(\frac{b_{1}}{2}+1-b_{2})} \\&& +\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)} \sum\limits_{b_{1} = 0}^{\infty}\sum\limits_{b_{3} = 0}^{\infty}\left[\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}(k_{1}(\alpha))^{b_{3}}} {b_{1}!b_{3}!(k_{0}(\alpha))^{b_{3}-\frac{b_{1}}{2}+1}q^{1-\frac{\alpha b_{1}}{2}+b_{3}+\alpha}}\frac{\Gamma(\frac{b_{1}}{2})}{\Gamma(\frac{b_{1}}{2}-b_{3})}\right] \\&& -\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)}\sum\limits_{a_{1} = 0}^{\infty}\sum\limits_{b_{3} = 0}^{\infty} \left[\frac{\left(-y\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}\left(k_{1}(\alpha)\right)^{b_{3}}}{a_{1}!b_{3}!\left(k_{0}(\alpha)\right)^{b_{3}-\frac{a_{1}}{2}+1}q^{1-\frac{\alpha a_{1}}{2}+b_{3}+\alpha}}\frac{\Gamma(\frac{a_{1}}{2})}{\Gamma(\frac{a_{1}}{2}-b_{3})}\right]. \end{eqnarray}$

(29)

Now taking inverse Laplace, have

$\begin{eqnarray} s(\xi, \tau)& = &\sum\limits_{b_{1} = 0}^{\infty}\sum\limits_{b_{2} = 0}^{\infty}\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}(k_{1}(\alpha))^{b_{2}}} {b_{1}!b_{2}!(k_{0}(\alpha))^{b_{2}-\frac{b_{1}}{2}}}\frac{t^{-\frac{\alpha b_{1}}{2}+b_{2}}\Gamma(\frac{b_{1}}{2}+1)}{\Gamma(\frac{b_{1}}{2}+1-b_{2})\Gamma(1-\frac{\alpha b_{1}}{2}+b_{2})} \\&& +\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)} \sum\limits_{b_{1} = 0}^{\infty}\sum\limits_{b_{3} = 0}^{\infty}\left[\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}(k_{1}(\alpha))^{b_{3}}} {b_{1}!b_{3}!(k_{0}(\alpha))^{b_{3}-\frac{b_{1}}{2}+1}}\frac{t^{-\frac{\alpha b_{1}}{2}+b_{3}+\alpha}\Gamma(\frac{b_{1}}{2})}{\Gamma(\frac{b_{1}}{2}-b_{3})\Gamma(1-\frac{\alpha b_{1}}{2}+b_{3}+\alpha)}\right] \\&& \!\!\!\!\!\!\!-\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)}\sum\limits_{a_{1} = 0}^{\infty}\sum\limits_{b_{3} = 0}^{\infty} \left[\frac{\left(-y\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}\left(k_{1}(\alpha)\right)^{b_{3}}}{a_{1}!b_{3}!\left(k_{0}(\alpha)\right)^{b_{3}-\frac{a_{1}}{2}+1}} \frac{t^{-\frac{\alpha a_{1}}{2}+b_{3}+\alpha}\Gamma(\frac{a_{1}}{2})}{\Gamma(\frac{a_{1}}{2}-b_{3})\Gamma(1-\frac{\alpha a_{1}}{2}+b_{3}+\alpha)}\right]. \end{eqnarray}$

(30)

Further, Eq (30) can be expressed in terms of more general function namely M-function ^[40],

$\begin{eqnarray} s(\xi, \tau)& = &\sum\limits_{b_{1} = 0}^{\infty}\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}} {b_{1}!(k_{0}(\alpha))^{-\frac{b_{1}}{2}}}M_{2}^{1}\left[(\frac{k_{1}(\alpha)} {k_{0}(\alpha)})t|_{(\frac{b_{1}}{2}+1, -1), (1-\frac{\alpha b_{1}}{2}, 1)}^{(\frac{b_{1}}{2}+1, 0)}\right]\\&& +\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)} \sum\limits_{b_{1} = 0}^{\infty}\frac{\left(-y\sqrt{\frac{r_{1}}{r_{2}\beta_{c}}}\right)^{b_{1}}} {b_{1}!(k_{0}(\alpha))^{-\frac{b_{1}}{2}+1}}M_{2}^{1}\left[(\frac{k_{1}(\alpha)} {k_{0}(\alpha)})t|_{(\frac{b_{1}}{2}, -1), (1-\frac{\alpha b_{1}}{2}+\alpha, 1)}^{(\frac{b_{1}}{2}, 0)}\right]\\&& -\frac{r_{3} {\rm{Gr}}}{\left(\frac{r_{2}r_{4} {\rm{Pr}}\beta_{c}}{r_{5}}-1\right)}\sum\limits_{a_{1} = 0}^{\infty} \frac{\left(-y\sqrt{\frac{r_{4}}{r_{5}} {\rm{Pr}}}\right)^{a_{1}}}{a_{1}!\left(k_{0}(\alpha)\right)^{-\frac{a_{1}}{2}+1}} M_{2}^{1}\left[(\frac{k_{1}(\alpha)}{k_{0}(\alpha)})t|_{(\frac{a_{1}}{2}, -1), (1-\frac{\alpha a_{1}}{2}+\alpha, 1)}^{(\frac{a_{1}}{2}, 0)}\right]. \end{eqnarray}$

(31)

5. Results and discussions

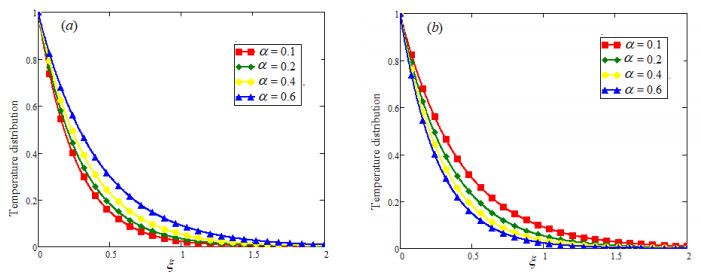
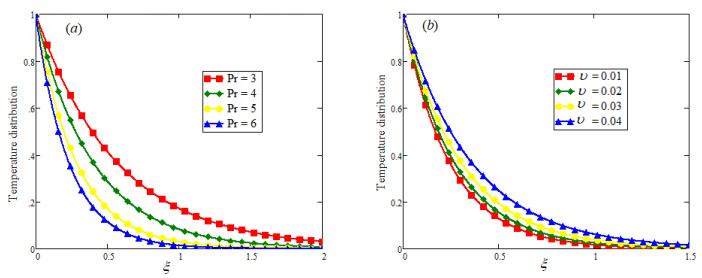
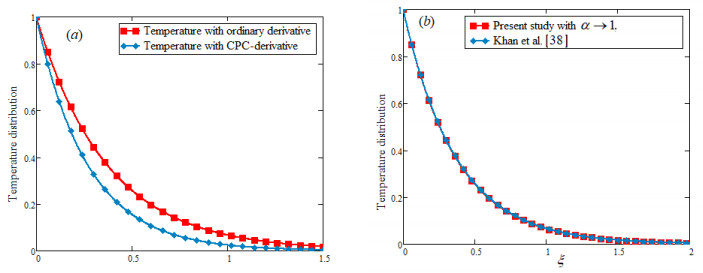
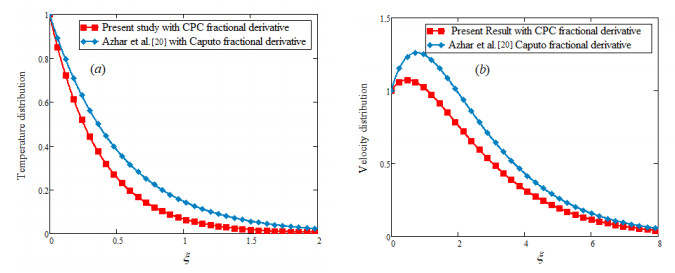
The main aim of this investigation is to explore the results for the flow of drilling nanofluid with constant proportional Caputo fractional derivative. Casson fluid flow model is consider with clay particles and explicit expression for temperature and velocity fields are established as solutions of governing equations via the Laplace transformation. The subjectivity of fractional parameter and other parameter of interest have been studied numerical by plotting the some 2-D graphs of temperature and velocity fields in Mathcad software. Temperature profile is plotted in to see the effect of fractional parameter $\alpha$ for large and small times. An interesting behavior is observed for large and small times that is temperature show increasing trend for large time while it is falling down for small time. The influence of Pr and volume fraction are highlighted in respectively. An increasing value of the Pr lessen the thermal conductivity of the fluid and due to this temperature of flowing fluid falls down with the elevated value of Pr. Thermal conductivity of nanofluid increases with the increasing volume fraction $\upsilon$ of clay nanoparticles that is why temperature of flowing fluid raises with increasing $\upsilon$ . presents the comparison between the ordinary and fractional temperature profiles. shows that temperature profile with constant proportional Caputo fractional derivative has the more decaying nature as compare to the ordinary temperature while it is tends to ordinary with increasing $\alpha$ and finally it overlaps with ordinary temperature as $\alpha\rightarrow1$ as shown in the Figure 4(b).

Figure 2. Temperature profile subject to

$\alpha$ variation for large t

$= 4$ and small

$t = 0.25$ times.

DownLoad: Full-Size Img PowerPoint

Figure 3. Temperature profile subject to Pr and time and volume fraction

$\upsilon$ variation, and

$\alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. Comparison Temperature profile for

$\alpha = 0.5$ and

$\alpha\rightarrow 1$ .

DownLoad: Full-Size Img PowerPoint

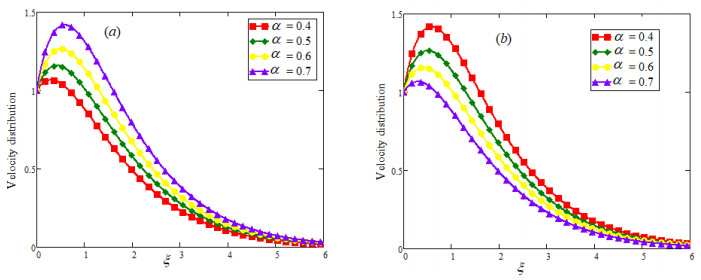
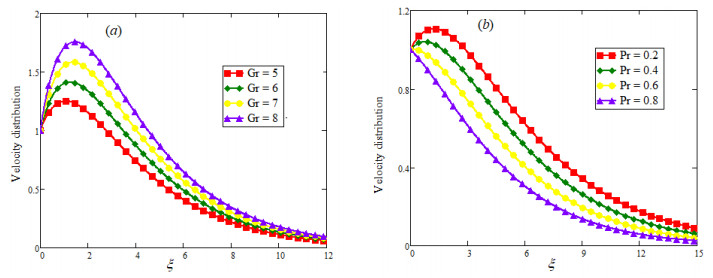
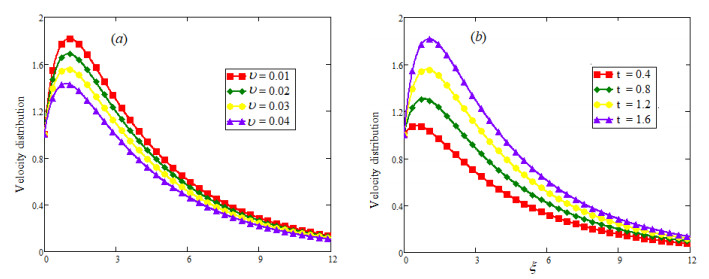
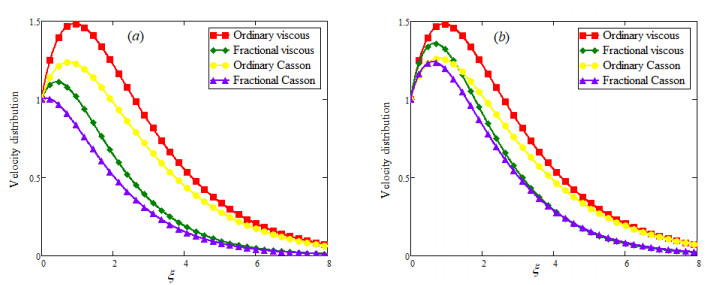
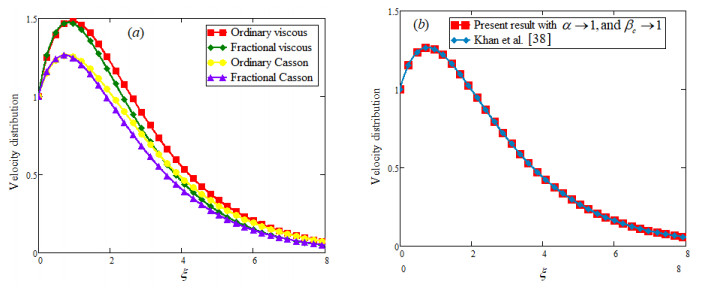
Velocity profiles also present a dual behavior due to $\alpha$ variation for large and small times and it is highlighted in . The effect of Gr and Pr have been explain in respectively and is noted that an increasing Gr (more bouncy effect) speeds up the fluid flow while an increasing Pr (more viscosity) create some hindrance to fluid flow which slows down the fluid flow. The influence of volume fraction $\upsilon$ and time t is illustrated in Figure 7(a), (b) and it is found that enhancing volume fraction of clay nanoparticles boosts the viscous effect for the nanofluid consequently it decreases the fluid velocity as depicted in the Figure 7(a). For a long time, the thermal boundary layer become more thick as compare to the momentum boundary layer that aided the fluid flow as shown in Figure 7(b). In , and , the fractional and ordinary velocity of viscous and Casson fluid are compared for the different values of fractional parameter $\alpha$ . Fraction nanofluid shows a decaying nature for both viscous and Casson fluid as shown in Figure 8(a) while both fractionalized fluids, viscous and Casson tend toward ordinary fluid and this aspect is bring into light in and . At last all velocity profiles concede with each other as both Casson fluid parameter $\beta_{c}\rightarrow 1$ and fractional parameter $\alpha \rightarrow 1$ as shown in Figure 9(b). Finally the temperature and velocity fields obtained by CPC are also compared with that obtained by Caputo fractional derivative and presented graphically in the Figure 10(a), 10(b). From outlines of the figures it is observed that temperature and velocity with CPC are of more decaying nature with respect to temperature and velocity with Caputo fractional derivative.

Figure 5. Velocity profile subject to

$\alpha$ variation for large t = 4 and small t = 0.25 times, and

$\alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. Velocity profile subject to positive and Pr variation and

$\alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. Velocity profile subject to volume fraction

$\upsilon$ and time t variation, and

$\alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. Comparison velocity profile for

$\alpha = 0.4$ and

$\alpha = 0.6$ .

DownLoad: Full-Size Img PowerPoint

Figure 9. Comparison velocity profile for

$\alpha = 0.8$ and

$\alpha\rightarrow1$ .

DownLoad: Full-Size Img PowerPoint

Figure 10. Comparison of Temperature and velocity profiles for among CPC and Caputo fractional derivatives with

$\alpha = 0.5$ .

DownLoad: Full-Size Img PowerPoint

6. Conclusion

The fractional Casson nanofluid flow with clay nanoparticles is modeled by utilizing constant proportional Caputo fractional derivative. Results for temperature and velocity field are established with the help of Laplace transformation. Regarding obtained results for temperature and velocity, the present study can be summarized withe following concluding remarks:

● Temperature and velocity profiles with constant proportional Caputo fractional derivative remain lower than the ordinary profiles.

● Velocity profile is an increasing function for $\alpha$ , Gr, and $t$ .

● Velocity is a decreasing function of Pr and $\upsilon$ .

● Temperature is a increasing functions of $\upsilon$ while it is decreasing for Pr.

● Velocity of Casson fluid in both cases (fractional and ordinary) show a more restrain as compare to the viscous one.

Acknowledgments

The authors are greatly obliged and thankful to the Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University Multan, Pakistan and University of Management and Technology Lahore, Pakistan for facilitating and supporting the research work.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	H. T. Alkasasbeh, M. Z. Swalmeh, A. Hussanan, M. Mamat, Effects of mixed convection on methanol and kerosene oil based micropolar nanofluid containing oxide nanoparticles, CFD Letters, 11 (2019), 55–68.
[2]	A. Raju, O. Ojjela, P. K. Kambhatla, A comparative study of heat transfer analysis on ethylene glycol or engine oil as base fluid with gold nanoparticle in presence of thermal radiation, J. Therm. Anal. Calorim., 2020.
[3]	H. W. Xian, N. Azwadi, C. Sidik, S. R. Aid, T. Ken, Y. Asako, Review on preparation techniques, properties and performance of hybrid nanofluid in recent engineering applications, Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 45 (2018), 1–13.
[4]	S. Aman, I. Khan, Z. Ismail, M. Z. Salleh, Applications of fractional derivatives to nanofluids: Exact and numerical solutions, Math. Model. Nat. Pheno., 13 (2018), 1–12. doi: 10.1051/mmnp/2018007
[5]	A. Hussanan, N. T. Trung, Heat transfer analysis of sodium Carboxymethyl Cellulose based nanofluid with Tiatania nanoparticles, Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 56 (2019), 248–256.
[6]	A. Bhattad, J. Sarkar, P. Ghosh, Discrete phase numerical model and experimental study of hybrid nanofluid heat transfer and pressure drop in plate heat exchanger, Int. Commun. Heat Mass, 91 (2018), 262–273. doi: 10.1016/j.icheatmasstransfer.2017.12.020
[7]	K. Farhana, K. Kadirgama, M. M. Noor, M. M. Rahman, D. Ramasamy, A. S. F. Mahamude, CFD modelling of different properties of nanofluids in header and riser tube of flat plate solar collector, In: IOP Conference Series: Materials Science and Engineering, 469 (2019), 012041.
[8]	I. Khan, Shape, effects of MoS2 nanoparticles on MHD slip flow of molybdenum disulphide nanofluid in a porous medium, J. Mol. Liq., 233 (2017), 442–451.
[9]	Z. Shah, P. Kumam, W. Deebani, Radiative MHD Casson Nanofluid flow with Activation energy and chemical reaction over past nonlinearly stretching surface through Entropy generation, Sci. Rep., 10 (2020), 4402. doi: 10.1038/s41598-020-61125-9
[10]	M. Saqib, Convection in ethylene glycol-based molybdenum disulfide nanofluid, J. Therm. Anal. Calorim., 135 (2019), 523–532. doi: 10.1007/s10973-018-7054-9
[11]	J. A. R. Babu, K. K. Kumar, S. S. Rao, State-of-art review on hybrid nanofluids, Renewable and Sustainable Energy Reviews, 77 (2017), 551–565. doi: 10.1016/j.rser.2017.04.040
[12]	N. S. Khan, S. Zuhra, Q. Shah, Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction, Appl. Nanosci., 9 (2019), 1797–1822. doi: 10.1007/s13204-019-01017-1
[13]	A. Bhattad, J. Sarkar, P. Ghosh, Discrete phase numerical model and experimental study of hybrid nanofluid heat transfer and pressure drop in plate heat exchanger, Int. Commun. Heat Mass, 91 (2018), 262–273. doi: 10.1016/j.icheatmasstransfer.2017.12.020
[14]	S. M. Aminossadati, B. Ghasemi, Natural convection cooling of a localised heat source at the bottom of a nanofluid filled enclosure, Eur. J. Mech. B Fluids, 28 (2009), 630–640. doi: 10.1016/j.euromechflu.2009.05.006
[15]	A. Dawar, Z. Shah, W. Khan, M. Idrees, S. Islam, Unsteady squeezing flow of MHD CNTS nanofluid in rotating channels with Entropy generation and viscous Dissipation, Adv. Mech. Eng., 10 (2019), 1–18.
[16]	M. A. Imran, M. Aleem, M. B. Riaz, R. Ali, I. Khan, A comprehensive report on convective flow of fractional (ABC) and (CF) MHD viscous fluid subject to generalized boundary conditions, Chaos Soliton. Fract., 118 (2019), 274–289. doi: 10.1016/j.chaos.2018.11.016
[17]	J. Hristov, Steady-state heat conduction in a medium with spatial non-singular fading memory, Derivation of Caputo-Fabrizio spacefractional derivative with Jeffreys kernel and analytical solutions, Therm. Sci., 21 (2017), 827–839. doi: 10.2298/TSCI160229115H
[18]	S. Aman, I. Khan, Z. Ismail, M. Z. Salleh, Applications of fractional derivatives to nanofluids: exact and numerical solutions, Math. Model. Nat. Pheno., 13 (2018), 1–12. doi: 10.1051/mmnp/2018007
[19]	N. A. Sheikh, F. Ali, M. Saqib, I. Khan, S. A. Jan, A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid, Phys. Fluids, 132 (2017), 54–62.
[20]	W. A. Azhar, D. Vieru, C. Fetecau, Free convection flow of some fractional nanofluids over a moving vertical plate with uniform heat flux and heat source, Phys. Fluids, 29 (2017), 082001. doi: 10.1063/1.4996034
[21]	K. A. Abro, M. N. Mirbhar, J. F. Gomez-Aguilar, Functional application of Fourier sine transform in radiating gas flow with non singular and non local kernel, J. Braz. Soc. Mech. Sci. Eng., 41 (2019), 400.
[22]	M. Arif, F. Ali, N. A. Sheikh, I. Khan, K. S. Nisar, Fractional model of couple stress fluid for generalized couette flow: A comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives, IEEE Access, 7 (2019), 88643–88655. doi: 10.1109/ACCESS.2019.2925699
[23]	M. Nazar, M. Ahmad, M. A. Imran, N. A. Shah, Double convection of heat and mass transfer flow of mhd generalized second grade fluid over an exponentially accelerated infinite vertical plate with heat absorption, J. Math. Anal., 8 (2017), 1–10.
[24]	M. Ahmad, M. A. Imran, M. Aleem, I. Khan, A comparative study and analysis of natural convection flow of MHD nonNewtonian fluid in the presence of heat source and first order chemical reaction, J. Therm. Anal. Clorim., 137 (2019), 1783–1796. doi: 10.1007/s10973-019-08065-3
[25]	C. H. Yu, Fractional derivatives of some fractional functions and their applications, Asian Journal of Applied Science and Technology, 4 (2020), 147–158. doi: 10.38177/AJAST.2020.4116
[26]	I. Podlubny, Geometric and physical interpretation of fractional integration and fractional differentiation, Fract. Calc. Appl. Anal., 5 (2002), 367–386.
[27]	N. A. Shah, X. Wang, H. Qi, S. Wang, A. Hajizadeh, Transient electro-osmatic slip flow of an Oldroyd-B fluid with time fractional Caputo-Fabrizio derivative, J. Appl. Comput. Mech., 5 (2019), 779–790.
[28]	C. H. Yu, Fractional derivatives of some fractional functions and their applications, Asian Journal of Applied Science and Technology, 4 (2020), 147–158. doi: 10.38177/AJAST.2020.4116
[29]	D. Baleanu1, J. Alzabut, J. M. Jonnalagadda, Y. Adjabi, M. M. Matar, A coupled system of generalized Sturm-Liouville problems and Langevin fractional differential equations in the framework of nonlocal and nonsingular derivatives, Adv. Differ. Equ., 239 (2020), 1–30.
[30]	D. Baleanu, K. Ghafarnezhad, S. Rezapour, On a strong-singular fractional differential equation, Adv. Differ. Equ., 350 (2020), 1–18.
[31]	A. Atangana, D. Baleanu, New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model, Therm. Sci., 20 (2016), 763–769. doi: 10.2298/TSCI160111018A
[32]	T. Abdeljawad, A. Fernandez, On a new class of fractional difference-sum operators with discrete Mittag-Leffler kernels, Mathematics, 7 (2019), 1–13.
[33]	F. Jarad, E. Uourlu, T. Abdeljawad, D. Baleanu, On a new class of fractional operators, Adv. Differ. Equ., 1 (2017), 247.
[34]	A. Atangana, A. Akgül, K. M. Owolabi, Analysis of fractal fractional differential equations, Alex. Eng. J., 59 (2020), 2477–2490. doi: 10.1016/j.aej.2020.03.022
[35]	E. K. Akgül, A. Akgül, D. Baleanu, Laplace transform method for economic models with constant proportional Caputo derivative, Fractal Fract., 4 (2020), 1–9.
[36]	M. N. Mirbahar, K. A. Abro, A. W. Shaikh, Calorimetric investigation for thermal plate of Casson fluid via fractional derivative, Journal of Nanofluids, 8 (2019), 1668–1675. doi: 10.1166/jon.2019.1720
[37]	K. A. Abro, I. Khan, K. S. Nisar, A. S. Alsagri, Effects of carbon nanotubes on magnetohydrodynamic flow of methanol based nanofluids via atanganabaleanu and caputo-fabrizio fractional derivatives, Therm. Sci., 23 (2019), 883–898. doi: 10.2298/TSCI180116165A
[38]	I. Khan, A. Hussanan, M. Saqib, S. Shafie, Convective heat transfer in drilling nanofluid with Clay nanoparticles: applications in water cleaning process, BioNanoSci., 9 (2019), 453–460. doi: 10.1007/s12668-019-00623-1
[39]	D. Baleanu, A. Fernandez, A. Akgül, On a fractional operator combining proportional and classical differintegrals, Mathematics, 8 (2020), 360–372. doi: 10.3390/math8030360
[40]	A. Atangana, A. Akgül, K. M. Owolabi, Analysis of fractal fractional differential equations, Alex. Eng. J., 59 (2020), 1117–1134. doi: 10.1016/j.aej.2020.01.005
[41]	A. Atangana, A. Akgül, Can transfer function and Bode diagram be obtained from Sumudu transform, Alex. Eng. J., 59 (2020), 1971–1984. doi: 10.1016/j.aej.2019.12.028
[42]	N. H. Sweilam, S. M. AL-Mekhlafi, D. Baleanu, A hybrid fractional optimal control for a novel Coronavirus (2019-nCov) mathematical model, J. Adv. Res., 2020, In press.
[43]	I. Khan, S. Shafie, Exact solutions for unsteady free convection flow of Casson fluid over an oscillating vertical plate with constant wall temperature, Abstr. Appl. Anal., 2015 (2015), 1–8.
[44]	S. M. Aminossadati, B. Ghasemi, Natural convection cooling of a localised heat source at the bottom of a nanofluidfilled enclosure, Eur. J. Mech. B Fluids, 28 (2009), 630–640. doi: 10.1016/j.euromechflu.2009.05.006
[45]	M. H. Matin, I. Pop, Forced convection heat and mass transfer flow of a nanofluid through a porous channel with a first order chemical reaction on the wall, Int. Commun. Heat Mass, 46 (2013), 134–141. doi: 10.1016/j.icheatmasstransfer.2013.05.001
[46]	H. C. Brinkman, The viscosity of concentrated suspensions and solutions, J. Chem. Phys., 20 (1952), 571–571. doi: 10.1063/1.1700493

This article has been cited by:

1.	Muhammad Imran Asjad, Muhammad Danish Ikram, Noman Sarwar, Taseer Muhammad, Sivanandam Sivasankaran, Sami Ahmed Abdu Subaihi, Ardashir Mohammadzadeh, Analysis of Fractional Bioconvection with Hybrid Nanoparticles in Channel Flow, 2022, 2022, 1563-5147, 1, 10.1155/2022/8600591
2.	Zaib Nisa, Ahmad Shafique, Mudassar Nazar, Muhammad Asjad, Khaled Mahmoud, Abdullah Alsubai, Mustafa Inc, A novel fractional study on free convection flow of Brinkmann hybrid nanofluid over an inclined plate, 2022, 26, 0354-9836, 229, 10.2298/TSCI22S1229N
3.	Kehong Zheng, Fuzhang Wang, Muhammad Kamran, Rewayat Khan, Ali Sikandar Khan, Sadique Rehman, Aamir Farooq, On rate type fluid flow induced by rectified sine pulses, 2022, 7, 2473-6988, 1615, 10.3934/math.2022094
4.	Ali Raza, Umair Khan, Aurang Zaib, Wajaree Weera, Ahmed M. Galal, A comparative study for fractional simulations of Casson nanofluid flow with sinusoidal and slipping boundary conditions via a fractional approach, 2022, 7, 2473-6988, 19954, 10.3934/math.20221092
5.	P.M. Patil, Madhavarao Kulkarni, J.R. Tonannavar, A computational study of the triple-diffusive nonlinear convective nanoliquid flow over a wedge under convective boundary constraints, 2021, 128, 07351933, 105561, 10.1016/j.icheatmasstransfer.2021.105561
6.	Ye-Qi Wang, Ahmad Shafique, Zaib Nisa, Muhammad Asjad, Mudassar Nazar, Mustafa Inc, Shao-Wen Yao, Unsteady flow of Casson nanofluid through generalized Fourier's and Fick's law for heat and mass transfer, 2022, 26, 0354-9836, 29, 10.2298/TSCI22S1029W
7.	Wan Faezah Wan Azmi, Ahmad Qushairi Mohamad, Lim Yeou Jiann, Sharidan Shafie, Unsteady natural convection flow of blood Casson nanofluid (Au) in a cylinder: nano-cryosurgery applications, 2023, 13, 2045-2322, 10.1038/s41598-023-30129-6
8.	Rusya Iryanti Yahaya, Mohd Shafie Mustafa, Norihan Md Arifin, Ioan Pop, Fadzilah Md Ali, Siti Suzilliana Putri Mohamed Isa, Hybrid nanofluid flow past a biaxial stretching/shrinking permeable surface with radiation effect: Stability analysis and heat transfer optimization, 2023, 85, 05779073, 402, 10.1016/j.cjph.2023.06.003
9.	Shajar Abbas, Mushtaq Ahmad, Mudassar Nazar, Zubair Ahmad, Muhammad Amjad, Hakim AL Garalleh, Ahmed Zubair Jan, Soret Effect on MHD Casson Fluid over an Accelerated Plate with the Help of Constant Proportional Caputo Fractional Derivative, 2024, 9, 2470-1343, 10220, 10.1021/acsomega.3c07311
10.	Xiao Xin, Rabia Safdar, Wasim Jamshed, Syed M. Hussain, Abdullah Alhushaybari, Aiedh Mrisi Alharthi, Application of constant proportional caputo (CPC) fractional derivative for natural convective casson nanofluid flow on an infinite cylinder, 2024, 1040-7790, 1, 10.1080/10407790.2024.2327497
11.	Aziz Ur Rehman, Muhammad Bilal Riaz, Jan Martinovic, MHD Radiative Casson Fluid Flow with Ramped Influence through a Porous Media via Constant Proportional Caputo Approach, 2024, 63, 1572-9575, 10.1007/s10773-024-05667-y

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2128) PDF downloads(82) Cited by(11)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(10)

AIMS Mathematics

Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate

Related Papers:

Abstract

Nomenclature

1. Introduction

2. Mathematical formulation

3. Model with constant proportional Caputo derivative

4. Solution of problem

4.1. Temperature distribution

4.2. Velocity field

5. Results and discussions

6. Conclusion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

Nomenclature

1. Introduction

2. Mathematical formulation

3. Model with constant proportional Caputo derivative

4. Solution of problem

4.1. Temperature distribution

4.2. Velocity field

5. Results and discussions

6. Conclusion

Acknowledgments

Conflict of interest

References

AIMS Mathematics

Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate

Related Papers:

Abstract

Nomenclature

1. Introduction

2. Mathematical formulation

3. Model with constant proportional Caputo derivative

4. Solution of problem

4.1. Temperature distribution

4.2. Velocity field

5. Results and discussions

6. Conclusion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

Nomenclature

1. Introduction

2. Mathematical formulation

3. Model with constant proportional Caputo derivative

4. Solution of problem

4.1. Temperature distribution

4.2. Velocity field

5. Results and discussions

6. Conclusion

Acknowledgments

Conflict of interest

References