In this paper, we will prove a sufficient condition for that there does not exist an open immersion between two affine schemes of finite type over a field k with the same dimension. The proof is based on the following fact: the complement of an open affine subset in a noetherian integral separated scheme has pure codimension 1. We will first prove it when k is a finite field, the key to the proof of this part is Lang-Weil estimation. Then we'll prove a general result over an arbitrary field by reducing to the case when k is finite. And the proof of the general result is much more complicated. In order to use the result over a finite field, at some point we must produce a scheme that is defined over Fq and an open immersion, also defined over Fq. One important lemma is that a morphism f:Spec(B)⟶Spec(A) between two integral domains with the same quotient field K is an open immersion if and only if B is a birational extension of A in K and B is flat over A. According to the general result, the following open immersions do not exist: SLn/k↪An2−1k, Spn/k↪A2n2+nk, SOn/k↪An2−n2k, PGLn/k↪An2−1k, where k is an arbitrary field.
1.
Introduction
The topology involved in this paper is the Zariski topology. The closed sets of affine space Ank are those of the form V(S)={x∈Ank∣f(x)=0,∀f∈S} where S is any set of polynomials in n variables over k. A variety is an integral separated scheme of finite type over an algebraically closed field.
It is well-known that GLm/k is an open subset of Am2k, where k is a field. A natural question is whether there exists an open immersion ϕ:SLm/k↪Am2−1k. If k is algebraically closed, it is easy to show that such an open immersion does not exist, by combining two classical results on algebraic groups. Indeed, if such an immersion exists, then the complement of its image is the zero locus of some polynomial function f. The restriction of this function to SLm/k is a regular invertible function on this connected algebraic group, and hence a scalar multiple of a character by a result of Rosenlicht(see [8]). Since every character of SLm is trivial, f is constant, and hence SLm/k is an affine space. But this contradicts the fact that every algebraic group with underlying variety an affine space is unipotent(see [6]). In this paper we study the nonexistence of some open immersions between affine varieties over a field k, and we will prove a theorem which can explain the nonexistence of ϕ in another way. In addition, there is a result which is similar in spirit: any injective endomorphism of an affine variety is also surjective(see [7]). The main theorem is Theorem 2.15.
Since an open subset of an irreducible affine scheme is dense, we can reduce to the case where the open immersion ϕ:X↪Y is dominant.We first prove the theorem when k is a finite field and then we prove a more general result by reducing to this case. As a simple application, we have the following conclusions: open immersions SLn/k↪An2−1k, Spn/k↪A2n2+nk, SOn/k↪An2−n2k, PGLn/k↪An2−1k do not exist, and open immersions SLn/k×kGa/k↪An2k, Spn/k↪SO2n+1/k, Spn/k↪SLn/k×kAn2+n+1k do not exist either, where k is an arbitrary field.
2.
Results
2.1. Result over a finite field
To prove the main result of this subsection, we require the Lang-Weil estimate and some other lemmas.
Let X be an irreducible scheme defined over a finite field Fq. Assume that X is embedded into a projective space of fixed dimension n, dim(X)=r, deg(X)=d, then we have universal estimates for #X(Fqk), in terms of r, d, and qk. More precisely, we show the following:
LEMMA 2.1 ([Lang-Weil]). Given nonnegative integers n, d and r, with d>0, there is a positive constant A(n,d,r), such that for every finite field k=Fq, and every absolutely irreducible subscheme X⊆Pnk of dimension r and degree d, we have
Proof. See [11].
LEMMA 2.2. Given n, d and r as in Lemma 2.1, there is a positive constant A1(n,d,r), such that for every finite field k=Fq, and every subscheme X⊆Pnk of pure dimension r and degree ≤d, we have
Proof. See Lemma 1 in [11].
If X is allowed to have components of smaller dimension, we still have
COROLLARY 2.3. If X is an r-dimensional scheme over k=Fq, then there is cX>0 such that #X(Fqe)≤cXqer for every e≥1.
Proof. The proof is omitted.
COROLLARY 2.4. If X is an r-dimensional absolutely irreducible scheme over Fq, then there is cX>0 such that |#X(Fqe)−qer|≤cXqe(r−12) for every e≥1.
Proof. The proof is omitted.
LEMMA 2.5. Let A be an integrally closed noetherian domain. Then
where the intersection is taken over all prime ideals of height 1.
Proof. See Theorem 38 in [1].
LEMMA 2.6. For any noetherian, integral, normal affine scheme X = Spec A, and any nonempty closed subscheme Z of X with codimension at least 2, X−Z is not an affine scheme.
Proof. If X−Z is affine, then i:X−Z→X is a morphism of affine schemes, hence i is totally determined by i#:Γ(X,OX)→Γ(X−Z,OX−Z)=Γ(X−Z,OX). Since X is integral, i# is injective.
Moreover, since Z does not contain any codimension 1 point of X, so for any f∈Γ(X−Z,OX), f is regular at all codimension 1 points.Hence by Lemma 2.5, f is regular on X bexause A is integrally closed. As a result, i# is surjective.
In sum, i# is both injective and surjective, so it is actualy an isomorphism. Therefore i is an isomorphism, which means Z is empty and we get a contradiction.
COROLLARY 2.7. If X is a noetherian, integral, separated scheme X, U is an affine open subset, then the complement of U has codimension 1 in X.
Proof. Replace X by its normalization, and U by its preimage inX. Then the codimension of the complement of U doesn't change, and so we reduce to the normal case. Intersecting U with the members of an open affine cover of X, we reduce to the case when X is affine.(X is separated, so the intersection of two open affines is open affine.)Then Lemma 2.6 applies.
We can now prove the main result of this subsection.
THEOREM 2.8. Assume X and Y are affine n-dimensional schemes over Fq, #X(Fqm)≠#Y(Fqm), if |#X(Fqm)−#Y(Fqm)|=o(qm(n−1))(m→∞m∈Z), then there does not exist an open immersion X↪Y.
o(qm(n−1)) represents a polynomial of q, denoted by f, such that limm→∞f(qm)qm(n−1)=0.
Proof. Suppose that there exists an open immersion X↪Y. Let Y=SpecR, V=Y∖X which is associated with an induced scheme structure R/I that is reduced, I⊂R is the defining ideal of V.
We denote by V¯Fq the scheme V×SpecFqSpec¯Fq.
Let X1,X2,…,Xl be the irreducible components of V¯Fq of maximal dimension r, there is a finite extention Fqe of Fq such that for some closed subscheme Vi of VFqe, we have Vi×SpecFqeSpec¯Fq=Xi, 1≤i≤l. This implies that each Vi is absolutely irreducible. Note that the dimension of any other irreducible component of VFqe is smaller than r, and dim(Vi⋂Vj)<r when i≠j.
Combining Corollary 2.3 with Corollary 2.4, we have
That is
Then we have
According to Corollary 2.7, r=n−1, we obtain
On the other hand,
this implies
This contradiction shows that there does not exist an open immersion X ↪ Y.
2.2. Result over an arbitrary field
We need the following four lemmas to prove the main theorem.
LEMMA 2.9. Let A⊆B be two integral domains. If B is faithfullly flat over A and qf(A) = qf(B). Then A=B.
qf(A) means the quotient field of A, and qf(B) is similar.
Proof. Take x∈B with x=b/a (a,b∈A). B is faithfully flat over A, so it follows that b=ax∈aB∩A=aA (cf.[[1], (4.C)]). Hence x=b/a∈A. Therefore A=B.
LEMMA 2.10. Let A be an integral domain with quotient field K and let B be an extension of A. B is a finitely generated A-algebra. Then the canonical morphism f:Spec(B)→Spec(A) is an open immersion ⟺ B is a birational extension of A in K and B is flat over A.
Proof. ⇒ B is flat over A if and only if BP is flat over Ap for every P∈B (p=P∩A). Since f is an open immersion, it follows that BP≅Ap, and BP is flat Ap. Furthermore f is birational, this implies that qf(B) = K.
⇐ Any flat morphism that is locally of finite type is open. Next we will show that this map is injective. Let P,P′∈Spec(B) with P∩A=P′∩A:=p, then Ap→BP is flat. As a flat extension of rings satisfies Going-Down Theorem(cf.[[1], (5.D)]), Spec(BP)→Spec(Ap) is surjective, it follows that BP is faithfully flat over AP(cf.[[1], (4.D)]). Hence Ap=BP by Lemma 2.9. Similary, Ap=BP′=BP. Hence P=P′. So Spec(B) is homeomorphic to an open subset U of Spec(A). Since open sets of the form D(g) form a base for the topology of Spec(A), take Bg⊂U, it is enough to prove Ag≅Bg. We have a surjective homomorphism Bg⊗AgBgϕ↠Bg, since Bg⊗AgBg⊂Bg⊗AgK=K, ϕ is also injective, namely ϕ is an isomorphism. As Bg is faithfully flat over Ag, we conclude that Ag≅Bg.
LEMMA 2.11. Let A⊂B⊂C be rings. Suppose that A is Noetherian, that C is finitely generated as an A-algebra and that C is either (1) finitely generated as a B-module or (2) integral over B. Then B is finitely generated as an A-algebra.
Proof. See Proposition 7.8 in [5].
LEMMA 2.12. Let k be a finitely generated Z-algebra. If k is a field, then k is finite.
Proof. We have a homomorphism Zf→k, if ker(f) = pZ(p is a prime), then k is a finitely generated Fp-algebra, so k is a finite algebraic extension of Fp(cf.[[5], (7.9)]), and k is a finite field.
If ker(f) = (0), we have Z⊂Q⊂k. Since k is a finitely generated Z-algebra, it is a finitely generated Q-algebra, similarly, k is a finite algebraic extension of Q, hence k is a finitely generated Q-module, by Lemma 2.11, Q is a finitely generated Z-algebra, a contradiction. Let Q=Z[c1,…,cs],ci=aibi,ai,bi∈Z,1≤i≤s, take p such that p and bi are coprime, then 1p∉Z[c1,…,cs], this contradiction shows that k is a finite field.
Suppose S0 is a scheme, and Aλ are commutative quasi-coherent OS0-algebras, then A=lim→Aλ is a quasi-coherent OS0-algebra. Denote by Sλ(resp.S) the spectrum of the OS0-algebra Aλ(resp.A), and let uλμ:Sμ→Sλ(for λ≤μ) and uλ:S→Sλ be respectively the S0-morphisms corresponding to homomorphisms φμλ:Γ(S0,Aλ)→Γ(S0,Aμ) and φλ:Γ(S0,Aλ)→Γ(S0,A); it is clear that (Sλ, uλμ) is a projective system in the category of S0-schemes.
Given two Sα-schemes Xα, Yα, we define two projective systems of (Xλ, vλμ) and (Yλ, wλμ) by setting Xλ=Xα×SαSλ, Yλ=Yα×SαSλ, vλμ=idXα×uλμ, wλμ=idYα×uλμ(for α≤λ≤μ), whose projective limits are respectively X=Xα×SαS, Y=Yα×SαS, the canonical morphisms vλ:X→Xλ and wλ:Y→Yλ are respectively equal to idXα×uλ and idYα×uλ. We denote by fλ the morphism Xλ→Yλ, and for α≤λ≤μ, we have fμ=fλ×idSμ:Xλ×SλSμ→Yλ×Sμ, f=fλ×idS:Xλ×SλS→Yλ×SλS.
LEMMA 2.13. Suppose S0 is quasi-compact, Xα and Yα are of finite presentation over Sα, let fα:Xα→Yα be an Sα−morphism.Then f is an open immersion if and only if there exists λ≥α such that fλ is an open immersion(in which case fμ is also an open immersion for μ≥λ).
Proof. See Theorem 8.10.5 in [13].
LEMMA 2.14. Let X and Y be affine n-dimensional integral schemes of finite type over a field k. If we have an open immersion Xf↪Y/k, then there exists a finitely generated Z-subalgebra R of k, affine scheme X, Y of finite type over S=SpecR, and an open immersion XfS↪Y/S, such that X×SSpeck≅X, Y×SSpeck≅Y, and fS×Sidk=f.
Proof. In order to use Lemma 2.13, we should find a field k′, two affine schemes X′, Y′ that are defined over k′, an open immersion f′:X′→Y′, also defined over k′, such that k′ is the quotient field of a finitely generated Z-subalgebra R′⊂k, and X=X′×Speck′Speck, Y=Y′×Speck′Speck, f=f′×idSpeck:X′×Speck′Speck→Y′×Speck′Speck, because k′=lim→s∈R′,s≠0R′s.
Write [x_]=[x1,…,xl], [y_]=[y1,…,ym], X=Speck[x_]/I, Y=Speck[y_]/J, where I=(f1,…,fs)k[x_] and J=(g1,…,gt)k[y_] are respectively the defining ideals of X and Y.
If we have an open immersion Xf↪Y/k, by Lemma 2.10, we have a flat and birational k-morphism f#:k[y_]/J→k[x_]/I. So we have an isomorphism qf{k[x_]/I}g→qf{k[y_]/J}.
Let g0 be the restriction to k[x_]/I of g.
Set φ=g0∘π, π:k[y_]↠k[x_]/I.
We have a homomorphism
¯fi,¯gi∈k[y_]/J, ¯fi,¯gi have no non-unit common factor, 1≤i≤l.
Set R0 = {the subring of k generated by identity 1, all the coefficients of f1,…,fs, g1,…,gt}.
Set R1 = {the subring of k generated by S0, all the coefficients of ¯fi, ¯gi and their inverses}.
It is noted that R1 is a finitely generated Z-algebra.
Consider the restriction to R1[x_] of φ
R1[x_] is noetherian, so kerφ1 is finitely generated.
Let b1,b2,…,bℓ be the generators of kerφ1
Set R2 = {the subring of k generated by R1, all the coefficients of Pij and their inverses. 1≤i≤ℓ, 1≤j≤s}
R2 is still a finitely generated Z-algebra.
Consider the restriction to R2[x_] of φ
Clearly we have kerφ2⊃(f1,…,fs)R2[x_].
We denote by IM(φ1) the image of φ1 in qf{k[y_]/J}, it is a subring of qf{k[y_]/J} generated by R1 and φ1(xi), so we have an exact sequence
IM(φ1)⊗R1R2 is the subring of qf{k[y_]/J} generated by R2 and φ1(xi), so kerφ2 is the image of (b1,…,bℓ)R1[x_]⊗R1R2 in R1[x_]⊗R1R2≅R2[x_], namely (b1,…,bℓ)R2[x_].
By (2.8) we have
(f1,…,fs)R2[x_]⊃(b1,…,bℓ)R2[x_]=kerφ2.
Hence kerφ2=(f1,…,fs)R2[x_].
On the other hand, we have a homomorphism of rings:
f#:k[y_]/J→k[x_]/I
Set ψ=f#∘ρ, ρ:k[y_]↠k[y_]/J.
We have a homomorphism
¯f′i,¯g′i∈k[x_]/I, ¯f′i,¯g′i have no non-unit common factor, 1≤i≤m.
Set R3 = {the subring of k generated by R2 and all the coefficients of ¯f′i, ¯g′i and their inverses}.
Consider the restriction to R3[y_] of ψ
Let c1,c2,…,cℓ′ be the generators of kerψ1
Qij∈k[y_], 1≤i≤ℓ′, 1≤j≤t.
Set R4 = {the subring of k generated by R3 and all the coefficients of Qij and their inverses. 1≤i≤ℓ′, 1≤j≤t}
Let ψ2 be the restriction to R4[y_] of ψ. Similarly, R4 is a finitely generated Z-algebra and kerψ2=(g1,…,gt)R4[y_].
The restriction to R4[y_]/J of f#
is birational according to the construction of R4.
Write k4=qf(R4). Obviously k4⊂k, the restriction to k4[y_]/J of f#
is still birational.
We have a commutative diagram
i1 is flat and f# is flat, so f∘i1=i2∘f#k4 is flat. As i2 is faithfully flat, f#k4 is flat.
According Lemma 2.10, fk4 is an open immersion.
Let k′=k4, R′=R4, X′=SpecR′[x_]/I, Y′=SpecR′[y_]/J, f′=fk4, then Lemma 2.13 applies.
THEOREM 2.15. Assume R is an integral domain which is a finitely generated Z-algebra, S=SpecR, ξ∈S is the generic point. X and Y are affine integral S-schemes of finite type, such that Xξ and Yξ are n-dimensional affine schemes. If for a sufficiently general closed point t∈S, #Xt(κ(t)m)≠#Yt(κ(t)m), and |#Xt(κ(t)m)−#Yt(κ(t)m)|=o(|κ(t)|m(n−1))(m→∞m∈Z), then there does not exist an open immersion Xξ↪Yξ("sufficiently general" is made precise in the proof).
Proof. κ(t)) is the residue field of the point t, because t is a closed point of S, κ(t)) is a finitely generated Z-algebra. According to Lemma 2.12, κ(t)) is a finite field. Set κ(t)=Fq, κ(t)m=Fqm. So #Xt(κ(t)m)=#(X×Sκ(t)m) makes sense, so does #Yt(κ(t)m).
Write [x_]=[x1,…,xl], [y_]=[y1,…,ym], X=SpecR[x_]/I, Y=SpecR[y_]/J, where I=(f1,…,fs)R[x_] and J=(g1,…,gt)R[y_] are respectively the defining ideals of X and Y.
Suppose there is an open immersion Xξfξ↪Yξ/κ(ξ), by Lemma 2.14, there exists a finitely generated Z-subalgebra R′ of κ(ξ), an open immersion
such that SpecR′[x_]/I×SpecR′Specκ(ξ)≅Xξ, SpecR′[y_]/J×SpecR′Specκ(ξ)≅Yξ, and fR′×SpecR′idκ(ξ)=fξ.
Set R″ = {the subring of κ(ξ) generated by R and R′}, then SpecR″[x_]/I×SpecR′Specκ(ξ)≅Xξ, SpecR″[y_]/J×SpecR′Specκ(ξ)≅Yξ, SpecR″[x_]/IfR″↪SpecR′[y_]/J is an open immersion, and fR″×SpecR″idκ(ξ)=fξ.
SpecR″⊂SpecR is a dense open subset, for a sufficiently general closed point t∈SpecR, we have t∈SpecR″.
Let P⊂R″ be the maximal ideal corresponding to t∈S, we have
The property of being an open immersion is stable under base change, so ˉfR″ is an open immersion.
R″/P is a finitely generated Z-algebra which is a field, according to 2.12, it is a finite field, set R″/P≅Fq.
Namely there exists an open immersion Xt/κ(t)↪Yt/κ(t).
|#Xt(κ(t)m)−#Yt(κ(t)m)|=o(|κ(t)|m(n−1))(m→∞m∈Z) implies
by Theorem 2.8, this can not happen. This contradiction shows that there does not exist an open immersion Xξ↪Yξ.
REMARK 2.16. If it happens that #Xt/κ(t)>#Yt/κ(t), there does not exist an open immersion X↪Y.
REMARK 2.17. Denote |#Xt(κ(t)m)−#Yt(κ(t)m)| by fm, if degfm≠m(dimX−1)(∀m∈Z), there does not exist an open immersion X↪Y.
REMARK 2.18. Given X and Y as in Theorem 2.15, if Y is quasi-projective, there does not exist an open immersion X↪Y. Regard X as an affine open subscheme of Y, for any affine open subscheme U⊂Y, U∩X is still affine because Y is separated over S. Then we come to the conclusion.
COROLLARY 2.19. Let X and Y be affine n-dimensional integral schemes of finite type over a field k. If there exists a finitely generated Z-subalgebra R of k and affine schemes X, Y of finite type over S=SpecR, such that X×SSpeck≅X, Y×SSpeck≅Y, and for a sufficiently general closed point t∈S, #Xt(κ(t)m)≠#Yt(κ(t)m) and |#Xt(κ(t)m)−#Yt(κ(t)m)|=o(|κ(t)|m(n−1))(m→∞m∈Z), then there does not exist an open immersion Xf↪Y/k.
Proof. Write [x_]=[x1,…,xl], [y_]=[y1,…,ym], X=Speck[x_]/I, Y=Speck[y_]/J, where I=(f1,…,fs)k[x_] and J=(g1,…,gt)k[y_] are respectively the defining ideals of X and Y.
Assume there is an open immersion Xf↪Y/k, by Lemma 2.14, there exists a finitely generated Z-subalgebra R′ of k, an open immersion
such that SpecR′[x_]/I×SpecR′Speck≅X, SpecR′[y_]/J×SpecR′Speck≅Y, and fR′×SpecR′idk=f.
Set R″ = {the subring of k generated by R and R′}, we have SpecR″[x_]/I×SpecR′Speck≅X, SpecR″[y_]/J×SpecR′Speck≅Y, SpecR″[x_]/IfR″↪SpecR′[y_]/J is an open immersion, and fR″×SpecR″idκ(ξ)=fξ.
It is noted that SpecR″⊂SpecR, then we come to the conclusion according to Theorem 2.15.
3.
Examples
EXAMPLE 3.1. Since
|#SLn/Fq(Fqm)−#An2−1Fq(Fqm)|=qmn2−m−(qmn−1)⋯(qmn−qmn−2m)qmn−m=qm(n2−3)+lower-degree terms+…
We have dimSLn/Fq=dimAn2−1Fq=n2−1, so for an arbitrary field k, there does not exist an open immersion SLn/k↪An2−1k.
EXAMPLE 3.2. Since
|#Spn/Fq(Fqm)−#A2n2+nFq(Fqm)|=qm(2n2+n−2)+lower-degree terms+…
We have dimSpn/Fq=A2n2+nFq=2n2+n, so for an arbitrary field k, there does not exist an open immersion Spn/k↪A2n2+nk.
EXAMPLE 3.3. Since
We have dimSOn/Fq=n2−n2, for n>2, so for an arbitrary field k, there does not exist an open immersion SOn/k↪An2−n2k.
EXAMPLE 3.4. Since
We have dimPGLn/Fq=n2−1, so there does not exist an open immersion PGLn/k↪An2−1k for an arbitrary field k.
EXAMPLE 3.5. Since
|#SLn/Fq×Ga/Fq(Fqm)−#An2−1Fq(Fqm)|=qmn2−m−(qmn−1)⋯(qmn−qmn−2m)qmn=qm(n2−2)+lower-degree terms+…
We have dimSLn/Fq×Ga/Fq=dimAn2Fq=n2, so for an arbitrary field k, there does not exist an open immersion SLn/k×kGa/k↪An2k, and Example 1 is a corollary of this.
EXAMPLE 3.6. We have dimSpn/Fq=dimSO2n+1/Fq=2n2+n, #SO2n+1/Fq>#Spn/Fq for n>2, so when n>2, there does not exist an open immersion Spn/k↪SO2n+1/k for an arbitrary field k.
EXAMPLE 3.7. There does not exist an open immersion Spn/k↪SLn/k×kAn2+n+1k for any field k.
Acknowledgments
The author thanks Professor KeZheng Li for his guide and useful discussions with him. The author thanks Professor Fei Xu and Professor Lei Fu.
Conflict of interest
The author declares that there are no conflicts of interest.










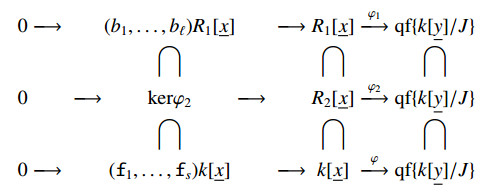






 DownLoad:
DownLoad: