Bifurcation for a fractional-order Lotka-Volterra predator-Cprey model with delay feedback control

1.   Introduction

Dynamical relationships between predator and prey exist widely in real world, which play a key role in linking complex food chains and food networks ^[1,2]. Previously, to unravel these dynamics and their biological functions, several predator–prey models have been proposed. Lotka-Volterra predator–prey system, one of the most celebrated predator–prey models, is being paid more and more attention in recent years ^{[3,4,5,6,7,8]}. Given the importance of the Lotka-Volterra model in the study of ecosystem, many efforts have been undertaken over the years to investigate its dynamical properties, including, dynamical behavior, stability, persistent property, anti-periodic solution, periodic solution and almost periodic solution^{[9,10,11,12,13,14,15]}. In 2008, Yan and Zhang ^[16] considered the following form of predator–prey model to investigate the effects of time delay on stability and bifurcation:

where $x(t)$ and $y(t)$ denote the population densities of prey and predator at time $t$, respectively; $\tau$ is the feedback time delay of the prey to the growth of the species itself; $r_1 > 0$ denotes intrinsic growth rate of the prey and $r_2 > 0$ denotes the death rate of the predator; $a_{ij}$$(i, j = 1, 2)$ are all positive constants.

As a matter of fact, fractional calculus is merged into complicated, dynamical systems which extremely renovate the theory of the design and control performance for complex systems. The scholars discovered that some real world problems in nature can be depicted more accurately by fractional-order systems in comparison with classical integer-order ones ^[17,18]. Furthermore, the biological process is in relation to the entire time information of the model in the light of the traits of the fractional derivative, whereas the classic integer-order derivative places a high value on the information at a given time ^[19,20]. Recently years, many scholars have done a lot of research on the basic theory of fractional differential equations and the dynamics analysis of fractional order predator–prey or eco-epidemiological models (see ^{[21,22,23,24,25,26,27,28,29]}). As in ^[30,31,32], the authors considered the fractional-order delayed predator–prey systems.

Normally, quite a few bifurcation control schemes can be adopted to handle bifurcation dynamics, such as dislocated feedback control, speed feedback control and enhancing feedback control. Actually, it is challenging to exhaustively control the dynamical properties of an involute system relying on a unique feedback variable. In ^[33], Xiao et al. found that the onset of Hopf bifurcations can be lagged or advanced by the proposed fractional-order PD controller by selecting proper control parameters. Paper ^[34], an extended delayed feedback controller is subtly designed to control Hopf bifurcation for a delayed fractional predator–prey model, and it is detected that both extended feedback delay and fractional order can delay the onset of bifurcation for the proposed system. It is point out that the performance of nonlinear fractional dynamic systems can be elevated by utilising bifurcation control methods ^[35,36]. In addition, several control design analysis methods is a valid tool for the amelioration of the stabilization/synchronization of nonlinear systems ^{[37,38,39,40,41,42,43]}. However, to the best of our knowledge, there are few papers to investigate the existence of Hopf bifurcation to fractional-order delay Lotka-Volterra predator–prey with feedback control by using time delay as a bifurcation parameter.

Inspired by the above discussions, in this paper, we consider the following fractional-order delayed Lokta-Volterra predator–prey with feedback control:

where $q\in(0, 1]$ is fractional order, and $k$ is negative feedback gains, $x^*$ is equilibrium point of system (1.1), other paraments are same as system (1.1). Obviously, system (1.2) degenerates into the model in ^[16] when $k = 0$ and $q = 1$.

The main contributions can be sum up in three key points:

1) One new fractional-order Lotka-Volterra predator–prey control model with feedback control and feedback gain is considered.

The joint effects of feedback gain and feedback delay on the controlled system are investigated.

2) Two primary dynamical properties—stability and oscillation—of the delayed fractional-order Lotka-Volterra predator–prey model with feedback control are investigated.

3) The influences of the order on the Hopf bifurcation are obtained.

4) One numerical simulation is given to illustrate the effectiveness of the proposed controllers.

Throughout of this paper, we address the following assumption:

$(\textbf{H1})$ $r_1a_{21}-r_2a_{11} > 0$.

Suppose $(\textbf{H1})$ holds, the positive equilibrium point $E^* = (x^*, y^*)$ of system (1.2) is unique, described by

Our main purpose of this work is by applying time delay as a bifurcation parameter, some conditions of bifurcation are gained for controlled system (1.2).

The rest of this paper is structured as follows. In Section 2, we state some basic necessary definitions and lemmas. In Section 3, we study the existence of Hopf bifurcation of system (1.2). In Section 4, simulation is illustrated to verify the theoretical results. To the end, a brief conclusion is given.

2.   Preliminaries

In this section, we introduce some definitions and lemmas of fractional derivatives, which serve as a basis for the proofs of main result of Section 3.

Generally speaking, there are three extensively used fractional operators, that is to say, the Riemann-Liouville definition, the Gr$\ddot{u}$nwald-Letnikov definition, and the Caputo definition. Since the Caputo derivative only requires the initial conditions which are based on integer-order derivative and represents well-understood features of physical state, it is more benefiting to real world questions. With this concept in mind, we shall apply the Caputo fractional-order derivative to model and analyze the stability of the proposed fractional-order algorithms in this paper.

Definition 2.1. ^[44] The Caputo fractional-order derivative is defined by

where $l-1\leq\alpha < l\in Z^+$, $\Gamma(\cdot)$ is the Gamma function, $\Gamma(s) = \int_0^\infty t^{s-1}e^{-t}dt$.

Definition 2.2. ^[44] The Laplace transform of the Caputo fractional-order derivatives is

If $\digamma^i(0) = 0$, $i = 1, 2, \ldots, n$, then $L\{D_t^{\alpha}\digamma(t); s\} = s^\alpha F(s).$

Lemma 2.1. ^[45] For the following autonomous model

in which, $0 < \alpha < 1$, $f\in R^{n}$, $A\in R^{n\times n}$ is asymptotically stable if and only if $|\arg(\lambda_i)| > \alpha\pi/2$$(i = 1, 2, \ldots, n)$, then each component of the states decays towards $0$ like $t^{-q}$. Furthermore, this model is stable if and only if $|\arg(\lambda_i)|\geq \alpha\pi/2$ and those critical eigenvalues that satisfy $|\arg(\lambda_i)| = \alpha\pi/2$ have geometric multiplicity one.

Consider the $n$-dimensional linear fractional-order system with multiple time delays:

where $\alpha\in(0, 1]$. The initial conditions are $u_{i}(t) = \psi_{i}(t), t\in[-\tau_{\max}, 0]$ for some continuous function $\psi_{i}(t)$, where $\tau_{\max} = \max_{1\leq i, j, \leq n}\{\tau_{ij}\}$. The stability of the zero solution of system (2.1) depends on the distribution of the roots of the associated characteristic equation as following:

Next section, we will establish some sufficient conditions for the existence Hopf bifurcation of system (1.2).

3.   Main results

By making the substitution $u_1(t) = x(t)-x^*, u_2(t) = y(t)-y^*$, then the equivalent system of system (1.2) can be obtained as

Linearizing model (3.1) at the zero, yields

From system (3.2), then we derive that associated characteristic equation is

where

Multiplying $e^{s\tau}$ both sides of Eq (3.3), then we obtain

It concludes that $s = i\omega = \omega(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2})$$(\omega > 0)$ is a purely imaginary root of Eq (3.4) if and only if

where

According to Eq (3.5), we get

It is clear from Eq (3.6) that

$(\textbf{H2})$ Eq (3.7) has leastwise one positive real root $\omega$.

By the aid of Eq (3.6), then we get

Define the bifurcation point

where $\tau^{(l)}$ is defined by Eq (3.8).

To obtain the condition of Hopf bifurcation with respect to $\tau$, further, we also assume that:

$(\textbf{H3})$ $\frac{\chi_1\varphi_1+\chi_2\varphi_2}{\varphi_1^2+\varphi_2^2}\neq0$,

where

Lemma 3.1. Let $s(\tau) = \xi(\tau)+i\omega(\tau)$ be a root of Eq (3.3) near $\tau = \tau_j$ satisfying $\xi(\tau_j) = 0$, $\omega(\tau_j) = \omega_0$, then the following transversality condition holds

where $\tau_0$ and $\omega_0$ are the bifurcation point and the critical frequency of system (1.2), respectively.

Proof. By exploit implicit function theorem and differentiating Eq (3.5) with respect to $k$, we obtain

It can be noted that $C'_3(s) = 0$, then we have

where

Let $C_l^r$, $C_l^i$ be the real and imaginary parts of $C_l(s)$, respectively. $C_l^{'r}$, $C_l^{'i}$ are the real and imaginary parts of $C_l^{'}(s)$, respectively. Let $\chi_1$, $\chi_2$ be the real and imaginary parts of $\chi(s)$, respectively. Let $\varphi_1$, $\varphi_2$ be the real and imaginary parts of $\varphi(s)$, respectively.

Based on Eq (3.9), then we get

Thus, $(\textbf{H3})$ insinuates that transversality condition holds. This completes the proof of Lemma 3.1. According to Lemma 3.1 it is not difficult to arrive at the following Theorem.

Theorem 3.1. Assume that (H1)–(H3) hold, for a fractional Lotka-Volterra predator–prey with feedback control system (1.2), the following results hold:

(i) $E^*$ is unstable for $\tau\in(0, \tau_0)$.

(ii) system (1.2) exhibits a Hopf bifurcation at $E^*$ when $\tau = \tau_0$, $E^*$ of delay fractional Lotka-Volterra predator–prey with feedback control model (1.2) will become asymptotically stable near $\tau = \tau_0$.

4.   Numerical example

In this section, we will give an example is provided to demonstrate the effectiveness of the proposed approach. The numerical solution is derived by using the Adams-Bashforth-Moulton predictor-corrector method^[46], and take step-length $\Delta t = 0.01$.

Example 4.1. Consider the following delayed fraction Lotka-Vollterra predatory–prey with feedback control model:

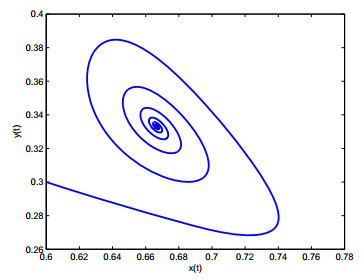
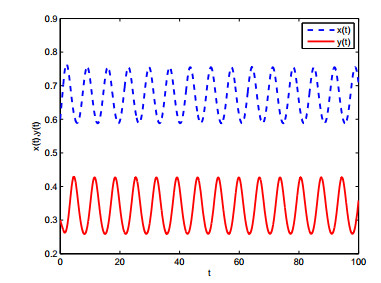
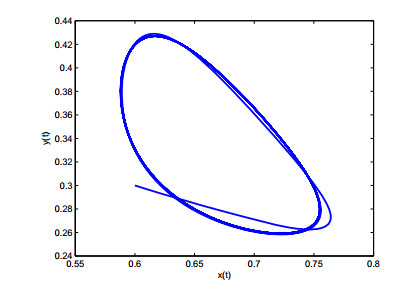
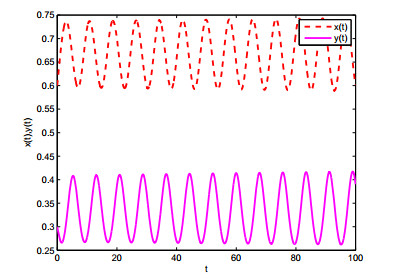
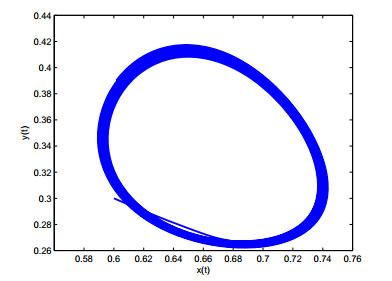
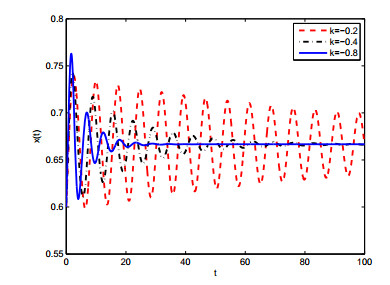
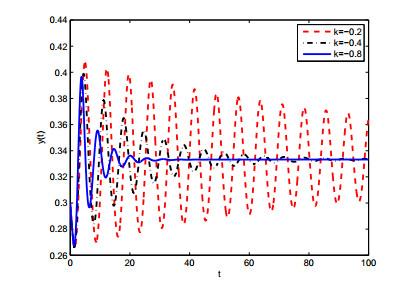
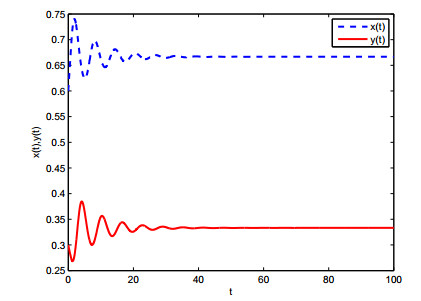
In this case, $r_1 = 1, a_{11} = -1, r_2 = 1, a_{22} = 2$, it is not difficult to calculate $r_1a_{21}-r_2a_{11} = 1*2-1*(-1) = 3 > 0$, therefore, condition of $(H_1)$ is satisfied. Furthermore, according to reference ^[16], we obtained $E^* = (\frac{2}{3}, \frac{1}{3})$. Choosing $k = -0.5$, then $\omega_0 = 0.9085$, $\tau_0 = 1.0229$. From Theorem 3.1, $E^*$ is unstable when $\tau = 0.93 < \tau_{0}$, which is simulated in Figures 1 and 2. Hopf bifurcation occurs from $E^*$ when $\tau = 1.16 > \tau_{0}$, as showed in Figures 3 and 4. Figures 5 and 6 display that system (4.1) turns unstable upon removing the controller. This advises that the introduced controller is fairly efficient. We further choose $k = -0.2, -0.4, -0.6$, then $\tau_{0} = 0.9825, 1.185, 1.324$, respectively. Figures 7 and 8 implies that the onset of bifurcation of system (4.1) can be delayed as $k$ decreases.

5.   Conclusion

The bifurcation control of a fractional-order Lotka-Volterra predator–prey model has been carefully studied by delay feedback control. The criteria of bifurcation have been derived for controlled systems by choosing delay as a bifurcation parameter. It detects that the emergence of bifurcation can be delayed with the decrement of feedback gain. A simulation example is finally used to verify the efficiency of the devised strategy. It is worth noting that there will be several future directions to apply the methods from employing time delay as a bifurcation parameter to more complex ones like models with different delays, or to study the Hopf bifurcation of fractional-order systems with higher dimension.

Acknowledgments

This work is supported by the National Natural Sciences Foundation of People's Republic of China under Grants 11961078, and the Natural Scientific Research Fund Project of Yunnan Province (Grant No.2018FH001-012), and the Construction Plan of Key Laboratory of Institutions of Higher Education in Yunnan Province. The authors are grateful to anonymous referees for their useful suggestions, which greatly improve the presentation of the paper.

Conflict of interest

All authors declare no conflict of interest.