Subalgebras of type (α, β) based on m-polar fuzzy points in BCK/BCI-algebras

1.   Introduction

$BCK$-algebras, one of the oldest branches of general algebras, first appeared in mathematical sciences in 1966 by Imai and Iséki ^[1], which are applied to several areas, such as topology, group theory, semigroups, graphs and functional analysis, etc. Such algebras generalize Boolean D-poset ($MV$-algebras) as well as Boolean rings. In the same year, as an extension of $BCK$-algebras, Iséki ^[2] introduced the idea of $BCI$-algebras. $BCK/BCI$-algebras are established from two distinct approaches: Propositional calculi and set theory. Several results and properties of $BCK/BCI$-algebras are discussed in the works ^[3,4].

Fuzzy set theory, initially established by Zadeh ^[5] in 1965, was applied by several researchers to generalize some of the essential ideas of algebraic structures. Fuzzy algebraic structures play a prominent role in different domains in mathematics and other sciences such as theoretical physics, topological spaces, real analysis, coding theory, set theory, logic, information sciences and the like. In 1994, bipolar fuzzy ($\mathscr{BF}$, for short) sets were developed by Zhang ^[6] and is a more platform that extends the crisp (classical) sets and fuzzy sets. Hybrid models of fuzzy sets have been implemented in several algebraic structures, such as hemirings ^[7], $BRK$-algebras ^[8] and $BCK/BCI$-algebras ^{[9,10,11,12,13,14,15,16]}. In many real life problems, multi-polar information plays a fundamental role in distinct areas of the science, such as neurobiology and technology. Data sometimes comes from $m$ components ($m\geq 2$), for example consider the following sentence "Harvard University Is a Good University". The degree of membership of this sentence may not be a real number in the standard interval $[0, 1].$ In fact, Harvard University is a good university in several components: good in ranking, location, facilities and education, etc. Any component may be a real number in the interval $[0, 1].$ If we have $m$ components, then the degree of membership of the fuzzy sentence is an element of $[0, 1]^m$, that is, a $m$-tuple of real number in $[0, 1].$

Based on these observations, Chen et al. ^[17] broadened the theory of $\mathscr{BF}$ sets to get the idea of $m$-polar fuzzy ($m$-$\mathscr{PF}$, for short) sets in 2014, and proved that $\mathscr{BF}$ sets and $2$-$\mathscr{PF}$ sets are cryptomorphic mathematical notions. In $m$-$\mathscr{PF}$ sets, the grades of membership functions $\mathcal{\widehat{W}}$ are extended from the unit interval [0, 1] into the cubic $[0, 1]^m.$ Recently, $m$-$\mathscr{PF}$ set theory was applied to some algebraic structures such as lie algebras ^[18,19] and groups ^[20]. In $BCK/BCI$-algebras, the notion of $m$-$\mathscr{PF}$ subalgebras was first initiated in 2018 by Al-Masarwah and Ahmad ^[21]. After that, in ^[22] they studied the normalizations of $m$-$\mathscr{PF}$ subalgebras in $BCK/BCI$-algebras. Various applications of $m$-$\mathscr{PF}$ sets and other hybrid models of fuzzy sets in the real life-issues in the field of decision making problems are studied in ^[23,24].

The framework of the fuzzy subetaoup, initially proposed by Rosenfeld ^[25] in 1971, is a fundamental concept of fuzzy algebras. The notion of "belongingness" of a fuzzy point with a fuzzy set was given by Murali ^[26]. Besides, the concept of "quasi-coincidence" of a fuzzy point with a fuzzy set ^[27], played a fundamental role to construct distinct innovative types of fuzzy subetaoups. In the literature, Bhakat and Das ^[28] first generalized the notion of fuzzy subetaoups to $(\alpha, \beta)$-fuzzy subetaoups. They proposed the idea of $(\in, \in \vee q)$-fuzzy subetaoups as a special case of $(\alpha, \beta)$-fuzzy subetaoups. In this aspect, Dudek et al. ^[29] and Narayanan et al. ^[30] extended these results to near-rings and hemirings. In $BCK/BCI$algebras, Xi ^[31] introduced the idea of fuzzy subalgebras in 1991. Jun ^[32] presented the study of $(\alpha, \beta)$-fuzzy subalgebras as a generalization of fuzzy subalgebras. Further, Muhiuddin and Al-Roqi discussed more results of this concept in ^[33]. Jana et al. ^[34] presented an $(\in, \in \vee q)$-intuitionistic fuzzy subalgebra in $BCI$-algebras. Also, Jana et al. ^[35] established the idea of $(\in, \in \vee q)$-$\mathscr{BF}$ subalgebras in $BCK/BCI$-algebras. This concept is a fundamental and useful generalization of Lee's ^[36] $\mathscr{BF}$ subalgebras.

Inspired by the previous studies and by using $m$-$\mathscr{PF}$ sets and $m$-$\mathscr{PF}$ points, we present a new idea called $m$-polar $(\alpha, \beta)$-fuzzy subalgebras in $BCK/BCI$-algebras and we establish some interesting characterization results. In particular, we introduce the concept of $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras and we give some related theorems. We provide conditions for an $m$-$\mathscr{PF}$ set to be an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra and an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra. We explore the characterizations of $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras in $BCK/BCI$-algebras by using level cut subsets. To show the novelty of this model, some contributions of different authors toward generalized $m$-$\mathscr{PF}$ subalgebras in $BCK/BCI$-algebras are analyzed in Table 1.

2.   Preliminaries

In the current section, we recall the basic concepts of $BCK/BCI$-algebras which will be very helpful in further study of the paper.

A structure $(\mathcal{P}, \ast)$ is called a $BCI$-algebra if $\mathcal{P}$ contains a constant $0$ and satisfies the following conditions: For all $h, k, l \in \mathcal{P},$

(Ⅰ) $(h \ast (h \ast k)) \ast k = 0,$

(Ⅱ) $((h \ast k) \ast (h \ast l)) \ast (l \ast k) = 0,$

(Ⅲ) $h \ast h = 0,$

(Ⅳ) $h \ast k = 0$ and $k \ast h = 0$ imply $h = k.$

If a $BCI$-algebra $(\mathcal{P}, \ast)$ satisfies $0 \ast h = 0,$ then $\mathcal{P}$ is said to be a $BCK$-algebra. In any $BCK/BCI$-algebra $(\mathcal{P}, \ast),$ the following valid: For all $h, k, l \in \mathcal{P},$

(1) $h \ast 0 = h,$

(2) $(h \ast k) \ast l = (h \ast l) \ast k,$

(3) $h \ast k \leq h,$

(4) $(h \ast k) \ast l \leq (h \ast l) \ast (k \ast l),$

(5) $h \leq k \Rightarrow h \ast l \leq k \ast l,$ $l \ast k \leq l \ast h,$

where $h \leq k \Leftrightarrow h \ast k = 0$.

A subset $C\neq \phi$ of a $BCK/BCI$-algebra $(\mathcal{P}, \ast)$ is a subalgebra of $(\mathcal{P}, \ast)$ if $h\ast k \in C,$ $\forall h, k \in C.$

Here we mentioned some of the related definitions and results which are directly used in our work. For details we refer the researcher to the works ^[3,4,37] for more information regarding $BCK/BCI$-algebras. From now on, let $\mathcal{P}$ denote a $BCK/BCI$-algebra unless otherwise specified.

Definition 2.1. ^[17] A function $\widehat{\mathcal{W}}:\mathcal{P} \rightarrow [0, 1]^m$ is defined from $\mathcal{P} (\neq \phi)$ to an $m$-tuple of real number in $[0, 1],$ is called an $m$-$\mathscr{PF}$ set. The membership degree of each element $h\in \mathcal{P}$ is denoted by

where $p_j\circ \mathcal{W}:[0, 1]^m\rightarrow [0, 1]$ is the $j$-th projection mapping. The smallest and largest values in $[0, 1]^m$ are $\widehat{0} = (0, 0, ..., 0)$ and $\widehat{1} = (1, 1, ..., 1),$ respectively.

Definition 2.2. ^[21] An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is called an $m$-$\mathscr{PF}$ subalgebra of $\mathcal{P}$ if for all $h, k \in \mathcal{P},$

i.e.,

for all $j = 1, 2, ..., m.$

3.   $m$-polar $(\alpha, \beta)$-fuzzy subalgebras

In the current section, we propose the concept of $m$-polar $(\alpha, \beta)$-fuzzy subalgebras, where $\alpha, \beta \in \{\in, q, \in \vee q, \in \wedge q\}, \alpha \neq \in \wedge q,$ and study some related properties.

An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ having the form

is called an $m$-$\mathscr{PF}$ point with support $h$ and value $\widehat{\eta} = (\eta_1, \eta_2, ..., \eta_m)$ and is denoted by $h_{\widehat{\eta}}.$

For an $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P},$ we say that

(1) $h_{\widehat{\eta}}$ is belong to $\widehat{\mathcal{W}},$ denoted by $h_{\widehat{\eta}}\in \widehat{\mathcal{W}},$ if $\widehat{\mathcal{W}}(h)\geq \widehat{\eta}$ i.e., $p_j\circ \mathcal{W}(h)\geq \eta_j$ for each $j = 1, 2, ..., m.$

(2) $h_{\widehat{\eta}}$ is quasi-coincident with $\widehat{\mathcal{W}},$ denoted by $h_{\widehat{\eta}} q \widehat{\mathcal{W}},$ if $\widehat{\mathcal{W}}(h)+\widehat{\eta} > \widehat{1}$ i.e., $p_j\circ \mathcal{W}(h)+ \eta_j > 1$ for each $j = 1, 2, ..., m.$

(3) $h_{\widehat{\eta}}$ is belong to $\widehat{\mathcal{W}}$ or $h_{\widehat{\eta}}$ is quasi-coincident with $\widehat{\mathcal{W}},$ denoted by $h_{\widehat{\eta}}\in \vee q \widehat{\mathcal{W}},$ if $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ or $h_{\widehat{\eta}} q \widehat{\mathcal{W}}.$

(4) $h_{\widehat{\eta}}$ is belong to $\widehat{\mathcal{W}}$ and $h_{\widehat{\eta}}$ is quasi-coincident with $\widehat{\mathcal{W}},$ denoted by $h_{\widehat{\eta}}\in \wedge q \widehat{\mathcal{W}},$ if $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ and $h_{\widehat{\eta}} q \widehat{\mathcal{W}}.$

(5) $h_{\widehat{\eta}} \overline{\alpha} \widehat{\mathcal{W}}$ if $h_{\widehat{\eta}} \alpha \widehat{\mathcal{W}}$ does not hold.

If $C$ is a nonempty subset of $\mathcal{P},$ then the $m$-polar characteristic function of $C$ denoted and defined by

Clearly, $\widehat{\chi}_{C}$ is an $m$-$\mathscr{PF}$ subset of $\mathcal{P}$.

Definition 3.1. An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is called an $m$-polar $(\alpha, \beta)$-fuzzy subalgebra of $\mathcal{P}$ if it satisfies the following condition:

for all $\widehat{\eta}, \widehat{\zeta} \in (0, 1]^m$ and $h, k \in \mathcal{P},$ where $\alpha \neq \in \wedge q.$

In Definition 3.1 $\alpha \neq \in \wedge q.$ To explain this, let $\widehat{\mathcal{W}}$ be an $m$-$\mathscr{PF}$ set of $\mathcal{P}$ such that $\widehat{\mathcal{W}}(h)\leq \widehat{0.5}$ $\forall h\in \mathcal{P}.$ Let $h\in \mathcal{P}$ be such that $h_{\widehat{\eta}}\in \wedge q \widehat{\mathcal{W}}$ for $\widehat{\eta}\in (0, 1]^m.$ Then, $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ and $h_{\widehat{\eta}} q \widehat{\mathcal{W}}$ i.e., $\widehat{\mathcal{W}}(h) \geq \widehat{\eta}$ and $\widehat{\mathcal{W}}(h) + \widehat{\eta} > \widehat{1}.$ It implies that $\widehat{1} < \widehat{\mathcal{W}}(h)+\widehat{\eta}\leq \widehat{\mathcal{W}}(h)+\widehat{\mathcal{W}}(h) = 2\widehat{\mathcal{W}}(h),$ so $\widehat{\mathcal{W}}(h) > \widehat{0.5}.$ This means that $\{h_{\widehat{\eta}}\mid h_{\widehat{\eta}} \in q \widehat{\mathcal{W}}\} = \phi.$

Example 3.1. Consider a $BCI$-algebra $\mathcal{P} = \{0, k, l, n\}$ with the operation $\ast$ which is given in Table 2:

Let $\widehat{\mathcal{W}}: \mathcal{P}\rightarrow [0, 1]^3$ be a $3$-$\mathscr{PF}$ set defined by:

Then, $\widehat{\mathcal{W}}$ is a $3$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

For any $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}.$ Consider the set $\widehat{\mathcal{W}}_{\widehat{0}} = \{h\in \mathcal{P} \mid \widehat{\mathcal{W}}(h) > \widehat{0}\}.$

Theorem 3.2. If $\widehat{\mathcal{W}}$ is a non-zero $m$-polar $(\in, \beta)$-fuzzy subalgebra of $\mathcal{P},$ then $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P},$ where $\beta\in\{\in, q\}.$

Proof. Let $\widehat{\mathcal{W}}$ be a non-zero $m$-polar $(\in, \beta)$-fuzzy subalgebra of $\mathcal{P}$ and $h, k\in \mathcal{P}.$ We consider the following:

(1) For $(\beta = \in).$ Let $h, k\in \widehat{\mathcal{W}}_{\widehat{0}}.$ Then, $\widehat{\mathcal{W}}(h) > \widehat{0}$ and $\widehat{\mathcal{W}}(k) > \widehat{0}.$ Note that $h_{\widehat{\mathcal{W}}(h)}\in \widehat{\mathcal{W}}$ and $k_{\widehat{\mathcal{W}}(k)}\in \widehat{\mathcal{W}}.$ If $\widehat{\mathcal{W}}(h\ast k) = \widehat{0},$ then $\widehat{\mathcal{W}}(h\ast k) = \widehat{0} < \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\}.$ Thus, $(h\ast k)_{\inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\}} \overline{\in} \widehat{\mathcal{W}},$ a contradiction. So $\widehat{\mathcal{W}}(h\ast k) > \widehat{0},$ i.e., $h\ast k\in \widehat{\mathcal{W}}_{\widehat{0}}.$

(2) For $(\beta = q).$ Let $h, k\in \widehat{\mathcal{W}}_{\widehat{0}}.$ Then, $\widehat{\mathcal{W}}(h) > \widehat{0}$ and $\widehat{\mathcal{W}}(k) > \widehat{0}.$ If $\widehat{\mathcal{W}}(h\ast k) = \widehat{0},$ then $\widehat{\mathcal{W}}(h\ast k)+ \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\} = \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\}\leq \widehat{1}.$ Thus, $(h\ast k)_{\inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\}} \overline{q} \widehat{\mathcal{W}},$ a contradiction. So $\widehat{\mathcal{W}}(h\ast k) > \widehat{0},$ i.e., $h\ast k\in \widehat{\mathcal{W}}_{\widehat{0}}.$ Hence, in any case, we have $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P}.$

Theorem 3.3. If $\widehat{\mathcal{W}}$ is a non-zero $m$-polar $(q, \in)$-fuzzy subalgebra of $\mathcal{P},$ then $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P}.$

Proof. Let $h, k\in \widehat{\mathcal{W}}_{\widehat{0}}$ for $h, k\in \mathcal{P}.$ Then, $\widehat{\mathcal{W}}(h) > \widehat{0}$ and $\widehat{\mathcal{W}}(k) > \widehat{0}.$ It follows $x_{\widehat{1}}q \widehat{\mathcal{W}}$ and $y_{\widehat{1}}q \widehat{\mathcal{W}}.$ Since $\widehat{\mathcal{W}}$ is an $m$-polar $(q, \in)$-fuzzy subalgebra of $\mathcal{P},$ we have $(h\ast k)_{\widehat{1}}\in \widehat{\mathcal{W}}.$ If $\widehat{\mathcal{W}}(h\ast k) = \widehat{0} < \widehat{1},$ then $(h\ast k)_{\widehat{1}}\overline{\in} \widehat{\mathcal{W}},$ a contradiction. So $\widehat{\mathcal{W}}(h\ast k) > \widehat{0},$ i.e., $h\ast k\in \widehat{\mathcal{W}}_{\widehat{0}}$ for $h, k\in \mathcal{P}.$ Hence, $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P}.$

Theorem 3.4. If $\widehat{\mathcal{W}}$ is a non-zero $m$-polar $(q, q)$-fuzzy subalgebra of $\mathcal{P},$ then $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P}.$

Proof. Let $h, k\in \widehat{\mathcal{W}}_{\widehat{0}}$ for $h, k\in \mathcal{P}.$ Then, $\widehat{\mathcal{W}}(h) > \widehat{0}$ and $\widehat{\mathcal{W}}(k) > \widehat{0}.$ Thus, $\widehat{\mathcal{W}}(h) + \widehat{1} > \widehat{1}$ and $\widehat{\mathcal{W}}(k) + \widehat{1} > \widehat{1}.$ It follows $x_{\widehat{1}}q \widehat{\mathcal{W}}$ and $y_{\widehat{1}}q \widehat{\mathcal{W}}.$ If $\widehat{\mathcal{W}}(h\ast k) = \widehat{0},$ then $\widehat{\mathcal{W}}(h\ast k) + \widehat{1} = \widehat{0} + \widehat{1} = \widehat{1},$ and so $(h\ast k)_{\widehat{1}}\overline{q} \widehat{\mathcal{W}}.$ This is impossible, and hence $\widehat{\mathcal{W}}(h\ast k) > \widehat{0}$ i.e., $h\ast k \in \widehat{\mathcal{W}}_{\widehat{0}}$ for $h, k\in \mathcal{P}.$ Thus, $\widehat{\mathcal{W}}_{\widehat{0}}$ is a subalgebra of $\mathcal{P}.$

In the following theorem, we give characterizations of an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra.

Theorem 3.5. For an $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P},$ the conditions (J) and (H) are equivalent, where

for all $h, k \in \mathcal{P}$ and $\widehat{\eta}, \widehat{\zeta} \in (0, 1]^m.$

Proof. (J) $\Rightarrow$ (H). Assume that (H) does not valid, i.e., there exist $h, k\in \mathcal{P}$ such that $\widehat{\mathcal{W}}(h\ast k) < \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}.$ Then, $\widehat{\mathcal{W}}(h\ast k) < \widehat{\eta} \leq \inf\{\widehat{\mathcal{W}}(h),$ $\widehat{\mathcal{W}}(k), \widehat{0.5}\}$ for some $\widehat{\eta}\in (0, 1]^m.$ Thus, $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ and $y_{\widehat{\eta}} \in \widehat{\mathcal{W}},$ but $(h\ast k)_{\widehat{\eta}} \overline{\in \vee q} \widehat{\mathcal{W}},$ a contradiction. Thus, $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}$ for all $h, k \in \mathcal{P}.$

(H) $\Rightarrow$ (J). Let $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}, k_{\widehat{\zeta}} \in \widehat{\mathcal{W}}.$ Then, $\widehat{\mathcal{W}}(h)\geq \widehat{\eta}$ and $\widehat{\mathcal{W}}(k)\geq \widehat{\zeta}.$ If $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}}\in \widehat{\mathcal{W}},$ then (J) holds. If $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}}\overline{\in} \widehat{\mathcal{W}},$ then $\widehat{\mathcal{W}}(h\ast k) < \inf\{\widehat{\eta}, \widehat{\zeta}\}$. Since

It implies that $\widehat{\mathcal{W}}(h\ast k) \geq \widehat{0.5}$ and $\inf\{\widehat{\eta}, \widehat{\zeta}\} > \widehat{0.5}.$ Hence, $\widehat{\mathcal{W}}(h\ast k)+ \inf\{\widehat{\eta}, \widehat{\zeta}\} > \widehat{0.5}+\widehat{0.5} = \widehat{1},$ implies $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} q \widehat{\mathcal{W}}.$ Thus, $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}}\in \vee q \widehat{\mathcal{W}}.$

Corollary 3.6. An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ if it satisfies the condition (H).

Theorem 3.7. An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ if and only if $\widehat{\mathcal{W}}_{\widehat{\eta}} = \{h\in \mathcal{P}\mid \widehat{\mathcal{W}}(h) \geq \widehat{\eta}\}$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0, 0.5]^m.$

Proof. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ and let $h, k\in \widehat{\mathcal{W}}_{\widehat{\eta}}$ for $\widehat{\eta}\in (0, 0.5]^m.$ Then,

Thus, we have

that is, $\widehat{\mathcal{W}}(h\ast k)\geq \widehat{\eta},$ which implies, $h\ast k\in \widehat{\mathcal{W}}_{\widehat{\eta}}.$ Hence, $\widehat{\mathcal{W}}_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}.$

Conversely, assume that $\widehat{\mathcal{W}}_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0, 0.5]^m.$ Suppose $h, k\in \mathcal{P}$ such that

Select $\widehat{\psi}\in (0, 0.5]^m$ such that

Then, $x_{\widehat{\psi}}\in \widehat{\mathcal{W}},$ $y_{\widehat{\psi}}\in \widehat{\mathcal{W}},$ but $(h\ast k)_{\widehat{\psi}}\overline{\in \vee q} \widehat{\mathcal{W}}.$ Which is a contradiction. Thus, $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}$ for all $h, k\in \mathcal{P}.$ Hence, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

In the following theorem, we give conditions for an $m$-$\mathscr{PF}$ set to be an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra.

Theorem 3.8. Let $C$ be a subalgebra of $\mathcal{P}$ and let $\widehat{\mathcal{W}}$ be an $m$-$\mathscr{PF}$ subset of $\mathcal{P}$ such that

(1) $\widehat{\mathcal{W}}(h) \geq \widehat{0.5},$ for all $h\in C.$

(2) $\widehat{\mathcal{W}}(h) = \widehat{0},$ for all $h\notin C,$

Then, $\widehat{\mathcal{W}}$ is an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Assume $C$ is a subalgebra of $\mathcal{P},$ $h, k\in \mathcal{P}$ and $\widehat{\eta}, \widehat{\zeta}\in (0, 1]^m.$ If $h_{\widehat{\eta}} q \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}} q \widehat{\mathcal{W}},$ then $\widehat{\mathcal{W}}(h)+\widehat{\eta} > \widehat{1}$ and $\widehat{\mathcal{W}}(k)+\widehat{\zeta} > \widehat{1}.$ Thus, $h, k\in C$ and so $h\ast k\in C$ because if not, then $h\notin C$ or $k\notin C.$ Thus, $\widehat{\mathcal{W}}(h) = \widehat{0}$ or $\widehat{\mathcal{W}}(k) = \widehat{0},$ and so $\widehat{\eta} > \widehat{1}$ or $\widehat{\zeta} > \widehat{1}.$ This is a contradiction. If $\inf\{\widehat{\eta}, \widehat{\zeta}\}\leq \widehat{0.5},$ then

Hence, $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}}\in \widehat{\mathcal{W}}.$ If $\inf\{\widehat{\eta}, \widehat{\zeta}\} > \widehat{0.5},$ then

and so $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} q \widehat{\mathcal{W}}.$ Thus, $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} \in \vee q \widehat{\mathcal{W}}.$ Hence, $\widehat{\mathcal{W}}$ is an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Corollary 3.9. Let $\phi \neq C\subseteq X$ and $\widehat{\chi}_{C}$ be the m-polar characteristic function of $C.$ Then, $C$ is a subalgebra of $\mathcal{P}$ if and only if $\widehat{\chi}_{C}$ is an $m$-polar $(\alpha, \in \vee q)$-fuzzy subalgebra of $\mathcal{P},$ where $\alpha \in\{\in, q\}.$

We consider a relation between an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra and an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra.

Theorem 3.10. Every $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$ Let $h, k\in \mathcal{P}$ be such that $h_{\widehat{\eta}}, k_{\widehat{\zeta}} \in \widehat{\mathcal{W}}$ for $\widehat{\eta}, \widehat{\zeta}\in (0, 1]^m.$ Then,

Suppose that $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} \overline{\in \vee q} \widehat{\mathcal{W}}.$ Then,

and

From Eqs (3.1) and (3.2), we get

Combining Eqs (3.1) and (3.3), we have

Thus,

Choose $\widehat{\psi}\in (0, 1]^m$ such that $\widehat{1}- \widehat{\mathcal{W}}(h\ast k)\geq \widehat{\psi} > \sup\{1-\widehat{\mathcal{W}}(h), 1-\widehat{\mathcal{W}}(k), \widehat{0.5}\}.$ It follows that $\widehat{\mathcal{W}}(h)+ \widehat{\psi} > \widehat{1}, \widehat{\mathcal{W}}(k)+ \widehat{\psi} > \widehat{1},$ and $\widehat{\mathcal{W}}(h\ast k)+ \widehat{\psi}\leq \widehat{1}.$ Thus, $x_{\widehat{\psi}} q \widehat{\mathcal{W}},$ $y_{\widehat{\psi}} q \widehat{\mathcal{W}},$ but $(h\ast k)_{\widehat{\psi}} \overline{\in \vee q} \widehat{\mathcal{W}},$ a contradiction. Hence, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Remark 3.11. The converse of Theorem 3.10 is not true in general. For example, a 3-polar $(\in, \in \vee q)$-fuzzy subalgebra $\widehat{\mathcal{W}}$ of $\mathcal{P}$ in Example 3.1 is not a 3-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P},$ since

but

The following corollary follows from Theorem 3.8 and Theorem 3.10.

Corollary 3.12. For a subalgebra $C$ of $\mathcal{P}$, let $\widehat{\mathcal{W}}$ be an $m$-$\mathscr{PF}$ subset of $\mathcal{P}$ satisfying conditions (1), and (2) of Theorem 3.8. Then, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

We give a condition for an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ to be an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$.

Theorem 3.13. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ and any $m$-$\mathscr{PF}$ point has the value $\widehat{\eta} \in (0, 0.5]^m.$ Then, $\widehat{\mathcal{W}}$ is an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$ For $h, k\in \mathcal{P},$ let $\widehat{\eta}, \widehat{\zeta}\in (0, 0.5]^m$ be such that $h_{\widehat{\eta}} q \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}} q \widehat{\mathcal{W}}.$ Then, $\widehat{\mathcal{W}}(h) > \widehat{1}-\widehat{\eta}\geq \widehat{\eta}$ and $\widehat{\mathcal{W}}(k) > \widehat{1}-\widehat{\zeta}\geq \widehat{\zeta},$ i.e., $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}} \in \widehat{\mathcal{W}}.$ Since $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P},$ it implies that $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} \in \vee q \widehat{\mathcal{W}}.$ Consequently, $\widehat{\mathcal{W}}$ is an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Theorem 3.14. Both $m$-polar $(\in, \in)$-fuzzy subalgebra and $m$-polar $(\in \vee q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ are an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Obviously, an $m$-polar $(\in, \in)$-fuzzy subalgebra of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$ Now, let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in \vee q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$ For any $h, k\in \mathcal{P},$ let $\widehat{\eta}, \widehat{\zeta}\in (0, 1]^m$ be such that $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}} \in \widehat{\mathcal{W}}.$ Then, $h_{\widehat{\eta}} \in \vee q \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}} \in \vee q \widehat{\mathcal{W}},$ it follows that $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}} \in \vee q \widehat{\mathcal{W}}.$ Thus, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Remark 3.15. The converse of Theorem 3.14 is not true in general. For example, a 3-polar $(\in, \in \vee q)$-fuzzy subalgebra $\widehat{\mathcal{W}}$ of $\mathcal{P}$ in Example 3.1 is not a 3-polar $(\in \vee q, \in \vee q)$-fuzzy subalgebra of $\mathcal{P},$ since

but

Also, it is not a 3-polar $(\in, \in)$-fuzzy subalgebra of $\mathcal{P},$ since

but

We give a condition for an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra to be an $m$-polar $(\in, \in)$-fuzzy subalgebra.

Theorem 3.16. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ such that $\widehat{\mathcal{W}}(h) < \widehat{0.5}$ for all $h\in \mathcal{P}.$ Then, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Let $h_{\widehat{\eta}}\in \widehat{\mathcal{W}}$ and $k_{\widehat{\zeta}}\in \widehat{\mathcal{W}}$ for $h, k\in \mathcal{P}$ and $\widehat{\eta}, \widehat{\zeta}\in (0, 1]^m.$ Then, $\widehat{\mathcal{W}}(h)\geq\widehat{\eta}$ and $\widehat{\mathcal{W}}(k)\geq\widehat{\zeta}.$ Since $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in\vee q)$-fuzzy subalgebra of $\mathcal{P},$ by using condition (H) in Theorem 3.5, we conclude that $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}.$ Since $\widehat{\mathcal{W}}(h) < \widehat{0.5}$ for all $h\in \mathcal{P},$ then $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k)\geq \inf\{\widehat{\eta}, \widehat{\zeta}\}.$ Therefore, $(h\ast k)_{\inf\{\widehat{\eta}, \widehat{\zeta}\}}\in \widehat{\mathcal{W}}.$ Hence, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in)$-fuzzy subalgebra of $\mathcal{P}.$

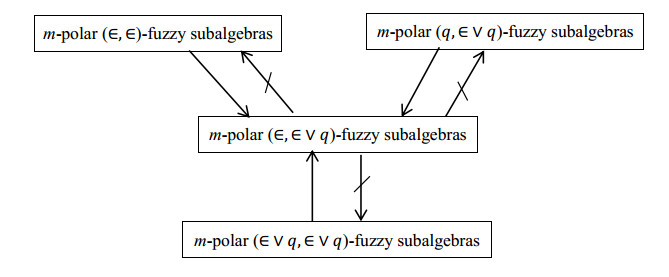
In the following figure, we summarize and display the relations between some types of $m$-polar $(\alpha, \beta)$-fuzzy subalgebras in where $\alpha, \beta\in\{\in, q, \in \vee q\},$ $\beta \notin q.$

Theorem 3.17. Let $\{\widehat{\mathcal{W}_j}\}_{j\in I}$ be a family of $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}.$ Then, the intersection, denoted by $\cap_{j\in I}\widehat{\mathcal{W}}_j,$ of $\{\widehat{\mathcal{W}_j}\}_{j\in I}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Proof. Let $\{\widehat{\mathcal{W}_j}\}_{j\in I}$ be a family of $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ and $h, k\in \mathcal{P}.$ Then, $\widehat{\mathcal{W}}_j(h\ast k) \geq \inf\{\widehat{\mathcal{W}}_j(h), \widehat{\mathcal{W}}_j(k), \widehat{0.5}\} \forall j\in I.$ Thus,

Therefore, $\big(\cap_{j\in I}\widehat{\mathcal{W}}_j\big)(h\ast k)\geq \inf\{\big(\cap_{j\in I}\widehat{\mathcal{W}}_j\big)(h),$ $\big(\cap_{j\in I}\widehat{\mathcal{W}}_j\big)(k), \widehat{0.5}\}.$ Hence, $\cap_{j\in I}\widehat{\mathcal{W}}_j$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

The following example shows that the union of two $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}$ may not be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}.$

Example 3.2. Let $\mathcal{P} = \{0, k, l, n\}$ be a $BCI$-algebra with the operation $\ast$ which is given in Example 3.1, and let $\widehat{\mathcal{W}}: \mathcal{P}\rightarrow [0, 1]^m$ be an $m$-$\mathscr{PF}$ set defined by:

Then,

Since $\mathcal{P}$ and $\{0, k\}$ are subalgebras of $\mathcal{P}$, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}$ by Theorem 3.7. Let $\widehat{\mathcal{F}}: \mathcal{P}\rightarrow [0, 1]^m$ be an $m$-$\mathscr{PF}$ set defined by:

Then,

Since $\mathcal{P}$ and $\{0, l\}$ are subalgebras of $\mathcal{P}$, $\widehat{\mathcal{F}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}$ by Theorem 3.7. The union $\widehat{\mathcal{W}}\cup \widehat{\mathcal{F}}$ of $\widehat{\mathcal{W}}$ and $\widehat{\mathcal{F}}$ is given by:

Hence,

Since $\{0, k, l\}$ is not a subalgebra of $\mathcal{P}$, it follows from Theorem 3.7 that $\widehat{\mathcal{W}}\cup \widehat{\mathcal{F}}$ is not an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$.

For any $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ and $\widehat{\eta}\in (0, 1]^m,$ we denote

and

The sets $\langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}$ and $[\widehat{\mathcal{W}}]_{\widehat{\eta}}$ are called $q$-level cut subset and $\in \vee q$-level cut subset of $\widehat{\mathcal{W}},$ respectively.

It is clear that

In the following two theorems, we discuss the relation between crisp subalgebras and $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras of $\mathcal{P}$ through level cut subsets.

Theorem 3.18. An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ if and only if $\langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}\neq \phi$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0.5, 1]^m.$

Proof. Assume $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$ Let $h, k\in \langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}.$ Then,

This implies that

By hypothesis

Thus, $\widehat{\mathcal{W}}(h\ast k) + \widehat{\eta} > \widehat{1},$ implies $(h\ast k)_{\widehat{\eta}} q \widehat{\mathcal{W}},$ i.e., $h\ast k\in \langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}.$ Therefore, $\langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}.$

Conversely, suppose $\langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0.5, 1]^m.$ Let $h, k\in \mathcal{P}$ such that

Then,

This implies

Select some $\widehat{\eta}\in (0.5, 1]^m$ such that

Then, $\widehat{\mathcal{W}}(h)+\widehat{\eta} > \widehat{1},$ $\widehat{\mathcal{W}}(k)+ \widehat{\eta} > \widehat{1}$ and $\widehat{\mathcal{W}}(h\ast k)+ \widehat{\eta} < \widehat{1}.$ Thus, $h_{\widehat{\eta}} q \widehat{\mathcal{W}},$ $y_{\widehat{\eta}} q \widehat{\mathcal{W}},$ but $(h\ast k)_{\widehat{\eta}} \overline{q} \widehat{\mathcal{W}},$ i.e., $h, k\in \langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}},$ but $h\ast k \notin \langle\widehat{\mathcal{W}}\rangle_{\widehat{\eta}},$ a contradiction. Thus, $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}$ for all $h, k\in \mathcal{P}.$ This shows that $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

Theorem 3.19. An $m$-$\mathscr{PF}$ set $\widehat{\mathcal{W}}$ of $\mathcal{P}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ if and only if $[\widehat{\mathcal{W}}]_{\widehat{\eta}}\neq \phi$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0, 1]^m.$

Proof. Let $\widehat{\mathcal{W}}$ be an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}$ and $\widehat{\eta}\in (0, 1]^m.$ Let $h, k\in [\widehat{\mathcal{W}}]_{\widehat{\eta}},$ so we have

that is

and

Case (1). If $\widehat{\eta}\in (0, 0.5]^m,$ then $\widehat{1}-\widehat{\eta} \geq \widehat{0.5} \geq \widehat{\eta}.$ It implies from (3.4) and (3.5) that

By hypothesis

Hence, $(h\ast k)_{\widehat{\eta}} \in \widehat{\mathcal{W}}.$

Case (2). If $\widehat{\eta}\in (0.5, 1]^m,$ then $\widehat{1}-\widehat{\eta} < \widehat{0.5} < \widehat{\eta}.$ It implies from (3.4) and (3.5) that

By hypothesis

Hence, $(h\ast k)_{\widehat{\eta}} q \widehat{\mathcal{W}}.$ Thus, $(h\ast k)_{\widehat{\eta}} \vee q \widehat{\mathcal{W}},$ i.e., $(h\ast k) \in [\widehat{\mathcal{W}}]_{\widehat{\eta}}.$ Therefore, $[\widehat{\mathcal{W}}]_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}.$

Conversely, Suppose that $[\widehat{\mathcal{W}}]_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P}$ for all $\widehat{\eta}\in (0, 1]^m.$ Assume $h, k\in \mathcal{P}$ such that

Select $\widehat{\eta}\in (0, 1]^m$ such that

Then, $h_{\widehat{\eta}} \in \widehat{\mathcal{W}}, k_{\widehat{\eta}} \in \widehat{\mathcal{W}},$ but $(h\ast k)_{\widehat{\eta}} \overline{\in \vee q} \widehat{\mathcal{W}}.$ Since $[\widehat{\mathcal{W}}]_{\widehat{\eta}}$ is a subalgebra of $\mathcal{P},$ we have $h\ast k\in [\widehat{\mathcal{W}}]_{\widehat{\eta}},$ a contradiction. Hence, $\widehat{\mathcal{W}}(h\ast k) \geq \inf\{\widehat{\mathcal{W}}(h), \widehat{\mathcal{W}}(k), \widehat{0.5}\}$ for all $h, k\in \mathcal{P}.$ Thus, $\widehat{\mathcal{W}}$ is an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra of $\mathcal{P}.$

4.   Conclusions

The objective of this article is to establish a new concept of $m$-$\mathscr{PF}$ subalgebras in $BCK/BCI$-algebras $\mathcal{P}$, called $m$-polar $(\alpha, \beta)$-fuzzy subalgebras, by using the notions of $m$-$\mathscr{PF}$ sets and $m$-$\mathscr{PF}$ points. As a special case of $m$-polar $(\alpha, \beta)$-fuzzy subalgebras, we have presented the idea of $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras, and investigated several related properties. Then, we have provided conditions for an $m$-$\mathscr{PF}$ set to be an $m$-polar $(q, \in \vee q)$-fuzzy subalgebra and an $m$-polar $(\in, \in \vee q)$-fuzzy subalgebra. Finally, we have discussed the relationship between crisp subalgebras and $m$-polar $(\in, \in \vee q)$-fuzzy subalgebras in $\mathcal{P}$ through level cut subsets. In our further research, we will focus on adopting this approach to some more algebraic structures, such as $KU$-algebras, $UP$-algebras, semigroups, $KU$-semigroups and Hemirings, and to some more complicated applications from the domains of information systems and computer sciences.

Acknowledgments

The authors are thankful to the editors and the anonymous reviewers for their valuable suggestions and comments on the manuscript.

Conflict of interest

The authors declare no conflict of interest.