Investigation of novel turbulator with and without twisted configuration under turbulent forced convection of a CuO/water nanofluid flow inside a parabolic trough solar collector

1.   Introduction

The introduction of fractional derivatives has significantly expanded the theoretical framework of calculus, enabling the resolution of a broader spectrum of mathematical and applied problems in fields such as physics ^[1], chemical kinetics systems ^[2], and control theory ^[3]. Fractional derivatives play a crucial role in multiple aspects of wave equations. In real-world physical environments, many media exhibit non-uniform properties. The fractional derivative wave equation accounts for these long-term correlations, providing a more precise description of wave behavior and uncovering patterns that traditional integer-order wave equations cannot capture. Therefore, it is of great significance to study the fractional wave equation. With the development of differential equation theory until now, the definition of fractional derivatives is varied. The well-known fractional derivatives include the Caputo derivative ^[4,5], Caputo-Fabrizio derivative ^[6], Riemann-Liouville derivative ^[7], Grünwald-Letnikov derivative ^[8], Atangana-Baleanu derivative ^[9], and conformable derivative ^[10], etc. To date, there have been a large number of methods to analyze and solve fractional nonlinear partial differential equations, such as the F-expansion method ^[11], generalized finite difference method ^[12], $\exp$($\phi(\xi)$)-expansion and the MAE methods ^[13], extended $(G'/G)$-expansion method ^[14], extended trial equation and modified auxiliary equation method ^[15], the dynamics approach ^[16], modified generalized Riccati equation mapping method ^[17], and Hirota method ^[18].

The Kadomtsev-Petviashvili (KP) equation ^[19] was initially introduced by Kadomtsev and Petviashvili in 1970. The equation describes the nonlinear wave phenomena, and can be regarded as a two-dimensional generalization of the Korteweg-de Vries (KdV) equation. The KdV-Sawada-Kotera-Ramani (KdV-SK-R) equation ^[20], which is a linear combination of the KdV equation and the Sawada-Kotera equation ^[21,22], can reduce to either the KdV or the Sawada-Kotera equation by eliminating specific terms. In 2022, Guo ^[23] incorporated a second-order derivative term into the KdV-Sawada-Kotera-Ramani equation, and thereby formulated a new nonlinear partial differential equation known as the (2+1)-dimensional Kadomtsev-Petviashvili-Sawada-Kotera-Ramani (KP-SK-R) equation. This development enables the previous equation to facilitate the description of more complex wave behaviors. Shortly thereafter, Wazwaz et al. ^[24] extended the (2+1)-dimensional KP-SK-R equation to its (3+1)-dimensional counterpart by introducing additional second-order derivative terms. Recently, Şenol et al. ^[25] extended the (3+1)-dimensional KP-SK-R equation by introducing the conformable fractional derivative.

Regarding the KP-SK-R equation, a significant amount of research has been devoted to its analysis. Gu et al. ^[26] derived soliton, breather, and lump solutions for the (2+1)-dimensional KP-SK-R equation using Hirota's bilinear form and the Duffing chaotic system. Althobaiti et al. ^[27] investigated the Lax-integrable three-dimensional sixth-order KP-SK-R equation via the Kudryashov method, further extending this equation to an $n$-dimensional framework further. Ma et al. ^[28] obtained hybrid solutions for the (3+1)-dimensional KP-SK-R equation through the Hirota bilinear method. Qasim et al. ^[29] derived exact solutions for the (3+1)-dimensional KP-SK-R equation using the Jacobi elliptic function expansion technique. Şenol et al. ^[25] formulated the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative by applying the exp$(-\phi(\xi))$-expansion and Kudryashov R function methods.

In an effort to further explore the properties of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative, this paper will continue to study the equation. The polynomial complete discrimination system method is capable of converting non-linear partial differential equations into polynomial equations. Subsequently, it solves these polynomial equations by leveraging the operational rules and discriminant system of polynomials. The solution process features a clear orientation and well-defined steps, rendering it highly amenable to calculation and implementation. Upon examination, it is evident that the (3+1)-dimensional KP-SK-R equation can be transformed into polynomial form via appropriate variable substitution and traveling wave transformation. Therefore, we propose to explore some new traveling wave solutions using the polynomial trial method in conjunction with the polynomial complete discrimination system method ^[30,31]. Moreover, by introducing external perturbations, we aim to observe the chaotic dynamic behavior inherent in this equation by leveraging the theory of plane dynamic systems ^[32].

The following work is divided into four parts: Section 2 gives the mathematical analysis for the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative. Section 3 analyzes chaotic behavior of the equation qualitatively. Section 4 gives some new exact solutions, and part of their graphs using trial method and polynomial complete discrimination system. Section 5 summarizes the whole work.

2.   Mathematical analysis

Definition 1 (^[10]). The $\alpha-$order conformable derivative of the function $f:[0, +\infty)\rightarrow R$ is defined as

If $f$ is $\alpha$-differentiable for an interval $(0, a), a > 0$, and $\lim\limits_{t\rightarrow 0^+}D_t^{\alpha}(f)(t)$ exists, then $D_t^{\alpha}(f)(0) = \lim\limits_{t\rightarrow 0^+}D_t^{\alpha}(f)(t).$

It has be verified that the fractional-order definition (1) satisfies the following properties:

Property 1. ^[10]

● $D_t^{\alpha}(t^k) = kt^{k-\alpha}$;

● $D_t^{\alpha}(af_1+bf_2) = aD_t^{\alpha}(f_1)+bD_t^{\alpha}(f_2)$;

● $D_t^{\alpha}(\frac{f_1}{f_2}) = \frac{f_2D_t^{\alpha}(f_1)-f_1D_t^{\alpha}(f_2)}{f_2^2}$;

● $D_t^{\alpha}(f_1f_2) = f_2D_t^{\alpha}(f_1)+f_1D_t^{\alpha}(f_2)$;

● $D_t^{\alpha}(f) = (t^{1-\alpha})\frac{df(t)}{dt}$

● If $f$ is a constant, then $D_t^{\alpha}(f)\equiv 0$.

Definition (^[33]). For a function $f$ with $n$ variables $z_i, i = 1, \cdots, n,$ the $\alpha$-order conformable derivative of $f$ respect to $z_i$ is defined as

According to Definitions 1 and 2, the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative ^[25] researched in this work is given as follows:

where $x, y, z, t$ are the wave variables, $t > 0$, $\kappa, \mu_1, \mu_2, \delta_1$, $\delta_2$, and $\delta_3$ are arbitrary constants, and $D_t^\alpha(\Phi_x)$ represents the $\alpha$-order derivative of $\Phi_x$.

Given the transformation

where $v$ represents the wave velocity, $a, b,$ and $c$ represent the wave width in the $x, y$, and $z$ directions respectively. Therefore, due to Property 1, we have

Subsequently, Eq (2.5) is substituted into Eq (2.3), leading to the ordinary differential form

where $\rho = av+\mu_1b^2+\mu_2c^2+\delta_1ab+\delta_2bc+\delta_3ac$. If Eq (2.6) is integrated twice with respect to $\zeta$ and the integration constant is assumed as zero, then we have

By using the polynomial trial method, we take the general trial equation

where $s_{j}, j = 1, \ldots, N,$ are coefficients to be determined. On the basis of the homogeneous balance principle, it results that $N = 2$. That is to say, $\phi$ fulfills the trial equation

Integrating Eq (2.9) with respect to $\zeta$, we have

where $d_0$ is the integral constant. From Eqs (2.9) and (2.10), we have

New algebraic equations about $\phi$ can be obtained by substituting both Eqs (2.9) and (2.11) into Eq (2.7) below:

where $r_3 = \frac{10}{3}a^6s_2^2+15a^4s_2+15a^2$, $r_2 = 5a^6s_1s_2+\kappa a^4s_2+15a^4s_1+3\kappa a^2$, $r_1 = 6a^6s_2s_0+a^6s_1^2+\kappa a^4s_1+15a^4s_0+\rho$, and $r_0 = a^6s_1s_0+2a^6s_2d_0+\kappa a^4s_0.$ The value of $d_0, s_j, j = 1, 2, 3,$ can be calculated by solving the equations $r_i = 0, i = 1, 2, 3,$ which are given as

or

It can be seen that $s_2$ is always negative.

3.   Dynamics of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative

In order to investigate the dynamics of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative, we analyze Eq (2.9) by employing the theory of plane dynamic systems ^[32].

3.1.   Chaotic behavior and sensitivity analysis

When an autonomous system is subjected to external periodic perturbations, its inherent nonlinear characteristics are activated, leading to a more complex phase space structure and heightened sensitivity to initial conditions. External periodic disturbances are typically modeled using nonlinear periodic functions. Introducing such an excitation function effectively adds an additional degree of freedom to the system, thereby increasing the dimensionality of the phase space. This results in a greater diversity and complexity of possible states and trajectories.

Let $h(\zeta) = Q_0\sin(\omega\zeta)$ be a periodic external disturbance, where $Q_0$ and $\omega$ stands for the amplitude and frequency respectively. When the periodic external disturbance is added to Eq (2.9), this equation is turned into the following form:

Denote $g = \phi'$ and $z = \omega\zeta$. Then, Eq (3.1) can be transformed into the three-dimensional dynamical system

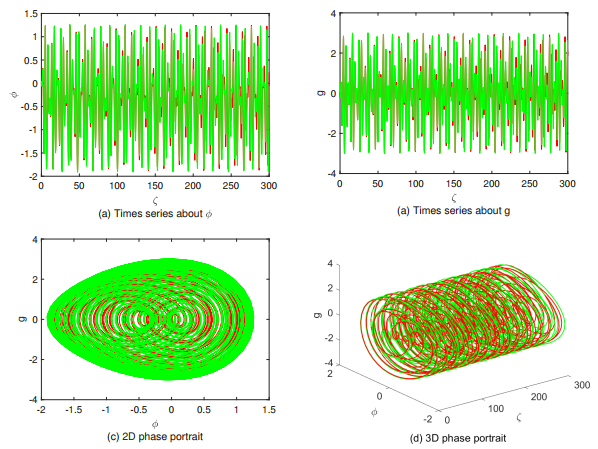
By taking the appropriate parameters, some two- and three-dimensional phase portraits of the periodically excited system (3.2) are shown to explain its chaotic behavior. Further, the sensitivity analysis is carried out simultaneously. Several sets of initial values are taken to observe the response of Eq (3.2), see Figure 1.

3.2.   Bifurcation diagram

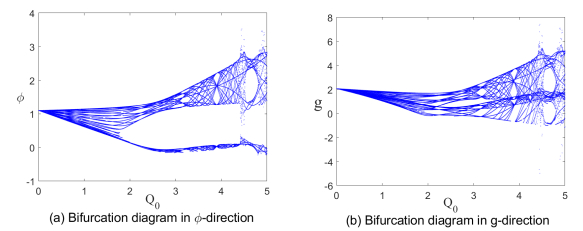
A bifurcation diagram provides a clear visualization of the critical points at which a system abruptly transitions from one state to another as parameters vary. Consequently, it delineates the stable and unstable regions of system parameters, facilitating the observation of various dynamic phenomena and underlying principles. Let $s_2 = -14, s_1 = 10, s_0 = 5$, $\omega = 2$ and the values range of $Q_0$ be from 0 to 5. With the aid of MATLAB software, the bifurcation diagrams in different two directions are given in Figure 2.

3.3.   Lyapunov exponent

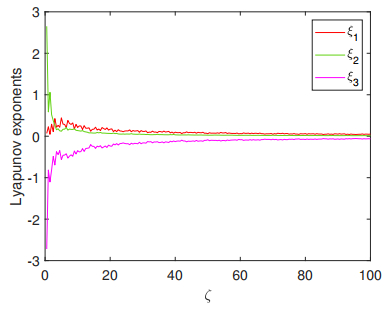
The Lyapunov exponent quantitatively measures the rate of divergence or convergence of two nearby trajectories in phase space over time. In multidimensional systems, different methods may yield distinct Lyapunov exponents. Positive and negative Lyapunov exponents respectively signify the directions of unstable and stable orbits. The presence of any positive Lyapunov exponent indicates chaotic behavior within the system. In this subsection, the Lyapunov exponents of Eq (3.2) with a set of fixed parameters are calculated by using Wolf algorithm, and its Kaplan-Yorke dimension $D_{KY}$ is obtained. After that, the graph of parameter-dependent Lyapunov exponents are provided when $Q_0$ runs the range of $[0, 5]$.

Let $s_2 = -5, s_1 = -15, s_0 = 1$, $\omega = 0.9$, and $Q_0 = 2$. From Figure 3, it can be seen that the Lyapunov exponents $\xi_1, \xi_2$, and $\xi_3$ converges to 0.032, 0.019, and $-0.05$, respectively.

Theorem 1. Under the conditions of $s_2 = -5, s_1 = -15, s_0 = 1$, $\omega = 0.9$, and $Q_0 = 2$, the Kaplan-Yorke dimension $D_{KY}$ of Eq (3.2) is bigger than 2.

Proof. The Kaplan-Yorke dimension $D_{KY}$ of Eq (3.2) is computed as follows:

Therefore, it can be known from Eq (3.3) that the conclusion holds.

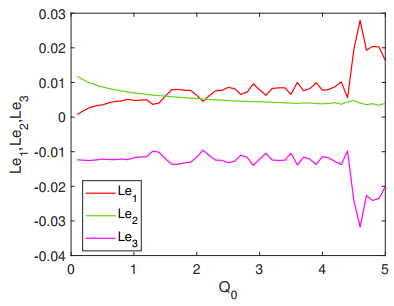
From the above, we can see that both the maximum Lyapunov exponent $\xi_1 > 0$ and the Kaplan-Yorke dimension $D_{KY} > 2$ verify the chaotic state of Eq (3.2). In Figure 4, it can be seen that as $Q_0$ increases in $[0, 5]$, the Lyapunov exponents $Le_1, Le_2$, and $Le_3$ present different degrees of chaos, and the maximum Lyapunov exponent $Le_1$ is almost always greater than 0.

4.   Traveling wave solutions of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative

In this section, we solve the function $\Phi$ for Eq (2.3) by using the third-order polynomial complete discrimination system method ^[31].

4.1.   Solving procedure

When applying the substitutions

Eq (2.10) takes the new form

The integral form of Eq (4.2) is

where $\zeta_{0}$ is the integration constant.

Let $F(u) = u^3+q_2u^2+q_1u+q_0$. The complete discrimination system of $F(u)$ is given as follows:

In the application of the polynomial discriminant system method, the signs of $\Delta$ and $H$ can reveal certain characteristics of the roots of the equation. In a cubic equation, when $\Delta = 0$, the equation has multiple roots. Specifically, when $\Delta = 0$ and $H < 0$, the cubic equation has one real root and a double root. When $\Delta = 0$ and $H = 0$, the equation has three equal real roots. When $\Delta > 0$ and $H < 0$, the equation has three distinct real roots. When $\Delta < 0$, the equation has no real roots. Therefore, the solution of the integral equation (4.3) will be discussed in four cases.

Theorem 2. Let $\alpha_1 = -\frac{q_2q_1-9q_0}{2(q_2^2-3q_1)}$ and $\alpha_2 = -q_2+\frac{q_2q_1-9q_0}{q_2^2-3q_1}$. If $\Delta = 0$ and $H < 0$, then the following two conclusions hold:

(i) When $\alpha_1 > \alpha_2$, Eq (2.3) has solutions involving a hyperbolic tangent and a hyperbolic cotangent as follows:

where $\alpha\in(0, 1)$, $a, b, c, v$ are arbitrary real numbers, $s_2, s_1, s_0, d_0$ are taken as the formulas (2.13) or (2.14), $q_2, q_1, q_0$ are taken as formulas (4.1) and satisfy that $\alpha_1 > \alpha_2$.

(ii) When $\alpha_1 < \alpha_2$, Eq (2.3) has a tangent solution

where the restrictions of $\alpha, a, b, c, v, s_2, s_1, s_0, d_0$ are the same as those of the solution $\Phi_1(x, y, z, t)$, while $q_2, q_1, q_0$ are taken as formulas (4.1) and satisfy that $\alpha_1 < \alpha_2$.

Proof. Suppose that $\Delta = 0$, and $H < 0$. Thereby, we have $F(\psi) = (\psi-\alpha_1)^2(\psi-\alpha_2).$ According to the cubic derivation formula, there are $\alpha_1 = -\frac{q_2q_1-9q_0}{2(q_2^2-3q_1)}$ and $\alpha_2 = -q_2+\frac{q_2q_1-9q_0}{q_2^2-3q_1}$. If $\alpha_1 > \alpha_2$, then Eq (4.3) has two solutions by utilizing the third-order polynomial complete discrimination system method as follows:

and

If $\alpha_1 < \alpha_2$, then Eq (4.3) has a solution by utilizing the third-order polynomial complete discrimination system method in the following:

Replacing $u, \zeta, \alpha_1$, and $\alpha_2$ in the above three equations by their specific expressions, the solutions of Eq (2.3) are obtained as the forms (4.5)–(4.7), respectively.

Theorem 3. If $\Delta = 0$ and $H = 0$, then Eq (2.3) yields a rational solution given by

where the restrictions of $\alpha, a, b, c, v, s_2, s_1, s_0, d_0$ are the same as those of the solution $\Phi_1(x, y, z, t)$, while $q_2, q_1$, and $q_0$ are taken as formulas (4.1) and satisfy that $\alpha_1 = -\frac{q_2}{3}$.

Proof. Suppose that $\Delta = 0$ and $H = 0$. Therefore, $F(\psi) = 0$ has three same real roots, i.e., $F(u) = (u-\alpha_1)^3$. Because of the cubic derivation formula, there is $\alpha_1 = -\frac{q_2}{3}$. By using the third-order polynomial complete discrimination system method, Eq (4.3) has a solution as follows:

Substituting $u, \zeta$, and $\alpha_1$ into the above equation with their specific expressions, the solution of Eq (2.3) is obtained as the form (4.8).

Theorem 4. Let

where $\theta = \arccos\frac{2q_2^3-9q_2q_1+27q_0}{2A^\frac{3}{2}}$and $A = -3H = q_2^2-3q_1$. If $\Delta > 0$ and $H < 0$, then the following two conclusions hold:

(i) When $\alpha_1 < u = (\frac{2}{3}s_2)^{\frac{1}{3}}\Phi < \alpha_3$, Eq (2.3) possesses a Jacobian elliptic solution of the form

where $\text{sn}$ is the Jacobian elliptic sine function, $m^2 = \frac{\sqrt{3A}\cos\frac{\theta}{3} -A\sin\frac{\theta}{3}}{\sqrt{3A}\cos\frac{\theta}{3} +A\sin\frac{\theta}{3}}$, and the restrictions of $\alpha, a, b, c, v, s_2, s_1, s_0, d_0$ are the same as those of the solution $\Phi_1(x, y, z, t)$, while $q_2, q_1$, and $q_0$ are taken as formulas (4.1) and satisfy that $\alpha_1 < u < \alpha_3$;

(ii) When $u = (\frac{2}{3}s_2)^{\frac{1}{3}}\Phi > \alpha_3$, Eq (2.3) possesses a Jacobian elliptic solution of the form

where $\text{cn}$ is the Jacobian elliptic consine function, $C_1 = -q_2+\sqrt{A}\cos\frac{\theta}{3}, C_2 = \frac{1}{2}(\frac{2}{3}s_{2})^{\frac{1}{3}}\Big(\sqrt{A}\cos\frac{\theta}{3} +\frac{\sqrt{3}}{3}A\sin\frac{\theta}{3}\Big)^{\frac{1}{2}}$, $m^2 = \frac{\sqrt{3A}\cos\frac{\theta}{3} -A\sin\frac{\theta}{3}}{\sqrt{3A}\cos\frac{\theta}{3} +A\sin\frac{\theta}{3}}$, and the restrictions of $\alpha, a, b, c, v, s_2, s_1, s_0, d_0$ are the same as those of the solution $\Phi_1(x, y, z, t)$, while $q_2, q_1$, and $q_0$ are taken as formulas (4.1) and satisfy that $u > \alpha_3$.

Proof. Suppose that $\Delta > 0$ and $H < 0$. Then, $F(u) = 0$ has three real different roots, that is, $F(u) = (u-\alpha_1)(u-\alpha_2)(u-\alpha_3)$. By the cubic derivation formula, we can obtain the specific form of $\alpha_1, \alpha_2$, and $\alpha_3$ in Eq (4.9). Furthermore, $\alpha_1 < \alpha_2 < \alpha_3$ because of $\theta\in (0, \pi)$. If $\alpha_1 < u = (\frac{2}{3}s_2)^{\frac{1}{3}}\phi < \alpha_3$, with the aid of the third-order polynomial complete discrimination system method, Eq (4.3) has the following solution:

If $u = (\frac{2}{3}s_2)^{\frac{1}{3}}\phi > \alpha_3$, then Eq (4.3) has the following solution:

Substituting the specific expressions of $u, \phi, \zeta, \alpha_1, \alpha_2$, and $\alpha_3$ into the above two equations, two solutions of Eq (2.3) are obtained as the forms (4.10) and (4.11), respectively.

Theorem 5. Let

If $\Delta < 0$ and $u = (\frac{2}{3}s_2)^{\frac{1}{3}}\Phi > \alpha_1$, then Eq (2.3) has a Jacobian elliptic solution as follows:

where $\text{cn}$ is the Jacobian elliptic cosine function, $m^2 = \frac{1}{2}+\frac{3(4q_2+\beta)}{8\big(2q_2^2+q_2\beta+\beta^2\big)}$, and the restrictions of $\alpha, a, b, c, v, s_2, s_1, s_0, d_0$ are the same as those of the solution $\Phi_1(x, y, z, t)$, while $q_2, q_1$, and $q_0$ are taken as formulas (4.1) and satisfy that $u > \alpha_1$.

Proof. Suppose that $\Delta < 0$. Then, $F(u) = 0$ has only one real root, that is, $F(u) = (u-\alpha_1)(u^2+\alpha_2u+\alpha_3)$. By the cubic derivation formula, we have

where $\beta$ is the form in Eq (4.12). If $u = (\frac{2}{3}s_2)^{\frac{1}{3}}\phi > \alpha_1$, then Eq (4.3) has the following solution by making use of the third-order polynomial complete discrimination system method

Substituting the specific forms of the variables $u, \phi, \zeta, \alpha_1, \alpha_1$, and $\alpha_3$ into the above equation and simplifying the expression yields the solution of Eq (2.3) given by (4.13).

4.2.   Graphical description

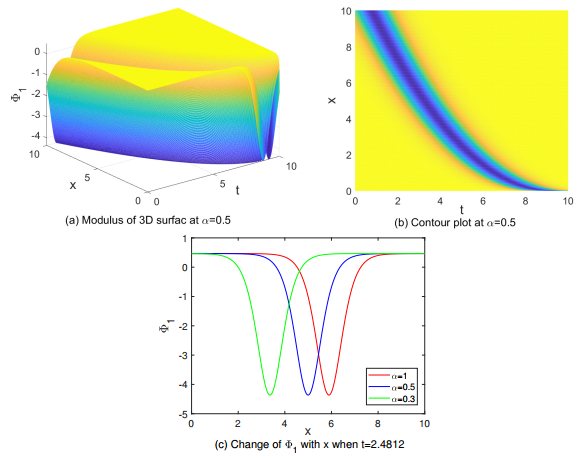
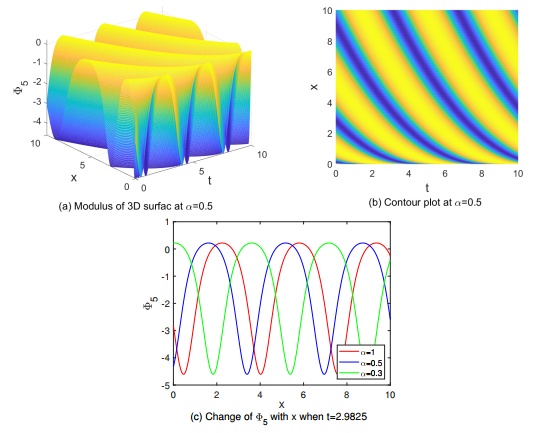
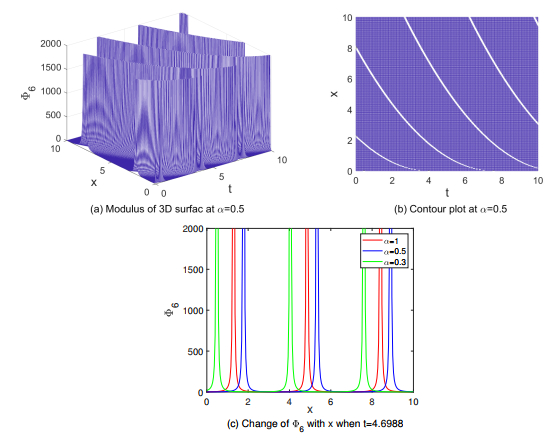
In order to visualize the structure of these traveling wave solutions, the figures of $\Phi_1$, $\Phi_5$, and $\Phi_6$ are shown in Figures 5–7 under some reasonable parameters by the aid of MATLAB software respectively. To compare the effect of fractional derivatives on the solution, different values of $\alpha$ are taken.

Figure 5 shows a dark soliton of the (3+1)-dimensional KP-SK-R equation. The amplitude of the wave is around $-4.3642$ to 0.4650, and the width is approximately 9.8997. Throughout the simulation range, as the value of $\alpha$ increases, the wave crest moves to the right while maintaining the amplitude and width unchanged. Figure 6 presents the elliptic periodic solution of the (3+1)-dimensional KP-SK-R equation. This solution is manifested as a waveform that shows periodic changes in space and time, and its shape is similar to the contour of an ellipse. Within one period, the wave completes a full oscillation along the lower $x$-axis. The period is approximately 3.5338, and the amplitude of the wave varies periodically between $-4.6051$ and 0.2183. Figure 7 shows the lower part of the graph of a quasi-periodic solution of the (3+1)-dimensional KP-SK-R equation. Some of its wave crests are very high, while some are very low, that is, the amplitude differences of the waves are very large. It can be observed from the figure that the period is approximately 3.5743, but the overall shape of the wave does not precisely repeat within fixed time or spatial intervals as the periodic solution does.

5.   Conclusions

The (3+1)-dimensional KP-SK-R equation can describe not only the wave phenomenon propagating in weakly nonlinear and weakly dispersive media, but also the shallow water wave phenomenon. Moreover, it finds application in solid-state physics for characterizing the collective vibrational behavior of atoms within the lattice. This study aims to derive a range of new soliton solutions and traveling wave solutions of the (3+1)-dimensional KP-SK-R equation and to probe its behavior under external perturbations. Therefore, four theorems regarding the solution are given. The newly derived exact solutions enhance the understanding of the model structure of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative. The introduction of external disturbances enables the observation of chaotic behavior within the system, thereby facilitating the exploration of the system's sensitivity and stability characteristics. Two and three-dimensional graphs visually depict the dynamic behavior. Overall, the findings reported herein significantly contribute to the theoretical development of the (3+1)-dimensional KP-SK-R equation with conformable fractional derivative and offer valuable insights into dispersion effects. Additionally, the trial method and polynomial discriminant system utilized in this research hold promise for extension to other fractional wave equations. In future research, building on the work presented in this paper, the stability of the traveling wave solutions of the (3+1)-dimensional KP-SK-R equation can be further investigated, the evolution of solutions under perturbation can be analyzed, and the asymptotic behavior of traveling wave solutions after long-term and long-distance propagation can be explored.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This paper is funded by Opening Fund of Geomathematics Key Laboratory of Sichuan Province (No. scsxdz2025-7).

Conflict of interest

The authors declare there is no conflicts of interest.