1. Introduction
Hydrogen peroxide a simple molecule with molecular formula H2O2, it is of great importance in numerous fields such as pharmaceuticals, mining, textile, environmental and food industry [1,2]. In living organisms, H2O2 is better recognized for its cytotoxic effects; apart from this it is also well known for its role as an signaling molecule in many processes like immune stomata closure, cell activation, apoptosis and root growth [3,4]. H2O2 is also known to be involved in therapeutic processes like wound healing, stem cell proliferation, anti-bacterial defense and neuronal protection [5,6,7,8,9,10]. Various biochemical reactions involving oxidase enzymes (alcohol oxidase, urate oxidase, amino acid oxidase, cholesterol oxidase, glucose oxidase) generate H2O2 as byproduct [11]. The aberrant production of H2O2 within the cell and its compartments may be correlated to severe pathological conditions such as diabetes, ageing, cancer [12,13,14]. The peroxo-oxygen of H2O2 is highly unstable and easily undergoes disproportion reaction hence widely used in home-made small explosions. History has witnessed several incidents where peroxide based small explosives have been used in terror attacks [15,16,17,18,19,20]. These types of explosives are easy to prepare and the raw materials are easily available [21,22,23]. These explosive lack aromatic rings or nitro functional groups to be spectroscopically detect hence easy pass through check points [24]. These types of explosives do not leave any traces behind after the explosion [25,26]. Considering all these, the through study and detection of H2O2 is of mere importance in academic as well as in the industry.
The development of low cost, high-speed, uncomplicated, highly selective and sensitive H2O2 sensors are very essential. So far, lots of researches were carried out in the qualitative determination of H2O2 following many different analytical techniques. Copious numbers of methods have been engaged in the investigation of H2O2 few of them are fluorescence, colorimetry, chemiluminescence, electrochemistry and many more [27,28,29,30,31]. Amongst these, electrochemical technique has engrossed enormous attention for the reason that of its ease in handling, rapid response, easy miniaturization, high sensitivity and selectivity. The sensitivity, stability and selectivity of a chemical sensor relying on electrochemical methods extensively depend on the structure and properties of the material used in the fabrication of sensor over the working electrodes [32]. In electrochemistry, H2O2 can either be oxidized or reduced at regular electrodes but these processes are generally limited by slow kinetics and over potential which relegate the sensing performance of the particular material. The interfering agents (uric acid, ascorbic acid, dopamine, bilrubin) occurring along with the H2O2 in real samples also downgrade the sensing performance. Thus, the current research is more focused on the modification of electrode so that the over potential can be reduced with simultaneous increase in the reaction kinetics.
After the discovery of existence of perfectly 2D crystal by Prof. Andre Geim and Konstatin Novoselov, graphene is one of the most celebrated discoveries presently in the field of material science [33]. The moment noble prize for its discovery was announced it took the centre stage and has been the main focus of research in both basic as well as applied science. Several unique properties of graphene make it a capable contender to be used as a sensor. As graphene being a 2D structure, it is the only allotrope of carbon where all the atoms are exposed from both the sides above and below for the chemical reaction. Graphene has the surface area of 2630 m2·g−1 which is amongst the highest in all the layered materials known till date and has extraordinary electronic properties and electron transport capabilities. The conductance of the graphene is extremely sensitive to the vicinity environment and even a small single molecule absorbed on the surface can alter the electronic characteristics drastically. It is highly conductive even in the low carrier density regimes. At higher carrier concentrations graphene monolayers achieves the conductance higher than any metal at room temperatures. This ensures that the graphene-based sensors to have a very low Johnson-Nyquist thermal noise which is comparable to semiconductor-based sensors. Graphene is also known for its exceptional flexibility and impermeability, high mechanical strength along with higher electric and thermal conductivities. Graphene shows good synergistic effects with most of the modifiers which may be organic, polymers, enzymes, metals, metal oxides, metal sulfides and many more. Graphene is biocompatible therefore very useful in various in-vivo applications.
In recent years, large numbers of reviews and research articles have been reported emphasizing on graphene and its composites [34,35,36,37,38,39,40]. Additionally, few numbers of reviews based on graphene based sensors or biosensors have also been reported. Li et al. synthesized 3D porous GO with MoS2 quantum dots for the determination of H2O2 which showed very encouraging results [34]. Wang et al. demonstrated a comprehensive study on graphene-based aptasensors focusing on molecule-interface interactions to design sensor and how these can be applied for bio-medical diagnostics [35]. Wang et al. reported an elaborated study on modification of graphene by bio-macromolecules such as DNA, protein, peptide, and others and discussed their biosensing capabilities [36]. Yang et al. and Wang et al. published review articles on different carbonaceous materials which could be used for fabricating sensors and biosensors [37,38]. Kuila et al. reported an article based on graphene based electrochemical biosensors, but all these reviews cover a broad range of analytes [39]. Zhang et al. showed comprehensive overview on the graphene-based nanomaterials for fabricating electrochemical H2O2 sensor [40]. The review covered enzymatic as well as the non-enzymatic graphene-based composites for the detection of H2O2. In past few years, the research in terms of modification and fabrication has gone a long way hence an updated review on graphene based H2O2 is very meaningful and necessary.
2. Synthesis and modification of graphene
There are numerous reports till date, highlighting the methods like exfoliation and cleavage of natural graphite, electric arc-discharge, chemical vapor deposition, and epitaxial growth on electrically insulating surfaces, micromechanical exfoliation of graphite and reduction of graphene oxide [41,42,43,44,45]. Although scientist knew the existence of 2D crystal graphene, nobody had the idea how to extract it from graphite. In 2004, Geim and Novoselov isolated pure single layer graphene using scotch-tape for continuously peeling the layers out of graphite [46]. Since its discovery, the researchers around the globe are in quest of developing the new method for the synthesis of graphene with very high surface area and keeping the thickness to one atomic dimension. Along with achieving graphene with the above mentioned properties, the scientific and industrial communities are also looking for the alternatives route of production of graphene with the aspect of decreasing the production cost hastily. Though there are so many methods present for the synthesis of graphene, chemical oxidation-reduction method is one of the most preferred methods for the synthesis of graphene. The graphene formed through the chemical oxidation-reduction method possess many advantages over other synthetic procedures like the surface modification become very easy, the defects present are very helpful in the electrochemical applications [47,48]. In chemical oxidation-reduction method, the graphite is treated with various strong oxidizing agents so that the layers may be intercalated with oxygen moieties and the distance between the layers raise. With the increase in the distance between the layers of graphite, it is easier to separate the layers with each other. Now this oxidized and loosened graphite is known as graphene oxide which is partially reduced to form partially reduced graphene oxide [49]. Different types of modification are done to enhance the properties of various composite in a desirable way and the modifications are done before the partially reduction process and then they are reduced to achieve partially reduced graphene oxide [50]. Chemically reduced graphene oxide, usually has abundant structural defects and functional groups which are advantageous for electrochemical applications. Therefore, this review mainly focuses on graphene preparation through chemical oxidation-reduction process. Theoretically, reduction of GO is supposed to remove the oxygen functionalities and restoration of sp2 C from sp3 C, in that way leaving it aromatic and defect free. Nevertheless experimentally, following any reduction process of GO significant quantity of oxygen functionalities and defects remain therefore called as reduced graphene oxide (RGO) rather than graphene.
Pristine graphene is hydrophobic in nature which makes it insoluble in polar solvents and easily stacks up due to the higher π–π interactions between the exfoliated layers. Therefore, the modification of graphene surface is important to address these issues. The types of modifications done on graphene surface are either covalent or non-covalent. Covalent modification generally includes electrophilic & nucleophilic substitution, cyclo-addition and condensation reactions. In this type of modification there is a formation of covalent bond between the graphene skeleton and the modifier. The functional groups present on the surface and the edges of the GO mainly participate in this type of surface modification. The functional groups present on the graphene are mainly hydroxyl, epoxy, carbonyl, and carboxyl therefore preferable functional groups to be present in the modifier might be amines, cyanide, isocyanide, dienophiles, pyrrolidine rings, alkylazides, etc. In this type of modification, there is considerable decrease in electrical conductivity of the composites as compared to the GO due to the increase in sp3 nature due to the formation of bonds between the GO and the modifier. He et al. developed facile and versatile method for the introduction of a variety of functional groups as well as polymers through nitrene cycloaddition [51]. These composite displayed enhanced chemical and thermal stabilities and also showed better dispersibility in the solvents. Yu et al. functionalized GO with –CH2OH terminated poly(3-hexylthiophene) through the formation of ester linkage with the –COOH of GO increasing its solubility in the organic solvents [52]. The earlier reports on the modification of GO with the organic moiety was carried out through the formation of amide bond between the –COOH group of GO and octadecylamine [53,54]. This led to the advancement of immobilization of enzymes onto the surface of GO resulting in the fabrication of enzyme based composite to be used as biosensors.
Graphene is a π-electronic system; most of its unique properties are acquired due to its endless conjugation involving continuous π electrons. In covalent modification, this π-system is disturbed due to the formation of sp3 bond which leads to the downfall of the desired property. Therefore, non-covalent modification with macromolecules, surfactants and aromatic moieties are of immense interest because this gives the freedom of tuning the graphene surface along with keeping its intrinsic properties intact. Non-covalent modifications generally include π–π, hydrogen bond and hydrophobic interaction. Mostly, π–π interactions and hydrogen bonding are involved and concurrently stabilizes the developed composites. Numerous works have been reported where GO was modified with large organic moiety having large number of π electrons such as methyl green, iron porphyrin, sufonated polyanaline, polystyrene, nafion, poly(3, 4-ethylenedioxythiophene) and many more.
3. Materials used for electrocatalytic hydrogen peroxide sensing
One of the key steps in the sensors is the ability of transfer of electron between the analytes and to the electrodes completing the circuit through the developed material without any interference. To attain uninterrupted electron transfer and to rise above all other constrains many researchers have developed different types of composite materials which can be for direct sensing of hydrogen peroxide. Many materials like enzymes, polymers, dyes, metals, metal oxides have been employed in the development of H2O2 sensor. For the better understanding of the readers the article has been divided into two main sections (enzymatic and non-enzymatic) giving the broad idea of the materials used.
3.1. Enzymatic sensor
As the biomolecules (enzymes) are used in the enzyme-based sensing of H2O2, these are better known as biosensors. Numerous metalloproteins (enzymes) having Fe at their redox centers such as horseradish peroxidase (HRP), hemoglobin (Hb), etc. are extensively investigated as the electro active materials for the direct electrochemical detection of H2O2. Detection mechanism depends on modified electrode irrespective of presence and absence of a mediator (materials enhancing the electron transfer) molecules. Enzymes are massive protein molecules with redox centers buried deep inside the gigantic structure, which are sometimes extremely hard to access that's why several mediators have been used to uphold the easy electron transfer between the redox centers and the modified active electrode. In the presence of mediator, the working mechanism of an enzymatic sensor can be formulated as follows [55].
|
H2O2+Ered→H2O+EoxEox+Mred→Ered+MoxMox+2H++2e−→MredNetReaction:H2O2+2H++2e−→2H2O
|
(1)
|
The above mechanism can be summarized as first of all, the immobilized enzyme (E) reduces the H2O2 present the solution and itself gets oxidized. The reduced form of the enzyme is again generated by the means of mediator (M) for further reduction of H2O2. In the regeneration process of reduced form of E the mediator undergoes oxidation which is finally electrochemically reduced at the surface of the electrodes resulting in the increase in the reduction current. The whole progression can be pictorially represented in Figure 1.
Depending upon the electron transfer pathways these types of biosensors can be further divided into mediated (use of mediator) and non-mediated (no use of mediator) biosensors. The mediated biosensors are those which use several electron-shutting mediators such as polymers, catechol, hexacyanoferrate and many more materials between the biomolecule and the electrode for the uninterrupted electron flow [56,57]. The mediator free sensors are those in which the electron transfer occurs directly between the biomolecule and the electrode without any intermediating molecule.
Generally, the electron transfer between the H2O2 and the enzyme active site is difficult because of its inaccessible position, so to prevail over this problem the use of mediator got popularized. The classes of sensors where mediators are used to complete the electron transfer are generally known as second generation biosensors. Graphene oxide (GO) serves as the pioneer for the synthesis of many composite materials and alone can also be used as material for sensing [58]. Zuo et al. used GO for immobilizing proteins (Cyt c, HRP, Mb) via incubation method for detection of H2O2 [59]. The sturdy hydrophobic property and electrostatic interactions involving the proteins and GO resulted in the healthier immobilization of proteins onto the GO surfaces. Their in-depth studies showed that the characteristics of the protein were unaltered in presence of GO signifying the creation of suitable microenvironment for the sensing applications. The presence of GO was noted with the sudden appearance of sharp peaks in the voltammograms which were otherwise absent with the use of only proteins molecules. It provides the information about the flow of electrons along with the restoration of catalytic activity of the biomolecules. The large surface area of GO assisted the augmentation of the sensing performance towards H2O2. Mani et al. synthesized GO-MWCNT-Pt composite and immobilized Mb (GO-MWCNT-Pt/Mb) over it [60]. The prepared composite provided suitable hold for the immobilization of Mb over itself. The successful immobilization and the synergistic dependence between them is evidenced from the enhanced results obtained; the sensitivity, LoD and linear range were found to be 1.99 μA·pM−1·cm−2, 6 pM and 10 pM to 0.19 μM respectively. Lu et al. fabricated H2O2 biosensor based on monolayer graphene HRP composite film [61]. The synthesis procedure involved a simple solution mixing pathway. Single layer graphene and tetrasodium 1, 3, 6, 8-pyrenetetrasulfonic acid (TPA) were mixed in 1:1 proportion which resulted in SLGnP-TPA and to this HRP in Phosphate Buffer Solution (PBS) of pH of about 5.0 was added and mixed well. The obtained composite was drop casted onto the glassy carbon electrode (GCE) surface and was dried in ambient temperature overnight to which minimal quantity of nafion was drop casted as binder onto the dried modified GC electrode. From the amperometric voltammograms the linear range and LoD, were found to be 6.3 × 10−7 to 1.68 × 10−5 M and 1.05 × 10−7 M, respectively. Li et al. demonstrated sequence-designed peptide nanofibers bridged conjugation of graphene quantum dots with GO which was used as a high performance electrochemical hydrogen peroxide biosensor [62]. Firstly, peptide nanofibres were self assembled onto which graphene quantum dots were adhered which was later anchored onto the graphene surface non-covalently through second self assembly process in the presence of hydrazine. The fabricated H2O2 biosensor had a linear range of 10 × 10−6 M to 7.2 × 10−3 M (R = 0.9994) with a detection limit of 0.055 × 10−6 M (S/N = 3). This strategy of fabrication of well-organized 2D hybrid nanomaterials has revealed quite a few advantages such as high efficiency, good reproducibility and relative simplicity.
3.1.1. Horseradish peroxidase (HRP)
Horseradish peroxidase (HRP) is one of the common and extensively studied enzymes for the construction of H2O2 biosensor. It contains Heme Fe(Ⅲ) at the active site. HRP is one of the most utilized enzymes for the biochemical applications. Xiao et al. constructed a novel HRP based H2O2 sensor by immobilizing HRP on to Au colloids supported over cysteamine and catechol being the mediator [63]. The glutaldehyde groups present on the cysteamine molecule forms the support to hold Au NPs. Using catechol as the mediator showed excellent electrocatalytic response towards the reduction of H2O2. The electrocatalytic response seemed to increase with the reduction in the Au colloidal size. The prepared composite showed a linear range of 0.39 μM to 0.33 mM with the response time merely being < 5 s and the LoD achieved as 0.15 μM. Zeng et al. synthesised self-assembled graphene-HRP hierarchial nanostructures for electrochemical biosensing [64]. Sodium dodecyl benzene sulfonate was used as the modifier to funtionalize graphene surface onto which HRP was successfully immobilized to obtain HRP-GNs hierarchical bionanocomposites. Slurry of thus obtained bionanocomposite was made and was deposited over the GC electrode surface for the fabricating electrodes which can be further used for electrochemical sensing of H2O2. The amperometry studies in 0.1 M PBS of pH 7.0 containing 0.1 mM hydroquinone as mediator at 0.08 V were established. The steady state current studies displayed a linear range from 1.0 × 10−6 to 2.6 × 10−5 M with a sensitivity of 0.22 A·M−1·cm−2 and LoD of 1.0 × 10−7 M. The reaction mechanism was summarized by the authors is as follows
|
HRP(Red)+H2O2→HRP(Ox)+H2OHRP(Ox)+Hydroquinone→HRP(Red)+BenzoquinoneBenzoquinone+2e−+2H+→Hydroquinone
|
(2)
|
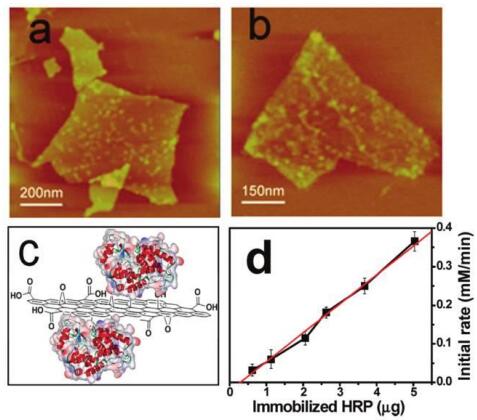
The direct electrochemistry without the utilization of any intermediate got vulgarized due to the convenience along with the capabilities of attaining better sensitivity and selectivity. These classes of sensors that were fabricated without the use of any intermediate mediators are branded as the third generation biosensors. Numerous studies in literature indicate that with the proteins anchored over the surface of graphene the parameters like selectivity and sensitivity can be enhanced enormously [65,66,67]. Zhang et al. demonstrated a successful route for immobilization of HRP onto the surface of graphene through simple incubation process done in a PBS buffer solution at 4 ℃ [68]. The results obtained were very encouraging, furthermore the authors also claim that the loading capacity of the HRP onto the graphene surface was the higher than any other reported materials. HRP was densily bonded to the surface of graphene and the catalytic reaction rates were found to be linear with the HRP loadings as shown in the Figure 2. Fan et al. encapsulated HRP into the graphene capsule (GRCAPS) and moreover anchored them onto the surface of PSS-GO to apprehend the direct electron transfer mechanism occurring at the electrode surface [69]. The fabricated biosensor showed a linear range of 0.01–12 mmol·L−1, LoD of 3.3 μmol·L−1 along with admirable anti-interfering property and long term stability.
Attributable to high aspect ratio, improved biocompatibility, astonishing catalytic properties along with elevated chemical stability, metal and their derivatives in nanodimensions have found good synergistic effect along with biomolecules which can further enhance the catalytic properties of graphene based HRP H2O2 sensors [70,71,72,73,74,75]. Zhang et al. fabricated Au-graphene-HRP-Nafion biocomposites modified screen-printed carbon electrodes [76]. HRP and graphene was co-immobilized in the nafion-based screen print carbon electrodes. The biosensor showed excellent electrochemical performance with linear range of 2.0 × 10−5 to 2.5 × 10−3 mol/L (R2 = 0.9994) and detection limit of 1.2 × 10−5 mol/L. The fabricated biosensor was cost-effective, fast, sensitive and showed strong anti-interference. Song et al. synthesised MoS2-GNS and tried immobilizing HRP on over its surfaces [77]. The prepared material showed exceptional performance towards the detection of H2O2. The steady state current studies displayed a linear range of 0.2 μM to 1.103 mM with LoD being 0.049 μM. Deng et al. demonstrated the preparation of a composite using ferrocene and chemically reduced graphene oxide (Fc-CRGO) utilizing π–π attraction as the dominant mode of interaction between them and have immobilized HRP over it [78]. The modified electrode showed admirable electrochemical properties like notable reduction of overpotential and fast kinetics being the significant once along with the lower LoD of 0.1 μM.
Zhou et al. demonstrated the synthesis of a novel H2O2 biosensor based on Au-graphene-HRP-chitosan biocomposite [79]. They prepared GNS by intercalation of –SO3− groups between the layers to keep them separate and then fabricated biosensor by co-immobilization of graphene and HRP into the bio-compatible chitosan which was later coated onto the GCE surfaces and then electrodeposted with Au NPs to obtain Au/graphene/HRP/CS/GCE. The modified electrode displayed excellent electrochemical performance towards electrochemical reduction of H2O2. The amperometric analysis was carried out at a variety of pH to determine the appropriate pH further electrochemical studies. The pH of 6.5 in 0.1 M PBS was established more appropriate with premier current response at a potential of −0.3 V. Strongly acidic or basic environment would easily denature the enzyme but faintly acidic nature was required to produce required H+ ions for HRP to reduce H2O2. The time taken to reach steady-state current was < 3 s, linear range was found to be 5 × 10−6 M to 5.13 × 10−3 M with a LoD of 1.7 × 10−6 M. The biosensor demonstrated a very good reproducibility with RSD of 4.2% and notable long term stability. Lv et al. demonstrated similar work by taking hemin, Au NP and graphene for the decomposition of H2O2 [80]. Firstly, graphene-hemin composite was synthesized through π–π interaction between them as the major force acting between them and then HAuCl4 was reduced in situ using ascorbic acid as the reducing agent. This ternary composite showed an elevated catalytic activity towards the decomposition of H2O2.
Wang et al. demonstrated the synthesis of flower like CuInS2-graphene hybrid for photochemical detection of H2O2 [81]. CuInS2-Graphene (GCIS) was synthesised as follows: at first GO was dispersed into teiethyl glycol under ultrasonication resulting exfoliated GO, which was then sonicated with a stoichiometric mixture of CuCl, InCl3 and sulphur powder before hydrothermal treatment at 200 ℃ for ~48 h. The dispersion for the electrode fabrication was prepared in the following manner, GCIS was firstly dispersed into chitosan acetic acid solution and ultrasonicated until homogenous solution was obtained and the pH ~ 5 was attained by adding NaOH solution. To thus prepared mixture 1-ethyl-3-(3-dimethylamino-propyl) carbodiimide was slowly added and ultrasonicated, later HRP dissolved in 0.1 M 7.0 pH PBS was added and incubated at 30 ℃ for not more than 3 h and stored overnight at 4 ℃ in refrigeration. Finally thus obtained final solution was drop casted onto the ITO electrode (HRP/GCIS/ITO). This electrode was utilized for all the electrochemical studies. The electrochemical studies were done in 0.1 M 7.0 pH PBS. The steady state current studies showed the linear range to be 5.0 × 10−7–5.3 × 10−4 M with the attainment of sensitivity of 4.7 × 10−7 M and the LoD being 11.2 μA·mM−1. The whole electrochemical process involved in detection of H2O2 can be represented as follows.
|
CIS+hν→CIS(h+e)CIS(e)+HRPox→HRPredH2O2+HRPred→H2O+HRPoxITO(e)+graphene→ITO+graphene(e)Graphene(e)+CIS(h)→Graphene+CISNetreaction:H2O2+ITO(e)→H2O+ITO
|
(3)
|
Radhakrishnan et al. prepared CeO2-rGO nanocomposite by one-pot synthesis method to be used as an H2O2 biosensor [82]. Hydrothermal method was employed by taking appropriate amounts of Ce(NO3)3·6H2O and GO and NaOH as reducing agent at 180 ℃ for 8 h. This composite was mixed with HRP in 7.0 pH 0.1 M PBS and drop casted onto the cleaned GC surface together with nafion as binder. The electrochemical measurements were undertaken in N2 saturated 7.0 pH PBS solution. With the addition of known concentration of H2O2 there was dramatical increase in the cathodic peak at 0.4 V along with the decrease in anodic peak. The calibration curve obtained for the detection of H2O2 displayed linear range of 0.1–500 μM, LoD of 0.021 μM and sensitivity of 4650 nA·mM−1. Nandidni et al. established electrochemical biosensor for the selective determination of H2O2 based on the co-deposition of palladium, horseradish peroxidase on functionalized-graphene composite on graphite electrode [83]. On the clean graphite electrode surface funtionalized GO was drop casted and then Pd and HRP was electrodeposited after complete drying of the f-GO casted graphite rod by galvonostatic electrodeposition method at a current density of −1.0 mA·cm−1 for 720 s. The electrode was cleaned with deionized water and then incubated for 30 min before storing it in PBS at 4 ℃. Electrochemical studies were carried out by using cyclic voltammetry (CV), differential pulse voltammetry (DPV) and amperometry. The DPV studies advocate that the cathodic peaks were highly stable for the reduction of H2O2. To optimise the pH and temperature the studies were conducted at varied conditions and the optimum condition obtained were at pH 7.0 and temperature 303 K. The amperometric studies were carried out at potential of −0.1 V in pH 7.0 PBS and the studies revealed the linear range of 25 μM to 3.5 mM, LoD of 0.05 μM, response time of < 2 s and the sensitivity of 92.82 μA·mM−1·cm−2. Nalini et al. demonstrated the synthesis of an amperometric hydrogen peroxide sensor functionalizing graphene through Ag NPs and enzyme deposits [84]. Direct preparation of electrodes was carried out through galvanostatic electrodeposition technique at a current density of −0.28 V for 600 s. The electrolyte was composed of 0.1 M KNO3, 1 mM AgNO3, 50 mg of f-graphene and 50 μl of HRP. The electrodeposition was carried out on the graphite electrode and nafion was drop casted after cleaning with DI water and was incubated for 30 min at room temperature for complete drying and stored at 4 ℃ in refrigerator till further use. The electrochemical studies were carried out through CV, DPV and amperometry. The CV displayed a pair of well-defined redox peaks which grew intensely compared to the voltammograms of composites prepared without graphene or Ag nanoflowers. Upon successive addition of small aliquots of H2O2 the cathodic peaks responded well and increased gradually with the increase in the strength of H2O2 used whereas the anodic peak was unaffected right through the experiment signifying that the prepared composite can be effectively used for the reduction of H2O2. The DPV studies were completed in the potential window of 0 to −0.8 V at a scan rate of 20 mV·s−1 and the current response were found proportional to the concentration of H2O2. The current response at a range of pH and temperature were also carefully noted to establish the most favourable operational pH and temperature. The studies divulge the optimum pH and temperature to be 7.0 and 308 K respectively. The amperometric studies were carried out at a potential of −0.5 V in PBS solution of pH 7.0, the linear range established was 25 μM to 19.35 mM, response time of < 3 s, LoD of 5 μM and the sensitivity of 272.2 μA·mM−1·cm−2. Interference test was not in favour of cholesterol, ascorbic acid, uric acid and dopamine which were done to determine the selectivity of the modified electrode towards the determination of H2O2 and the results assured highly selective towards H2O2.
3.1.2. Haemoglobin (Hb)
Although HRP has attracted the scientific community extensively for the fabrication of enzymatic H2O2 biosensor, few other macromolecules other than HRP have also been used in the fabrication of enzyme based H2O2 sensors. Liu et al. established a unique microwave assisted hydrothermal synthesis, for the preparation of Au NPs-graphene composite and later they have implanted haemoglobin (Hb) into it to form AuNPs-Gr/Hb composite which was used for H2O2 biosensing [85]. The retention of the secondary structure of the biomolecule Hb was confirmed by the FT-IR studies (Hb was not denatured). The enhancement in the electrochemical character after the successful immobilization suggests excellent biocompatibility. From the amperometric study, the LoD was found to be 0.03 μM·L−1. These heartening results were accredited to the following reasons: (ⅰ) the high surface area of graphene in AuNPs-Gr composite which can be used for the embodiment of Hb into it, and (ⅱ) Au NPs are non-destructive towards Hb and offer appropriate microenvironment for Hb in electron transfer process. Cheng et al. demonstrated a novel electrochemical biosensor for detection of H2O2 based on carboxymethyl cellulose functionalized reduced graphene oxide along with haemoglobin (Hb) as a hybrid nanocomposite film [86]. The preparation involved the mixing of appropriate amounts of GO and carboxymethyl cellulose under ultrasonication and reduction with NaBH4 at 80 ℃ for 24 h. The obtained rGO-CMC composite was mixed with haemoglobin (Hb) in 1:2 volume ratio and then drop casted onto cleaned surface of GC electrode. The CV studies suggested that the presence of Hb is responsible for the production of the redox peaks which were otherwise absent in the only rGO-CMC/GCE and the peaks got broadened with the addition of each drop of H2O2 signifying that the composite rGO-CMC/Hb/GCE is suitable to be used for the sensing of H2O2. The amperometric studies showed that the current increased linearly with the concentration of H2O2 in the range of 0.083 to 13.94 μM, with detection limit of 8.08 × 10−8 M. Wang et al. immobilized Hb on graphene/Fe3O4 nanocomposite for the determination of H2O2 [87]. The Fe3O4 particles were prepared by simple method by solvothermal co-precipitation in a teflon lined autoclave at 200 ℃ for 8 h. Then mixed with poly(diallyl dimethyl ammonium chloride) (PDDA) funtionalized GO under reflux to obtain GE/Fe3O4 nanocomposite. Prior to electrode preparation, the nanocomposite was mixed with Hb and then drop casted onto the surface of GCE and allowed to dry in ambient conditions. This electrode was used throughout the electrochemical studies. The studies to determine the optimum pH were carried out at a range of pH and the studies revealed that there was minimalistic change in the current response in the pH range of 5.0 to 7.0 but the peaks shifted slightly to the negative values with the increase in the pH but beyond the pH 7.5 the current response began to decrease which may be due to the denaturation of Hb at higher pH. The amperometric voltammograms showed the LoD to be 6 μM. The material displayed exceptional reproducibility of > 95% even after continuous use for 2 weeks. Wang et al. demonstrated H2O2 sensor based on Hb adsorbed on to the Au nanorods and GO coated with polydopamine [88]. In the synthetic procedure, first of all polydopamine coated rGO was synthesised and Au nanorods by seed mediated synthesis procedure were prepared separately. The amperometric studies were carried out in 0.1 M PBS of pH 7.2 at a potential of −0.2 V, meticulous study of the voltammograms revealed linear range to be 0.0036–6.0 mM and the LoD of 0.002 mM. The interference test were carried out against Na+, Cl−, K+, NO3−, CO32−, SO42−, Mg2+ and Ca2+ and these analytes were unable to disturb the steady state produced by the modified electrode significantly. This suggested that the modified electrode was highly selective and can be successfully used in the detection of H2O2 in the presence of many other interfering analytes. After 22 days of continuous usage of the electrode, there was 11.4% drop off in the current response portraying its long term stability and excellent repeatability.
Zhang et al. demonstrated the immobilization of Hb on Au/graphene-chitosan nanocomposite and using it efficiently as an H2O2 biosensor [89]. Separately GO was reduced using hydrazine to prepare rGO and Au NPs were synthesised by citrate reduction technique. The electrode was fabricated using layer by layer assembly technique. Firstly, rGO suspension in chitosan (CS) was prepared and drop casted on to the GCE surface and allowed to dry completely in ambient condition. Then the electrode was immersed into the Au NP solution and kept undisturbed for 4 h to dry in ambient conditions. Then, Hb was drop casted and allowed to dry so as to get the electrode titled as Hb/Au/GR-CS/GCE. From CV voltammograms, it is apparent that the introduction of Hb caused the appearance of the redox peaks which were otherwise absent. The amperometric studies were conducted to establish the catalytic activity of modified electrode towards the detection of H2O2. The studies revealed the linear range to be 2–935 μM which was a lot superior to the modified electrode without Au which typically had the value of 2–635 μM. The response time was < 3 s to reach 95% steady state current, LoD was found to be 0.35 μm which is also lesser compared to electrode without Au which had the value of 0.51 μM. The sensitivity was established to be 347.1 mA·M−1·cm−2 which is 1.56 times greater in comparision to the electrode without Au, i.e., Hb/GR-CS/GCE. He et al. demonstrated the fabrication of an Hb based H2O2 biosensor with ionic liquid functionalized rGO [90]. Graphene oxide was chemically reduced using hydrazine monohydrate and redispersed in chitosan under ultra-sonication for 30 mins in the presence of 1-Butyl-3-methylimidazolium hexafluorophosphate and DMF. Hb and PBS were also added to the above mixture and then the solution was drop casted on to the clean carbon ceramic electrode and dried. Later, nafion was drop casted onto the dry electrode and was completely dried prior to electrochemical characterization. The TEM image showed highly loosened, crumbled and folded sheet of rGO. The CV voltammograms showed the boost in the current response compared to the bare carbon ceramic electrode. The CV voltammograms displayed the sharp well defined redox peaks after the introduction of Hb on the electrode. The introduction of H2O2 into the PBS resulted in the steady increase of cathodic peaks and simultaneous decrease in the anodic peaks as the concentrations of H2O2 was increased. The amperometric studies were carried out in pH 7.0 PBS at a potential of −0.30 V. The steady state response time, linear range and LoD from the voltammograms were found to be 2–4 s, 8.0 × 10−7 to 1.8 × 10−4 M and 3.0 × 10−7 M respectively. The possible mechanism postulated by the authors is as follows
|
Hb[Heme(Fe3+)]+H2O2→Compound1+H2OCompound1+H2O2→Hb[Heme(Fe3+)]+H2O+O2Hb[Heme(Fe3+)]+H++e−→Hb[Heme(Fe2+)]atelectrodeHb[Heme(Fe2+)]+O2→Hb[Heme(Fe2+)]−O2fastHb[Heme(Fe2+)]−O2+H++e−→Hb[Heme(Fe3+)]+H2Oatelectrode
|
(4)
|
The overall reaction is
Xie et al. synthesised graphene anchored with ZnO and Au NPs and immobilized Hb over the modified graphene and successfully used it for H2O2 biosensing [91]. GO was chemically reduced with hydrazine at ~80 ℃, Au NPs were synthesised by citrate reduction, ZnO NPs were synthesised by NaOH reduction. All the NPs were synthesised separately and were assembled on electrode to construct the modified electrode for electrochemical measurements. The electrode for the electrochemical analysis was prepared as follows: graphene dispersion in DMF was drop casted on to the GCE and allowed to dry under ambient condition. Then ZnO dispersion in APS was casted over the graphene coated electrode and allowed to dry completely, and then it was washed with DI water dipped in Au NPs solution for at least 12 h. Later, Hb in pH 7.0 PBS was casted over that and allowed to dry completely and before finishing it off with a layer of nafion to prevent any sort of leakage. SEM images showed the morphology of graphene as a sheet with lot of wrinkles, ZnO was nicely assembled as flowers. Amperometric study was carried out in PBS of pH 7.0 at −0.3 V, the response time was found to be ~2 s and linear range of 6.0 to 1130 μM.
3.1.3. Others
Other enzymes such as catalase and oxidase have also been investigated for the fabrication of H2O2 biosensors, only a small number of them are described as it is outside the scope of this article to cover all. Zhou et al. demonstrated modification of graphene with chitosan and Ag NPs in company with sarcosine oxidase (SOX) enzyme [92]. Graphene was dispersed into chitosan solution of acetic acid through ultrasonication forming homogenous solution. SOX was dispersed in 1.0 M PBS of pH 7.4. The GCE was cleaned properly; modified graphene was drop casted and allowed to dry completely under infrared light in air before immersing into AgNO3 solution containing NH4NO3. Electrodeposition was carried out at −0.2 V for 45 s followed by washing with DI water. The electrode was then dried under nitrogen blowing, SOX was dropped onto the electrode surface and dried in air at room temperature. The obtained electrode was denoted as SOX/AgNPs/graphene-chitosan/GCE. The amperometric studies carried out in 0.1 M PBS of pH 7.0 showed the linear range of 1.0 to 177 μM, LoD of 1.0 μM and the response time of 6 s. The electrode was tested for 2 weeks on daily basis and the RSD was 12% which recommends the stability and the repeatability of the electrode. Huang et al. investigated electrochemistry of catalase enzyme at amine-functionalized graphene/Au NPs nanocomposite film for determination of H2O2 [93]. Au NPs were prepared by citrate reduction and were stored in dark bottles at 4 ℃. Carboxylic acid funtionalized graphene was prepared in Lindberg tube furnace at 1050 ℃ which was dried and processed for amine functionalization by treating it with NH2(CH2)2NH2. The electrode for the electrochemical studies was prepared by simple drop casting amine modified graphene, drying and dipped into the Au NPs solution. This allowed the adsorption of Au NPs on the surface of amine modified graphene on GCE. The immobilization of catalase enzyme was done by immersing it in the solution of catalase in PBS of pH 7.0 for 10 h at 4 ℃. The assembled electrode was labelled as Cat/AuNPs/graphene-NH2/GCE. The amperometry was performed at 0.3 V in PBS of pH 7.0, the results showed the linear range of 0.3 to 600 μM, LoD of 50 nM and sensitivity of 13.4 μA·mM−1. Zhang et al. demonstrated electrochemical biosensor for H2O2 based on well dispersed Au NPs on GO immobilized with thiuonine conjugated catalase enzyme [94]. GO was prepared by the most commonly followed technique, i.e., modified Hummers' method and Au NPs were anchored over its surface by vigorous mixing with HAuCl4 at 90 ℃ for 2 h. Thionine conjugated catalase enzyme was prepared by mixing proper amounts of enzymes in 0.01 M PBS of pH 9.5. Glutaraldehyde was added under stirring conditions and the pH was raised to 10.0 to promote the conjugation of amino groups of both the enzymes and glutaldehyde acted as the cross-linker. The electrode was prepared by first drop casting the Au NPs anchored graphene and allowing it to dry completely then incubating the electrode in conjugated enzymes at 4 ℃ for 6 h. The electrochemical behaviour was studied in ABS of pH 5.8, the linear range was found to be 0.1 μM–2.3 mM with the LoD of 0.01 μM. Graphene based enzymatic H2O2 biosensors have been summarized in Table 1 along with their sensing performances.
Table 1. Performance of graphene based H2O2 biosensors.
| Material |
Electrode Performance |
Ref. No. |
| Linear Range (μM) |
Detection Limit (μM) |
Sensitivity |
| RGO-MWCNT-Pt/Mb |
1 × 10−5–1.9 × 10−4 |
6 × 10−6 |
1.990 × 109 μA·mM−1·cm−2 |
[60] |
| SLGnP-TPA/HRP |
6.3 × 10−4–1.68 × 10−2 |
0.105 |
- |
[61] |
| Au-Cysteamine/HRP |
0.39–330 |
0.15 |
- |
[63] |
| HRP-GNs(SDBS) |
1.0 × 10−3–2.6 × 10−2 |
10 |
220 μA·mM−1·cm−2 |
[64] |
| PSS-GO-GRCAPS/HRP |
10–12000 |
3.3 |
- |
[69] |
| Au-G-HRP-Nafion |
20–2500 |
12 |
- |
[76] |
| Fc-RGO/HRP |
0.35–150 |
0.1 |
- |
[78] |
| Au/graphene/HRP/CS |
5.0–5130 |
1.7 |
- |
[79] |
| CuInS2-Graphene/HRP |
0.5–530 |
47.0 |
11.2 μA·mM−1 |
[81] |
| CeO2-rGO/HRP |
0.1–500 |
0.021 |
4.65 μA·mM−1 |
[82] |
| Pd-HRP-RGO |
25–3500 |
0.05 |
92.82 μA·mM−1·cm−2 |
[83] |
| Ag-HRP-RGO |
25–19350 |
5 |
272.2 μA·mM−1·cm−2 |
[84] |
| AuNPs-Gr/Hb |
0.1–70 |
0.03 |
- |
[85] |
| rGO-CMC/Hb |
0.083–13.94 |
0.08 |
- |
[86] |
| GE/Fe3O4/Hb |
100–1700 |
6.00 |
0.3837 μA·mM−1 |
[87] |
| Hb/AuNRs-GOs@Pdop |
3.6–6000 |
2.00 |
0.3293 μA·mM−1 |
[88] |
| Hb/Au/GR-CS |
2–935 |
0.35 |
3.471 × 105 μA·mM−1·cm−2 |
[89] |
| Hb-ionic liquid (IL)-GE |
0.8–180 |
0.30 |
0.0134 μA·mM−1 |
[90] |
| Hb/AuNPs/ZnO/Gr |
6.0–1130 |
0.8 |
- |
[91] |
| SOX/AgNPs/graphene-chitosan |
1.0–177 |
1.0 |
0.0024 μA·mM−1 |
[92] |
| Catalase/AuNPs/graphene-NH2 |
0.3–600 |
0.05 |
13.4 μA·mM−1 |
[93] |
| TCA/AuNP-GO |
0.1–2300 |
0.01 |
0.0009 μA·mM−1 |
[94] |
| PB-RGO |
0.05–120 |
45 |
- |
[95] |
| PB-RGO |
0.05–1000 |
0.4 |
- |
[96] |
| rGO-CS/PB |
10–400 |
0.213 |
816.4 μA·mM−1·cm−2 |
[97] |
3.2. Persian Blue: Artificial peroxidase enzyme
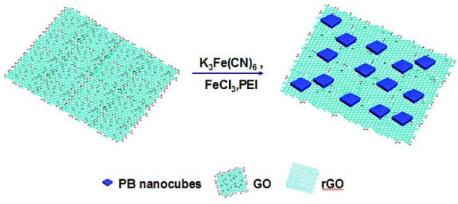
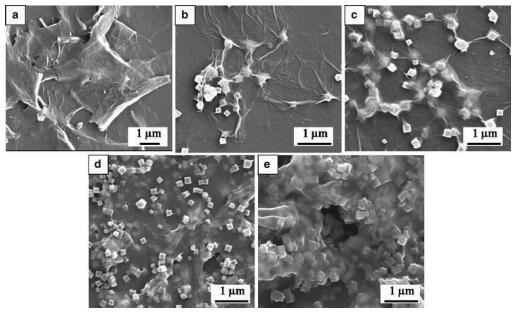
Persian Blue (PB) has received profuse consideration in the field of sensor due to its distinctive structure and electro-catalytic activity. Regardless of the fact that it is studied very commonly it has a few drawbacks, it is supposed to be used only in acidic conditions or else it will decompose rapidly it has small electrochemical stability. To prevail over these limitations researchers have dedicated their much valuable time in hunting an appropriate support which can enhance the stability and sensitivity satisfactory towards H2O2 determination. Many renowned researchers have postulated graphene to be a suitable support for PB [98,99]. Li et al. synthesized PB-rGO composite by electrochemical deposition method and found that the composite showed better response towards H2O2 than the PB or graphene alone [100]. Cao et al. synthesized PB nanocubes ornamented on graphene layers through in-situ wet chemical method and the overall synthetic scheme is depicted in the Figure 3 [95]. They have followed a simple synthetic route with controllable size of PB nnaoparticles with the small changes in the concentration of the precursors. The composite displayed a wider linear range of 0.05–120 µM and lesser LoD of 45 nM. Qian et al. synthesized PB-GO composite by solution mixing route treating GO and K3Fe(CN)6 at 80 ℃ for 3 h [96]. GO was successfully reduced to rGO along with conversion of K3Fe(CN)6 to PB nanocubes of the dimensions ~200 nm. The distribution of PB was seen homogenous throughout the surface of rGO sheets. The distribution and the morphology can be studied from FESEM image as shown in the Figure 4. The linear range was found to be 0.5 μM–1.0 mM and LoD of 0.4 μM.
In recent years, researchers worked to immobilize PB on the rGO surfaces. To accomplish this they have come about with an alternative, firstly covalently or non-covalently functionalizing the graphene surface with different polymers like chitosan, nitrobenzene, and polyethylene later immobilizing the PB NPs over it [101,102,103]. Yang et al. synthesized graphene-chitosan/Prussian blue (rGO-CS/PB) hybrids via mixing K3Fe(CN)6 and FeCl3 with chitosan functionalized graphene [97]. As graphene is well known to have negative charge and chitosan being positively charged there can electrostatic interaction to form a stable hybrid. The cationic charges present on the chitosan surface in the chitosan-graphene can hybrid provide the anchorage to the negatively charge PB. This strategy was successful in homogenously adhering PB NPs on the chitosan-graphene hybrid forming a composite (rGO-CS/PB). The hybrid displayed a wide linear range of 0.01 to 0.4 mM, LoD of 0.213 μM and attained a sensitivity of 816.4 μA·mM−1·cm−2 towards H2O2.
3.3. Non-enzymatic sensor
Taking into consideration the intrinsic flaws of inadequate stability and repeatability of the enzymatic electrochemical sensors, the scientific community curved towards the development of new electrochemical sensors which can be fabricated without using any of the bio-molecules and were called as non-enzymatic sensors. Non-enzymatic electrochemical sensor depends directly on the electrochemistry of the electrode material with the analytes. With superior properties for instance better sensitivity, stability and simplistic fabrication, the scientific community is putting much more effort in exploring high performance electrode material nonenzymatic sensors [104].
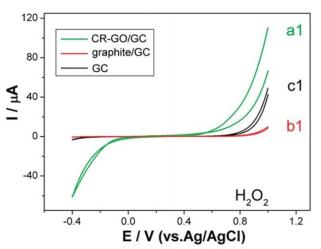
Zhou et al. used chemically reduced GO (CR-GO) for the detection of H2O2. It showed noteworthy elevations in the electrochemical behavior compared to that of graphite or bare GCE [105]. The CV results obtained for CR-GO are depicted in the Figure 5, thorough examination of the voltammograms reveal the onset oxidation/reduction potentials as 0.20/0.10 V, 0.80/0.35 V, and 0.70/0.25 V for CR-GO/GC, graphite/GC, and GC electrodes respectively. The linear range obtained was 0.05–1500 μM at a potential of −0.2 V. The elevated results were attributed to the defects created on the plane edges of the graphene [106,107,108]. In an another work reported by Takahashi et al., directly electrodeposited rGO on to the GC electrode by scanning through a potential of −1.5 to 0.6 V in the aqueous GO solution which showed an enhanced electrocatalytic activity and better selectivity towards H2O2 compared to bare electrode [109].
Obtaining monolayered or 2–3 layered graphene is very difficult and the conversion of hydrophilic GO to hydrophobic rGO leads to self stacking of the graphene layers, which results in the downfall of the overall electrocatalytic activity [110,111]. Therefore, research began to focus on inserting spacers or dispersants in between the layers of the graphene so that the restacking can prevent. Lv et al. introduced DNA molecules on the graphene sheets surface by self-assembly process using the π–π interaction between the graphene's aromatic rings and the nitrogen bases in the DNA structure [112]. As obtained rGO/DNA composite provided elevated electron transferability along with improved ability to get dispersed in an aqueous environment. rGO/DNA modified electrode showed higher sensitivity, lower response times along with wider detection limits in comparison to the only rGO modified electrode. Woo et al. used MWCNTs as the spacer molecules in between the layers of graphene by simple in-situ synthesis method [113]. The author's claim that the MWCNTs can successfully bridge between the graphene sheets preventing restacking and improving the electrochemical performance. MWCNT-graphene composite displayed good performance against H2O2 with the linear range of 20 μM–2.1 mM and limit of detection of 9.1 μM. In recent past, photochemical synthesis of metal-graphene composites gained attention due to controllable kinetics and mild reaction kinetics [114]. Gu et al. reported a simple method for functionalizing the graphene surface with noble metal NPs (Ag, Pd, Au, and Pt) through UV assisted ZnO photo catalysis [115]. Firstly, ZnO-G was synthesized in presence of PVP by utilizing the self-assembly process which aided in easy synthesis of desired composite. Then the positively charged ZnO nanorods were easily adhered to the negatively charged graphene. The obtained GS/ZnO2 was anchored with metal nanoparticles in the presence of ethanol by adding the metal salts (of Ag, Pd, Au, Pt) leisurely and irradiated with UV light. This resulted in the embedment of metal NPs onto the GS/ZnO surface. The authors reported that different morphologies of GS/ZnO@M corresponding to different metals and showed improved electrocatalytic activity with superior sensitivity.
3.3.1. Gold based composites
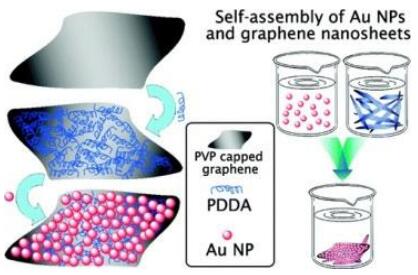
In recent past, many efforts have been put into the use of Au NPs as the electrochemical sensors especially for the H2O2 sensing owing to its high conductivity and catalytic properties [116]. Self-assembly is proved to be one of the most important strategies in the synthesis of Au NPs-graphene hybrid composites [117,118,119,120,121,122]. In this self-assembly process various types of forces acted in between rGO and the Au NPs. Fang et al. used poly(N-vinyl-2-pyrrolidone) (PVP) and poly(diallyldimethyl ammonium chloride) (PDDA) functionalized rGO along with Au for H2O2 sensing [123]. The synthetic procedure followed is illustrated in Figure 6. Microscopic images demonstrate that the Au NPs are uniformly distributed over the graphene surface as depicted in Figure 7. They claim that the presence of PVP avoided the restacking of the graphene layers. The presence of Au NPs over the graphene sheets led to the rough surfaces. The synthesized composite showed a linear range of 0.5 μM to 0.5 mM, LoD of 0.44 μM and response time of 6 s. Xi et al. followed a similar approach but using bovine serum albumin functionalized graphene and citrate capped Au NPs [124]. They fabricated thin films of Au NPs embedded porous graphene sheet (AuEPG). The formation of porous structure increased the surface area considerably in addition to the permeability giving the composite the linear range of 0.5 μM to 4.9 mM, LoD of 0.1 μM and the sensitivity of 75.9 μA·mM−1 against H2O2.
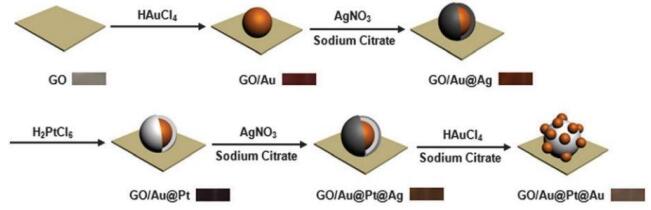
Besides the self-assembly process chemical reduction process for the synthesis of Au NPs is well followed in the research community [125,126]. Hu et al. followed co-reduction process by using hexamethylenetetramine (HMTA) with AuCl4 and GO for the synthesis of graphene-Au NPs composite along with sodium oleate as surfactant [127]. The synergistic effect between the Au NPs and the graphene in the prepared composite resulted in improved electrocatalytic activity and stability. Maji et al. [128] followed in-situ method to prepare sandwich-like periodic mesoporous silica-coated rGO which was deliberately anchored with ultra-small Au NPs (rGO-PMS@AuNPs). While evaluating the sensing ability against H2O2 of the synthesised composite fabricated on the electrode, they obtained the linear range of 0.5 μM to 50 mM, LoD of 60 nM, sensitivity of 39.2 μA·mM−1·cm−2 and the attainment of steady state current in < 2 s. Moreover, the fabricated sensor was tested for H2O2 in human urine and in tumour cells which produced comparative results. Ju et al. followed a new approach, i.e., green synthesis without the use of any reducing agents or surfactants [129]. They first have synthesised nitrogen doped graphene quantum dots (N-GQDs) through hydrothermal treatment of citric acid and dicyandiamide at 180 ℃/12 hrs. Later, they refluxed it with HAuCl4 to achieve AuNPs-N-GQDs. The composite showed homogenous distribution without much agglomeration. The electrode was also tested for real sample analysis against human serum and cervical cancer cells for H2O2 which produced similar results. The electrochemical studies showed a sensitivity of 186.22 μA·mM−1·cm−2 and LoD of 0.12 μM. These enhanced results at very low loading were mainly because of the synergestic effect between the Au NPs and graphene and it attracted enormous research attention [130,131,132]. Li et al. demonstrated the synthesis of bimetallic triple-layered core shell structure of GO/Au@Pt@Au with peroxidase like activity [133]. The synthetic procedure is shown in the Figure 8. The synthesised triple-layered core shell structure can serve as the bi-directional H2O2 sensor. From the electrochemical analysis the composite displayed the linear range of 0.05–17.5 mM and LoD 0.02 mM at a potential of 0.5 V. On the other hand, linear range of 0.5–110 mM and LoD 0.25 mM at a potential of −0.3 V were obtained. Shang et al. [134] used nitrogen doped graphene as the suitable support for hallow bimetallic AuPd NPs. Hollow bimetallic AuPd NPs were synthesised by following co-reduction method and by reducing HAuCl4 and Na2PdCl4 and using Co NPs as sacrificial template. The fabricated H2O2 sensor exhibited a sensitivity of 5059.5 μA·mM−1·cm−2 with the detection range of 0.1 to 20 μM and LoD of 0.02 μM. Wang et al. synthesized graphene by CVD growth on the Ni foam using CH4 as the carbon source and then electrophoretically deposited Au NPs on to the surface of graphene followed by H2O2 sensing [135]. The FE-SEM studies suggested the successful decoration of AuNPs over the graphene surfaces. The electrochemically studies showed the sensitivity of 47.4 μA·mmol·L−1·cm−2 with a linear range of 0.05–1.75 mmol·L−1. It showed good selectivity against glucose and ascorbic acid. Liu et al. synthesized Au NPs decorated graphene on Ni foam by simple dip technique [136]. Firstly, Ni foam of known dimensions were pretreated in acetone, ethanol and water then dipped in GO solution and dried for 3 times. Then, the GO coated Ni foam was treated with ascorbic acid to obtain RGO, which was again treated with the solution containing Au NPs. The Au NPs got anchored onto the surface of graphene. The Raman studies suggested the successful reduction of GO and other structural characterization prove the decoration of GO surface with Au NPs. The electrochemical characterization suggested the linear range of 0.003 to 1.06 mM, detection limit of 1.60 μM and the sensitivity of 156 μA·mM−1·cm−2. The selectivity was evaluated against glucose, ascorbic acid, uric acid, dopamine, sucrose and citric acid and the prepared electrode was found selective towards H2O2 in the presence of the above mentioned electrolytes.
3.3.2. Silver based composites
Even though Au based graphene composites for non-enzymatic H2O2 detection is one of the most attractive groups of sensors but owing to the cost and restricted reserve for large scale production has hindered it use. Ag-based sesnors can provide similar electrocatalytic property and at a much cheaper cost which has attracted researchers from all over the globe. In the quest for synthesis of Ag NPs supported graphene researchers have synthesized Ag NPs of different morphologies through many different procedures. Liu et al. [137] have also shown the use of metal oxides on the graphene surface for the utilization of the prepared composites for the electrochemical sensing. Most often used method for the synthesis of Ag NPs from Ag precursors is chemical reduction process [138,139]. Tian et al. [140] used microwave irradiation and NaBH4 for co-reduction synthesis of Ag NPs anchored sulphur doped graphene (Ag/SG) using AgNO3 as the Ag precursor. The studies have shown that they attained the linear range of 0.1–136.5 mM, LoD of 0.14 μL along with the attainment of steady state currents within < 2 s. Zhang et al. used mild reducing agent ethylene glycol (EG) because of its non-toxic nature [141]. The Ag nanowire decorated graphene was synthesised in the presence of PVP at 160 ℃/1–1.5 hrs. The linear range for the detection of H2O2 was found to be 10.0 μM to 34.3 mM, LoD of 1 μM and sensitivity of 12.37 μA·mM−1·cm−2. Following an analogous approach, Yu et al. synthesised Ag nanorods decorated graphene sheets (AgNR-rGO) using EG as the reducing agent [142]. The FESEM images of the AgNR-rGO are depicted in the Figure 9. The electrochemical study reveals the linear range to be 0.1–70 mM, LoD to be 2.04 μM and was stable over a very long period of time.
In past few years, in-situ reduction attracted more researchers and got popularised for the synthesis of Ag NPs-graphene based composites. In the synthetic procedures, several polymers were in use to obstruct the restacking of graphene sheets, on to which the metal particles were anchored. Liu et al. used poly[(2-ethyldimethylammonioethyl methacrylate ethyl sulfate)-co-(1-vinylpyrrolidone)] (PQ11) as the reducing as well as the stabilizing agent in the synthesis of AgNPs/graphene nanosheets (AgNP/GNs) composite [143]. In the typical synthetic procedure, graphene was first funtionalized with PQ11 following the absorbtion of AgNO3 over the functionalized surface and was later reduced to form AgNP/GNs composite. They fabricated non-enzymatic sensor for the detection of H2O2 and observed the linear range of 100 μM to 40 mM, LoD of 28 μM and amperometric response time of < 2 s. With similar approach, Liu et al. used aniline grafted AgNP/rGO [144]. From the current-time response curve, the linear range was seen to be 100 μM to 80 mM with the LoD of 7.1 μM. Yang et al. demonstrated a simple strategy to obtain Ag NPs of high quality and in a controlled way [145]. Ag NPs were synthesized following a hydrothermal route with TWEEN 80 as the reducing and stabilizing agent, which was later non-covelently combined with graphene to achieve AgNPs-TWEEN-GO. The microscopic images showed even distribution of Ag NPs over graphene as shown in the Figure 10. It showed superb electrochemical properties with wide linear range and very lower detection limits.
Electrodeposition is another efficient technique for the synthesis of Ag NPs anchored graphene [146,147,148,149,150]. Zhu et al. synthesised Ag NPs-GO composite by surface treating GO with Sn2+ attracted by the COO− functionalities [151]. Then Ag NP anchored onto the surface of GO by reducing Ag+ and subsequently oxidizing Sn2+ to Sn4+. The electrochemical measurement shows that they have achieved the LoD of 0.5 μM. Taking the silver mirror reaction as an inspiration, Bai et al. decorated Ag NPs over the surface of manganese oxyhydroxide-rGO (Ag-MnOOH-GO) [152]. Initially, MnOOH was synthesised and utilizing the hydrogen bonding it was successfully incorporated onto the graphene surface, this composite's produced a rough surface which was hostile enough to host Ag[(NH3)2OH]+ which was later reduced to Ag in the presence of CH2O gas. The prepared Ag-MnOOH-GO composite displayed a linear range of 0.5 μM to 17.8 mM with the LoD being 0.2 μM.
In addition to the afore mentioned synthetic procedures, hydrothermal synthesis is also a very common and largely followed technique as it can be performed without using any hazardous chemical reducing agents. Lorestani et al. demonstrated a facile one step hydrothermal method for the synthesis of Ag NPs modified MWCNT anchored graphene sheets utilizing GO, MWCNT and Ag(NH3)2OH as the precursor materials [153]. The FESEM images validate the homogenous distribution throughout the surface of graphene. It also elucidates the size distribution of the Ag NPs. Amperometric studies reveal that the steady state was achieved in < 3 s with linear range of 100 μM to 100 mM and LoD of 0.9 μM.
Nia et al. synthesized a novel H2O2 sensor using graphene decorated with polyppyrrole nanofibres-silver nanoparticles as the electro-active material [147]. The material was synthesed following two different methods. In the first method, AgNO3 solution was treated with ammonia to obtain Ag(NH3)2OH, which was mixed with GO and sonicated. Thus, the obtained solution was casted onto the clean GCE and the CV was performed in presence of 0.1 M 7.2 pH PBS buffer of 0.1 M pyrrole monomer and 0.1 M LiClO4 in the potential range of −1.5 to 0.8 V vs SCE and the obtained product was designated CV-PPyNFs-AgNPS-rGO. In the second method, they reduced the Ag(NH3)2OH-GO solution deposited on the GCE by electrochemical reduction to achieve AgNPs-rGO followed by the deposition polypyrrole on the surface of AgNPs-rGO. The results showed that the GO was reduced at the negative potentials and the polymerization of the pyrrole monomers took place in the positive potentials. The electrochemical measurements demonstrate the linear range of 0.1 to 5 mM, LoD of 0.085 μM. Yang et al. designed and synthesized a rigid chain liquid crystalline polymer-rGO composite for the detection of H2O2 [154]. The synthesized poly-(2, 5-bis((2-ferroceneylethyl)oxy carbonyl)styrene) (PFECS) is shown in the Figure 11. On a clean GCE, ~5 μl GO was deposited and reduced by CV in 0.02 M PBS of pH 5.6 in the potential range of 0 to −1.4 V which was dried in ambient temperature then 5 μl PFECS of conc. 1 mg·mL−1 in DCM was deposited over the rGO and was allowed to dry in ambient conditions and stored at 4 ℃ until further used. The CV studies showed that the introduction of the rGO increased the current response in the potential window of 0 to 0.7 V and thus proving its introduction to be beneficial. The current-time curves reveal linear range of 10 μM to 19 mM, with a sensitivity of 117.142 μA·mM−1·cm−2.
3.3.3. Platinum based composites
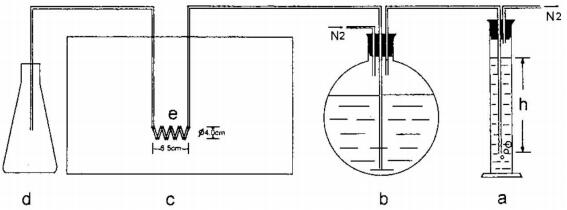
Pt NPs are another group of metal which have attracted enormous research in the field of metal-graphene based nnaocomposites for H2O2 sensing due to its grander electrocatlytic properties [155,156]. Vanegas et al. stated that the decoration of Pt NPs over the graphene has led to large active surface area which would assists in the adhesion of molecules and further more accelerates the electron transfer rates, which is helpful in the sensing [157]. In recent years, many new methods of synthesis of Pt NPs/graphene composite have been successfully demonstrated such as chemical reduction, photochemical reduction and many more [158,159,160]. Among numerous methods present, microwave assisted synthesis was more influential on researchers because of its even and rapid heating [161,162]. Figure 12 shows the reaction equipment system used by Tu et al. those times for rapid heating. Liu et al. used microwave assisted synthesis route with porous graphene (PG) and H2PtCl6 being the precursor and EG the reducing agent [163]. Firstly, GO and CaCO3 were mixed evenly to form a slurry and then heat treated before washing with HCl to form PG. PG was re-dispersed in EG along with Pt precursor and stirred vigorously so that the Pt NPs got adhered on to the surface of PG, then it was microwave treated to yield Pt/PG. The modified electrode was tested against known concentrations of H2O2 and the linear range was found to be 1 to 1477 μM with a sensitivity of 341.14 μA·mM−1·cm−2 and LoD of 0.50 μM.
Bragaru et al. has proposed that the homogenous distribution of Pt NPs over rGO improved the stability for which graphene's surface treatment with polyelectrolytes is very important [164]. Guo et al. demonstrated microwave assisted synthesis of Pt/rGO hybrids from a water/EG solution of H2PtCl6 and GO with poly(methacrylic acid sodium salt) (PMMA) [165]. PMMA is helpful in enhancing the stability of graphene sheets by hydrophobic interaction as well as controlling the shape and size of the forming Pt NPs. The electrochemical investigation of Pt NPs/graphene electrocatalytic capability towards H2O2 showed the linear range of 1–500 μM with detection limit of 80 nM.
The use of bimetallic nanocatalysts got popularized in order to reduce the cost of the catalysts and simultaneously improving the catalytic characters of the nanocatalysts [166]. Liu et al. came up with a simple and facile strategy of immobilizing PtAu NPs over the surface of cetyl trimethyl ammonium bromide (CTAB) modified graphene [167]. In a typical synthesis procedure the graphene was first modified with CTAB utilizing the electrostatic attractions between the negatively charged graphene and positively charged CTAB, then PtCl6− and AuCl4− were attracted onto the positively charged CTAB and was then in-situ reduced by employing NaBH4 leading to formation of PtAuNPs-CTAB-GR composite. The amperometric studies reveal the linear range of 5 nM to 4.8 μM and LoD of 1.7 nM.
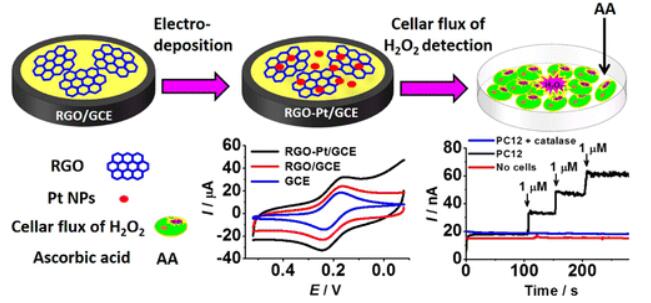
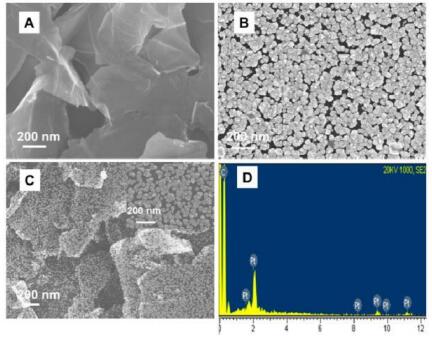
Apart from the chemical reduction procedures, electro-deposition is another technique followed in order to yield higher quality of composites along with controlling the shape of the forming NPs [168]. Zhang et al. electro-deposited Pt NPs on the rGO sheets from a solution containing 2 mM K2PtCl6 and 20 mM HCl by performing cyclic voltammetry [169]. The schematic for the RGO-Pt modified GCE for the detection of H2O2 from the cells is shown in the Figure 13. The microscopic images shown in Figure 14 revealed that the Pt NPs densely and uniformly distributed throughout the surface of graphene. The amperometric studies show that the linear range of 0.025–2 mM and a sensitivity of 459 ± 3 mA·M−1·cm−2 were achieved. The fabricated sensor was also tested for H2O2 in living cells and gave a wide range of linearity with lower detection limits. Apart from afore mentioned techniques sputtering deposition and photochemical reduction techniques also employed in the synthesis of Pt NPs-graphene composites [170,171].
3.3.4. Palladium based composites
Pd NPs-graphene based electrocatalyst are another group of composite materials where researchers have been extensively working. It also follows similar synthetic techniques such as chemical reduction, photochemical reduction, electrochemical reduction, impregnation adsorption etc. In most of the cases, GO or f-GO was co-reduced in the presences of Pd precursor either by electrochemical reduction, hydrothermal reduction or the use of various available reducing agents [172,173,174]. You et al. through electrochemical reduction have synthesised aminothiophenol (ATP)-functionalized GO decorated with Pd NPs [175]. The Pd NPs showed an even distributed without much agglomeration on the ATP funtionalized graphene layers. The electrochemical studies demonstrated the linear range to be 0.1 μM–10 mM, LoD to be 0.016 μM and sensitivity to be 492.09 μA·mM−1·cm−2.
3.3.5. Cobalt based composites
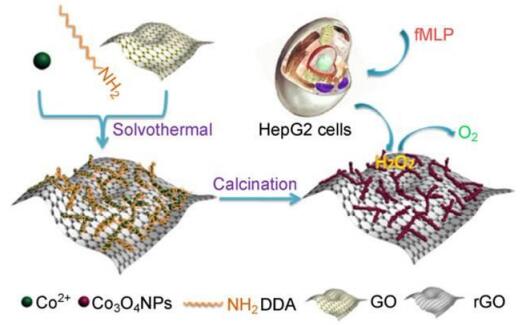
Recently, due to higher catalytic activities, good stability and abundance in occurrence non-noble metals have attracted good amount of research attention in the fabrication of economical and equally capable H2O2 sensors. For the afore mentioned reasons the researches are now greatly focusing on to the oxides and sulfides of other transition metals [176,177,178,179,180]. The synergistic chemical coupling between the graphene and the metal-oxide/sulfide was found beneficial towards the electrochemical sensing of H2O2. Kong et al. synthesized Co3O4 nano wires decorated rGO (Co3O4-rGO) via hydrothermal method, which was followed by thermal treatment [181]. The one-dimensional wires formed web-like structures due to the interaction with each other on the surface of rGO sheets. The synthetic procedure and the electrocatalytic mechanism are depicted in the Figure 15. The prepared composites exhibited an excellent electocatalytic performance against H2O2. The linear range of 0.015–0.675 mM, sensitivity of 1.14 mA·mM−1·cm−2 and LoD of 2.4 μM with excellent selectivity are reported. In another work, Li et al. prepared CoOx-rGO composite by electodepositing CoOx on the electrochemically reduced graphene oxide [182]. This method of synthesis provided the homogenous distribution of CoOx on the graphene sheets thus enhancing catalytic activities resulting in elevated performance. The sensitivity and the LoD were reported to be 148.6 mA·mM−1·cm−2 and 0.2 μM respectively. Zheng et al. synthesized cobalt-tetraphenylporphyrin/rGO (CoTPP/RGO) nanocomposite by non-covalent self-assembly method [183]. CoTPP molecules were adhered on the surface of the rGO sheets through non-covelent π–π interaction and got flattened over the rGO surface. The flattening of the CoTPP molecules further decreased the distance between the layers of the graphene sheets, which enhanced π–π stacking further. CoTPP/RGO showed excellent catalytic property towards oxidation as well as towards reduction of H2O2. Hosu et al. via chemical co-reduction route through ultra-sonication at 90 ℃/5 h in DMF containing GO and cobalt phthalocyanine tetracarboxylic acid [184]. The synthesized rGO/CoPc-COOH displayed greater stability, higher selectivity, better response time along with sensitivity and LoD being 14.5 nA·nM−1 and 60 μM, respectively. Kubendhiran et al. synthesized CoS/RGO by electrochemical co-precipitation method taking GO drop casted GC electrode and performed 15 consecutive CV cycles in an electrolyte containing Co2+ salt and thiourea at a scan rate of 50 mV·s−1 in the potential range of −1.4 to 0.2 V. The electrochemical study showed the linear range of 0.1 to 2542.4 µM with LoD of 42 nM and sensitivity of 2.519 μA·µM−1·cm−2 [185].
3.3.6. Iron based composites
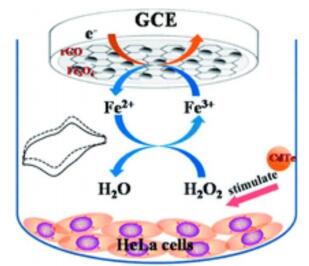
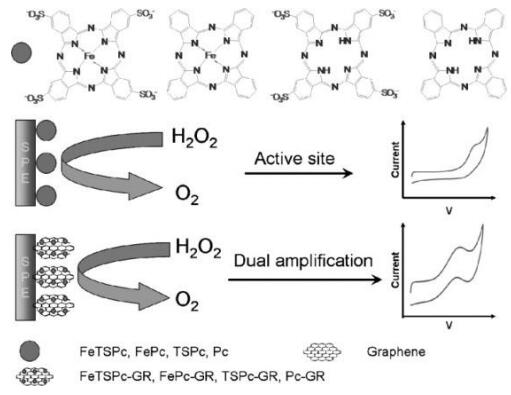
In recent past, iron oxides have received tremendous attention owed to low cost, recyclability, easy handling and admirable catalytic performance. Many researchers state that the graphene is the most appropriate support for the iron oxide as it stopped it from agglomeration and have one of the finest synergestic effects [186,187]. Karimi et al. in the basic medium via self-redox assembly have prepared Fe2O3-rGO taking sodium ferrate and GO as the precursors and reaction time was merely 15 min [188]. The synthesized composite showed a linear range of 0.05 to 9.0 mmol·L−1, LoD of 6.0 μmol·L−1 with longer stability and RSD of just 1.9%. Recent research claimed that Fe3O4 would be more beneficial as sensing material with graphene over Fe2O3 due to its higher conductivity, better catalytic property and greater stability [189,190,191]. The proposed mechanism is depicted in the Figure 16. Ye et al. synthesized 35–45 nm sized Fe3O4 particles over GO through co-precipitation method without the use surfactants or reducing agents [192]. The XRD analysis states that the nanoparticles formed were of fcc lattice and TEM images show that the Fe3O4 particles only are present on the rGO sheet. In addition to iron oxides, many iron complexes are also used as the electrode materials for the selective determination of H2O2 [193]. Zhu et al. through non-covelent functionalization synthesized iron-tetrasulfophthalocyanine-graphene nanocomposite (FeTsPc-GR) [194]. The modified electrode displayed excellent electrochemical performance with linear range of 2 × 10−7 to 5 × 10−3 M, LoD of 8.0 × 10−8 M and sensitivity of 36.93 ± 0.05 mA·mM−1·cm−2. The oxidative mechanism of H2O2 is illustrated in the Figure 17.
3.3.7. Copper based composites
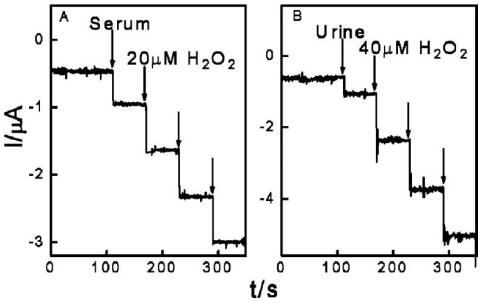
Copper oxides and sulfides are an additional group of metal derivatives which forms stable composites with graphene and have attracted researchers enormously around the globe in the field of H2O2 sensors [195,196,197]. Bai et al. synthesized CuS/RGO composite by taking Cu and S precursors as CuCl2 and Na2S, respectively following a hydrothermal method at 180 ℃/24 hrs [198]. The prepared composite offered a wide range of activity from 5–1500 μM and the LoD of 0.27 μM. The prepared composite was tested against real samples of various cancer patients in their serum and urine and the results were satisfactory comparable as shown in the Figure 18. Liu et al. synthesized rGO wrapped Cu2O nanocubes and the composite was used for sensing H2O2 [199]. They compared the materials with graphene and without graphene in the composites and shown the advantage of addition of graphene in terms of enhanced current response. The size and morphology of Cu2O NPs as well as its distribution over the graphene layers is evident from the microscopic images. The composite exhibited a good response time of < 7 s at a potential of −0.4 V. The linear current responses obtained for the H2O2 concentration ranges was between 0.6–7.8 mM (correlation coefficient R = 0.9970; Cu2O) and 0.3–7.8 mM (R = 0.9989; Cu2O/GNs). The limits of detection (LOD) were calculated to be 64.4 mM (Cu2O) and 20.8 mM (Cu2O/GNs) in the linear concentration range (S/N = 3). To examine the long-term electrochemical stability accelerated durability tests (ADT) were carried out in 0.1 M PBS solution of pH 7.4 by applying cyclic potential scan from −0.67 to 0.52 V at a scan rate of 0.1 V s. Liu et al. prepared a nanocomposite containing Cu2O, PANI, RGO by following an alkothermal reaction at 160 ℃ for 6 h [200]. The microscopic studies showed the homogenous distribution of Cu2O over the graphene surface. The electrochemical studies showed the linear range of 0.8 μM to 12.78 mM with sensitivity and LoD being 39.4 μA·mM−1·cm−2 and 0.5 μM. It showed the stability of 96% after 30 days of usage. The reproducibility of the six electrode fabricated independently showed a standard deviation of only 3.5% suggesting high reproducibility of the electrodes.
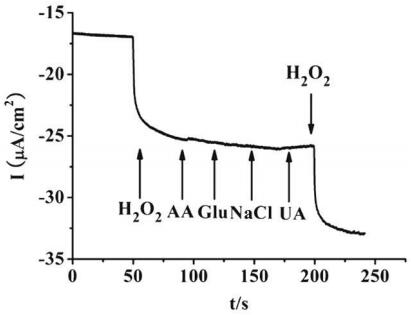
The amperogram is depicted in the Figure 19 which shows that the prepared composite had high selectivity towards H2O2 in the presence of various physiologically co-existing analytes. Kumar et al. synthesized Cu2O-GNP composite using a two-step electrodeposition technique where both Cu2O and GNP were synthesized from their particular precursors Cu2+ salt and a graphite rod respectively [201]. The authors reported synthesis of homogenousously distributed ultra small Cu2O NPs of dimensions 20 nm over the graphene surface. The electrochemical study showed the linear range of 0.2 to 1057.6 μM with the sensitivity of 52.8595 μA·μM−1·cm−2 and LoD of 34.32 nM. The electrode showed the stability of ~92% after 120 days of usage. Ding et al. demonstrated the use of Cu2O microsphere anchored graphene for the detection of H2O2. The synthesis was accomplished through one-step reduction process [202]. Initially, Cu precursor and GO in the presence of SDS were taken and stirred followed by the addition of weighed amounts of sodium ascorbate and NaOH were added and stirred for some more time. The electrochemical studied showed the linear response range of 0.005 to 2.775 mM (correlation coefficient 0.9974) and a detection limit of 0.0108 mM with excellent selectivity towards H2O2 in the presence of other analytes. Zhu et al. demonstrated the H2O2 sensing by synthesizing graphene by CVD growth on the Ni foam on to which Cu NPs were loaded [203]. Firstly, Ni foam was cleaned using ethanol, acetone and water, and then heat treated at 1000 ℃ in the tube furnace under controlled H2 atmosphere to remove the surface oxidation particles. Then graphene was grown using 10 sccm CH4 and 50 sccm H2 gas for 10 mins. Graphene coated Ni foam was inserted into the solution of CuSO4, due to galvanometric displacements reactions the Cu NPs were formed on the graphene surface. The electrochemical studies were done in 0.1 M PBS (pH 7.4). The amperometry studies showed the linear range from 50 μM to 9.65 mM and detection limit 1 μM.
3.3.8. Manganese based composites
Manganese derivatives combined with rGO are also found very capable as the electrode materials for H2O2 detection [204,205,206]. Through one step electrochemical method, Dong et al. synthesized MnO2 nanowires anchored on graphene nanohybrid paper [207]. They found higher selectivity, sensitivity and greater reproducibility. The shape and structure of the nanoparticle plays an important role in the determination of the electrochemical properties of the electrode material. Feng et al. after studying different morphologies of MnO2 determined that the sheet like structure of the MnO2 is more appropriate for sensing application as it has provide much more number of sites for the H2O2 to interact [208]. Therefore, later on the research much focuses on synthesis of sheet like MnO2 which could be anchored on the sheets like graphene for far better results. Mahmoudian et al. synthesized MnO2 nanotubes/reduced graphene oxide nanocomposite following a hydrothermal synthetic route at 150 ℃ for 12 h [209]. The microscopic studies showed a number of rods converging onto each another and forming a web like structure over the surface of graphene. The composite showed elevated electrochemical results with a linear range of 0.1–80 mM, LoD of 1.25 µM and the sensitivity of 194.5 A·mM−1·cm−2. Li et al. synthesized MnO2/graphene oxide nanocomposite through solution mixing at refluxing condition [210]. The sensor displayed a linear range of 5–600 µM, sensitivity of 38.2 mA·mM−1·cm−2 and LoD of 0.8 M. They fabricated 10 individual sensors and were tested for reproducibility and the standard deviation was found to be 3.8% and also showed long term stability. The fabricated sensors were used to test real samples and the results were satisfactory and the authors credited the catalytic behavior of MnO2. Graphene based non-enzymatic H2O2 sensors have been summarized in Table 2 along with their sensing performances.
Table 2. Performance of graphene based H2O2 sensors.
| Material |
Electrode Performance |
Ref. No. |
| Linear Range (μM) |
Detection Limit (μM) |
Sensitivity |
| CR-GO |
0.05–1500 |
0.05 |
- |
[105] |
| graphene-MWCNT |
20–2100 |
9.1 |
32.91 μA·mM−1·cm−2 |
[113] |
| GN/Au-NPs |
0.5–500 |
0.22 |
- |
[123] |
| AuEPG |
0.5–4900 |
0.1 |
75.91 μA·mM−1 |
[124] |
| RGO-PMS@AuNPs |
0.5–50000 |
0.06 |
39.2 μA·mM−1·cm−2 |
[128] |
| Au NPs-N-GQDs |
0.25–13327 |
0.12 |
186.22 μA·mM−1·cm−2 |
[129] |
| GO/Au@Pt@Au |
0.05–17500 |
0.02 |
- |
[133] |
| NG-hAuPd |
0.1–20 |
0.02 |
5095.5 μA·mM−1·cm−2 |
[134] |
| Au NPs/RGO/Ni foam |
50–1750 |
- |
47.4 μA·mM−1·cm−2 |
[135] |
| Au NPs/RGO/Ni foam |
3–1060 |
1.60 |
156 μA·mM−1·cm−2 |
[136] |
| Ag/S-RGO |
100–136500 |
0.14 |
- |
[140] |
| Ag NWs-graphene |
10–34300 |
1.0 |
12.37 μA·mM−1·cm−2 |
[141] |
| AgNR-rGO |
100–70000 |
2.04 |
- |
[142] |
| AgNP/rGO |
100–80000 |
7.1 |
- |
[144] |
| AgNPs-TWEEN-GO |
20–23100 |
8.7 |
0.7459 μA·mM−1·cm−2 |
[145] |
| PpyNFs/AgNPs-rGO |
100–5000 |
1.099 |
0.7367 μA·mM−1 |
[147] |
| AgNPs-GO |
10–20000 |
0.5 |
- |
[151] |
| Ag-MnOOH-GO |
0.5–17800 |
0.2 |
59.14 μA·mM−1·cm−2 |
[152] |
| AgNPs-MWCNT-rGO |
100–100000 |
0.9 |
330 μA·mM−1 |
[153] |
| Pt/PG |
1–1477 |
0.5 |
341.14 μA·mM−1·cm−2 |
[163] |
| PtNPs-GO-PDDA |
500–50000 |
1.3 |
- |
[164] |
| PtAuNPs-CTAB-GR |
0.005–4.8 |
0.001 |
165.4 μA·mM−1 |
[167] |
| RGO-Pt |
25–2000 |
0.2 |
4.59 × 105 μA·mM−1·cm−2 |
[169] |
| GO-ATP-Pd |
0.1–10000 |
0.01 |
492.09 μA·mM−1·cm−2 |
[175] |
| Co3O4-rGO |
15–675 |
2.4 |
1140 μA·mM−1·cm−2 |
[181] |
| CoOxNPs/ERGO |
5–1000 |
0.2 |
148.6 μA·mM−1·cm−2 |
[182] |
| rGO/CoPc-COOH |
100–12000 |
60 |
14.5 μA·mM−1 |
[184] |
| CoS/RGO |
0.1–2542.4 |
42 |
2519 μA·mM−1·cm−2 |
[185] |
| rGO-Fe2O3 |
50–9000 |
6.0 |
85 μA·mM−1 |
[188] |
| FeTSPc-GR-Nafion |
0.2–5000 |
0.08 |
36930 µA·mM−1·cm−2 |
[194] |
| CuS/RGO |
5–1500 |
0.27 |
35 μA·mM−1 |
[198] |
| Cu2O/GNs |
300–7800 |
20.8 |
- |
[199] |
| Cu2O-PANI-RGO |
0.8–12780 |
0.5 |
39.4 μA·mM−1·cm−2 |
[200] |
| Cu2O-GNP |
0.2–1057.6 |
0.03432 |
52859.5 μA·mM−1·cm−2 |
[201] |
| Cu2O-RGO |
50–2775 |
0.0108 |
52859.5 μA·mM−1·cm−2 |
[202] |
| Cu/RGO/Ni Foam |
50–9650 |
1 |
- |
[203] |
| MnO2/RGO |
100–80000 |
1.25 |
1.945 × 105 µA·mM−1·cm−2 |
[209] |
| GO/MnO2 |
5.0–600 |
0.8 |
38.2 μA·mM−1·cm−2 |
[210] |
4. Conclusions and future prospects
The article mainly concentrated on the recent advancements in the field of graphene based electrochemical H2O2 sensors. The article focused on the utilization of various electrocatalytic active materials to effectively reduce the over potentials for H2O2 oxidation or reduction. Though the earlier studies based on conventional materials showed considerable achievements but with the emergence of nanotechnology in the past decade enormously promoted the progress in this field. The unique properties of nanomaterials largely improved the sensitivity and selectivity of the electrochemical sensors. Graphene based materials received great attention due to its unique and attractive properties as well as were extensively applied in the field of electrochemical sensors. In this article, we highlighted the synthesis and application of various graphene based nanomaterials for the fabrication of electrochemical sensors for the H2O2 determination. In this article we have discussed about the various techniques followed and how the techniques enhance the electrochemical properties. In particular, recent developments in the various enzyme based biosensors for the determination of H2O2 with graphene based materials as the immobilized matrix have been summarized. Then the synthesis and application of various graphene supported metal derivatives as nanocatalyst for the construction of electrochemical sensors for the determination of H2O2 have been discussed in detail.
The research based on the artificial enzymes which can mimic natural enzyme is very meaningful. Natural enzymes are very difficult to manipulate during the construction of biosensor as they are very susceptible to environment and gets denatured easily. The poor stability of natural enzymes limits its usage in the fabrication of biosensors and long term usage in real application. In addition, the cost of the enzymes is very high compared to artificial enzymes which are robust and can be easily tailored as per the requirement.
Despite substantial progress has been made in the design and application of graphene based nanomaterials for electrocatalytic determination of H2O2, the development of new methods and techniques in the synthesis of graphene based nanomaterials with novel structures and extraordinary activities is still imperative. Moreover, in-depth understanding of structure-property relationship of graphene based nanocatlyst and exploring them more extensively for successfully applying them as electrochemical H2O2 sensor still needs continuous study and expansion. Better understanding of the chemistry and physics of the surface of the graphene and its interface interaction with the other molecules and the charge transport kinetics will give better knowledge of applying it as nano-scaffold in the field of sensors and biosensors. The adsorption mechanism of molecules on the graphene surface and the thorough understanding of their orientation may lead to further advancement of graphene composites in this field.
A wide range of new electrocatalytic nanomaterials are introduced every day and are expected to continuously advance and develop the electrochemical sensors for the accurate H2O2 determination. All the developments will facilitate the better understanding of physiological process participated by the H2O2 in living organism. Furthermore, tremendous influence of H2O2 sensing on clinical diagnostic, food safety, pharmaceutical development, environmental monitoring will progressively appear in near future.
Acknowledgments
Authors are thankful to the Director of CSIR-CMERI. Authors are also thankful to the Council of Scientific and Industrial Research (CSIR), New Delhi, India for funding Fast Track Translational Project (MLP-210812).
Conflict of interest
There is no conflict to declare.









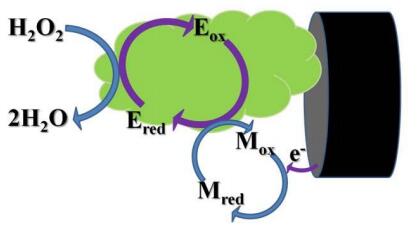
 DownLoad:
DownLoad: