1. Introduction
Electrohydrodynamic (EHD) casting has been used to make various forms of materials including fibers, coatings, films, and particles for applications in optoelectronics, energy conversion, sensing, and guided tissue regeneration. As for fiber preparation, the existing EHD casting process can easily generate randomly distributed fibers, but it is hard to control the orientation of the fibers. The 3D printing technology allows materials to be placed in controlled ways. Nevertheless, the resolution of 3D printing is still limited. Nanofibers can hardly be made directly through 3D printing. Integrating the electrohydrodynamic casting into 3D printing results in a new additive manufacturing technology, which allows the production of composite materials containing well-aligned 2D and/or 3D nanofibers for special applications. Based on the recent experimental research, a new manufacturing machine has been designed by attaching an electrohydrodynamic processing unit to a 3D printer. This electrohydrodynamic processing unit can be driven by the 3D printer to generate pre-programmed x–y–z three directional motions so that the nanofibers produced can be placed in the way as fully controlled by pre-set programs. Fundamental studies have been carried out to understand the science underpinning the new manufacturing technology. The objective of this paper is to provide a review of preparing 2D and 3D nanostructured composite materials through the layer-by-layer additive manufacturing process under the action of an electrohydrodynamic force. The nanostructured composite materials made by the new manufacturing technology have the properties of high surface areas and enhanced surface activities. Such properties could significantly increase the sensitivity of the materials to external signals and enhance the photon induced electron-hole pair generation at the surface of the materials. Based on earlier studies [1], at the metallic nanoparticle containing surface, an enhanced plasmonic effect has been found. The plasmonics increased the sensitivity of materials to sunlight. Consequently, the electron-hole pair generation in solar cells can be increased [2]. It is expected that the similar phenomena may also exist in the electrohydrodynamically cast composite materials containing functional nanoparticles, which is significant in promoting the performance of the composites for energy conversion.
Manufacturing composite materials containing nanofibers and nanoparticles via the innovative process in which the electrohydrodynamic (EHD) casting is integrated into the 3D printing has caught much attention. The EHD casting works by exposing a small jet of the selected material to a relatively high voltage, usually in the range of 5 kV to 30 kV. This high voltage causes the material undergoing stretching and bending to form nanofibers as it gets farther away from the jet. The traditional EHD manufacturing process can only produce randomly oriented nanofibers. To control the fiber orientation for the practical applications in optoelectronics, energy conversion, sensing, and guided tissue regeneration, a new manufacturing technology of combining 3D printing and EHD has developed. The existing 3D printing technology allows materials to be placed in the ways as planned. However, the resolution of 3D printing is limited. Nanofibers can hardly be made directly through 3D printing. Integrating the EHD casting into 3D printing is necessary for the new additive manufacturing technology. The new technology should make the production of composite materials containing well-aligned 2D and/or 3D nanofibers for special applications possible.
This review paper deals with the following issues: (1) how to design and make a new manufacturing machine consisting of an EHD casting system and a 3D printer, (2) how to use the machine to manufacture composite materials with functional nanoparticles uniformly distributed in polymer fibers, (3) how to perform heat treatment on the nanofiber composites to convert the polymer fibers into partially carbonized fibers, (4) how to test the functions of the composite materials for sensing and energy conversions, and (5) how to characterize the micro and nanostructures of the composite materials to understand the structure-property relations. It should be indicated that nanostructures such as nanofibers, nanotubes or nanoscale pores in functional composite materials can enhance the sensing and energy conversions performances due to the high surface areas of the active components. It is because such nanoscale features have the capability of maintaining the high surface areas and allow the improved properties for sensors and energy converters.
EHD forces include the electric repulsion, the fluid pump pressure, and the body force: gravity. Such forces may facilitate the uniform distribution of nanoparticles into polymer nanofibers. The manufactured composite materials may have enhanced thermoelectric and photovoltaic properties due to the special structure formation in the combined EHD casting and 3D printing processes. It is possible to make high performance sensors and energy converters with multiple components and 3D printed architectures. To show this technology, materials consisting of dispersed different nanoparticles in polyacrylonitrile (PAN) nanofibers are made. The nanoparticles are made from bismuth telluride and/or antimony telluride alloy compounds. Both of them are intrinsic narrow band semiconductors. Therefore, these nanoparticles can generate the thermoelectric and photovoltaic functions. The polyacrylonitrile polymer was mixed with the Bi-Te and Sb-Te alloy nanoparticles in a dimethylformamide (DMF) solvent. The uniform dispersion of the nanoparticles in the polymer nanofibers to form composites can be achieved via combined EHD casting and 3D printing. Then the high temperature heat treatment on the composites in hydrogen gas was conducted to convert the polymer nanofibers into partially carbonized fibers. The partially carbonized fibers are expected to have tuned electrical conductivities depending on the heat treatment temperatures. The higher the heat treatment temperature is, the better the conductivity of the carbon fibers. The carbon fibers will serve as electrical connectors to the Bi-Te or Sb-Te nanoparticles. The Seebeck coefficient of the composite materials was measured. Since such nanocomposites have the low-dimensional structures with high interface areas for phonon scattering, they are expected to have enhanced thermoelectric properties, i.e., high Seebeck coefficient, high electrical conductivity, and low thermal conductivity, which are required for effective energy conversions and sensing. In thermoelectric energy conversion process, the driving force for the energy conversion is the temperature gradient. The low thermal conductivity of the materials is the key factor that keeps the temperature difference for high thermoelectric energy conversion efficiencies. Morphology analysis was performed to understand the effects of some important manufacturing parameters such as nanoparticle content, polymer concentration, applied EHD casting voltage, pump pressure, 3D printing speed, and heat treatment temperature on the structure development of the composite materials. The structure-property relation for the composite materials will also be discussed in the paper.
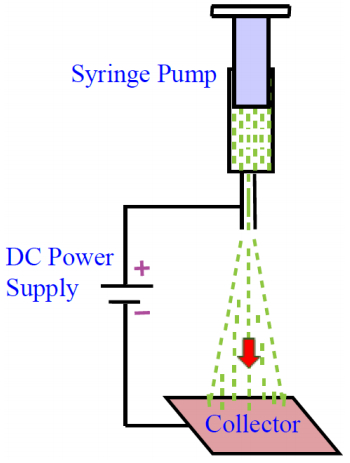
Electrohydrodynamic (EHD) casting as schematically shown in Figure 1 can be realized by exposing a small jet of the desired material to a relatively high DC voltage, usually in the range of several kilovolts to several ten kilovolts. The DC voltage causes the material to undergo stretching and bending as it gets farther away from the voltage point in the pattern of a Taylor cone [3]. EHD casting [4] allows the size of a droplet or jet from a fluid much smaller than the size of the injection needle. This is because the fluid to be cast is electrified and forms a Taylor cone. Fine droplets or jets then come out from the Taylor cone under the action of the electric force. Such a new casting method can eliminate the resolution limit from the size of the needle for casting. There is another advantage of low cost. The EHD process has made the production of nanoscale fibers cheaper and easier to accomplish than other developed methods such as chemical vapor deposition [5], X-ray lithography [6], and electron beaming writing followed by ion etching [7]. Therefore, the EHD process has been used for making nanofibers [8], particle-connected-by-nanofiber composites [9], nanofiber networks [10], nanoparticles [11], and microscale metal patterns [12].
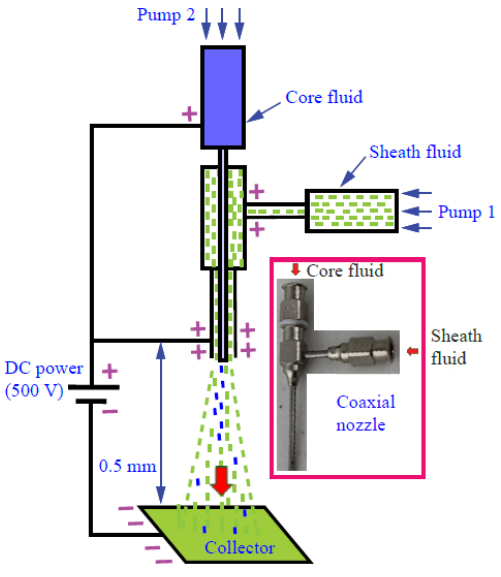
In addition to the single jet EHD, coaxial EHD has been studied for making nanofibers [13] and nanoscale spherical capsules [14]. During the coaxial EHD process, a coaxial nozzle as shown in Figure 2, is used. The main advantage of using a coaxial nozzle is that multiple components can be cast simultaneously. Other advantages include: (1) allowing high concentration polymers to be processed, (2) generating in-situ mixing of various solutions through interfacial mass transfer, and (3) controlling the delivery amount of each component by varying the pumping rate. For example, the outer liquid surrounds and encapsulated the inner one, which allows core-shell biodegradable nanofiber made for hydrogen storage [15], tissue repair [13], sustained drug release [16,17], and biochemical sensing [18]. Besides the biodegradable polymers, various other core and shell materials were used [19]. The core and the shell materials could be miscible or immiscible [20] depending on the structure to be made. Among the various core-shell materials, polyacrylonitrile (PAN) has caught much attention because it can be easily to be processed into submicron sized fibers [21], serving as the precursor for carbon nanofibers [22,23].
Controlling the structure in two dimensional (2D) and three dimensional (3D) forms has caught great interest [24]. For example, inkjet printing has been used for scaffolds generation [25]. Although microfabrication technology was used for cell culture formation [26], the more commonly used practice is 3D printing for generating biostructure tissues [27,28]. Combining the 3D printing with other technologies, for example, electrospraying, has recently been studied due to the better controllability of the deposition [29]. Such a combined process has been used for the p-typed conductive transparent oxide structure preparation [30]. Generally, 3D printing is frequently used for food fabrication [31] and biofabrication [32,33,34,35,36,37,38,39]. Although 3D printing can spatially control the material deposition very well, it has limited resolution, i.e., at millimeter or several hundreds of micrometer scales. For nanoscale resolution, electrohydrodynamic processing is the best [40]. Electrohydrodynamic processing including electrospinning and electrospraying is suitable for generating the required hierarchical scaffords, for example, micro and nanomotifs in bone structure [41]. EHD processing has also found applications for neural tissue regeneration [42], and functional gradient nanocomposites preparation [43].
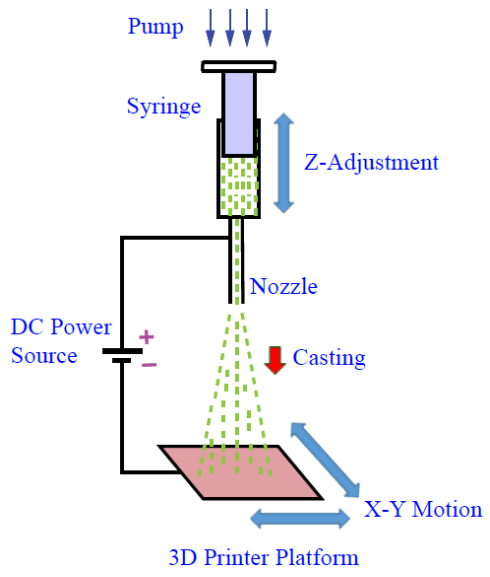
In order to preserve the controllability of 3D printing while keep the nanoscale feature formation capability, one of the ways is to develop a combined additive manufacturing process [44]. In view of this trend, a hybrid printing approach using multiple printing heads including inkjet printing head and electrospinning head has been proposed [45]. It should be able to resolve the challenge issue on porosity control in cell structure printing [46]. It can also achieve the better resolution of printed features that are normally impossible to get from the traditional rapid prototyping process [47]. Neural tissue generation as discussed in [48] could potentially be improved. Nutrient mixing and diffusion in tissue structure as mentioned in [49] can be controlled better by depositing the tailored pore architectures. Other related progress in this direction includes the indirect 3D printing [50], modified 3D writing [51]. Both approaches can generate the nanoscale features as shown by electrospinning [52]. Considering the promising development in this direction, it is the major objective of this review article to introduce the better controllability of the nanostructures by integrating the near field electrohydrodynamic processing into 3D printing. Traditional far-field electrospinning and electrospraying use high voltage over 10 kV, which causes issues such as high power consumption, sever electric discharging, electric shock and fire safety. On the contrary, near-field method uses less than 0.5 kV electrical power source to drive the electrohydrodynamic process. This provides the logic of integrating the unit into a 3D printer to form a new machine which overcomes the above mentioned disadvantages associated with the existing EHD machines. The schematic of the new machine is illustrated in Figure 3.
As p-type semiconducting materials, Sb-Te alloys in single crystal state and in conventional sintered polycrystalline form have been studied for thermoelectric energy conversion. Besides the thermoelectric application, Sb-Te based compounds doped with Ge and Sn have been used as phase-change materials (PCMs) in rewritable optical data storage media [53]. Sb-Te materials can be processed by pulsed current sintering [54], electrodeposition [55], radio-frequency magnetron sputtering [56], and thermal evaporation [57]. Sb-Te film can also be deposited from choline chloride containing ionic liquids [58]. To make flexible energy converters, Sb-Te film was deposited on a Kapton™ polyimide substrate with presetting curvatures followed by mechanical deformation [59] or by screen printing [60]. Sb-Te alloy takes a distorted rock salt crystal structure [53,61].
Through doping with some other elements such as Ag, In, Bi, Se, Pb and Cu [62,63,64], the thermoelectric, transport and corrosion properties of Sb-Te alloys can be improved. The carrier concentration in Bi-containing Sb-Te alloys can be controlled by a tellurium-evaporation-annealing process [65]. Oxygen removing through hydrogen reduction [66] and hot pressing [67] has been found to enhance the electrical conductive behavior of Sb-Te materials. While the thermal conductivity of the Sb-Te alloys can be suppressed by controlling the crystal orientation [68] and grain size of the alloys [69].
Nanostructured Sb-Te alloys in the form of electrodeposited or sputtered thin films [70,71,72,73], particles [74], and nanowires [75] show interesting properties. Nanocomposites consisting of lead telluride nanoinclusions in the bismuth antimony telluride matrix were made by an incipient wetness impregnation approach followed by hot pressing [76]. The study reveals that nanosized PbTe in the bulk Bi-Sb-Te matrix results in a special doping effect and changes the transport properties of the matrix alloy. Due to the interface effect, such a composite material system provides the decreased thermal conductivity without sacrificing the electrical conductive property. Since the introduction of low temperature processing method for complex Sb-Te alloys [77], it is possible to make carbon/Sb-Te composites and polymer/Sb-Te composite materials. For example, through aerosol deposition at room temperature, Bi-Sb-Te can be deposited on the polyethylene terephthalate polymer to form thermoelectric legs [78]. Although vacuum infiltration followed by cold pressing was used for preparing multi-walled carbon nanotube/Bi-Te composites [79], there is no early work reported on making partially carbonized nanofiber/Sb-Te composite materials.
Bismuth based metallic alloys possess a semiconducting behavior. For example, bismuth telluride has a narrow energy band of Eg = 0.19 eV [80]. Another important bismuth alloy, Bi2Se3, shows the band gap around 0.35 eV [81]. They are suitable for thermoelectric energy conversion. They also find applications for infrared radiation monitoring and temperature sensing. Bismuth telluride may be embedded into an insulating material, for example alumina, to form a composite material. Such a composite offers enhanced thermoelectric figure-of-merit [82,83]. It is expected that the electrical conductivity and Seebeck coefficient of the composites could be dramatically increased, while the thermal conductivity could be kept as low as possible by selecting the suitable insulating matrix and controlling the bismuth alloy filler loading amount. This approach could provide a way for the improvement of the thermoelectric performance of polymeric materials. Polymeric composite materials (ultrahigh molecular weight polyethylene based) with separated networks of CNT/Bi2Te3 hybrids were made [84]. However, the Seebeck coefficient of the polyethylene composite is only about 29 μV/K, which is much lower than that of the pure Bi-based thermoelectric materials. Electrodeposition of polyaniline and Bi2Te3 simultaneously was conducted. It is found that the thermoelectric power of the composite material in the high temperature range (380~420 K) is higher than that of the pure polyaniline [85].
To increase the phonon scattering, incorporating nanoscale entities into the Bi-Te alloy matrix has also been considered. The dispersion of SiC nanoparticles in Bi2Te3 reduced the thermal conductivity but did not significantly increase the electrical resistance of the alloy resulting in the 18% increase in the figure of merit [86]. Carbon nanotube addition also resulted in the increasing phonon scattering in Bi2Te3
[87]. Scattering of phonons is also anticipated in quantum-confined structures as can be made by epitaxial growth [88], hydrothermal synthesis [89,90], electrodeposition [91], and combined solution chemical method and thermal processing [92]. The mechanism for the increased phonon scattering may be due to the interface reflection effect as discussed in [93] for the Al2O3/Bi2Te3, and in [94] for silicon films.
Progress has been made in manufacturing Bi-based alloys and the Bi2Te3-containing composite materials. Bi-based alloys are typically manufactured through spark plasma sintering and corrosion [95,96], mechanical alloying [97], self-assembling [98], organic-assisted growth [99], and interface reaction [100]. For composite materials, several major methods have been used including chemical reaction approach [101], mechanical alloying [102], plasma sintering [103], electrochemical synthesis [104,105], and aerosol deposition [106]. Recently, carbon-based or carbon mixing with bismuth based alloys composite materials have caught much attention for thermoelectric applications [87,95,98,107,108,109]. Due to the low figure of merit, the thermoelectric performance of the composite materials still remains to be improved. Considering the promising development in this direction and some unsolved issues in this field, it is worthy of discussing how to better integrate the near field electrohydrodynamic processing into 3D printing. In the rest of the paper, how to manufacture composite materials containing nanofibers and nanoparticles by the innovative process in which the electrohydrodynamic (EHD) casting is integrated into 3D printing will be reviewed first. Then, a scalable manufacturing process ensuring high process yield, process and product repeatability and reproducibility, along with optimized quality control will be shown. Finally, energy conversion and sensing functions of the nanocomposite materials will be presented.
2. Materials, manufacturing and characterization
The integration of EHD casting into 3D printing to make composite materials containing carbon nanofibers and a bismuth telluride and/or antimony telluride particles is presented. Specifically, a new manufacturing machine is designed and made. This machine consists of an EHD casting unit installed on a 3D printer. Manufacturing bismuth telluride and antimony telluride particle loaded carbon nanofiber composite materials by the new machine is performed. First, Bi2Te3 and Sb2Te3 particles were dispersed into a polyacrylonitrile (PAN) polymer nanofiber mat through the EHD force-assisted 3D printing process. Then, stabilizing the PAN at intermediate temperatures and carbonizing the polymer through high temperature annealing were carried out to obtain carbon fiber composite materials. The functions of the composite materials for energy conversions and sensing were validated. Fiber mats with controlled architectures or patterns can be manufactured through the combined EHD casting and 3D printing process.
Characterization of the composite materials was conducted, which includes examining the structure of the materials and testing their energy conversion performances. Specifically, the scanning electron microscopic (SEM) analysis was performed to reveal the morphologies and the compositions of the composite materials. Energy conversion properties of converting heat and photon energy into electricity were revealed. Hyperthermia behavior of converting electromagnetic wave energy into heat was also studied. The thermoelectric, hyperthermia, and photovoltaic effects of the composite materials were evaluated with the emphasis on thermoelectric behavior. To make multiple component composites, the EHD unit consisting of a coaxial nozzle was designed. The EHD force-assisted 3D printing machine was made by attaching the EHD unit to a 3D printer. The as mentioned composite materials were made using the new machine. Seebeck coefficient of the composites was measured using an HP 34401A multimeter. The electrical conductivity maps of the composites were generated using an atomic force microscope (AFM).
3. Integrating near-field electrohydrodynamic casting into 3D printing
First of all, the near-field EHD casting was performed to make sure the size and orientation of nanofibers can be controlled. Our preliminary work indicated that by changing the voltage and the distance from the fiber collector, the diameters of the fibers can be easily controlled in the range from several ten nanometers to several hundred nanometers. The micro and nanofibers prepared by the far-field EHD casting at a high voltage of 15 kV were found randomly distributed. On the contrary, the controlled deposition of nanofibers by integrating near-field EHD processing into 3D printing generated well-aligned polyvinylpyrrolidone (PVP) nanofibers.
More precise controlling the size of the nanofibers was performed to understand the effect of manufacturing parameters on the quality of the fibers. The orientation of the nanofibers can be better controlled by optimizing the near-field EHD casting parameters. The regular fiber alignment is critical for some applications such as guided tissue regeneration, fast responsive sensing, and high efficiency energy conversions. Therefore, it is necessary to use a near-field EHD process to generate nanostructure. To obtain better controllability of the fiber orientation, the voltage was kept in the range from 0.5 to 1.2 kV. The near field condition was maintain by keep the space between positively charged nozzle and the negatively charged fiber collector as close as 500 microns, which is the gap between the tip of the extruder to the flatbed of the 3D printer.
4. Improved EHD casting system design
A coaxial nozzle was designed first for the EHD casting. Secondly, integrating the near-field EHD casting unit into a 3D printer was done. The integrated machine allowed fiber materials to be placed much more precisely than those shown in earlier work. It must be noted that if just the 3D printing was used, the resolution would be only in the millimeter range. Consequently, no nanofibers could be made directly through 3D printing. Therefore, the design of a new manufacturing machine should attach an EHD casting unit to a 3D printer. Such a new machine runs by using the 3D printer for generating pre-programmed x–y–z three directional motions so that the nanofibers came out from the EHD casting unit could be placed in the way as designed by the computer programming. The fluid control unit in the EHD casting system allows polymer solutions to be delivered with the required amount.
To show that integrating the EHD casting into 3D printing could lead to a new additive manufacturing technology which allows to produce aligned three dimensional nanostructures with multiple components, nozzles with a coaxial structure was made. Different solutions can be delivered to the tip of the coaxial nozzle.
5. Manufacturing nanoparticle loaded composite fibers
The solvent used was dimethylformamide (DMF). Bi2Te3 and Sb2Te3 raw powders were used as the functional components in the composite materials to be made. The polyacrylonitrile (PAN) polymer was dissolved in the solvent. Generally, the PAN solution was prepared by adding approximately 10% in weight of the PAN powder into the DMF solvent. For a typical experiment, 10 g PAN polymer was added into 90 ml DMF solvent and stirred for an hour to allow the PAN powder to dissolve into the solvent. Then 10 g refined Bi2Te3 or Sb2Te3 powders with the nominal size less than 1 µm were added into the PAN solution.
The solution containing PAN polymer, Bi2Te3 or Sb2Te3 powders, and DMF solvent were filled in a plastic vessel as the sheath fluid. The core fluid only consisting of the PAN polymer in DMF will also be loaded into another plastic vessel. The two plastic vessels were connected with two precision syringe pumps. The two pumps can precisely control the injection flow rate of the two solutions. The distance between the tip of the nozzle for injection and the receiving target may be kept at a distance of 0.5 mm. A constant flow rate of the solutions injected by the syringe pumps may be kept at 0.1 mL/min. Under ambient temperature, pressure and humidity conditions, a DC voltage of 0.8 kV can be applied at the tip of the nozzle to electrify the solutions. This electrified state allows the mixture material to overcome the surface tension of the solutions. The cast fibers can be collected on the flatbed of the 3D printer. The electric potential difference between the tip of the nozzle and ground collector leaded the charged jet to cast fibers on the collector continuously. The 3D printer allows the control of the orientation of the cast nanofibers. In other words, the collector may be set on an x–y–z table, which can translate in x-, y-and z-directions as shown in Figure 3. From this processing step, the product collected is a composite mat containing Bi-Te or Sb-Te nanoparticles within the PAN nanofibers.
6. Stabilization and carbonization
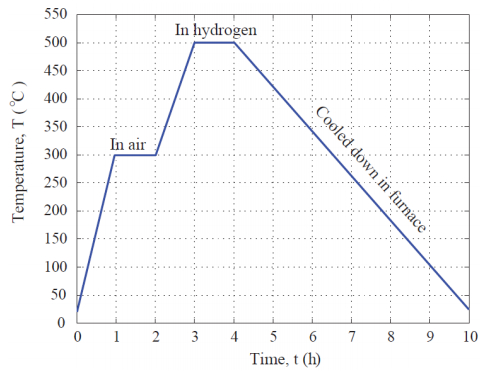
In order to form electrically conductive network around the Bi-Te and Sb-Te particles, the PAN nanofibers were stabilized and converted into partially carbonized nanofibers through the heat treatment in protective atmosphere. The heat treatment can be divided into two steps as shown in Figure 4.
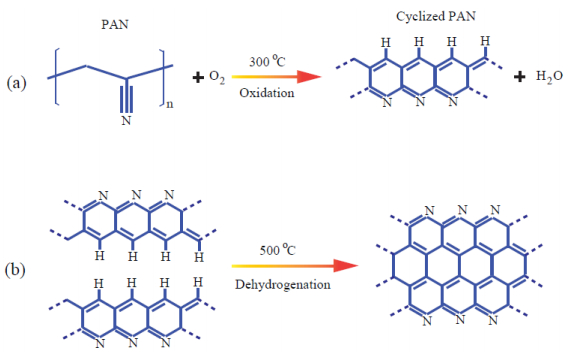
First, the composite specimen was out in the quartz tube and heated up to 300 ℃ in ambient atmosphere. After being kept at 300 ℃ for one hour, the composite fiber material was heated up slowly to 500 ℃. Hydrogen was inducted carefully into the chamber during the heating from 300 to 500 ℃. This prevents the Bi-Te or Sb-Te being oxidized. The PAN fiber started partial carbonizing. After the material was heat treated at 500 ℃ for one hour, it was cooled down naturally with the furnace to the room temperature. It is believed that the PAN polymer underwent cyclization and oxidation when it is heated in the temperature range from 200 to 300 ℃ in air [110,111,112]. In this work, a stabilizing temperature of 300 ℃ was used. The PAN molecules were cyclized and transformed into a non-meltable ladder structure as reported earlier [113,114,115]. Figure 5a shows the cyclized structure developed from the oxidation of PAN molecules in air around 300 ℃. Some oxygen in the functional groups such as = O and –OH attached to the backbone structure of cyclized polymeric carbon [116,117] was removed due to the exposure to the hydrogen atmosphere. At even higher temperature of 500 ℃ in protective atmosphere, the cyclized structure became condensed and formed 2D networks as shown in Figure 5b. In order to determine the elemental compositions of the composite materials, energy dispersive X-ray diffraction spectra (EDS) were obtained by mapping the selected areas on the materials.
7. Energy conversion and sensing behavior characterization
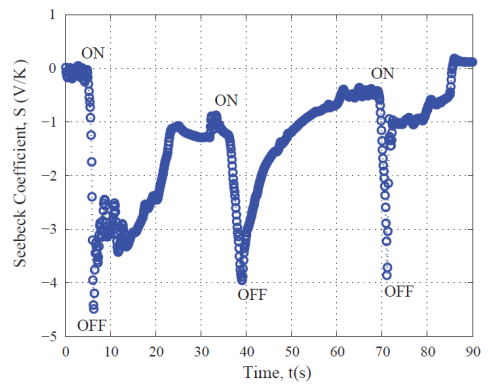
The thermoelectric response of the Bi2Te3/carbon nanofiber (CNF) and Sb2Te3/carbon nanofiber (CNF) composites was examined using a thermal wave testing method. Here we focus on the results obtained from the tests on the Bi2Te3/carbon nanofiber (CNF) composite. During the experiment, a 1.5 kW Drill Master heating gun was used to blow hot air towards the composite material specimen. Preliminary study of a Bi2Te3/carbon nanofiber (CNF) specimen with the width × length dimension of 15 mm × 50 mm shows promising results. When the 110 V AC power supply to the heat gun was ON, the open circuit voltage of the specimen dropped about 0.5 V. The temperature of the hot air reached the surface of the specimen was around 150 ℃. The room temperature of the cold and was about 23 ℃ under the test condition. As known, the Seebeck coefficient can be calculated by the following equation.
where ΔV is the voltage difference generated, and ΔT refers to the temperature difference between the hot and cold ends.
As plotted in Figure 6, the estimated value of S for the Bi2Te3/carbon nanofiber (CNF) material is about –4 mV/K. These results provide us important information. First, the composite material shows a general n-type behavior because the voltage dropped to a negative value when the specimen was heated. Second, the best carbon based composite materials—the stacked graphene sheets based thermoelectric material can only reach a Seebeck coefficient value of –90 µV/K [109]. The result from our current study shows that the Bi2Te3/CNF composite mat is more than 44 times stronger than the currently existing carbon composite materials.
Based on the strong thermoelectric effect of the Bi2Te3/CNF composite material, tests on the sample as a prototyped sensor to monitor the warm air flow due to exhaling and inhaling of human were made. The results from the preliminary study were obtained [23]. First, a relatively short exhaling phase (5 s) was followed by a longer inhaling stage (15 s) in a complete cycle and the test results are plotted. Interestingly, the warm air from the exhaling stage caused the negative voltage generation. The surface temperature of the hot end of the specimen can be monitored by an INF165 infrared thermometer available from UEi Test Instruments, Beaverton, OR. The hot end surface temperature of the specimen was around 31 ℃. And the cold end surface temperature was about 26 ℃. From the voltage difference in the exhaling and inhaling stages, it was found that the Seebeck coefficient was approximately 4 mV/K. This value is consistent with the result as obtained by the heat gun testing experiment shown in Figure 6. The test results related to a short exhaling phase (5 s) followed by a short inhaling stage (5 s) in a full cycle are also obtained. It was found that due to the short recovery time for the temperature in the inhaling cycle, the voltage changed in a relatively small range. The data revealed a general trend of decreasing in the open circuit voltage.
The breathing pattern of a patient with coughing symptom may be monitored. It was found that the breathe-in signals were momentarily strong because the air came out due to the coughing as shown by the sharp drop of the voltage. Because of the reflexing actions, the period right after the breathe-in and the following breath-out signals reveal irregularity as evident by the zig-zag patterns. The implication of the test results is that an inexpensive sensor may be built based on the highly sensitive thermoelectric responses of the Bi2Te3/CNF composite material.
In addition to manufacturing the above composites containing particles and fibers, integrating electrohydrodynamic casting into 3D printing can also generate new structures. For example, co-casting two immiscible fluids, silicone oil as the core fluid and 10% polyacrylonitrile in dimethylformamide as the sheath fluid, resulted in the formation of PAN polymer nanofiber networks [10]. The high temperature heat treatment in Ar or H2 can convert the polymer nanofiber networks into carbon networks. Such a unique network structure showed p-type semiconducting behavior. It has been found long time ago that the electrical resistivity of the partially carbonized fibers can be tuned in a wide range [118]. Based on this unique electrical transport behavior, the electrohydrodynamic cast composite fibers could be potential candidates for applications in optoelectronic devices.
8. Conclusions
Integrating the electrohydrodynamic casting into 3D printing represents a new manufacturing technology. This new technology has been successfully used for making Bi-Te/PAN nanofiber composite materials. It is also scalable to produce fiber mats. The high temperature heat treatment converts the composite nanofibers to polymeric carbon nanofibers (CNFs). Morphology analysis reveals the uniform distribution of the Bi-Te particles in the partially carbonized nanofiber (CNF) matrix. The CNFs form networks connecting the Bi-Te particles. Thermoelectric response tests indicate that the absolute value of the Seebeck coefficient of the Bi-Te/CNF, 4 mV/K, is much higher than that of the currently available carbon based thermoelectric materials or Bi-Te alloys. Photovoltaic response measurement of the heat treated Bi-Te/CNF composite mat specimen shows a semiconducting behavior. Bi-Te is infrared (IR) radiation sensitive due to its narrow band structure. In addition, the CNF in the Bi-Te/CNF composite material is sensitive to the visible light. Therefore, the composite material generates responses in a wider spectrum range than the existing materials. It has the potential to be made as optical-electric sensors working in the frequency range from IR irradiation to the visible light.
Acknowledgements
This work was sponsored by National Science Foundation (NSF) under Grant Number CMMI-1333044. The partial support by the 2017–2018 California State Polytechnic University Pomona Provost's Teacher-Scholar program is also acknowledged.
Conflict of interest
The author declares that there is no conflict of interest.









 DownLoad:
DownLoad: