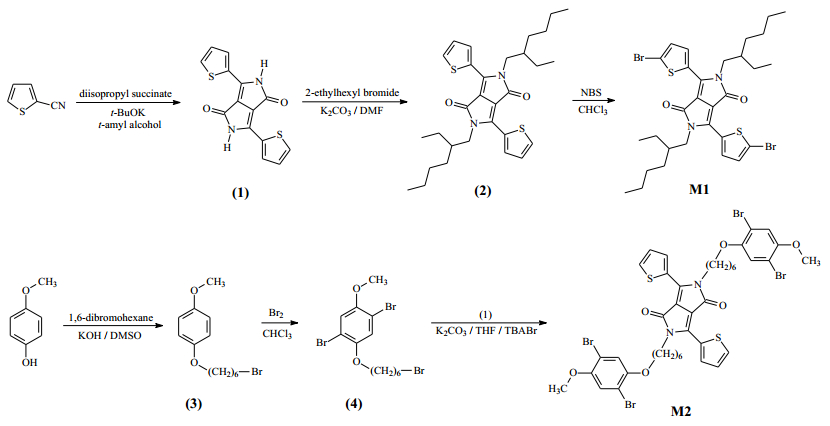
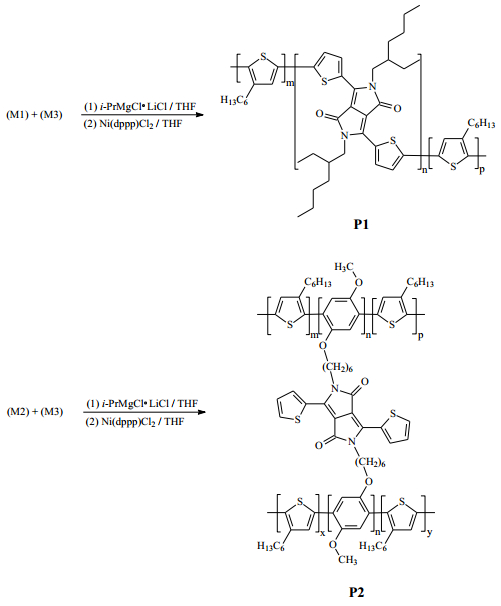
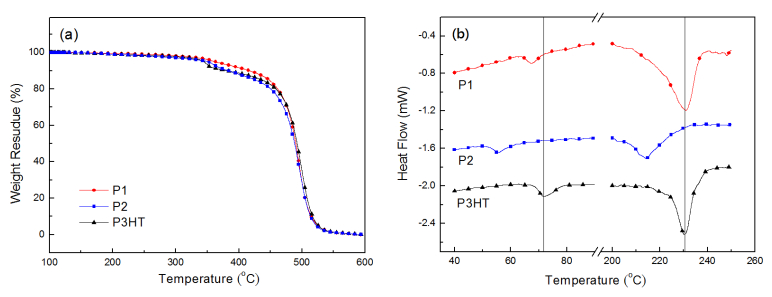
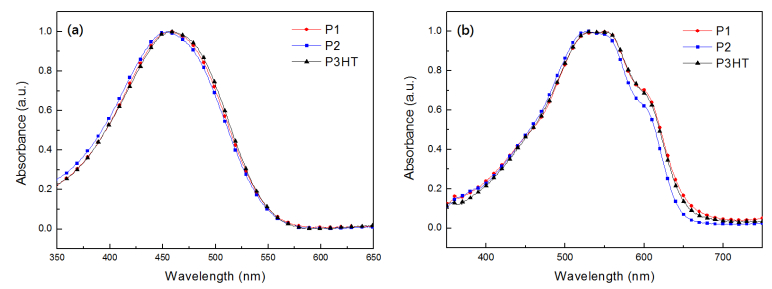
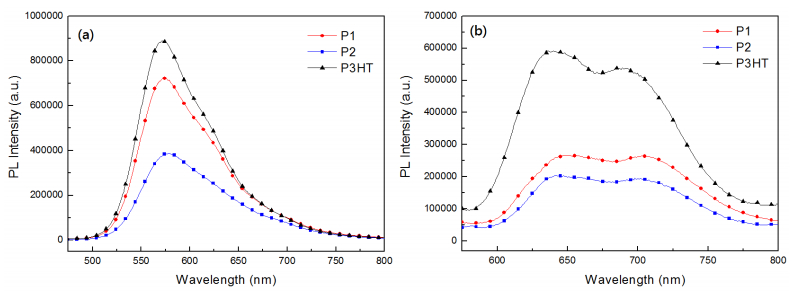
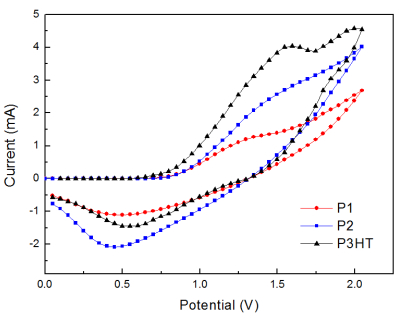
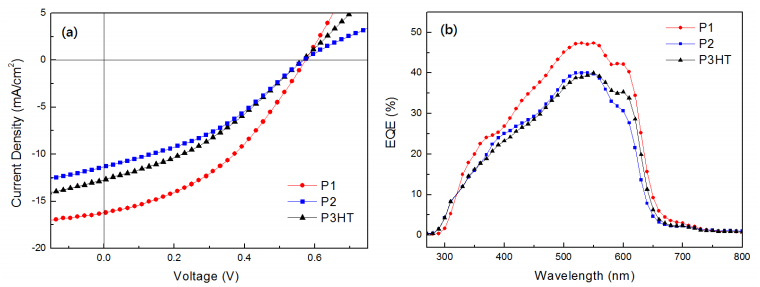
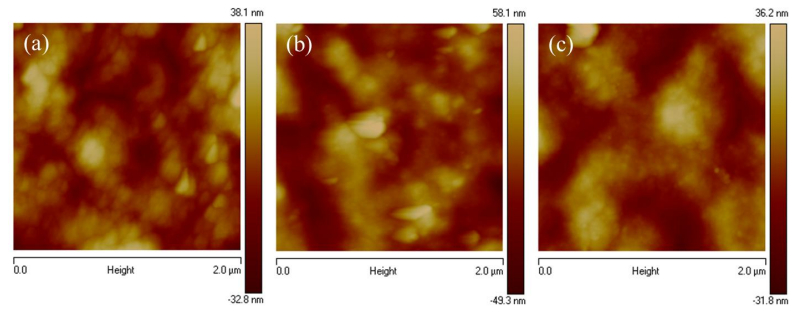
Two novel polythiophene derivatives with linear or hyperbranched architectures using diketopyrrolopyrrole (DPP) as linking groups as well as normal poly(3-hexylthiophene) (P3HT) were synthesized via the Universal Grignard metathesis polymerization. The molecular weights of the linear polythiophene containing DPP linking moieties are higher than those of P3HT, while molecular weights of the hyperbranched one are smaller. The main decomposition temperatures of polymers were measured at 470 °C from TGA experiments. The UV-vis absorption behaviors of the DPP-containing polymers are similar to that of P3HT; moreover, these DPP-containing polythiophenes show distinct PL decay both in solution and thin film states. The electrochemical experiments reveal that the incorporation of DPP groups resulted in lowering HOMO levels of polymers. All polymers were blended with PC61BM and used as active layers for the fabrication of inverted polymer solar cells. The power conversion efficiency of devices based on linear and hyperbranched polythiophenes reached 3.74% and 2.38%, respectively, revealing comparable or even higher efficiency than the one based on normal P3HT.
1.
Introduction
Recently, the world interests in dealing with the risk of the new virus (SARS-CoV-2) or (COVID-19). This novel coronavirus emerged recently from China with a total of 45171 confirmed pneumonia cases. It is the third highly pathogenic human coronavirus that occurs in the last two decades after coronavirus and coronavirus of Severe Acute Respiratory Syndrome (SARS) [1]. In both hospital and family settings, the person-to-person transmission was documented [1]. Consequently, further spread in public and healthcare environments is crucial. The transfer of coronaviruses from contaminated dry surfaces, including self-inoculation of the nose, eye, or mouth mucous membranes, was proposed, emphasizing the importance of a thorough comprehension of the persistence of coronavirus on inanimate surfaces [1]. A series of public social distancing measures to reduce transmission rates of COVID-19 were implemented in the context of the emergency response. As a result, many researchers have published several papers in order to study and examine this virus, such as ([1,2,3,4,5,6,7,8,9,10,11,12]).
Pawlak's [13] methodology for dealing with rough sets has been proposed to solve the problems of the inexact and ambiguous knowledge. This theory is centered on equivalence relations induced from the data composed from the studied real-life problem. Therefore, the application of this theory is restricted by the equivalence relation, since it is only dealing with an information-system with whole information. So, to handle complex and difficult applied problems, many authors proposed numerous generalizations such as similarity relation [14], pre-order relation [15], reflexive relation [16], general binary relation [17,18,19], topological approaches [20,21,22,23,24] and coverings [25,26]. Most of them failed in satisfying Pawlak's rough set properties.
The central aims of the current work are divided into three objectives. Firstly, we define for the first time; a new generalized neighborhood called (initial-neighborhood) induced from a binary relation. Properties of this neighborhood are examined and the special cases of the binary relation for this neighborhood are studied. Based on this new neighborhood, we introduce new generalized rough approximation operators called (initial-rough approximations). These approximations are a generalization to Pawlak's rough sets and their applications. The properties of the suggested approximations are studied and the relationships among them and the previous works such as (Yao's approach [17], Allam et al.'s approach [18], and Dai et al.'s approach [27]) are established. Many examples and counterexamples to illustrate these relationships are investigated. Moreover, we will prove that the proposed approximations satisfy all characteristics of Pawlak's rough sets in the general case. Decision-making problems need some accurate tools to make an accurate decision. In 2020, Zhang et al. [28] and Zhan et al. [29] presented different types of multi-criteria decision-making methods based on a fuzzy rough set model with fuzzy α-neighborhoods and applied them in decision-making problems. On other hand, Ghorui et al. [8] have successes in the identification of dominant risk factors involved in the spread of COVID-19 using a hesitant fuzzy MCDM methodology.
Topology and its applications [30] have been pivotal subjects in many real-life applications (such as [31,32,33,34,35,36]). In (2013), M. Lellis Thivagar and C. Richard [36] presented the concept of a "nano-topology" based on a general topology induced from Pawlak's rough set approximations. They have exposed numerous applications of this model in resolving various applied problems in the economics, engineering, social science, and the medical sciences, etc. Nano-topology represents a minimal topology that can be constructed from the rough approximations which consist of three open sets namely (the lower approximation, upper approximation, and the boundary region of a rough set) beside the universe and the empty set. So, this notion depends basically on an equivalence relation and thus this restricts the application field. Accordingly, the second aim is to extend this notion to any binary relation, and hence we will induce generalized nano-topologies using the suggested approximations. In addition, we will state and prove the conditions that any generalized rough set approximations generate generalized nano-topology such as (Yao [17], Allam [18], and Dai [27] approximations). We will prove that the proposed method is more accurate than the others methods. Moreover, we study its properties and give some examples of these topologies.
On the other hand, we will introduce a new method to make a topological reduction of the attributes generated from a multi-information table. In the multi-information table, the suggested relation is a general binary relation (for example, a reflexive relation), so Pawlak's approach cannot be applied and hence we cannot use M. Lellis Thivagar and C. Richard [36] method in this case. Accordingly, the suggested method in the current paper can be used, and hence we can apply the notion of generalized nano-topology in decision-making.
The third purpose of our contribution is to create a specific effect of such crucial mathematical ideas with continuous nature and to propose a novel methodology for mathematical exploration in real-life problems. In fact, we introduce a medical application in decision-making on coronavirus disease (COVID-19). Thus, we determine the impact factors in infection caused by Coronavirus "COVID-19". Finally, we also give some algorithms which can be used to have the infected values with COVID-19 for a sample of ten patients. These results may help the doctor to make the best decision. Therefore, we can say that the suggested approaches may be useful in discovering the vagueness of the data and help in the decision-making of real-life problems such as in the medical diagnosis which needs accurate decisions.
2.
Pawlak's rough sets and generalized rough sets
The main objective of the current article is to present the basic definitions and results that used through the paper.
2.1. Pawlak rough set theory
Definition 2.1.1 [37] Suppose that A and B are two sets. A binary relation R from A to B (or between A and B) is defined by a subset of the Cartesian product A×B, that is the set of ordered pairs (θ,ω)∈R where θ∈A and ω∈B.
Note that: The binary relation R can be from A to itself, and then R is said to be a binary relation on A. In addition, the ordered pair (θ,ω) can be represented by θRω and we say that ω is related to θ by R. Accordingly, θ is a predecessor of ω and ω is a successor of θ and thus we describe the θR={ω∈A:θRω} (resp. Rθ={ω∈A:ωRθ}) as after set (resp. fore set) of the element θ∈A.
Definition 2.1.2 [37] A binary relation R on a set A is said to be:
(i) Reflexive: if for every θ∈A,θRθ.
(ii) Symmetric: if for every θ,ω∈A and θRω, then ωRθ.
(iii) Transitive: if for all θ,ω,ρ∈A, θRω and ωRρ, then θRρ.
(iv) Similarity or tolerance: if R is a reflexive and symmetric.
(v) Pre-order or dominance: if R is a reflexive and transitive.
(vi) Equivalence: if R is a reflexive, symmetric and transitive relation.
Definition 2.1.2 [13] Consider U is a finite set called (universe), and B represents an equivalence relation on U, we write U/B to symbolize the class of all equivalence classes of B and [α]B to indicate an equivalence class in B containing an element x∈U. Then, the pair (U,B) is called an approximation space and for any A⊆U, we propose the Pawlak-lower and Pawlak-upper approximations of A by: B∗(A)={α∈U:[α]B⊆A} and B∗(A)={α∈U:[α]B⋂A≠∅}, respectively. Accordingly, we define the following regions:
 The boundary region of A⊆U: BNDB(A)=B∗(A)−B∗(A).
The boundary region of A⊆U: BNDB(A)=B∗(A)−B∗(A).
 The positive region of A⊆U: POSB(A)=B∗(A).
The positive region of A⊆U: POSB(A)=B∗(A).
 The negative region of A⊆U: NEGB(A)=U−B∗(A).
The negative region of A⊆U: NEGB(A)=U−B∗(A).
The accuracy of Pawlak's approximation is: μB(A)=|B∗(A)||B∗(A)|, where B∗(A)≠φ.
Remark 2.1.1 According to Pawlak in [13], we notice that:
(i) A is called an exact set if B∗(A)=B∗(A) and we refer to the pair (B∗(A),B∗(A)) by rough sets with respect to B.
(ii) If BNDB(A)=φ, then A is an exact set with respect to B and thus μB(A)=1. On the other hand, A is a rough set with respect to B if BNDB(A)≠φ and μB(A)≠1.
(iii) If a subset A is defined by a predicate P and x∈U, we get the next interpretation:
- x∈POSB(A) interprets to x certainly has property P.
- x∈BNDB(A) interprets to x possibly has property P.
- x∈NEGB(A) interprets to x definitely does not have property P.
Thus, a boundary region represents the doubtful (or uncertainty) region. So if we reduce this region, then we can make an accurate decision.
Proposition 2.1.1 [13] Suppose that φ represents an empty set and Ac is a complement of A in U. For each A,B⊆U, the followings are held:
Note that: The properties (L9) and (U9) mean that the lower and upper approximations are exact sets while the properties (L10) and (U10) illustrate that the elements in U/B, are exact sets.
2.2. Yao's rough sets
Definition 2.2.1 [17] If R is a binary relation on the universe U. Then, for each α∈U, we propose its "right neighborhood" as follows:
Definition 2.2.2 [17] If R is a binary relation on the universe U. Then, the right-lower and right-upper approximations of A⊆U are proposed, respectively, by
Definition 2.2.3 If R is a binary relation on U. The right-positive, right-negative and right-boundary, region and the right-accuracy of approximations of a subset A⊆U are defined, respectively, by:
Note that: If κr(A)=1, then Bndr(A)=φ and A is a right-exact set. Else, it is a right-rough set. The above approximations satisfy the properties (L3–L7), and (U2, U4–U7) in a general case. The remainder properties of Pawlak are satisfied for some cases of relation, as Theorem 2.2.1 illustrates.
Theorem 2.2.1 [17] If R is a pre-order relation on the universe U and A⊆U. Then, the right-lower and right-upper approximations of A, defined by Definition 2.2.2, satisfy the properties of Pawlak; rough sets in Proposition 2.1.1.
2.3. Allam et al.'s rough sets
Definition 2.3.1 [18] If R is a binary relation on the universe U. Then, for each α∈U, we propose its "minimal right neighborhood" (in briefly, minimal-neighborhood) as follows:
Definition 2.3.2 [18] If R is a binary relation on U. Then, the minimal-lower and minimal-upper approximations of A⊆U are given, respectively, by
L_⊓(A)={α∈U:N⊓(α)⊆A} and ¯U⊓(A)={α∈U:N⊓(α)∩A≠φ}.
Definition 2.3.3 [18] If R is a binary relation on U. Then, the minimal-positive, minimal-negative and minimal-boundary, region and the minimal-accuracy of minimal-approximations of a subset A⊆U are defined, respectively, by:
Note that: If κ⊓(A)=1, then Bnd⊓(A)=φ and A is a minimal-exact set. Otherwise, it is a minimal-rough set. The above approximations satisfy the properties (L3–L7), and (U2, U4–U7) in a general case. The rest properties of Pawlak are satisfied for some cases of relation, as Theorem 2.3.1 illustrates.
Theorem 2.3.1 [18] If R is a reflexive relation on U and A⊆U. Then, the minimal-lower and minimal-upper approximations of A, defined by Definition 2.3.2, satisfy the properties of Pawlak's rough sets in Proposition 2.1.1.
2.4. Dai et al.'s rough sets
Definition 2.4.1 [27] If R is a binary relation on the universe U. Then, for each α∈U, we define its "maximal right neighborhood" (in briefly, maximal-neighborhood) as follows:
Definition 2.4.2 [27] If R is a binary relation on U. Then, the maximal-lower and maximal-upper approximations of A⊆U are defined, respectively, by
L_⨆(A)={α∈U:N⨆(α)⊆A} and ¯U⨆(A)={α∈U:N⨆(α)∩A≠φ}.
Definition 2.4.3 [27] Consider R is a binary relation on U. The maximal-positive, maximal-negative and maximal-boundary, region and the maximal-accuracy of maximal-approximations of a subset A⊆U are defined, respectively, by:
Note that: If κ⨆(A)=1, then Bnd⨆(A)=φ and A is a maximal-exact set. Else, it is a maximal-rough set. The above approximations satisfy the properties (L3–L7), and (U2, U4–U7) in a general case. The remainder properties of Pawlak are satisfied for some cases of relation, as Theorem 2.4.1 illustrates.
Theorem 2.4.1 [27] If R is a similarity relation on the universe U and A⊆U. Then, the maximal-lower and maximal-upper approximations of A, that defined by Definition 2.4.2, satisfy the properties of Pawlak's rough sets in Proposition 2.1.1.
3.
Generalized rough sets based on a new type of generalized neighborhoods
The main objective of the current section is to suggest new generalized rough set approximations called "initial-approximations" based on a new neighborhood called "initial-neighborhood". This neighborhood is established from a general binary relation and then no restricted conditions on the application field. So, the existing section is divided into three subsections. The first one is dedicated to suggesting the new generalized neighborhood "initial-neighborhood" generated from a general binary relation. Besides, its properties are studied and the relationships between it and the other neighborhoods are examined with counterexamples. In the second subsection, we generate new generalized rough sets based on the initial-neighborhood. These approximations satisfy all properties of Pawlak's rough sets without any restrictions. Finally, in the last subsection, we introduce many comparisons between the suggested methods and the others that existing in the literature.
3.1. Initial neighborhood and its properties
The concept of "initial-neighborhood", generated from a general binary relation, is introduced and its properties are studied in the current subsection. Moreover, we study the different cases of it in different kinds of the binary relation. Besides, the connections between this neighborhood and the other types are investigated with counterexamples.
Definition 3.1 Consider R is a binary relation on the universe U. For each α∈U, we define its initial right neighborhood (in briefly, initial-neighborhood) as follows:
The key goal of the next results is to present the elementary properties of the initial-neighborhoods.
Lemma 3.1 If R is a binary relation on U. Then, for each α∈U:
(i) α∈Ni(α).
(ii) Ni(α)≠φ.
(iii) If β∈Ni(α), then Ni(β)⊆Ni(α).
Proof:
The proof of (i) and (ii) is follows from Definition 3.1.
The proof of (iii) is follows by using Definition 3.1, if β∈Ni(α). Then Nr(α)⊆Nr(β) (1)
Now, let γ∈Ni(β). Then Nr(β)⊆Nr(γ). Therefore, by (1), Nr(α)⊆Nr(γ) and this implies γ∈Ni(α). Consequently, Ni(β)⊆Ni(α).
Note that: In Lemma 3.1 (iii), it needn't be Ni(β)=Ni(α) generally. The next example demonstrates this fact.
Example 3.1 Consider U={a,b,c,d} and R={(a,a),(b,a),(a,d),(c,b)} is a binary relation on U. Then we get the following:
Clearly, a∈Ni(b) and Ni(a)≠Ni(b).
Remark 3.1 Suppose that R be a binary relation on U. For each α∈U, the right-neighborhood and initial-neighborhood are independent (not comparable) in general as demonstrated in Example 3.1.
The next examples show that the right-neighborhood and initial-neighborhood are not comparable in case of R is a reflexive, symmetric and transitive relation, respectively.
Example 3.2 Consider U={a,b,c,d} and R={(a,a),(a,b),(a,c),(b,b),(b,c),(b,d), (c,c),(d,d)} is a reflexive relation on U. Then we get the following:
Example 3.3 Consider U={a,b,c,d} and R={(a,b),(b,a),(b,c),(c,b),(c,d),(d,c)} is a symmetric relation on U. Then we get the following:
Example 3.4 Consider U={a,b,c,d} and R={(a,a),(a,b),(b,d),(c,c),(a,d)} is a transitive relation on U. Then we get the following:
The subsequent results clarify the relationships among the suggested neighborhood "initial-neighborhood" and the previous neighborhoods (right-neighborhood, minimal-neighborhood and maximal-neighborhood).
Lemma 3.2 If R is a reflexive relation on the universe U. Then, for each α∈U:
Proof:
(i) Let β∈N⊓(α), then β belongs to every right-neighborhood contains α. Since R is a reflexive relation, then α∈Nr(α) and this implies β∈Nr(α).
(ii) Let β∈Nr(α) and since α∈Nr(α). Then, β∈⋃α∈Nr(γ)Nr(γ)=N⨆(α).
(iii) Let β∈Ni(α), then Nr(α)⊆Nr(β). But α∈Nr(α), thus α∈Nr(β). Accordingly, Nr(β)⊆⋃α∈Nr(γ)Nr(γ) and hence β∈⋃α∈Nr(γ)Nr(γ)=N⨆(α).
(iv) Follows from (i) and (ii).
Note that: The next example shows that:
(i) The initial-neighborhood Ni(α) and the minimal-neighborhood N⊓(α) of each element α∈U are independent in the case of R is a reflexive relation on U.
(ii) The reverse relations in Lemma 3.2 needn't be true in general.
Example 3.5 Consider U={a,b,c,d} and R={(a,a),(b,b),(b,c),(c,c),(c,d),(d,d)} is a reflexive relation on U. Then, we get the following neighborhoods:
Lemma 3.3 If R is a similarity relation on U, then, for each α∈U:
(i) Ni(α)=N⊓(α).
(ii) N⊓(α)⊆Nr(α)⊆N⨆(α).
(iii) Ni(α)⊆Nr(α)⊆N⨆(α).
Proof:
(i) First, let β∈Ni(α), then Nr(α)⊆Nr(β). Since R is a reflexive relation, then α∈Nr(α) and this implies α∈Nr(β). Since R is a symmetric relation, then β∈Nr(α). Accordingly, β∈⋂α∈Nr(γ)Nr(γ)=N⊓(α) and hence Ni(α)⊆N⊓(α). Conversely, if β∈N⊓(α). Then β∈⋂α∈Nr(γ)Nr(γ) and thus β∈Nr(α). Since R is a symmetric relation, then α∈Nr(β). Thus, Nr(α)⊆Nr(β) and hence N⊓(α)⊆Ni(α).
(ii) By using Lemma 3.2, the proof is obvious.
(iii) The proof follows from (i) and (ii).
Note that: The subsequent example proves that the reverse relations in Lemma 3.3 needn't be correct generally.
Example 3.6 Consider U={a,b,c,d} and R={(a,a),(a,b),(b,a),(b,b),(b,c),(c,b), (c,c),(d,d)} is a similarity relation on U. Then we get the next neighborhoods:
Lemma 3.4 If R is an equivalence relation on U, then, for each α∈U:
Proof:
Straightforward.
3.2. Generalized rough sets based on initial neighborhoods
Based on the generalized neighborhood (initial-neighborhood), new generalized rough sets (called initial-approximations) are constructed and their properties will be examined. We will prove that these approximations represent a generalization to Pawlak's rough sets and some of their generalizations.
Definition 3.2 Consider R is a binary relation on U. The initial-lower and initial-upper approximations of A⊆U are proposed, respectively, by
Definition 3.3 Suppose that R is a binary relation on U. The initial-positive, initial-negative and initial-boundary regions and the accuracy of initial-approximations of a subset A⊆U are given, respectively, by:
Remark 3.2
(i) Obviously 0≤κi(A)≤1, for each A⊆U.
(ii) If κi(A)=1, then Bndi(A)=φ and A is an initial-exact set. Otherwise, it is an initial-rough set.
The next theorem gives the main properties of the initial-approximations.
Theorem 3.1 Suppose that R is a binary relation on U and A,B⊆U. Thus, the initial-lower and upper approximations satisfy the following statements:
Proof:
The properties (L1–L3) and (U1–U3) are obvious. So, we prove the rest properties as follows:
(L4) Let A⊆B and z∈L_i(A), then Ni(z)⊆A. Therefore, Ni(z)⊆B and this implies z∈L_i(B). Accordingly, L_i(A)⊆L_i(B).
(L5) Firstly, since A⋂B⊆A and A⋂B⊆B. Then L_i(A⋂B)⊆L_i(A)⋂L_i(B).
Now, let z∈L_i(A)⋂L_i(B). Therefore, Ni(z)⊆A and Ni(z)⊆B. Thus Ni(z)⊆(A⋂B) and accordingly z∈L_i(A⋂B). Hence L_i(A)⋂L_i(B)⊆L_i(A⋂B).
(L6) Since A⊆(A⋃B) and B⊆(A⋃B). Then, L_i(A)⋃L_i(B)⊆L_i(A⋃B).
(L7) (¯Ui(A))c=({x∈U:Ni(x)∩A≠φ})c={x∈U:Ni(x)∩A=φ}={x∈U:Ni(x)⊆Ac}=L_i(Ac).
(L8) First, L_i(L_i(A))⊆L_i(A), by using (L4). Now, let x∈L_i(A), then Ni(x)⊆A. We need to prove that Ni(x)⊆L_i(A) as follows:
Let y∈Ni(x), then Ni(y)⊆Ni(x) and thus inr(y)⊆A. So, y∈L_i(A) and this implies Ni(x)⊆L_i(A). Accordingly, x∈L_i(L_i(A)) and hence L_i(A)⊆L_i(L_i(A)).
By a similar way, we can prove the properties (U4)–(U8).
Remark 3.3 The reverse relations in (L6) and (U6) in Theorem 3.1 need not be right generally as demonstrated in Example 3.5.
Example 3.7 In Example 3.1, let A={a,b,c}, B={a,b,d}, C={b,c,d} and D={a,c,d}. Then, we get L_i(A)={a,b,c}, L_i(B)={a,b}, and L_i(A∪B)=U. Thus L_i(A)∪L_i(B)≠L_i(A∪B). Similarly, ¯Ui(C∩D)≠¯Ui(C)∩¯Ui(D).
Remark 3.4 Theorem 3.1 proved that the proposed approximations (initial-approximations) satisfy all properties of Pawlak approximations, in the general case, without adding any restrictions or conditions on the relation. Accordingly, we can say that our methodology represents a generalization to Pawlak's rough set theory. The following result confirms this fact.
Lemma 3.5 If R is an equivalence relation on U and A⊆U. Then, L_i(A)=B∗(A) and ¯Ui(A)=B∗(A), that is Pawlak approximations coincide with the initial-approximations in this case.
Proof: By Lemma 3.4, the proof is obvious.
3.3. Comparisons among Yao's method, Allam's method, Dai's method and current method
The current subsection is devoted to introducing numerous comparisons between the suggested approaches in the previous subsection and the other methods (such as Yao [17], Allam [18], and Dai [27]). We investigate several results to illustrate that the suggested technique is more accurate and stronger than the other methods. Besides, we will discuss the different types of relations in the different approaches. Moreover, we will show that the previous methods make some contradictions to Pawlak's rough set theory in the general case and hence they restrict the application fields. On the other hand, we prove that the proposed approach extends the application fields and does not make any contradiction to Pawlak's rough set theory.
Firstly, we introduce a comparison between the proposed method and the previous one (Yao, Allam, Dai approaches) in a general case of the binary relation to identifying the best method in real-life problems.
Example 3.8 Consider U={a,b,c,d} and R={(a,a),(a,d),(b,a),(c,b)} is a binary relation on U. Then, we get the subsequent neighborhoods:
Therefore, we calculate the approximations of all subsets of U using the current method and the previous methods (Yao [17], Allam [18], Dai [27] approaches) as shown in Table 1.
Remark 3.5 From Table 1, we can notice the following:
(i) Yao, Allam, and Dai methods are not suitable to approximate the rough sets in the general case, since they couldn't be applied for any relation (since the main properties of the approximations didn't hold) and thus these methods restrict the applications of rough set theory, for instance:
o L_k(A)⊈A⊈¯Uk(A), for every A⊆U and k∈{r,⊓,⨆}.
o ¯Uk(U)≠U and L_k(φ)≠φ.
For example, see the red highlighted cells in Table 1. Accordingly, these methods make some contradictions to the Rough set theory. Besides, all subsets are rough according to these methods and this represents vagueness for data.
(ii) On the other hand, our methods in the present paper are the best methods for approximating the sets in the general case, since the initial-approximations satisfy all properties of Pawlak's rough sets without any conditions or restrictions. Moreover, there are exact subsets in our approaches and this means that the suggested method can help in discovering the vagueness in the data.
The subsequent results familiarize the relationships between the methods of Yao, Allam, Dai and the current approaches.
Theorem 3.3 If R is a reflexive relation on U, then, for each A⊆U:
Proof:
We will demonstrate only the first statement and the others similarly.
Let x∈L_⨆(A), then N⨆(x)⊆A. By using Theorem 3.1, we obtain Nr(x)⊆A and this implies x∈L_r(A).
Corollary 3.2 Consider R is a similarity relation on the universe U and A⊆U. If A is a maximal-exact set, then A is an initial-exact set.
Note that: According to Example 3.5, we notice that:
(i) The initial-approximations, minimal-approximations and right-approximations needn't be a comparable (i. e. independent) in the case of R is a reflexive relation on U. For instance, if A={b,d}. Then we get: L_i(A)={b}. But: L_r(A)={d}, and L_⊓(A)={d}.
(ii) The reverse relations in Theorem 3.3 needn't be true in general. For instance, if A={a,b}. Then we get: L_i(A)=A. But: L_⨆(A)={a}⊊A.
Theorem 3.4 If R is a similarity relation on U, then, for each A⊆U:
(i) L_i(A)=L_⊓(A) and ¯Ui(A)=¯U⊓(A).
(ii) L_⨆(A)⊆L_r(A)⊆L_i(A).
(iii) ¯Ui(A)⊆¯Ur(A)⊆¯U⨆(A).
Proof:
(i) The proof of (i) follows from Lemma 3.3.
(ii) Let x∈L_⨆(A), then N⨆(x)⊆A. By using Lemma 3.1, we obtain:
- N⨆(x)⊆A⇒ Nr(x)⊆A and this implies x∈L_r(A).
- Nr(x)⊆A⇒ N⊓(x)⊆A and this implies x∈L_⊓(A).
(iii) By similar way like (ii).
Corollary 3.3 If R is a similarity relation on U, then, for each A⊆U:
(i) Bndi(A)=Bnd⊓(A) and κi(A)=κ⊓(A).
(ii) Bndi(A)⊆Bndr(A)⊆Bnd⨆(A).
(iii) κ⨆(A)≤κr(A)≤κi(A).
Corollary 3.3 If R is a similarity relation on the universe U and A⊆U. Then we get:
(i) If A is a minimal-exact set ⟹A is an initial-exact set.
(ii) If A is a maximal-exact set ⟹A is a right-exact set ⟹A is an initial-exact set.
Note that: The opposite of the previous results is not correct generally as Example 3.9 explains.
Example 3.9 According to Example 3.6, we compute the approximations of all subsets of U using the current method and the previous methods (Yao and Dai methods) as illustrated in Table 2.
Remark 3.6 According to Table 2, we note the next:
(i) The proposed method is more accurate than the other methods such as (Yao and Dai methods), that is: Bndi(A)⊆Bndk(A) and κk(A)≤κi(A) for every A⊆U and k∈{r,⨆}.
(ii) Every an exact set in Yao and Dai is also exact in the current method. The converse is not true.
4.
Generalized nano-topology and its applications
The core aim of this section is to extend the notion of Nano-topology [36] into any generalized rough sets. In fact, we generate a nano-topology induced from generalized rough set approximations. The necessary condition for generating this topology is proposed. Moreover, we illustrate the conditions for generating generalized nano-topology using Yao [17], Allam [18], and Dai [27] approximations. Besides, we demonstrate a medical application to show how we can use these types of techniques in deciding the impact factors of COVID-19 infections. These new types of basic models, as well as the procedure for decision-making techniques and the algorithm for applying the new approach in a medical setting, are described in detail.
4.1. Generalized nano-topology and its properties
Definition 4.1 Consider U is a finite set, and let L_(A) and ¯U(A) be the lower and upper approximations of A⊆U. The class TGn={U,φ,L_(A),¯U(A),Bnd(A)}, where Bnd(A) is the boundary region of A⊆U, is a topology on U if L_(A) and ¯U(A) satisfy Pawlak's rough set properties (L1-L8) and (U1-U8). Accordingly, TGn is said to be a "generalized nano-topology" (in briefly, Gn -topology) generated by the generalized rough approximations of A⊆U.
Note that: The above definition introduces the condition of generating a nano-topology by using any generalized rough sets. So, the following result illustrates the method of generating Gn -topology via Yao, Allam, Dai and the suggested approximations.
Theorem 4.1 Consider R to be a binary relation on a finite set U and A⊆U. The class TGnk={U,φ,L_k(A),¯Uk(A),Bndk(A)} is a Gn -topology on U if and only if
(i) Yao's approach (For k=r): R is a pre-order relation.
(ii) Dai's approach (For k=⨆): R is a similarity relation.
(iii) Allam's approach (For k=⊓): R is a reflexive relation.
(iv) Current approach (For k=i): R is a general binary relation.
Proof:
We only prove (iv) and the others by a similar way (using Theorems 2.2.1, 2.3.1 & 2.4.1).
(1) Firstly, it is clear that φ∈TGni.
(2) By using Theorem 3.1, we get ∀A,B∈TGni⇒A∩B∈TGni.
(3) By using Theorem 3.1, we get ∀A,B∈TGni⇒A∪B∈TGni.
Lemma 4.1 Let U be a finite set, and A⊆U. Then the base of the Gn -topology TGN is given by the class: BGnk={U,L_k(A),Bndk(A)}, for each k∈{r,i,⊓,⨆}.
Proof:
Straightforward.
The next example clarifies that the topologies TGnr and TGni are independent.
Example 4.1 Consider U={a,b,c,d} and R={(a,a),(a,b),(a,c),(b,b), (b,c),(c,c),(d,d)} is a pre-order relation on U. Then we get the following neighborhoods:
Nr(a)={a,b,c}, Nr(b)={b,c}, Nr(c)={c} and Nr(d)={d}.
Ni(a)={a}, Ni(b)={a,b}, Ni(c)={a,b,c} and Ni(d)={d}.
Therefore, the Gn -topologies of a subset X={a,c} are:
Using Yao's approach: TGnr={U,φ,{c},{a,b,c},{a,b}}.
Using initial approach: TGni={U,φ,{a},{a,b,c},{b,c}} .
Obviously, TGnr⊈TGni.
The subsequent example explains that TGn⨆ and TGni needn't be comparable.
Example 4.2 Consider Example 3.9, Therefore, Gn -topologies of a subset X={c,d} are:
Using Dai's approach: TGn⨆={U,φ,{d},{a,b,c}}.
Using initial approach: TGni={U,φ,{d},{c,d},{c}}.
Obviously, TGn⨆⊈TGni.
4.2. A medical application via a nano- topology in decision-making of COVID-19
The fast diffusion of the COVID-19 epidemic has caused widespread societal, economic, and political disruption. COVID-19 can be spread through physical contact between people. Unfortunately, no successful therapy exists at this time. Wearing masks, washing, sterilizing, and social distancing are the only preventive measures available. So, the importance of an accurate decision to diagnosis the infection of this virus is very useful to avoid the spread of the COVID-19. This subsection aims to demonstrate the significance of our approach in obtaining better and accurate tools to identify deciding factors of infections for COVID-19 in humans. In the present application, we use a general binary relation to illustrate the significance of the suggested technique in decision-making. Therefore, the other methods (such as Pawlak [13], M. Lellis Thivagar and C. Richard [36], Yao [17], Allam et al. [18], and Dai et al. [27]) can't apply here and hence we can say that our technique extends the application field of rough sets. Accordingly, we demonstrate that the suggested tools are more accurate than the other methods.
Our approach is based on removing redundant attributes to produce the successfully reduced set and formulate the core set of attributes. According to [12], we would like to mention that the information obtained in this Corona-virus analysis is from 1000 patients. Since the attributes in rows (objects) were identical, 1000 patients were reduced to 10 patients, and the most symptoms of COVID-19 are: Difficulty breathing, Chest pain, Dry cough, Headache, High Temperature, Loss of taste or smell. So, the application can be described as follows:
The set of objects as U={p1,p2,...,p10} denotes 10 listed patients, the attributes as {a1,a2,...,a6} = {Difficulty breathing, Chest pain, Dry cough, Headache, High Temperature, Loss of taste or smell}and Decision COVID-19 {d}, as follows in Information was collected by the World Health Organization as well as through medical groups specializing in corona virus (COVID-19).
Consider the following information system in the Table 3:
We are again drawing the consistent part of Table 3 by the next Table 4.
From Table 4, we obtain the symptoms of every patient are:
V(p1)={a1,a2,a4,a5,a6} , V(p2)={a1,a2,a3,a4,a5,a6}, V(p3)={a1,a2,a4,a6}, V(p4)={a1,a2}, V(p5)={a1,a2,a4}, V(p6)={a1,a3,a4,a5}, V(p7)={a4,a5}, V(p8)={a4,a5}, (p9)={a6} and V(p10)={a3,a4,a5}.
Now, we can generate the following relation:
We apply this relation for all attributes in the table to induce the neighborhoods as follows: R={(p1,p1),(p1,p2),(p2,p2),(p3,p1),(p3,p3),(p3,p2),(p3,p3),(p4,p4),(p4,p1),(p4,p2), (p4,p3),(p4,p5),(p5,p1),(p5,p3),(p5,p5),(p5,p2),(p6,p2),(p6,p6),(p7,p1),(p7,p2),(p7,p6), (p7,p7),(p7,p8),(p7,p9),(p7,p10),(p8,p1),(p8,p2),(p8,p6),(p8,p7),(p8,p8),(p8,p9),(p8,p10), (p9,p1),(p9,p2),(p9,p3),(p9,p9),(p10,p2),(p10,p6),(p10,p10)}.
Thus, the right neighborhoods of each element in U of this relation are:
Nr(p1)={p1,p2} , Nr(p2)={p2}, Nr(p3)={p1,p2,p3}, Nr(p4)={p1,p2,p3,p4,p5},
Nr(p5)={p1,p2,p3,p5} , Nr(p6)={p2,p6} Nr(p7)={p1,p2,p6,p7,p8,p10},
Nr(p8)={p1,p2,p6,p7,p8,p10} , Nr(p9)={p1,p2,p3,p9} and Nr(p10)={p2,p6,p10} .
Accordingly, the initial neighborhoods are:
Ni(p1)={p1,p3,p4,p5,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4}, Ni(p5)={p4,p5}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,p8}, Ni(p8)={p7,p8}, Ni(p9)={p9} and Ni(p10)={p7,p8,p10} .
Now, from Table 4, we get two cases are:
Case 1: (Patients infected with COVID-19)
The set of infected patients with COVID-19 is X={p1,p2,p6,p7,p9,p10}, then we get:
L_i(X)={p9} , ¯Ui(X)={p1,p2,p3,p6,p7,p8,p9,p10} and Bi(X)={p1,p2,p3,p6,p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 1: When the attribute a1 "Difficulty breathing" is removed:
Therefore, the symptoms of every patient are:
V(p1)={a2,a4,a5,a6} , V(p2)={a2,a3,a4,a5,a6}, V(p3)={a2,a4,a6}, V(p4)={a2}, V(p5)={a2,a4}, V(p6)={a3,a4,a5}, V(p7)={a4,a5}, V(p8)={a4,a5}, (p9)={a6} and V(p10)={a3,a4,a5} .
Thus, the right neighborhoods of each element in U of this relation are:
Nr(p1)={p1,p2} , Nr(p2)={p2}, Nr(p3)={p1,p2,p3}, Nr(p4)={p1,p2,p3,p4,p5},
Nr(p5)={p1,p2,p3,p5},Nr(p6)={p2,p6} , Nr(p7)={p1,p2,p6,p7,p8,p10},
Nr(p8)={p1,p2,p6,p7,p8,p10} , Nr(p9)={{p1,p2,p3,p9} and Nr(p10)={p2,p6,p10} .
Accordingly, the initial neighborhoods are:
Ni(p1)={p1,p3,p4,p5,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4}, Ni(p5)={p4,p5}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,(p8}, Ni(p8)={p7,p8}, Ni(p9)={p9} and Ni(p10)={p6,p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 2: When the attribute a2 "Chest pain" is removed:
By the same manner as in Step 1, we get the initial neighborhoods are: Ni(p1)={p1,p3,p4,p5,p6,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4}, Ni(p5)={p4,p5}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,p8}, Ni(p8)={p7,p8}, Ni(p9)={p9} and Ni(p10)={p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 3: When the attribute a3 "Headache" is removed:
By the same manner as in Step 1, we get the initial neighborhoods are:
Ni(p1)=U , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4}, Ni(p5)={p4,p5}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,p8,p10}, Ni(p8)={p7,p8,p10}, Ni(p9)={p9} and Ni(p10)={p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 4: When the attribute a4 "Dry cough" is removed:
By the same manner as in Step 1, we get the initial neighborhoods are:
Ni(p1)={p1,p3,p4,p5,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4,p5}, Ni(p5)={p4,p5}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,p8}, Ni(p8)={p7,p8}, Ni(p9)={p9} and Ni(p10)={p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 5: When the attribute a5 "High Temperature" is removed:
By the same manner as in Step 1, we get the initial neighborhoods are:
Ni(p1)={p1,p3,p4,p5,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p1,p3,p4,p5,p7,p8,p9}, Ni(p4)={p4}, Ni(p5)={p4,p5,p7,p8}, Ni(p6)={p6,p7,p8,p10}, Ni(p7)={p7,p8}, Ni(p8)={p7,p8}, Ni(p9)={p9} and Ni(p10)={p7,p8,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Step 6: When the attribute a6 "Loss of taste or smell" is removed:
By the same manner as in Step 1, we get the initial neighborhoods are:
Ni(p1)={p1,p3,p4,p5,p6,p7,p8,p9} , Ni(p2)=U, Ni(p3)={p3,p4,p5,p9}, Ni(p4)={p4,p9}, Ni(p5)={p3,p4,p5,p9}, Ni(p6)={p6,p7,p8,p9,p10}, Ni(p7)={p7,p8,p9}, Ni(p8)={p7,p8,p9}, Ni(p9)={p9} and Ni(p10)={p7,p8,p9,p10} .
Therefore, by using Theorem 4.1 and Lemma 4.1, the Gn -topology and its basis of X are:
Hence, from Steps (1–6), we observe that: the CORE is {a5, a6}, that is the impact factors to determine COVID-19 infection are "High Temperature and Loss of taste or smell".
Case 2: (Patients are not infected with COVID-19)
The set of infected patients with COVID-19 is Y={p3,p4,p5,p8}. By made the same steps like as Case (1), we obtain the same results.
Observation: From the CORE, we observed that "High Temperature and Loss of taste or smell" are the key factors for COVID-19 infection. Hence, these attributes are not dispensable attributes that represent the impact factors for COVID-19 infection.
At the end of the paper, we introduce an algorithm for decision making using our approaches.
5.
Discussion and conclusions
In our daily life, we often look some difficulties in which the correct decision-making is highly crucial. But in most of these cases, we become disordered about the precise solution. To obtain the best practicable explanation to these problems, we have to consider several factors involving to the solution. One of the significant subjects on rough sets is minimizing the boundary region, which aims to maximize the accuracy measure of decision-making. Neighborhoods, that generating from relations, are one of the techniques that have been used to achieve this goal. For this reason, in the current work, we have achieved three different goals. The first achievement is to introduce a new generalized neighborhood (initial-neighborhood) induced from a general binary relation without any extra restrictions. Besides, we have studied its properties in different cases of the relation and investigated the relationships with the other types of neighborhoods. Based on the suggested neighborhoods, we established new generalized rough sets (called initial-approximations). Theorem 3.1 and its consequences proved that these approximations represent a generalization to Pawlak's rough sets and their extensions. Many comparisons among the proposed approximations and the previous approaches such as (Yao [17], Allam et al. [18], and Dai et al. [27] methods) were investigated with counterexamples. In fact, we have illustrated that the proposed techniques extend the applications because it was used a general binary relation to define the approximations, and hence we can solve any real-life problem. On the other hand, we proved that the other methods couldn't apply to solve these problems in the general case as illustrated in Table 1. M. Lellis Thivagar and C. Richard [36] have introduced the notion of nano-topology based on Pawlak's rough sets [13] which restrict the application fields. So, our second goal, we have extended the concept of nano-topology to generalized nano-topology (Gn -topology) in order to emphasize the application field of this approach. Theorem 4.1 showed the condition of generating Gn -topology by Yao, Allam, and Dai methods.
Finally, we have used the suggested techniques to identify the impact factors (symptoms) of Corona-virus infection. The approach used here can be applied to analyze data of COVID-19 with quantitative or qualitative data by coding the data into the consistent part such as Table 4. In this application, we use a general binary relation to illustrate the significance of the suggested technique in decision-making. Therefore, Pawlak's approach and other methods couldn't apply here and hence we can say that our method extends the application field of rough sets. We have applied a topological reduction using a Gn -topology generated from the initial-approximations for data of 10 patients and hence we identified the impact factors of COVID-19 infection. Consequently, we may help the doctor to make an accurate decision about the diagnosis of patients. At the end of the paper, we introduced an algorithm for our method to be useful tools in the decision-making of any real-life problem.
Acknowledgements
Firstly, we would like to express thanks and appreciation to the editor and anonymous referees for the careful reading and thoughtful comments that helped in improving the paper. Besides, the Authors would like to express their gratitude to the ministry of education and the deanship of scientific research-Najran University-Kingdom of Saudi Arabia for their financial and Technical support under code number [NU/ESCI/18/003]. This research work supported by the Deanship of the Scientific Research at Najran University, Najran, Saudi Arabia [NU/ESCI/18/003].
Conflict of interest
The authors declare no conflicts of interest in this paper.









 The boundary region of
The boundary region of  DownLoad:
DownLoad: