Theoretical evaluation of the power efficiency of a moored hybrid floating platform for wind and wave energy production in the Greek seas

1.   Introduction

Predator-prey interaction is one of the most important subjects in the bio-mathematical literature. Therefore, many ecologists, mathematicians and biologists have investigated the dynamical behavior of the predator-prey system describing the interaction between prey and predator. The Lotka-Volterra predator-prey system, which is a fundamental population model, was introduced by Lotka ^[1] and Voltera ^[2]. The Lotka-Volterra model assumes that "the prey consumption rate by a predator is directly proportional to the prey abundance. This means that predator feeding is limited only by the amount of prey in the environment. While this may be realistic at low prey densities, it is certainly an unrealistic assumption at high prey densities where predators are limited, for example, by time and digestive constraints ^[3]." Since this model has neglected many real situations and complexities, it has been modified over the years by numerous researchers to ensure an accurate explanation and better understanding ^{[3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]}. Additionally, many ecological concepts, such as diffusion, functional responses, time delays and the Allee effect, have been added to the predator-prey system to facilitate a more accurate description ^{[7,13,14,15,16,20,23,24,25,26,27,28]}. It is known to all that one of the important modifications to the system is immigration. The concept of immigration, which affects the population growth rate, is an external factor expressed for an organism that establishes a particular habitat. Both immigration and migration happen when there is shortage of basic needs due to human activities. Especially, predator-prey interactions may be disrupted due to different reactions to climate change. Sometimes, regular and seasonal migration and immigration drive living organisms to adopt traveling and nomadic lives ^[29]. Additionally, the process of immigration is a significant phenomenon that helps the ecosystem to achieve a state of stability. Specially, discrete-time systems that take into account seasonal events, such as immigration are more realistic ^{[6,11,12,26,27,30,31,32,33,34,35]}. There have also been many studies on the role of immigration and its impact on population dynamics. Sugie et al. studied the existence and uniqueness of limit cycles in a predator-prey system with constant immigration in ^[26]. Zhu et al. investigated the local and global stability in a delayed predator-prey system with constant-rate immigration ^[27]. Also, they showed the existence of the global Hopf bifurcation. Tahara et al. analyzed the asymptotic stability of the predator-prey systems by adding an immigration factor to the prey and predator populations in a classical Lotka-Volterra system ^[36].

Rana ^[23] investigated the dynamics of a discrete-time predator-prey system of Holling I type. The author analyzed the existence and local stability of positive fixed points in the system and showed that the system undergoes flip and Neimark-Sacker bifurcations. Also, Rana observed that, when the prey is in a chaotic dynamic state, the predator can tend to extinction or to a stable equilibrium. It is important to consider the effects of the presence of some number of immigrants because most predator-prey systems in nature are not isolated. The immigration effect of the predator-prey system has been rarely studied in literature. Therefore, we will investigate a discrete-time predator-prey system with constant immigration of the prey population, as follows:

where $X_{t}$ and $Y_{t}$ represent the population densities of the prey and predator at time $t$, respectively. $r$ is the intrinsic growth rate of the prey, $a$ is the per capita searching efficiency of the predator, $b$ is the conversion rate of the predator, $d$ is the death rate of the predator and $s$ is the prey immigration rate. All parameters, $r, a, b, d$ and $s,$ are positive constants. The predator-prey system given by $(1.1)$ assumes that the prey grows logistically with an intrinsic growth rate $r$ and a carrying capacity of one in the absence of predation.

The contributions of this study are given as follows:

(1) The intended system consists of two interacting species, where one species is the food source for the other. In this paper, we have analyzed the immigration effect on the prey population in the system.

(2) The stability of the considered system is analyzed for possible fixed points.

(3) It has been shown that the proposed system undergoes both flip and Neimark-Sacker bifurcations.

(4) The OGY method has been applied to the system to control the chaos due to the emergence of the Neimark-Sacker bifurcation.

(5) Some numerical examples have been presented for our discrete-time predator-prey system with immigration in order to support the accuracy of our theoretical results.

Our task is to discuss the dynamics of a modified discrete-time predator-prey system with immigration of the prey population. The rest of the paper is organized as follows. In Section 2, the existence conditions and stability of the fixed points of the system are investigated. In Section 3, Neimark-Sacker and flip bifurcation analysis is explored by choosing $r$ as a bifurcation parameter. Next, the directions of both Neimark-Sacker and flip bifurcations are obtained by using normal form theory ^[21,37]. In Section 4, an OGY feedback control strategy is implemented to control the chaos due to the emergence of Neimark-Sacker bifurcation. In Section 5, some numerical simulations are demonstrated out to support the accuracy of our theoretical finding. In the end, a brief conclusion is given.

2.   Existence and stability of the fixed points

In this section, we will examine the existence and stability of the fixed points of a discrete system with immigration of the prey in the close first quadrant $R_{+}^{2}.$ To find the fixed points of the system given by $(1.1),$ we can rewrite system $(1.1)$ in the following form:

Solving the algebraic equation, we get that system $(1.1)$ has the following fixed points:

We have obtained the following lemma regarding the existence of the fixed points of system $(1.1)$.

Lemma 2.1. For system $\mathit{(1.1)}$, the following statements hold true:

i) System $\mathit{(1.1)}$ always has an axial positive fixed point $E_{1} = \left(\frac{(r-1)+\sqrt{(r-1)^{2}+4rs}}{2r}, 0\right).$

ii) System $\mathit{(1.1)}$ has a unique positive fixed point $E_{2} = \left(\frac{d+1}{b}, \frac{(d+1)b(r-1)-r(d+1)^{2}+sb^{2} }{ab(d+1)}\right)$ if $(d+1)b(r-1)+sb^{2} > r(d+1)^{2}.$

Now, we investigate the stability of the coexistence fixed point $E_{2}$ of system $(1.1)$ only. The Jacobian matrix of system $(1.1)$ evaluated at the unique positive fixed point $E_{2} = \left(\frac{ d+1}{b}, \frac{(d+1)b(r-1)-r(d+1)^{2}+sb^{2}}{ab(d+1)}\right)$ is given by

Then, the characteristic polynomial of $J(E_{2})$ is given by

In order to analyze the dynamics of the unique positive fixed point $E_{2} = \left(\frac{d+1}{b}, \frac{(d+1)b(r-1)-r(d+1)^{2}+sb^{2}}{ab(d+1)} \right)$ of system $(1.1)$, we present Lemma 2.2 ^[8,18,19]:

Lemma 2.2. Let $F(\lambda) = \lambda ^{2}+B\lambda +C,$ where B and C are two real constants, and let $F(1) > 0.$ Suppose $\lambda _{1}$ and $\lambda _{2}$ are two roots of $F\left(\lambda \right) = 0.$ Then, the following statements hold true:

i) $\left\vert \lambda _{1}\right\vert < 1$ and $\left\vert \lambda _{2}\right\vert < 1$ if and only if $F(-1) > 0$ and $C < 1,$

ii) $\left\vert \lambda _{1}\right\vert > 1$ and $\left\vert \lambda _{2}\right\vert > 1$ if and only if $F(-1) > 0$ and $C > 1,$

iii) ( $\left\vert \lambda _{1}\right\vert < 1$ and $\left\vert \lambda _{2}\right\vert > 1)$ or ( $\left\vert \lambda _{1}\right\vert > 1$ and $\left\vert \lambda _{2}\right\vert < 1)$ if and only if $F(-1) < 0,$

iv) $\lambda _{1}$ and $\lambda _{2}$ are a pair of conjugate complex roots, and $\left\vert \lambda _{1}\right\vert = \left\vert \lambda _{2}\right\vert = 1$ if and only if $B^{2}-4C < 0$ and $C = 1,$

v) $\lambda _{1} = -1$ and $\left\vert \lambda _{2}\right\vert \neq 1$ if and only if $F(-1) = 0$ and $C\neq \pm 1.$

Assume that $\lambda _{1}$ and $\lambda _{2}$ are the roots of the characteristic polynomial at the positive fixed point $(x, y)$. Then, the point $(x, y)$ is called a sink if $\left\vert \lambda _{1}\right\vert < 1$ and $\left\vert \lambda _{2}\right\vert < 1$ and it is locally asymptotically stable. $(x, y)$ is known as a source or repeller if $\left\vert \lambda _{1}\right\vert > 1$ and $\left\vert \lambda _{2}\right\vert > 1;$ thus, a source is always unstable. The point $(x, y)$ is called a saddle point if ($\left\vert \lambda _{1}\right\vert < 1$ and $\left\vert \lambda _{2}\right\vert > 1)$ or ($\left\vert \lambda _{1}\right\vert > 1$ and $\left\vert \lambda _{2}\right\vert < 1).$ And, $(x, y)$ is called non-hyperbolic if either $\left\vert \lambda _{1}\right\vert = 1$ or $\left\vert \lambda _{2}\right\vert = 1.$

Now, we will discuss the topological classification of the unique positive fixed point $\left(\frac{d+1}{b}, \frac{(d+1)b(r-1)-r(d+1)^{2}+sb^{2}}{ ab(d+1)}\right)$ of system $(1.1),$ and we will apply Lemma 2.2 to prove the following lemma. From Eq $\mathit{(2.2)}$, we can obtain $\ F(1) = \frac{(d+1)b(r-1)-r(d+1)^{2}+sb^{2}}{b} > 0$ if $(d+1)b(r-1)+sb^{2} > r(d+1)^{2}.$

Lemma 2.3. Assume that $(d+1)b(r-1)+sb^{2} > r(d+1)^{2};$ then, for a unique positive fixed point $E_{2}$ of system $\mathit{(1.1)},$ the following holds true.

i) $E_{2}$ is a sink-type fixed point if the following conditions hold:

and

ii) $E_{2}$ is a source (repeller)-type fixed point if the following conditions hold:

and

iii) $E_{2}$ is a saddle-type fixed point if the following condition holds:

iv) Assume that $\lambda _{1}$ and $\lambda _{2}$ are the roots of Eq $\mathit{(2.2)}$; then $\lambda _{1} = -1$ and $\left\vert \lambda _{2}\right\vert \neq 1$ if and only if $r = r_{1}$ and $r\neq r_{2}, r_{2}+\frac{2b}{d^{2}-bd+3d-b+2}$.

v) The roots of Eq $\mathit{(2.2)}$ are complex with modules of one if and only if

where $r_{1} = -\frac{(2d+3-d^{2}-sb(1-d))b}{(d+1)^{2}(b-d-3)}$ and $r_{2} = \frac{((d+1)^{2}-sbd)b}{(d+1)^{2}(b-(d+2))}.$

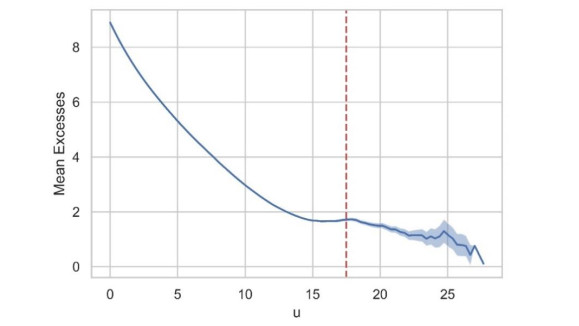
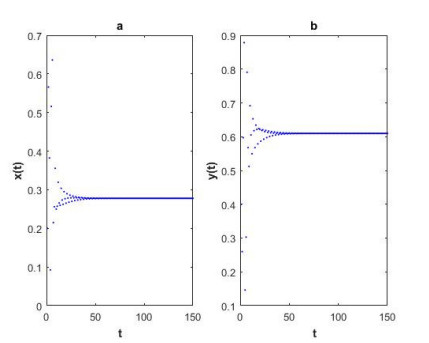
Example 2.1. For the parameter values $a$ = 3.5, $b$ = 4.5, $d$ = 0.25, $s$ = 0.75, $r$ = 0.5 and the initial condition $\left(x_{0}, y_{0}\right) = (0.25, 0.6),$ the positive unique fixed point of system $(1.1)$ is obtained as $\left(x^{\ast }, y^{\ast }\right) = (0.27777778, 0.58888889).$ Figure 1 shows that the fixed point $\left(x^{\ast }, y^{\ast }\right)$ of system $(1.1)$ is locally asymptotically stable, with $x(t)$ and $y(t)$ being the prey and predator populations at time $t$, respectively.

3.   Bifurcation analysis

In this section, we will investigate flip and Neimark-Sacker bifurcations of the coexistence fixed point $E_{2}$ by using the bifurcation theory in the sense of ^[15].

3.1.   Neimark-Sacker bifurcation at the point $E_{2}$

In this subsection, we investigate the existence conditions for the Neimark-Sacker bifurcation around coexistence fixed point by choosing the parameter $r$ as a bifurcation parameter. Furthermore, the direction of the Neimark-Sacker bifurcation is given by applying bifurcation theory.

When the term $(v)$ of Lemma 2.3 holds, we say that two eigenvalues of $J\left(E_{2}\right)$ are a pair of complex conjugates with a modulus of one. Therefore, we can write the following set:

$NSB_{E_{2}}$ =

where $r_{2} = \frac{((d+1)^{2}-sbd)b}{(d+1)^{2}(b-(d+2))}.$

The Neimark-Sacker bifurcation appears when the parameter r varies in a small neigborhood of $NSB_{E_{2}}$. The eigenvalues of system $(1.1)$ under these conditions are obtained by

where

It is easy to see that

From the transversality condition, we get

If the nonresonance condition $B = -trJ_{E_{2}}\left(r_{NS}\right) \neq 0, -1$, then

which obviously satisfies

where $\alpha = \frac{2K-sb}{K^{2}}$. Assume that $q, p\in \mathbb{C} ^{2}$ are two eigenvectors of $J\left(NSB_{E_{2}}\right)$ and the transposed matrix $J^{T}\left(NSB_{E_{2}}\right)$ corresponding to $\lambda$ and $\overline{\lambda },$ respectively. We have

and

To achieve the normalization $< p, q > = 1,$ where $< ., . >$ means the standard scalar product in $C^{2}$, we can set the normalized vectors as

From Taylor expansion, substituting $x_{t}+x^{\ast }$ into $X_{t},$ and $y_{t}+y^{\ast }$ into $Y_{t},$ the fixed point $E_{2}$ of system $(1.1)$ results in the origin $\left(0, 0\right),$ and system $(1.1)$ converts to

where $J\left(E_{\ast }\right) = J(x^{\ast }, y^{\ast }),$ and

where $X_{t} = \left(x_{t}, y_{t}\right) ^{T}$. System $\left(3.10\right)$ can be expressed as

where $B\left(x, y\right) = \left(\begin{array}{c} B_{1}\left(x, y\right) \\ B_{2}\left(x, y\right) \end{array} \right)$ and $C\left(x, y, u\right) = \left(\begin{array}{c} C_{1}\left(x, y, u\right) \\ C_{2}\left(x, y, u\right) \end{array} \right)$ are symmetric multi-linear vector functions of $x, y, u\in R^{2}.$ We define the functions $B\left(x, y\right)$ and $C\left(x, y, u\right)$ by the following formulas:

For $r$ near to $r_{NS}$ and $z\in \mathbb{C}$, we use the transformation $X = zq+\overline{z}\overline{q};$ then, system $\left(3.11\right)$ becomes

where $\lambda \left(r\right) = \left(1+\varphi \left(r\right) \right) e^{i\arctan \left(r\right) },$ with $\varphi (r_{NS}) = 0,$ and $g\left(z, \overline{z}, r\right)$ is a smooth complex-valued function. After Taylor expression of $g$ with respect to $\left(z, \overline{z}\right),$ we obtain

Given the symmetric multi-linear vector functions, the Taylor coefficients $g_{kl}$ can be expressed by the following formulas:

The coefficient $\beta _{2}(r_{NS}),$ which determines the direction of the appearance of the invariant curve in a generic system exhibiting the Neimark-Sacker bifurcation, can be calculated as follows:

where $e^{i\arctan \left(r_{NS}\right) } = \lambda \left(r_{NS}\right).$

From the above analysis, we have the following theorem:

Theorem 3.1.1. Suppose that $E_{2{\rm{ }}\ }$is a positive unique fixed point of system $\mathit{(1.1)}$. If Eq $\mathit{(3.5)}$ holds, $\beta _{2}\left(r_{NS}\right) \neq 0$ and the parameter $r$ changes its value in a small vicinity of $NSB_{E_{2}}$; then, system $\mathit{(1.1)}$ passes through a Neimark-Sacker bifurcation at the fixed point $E_{2}.$ Moreover, if $\beta _{2}\left(r_{NS}\right) < 0$ $\left(\beta _{2}\left(r_{NS}\right) > 0\right),$ then the Neimark-Sacker bifurcation of System $\mathit{(1.1)}$ at $r = r_{NS}$ is supercritical (subcritical) and there exists a unique closed invariant curve bifurcation from $E_{2}$ for $r = r_{NS},$ which is attracting (repelling).

3.2.   Flip bifurcation at the point $E_{2}$

In this subsection, we will discuss the existence conditions for and direction of the flip bifurcation at a unique positive fixed point $E_{2}$ of system $(1.1)$ by choosing $r$ as a bifurcation parameter.

If Lemma 2.3 $(iv)$ holds, we see that one of the eigenvalues of $J(E_{2})$ is $-1$ and the other eigenvalue is neither $1$ nor $-1.$ Therefore$,$ there can be a flip bifurcation of the fixed point $E_{2}$ if the parameter $r$ varies in the small neighborhood of $FB_{E_{2}},$ where

The eigenvalues of system $(1.1)$ under these conditions are given by

In order to be $\lambda _{2}(r_{1})\neq \pm 1,$ we have

Suppose that $q, p\in R^{2}$ are two eigenvectors of $J\left(FB_{E_{2}}\right)$ and the transposed matrix $J^{T}\left(FB_{E_{2}}\right),$ respectively, for $\lambda _{1}(r_{1}) = -1.$ Then, we have

By direct calculation, we obtain

and

To achieve the normalization $< p, q > = 1,$ where $< , >$ means the standard scalar product in $R^{2}$, we can write the normalized vectors $p$ and $q$ as

Assume that $x_{t} = X_{t}-x^{\ast },$ $y_{t} = Y_{t}-y^{\ast }$ and $J\left(E_{\ast }\right) = J(x^{\ast }, y^{\ast }).$ We transform the fixed point $E_{2}$ of system $(1.1)$ into the origin $\left(0, 0\right).$ By Taylor expansion, system $(1.1)$ can be taken as

where

where $X_{t} = \left(x_{t}, y_{t}\right) ^{T}$. System $\left(3.23\right)$ can be expressed as

where $B\left(x, y\right) = \left(\begin{array}{c} B_{1}\left(x, y\right) \\ B_{2}\left(x, y\right) \end{array} \right)$ and $C\left(x, y, u\right) = \left(\begin{array}{c} C_{1}\left(x, y, u\right) \\ C_{2}\left(x, y, u\right) \end{array} \right)$ are symmetric multi-linear vector functions of $x, y, u\in R^{2}$ that are defined as follows:

The sign of the coefficient $\beta _{2}(r_{FB})$ determines the direction of the flip bifurcation, and it can be calculated as follows:

From the above analysis, we have the following theorem:

Theorem 3.2.1. Suppose that $E_{2{\rm{ }}\ }$is a positive unique fixed point of system $\mathit{(1.1)}$. If the condition given by $\mathit{(3.19)}$ holds, $\beta _{2}\left(r_{F}\right) \neq 0$ and the parameter $r$ changes its value in a small vicinity of $FB_{E_{2}};$ then, system $\mathit{(1.1)}$ experiences a flip bifurcation at the fixed point $E_{2}.$ Moreover, if $\beta _{2}\left(r_{F}\right) > 0$ $\left(\beta _{2}\left(r_{F}\right) < 0 \right)),$ then there exists stable (unstable) period-2 orbits that bifurcate from $E_{2}$.

4.   Chaos control

In dynamical systems, it is desirable to optimize the system according to some performance criteria and avoid chaos. In order to stabilize the chaos in the case of unstable trajectories of the systems, different control techniques are applied. Therefore, chaos control is one of the attractive topics of current studies ^[8,9,10].

Chaos control can be obtained by applying various methods to the discrete-time systems. To control the chaos in system $(1.1)$, we chose to explore a feedback control strategy and apply the OGY method to system $(1.1)$ in the sense of ^[22]. In order to apply OGY techniques to system $(1.1),$ we rewrite it as follows:

where $r$ is a controlling parameter. Furthermore, $r$ is restricted to lie in some small interval $\left\vert r-r_{0}\right\vert < \mu,$ where $\mu > 0$ and $r_{0}$ denotes the nominal value belonging to the chaotic region. We apply a stabilizing feedback control strategy in order to move the trajectory toward the desired orbit. Suppose that $\left(X^{\ast }, Y^{\ast }\right)$ is an unstable fixed point of system $(1.1)$ in the chaotic region produced by the emergence of Neimark-Sacker bifurcation; then, system $(4.1)$ can be approximated in the neighborhood of the unstable fixed point $\left(X^{\ast }, Y^{\ast }\right)$ by the following linear map:

where

and

On the other hand, system $(4.1)$ can be controlled provided that the following matrix exists:

which has a rank of $2.$ We suppose that $\left[r-r_{0}\right] = -K\left[\begin{array}{c} X_{t}-X^{\ast } \\ Y_{t}-Y^{\ast } \end{array} \right];$ where $K = \left[\rho _{1}{\rm{ }}\ \rho _{2}\right],$ then, system $(4.2)$ can be written as follows:

The corresponding controlled system given by $(1.1)$ can be written as

where $-\rho _{1}\left(X_{t}-X^{\ast }\right) -\rho _{2}\left(Y_{t}-Y^{\ast }\right)$ is the control force; $\rho _{1}$ and $\rho _{2}$ are defined as the feedback gains. Furthermore, the fixed point $\left(X^{\ast }, Y^{\ast }\right)$ of system $(4.4)$ is locally asymptotically stable if and only if both eigenvalues of the matrix $A-BK$ lie in an open unit disk. The Jacobian matrix $A-BK$ of the controlled system given by $(4.4)$ can be written as follows:

The characteristic equation of the Jacobian matrix $A-BK$ is given by

Let $\lambda _{1}$ and $\lambda _{2}$ be roots of the characteristic equation given by $(4.5);$ then,

are valid. In order to obtain the lines of marginal stability, we must solve the equations $\lambda _{1} = \pm 1$ and $\lambda _{1}$ $\lambda _{2} = 1.$ These constraints ensure that the absolute value of $\lambda _{1}$ and $\lambda _{2}$ is less than $1.$ Assume that $\lambda _{1}\lambda _{2} = 1;$ then, the second part of Eq $(4.6)$ implies that

Moreover, we suppose that $\lambda _{1} = 1;$ then, using Eq $(4.6),$ we get

Finally, taking $\lambda _{1} = -1$ and using Eq $(4.6),$ we get

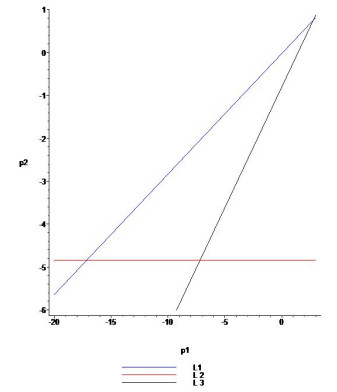
Then, stable eigenvalues lie within the triangular region in the $\rho _{1}\rho _{2}$ plane bounded by the straight lines $L_{1},$ $L_{2}$ and $L_{3}$ for particular parametric values.

5.   Numerical analysis

In this section, we will give three examples to illustrate the results obtained in the above sections. Computer algebra systems such as Mathematica, Maple and Matlab were used for the calculations and graphic drawings.

Example 5.1. With this example, our aim is to present numerical simulations to validate the above theoretical results by choosing $r$ as the bifurcation parameter for system $(1.1)$ around the fixed point $E_{2 {\rm{ }}\ }.$ The parameter values were taken from ^[23]. The Neimark-Sacker bifurcation point $r_{NS}$ was obtained as $r_{NS} = 0.70339999998.$ By taking the parameter values $(r_{NS}, a, b, d, s) = (0.70339999998, 3.5, 4.5, 0.25, 0.9)$, the positive fixed point of system $(1.1)$ has been evaluated as $E_{2} = \left(0.2777777778, 0.7852698412\right).$ Using these parameter values, we get the following Jacobian matrix:

The eigenvalues were calculated to be:

Let $q, p\in C^{2}$ be complex eigenvectors corresponding to $\lambda _{1, 2},$ respectively:

and

To obtain the normalization $\langle p, q\rangle = 1,$ we can take the normalized vectors to be

and

To compute the coefficients of normal form, we can transform the fixed point $E_{2}$ to the point $\left(0, 0\right)$ by changing the following variables:

Hence, we can compute the coefficients of the normal form of the system by using the formulas given by Eq $(3.15),$ as follows:

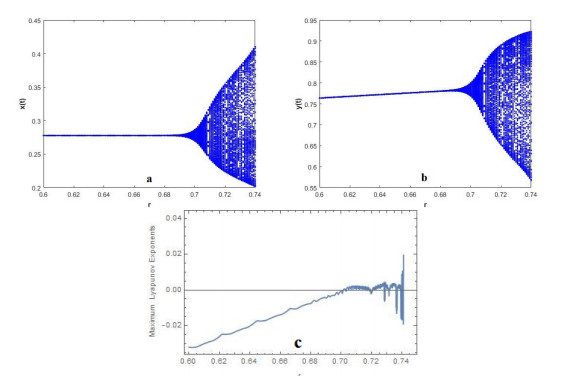
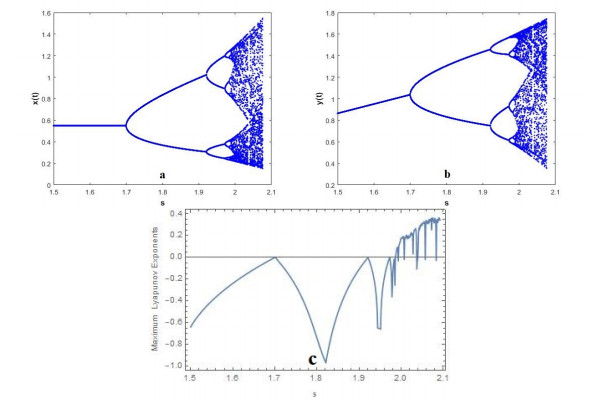
From Eq $(3.16)$, the critical part is then obtained as $\beta _{2}\left(r_{NS}\right) = -17.302665 < 0.$ Therefore, the Neimark-Sacker bifurcation is supercritical and it shows the correctness of Theorem 3.1.1. The bifurcation diagram, maximum Lyapunov exponents and this phase portraits of system $(1.1)$ are shown in Figures 2 and 3.

The bifurcation diagrams in Figure 2(a) and (b) show that the stability of $E_{2}$ happens for $r < 0.7039999998$, but there is a loss of stability at $r = 0.7039999998,$ and an attractive invariant curve appears if $r > 0.7039999998.$ We computed the maximum Lyapunov exponents to detect the presence of chaos in the system. The existence of chaotic regions in the parameter space is clearly visible in Figure 2(c).

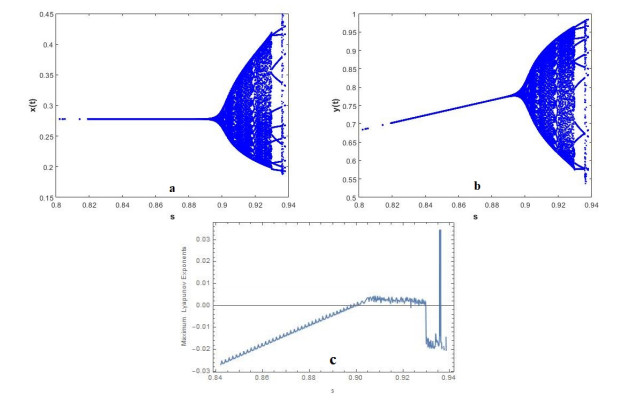
Now, we present the Neimark-Sacker bifurcation diagrams and maximum Lyapunov exponents for system $(1.1)$ by choosing the immigration parameter $s$ instead of $r$ as a bifurcation parameter.

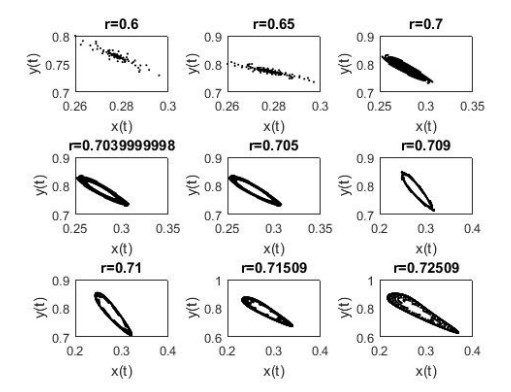
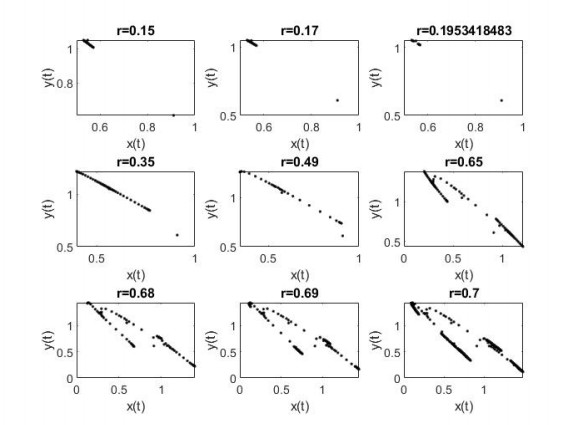
The phase portraits for different values of $r$ are displayed in Figure 4, which clearly depicts the process of how a smooth invariant circle bifurcates from the stable fixed point $E_{2} = \left(0.27777778, 0.7852698412\right).$ When $r$ exceeds $0.7039999998,$ there appears a circular curve enclosing the fixed point $E_{2},$ and its radius becomes larger with respect to the growth of $r.$

Example 5.2. Let $(r_{F}, a, b, d, s) = (0.1953418483, 2.1, 2, 0.1, 1.7)$. The positive fixed point of system $(1.1)$ has been evaluated as $E_{2} = \left(0.55, 1.037529963\right).$ Also, the flip bifurcation point $r_{F}$ was obtained as $r_{F} = 0.1953418483$. Using these parameter values, we can obtain the following Jacobian matrix:

The eigenvalues were calculated to be

Let $q, p\in R^{2}$ be eigenvectors of $J$ and the transposed matrix $J^{T},$ respectively, for $\lambda _{1} = -1.$ Then, we have

Direct computation gives

and

To obtain the normalization $\langle p, q\rangle = 1,$ we can take the normalized vectors to be

and

Then, the symmetric multi-linear vector functions can be obtained as follows:

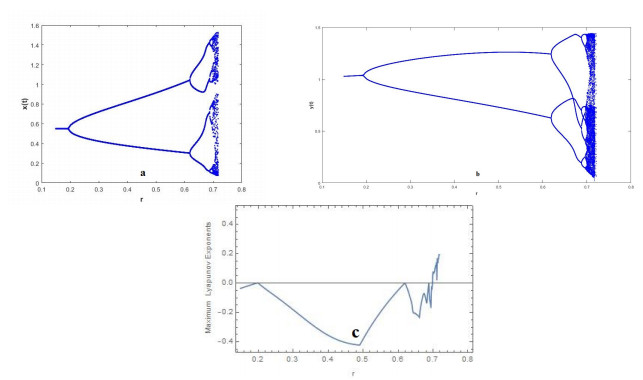
From Eq $(3.26)$, the critical part is obtained as $\beta _{2}\left(r_{F}\right) = 0.6745625580 > 0.$ Therefore, unique and stable period-2 orbits bifurcate from $E_{2},$ and it shows the correctness of Theorem 3.2.1. The bifurcation diagram, maximum Lyapunov exponents and this phase portraits of system $(1.1)$ are shown in Figures 5 and 6.

From Figure 5(a) and (b), we see that the fixed point $E_{2} = \left(0.55, 1.037529963\right)$ is stable for $r < 0.1953418483,$ and loses its stability at $\ $the flip bifurcation parameter value $r = 0.1953418483.$ We also observe that, if $r > 0.1953418483,$ the flip bifurcation giving a 2-periodic orbit occurs. Moreover, the maximum Lyapunov exponents were computed, and the existence of chaotic regions in the parameter space is clearly visible in Figure 5(c).

We present the flip bifurcation diagrams and maximum Lyapunov exponents for system $(1.1),$ which were obtained by choosing the immigration parameter $s$ instead of $r$ as a bifurcation parameter.

In Figure 7, we present the phase portraits of system$(1.1)$ for different values of $r.$

Example 5.3.In order to discuss the OGY feedback control method for system (1.1), we take $r_{0} = 0.73$ and $(a, b, d, s) = (3.5, 4.5, 0.25, 0.9).$ In this case, system (1.1) has unique positive fixed point $(X^{\ast }, Y^{\ast }) = (0.2777777778, 0.7906349207),$ which is unstable. Then, the corresponding controlled system is given by

where $K = \left[\rho _{1}{ \ }\rho _{2}\right]$ is a matrix and $(X^{\ast }, Y^{\ast }) = (0.2777777778, 0.7906349207)$ is an unstable fixed point of system $(1.1)$. We have

and

Then, it is easy to check that the rank of Matrix $C$ is 2. Therefore, system $(5.1)$ is controllable. Then, the Jacobian matrix $A-BK$ of the controlled system given by $(5.1)$ is

Moreover, the lines $L_{1},$ $L_{2}$ and $L_{3}$ of marginal stability are given by

Then, the stable triangular region bounded by the marginal lines $L_{1},$ $L_{2}$ and $L_{3}$ for the controlled system given by (5.1) is shown in Figure 8.

6.   Conclusions

Since most predator-prey systems in the wild are not isolated, it is important to consider the effects of the presence of some number of immigrants. The immigration effect of the predator-prey system has rarely been studied in the literature. Therefore, we considered a discrete-time predator-prey system with a constant-rate immigration of the prey and investigated the dynamics of modified system $(1.1)$ around coexistence fixed point in this paper.

In the case of $s = 0$, we obtained the trivial fixed point, non-predatory fixed point for $r > 1$ and coexistence fixed point for $r > \dfrac{b}{b-d-1}$. In the case of $s\neq 0,$ the origin is not a fixed point. System $(1.1)$ has two fixed points, namely, $E_{1}$ and $E_{2}.$ Moreover, simple calculations showed that, if $(d+1)b(r-1)+sb^{2} > r(d+1)^{2},$ then system $(1.1)$ has a unique positive fixed point $E_{2}.$ As $r$ is varied, the system exhibits several complicated dynamical behaviors, including the emergence of Neimark-Sacker and flip bifurcations, an invariant circle, a period-2 orbit and chaotic sets. We presented some figures to explain the theoretical analysis in Section 4. In Figure 2 and Figure 5, the bifurcation, maximum Lyapunov exponents and phase portraits are given for some parameter values. Figure 2 and Figure 5 show that, when the bifurcation parameter $r$ passes a critical bifurcation value, the stability of the coexistence fixed point of the system changes from stable to unstable. In Figure 2(c) and Figure 5(c), the computation of the maximum Lyapunov exponents confirm the presence of chaotic behavior in the system. In Figure 4 and Figure 7, the phase portraits of the system for different values of the $r$ parameter are plotted. Moreover, the Neimark-Sacker bifurcation has been successfully controlled with an OGY control strategy. From our numerical investigation, it is clear that an OGY method based on a feedback control strategy can restore the stability. This control method is effective in order to advance or completely eliminate the chaos due to the emergence of Neimark-Sacker bifurcation. In this study, because of consistency with the biological facts, we used the same parameter values that were used in ^[23]. As a final point, we can say that the parameter $r$ has a strong effect on the stability of system (1.1) for the control of two populations.

On the other hand, the biological meaning of the term $s$ being included in the system is that a small number of immigrants is added persistently to the prey population in each generation. A very small immigration into the system occurs as a stabilizing factor for the system. A positive immigration factor is enough to change the quality of the dynamics of the system. Specially, adding the term $s$ contributes to asymptotic stability. This means that adding a small immigration $s$ may imply that cyclic population can be stabilized.

When the immigration effect is applied to a small number of species, the level of the species increases significantly. In the same way, when the harvesting effect is applied to a large number of species, the level of the species is significantly reduced ^[38]. Thanks to these two external factors, all species in the ecosystem can be preserved to stabilize the unstable system. In a future study, we plan to explore the effects of these factors on the population model.

Conflict of interest

The authors declare no conflicts of interest in this paper.