Impact of COVID-19 on tourism sector: a case study of Rajasthan, India

1.   Introduction

Coronavirus disease (COVID-19) is a dangerous disease caused by a recently discovered coronavirus, first case reported in China (Wuhan city). The infection spreads mostly by discharge from the nose or droplets of saliva as an infectious person sneezes or coughs. As on 2021, in India there are three vaccine namely (Covishield, Covaxin, and Sputnik V) vaccines for COVID-19 available for the peoples of India, availed by Central Government of India. Most of them are very much effective against COVID-19 disease, but no one make you fully immune against COVID-19. In some countries, it was found that they can mutate in different forms and affect the human body more aggressively. However, many ongoing research and clinical trials are evaluating potential treatments and cure ^[1]. On the 11^th of March 2020, the WHO, World Health Organization has declared this outbreak a Worldwide Pandemic. After that many countries, including India, have shut-down its socio-economic and cultural institutions, except sectors related to essential services. At this time, the COVID-19 pandemic has emerged as an opportunity as well as the biggest challenge for the world and countries individually. From the government's point of view, opportunity in the sense of expanding the medical facilities as well as innovating for the peoples and society so that during the lockdown and social distancing protocols how the people utilize their time, money, and efforts in a tough time. For private peoples, they have to learn how to make the product for the end-user by following governmental guidelines as well as how to sell that product at customers doorstep so that both will be safe and benefitted. Schools and Colleges, have to learn how to teach the children's in a digital way so that both of them will be safe. Peoples have to learn how to expand their social relationship without affecting others.

Today's era comes in the digital age, where networking in social media become a major necessity for our day-to-day life. For any information or news, we tend to approach such platforms where the chances are high that we can get exposed to false information. Most likely in the case of the COVID-19 pandemic, all platforms of social media had flooded with many kinds of false information connecting to its origin, spread, cure, precautions, vaccines, etc. Some of them were correct, but most of them were fake news, which was creating a panic situation among peoples. To ignore such untrue information and keeping the chaos down, geospatial technology can be used for monitoring based on available data (count of reported cases) in India and around the globe. GIS offers an interactive way to monitor the effects of the virus on a real-time basis. The best example is Aarogya Setu mobile app the working of app is purely based on geospatial technology. "Aarogya Setu is a smartphone application that informs users about their COVID-19 infection risk. On April 2, the Indian government introduced the Aarogya Setu smartphone app to safeguard Indian residents against the widespread spread of coronavirus. The software makes use of a GIS location system and a contact tracking technique based on Bluetooth. It keeps track of all the individuals who come into touch with as you go about your daily routine. If any of contacts tests positive, the app will notify you. The COVID-19 pandemic is also covered by the Aarogya Setu app, which gives relevant and tailored medical warnings."

With the geospatial technology, we are able to map the distribution pattern of COVID-19 cases in India, adding infectious cases, as well as evolving trends among the peoples and countries ^[2]. It is believed that geographic accuracy is mandatory while detecting and responding to any infectious disease outbreak and pandemic situations ^[3]. Geospatial data science plays a vital role to understand, analyses, and visualize the spatial distribution of any phenomenon occurring in various countries. Similarly, Geospatial innovations offer a scope of chances for the improvement of current tourism applications utilizing digital maps ^[4].

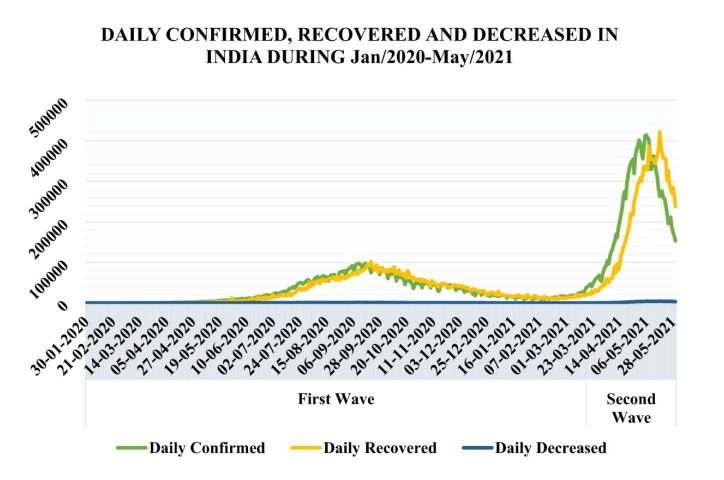
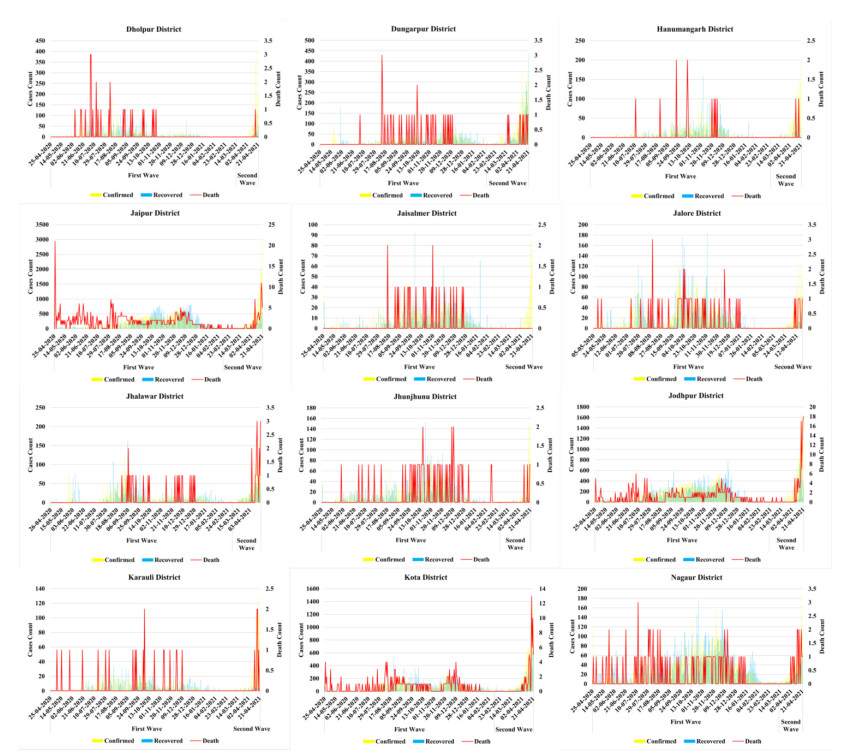
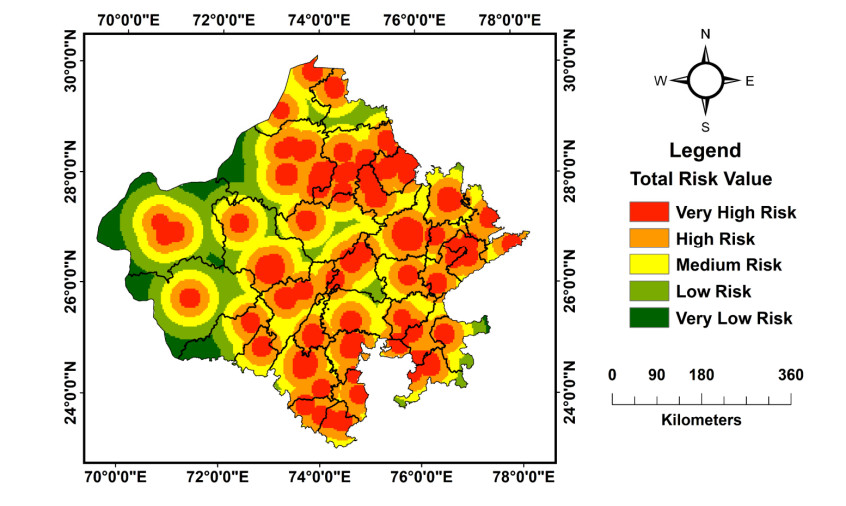
The spread of COVID-19 in India has started in January 2020. On March 24, the Government of India ordered a 21-days nation-wide lockdown to break the chain of the spread of COVID-19 ^[5,6]. At that point, the total count of cases in India was relatively low, with only 564 confirmed cases all over the country. However, total tests conducted at that point were also low, around 3298 tests till that day ^[7], because of this it was impossible to know the exact number of true infections, all contaminated zones or hotspots., and the rate of the spread of disease. But now the COVID-19 cases has been increasing day by day, now India is among most adversely affected country throughout the world. Poor management and unnecessary steps taken by the government is one of the reasons behind this situation. The current status of the COVID-19 pandemic in India are shown below Figure 1A and B.

Afterward, during starting of First Wave it has been found by many research and experts that the decision to impose lockdown in India was taken in the face of deep uncertainty, and it required understanding of the coming consequences to livelihoods against the risk of an uncontained outbreak of the COVID-19 ^[8,9]. Some researchers and experts said that the Second Wave of COVID-19 started at the start of May month, 2021 and it is more aggressive than the first one because the COVID-19 virus is mutating very rapidly and affecting the lungs and immune system of human body. Due to this people require ventilators for breathing oxygen. The most affected states are Maharashtra, Delhi, Uttar Pradesh, Karnataka and Tamil Nadu etc. ^[10].

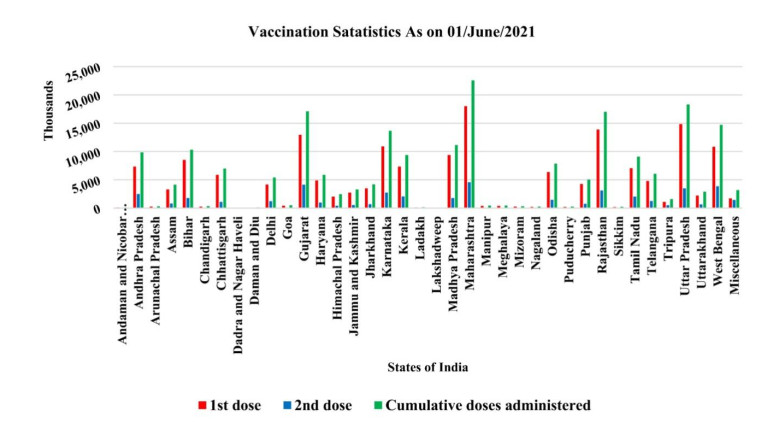
The Second Wave of COVID-19 is much worse than expected for India; more than four thousand people died every day as per government records and more than 2343152 active cases as of 28 May 2021. In the flow of the second wave, the country's health care system and economic structure totally collapsed, which also shows the poor infrastructure ^[10]. It is very crucial for any country to develop and maintain the health facilities at a vast scale for the peoples. After the Second Wave of COVID-19 experts are analyzing that Third Wave of COVID-19 is more severe, in which most likely the chance of low age group children might be affected at large scale. So, the government must focus on this situation either new generation will be affected at large scale. Vaccination is the only solution to beat this epidemic. As of now, there is no vaccine for lower age group children but the government is working on it. "Vaccination is the only way fight against COVID-19 pandemic situation." The current status of Vaccine is mentioned below in Table 1 and Figure 2.

2.   Impact of COVID-19 on tourism sector

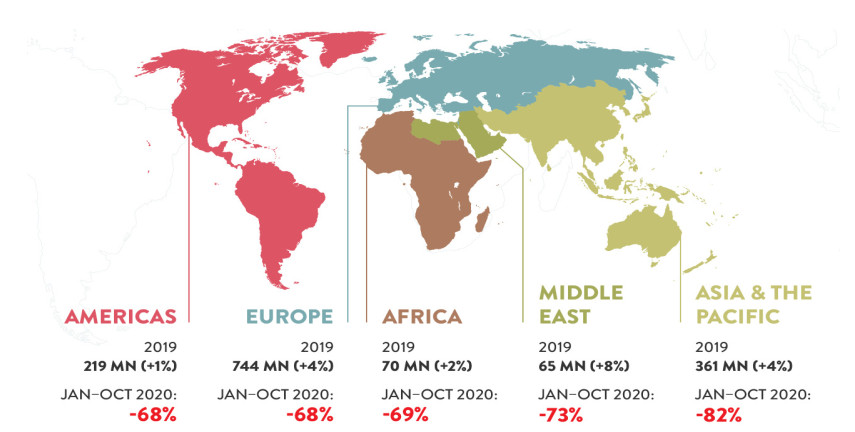
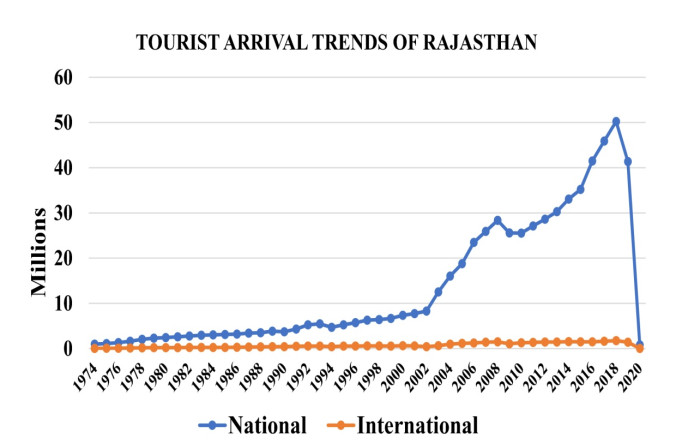
As a consequence of the COVID-19 epidemic, the globe is facing an unparalleled global health, social, and economic crises. Travel and tourism are among the worst-affected industries, with worldwide demand plummeting as a result of worldwide travel restrictions, including the closure of several borders to control the infection. International tourist arrivals (overnight visitors) fell by 72 percent in January-December 2020 compared to the same period last year, according to the latest UNWTO World Tourism Barometer, and continue to decline, hampered by slow virus containment, low traveler confidence, and significant travel restrictions still in place due to the COVID-19 pandemic. In comparison to the same period last year, there were 900 million fewer international tourist arrivals in the first ten months of this year, resulting in a loss of US$ 935 billion in international tourism export revenues, more than ten times the loss experienced in 2009 as a result of the global economic crisis. Between January and December 2020, arrivals in Asia and the Pacific fell by 82 percent. This ten-month period showed a 73 percent dip in the Middle East and a 69 percent dip in Africa. International arrivals fell by 68 percent in both Europe and the Americas. According to current patterns, foreign arrivals are expected to fall by 70% to 75% for the whole year of 2020. Figure 3. This would mean that international tourism could have returned to levels of 30 years ago. In 2020, the predicted drop in international tourism will equate to a loss of nearly 1 billion visitors and US＄ 1.1 trillion in tourist revenue. This drop in foreign tourism might result in a worldwide economic loss of more than US$ 2 trillion in 2019, accounting for more than 2% of global GDP. In the future, it is believed that the announcement and implementation of a vaccination would gradually boost consumer trust and help to reduce travel restrictions. International tourism is expected to return in the second half of 2021, according to UNWTO's expanded scenarios for 2021–2024. In terms of foreign immigration, however, a restoration to 2019 levels might take 2½ to 4 years.

In Indian context the tourism sector has been badly affected due to COVID-19. If we compare two-year trends (2019–2020) the difference is visible as per Table 2. The tourism sector is most revenue generating sector but due pandemic effect it goes in negative figures. As off now the Indian government requires fund to fight against COVID-19 Pandemic. For that purpose, they have very limited resources for earning. Among all the resources tourism is one of them, so this study it is important to analyze the sector at a vast scale to understand how the COVID-19 situation affecting tourism sector for that Rajasthan is chosen as a study area, because Rajasthan is most preferred destination for tourism activity.

In the long term, it has also impacted on the sustainable development and climate change agenda (s) of the nation as well as for the Rajasthan as a state. In current scenario India suspended all its tourist activities as the majority of the confirmed cases were linked to the other countries.

3.   COVID-19 in Rajasthan

In Jaipur, the city of Rajasthan, the 1^st case of coronavirus was found on the 2^nd of March 2020 ^[11]. In fact, on 19^th March 2020, Rajasthan imposed a statewide lockdown. Rajasthan was the first state to imposed such kind of massive lockdown due to the heavy flow of COVID 19 cases ^[12]. Among them Bhilwara city was highly affected by COVID-19 due to that there was an essential need to impose more constrictive lockdown in the city Figure 4. At that time the administration had decided more restrictive curfew to disrupt the spread of the virus, which has a major economic effect on the state.

Due to falling state revenues, the government will be forced to slash big spending on basic necessities, which is necessary to revive the state's economy ^[13,14]. The state officials are already restructuring the budget for new financial year, which promised a modest but important boost to the state's economy. Some specific departments may have to minimize their daily expenses up to 25 percent which ultimately results enough amount of revenue to tackle the current situation. The problems in Rajasthan give a snapshot into what awaits the rest of the nation as new cases of COVID-19 begin to escalate and the lockdown that started on the night of March 24 to May 3, 2020 ^[12,15]. It further stresses the importance of offering financial aid to state governments whose budgets have failed due to a number of causes. The economy of Rajasthan, like most of the world, was tussling much before the epidemic. Because of the lockdown, the slowdown of the economy spreading very fast which results in the closure of many states industries and establishments which are likely to get decreased the income of the state by Rs 17,500 crores during 2019–2020, a 12.5 percent downfall compared to the past year, as per recent report submitted by DOIT Rajasthan ^[16].

In the last quarter of March alone, it is reported that coronavirus-related restrictions cost approx. Rs 3,500 crores, a 50 percent downfall compared to the past year. Another prediction exercise by the finance department of the state government estimates April revenues to decrease approx. Rs 1500 crores, a 60 percent downfall year-by-year, owing to the lockdown extension until May 3, 2020 ^[17]. Although Jaipur state officials worry about their numbers, according to experts, the countryside is braced for acute hunger and unemployment, and cautioned that the closing of local businesses and factories has adversely affects the livelihoods of the neediest citizens of district ^[18].

In 2018, travel and tourism have contributed about 9 percent share of GDP in India. As a result, it's evident that the country's growth is being significantly ^[19,20] helped by the tourism industry ^[21]. Protecting this sector will also be a significant investment in potential economic opportunities for nations. Therefore, if we are to reflect on India's potential growth through the tourism business, we need to secure all the service providers in the tourism industry.

4.   Objectives of the study

The main objectives of this paper are as follows: a) Assessing and mapping the affected parts of Rajasthan at initial days and evaluating the risk of the pandemic on tourism, and b) Initially tracking and forecasting the cases of COVID-19 in the study area.

5.   Study area description

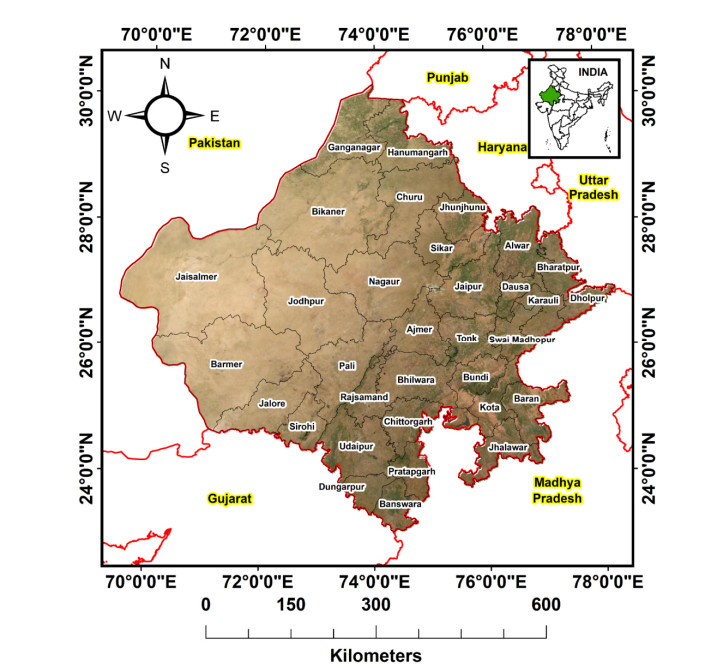
From a tourism point of view, Rajasthan has always been a crucial part of India. It covers an area of 342239 square kilometers in total, making the largest state geographically in the country ^[22]. Geographical state boundaries are linked to 5 states that are Haryana, Gujarat, Punjab, Madhya Pradesh (MP), and Uttar Pradesh (UP) Figure 5, and also has 1071 kilometers lengthy western international boundary with neighboring country Pakistan ^[23]. Rajasthan is already one of the famous and most favored tourist destinations among national and foreign visitors. All the destinations have a very high flow of visitors throughout the year.

As per (Statista Research Department, Feb 10, 2021) domestic tourists accounted for nearly 52 million visitors to Rajasthan in 2019, while international visitors accounted for about 1.6 million which is good amount ^[24]. In terms of natural wealth, cultural history, historical and archaeological treasures and unique wildlife, the state is renowned for its richness. For visitors visiting Rajasthan, the palaces and forts, heritage hotels, vibrant festivals and fairs, local handicraft, etc., have become a ultimate selling enthusiasm. The western regions of the state offer a spectacular view of the desert. This draws a large number of tourists, particularly international visitors. ^[25]. In the past, the tourism sector in Rajasthan has been affected at various levels from time to time, but in the year 2020, it has been disturbed and destructed drastically.

COVID-19 pandemic has become one of the major concerns for the tourism sector. It has affected tourism on a very large scale. Hence, there is a need to rejuvenate the tourism sector by developing a proper monitoring system of COVID-19 cases, so that people feel safe while traveling and the government can control the heavy spread of the virus among the people.

6.   Research framework

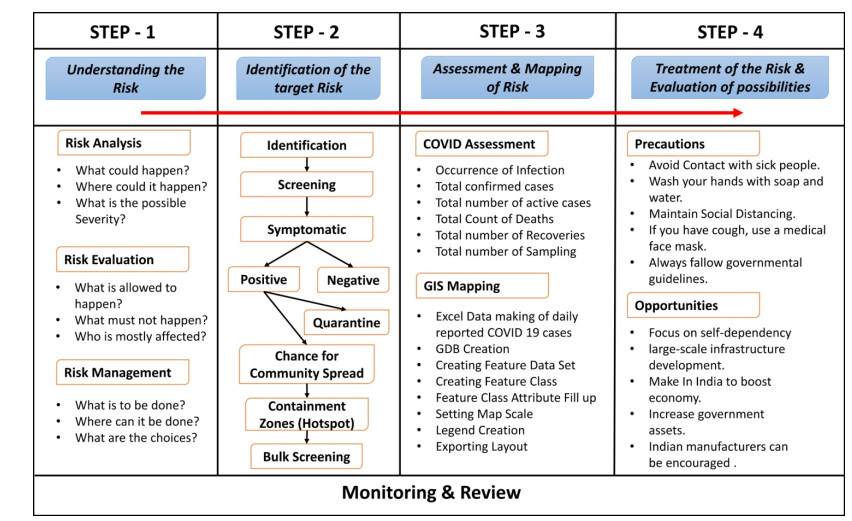
The research paper is purely focused on the COVID-19 pandemic in Rajasthan, India, and how the geospatial technology can help to identify logical possibilities of the current and future situation during the pandemic Figure 6. The research is following the current trend of COVID-19 cases and the analysis which can help to project future trends. So that proper monetization and effective control measures can be implemented by the government. In India, Rajasthan plays a crucial part in the tourism sector at national as well as international level and the spread of COVID-19 has been seen increasing due to tourism ^[26]. Example: Haridwar Kumbh, Pilgrimage tourism one of the largest and biggest tourism event organized by government is the best place for corona virus to spread among the people. More than 2000 positive cases was found during Kumbh mela ^[27]. This force me to do this research for my country, for fulfilling this I have selected Rajasthan as a study area. The methodology consists of four main phases. In the first phase understanding the risk of the pandemic situation at three primary levels after that identification of target risk using geospatial technology comes under the second phase. Assessment and mapping of pandemic risk is the third phase. In the fourth phase, treatment of the risk and evaluation of future occurrence possibilities.

7.   Result

Tourism has always been a major contributor to job growth and a major source of foreign income for the country. This sector not only supports urban workers but also offers livelihoods for people through social strata in rural areas. It is a mediator of the aviation sector, automobile sector, hospitality, commercial, etc. It is one of the primary drivers to generate revenue for Rajasthan. Due to COVID-19, Tourism has become the most adversely affected sector. It has been found that the national and international arrival trends are highly affected at large scale, it can be seen from the flow chart Figure 7, which is not good for the Tourism industry. The closure of hotels, dharamshala, resorts etc., and airport flights have been halted after the start and spread of the COVID-19 pandemic has already resulted in a projected revenue loss of 1.25 trillion rupees for the Indian tourism industry by 2020. A CARE ratings agency research says that the amount corresponds to a 40 percent downfall in total revenue over the fiscal year 2019. The study predicts the impact of the epidemic on tourism between January and February 2020 which shows downfall of 50 percent, and it may be getting stronger by 70 percent downfall in March alone, since the termination of numerous global flights. In April–June, the Indian tourism sector is forecast to make a projected loss of revenue approx. Rs. 69,400 crosses, describing a y-o-y (year-on-year) downfall of 30 percent.

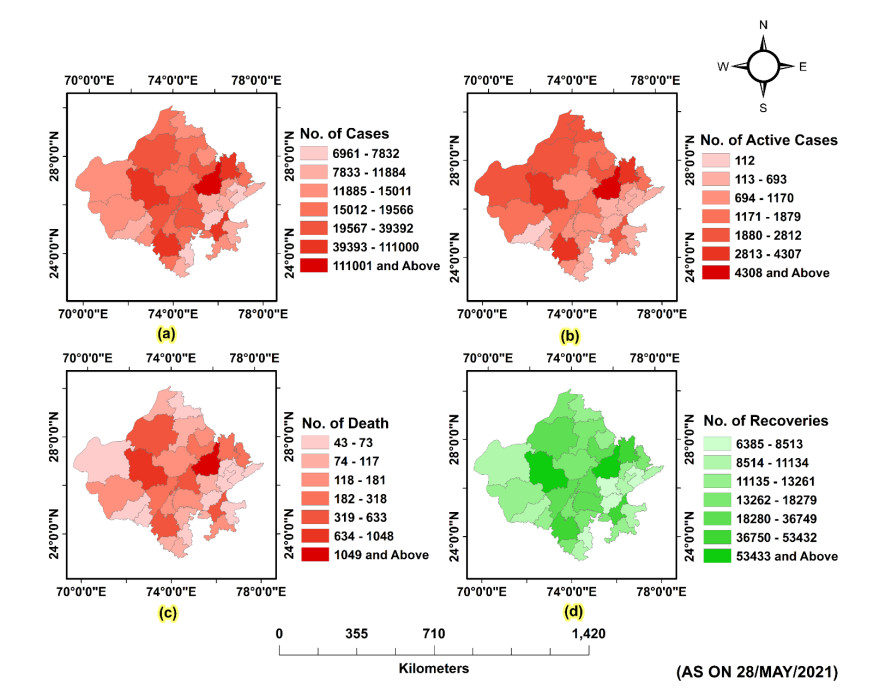
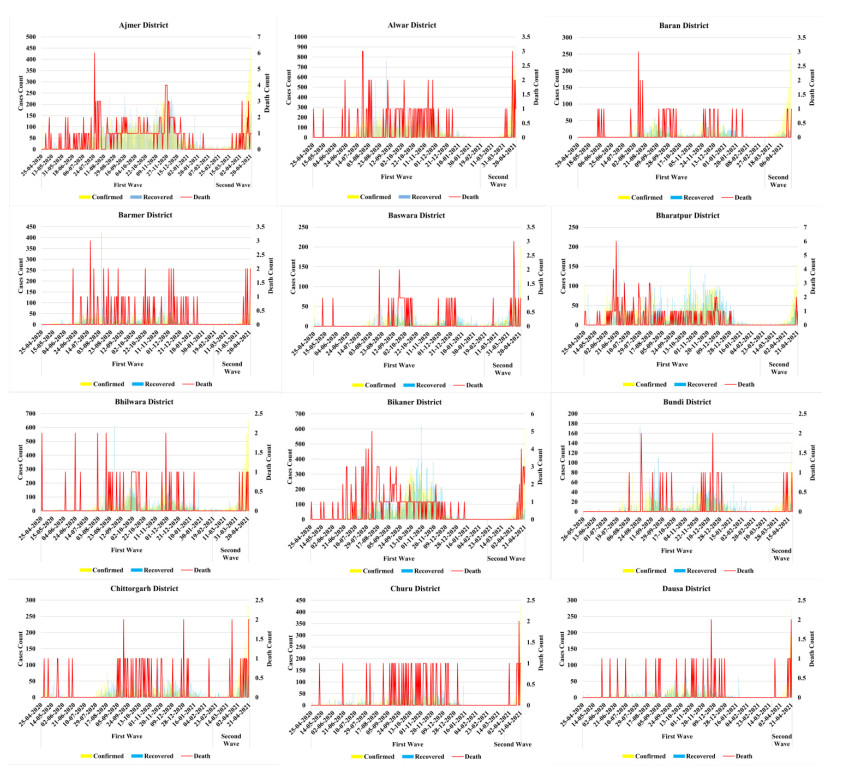
In Rajasthan, daily new cases are coming in all the 33 districts Figure 8. So, collecting all the data and multi-scale mapping it using Geospatial Technology makes it more understandable to the government agencies for future prediction and establishing hotspots/containment zones play a crucial role in minimizing the cases. Assessment and mapping in geospatial technology also allow upgradation of the data and the information for the epidemic with time.

India's government agency, the Ministry of Health and Family Welfare (MoHFW), has proposed a district wise categorization to tackle COVID-19 pandemic in the form of different hotspots naming red zone, yellow zone and green zone representing (high, medium and low) based on recorded cases using Geospatial Technology. Districts with no found cases are categorized as green zone. As per the government, if there is no new case is found for 28 days, a hotspot district will be transferred to the green zone. In India, based on the doubling rate of reported COVID-19 cases, states are directed to recognize hotspots. According to the Ministry, this detection and tracking of hotspots will be performed regularly. In the red hotspot zones, strict containment strategies need to be enforced. Demarcation of Rajasthan district is done by government agencies which are shown above.

8.   Discussion

Combined with the context of large-scale population flow, the uncertain dissemination of COVID-19 has contributed to the immediate need for science and technical assistance to monitor and prevent the spread of the disease. Geospatial technologies may play an important role in the battle against this pandemic, in the prediction of the spatial spread of the disease, in the spatial avoidance and management of the epidemic, in the spatial distribution of money, and in the spatial detection of social opinion.

In the current scenario of COVID-19 in India, Geospatial Technology can help in the (a) Rapid collection of a large number of data and information systems for the epidemic. (b) Processing, acquisition, and integration of problem-oriented data. (c) Rapid multi-scale mapping for the epidemic, and upgradation with time. (d) Comparative study of spatio-temporal tracking and analyzing the containment zones. (e) Managing the demand and supply for medical amenities. (f) Evaluation of the risks of commodity procurement and shipping. (g) Estimation of the population flow and epidemic spread. (h) Monitoring social activities at a time of the epidemic, etc.

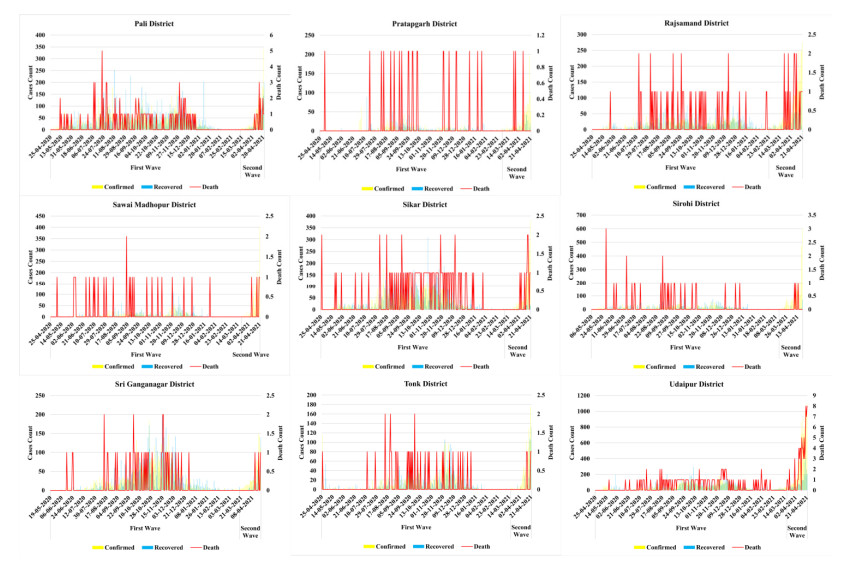
Through all the data provided by the Rajasthan Government, early and fast detection of possible danger areas of infection with COVID-19 is increasingly crucial for mega-states adopting targeted infection prevention and control initiatives, which would be a first step towards improving the tourism sector in Rajasthan. In this analysis, communities with confirmed cases from 1 March to 19 June were obtained and considered to be unique disease data for Rajasthan. Evaluation of spatio-temporal variations in epidemics prior to the use of Ecological Niche Models (ENM) to compile disease data and socio-economic variables to classify most possible danger zones of this infection in Rajasthan Figure 8.

It is very important to take a risk zone for the analysis of the infected areas. Based on size of population of Rajasthan different buffer zones has been created from outside the city's urban boundary at (20, 40, 60, 80,100 m) by this we can clearly map the chances of high infection in the community which can be mapped with Red. The community with high risk is mapped as orange which can clear that the community is going to infected soon or have a high risk of infection. And the community with medium risk is mapped as yellow which clears that community has medium risk which is going to be infected later stage. A community with a low risk of infection is mapped as light green and dark green is mentioned as no risk of infection. It is essential to know the risk factors in the community if we analyze the pattern of COVID-19 cases.

Risk zone analysis shows that the approach can be used as an early forecasting technique to classify possible risk areas for contamination with COVID-19 on a fine scale. This paper recommends that local health authorities should keep an eye on the disease in each area and ensure that their measures in the zones are properly applied and adapted. In this study, we analysed the spatial and temporal dynamics of newly issued communities with reported cases of COVID-19 before exploring feasibility and early detection of possible risk areas for infection in Rajasthan. Several notable findings that have been achieved and would provide a valuable guidance for regions with increasingly local dissemination and focused containment measures to tackle the outbreak of this disease. Even as the Coronavirus pandemic sparks an unparalleled global attack on life and livelihoods, pushing the planet into a slowdown that, in terms of size, may well be reminiscent of the Great Depression, India seems to be the odd one in dealing with the crisis. The leadership of every major economy, including those that have been singing waves of globalization, is undergoing some form of government interference and expansionary fiscal policy.

9.   Conclusions

The COVID-19 pandemic is the biggest threat to any nation has ever faced, as international and domestic travel has severely impacted by up to 45 percent in 2020, which is equal to a four-month travel loss. Geospatial Technology is one of the important tools which helps in understanding the current tourism-related activities as well as the pandemic situation in a very efficient and effective way. Geographic Information System (GIS) technology provides a way through mapping and interpreting the spread of COVID-19 concerning tourism in space and time so that the decisions can be taken about strategies and measures to monitor the spread of the pandemic the best example is Arogya Setu Android App which utilizes Bluetooth based contact tracing technology to help the community. Evaluation of maps offer a common research framework that incorporates all forms of related data, both primary and secondary. Maps can aid a better way in terms of visualization, interpretation and reaction planning for policy makers in a constantly shifting world. Site intelligence offers gathering of real-time information about the effects of COVID-19 pandemic on the workforce, businesses and facilities Figure 9.

It also helps many policy and decision-makers to estimate the valuable resources required to keep organizations running. GIS offers a location-based solution to tracking community-based activity of virus in predefined area. Leverage maps will help to explain new issues and introduce a framework that incorporates essential data, events and services. The first and second wave of COVID-19 has almost gone, now the government must focus on third wave. The experts and researchers suggest that it is going to be very tough situations for the kids because virus is mutating very fast and affecting the population on a large scale in a very mean time. So, there is only one solution left, vaccinate each and every one. Government is already started vaccination to major age groups, but the children-based vaccine is on trial phase. Now there is an immense need to accelerate the trials and come up with proper vaccine. This will help in constraining the COVID-19 cases and accordingly, the government can take effective measures. When COVID-19 cases will stop spreading; people will start feeling safe, the economy will boost, commercial activities; hotels and hospitality sectors, Tourist destinations will get back to its stage; in this way, Tourism Industry will revive itself.

Acknowledgments

I express my deep gratitude to Dr. Shruti Kanga and Dr. Suraj Kumar Singh for several enlightening discussions and comments about this research paper.

Conflict of interest

The authors declare no conflict of interest.