Understanding of the carbon cycle is particularly important because of the role of carbon dioxide as a greenhouse gas. Carbon cycle models play an essential role in the interpretation of observational data. The analysis of the carbon cycle involves statistical estimation in various contexts. These include various types of model calibration, including the estimation of feedbacks. A range of inverse calculations are involved in estimating the spatial and/or temporal dependence of carbon dioxide sources and sinks, given observations of concentrations. The uncertainties in these estimates propagate into uncertainties in projections of future carbon cycle behavior. These disparate analyses are discussed in terms of a modeling spectrum that runs from empirical statistical models through to reductionist mechanistic models. The use of the modeling spectrum allows a comparison of di erent modeling approaches. Comparing di erent levels of modeling can provide a basis for assessing the extent to which estimation is being applied consistently.
1.
Introduction
Associating graphs to algebraic structures and studying their algebraic properties employing the methods in graph theory has been an interesting topic for mathematicians in the last decades and continuously arousing people's wide attention. For instance, Cayley graphs of groups [14], power graphs of groups ([2,15,24]), zero-divisor graphs of semigroups [17], zero-divisor graphs of commutative rings [5], total graphs of rings [1], unit graphs of rings [6], zero-divisor graphs of modules [9]. Bosák initiated the study of the intersection graphs of semigroups in [10]. Later, Csákány and Pollák defined the intersection graph of subgroups of a finite group and studied the graphic properties in [16]. In the recent years, several interesting properties of the intersection graphs of subgroups of groups have been obtained in the literature. In 1975, Zelinka investigated the intersection graphs of subgroups of finite abelian groups [33]. Akbari, Heydari and Maghasedi obtained some properties of the intersection graphs of subgroups of solvable groups in [7]. Shen classified finite groups with disconnected intersection graphs of subgroups in [29]. Ma gave an upper bound for the diameter of intersection graphs of finite simple groups in [23]. Rajkumar and Devi defined the intersection graph of cyclic subgroups of groups and obtained the clique number of intersection graph of subgroups of some non-abelian groups [26,27]. Recall that, for a finite group G, the intersection graph of subgroups of G, denoted by Γ(G), is a graph with all non-trivial subgroups of G as its vertices and two distinct vertices H and K are adjacent in Γ(G) if and only if H∩K≠1.
The thickness of a graph, as a topological invariant of a graph, was first defined by Tutte in [30]. The problem is the same as determining whether K9 is biplanar or not, that is, a union of two planar graphs and it was showed in [11]. Tutte generalized the problem by defining the concept of the thickness of a graph. It is an important research object in topological graph theory, and it also has important applications to VLSI design and network design (see [4,28]). Outerthickness seems to be studied first in Geller's unpublished manuscript, where it was shown that θ0(K7) is 3 by similar exhaustive search as in the case of the thickness of K9. It is known that determining the thickness of a graph is NP-hard [22]. Until now, there are only a few results on the thickness of graphs. The attention has been focused on finding upper bounds of thickness and outerthickness. In 1964, Beineke, Frank and Moon obtained the thickness of the complete bipartite graph [13]. Beineke and Harary obtained the thickness of the complete graph ([3,12]). Chartrand, Geller and Hedetniemi conjectured that planar graph has an edge partition into two outerplanar graphs in [21]. Guy and Nowwkowski obtained the outerthickness of the complete graph and complete bipartite graph in [19,20]. In [18], Ding et al. proved that every planar graph has an edge partition into two outerplanar graphs.
For the planarity of intersection graph of subgroups of a finite group, Ahmadi and Taeri, Kayacan and Yaraneri independently classified all finite groups with planar intersection graphs in [8,25], respectively. By their main theorem, it is easy to obtain the planarity of intersection graph of subgroups of a finite abelian group.
Theorem 1.1. [8,25] Let G be a finite abelian group. Then Γ(G) is planar if and only if G is one of the following groups:
Zpα(α=2,3,4,5),Zpαq(α=1,2),Zpqr,Zp⊕Zp,Z2⊕Z2p, where p,q,r are distinct primes.
Motivated by the above theorem, the aim of this paper is to classify finite abelian groups whose thickness and outerthickness of intersection graphs of subgroups are 1 and 2, respectively. We also investigate the thickness and outerthickness of intersection graphs of subgroups of some finite non-abelian groups in the last section.
2.
Preliminaries
Let us recall some basic definitions and notations in graph theory. Let Γ be a graph with vertex set V(Γ) and edge set E(Γ), and all graphs in this paper are simple graphs, that are, undirect, no loops and no multiple edges. We use Kn to denote the complete graph on n vertices and Km,n to denote the complete bipartite graph with one partition consisting of m vertices and another partition consisting of n vertices. The degree of a vertex v in Γ, denoted by degΓ(v), is the number of vertices incident to v. If degΓ(v)=k, then the vertex is denoted by vk. A subgraph Γ′ of Γ is provided V(Γ′)⊆V(Γ) and E(Γ′)⊆E(Γ). A clique of a graph Γ is a complete subgraph of Γ. A maximal clique of a graph is a clique such that adding any vertex into the clique cannot be a clique. The clique number of a graph Γ is the number of vertices in a maximal clique in Γ with maximum size and it is denoted by ω(Γ). A subgraph H of Γ is a spanning subgraph of Γ if V(H)=V(Γ). The union of graphs Γ1 and Γ2 is the graph Γ1∪Γ2 with vertex set V(Γ1)∪V(Γ2) and edge set E(Γ1)∪E(Γ2). Let Γ1+Γ2 be a graph obtained from the union Γ1∪Γ2 by adding edges between each vertex in Γ1 and each vertex in Γ2. If Γ2 has exactly one vertex v, we shall use Γ1+v instead of Γ1+Γ2. A graph is planar if it can be drawn in a plane such that no two edges intersect expect at their end vertices. An outerplanar graph is a planar graph that can be embedded in the plane without crossings in such a way that all the vertices lie in the boundary of the unbounded face of the embedding. Recall that the thickness of a graph Γ, denoted by θ(Γ), is the minimum number of planar subgraphs whose union is Γ. Similarly, the outerthickness θ0(Γ) is obtained where the planar subgraphs are replaced by outerplanar subgraphs in the previous definition. Obviously, the thickness of a planar graph is 1 and the outerthickness of an outerplanar graph is 1.
The following lemmas are obvious and are used frequently later.
Lemma 2.1. [32,Lemma 2.1] If Γ1 is a subgraph of Γ2, then θ(Γ1)≤θ(Γ2) and θ0(Γ1)≤θ0(Γ2).
Lemma 2.2. [12,19,3] (1) θ(Kn)={⌊n+76⌋n≠9,103n=9,10.
(2) θ0(Kn)={⌈n+14⌉n≠73n=7.
where ⌈x⌉ denotes the least integer greater than or equal to x, ⌊x⌋ denotes the largest integer greater than or equal to x
By Lemma 2.2, one can see that θ(Kn)≥3 for n≥9, θ0(Kn)≥3 for n≥7.
From Euler's formula, a planar graph Γ has at most 3|V|−6 edges and an outerpalnar graph Γ has at most 2|V|−3 edges, furthermore, one can get the lower bound for the thickness and outerthickness of a graph as follows.
Lemma 2.3. [13] If Γ=(V,E) is a graph with |V|=n and |E|=m, then θ(Γ)≥⌈m3n−6⌉ and θ0(Γ)≥⌈m2n−3⌉.
Lemma 2.4. Let Γ be a graph. If θ(Γ)=k, then θ(Γ+vk)=k. In particular, if Γ is a complete graph, then θ(Γ+vt)=k(1≤t≤2k).
Proof. If Γ is a planar graph, then Γ+v1 is clearly a planar graph. If Γ is not a planar graph, then we may assume that {Γ1,Γ2,⋯,Γk} is a planar decomposition of Γ, where each Γi is a spanning subgraph of Γ, then Γi+v1 are planar graphs. Hence {Γ1+v1,Γ2+v1,⋯,Γk+v1} is a decomposition of Γ+vk. Thus, θ(Γ+vk)≤k. By Lemma 2.1, θ(Γ+vk)≥θ(Γ)=k and thus θ(Γ+vk)=k. In particular, if Γ is a complete graph, then θ(Γ+vt)=k(1≤t≤2k).
Lemma 2.5. [31] A graph is outerplanar if and only if it has no subgraph homeomorphic to K4 or K2,3.
3.
Classification of finite abelian groups
The aim of this section is to classify finite abelian groups whose intersection graphs have thickness and outerthickness 1 and 2. We first consider the case of finite cyclic groups.
Theorem 3.1. Let G=Zn be a cyclic group of order n and Γ(G) is not an empty graph. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G is one following groups:
where p1, p2, p3 and p are distinct primes.
(2) θ(Γ(G))=2 if and only if G is one following groups:
where p1, p2, p3, p4 and p are distinct primes.
Proof. Suppose that n=pα11pα22⋯pαss with α1≤α2≤⋯≤αs. Then we have V(Γ(Zn))=s∏i=1(αi+1)−2. We complete our proofs by discussing the number of prime divisors of n.
Case 1. s≥5. It is clear that
are nine non-trivial subgroups of G. Note that any pair of these nine subgroups has non-trivial intersection. So they form a complete graph K9, which is a subgraph of Γ(G). Thus, ω(Γ(G))≥9. By Lemma 2.1, θ(Γ(G))≥θ(K9)=3.
Case 2. s=4. If α4≥2, then G has at least nine non-trivial subgroups, namely,
Note that any pair of these nine subgroups has non-trivial intersection. So they form a complete graph K9, which is a subgraph of Γ(G). Thus, θ(Γ(G))≥θ(K9)=3 by Lemma 2.1. If α4=1, then G≃Zp1p2p3p4. So, G has totally 14 non-trivial subgroups, namely,
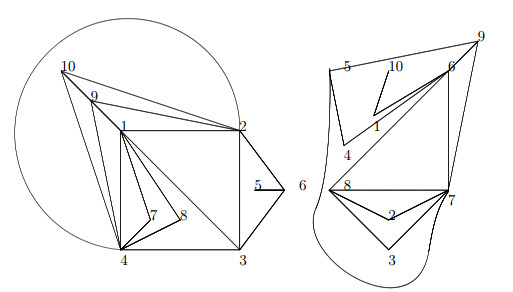
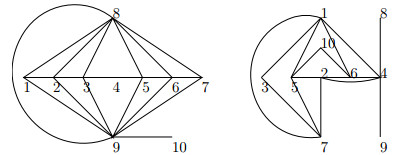
Note that ⟨p1⟩,⟨p2⟩,⟨p3⟩, ⟨p1p2⟩, ⟨p1p3⟩, ⟨p2p3⟩, ⟨p1p2p3⟩ form K7 as a subgraph of Γ(G). So ω(Γ(Zp1p2p3p4))≥7 and V(Γ(Zp1p2p3p4))=14. By Lemma 2.1 and Lemma 2.2, 2=θ(K7)≤θ(Γ(Zp1p2p3p4))≤θ(K14)=3. A planar decomposition of Γ(Zp1p2p3p4) shown in Figure 1 deduces that θ(Γ(Zp1p2p3p4))=2.
Case 3. s=3. If α3≥3, then
are nine non-trivial subgroups of G. Any pair of these nine subgroups has non-trivial intersection. So they form K9, which is a subgraph of Γ(G). By Lemma 2.1, θ(Γ(G))≥θ(K9)=3. If α2=α3=2, then
are nine non-trivial subgroups of G. Any pair of these nine subgroups has non-trivial intersection. They also form K9 as a subgraph of Γ(G). So θ(Γ(G))≥θ(K9)=3 by Lemma 2.1.
If α1=α2=1,α3=2, then G has totally ten non-trivial subgroups, namely,
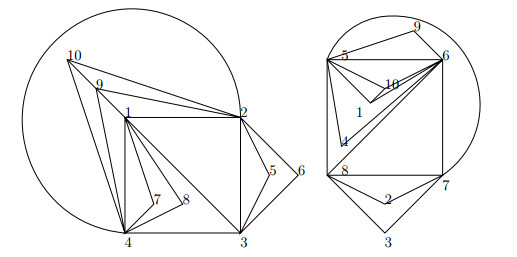
Note that ⟨p1⟩, ⟨p2⟩, ⟨p3⟩, ⟨p1p2⟩, ⟨p1p3⟩, ⟨p2p3⟩, ⟨p1p2p3⟩ form K7 as a subgraph of Γ(G). Then ω(Γ(G))≥7 and V(Γ(G))=10. By Lemma 2.1 and Lemma 2.2, 2=θ(K7)≤θ(Γ(G))≤θ(K10)=3. We can give a planar decomposition of Γ(Zp1p2p23) as shown in Figure 2. Thus, θ(Γ(G)=2.
If α1=α2=α3=1, by Theorem 1.1, Γ(Zp1p2p3) is a planar graph. So θ(Γ(Zp1p2p3))=1.
Case 4. s=2. In this case, it easy to see that Γ(G)≅Kα1α2−1+(Kα1∪Kα2). Then ω(Γ(Zpα11pα22))=α1α2−1+α2. If α1α2−1+α2≥9, then θ(Γ(G))≥θ(K9)=3. So α1α2−1+α2≤8 and implies that α2≤4.
If α2=4, then α1=1. So, Γ(G)≃K3+(K4∪K1). By Lemma 2.1 and Lemma 2.2, 2=θ(K7)≤θ(Γ(Zp1p42))≤θ(K8)=2. This deduces that θ(Γ(Zp1p42))=2.
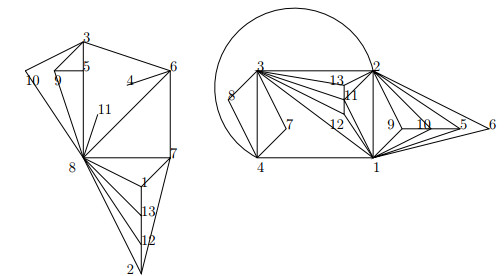
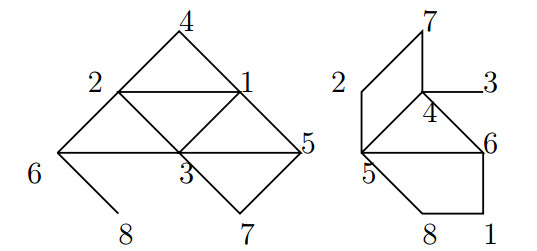
If α2=3, then α1≤2. If α1=2, then Γ(G)≃K5+(K3∪K2), By Lemma 2.1 and Lemma 2.2, 2=θ(K8)≤θ(Γ(Zp21p32))≤θ(K10)=3. A planar decomposition of Γ(Zp21p32) as shown in Figure 3 deduces that θ(Γ(Zp21p32))=2. If α1=1, then Γ(G)≃K2+(K3∪K1). By Lemma 2.1 and Lemma 2.2, 2=θ(K5)≤θ(Γ(Zp1p32))≤θ(K6)=2. So, θ(Γ(Zp1p32))=2.
If α2=α1=2, then Γ(G)≃K3+(K2∪K2). By Lemma 2.1 and Lemma 2.2, 2=θ(K5)≤θ(Γ(Zp21p22))≤θ(K7)=2. Thus, θ(Γ(Zp21p22))=2.
If α2=2 and α1=1 or α1=α2=1, then by Theorem 1.1, Γ(Zp1p2) and Γ(Zp1p22) are planar graphs. So, θ(Γ(Zp1p2))=θ(Γ(Zp1p22))=1.
Case 5. s=1. In this case, Γ(Zpα)≃Kα−1. By Lemma 2.2, it deduces that if α=2,3,4,5, then θ(Γ(Zpα))=1; and if α=6,7,8,9, then θ(Γ(Zpα))=2.
This completes the proof.
For the outerthickness of Γ(G) of a cyclic group G, we have following theorem.
Theorem 3.2. Let G=Zn be a cyclic group of order n and Γ(G) is not an empty graph. Then the following statements are hold.
(1) θ0(Γ(G))=1 if and only if G is one following groups: Zpα(α=2,3,4), Zp1pα2(α=1,2), Zp1p2p3, where p1, p2, p3 and p are primes.
(2) θ0(Γ(G))=2 if and only if G is one following groups: Zpα(α=5,6,7), Zp21p22, Zp1p32, where p1, p2 and p are primes.
Proof Suppose that n=pα11pα22⋯pαss with α1≤α2≤⋯≤αs. According to the proof of Theorem 3.1, if s≥4, then θ0(Γ(G))≥3. We proceed with three cases.
Case 1. s=3. Again according to the proof of Theorem 3.1, if θ0(Γ(G))≤2, then G≃Zp1p2p3. In this case, it is clear that Γ(G) contains no subgraph homeomorphic to K4 or K2,3. By Lemma 2.5, Γ(Zp1p2p3) is an outerplanar graph. So, θ0(Γ(Zp1p2p3))=1.
Case 2. s=2. In this case, Γ(G)≃Kα1α2−1+(Kα1∪Kα2). Then ω(Γ(G))=α1α2−1+α2. If α1α2−1+α2≥7, then θ0(Γ(G))≥3. So α1α2−1+α2≤6. This deduces that α2≤3.
If α2=3, then α1=1. So Γ(G)≃K2+(K3∪K1). By Lemma 2.1 and Lemma 2.2, 2=θ0(K5)≤θ0(Γ(Zp1p32))≤θ0(K6)=2. Hence θ0(Γ(Zp1p32))=2.
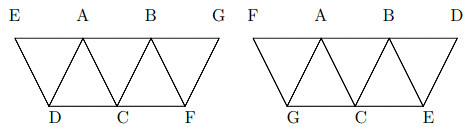
If α2=2,α1=2, then Γ(G)≃K3+(K2∪K2). By Lemma 2.1 and Lemma 2.2, 2=θ0(K5)≤θ0(Γ(Zp21p22))≤θ0(K7)=3. An outerplanar decomposition of Γ(Zp21p22) as shown in Figure 4 deduces that θ0(Γ(Zp21p22))=2.
If α2=2,α1=1, then Γ(G)≃K1+(K2∪K1). It is clear that Γ(G) contains no subgraph homeomorphic to K4 or K2,3. By Lemma 2.5, Γ(Zp1p22) is an outerplanar graph. Then, θ0(Γ(Zp1p22))=1.
If α1=α2=1, then Γ(G)≃K2. So, Γ(Zp1p2) is an outerplanar graph and thus θ0(Γ(Zp1p2))=1.
Case 3. s=1. In this case, Γ(Zpα)≃Kα−1. By Lemma 2.2, it deduces that if α=2,3,4, then θ0(Γ(Zpα))=1; and if α=5,6,7, then θ0(Γ(Zpα))=2. The proof is complete.
Now, we consider the case of finite non-cyclic groups. Let G be a finite Abelian group but not a cyclic group. Then by fundamental theorem of finite abelian group, we have G≃G1⊕G2⊕⋯⊕Gs, where Gi(i=1,2,⋯,s) is a cyclic group of prime power order.
Lemma 3.3. Let G≃G1⊕G2⊕⋯⊕Gs, where s≥2 and Gi(i=1,2,⋯,s) is a cyclic group of prime power order. If s≥4, then θ(Γ(G))≥3.
Proof. Set
Then they are nine non-trivial subgroups of G. Note that any pair of these nine subgroups has non-trivial intersection. So they form K9, which is a subgraph of Γ(G). Thus, θ(Γ(G))≥θ(K9)=3.
Theorem 3.4. Let G be a finite non-cyclic abelian group. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G is one following groups: Z2⊕Z2p, Zp⊕Zp, where p is a prime.
(2) θ(Γ(G))=2 if and only if G is one following groups: Z3⊕Z3q, Z5⊕Z5q, Z4⊕Z4, Z2⊕Z8, Z2⊕Z2⊕Z2, where q is a prime.
Proof. Let the number of distinct prime factors of order of |G| be s. By Lemma 3.3, we know that if θ(Γ(G))≤2, then s≤3. By assumption that G is not cyclic, we have three cases for our discussion.
Case 1. G≃Zpα⊕Zpβ⊕Zpγ, p is a prime.
Case 2. G≃Zpα⊕Zpβ⊕Zqγ, p,q are distinct primes.
Case 3. G≃Zpα⊕Zpβ, p is a prime.
For the Case 1, if there is at least one in {α,β,γ} greater than 1, then we may assume γ≥2. Set
It is easy to see that they are nine non-trivial subgroups of G. Note that any pair of these nine subgroups has non-trivial intersection. So they form K9, which is a subgraph of Γ(G). Thus, θ(Γ(G))≥θ(K9)=3.
Now, we consider the case of α=β=γ=1. If p≥3, we let
They also form K9 and θ(Γ(G))≥θ(K9)=3.
If p=2, then G≃Z2⊕Z2⊕Z2. G has totally 14 non-trivial subgroups, namely,
It is easy to see that Γ(G)=K7+7v3. By Lemma 2.4, we get θ(Γ(G))=θ(K7)=2.
For the Case 2, we may assume α≤β. If β≥2, we let
Note that Di∩Dj=D1 for all i≠j. So, they form a K9 and θ(Γ(G))≥θ(K9)=3.
If γ≥2, then we let
Note that Ei∩Ej=E1 for all i≠j. So, they form a K9 and θ(Γ(G))≥θ(K9)=3.
Now, let G≃Zp⊕Zp⊕Zq. Then all non-trivial subgroups of G are:
It is not difficult to see that Γ(G)=(Kp+3−e)+(p+1)v2. If p≥7, then θ(Γ(G))≥θ(K9)=3. So, p≤5. By Lemma 2.2, if p=2, then θ(Γ(G))=1; and if p=3,5, then θ(Γ(G))=2.
For the Case 3, G≃Zpα⊕Zpβ. We may assume that β≥α. If α≥2 and β≥3, then we set
They are non-trivial subgroups of G. Also, F1=Fi∩Fj for all i≠j. It follows that they form K9 as a subgraph of Γ(G). Thus, θ(Γ(G))≥θ(K9)=3.
If α=β=2, then G≃Zp2⊕Zp2. Now, G has totally p+1 subgroups of order p, i.e., ⟨(0,p)⟩, ⟨(p,0)⟩, ⟨(p,p)⟩, ⋯⟨(p2−p,p)⟩; G has totally p2+p+1 subgroups of order p2, i.e., Q=⟨(0,p),(p,0)⟩, ⟨(1,0)⟩, ⟨(0,−1)⟩, ⟨(1,−1)⟩, ⋯ ⟨(p2−1,−1)⟩; ⟨(1,p)⟩, ⟨(1,2p)⟩, ⟨(1,3p)⟩, ⋯ ⟨(1,p2−p)⟩; G has totally p+1 subgroups of order p3, i.e., ⟨(0,1),(p,0)⟩, ⟨(0,p),(1,0)⟩, ⟨(0,p),(p,0),(1,1)⟩, ⟨(0,p),(p,0),(1,2)⟩, ⋯ ⟨(0,p),(p,0),(1,p−1)⟩. It is not difficult to see that Γ(Zp2⊕Zp2)≃Kp+2+(p+1)Kp+1. So, ω(Γ(Zp2⊕Zp2))=2p+3,V(Γ(Zp2⊕Zp2))=p2+3p+3. If p≥3, then ω(Γ(G))≥9 and θ(Γ(G))≥3. So p=2. By Lemma 2.1 and Lemma 2.2, 2=θ(K7)≤θ(Γ(Z4⊕Z4)≤θ(K13)=3. On the other hand, a planar decomposition of Γ(Z4⊕Z4) shown in Figure 5 gives θ(Γ(Z4⊕Z4))=2.
If α=1, then G≃Zp⊕Zpβ. All subgroups of G can be listed below.
⟨(0,1)⟩,⟨(1,1)⟩,⋯⟨(p−1,1)⟩,
⟨(0,p)⟩,⟨(1,p)⟩,⋯⟨(p−1,p)⟩,
⟨(0,p2)⟩,⟨(1,p2)⟩,⋯⟨(p−1,p2)⟩,
⋯⋯
⟨(0,pβ−1)⟩,⟨(1,pβ−1)⟩,⋯⟨(p−1,pβ−1)⟩.
It is clear that Γ(G)≃Kβ−1+(Kpβ−p+1∪pK1). So Kβp+β−p is a subgraph of Γ(G). If β≥4, then ω(Γ(G))≥9 and θ(Γ(G))≥3. So, β≤3.
If β=3, then p=2 and G≃Z2⊕Z8. So Γ(G)≃K2+(K5∪2K1) and θ(Γ(Z2⊕Z8)≥θ(K7)=2. By Lemma 2.4, θ(Γ(Z2⊕Z8))=θ(K7)=2.
If β=2, then p≤5. If p=2, then G≃Z2⊕Z4 and Γ(G)≃K1+(K3∪2K1). So, θ(Γ(Z2⊕Z4))≥θ(K4)=1. By Lemma 2.4, θ(Γ(Z2⊕Z4))=θ(K4)=1. If p=3, then G≃Z3⊕Z9 and Γ(G)≃K1+(K4∪3K1). Thus, θ(Γ(Z3⊕Z9))≥θ(K5)=2. By Lemma 2.4, θ(Γ(Z3⊕Z9))=θ(K5)=2. If p=5, then G≃Z5⊕Z25 and Γ(G)≃K1+(K6∪5K1). Thus, θ(Γ(Z5⊕Z25))≥θ(K7)=2. By Lemma 2.4, then θ(Γ(Z5⊕Z25))=θ(K7)=2.
If β=1, then G≃Zp⊕Zp. So, Γ(G)≃(p+1)K1. By Theorem 1.1, θ(Γ(Zp⊕Zp))=1.
This completes our proof.
Theorem 3.5. Let G be a finite non-cyclic abelian group. Then the following statements are hold.
(1) θ0(Γ(G))=1 if and only if G≃Zp⊕Zp, where p is a prime.
(2) θ0(Γ(G))=2 if and only if G≃Z2⊕Z2p or Z3⊕Z3p, where p is a prime.
Proof. Suppose G≃G1⊕G2⊕G3⊕⋯⊕Gs, where s≥2 and Gi(i=1,2,3,⋯,s) are cyclic groups. According to the proof of Theorem 3.4, if θ0(Γ(G))≤2, then G≃Zp⊕Zp or G≃Zp⊕Zp⊕Zq or G≃Zp⊕Zp2.
Case 1. G≃Zp⊕Zp. In this case, Γ(G)≃(p+1)K1. It is clear that Γ(G) contains no subgraph homeomorphic to K4 or K2,3. By Lemma 2.5, Γ(Zp⊕Zp) is an outerplanar graph, then θ0(Γ(Zp⊕Zp))=1.
Case 2. G≃Zp⊕Zp⊕Zq. Again by the proof of Theorem 3.4, we know that ω(Γ(Zp⊕Zp⊕Zq))=p+2. If p≥5, then θ0(Γ(G))≥θ0(K7)=3. So p=2, 3. If p=2, then G≃Z2⊕Z2q. It is easy to see that Γ(Z2⊕Z2q)=(K5−e)+3v2. By Lemma 2.1 and Lemma 2.2, 2=θ0(K4)≤θ0(Γ(Z2⊕Z2q))≤θ0(K5)=2. Thus, θ0(Γ(Z2⊕Z2q))=2. If p=3, then G≃Z3⊕Z3q. It is easy to see that Γ(Z3⊕Z3q)=(K6−e)+4v2. By Lemma 2.1 and Lemma2.2, 2=θ0(K5)≤θ0(Γ(Z3⊕Z3q))≤θ0(K6)=2. So θ0(Γ(Z3⊕Z3q))=2.
Case 3. G≃Zp⊕Zp2. In this case, Γ(Zp⊕Zp2)≃K1+(Kp+1+pK1). Thus, ω(Γ(G))=p+2. If ω(Γ(G))≥7, then θ0(G)≥3. Thus, p=2,3. If p=2, then G≃Z2⊕Z4 and Γ(G)≃K1+(K3∪2K1). By Lemma 2.4, θ0(Γ(Z2⊕Z4))=θ0(K4)=2. If p=3, then G≃Z3⊕Z9 and Γ(G)≃K1+(K4∪3K1). By Lemma 2.4, θ0(Γ(Z3⊕Z9))=θ0(K5)=2.
The proof is complete.
Combine Theorems 3.1–3.5, we get the following theorem.
Theorem 3.6. Let G be a finite abelian group and let p1,p2,p3,p4 and p be primes. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G is one following groups:
(2) θ(Γ(G))=2 if and only if G is one following groups:
(3) θ0(Γ(G))=1 if and only if G is one following groups:
(4) θ0(Γ(G))=2 if and only if G is one following groups:
4.
Some finite non-abelian groups
In this section, we investigate the thickness and outerthickness of intersection graphs of subgroups of some finite non-abelian groups. For a positive integer n, τ(n) denotes the number of positive divisor of n; σ(n) denotes the sum of all the positive divisors of n. Sn and An are denoted the symmetric group and alternating group of degree n acting on {1,2,3,⋯,n}, respectively.
For any integer n≥3, the dihedral group of order 2n is defined by
For any integer n≥2, the generalized quaternion group of order 4n is defined by
For any prime p and integer α≥3, the modular group of order pα is defined by
For any integer n≥4, the quasi-dihedral group of order 2n is defined by
Lemma 4.1. [27] The following statements are hold.
(1) For n≥3, n=pα11pα22⋯pαkk, V(Γ(Dn))=τ(n)+σ(n)−2 and ω(Γ(Dn))=σ(n)−n−1+∏ki=1αi.
(2) Let n≥2 be an integer and 2n=2α1pα22⋯pαkk, where p2,…,pk are distinct odd primes and αi≥1. Then V(Γ(Qn))=τ(2n)+σ(n)−2 and ω(Γ(Qn))=σ(n)−1+α1∏ki=2(αi+1).
(3) For α≥4, V(Γ(QD2α))=α+3(2α−1−1) and ω(Γ(QD2α))=α+2α−1−3.
Theorem 4.2. Let G=Sn. Then the following statements are hold.
(1) If n=3, then θ(Γ(G))=1.
(2) If n≥4, then θ(Γ(G))≥3.
Proof. If G=S3, then it is easy to see that Γ(S3)≃4K1, which is a planar graph. So, θ(Γ(G))=1. If n≥4, then we set
S1={(1),(12),(34),(12)(34)},
S2={(1),(12),(13),(23),(123),(132)},
S3={(1),(12),(14),(24),(124),(142)},
S4={(1),(13),(14),(34),(134),(143)},
S5={(1),(23),(24),(34),(234),(243)},
S6={(1),(13),(24),(13)(24),(14)(23),(12)(34),(1234),(1432)},
S7={(1),(14),(23),(13)(24),(14)(23),(12)(34),(1243),(1342)},
S8={(1),(13),(24),(13)(24),(14)(23),(12)(34),(1324),(1423)},
S9={(1),(123),(132),(124),(142),(134),(143),(234),(243),(13)(24),(14)(23),(12)(34)}.
Then they are nine non-trivial subgroups of Sn and form a complete graph K9 as a subgraph of Γ(Sn). Thus, θ(Γ(G))≥θ(K9)≥3.
Theorem 4.3. Let G=An. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if n=4.
(2) If n≥5, then θ(Γ(G))≥3.
Proof. If G≃A4, then Γ(A4)≃4K1∪K1,3, which is a planar graph. So, θ(Γ(G))=1. If n≥5, we let
L1={(1),(12345),(13524),(14253),(15432),(12)(35),(13)(45),(14)(23),(15)(24),(25)(34)},
L2={(1),(12453),(13542),(14325),(15234),(12)(34),(13)(25),(14)(35),(15)(24),(23)(45)},
L3={(1),(12354),(13425),(14532),(15243),(12)(34),(13)(45),(14)(25),(15)(23),(24)(35)},
L4={(1),(12435),(13254),(14523),(15342),(12)(45),(13)(24),(14)(35),(15)(23),(25)(34)},
L5={(1),(12534),(13245),(14352),(15423),(12)(45),(13)(25),(14)(23),(15)(34),(24)(35)},
L6={(1),(12543),(13452),(14235),(15324),(12)(35),(13)(24),(14)(25),(15)(34),(23)(45)},
L7={(1),(123),(124),(134),(234),(132),(142),(143),(243),(13)(24),(14)(23),(12)(34)},
L8={(1),(123),(125),(135),(235),(132),(152),(153),(253),(12)(35),(13)(25),(15)(23)},
L9={(1),(124),(125),(145),(245),(142),(152),(154),(254),(12)(45),(14)(25),(15)(24)}.
Then they are nine non-trivial subgroups of An and form a complete graph K9 as a subgraph of Γ(An). Thus, θ(Γ(G))≥θ(K9)≥3.
Theorem 4.4. Let G=Dn(n≥3) be the dihedral group of order 2n. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G≃D4 or Dp, where p is an odd prime.
(2) θ(Γ(G))=2 if and only if G≃D6,D9, D25 or D10.
Proof. For n≥3, let n=pα11pα22⋯pαkk with α1≤α2≤⋯≤αk. By Lemma 4.1, we know that ω(Γ(Dn))=σ(n)−n−1+∏ki=1αi. If k≥2 and αk≥2, then ω(Γ(Dn))≥p1+pk+p1pk≥11. Thus, if θ(Γ(G))≤2, then n=p1p2 or n=pα.
If n=p1p2, then by Lemma 4.1, ω(Γ(Dn))=σ(n)−n−1+∏ki=1αi=p1+p2+1. If p1+p2+1≥9, then θ(Γ(Dn))≥3. Thus, if θ(Γ(Dn))≤2, then p1+p2+1≤8. Thus, p1=2, p2=3 or p1=2, p2=5.
If p1=2, p2=3, then ω(Γ(D6))=6. So, θ(Γ(D6))≥θ(K6)=2. Note that degΓ(D6)(⟨aib⟩)=τ(6)−2=2 and V(⟨aib⟩)=6. By Lemma 2.4, θ(Γ(D6))=θ(Γ(D6)−6v2). On the other hand, V(Γ(D6)−6v2)=τ(6)−1+σ(6)−6−1=8, then 2=θ(K6)≤θ(Γ(D6)−6v2)≤θ(K8)=2. Hence, θ(Γ(D6))=2.
If p1=2 and p2=5, then ω(Γ(D10))=8. So, θ(Γ(D10))≥θ(K8)=2. Note that degΓ(D10)(⟨aib⟩)=τ(10)−2=2 and V(⟨aib⟩)=n=10. By Lemma 2.4, θ(Γ(D10))=θ(Γ(D10)−10v2). As V(Γ(D10)−10v2)=τ(10)−1+σ(10)−10−1=10, we have 2=θ(K8)≤θ(Γ(D10)−10v2)≤θ(K10)=3. On the other hand, a planar decomposition of Γ(D10)−10v2 as shown in Figure 6 deduces that θ(Γ(D10))=2.
If n=pα, then by Lemma 4.1, ω(Γ(Dn))=pα−pp−1+α. If ω(Γ(Dn))≥9, then θ(Γ(Dn))≥3. So, α≤2.
If α=1, then Γ(Dp)≃(p+1)K1 and thus θ(Γ(Dp))=1. If α=2, then ω(Γ(Dp2))=p+2. Note that degΓ(Dp2)(⟨aib⟩)=τ(p2)−2=1, V(⟨aib⟩)=n=p2, and V(Γ(Dp2))=τ(n)+σ(n)−2=1+p+p2+3−2=p2+p+2. So, Γ(Dp2)=Kp+2+p2v1. By Lemma 2.4, θ(Γ(Dp2))=θ(Kp+2). Since p+2≥9 deduces θ(Γ(Dp2))≥3, we have p+2≤8, that is, p=2,3,5. By Lemma 2.2, we get if p=2, then θ(Γ(D4))=1; and if p=3,5, then θ(Γ(D9))=θ(Γ(D25))=2.
Theorem 4.5. Let G=Qn. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G=Q2.
(2) θ(Γ(G))=2 if and only if G≃Q3 or Q5.
Proof. Let n≥2 be an integer and 2n=2α1pα22⋯pαkk, where pi are distinct primes and αi≥1. By Lemma 4.1, ω(Γ(Qn))=σ(n)−1+α1∏ki=2(αi+1). If k≥2, then ω(Γ(Qn))≥1+p1+p2+p1p2−1+1×2×2=4+p1+p2+p1p2>4+2+3+2×3>9 and θ(Γ(Qn))>3. So, if θ(Γ(Qn))≤2, then we have n=pα.
If n=2α, ω(Γ(Q2α))=σ(n)−1+α1∏ki=2(αi+1)=2α+1−1+α,V(Γ(Q2α))=τ(2n)+σ(n)−2=2α+1−1+α, then Γ(Q2α) is a complete graph. If 2α+1−1+α≥9, then θ(Γ(Qn))≥3. So, if θ(Γ(Qn))≤2, then 2α+1−1+α≤8 and thus α=1. In this case, θ(Γ(Q2))=1.
If n=pα and p≠2, then ω(Γ(Qn))=σ(n)−1+α1∏ki=2(αi+1)=1+p+p2+⋯+pα−1+pα+1×(α+1)−1=pα+1−1p−1+α≥9, then θ(Γ(Qn))≥3. So, if θ(Γ(Qn))≤2, then pα+1−1p−1+α≤8, then α=1.
For α=1, ω(Γ(Qn))=σ(n)−1+α1∏ki=2(αi+1)=p+2 and V(Γ(Qn))=τ(2n)+σ(n)−2=p+3. So, θ(Kp+2)≤θ(Γ(Qn))≤θ(Kp+3). If ω(Γ(Qn))=p+2≥9, then θ(Γ(Qn))≥3. So, if θ(Γ(Qn))≤2, then p+2≤8, then p=3,5.
By Lemma 2.1 and Lemma 2.2, 2=θ(K5)≤θ(Γ(Q3))≤θ(K6)=2 and 2=θ(K7)≤θ(Γ(Q5))≤θ(K8)=2, then θ(Γ(Q3))=θ(Γ(Q5))=2.
Theorem 4.6. Let G=QD2α. Then θ(Γ(G))≥3.
Proof. For α≥4, by Lemma 4.1, we have ω(Γ(QD2α))=α+2α−1−3≥9. Thus, θ(Γ(QD2α))≥θ(K9)=3.
Theorem 4.7. Let G≃Mpα. Then the following statements are hold.
(1) θ(Γ(G))=1 if and only if G=M8.
(2) θ(Γ(G))=2 if and only if G≃M27,M125 or M16.
Proof. If pα=8, then Γ(M8)≃Γ(D4). So θ(Γ(M8))=1. If pα≠8, then Γ(Mpα)≃Γ(Zp⊕Zpα−1). If θ(Γ(G))≤2, then by the proof of Theorem 3.5, we know α=3,4. If α=3, then Γ(Mp3)≃K1+(Kp+1∪pK1). By θ(Γ(G))≤2, we get p=3,5. By Lemma 2.4, θ(Γ(M27))=θ(K5)=2 and θ(Γ(M125))=θ(K7)=2. If α=4, then p=2. By Theorem 3.5, θ(Γ(M16))=θ(Γ(Z2⊕Z8))=2.
Theorem 4.8. Let G=Sn. Then the following statements are hold.
(1) If n=3, then θ0(Γ(G))=1.
(2) If n≥4, then θ0(Γ(G))≥3.
Proof. If G=S3, then Γ(S3)≃4K1, which is an outerplanar graph. So θ0(Γ(S3))=1. By the proof of Theorem 4.2, if n≥4, then θ0(Γ(G))≥θ0(Γ(K9))=3.
Theorem 4.9. Let G≃An. Then the following statements are hold.
(1) If n=4, then θ0(Γ(G))=1.
(2) If n≥5, then θ0(Γ(G))≥3.
Proof. Note that Γ(A4)≃4K1∪K1,3. It is clear that Γ(A4) contains no subgraph homeomorphic to K4 or K2,3. By Lemma 2.5, Γ(A4) is an outerplanar graph. So θ0(Γ(A4))=1. By the proof of Theorem 4.3, if n≥5, then θ0(Γ(G))≥θ0(K9)=3.
Theorem 4.10. Let G≃Dn. Then the following statements are hold.
(1) θ0(Γ(G))=1 if and only if G≃Dp, where p is a prime.
(2) θ0(Γ(G))=2 if and only if G is one following groups: D4, D6, D9.
Proof. For n≥3, let n=pα11pα22⋯pαkk with α1≤α2≤⋯≤αk. According to the proof of Theorem 4.4, if θ0(Γ(Dn))≤2, then n=p1p2 or pα.
If n=p1p2, then ω(Γ(Dn))=σ(n)−n−1+∏ki=1αi=p1+p2+1. If p1+p2+1≥7, then θ0(Γ(Dn))≥3. So, if θ0(Γ(Dn))≤2, then p1+p2+1≤6, that is, p1=2, p2=3. As ω(Γ(D6))=2+3+1=6, we know θ0(Γ(D6))≥θ0(K6)=2. An outerplanar decomposition of Γ(D6)−6v2 as shown in Figure 7 gives θ0(Γ(D6))=2.
If n=pα, then ω(Γ(Dn))=σ(n)−n−1+∏ki=1αi=p+p2+⋯+pα−1+α=pα−pp−1+α≥7, then θ0(Γ(Dn))≥3. So, if θ0(Γ(Dn))≤2, then pα−pp−1+α≤6, so α=1,2.
If α=1, then Γ(Dp)≃(p+1)K1. So, θ0(Γ(Dp))=1.
If α=2, Γ(Dp2)=Kp+2+p2v1. By Lemma 2.4, θ0(Γ(Dp2))=θ0(Kp+2). As p+2≥7, then θ0(Γ(Dp2))≥3. So, if θ0(Γ(Dp2))≤2, then p+2≤6, then p=2,3. By Lemma 2.2, we get if p=2, then θ0(Γ(D4))=θ0(K4)=2; and if p=3, then θ0(Γ(D9))=θ0(K5)=2.
Theorem 4.11. Let G≃Qn. Then the following statements are hold.
(1) θ0(Γ(G))≥2.
(2) θ0(Γ(G))=2 if and only if G≃Q2 or Q3.
Proof. According the proof of Theorem 4.5, if θ0(Γ(Qn))≤2, then n=pα.
If n=2α, again by the proof of Theorem 4.5, we have Γ(Q2α)=K2α+1−1+α. If 2α+1−1+α≥7, then θ0(Γ(Qn))≥3. So θ0(Γ(Qn))≤2, then 2α+1−1+α≤6, so α=1. In this case, θ0(Γ(Q2))=2.
If n=pα and p≠2, then ω(Γ(Qn))=pα+1−1p−1+α≥7 deduces θ0(Γ(Qn))≥3. So, if θ0(Γ(Qn))≤2, then pα+1−1p−1+α≤6 and α=1.
In this case, ω(Γ(Qn))=σ(n)−1+α1∏ki=2(αi+1)=p+2 and V(Γ(Qn))=τ(2n)+σ(n)−2=p+3. So, θ0(Kp+2)≤θ0(Γ(Qn))≤θ0(Kp+3). If ω(Γ(Qn))=p+2≥7, then θ0(Γ(Qn))≥3. So, if θ0(Γ(Qn))≤2, then p+2≤6, so p=3. By Lemma 2.1 and Lemma 2.2, 2=θ0(K5)≤θ0(Γ(Q3))≤θ0(K6)=2, then θ0(Γ(Q3))=2.
Theorem 4.12. Let G≃QD2α. Then θ0(Γ(G)≥3.
Proof. For α≥4, by Lemma 4.1, we have ω(Γ(QD2α))=α+2α−1−3≥9. Thus, θ0(Γ(QD2α))≥θ0(K9)=3.
Theorem 4.13. Let G=Mpα. Then the following statements are hold.
(1) θ0(Γ(G))≥2.
(2) θ0(Γ(G))=2 if and only if G≃M8 or M27.
Proof. If pα=8, then Γ(M8)≃Γ(D4). By Theorem 4.4, θ0(Γ(M8))=2. If pα≠8, then Γ(Mpα)≃Γ(Zp⊕Zpα−1). By the proof of Theorem 4.7, we get α=3,p=3. In this case, we have θ0(Γ(M27))=2.
5.
Conclusions and further work
In this paper, we classify all finite abelian groups whose thickness and outerthickness of subgroup intersection graphs are 1 and 2, respectively. We also investigate the thickness and outerthickness of subgroup intersection graphs for some finite non-abelian groups. The method is finding a forbidden subgraph of Γ(G), like K9 and then determining the remaining cases. The key point is how to separate Γ(G) into two planar graphs. Next, one can consider to determine all finite abelian groups G whose Γ(G) has thickness or outerthickness 3. For a general finite group G, how to determine the thickness and outerthickness of Γ(G) is a challenge. Of course, investigating other properties of Γ(G) is a valuable exploration.
Acknowledgments
We would like to thank the referees for a careful reading of the paper and for their valuable comments. This work was supported by the National Natural Science Foundation of China (Grant No. 11661013, 11961050), the Guangxi Natural Science Foundation (Grant No. 2020GXNSFAA159103, 2020GXNSFAA159053) and High-level talents for scientific research of Beibu Gulf University (2020KYQD07). The second author is supported by the Science and Technology Research Project of Jiangxi Education Department.
Conflict of interest
The authors declared that they have no conflicts of interest to this work.










 DownLoad:
DownLoad: