Notation
n,nu,nw,ny are the number of states, inputs, input noise, and outputs, respectively.
q is the dimension of the nonlinearity (q≤n).
u∈Rnu is the vector of known inputs.
˜ueq is the equivalent output of the nonlinearity function.
v∈Rny is a vector of unknown measurement noise.
w∈Rnw is a vector of unknown input disturbance.
wext=col(w(t),x(t),ϕ(t,u,x),u(t)) are the extended errors.
x∈Rn is the state vector.
ˆx∈Rn is the state estimate vector.
˜x=x−ˆx is the state estimation error vector of the system.
xd is the state of delayed measurement.
ˆxa is the approximation of ˆx (when delay is approximated).
˜xa is the approximation of ˜x (when delay is approximated).
y∈Rny is the vector of measurement.
˜yeq is the equivalent input to the nonlinearity.
yˉδ is the effect of error in modeling the delay.
zeq is the state of the augmented equivalent system.
x,y,u are the states, output, and input of system used in the proof of bounded real lemma.
A,ΔA∈Rn×n are the nominal system matrix and its deviation, respectively, with Asys=A+ΔA.
AΓ is a delay system matrix.
Ad,Bd, and Cd are the system matrices of delay.
ˉA,ˉC,ˉL,ˉE,ˉFext,ˉG are system matrices in extended state space.
E,ΔE∈Rn×qare the nominal nonlinearity gain matrix and its deviation, respectively, with Esys=E+ΔE.
F∈Rn×nw is the gain matrix for input disturbance.
Fext=[F ΔA ΔE ΔH] is the extended error-gain matrix.
G is the matrix gain used in matrix Lipschitz condition.
H,ΔH∈Rn×nuare the nominal input-gain matrix and its deviation, respectively, with Hsys=H+ΔH.
L is the observer gain.
K is the degree of rational approximation of delay.
ˉP is a Lyapunov matrix in the extended state-space.
Q∈Rny×ny,Rext∈Rnwext×nwext, and W∈Rn×n are weighting matrices.
T is the time period of the moving time-averaged Lyapunov function.
V1:Rn1→R and V2:Rn2→R, V:R×Rn→R are arbitrary functions.
V(t,x) is an average energy function.
VI(τ,x) is an energy function (being averaged).
A,B,C,D are arbitrary matrices.
G(s) is the transfer function from the output to the input of the nonlinearity.
Gd(s) is the transfer function of delay.
Gd′(s) is the approximate rational transfer function of delay.
U,V,W,Z are arbitrary matrices used in the matrix inverse lemma.
V is an arbitrary energy function used in the proof of bounded real lemma.
Vt:=V(t,x)/∂t,Vx:=V(t,x)/2∂x are partial derivatives of V.
T is the inverse-projection matrix with TT=[ˉ0TKny×nIn×n]T.
γ is H∞ norm of the system used in the proof of bounded real lemma.
γC is the effective bound on the error dynamics.
ε,ϵϕ is an arbitrary constant.
δGd is the approximation error transfer function.
ˉδGd is an equivalent approximation error transfer function.
ςk,ˉςk are Taylor coefficients.
ϕ=ϕ(t,u,x):R×Rm×Rn→Rq is the vector nonlinearity.
˜ϕ=˜ϕ(t,u,ˆx,˜x)=ϕ(t,u,x)−ϕ(t,u,ˆx) is the error in the nonlinearity.
ω is the frequency.
ωmax is the frequency where gain of GNL is maximum.
ωδ is the frequency at which the gain of δGdis maximum.
Γ is the time delay.
Θ(ω) is the matrix frequency gain function of the observer error dynamics.
ˉΘ(ω) is the matrix frequency gain function of the observer error dynamics with equivalent delay.
Ξ,Ω are arbitrary matrices in extended state space.
1.
Introduction
All physical systems exhibit varying levels of nonlinearities. While some nonlinearities may be negligible, it is often necessary to implement a nonlinear controller to ensure stability and system performance [1]. Many advanced control techniques, such as backstepping and sliding mode control, use all system states [1]. Since not all system states are directly measured, it is often necessary to utilize a nonlinear observer to estimate unmeasured states. Physical systems also experience at least a small amount of delay between sensing and activation due to physical limits on processing and communication speed. Non-trivial amounts of delay are known to destabilize systems [2] and observers [3,4,5]. Most observer designs tend to neglect modeling uncertainties, unknown inputs, and measurement noises [6,7,8,9,10]. Hence, this paper focuses on developing observers for systems with measurement delays.
Lipschitz [11,12,13,14,15] and matrix Lipschitz [16,17] nonlinearities are the most common classes of nonlinearities considered in the literature. Here, the observer design problem is formulated as a solution to a linear matrix inequality (LMI). LMI-based formulation is particularly attractive owing to the availability of fast commercial solvers. Such LMI-based designs have been extended to delay-free Lipschitz and matrix Lipschitz nonlinear systems with input disturbances and measurement noise [6,7,8], as well as to perform sensor fault detection [18], actuator fault detection [19], and unknown parameter estimation [9,10]. Other literature has utilized high-gain sliding mode observers [20,21,22] to improve the robustness of systems without measurement noises or measurement delays. More recent literature has used a new time-averaged Lyapunov function to design sliding mode nonlinear observers for systems with sensor noise [23,24]. High-gain observers have also been used for extended state observers for uncertain nonlinear systems without sensor noise or measurement delay [25]. Fault reconstruction algorithms have also been extended to noise-free one-sided Lipchitz nonlinear descriptor systems [26]. However, these results require systems with special structures and cannot be extended to general systems.
The most common method for analyzing the stability of a system with delay is through the use of Lyapunov–Krasowskii (LK) or Lyapunov–Razumikhin (LR) functionals. LK and LR are constructed by adding a quadratic integral term to the traditional quadratic Lyapunov function. While there is ample literature on control [27,28,29,30] and parameter estimation [31,32,33] in systems with non-measurement delay (i.e., delay only in the state dynamics with, e.g., no measurement delay), this review instead focuses on the literature on measurement delay. Zhou et al. [34] proposed an observer for a stochastic linear system to implement non-fragile observer-based H∞ control. Kazantzis and Wright [35] used a linearizing transform (potentially through feedback linearization) on a noise-free nonlinear system. These works do not, however, provide an explicit method for calculating the observer gain. Cacace et al. [36] presented a state observer for drift observable nonlinear systems where the output measurements are affected by a known and bounded time-varying delay. Majeed et al. [3] developed a nonlinear observer-based control of a noise-free Lipschitz nonlinear system whose stability is demonstrated using an LK functional. He and Liu [4,5] designed a noise-free nonlinear observer for a system in feedback linearization. However, these works do not provide an explicit design procedure. Vafaei and Yazdanpanah [37] proposed a "chain observer" for a Lipschitz nonlinear system; again, the overall stability was demonstrated using the LF functional. Chakrabarty et al. [38] presented an LMI-based sufficient condition for the design of state and unknown input observers, which as in earlier results, requires the underlying system dynamics to be stable. Huong [39] proposed an observer design for a noise-free linear system with sensor delay without utilizing LK/LF functionals. However, the observer design relies on the existence of an esoteric state transformation that would be difficult to extend to nonlinear systems with noise.
More recently, Targui et al. [40] designed an observer for a noise-free nonlinear system adding a state-integral term. The state-integral term aims to project the sensor measurement to the current time. However, the need for an additional integration term would make the observer design impractical, and the conditions for the observer design are conservative. Furthermore, satisfying the provided condition does not appear to guarantee observer stability (a more detailed explanation is provided in the Appendix). Guarro et al. [41] proposed a hybrid observer for a linear system, which uses a similar state-integral term to project sensor measurements to current time. There have been other variations of LK/LF functionals for specific systems such as wind turbines [42] or using neural networks [43] for noise-free systems that also require inherent system stability.
It should be noted that all LMI-based formulations require us to find an observer gain that would make the LMI negative. The LK- and LR-based formulation used in previous literature typically result in a positive definite term being added to the LMI. In the case of observers, this implies that previous literature can only design stable observers when the underlying system is stable. Further, LK- and LR-based formulation would require the delay to be smaller than the time scale of the error dynamics [44]. Additionally, most previous results have focused on linear or nonlinear systems without any noise. Hence, this paper aims to develop an observer design that can be applied to any magnitude of delay. The observer design would make the nominal observer stable or would guarantee a L2 performance in the presence of modeling uncertainties, sensor noise, and input disturbance. The key contributions of this paper lie in developing a new observer design procedure that
● can be implemented on a very wide class of nonlinear systems in the presence of measurement noise and disturbances,
● works for large measurement delays,
● does not require stability of the underlying system,
● is robust to modeling uncertainties,
● can guarantee stability in the absence of noise and L2 performance in the presence of modeling uncertainties, sensor noise, and input disturbance,
● provides both necessary and sufficient conditions for the existence of the observer.
Additionally, the implementation of the algorithm has been demonstrated using multiple illustrative examples. The methodology for calculating the explicit solution can be extended to intermittent measurements. A previous observer design by Targui et al. [40] was shown to produce an unstable observer for certain systems.
2.
Materials and methods
2.1. System model
Consider a nonlinear system with measurement delay given by
v,w can be zero-mean white noises. The C-matrix is assumed to not deviate from its nominal value as any error in the C-matrix can be incorporated in ΔA,ΔE, and ΔH. The nonlinearity ϕ=ϕ(t,u,x):R×Rm×Rn→Rq is assumed to satisfy a matrix Lipschitz condition
The matrix Lipschitz condition is a fairly general condition as all nonlinear systems would become matrix Lipschitz in a small neighborhood around their normal operating point. (Note: we may assume σmax(G)=1 or σmax(E)=1). We can construct an observer using the nominal system as follows:
The estimation error dynamics can be written as
We will now determine observer gains that can drive ˜x to an invariant subspace when w≠0,v≠0 and [ΔA ΔE ΔH]≠0, or drive ˜x→0 when w=0,v=0 and [ΔA ΔE ΔH]=0. To this end, we will define preliminary lemmas in section 2.2 that will help us formulate LMIs. Next, we will create a state-space approximation of the delay and define a bound on the approximation error in section 2.3.
2.2. Preliminary results
Lemma 1: S-Procedure Lemma [45]: If V1:Rn1→R and V2:Rn2→R be such that V2≤0, then V1<0 iff ∃ε>0 such that
Proof: If V1<0, then we can choose ε≤min(−V1)max(−V2) to obtain Eq (2.7). Now, if Eq (2.7) is valid, since ε>0, and V2≤0, −εV2≥0. Hence, we find that 0>V1−εV2≥V1.
Lemma 2: Time-averaged Lyapunov function [23,24] or, equivalently, the moving average function: If there exists a moving average function
s.t., VI(τ,x)>0 ∀x≠ˉ0, 1T∫tt−T˙VI(τ,x)dτ<0, when 1T∫tt−TxTWxdτ>D then the system achieves a L2 performance 1T∫tt−TxTWxdτ≤D.
Proof: Note that
hence
Using LaSalle's invariance principle [46], we can show that the system converges to a subspace where ˙V=0, which corresponds to 1T∫tt−TxTWxdτ≤D.
Lemma 3: Matrix inverse lemma or Woodbury lemma [47]:
Lemma 4: Bounded real lemma extended to a system with delay: Consider a system with a transfer function
and an equivalent state space representation
Let ∃V=V(t,x):R×Rn→R be an energy function satisfying
For this system, the following statements are equivalent:
ⅰ. The H∞ norm of the transfer function is bounded by γ
ⅱ. ∃V satisfying Eq (2.14) and ϵϕ∈R≥0 s.t., ∀x,
ⅲ. ∃V satisfying Eq (2.14) and ϵϕ∈R≥0 s.t. ∀x,u
ⅳ. The system is stable with an input |u|≤γ−1|Gx|.
Proof: Since (ETVTx−ϵϕu(t))Tϵ−1ϕ(ETVTx−ϵϕu(t))≥0
Adding Eq (2.19) to Eq (2.17) yields Eq (2.18); hence, ii ⇒ iii. If iii is valid, substituting u(t)=ETVTx into Eq (2.18) yields Eq (2.17) (u(t)=ETVTxcorresponds to the value of u that optimizes Eq (2.18)). Hence, ii ⟺ iii. Now, from Eq (2.13), Ax(t)+AΓx(t−Γ)+Eu(t)=˙x(t); substituting Ax(t)+AΓx(t−Γ)+Eu(t) with ˙x(t) into Eq (2.18) and integrating the result yields
Thus, when |u|≤γ|y|, we can choose V(t,x)+ϵϕ∫t0(yT(t)y(t)−γ2uT(t)u(t))dτ>0 as our Lyapunov candidate to demonstrate stability. Hence, ⅲ ⟺ ⅳ.
When x(0)=ˉ0, V(0,x(0))=0. Since V(t,x)≥0, we find that Eq (2.20) yields
or ⅱ-ⅳ ⇒ ⅰ. To show ⅰ⇒ⅳ, let us consider |u|≤γ−1|y|. This is equivalent to interconnecting G(s) with another system ||G′||∞≤γ−1. Since ||G||∞||G′||∞<1, it follows from the small gain theorem [46] that the interconnected system is stable. Thus i ⇒ ⅳ.
2.3. Modeling feedback delay
2.3.1. State-space representation of the delay
A time delay can be approximated in the Laplace domain using Kth-degree numerator and denominator polynomials as follows [48]
where ςk=(2K−k)!/[ΓK−kk!(K−k)!], ˉςk=2ςk if k is even,else 0.
Notice that owing to symmetry, |Gd′(jω)|=1. The state-space representation of the delay can now be constructed such that
In the controller canonical form, Ad,Bd, and Cd are given by
If ˜x is known, then the approximation of the delayed measurement xd≈C˜x(t−Γ) is written as
In order to construct the overall approximate dynamics, we also need to replace ˜x with ˜xa. Hence, the approximate observer dynamics can be written as
where ˜xa is the approximation of ˜x, and ˆxa is the approximation of ˆx. In the extended space,
where
This can be easily extended to multiple sensors by stacking the state-space representation of the delay for the individual sensors.
2.3.2. Approximation error
Let us define the approximation error as
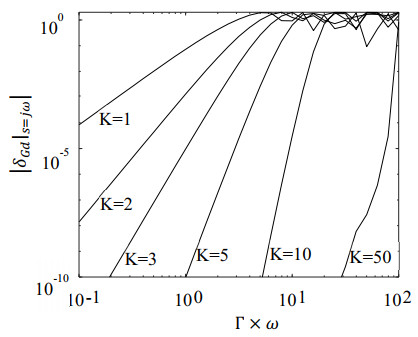
Figure 1 plots |δGd(jω)| vs. Γω for various values of K.
Lemma 5: For δGd(s) defined by Eq (2.31), T defined by Eq (2.30), ˉA,ˉL, and ˉC defined by Eqs (2.28) and (2.29), and ∀Ω,Ξ,
Proof: From Eqs (2.31) and (2.23), we can deduce that
Hence,
Using Lemma 3 we find that
Substituting Eq (2.34) into Eq (2.35) and substituting for ˉA,ˉC, and ˉL from Eq (2.28) yields Eq (2.32).
2.3.3. Estimating the bound on the approximation error
We will now determine a bound on the approximation error that can then be used in the observer design. Since |Gd′(jω)|=|Gd(jω)|=1, Eq (2.31) yields ||δ(s)||∞=2. However, from Figure 1, it is clear that if we are only interested in frequencies below a particular threshold, it may be possible to define a lower effective bound for δGd(jω).
Definition 1: The effective bound on the error of Kth Padé approximation is defined as γC>0, s.t., ∀Ω,Ξ and ˉA,ˉC,and ˉL as defined in Eq (2.28), ∃ˉδGd:||ˉδGd(s)||∞≤γC such that,
Lemma 6: Suppose GNL(s):=Ω[sI−A+LGd(s)C]−1Ξ, is strictly proper, then
where
Proof: Let ωmaxbe the frequency at which the H∞ norm is reached or |GNL(jωmax)|=||GNL||∞. Since GNL(s) is strictly proper, |GNL(jω)|→0 as ω→0. Hence, ∃ωδ≿ωmax s.t. ∀ω≥ωδ, |GNL(jω)|≤||GNL||∞/(1+4|ˉL||ˉC|). Now, consider
Let ΔδGd=ˉδGd(jω)−δGd. Hence
Now
Substituting Eqs (2.39) and (2.42) into Eq (2.43) and simplifying yields,
Since ||δ(s)||∞=2, for ∀ω≥ωδ, |ΔδGd(ω)|≤4. From Eq (2.38), ˉΘ(ω)<||GNL||∞∀ω≥ωδ. Hence, we are only interested in |ˉδGd(jω)| for ω≤ωδ. Since for ω≤ωδ, ˉδGd(jω)=δGd(jω), it follows that γC≈|δGd(jωδ)|.
To illustrate the utility of Lemma 6, suppose it is known that ωδ=0.1/Γ, then for K=2, the effective bound on |δGd(jω)| is 2×10−10.
Note: We can choose ωδ≈−Re(λminˉA−ˉLˉC).
Note: In principle, γC can be made arbitrarily small by increasing K. However, notice that ς0=(2K)!/[ΓKK!], and ςK−1=(K+1)K/Γ; as we increase K, the variation between the smallest and the largest values of ςk will increase and ˉA and ˉC will become less well conditioned. While there is no strict upper limit for K, a very large K may cause computation problems.
2.4. Observer stability
Theorem 7: The noise-free, disturbance-free, and uncertainty-free nominal error dynamics, Eq (2.6) with w=0,v=0 and [ΔAΔEΔH]=0, is stable ∀ϕ satisfying Eq (2.4) if, for the Kth Padé approximation of the delay, ∃ˉP∈R(n+Kny)×(n+Kny)>0,ϵϕ>0, and ϵC>0 s.t.,
where
and ˉ0-s are zero matrices of appropriate dimensions, ˉA,ˉC,ˉL,ˉE and ˉG are defined in Eq (2.28), and γC>0 is the effective bound on the error dynamics as defined in Definition 1.
Further, conditions Eq (2.45) become necessary and sufficient as γC→0.
Proof: For Ξ=E and Ω=G in Definition 1, ∃||ˉδGd(s)||∞≤γC
For such a ˉδGd, the state-space form of ˉG[sI−(ˉA−ˉL(1+ˉδGd(s))ˉC)]−1ˉE can be written as
Multiplying Eq (2.45) by [zTeq ˜uTeq yTˉδ] on the left and col(zeq˜ueqyˉδ) on the right,
Noting that ˉAzeq(t)−ˉLˉCzeq(t)−ˉLyˉδ(t)+ˉE˜ueq(t)=˙zeq(t) (from Eq (2.48)), we find
Integrating the above equation yields
Since ||ˉδGd(s)||∞≤γC,
Applying Lemma 1 to Eqs (2.53) and (2.54), we find
Thus when zeq(0)=0, ∫t0˜yTeq(τ)˜yeq(τ)dτ<∫t0˜uTeq(τ)˜ueq(τ)dτ or,
From Eqs (2.47) and (2.57), we can deduce that
Replacing u with ˜ϕ and AΓ with −LC, in Lemma 4, it is clear that Eq (2.57) ⟺ ∃V=V(t,˜x):R×Rn→R satisfying V(t,˜x)>0 ∀˜x≠ˉ0,V(t,ˉ0)=0, and ϵϕ∈R≥0 s.t ∀˜x,˜ϕ
Since ϕ(t,u,ˆx,˜x) satisfies Eq (2.4),
Let us define a candidate Lyapunov function for the system Eq (2.6) as
Since V>0 ∀˜x≠ˉ0,and ˙V<0, the system Eq (2.6) is stable.
On the limit γC→0,
If on the limit γC→0, ∄ˉP satisfying Eq (2.45), then ||G[sI−A+LGdC]−1E||∞>1. Subsequently, ∃ϕ, for instance ϕ=sin(Gx) that would make the observer unstable. Hence the condition becomes necessary when γC→0.
Note: It is clear from the above theorem that we need to make γC as small as possible. Without the concept of effective bound, however, we would need to use γC=2 (since ˉδ=δ and ||δ(s)||∞=2).
Lemma 8: Given weighting matrices W∈Rn×n, Rext∈Rnwext×nwext, and Q∈Rny×ny, the observer Eq (2.5) can eventually guarantee the following performance
for all nonlinearities ϕ satisfying Eq (2.4), if for the Kth Padé approximation of the delay ∃ˉP>0,ϵϕ>0,ϵC>0, and ϵW>0 s.t.,
where N=ϵWTWTWTT+ˉATˉP+ˉPˉA−ˉPˉLˉC−ˉCTˉLTP+ϵϕγ2ϕˉGTˉG+ϵCγ2CˉCTˉC, ˉ0 is a zero matrix, ˉA,ˉC,ˉL,ˉE,and ˉG are the systems matrices for the error dynamics defined in Eq (2.28), and γC>0 is the effective bound on the approximation error as defined in Definition 1.
Further, Eq (2.63) becomes necessary and sufficient on the limit γC→0.
Proof: Let E:=[EFext(ϵW/ϵϕR)−1/2L(ϵW/ϵϕQ)−1/2] and G:=col(G,(ϵW/ϵϕ)1/2W). By multiplying Eq (2.63) by diag(I,I,(ϵWϵϕR)−1/2,(ϵWϵϕQ)−1/2,I) on both sides, we find
Following the proof of Theorem 7, we can show that
Replacing u with col(˜ϕ,(ϵWϵϕQ)1/2v,(ϵW/ϵϕRext)1/2wext), G with G and E with E in Lemma 4, we find ∃V satisfying Eq (2.14), s.t.,
Hence, if we define
Notice that ˙V<0 when
Hence, from Lemma 2, the system will converge to
It also follows from the proof of Theorem 7 that the condition becomes necessary when γC→0.
Note: While not strictly necessary, if w and v are zero-mean white Gaussian noises, then we can choose (R)−1 equal to the covariances of v and (Q)−1 equal to the covariances of w.
Notice that Eq (2.63) ceases to be a linear matrix inequality if L is unknown. Hence, we will require an iterative procedure for determining L. Such an iterative method would require a method of evaluating the fitness of a chosen L.
Lemma 9: For the system
If ∃ˉP:I≥ˉP>0,ϵϕ>0,ϵC>0andϵW>0, s.t.,
where N=ϵWTWTT+ˉATˉP+ˉPˉA−ˉPˉLˉC−ˉCTˉLTP+ˉGTˉG+ϵCγ2CˉCTˉC+γSI, then if γS>0, system Eq (2.70) has the performance
with an exponential rate ≥γS.
Proof: Defining ˙V by multiplying Eq (2.71) by [zTeq ˜ϕTeq yTˉδ vTwT] on the left and col(zeq,˜ϕeq,yˉδ,v,w) on the right, and following the proof of Theorem 7, we can show that
Since I≥ˉP, it is evident that Eq (2.73) ensures that for V(t)=1T∫tt−T˜xT(τ)ˉP˜x(τ)dτ, when Eq (2.72) is not satisfied
Q.E.D.
For numerical stability, we may need to impose the constraint ˉP≥10−5I and iteratively solve Eq (2.71) and move in the direction of increasing γS until γS>0.
3.
Results
3.1. Simple 2-D problem
3.1.1. Observer design
We will use a simple example to show that the proposed observer design works better than other algorithms from the literature. Consider a second-order unstable system with a dead-zone nonlinearity.
Notice |ϕ(x1a)−ϕ(x1b)−5(x1a−x1b)|≤5|x1a−x1b|. Hence,
The parameters of this system were chosen arbitrarily such that the eigenvalues of A are stable while those of A+EG are unstable. Assuming that our observer eigenvalues would be of the same order of magnitude as our open-loop system, Γ×|Re(λmax)| 5. From Figure 1, let us choose K = 6 with γ=10−5. We can solve the equation to get L=[2.2 2.6]T, with
3.1.2. Comparison with previous literature
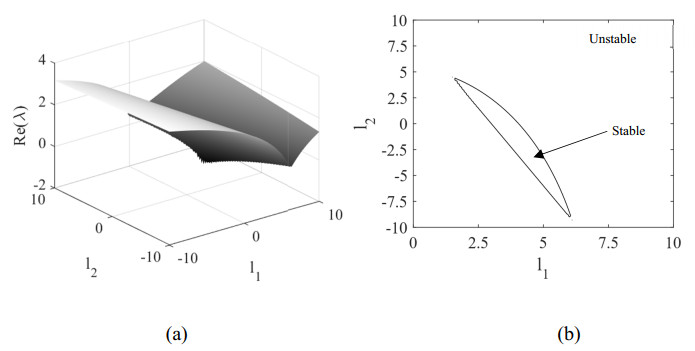
Since much of the literature on delay observers has focused on linear systems, let us consider an equivalent linear system with xdead=0, wherein Aeq=A+EG. The eigenvalues of Aeq are 1.8541 and -4.8541, and the system is unstable without feedback. We know that for a given L, the linear observer would be stable if all of the eigenvalues of the characteristic equations det(sI−A+Le−ΓsC)=0 have negative real parts. Since L only has two elements, we have solved for the roots of the characteristic equations for different values of L. Figure 2 plots the maximum of the real part of the eigenvalues (either the least negative or the most positive eigenvalue), as well as the stability boundary wherein this maximum of the real part of the eigenvalues is zero.
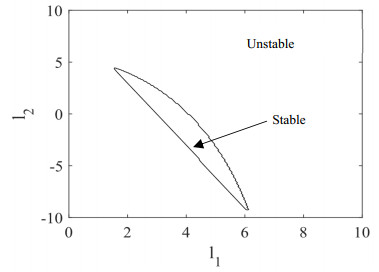
Figure 3 plots the stability boundary obtained by applying the observer design proposed in this paper. This boundary matches the theoretical stability boundary in Figure 2.
We are unable to make a direct comparison to literature results as there are no equivalent explicit procedures for observer design for systems with measurement delay. Hence, we select possible observer gains over a dense grid (L=[l1l2]T, −100≤l1≤100, and −100≤l2≤100). For each L, we examined the feasibility of the LMI that was proposed in Fridman and Shaked [44,49], by attempting to find P1>0, P2,P3,P4, s.t.,
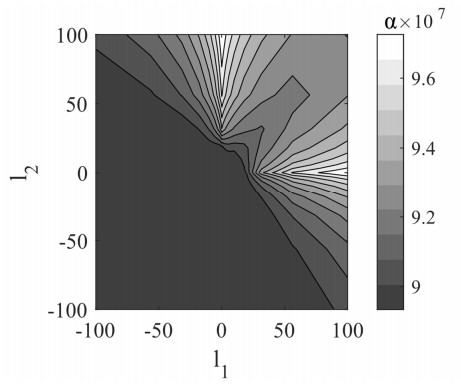
As we were unable to find any L, we aimed to get a better understanding of feasibility by making M<α under the constraint P1≥10−5I (without this constraint, it is possible to make P1, P2,P3,P4 arbitrarily small, which will lead to numerical problems). Figure 4 plots the minimum α for L=[l1l2]T, −100≤l1≤100, and −100≤l2≤100 (the plot was generated by minimizing α using LMI solver for every combination of l1 and l2 in the given range). It is seen that α>0, indicating that an observer design is not possible.
We similarly attempted to solve the following LMI that was proposed by Park et al. [50] (presented in Fridman [44]), P1>0, P2>0,P3>0, s.t.,
The LMI was similarly found to be infeasible. This is expected since the condition based on earlier literature requires the eigenvalues of ΓLC to lie within a unit circle [44], while Figure 2 indicates a different stability boundary. We were similarly unable to design a nonlinear observer for the system based on the methodology proposed in Targui et al. [40], as for every L, we were unable to find P>0 such that
3.2. Robotic link with an elastic joint
In this example, we consider an unstable nonlinear system with
This system is an unstable variation of the elastic joint robotic arm studied in the literature [6,24]. Notice that the eigenvalues of A are 0.2385,−0.6250±8.2501j,−1.4885. The real system is assumed to have a mass that is 1% lower than the nominal system. This would result in
We will further assume that the input disturbance is given byw (0,10−2), the noise in the sensor is given by v (0,10−2), and the sensor measurements are delayed by Γ=0.1s. If we solve for L by ignoring the delay, we can obtain
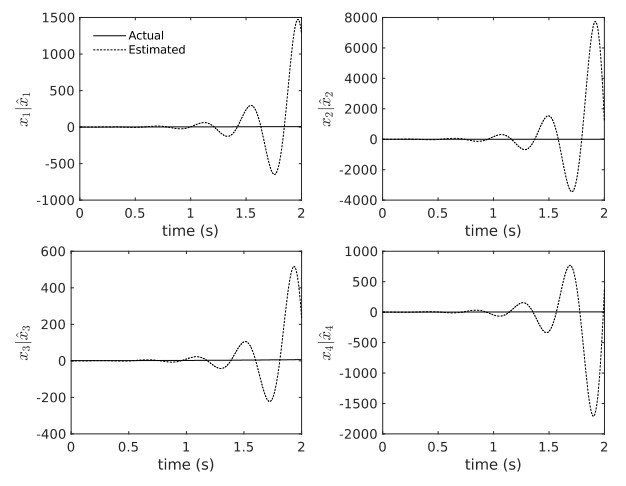
Notice that ||E(sI−A+Lignore delayC)G||∞<1, and the observer is stable in the absence of delay. However, Figure 5 shows that the observer is unstable (when by u=sin(t)).
We will use K=3 and γC=10−5, and set W=I. Applying the proposed algorithm for a delay time of 0.1 s on outputs, we obtain:
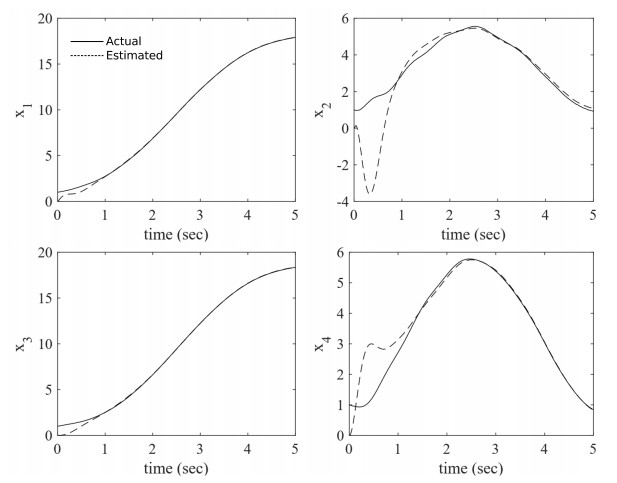
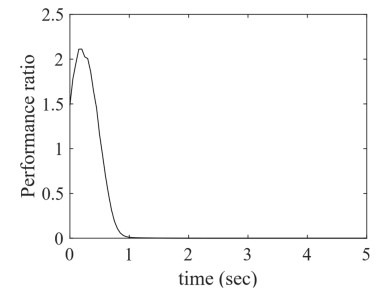
Figure 6 shows the observer states, and Figure 7 shows that the performance ratio ∫tt−T˜xT(τ)W˜x(τ)dτ/∫tt−T(vT(τ)Qv(τ)+wText(τ)Rextwext(τ))dτ is less than 1.
4.
Discussion
This section discusses potential stability issues with the nonlinear delay observer that was proposed in Targui et al. [40]. Targui et al. [40] considered a noise-free system and an observer of the form
The error dynamics of ˜x=x−ˆx is given by Eqs (4.1)-(4.3)
Using
They obtain
Using the following LK functional
The authors show that the observer design would be stable if
We will now provide an example where the error dynamics could be unstable despite satisfying Eq (4.8). Consider the unstable linear system
Here, A=1, C=1, G=0 and Γ=0.75. We can construct an observer of the form Eq (4.3)
Since G=0, we can set ϵ1,ϵ3→∞. Notice Eq (4.14) is satisfied for l=5, and P=1,ϵ2=5,ϵ1,ϵ3→∞, since
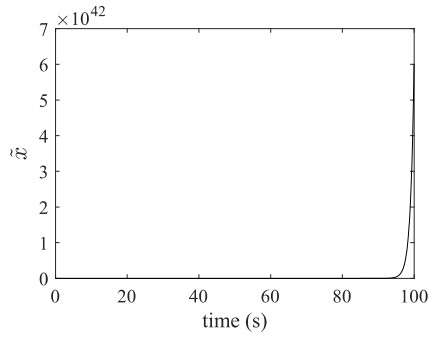
Hence, the observer should be stable. Figure 8 shows the error dynamics for the above system for u=sin(100t). It is evident from the figure that the observer is unstable, and the observer design proposed by Targui et al. [40] may not be viable.
We will provide further analysis to get to the root of the problem. Let us begin by considering a more general form of the above system using A=a, L=l, G=0.
As before, since G=0, we can set ϵ1,ϵ3→∞. Hence, Eq (4.8) can be written as
Taking Schur's complement, we find that we need
Setting dM/dϵ2=0 yields
Notice that ϵ2=P|la| is a minimum as d2M/dϵ22>0. Hence, substituting in Eq (4.15) we find
Since P>0, we need
Since l would usually be positive, we need
There does not seem to be an upper bound for stability (which contradicts our understanding of system delay). It should be noted that even if the observer would work under most normal circumstances, it would be extremely difficult to implement.
5.
Conclusions
This paper has developed an observer design procedure for a nonlinear system in the presence of unknown input disturbance, sensor delay, and sensor noise. Necessary and sufficient conditions have been presented for the observer stability in the form of linear matrix inequalities. The observer design procedure was demonstrated for a simple 2D system and an elastic joint robotic arm with delay. Additionally, the paper provided a means of calculating the H∞ gain of the state-space representation of a delay system, which can be extended to a robust control of the system with delay.
The proposed design procedure is less conservative than results that use Lyapunov–Krasowskii (LK) or Lyapunov–Razumikhin (LR) functionals. In the future, the proposed observer design may be extended to systems with variable delay and to hybrid systems by treating the discrete-time digital signal as a delayed measurement. Additionally, controller and observer designs are often dual problems, and it will be possible to adapt these results to several controller designs.
Use of AI tools declaration
The author declares that they have not used any Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The author would like to thank Alireza Beigi, Divya Rao Ashok Kumar, and Amirmasoud Ghasemi Toudeshki at SFU, for their assistance with a few of the simulations used in the paper. The authors would like to acknowledge funding support from NSERC through the Discovery grant (RGPIN/02971-2021).
Conflict of interest
The author declares that there is no conflict of interest.









 DownLoad:
DownLoad: