CNN-Trans-SPP: A small Transformer with CNN for stock price prediction

1.   Introduction

In recent years, the number of financial activities has surged alongside rapid economic development, leading to increasingly complex trends. Simultaneously, the advancement of information technology has resulted in the accumulation of vast amounts of financial transaction data. Leveraging this historical data to uncover patterns in financial activities and predict their evolution has become a key focus in both academic and financial research. This approach benefits investors and profit-driven organizations by enabling informed decision-making at the micro-level, with the goal of maximizing profits. However, the inherent non-linearity and complexity of financial data make accurate financial price prediction an exceptionally challenging task ^[1].

In the early days, researchers primarily adopted statistical models and econometric methods to construct prediction model. An assumption for using these models was that the data should exhibit linear characteristics, which did not align with the nonlinear nature of financial data. Subsequently, some nonlinear machine learning models were widely used in financial forecasting, including support vector machines (SVM), neural networks, and others. Recently, with the widespread adoption of deep learning models across various domains, techniques such as convolutional neural networks (CNNs) and long short-term memory (LSTM) networks have also been extensively employed in financial forecasting. These models are particularly effective in addressing nonlinear problems ^[2]. To further enhance feature representation, people attempt to use transformer models in varied fields. This paper aims to introduce the transformer model into stock price prediction, combining it with CNN to extract local features effectively. Additionally, to make predictions more practical, this work also explores multi-step forecasting, allowing for a more comprehensive understanding of future trends in stock prices.

The primary contributions of this paper are summarized as follows:

● We propose a small hybrid model that can fully leverage the advantages of CNNs and transformers.

● We not only achieved one-step prediction, but also achieved multi-step prediction for stock price prediction. This can obtain stock trends on a larger time scale, which is beneficial for making decisions.

● We selected four types of stock data to demonstrate the generalization ability and adaptability of our method. Experiments have shown that our proposed method achieves better performance.

The remainder of the paper is organized as follows: Section 2 provides an overview of recent literature on stock price prediction. In Section 3, we introduce the proposed fusion approach. Section 4 presents the experimental setup, followed by a discussion of the results. Finally, Section 5 concludes the paper and outlines directions for future research.

2.   Related works

2.1.   Traditional methods for stock forecasting

Researchers have made significant advancements in predicting stock prices. Early efforts primarily utilized time series analysis models such as autoregressive conditional heteroskedasticity (ARCH) ^[3] and generalized autoregressive conditional heteroskedasticity (GARCH) ^[4]. To better address the nonlinearity and volatility of financial data, machine learning models, including artificial neural networks (ANN) ^[5] and support vector machines (SVM) ^[6], have been widely applied. Tay et al. were the first to apply SVM to stock market prediction ^[7]. Birgul et al. used ANN to predict stock returns ^[8], and Kara et al. further confirmed the significant performance of ANN and SVM models in predicting stock prices ^[9].

However, these models have drawbacks, such as being prone to local optima and parameter tuning difficulties. To address these issues, researchers have proposed hybrid models based on these traditional approaches to enhance performance. Armano et al. introduced a hybrid neural network model that uses a genetic classifier to control the activation of feedforward neural networks ^[10]. Fu et al. proposed the Bayesian Ying Yang neural network, inspired by the ancient Chinese Ying-Yang philosophy ^[11]. Additionally, Choudhary et al. developed a hybrid model combining a genetic algorithm with SVM, which was applied to stock market prediction ^[12]. Vijh et al. ^[13] combined an artificial neural network with random forest techniques to predict the next day's stock closing price, demonstrating the effectiveness of their model. Meanwhile, Chandar et al. ^[14] assessed the efficiency of a hybrid prediction model using a multi-layer perceptron (MLP) and cat swarm optimization (CSO) algorithm. In our previous work ^[15], we also proposed a hybrid model combining particle swarm optimization with SVM. The experimental results showed that the hybrid model outperforms single models.

2.2.   Deep learning methods for stock forecasting

With the rise of deep learning technology, deep neural networks have been increasingly employed for stock market prediction. Wanjawa et al. applied deep neural networks to predict three stocks on the New York stock exchange, achieving favorable prediction results ^[16]. CNNs, known for their exceptional performance in image recognition, have also been utilized in stock prediction tasks. Tsantekidis et al. constructed a 1-D CNN for stock price prediction, demonstrating that CNN outperforms multi-layer perceptron and SVM models ^[17]. Gudelek et al. used a 2-D CNN to predict stock price trends by classifying trading images ^[18].

Furthermore, recurrent neural networks (RNNs) are crucial for addressing sequential problems and have been widely applied in fields such as speech recognition and natural language processing. Samarawickrama et al. employed RNNs for daily stock price prediction of listed companies, achieving superior results compared to feedforward neural networks ^[19]. Roondiwala et al. used LSTM networks to predict the stock returns of NIFTY 50 ^[20]. Selvin compared the performance of three different models (i.e., RNN, CNN, and LSTM—in predicting stock prices of NSE-listed companies, finding that RNN and LSTM) were capable of capturing long-term dependencies in the data, while CNN excelled at capturing short-term dependencies ^[21]. Building on these findings, Lu et al. proposed a CNN-LSTM hybrid model ^[22]. This model utilized CNNs to extract local features, followed by LSTM networks to learn temporal features. The results once again demonstrated the superiority of the hybrid model over single models.

In recent years, transformer models ^[23] have set new benchmarks in natural language processing and are increasingly being utilized in areas such as image recognition ^[24] and multimodal tasks ^[25]. Lai et al. ^[26] introduced a differential transformer model for predicting stock movement, incorporating a temporal attention-augmented bilinear layer and a temporal convolutional network to filter noise from the data. Tao et al. ^[27] developed the series decomposition transformer with period-correlation (SDTP) to discern relationships in historical data, thereby enhancing trend prediction in the stock market with high accuracy and generalizability. Mishra et al. ^[28] combined a transformer with GARCH and LSTM models to improve volatility forecasting and financial risk assessment. Recently, Shi et al. ^[29] proposed a new model called manbaStock, which effectively mines historical stock market data to predict future stock prices without handcrafted features.

Research literature indicates that transformers excel at capturing global features, while CNNs are more effective at representing local features. Therefore, in this paper, we combine the strengths of CNNs and Transformers to propose a hybrid model for stock price prediction (CNN-Trans-SPP).

3.   The models for stock price prediction

3.1.   Problem description and modeling

The task of stock price prediction involves forecasting the price for the next day or several days using stock trading data from the previous days. Predicting the stock price for only the next day is referred to as single-step prediction, while forecasting the stock prices for several consecutive days is known as multi-step prediction. In this paper, we focus on predicting the opening price of the next day by leveraging trading data from the previous five days. The formal description of the single-step prediction task is shown in Eqs (3.1) and (3.2).

Here, $\boldsymbol{x_{t}}$ represents the trading data, which includes the opening price, high price, low price, closing price, and trading volume. $\boldsymbol{t}$ denotes a specific day in the time series.

For the multi-step prediction task, we predict the opening prices for the next three days using the trading data from the previous five days. The multi-step prediction is formalized as shown in Eq (3.3).

3.2.   The proposed framework of CNN-Trans-SPP

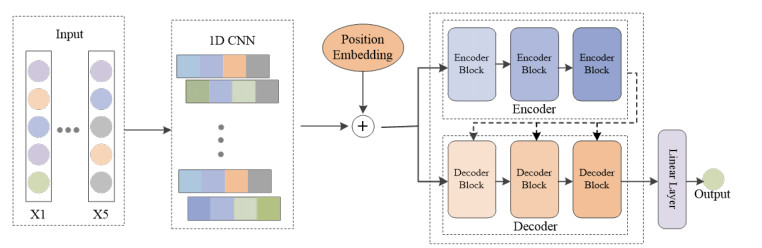
The CNN-Trans-SPP model consists of five parts: Conv1d embedding, position encoding, encoder, decoder, and linear layer, as shown in Figure 1. Conv1d embedding layer consists of 252 convolutional kernels. For position encoding, transformer model captures the relative position information by the functions of sine and cosine. However, an absolute position information is more beneficial for time series prediction tasks. Therefore, we utilize tabular position encoding, which limits the range of position values to [0, 1] and evenly distributes each element. The corresponding formula is shown in Eq (3.4).

Figure 1.  CNN-Trans-SPP framework.

DownLoad: Full-Size Img PowerPoint

where, $y_i$ denotes the position value of the $i-th$ element. $k$ denotes the length of time series. Then, a linear layer is utilized for embedding the position value. Encoder consists of 3 encode blocks, which include mutil-head attention mechanism, residual layer, and feedforward neural network layer. Compared to the encoder, decoder consists of 3 decode blocks, which has an additional encoding and decoding attention mechanism.

3.3.   LSTM model

LSTM is an advanced form of RNN designed to overcome the challenges of vanishing or exploding gradients during training. LSTM excels at capturing long-term dependencies and is particularly effective for time series prediction ^[30,31]. LSTM replaces the hidden neurons of RNN with memory cells, which are capable of selectively retaining or discarding information through a gated mechanism. Specifically, LSTM utilizes three gates: the input gate, forget gate, and output gate. The architecture of an LSTM memory cell is illustrated in Figure 2. The functioning of LSTM can be mathematically expressed through the Eqs (3.5)–(3.9).

Figure 2.  Structrue of LSTM cell.

DownLoad: Full-Size Img PowerPoint

The forget gate $f_{(t)}$ determines how much of the previous cell state $c_{(t-1)}$ is retained or discarded. The input gate $i_{(t)}$ governs the integration of current input information into the updated cell state $c_{(t)}$. The output gate $o_{(t)}$ controls the output derived from the current cell state, which is then forwarded to the next memory cell. In Eqs (3.2)–(3.6), $W$ and $U$ represent the weight matrices to be optimized, while $b$ denotes the bias term. The symbol $\sigma$ stands for the sigmoid activation function, and $\otimes$ represents element-wise multiplication.

3.4.   Attention-based LSTM model

The attention mechanism was initially introduced in computer vision, where it mimics the human visual system by focusing on key local features while filtering out irrelevant information. Incorporating the attention mechanism into deep learning models helps to manage information overload, thereby improving both efficiency and performance. Specifically, this mechanism enables the model to train a learnable vector, calculated using a softmax function, to produce weighted outcomes. In the context of LSTM models, the attention mechanism can be integrated across time steps, allowing the model to concentrate on important temporal contexts.

4.   Experimental results and analysis

4.1.   Experimental data

The experimental data used in this study were obtained from securities treasure, a free and open-source securities data platform. To validate the performance of CNN-Trans-SPP, we selected eight representative stocks from companies listed on the Shanghai stock exchange and the Shenzhen stock exchange, spanning four different sectors: finance, technology, agriculture, and industry. The daily data for each stock include five features: opening price, closing price, highest price, lowest price, and trading volume. The selected stock names and their corresponding codes are presented in Table 1.

Table 1.  The names and codes of the selected stocks.

Category	Stock name	Stock code
Finance	China Bank (CB)	601988
	Ping An Bank (PAB)	000001
Technology	Inspur Group (IG)	000977
	Tongfang Co. (TC)	600100
Agriculture	Longping Hi-Tech (LHT)	000998
	Denghai Seeds (DS)	002041
Industry	China Heavy Industries (CHI)	601989
	XCMG Machinery (XCMG)	000425

---

 | Show Table

DownLoad: CSV

4.2.   Evaluation metrics

To verify the effectiveness of the proposed methods, we utilized three widely adopted quality metrics: root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE). RMSE is frequently used to evaluate the performance of regression models and is particularly sensitive to outliers and extreme values, meaning larger errors have a more pronounced impact on RMSE, as shown in Eq (4.1). MAPE offers an intuitive explanation of model performance and is applicable to various data types. Unlike RMSE, MAPE is not influenced by outliers, making it more robust, as demonstrated in Eq (4.2). MAE provides a linear evaluation of error magnitude and offers a straightforward representation of errors. However, it does not differentiate between the impacts of small and large errors, as illustrated in Eq (4.3). In these equations, $y_i$ and $\hat{y}_i$ represent the actual and predicted values, respectively, while $N$ denotes the number of samples.

4.3.   Experimental results and discussion

4.3.1.   Data preprocessing

We select five features for the stock: the opening price, highest price, lowest price, closing price, and trading volume for each day. The data from the previous four days is used as input to predict the opening price for the next day or the next three days. We apply the min-max normalization to each of the five features. The normalization formula is $x_{norm} = (x-x_{min}(x_{max}-x_{min}))$, where $x$ denotes the original value, $x_{norm}$ denotes the normalized value, $x_{min}$ and $x_{max}$ are minimum and maximum values, respectively. We choose 80% of the data as the training set and the rest as the test set. For LSTM models, the normalized features from the previous four days are used as the input for each step of the LSTM and ALSTM models. For the CNN-Trans-SSP and MLP-Trans-SPP, the normalized features from the previous four days are mapped to a feature vector of size 512 using either 1D convolution or a linear layer. Subsequently, positional encoding is added, and this serves as the input to the transformer model.

4.3.2.   Experimental settings

In the single-step prediction experiments, we employed an LSTM model with an input layer of 5 nodes, a hidden layer of 64 nodes, and an output layer of 1 node. The time step was set to 5. We conducted experiments on PAB stock, setting the number of hidden layer nodes to 16, 32, 48, 64, and 80. The results obtained for the MAPE metric were 1.13%, 0.94%, 0.89%, 0.82%, and 0.91%, respectively. Therefore, we set the number of hidden layer nodes to 64. During the training phase, the learning rate was set to 0.001, and the number of epochs was set to 1000. For the attention-based LSTM, we used the same network structure as the standard LSTM to facilitate a direct comparison of effectiveness. The only difference was that the learning rate was adjusted to 0.0001. In the multi-step prediction experiments, we utilized an LSTM model with an input layer of 5 nodes, a hidden layer of 64 nodes, and an output layer of 3 nodes. All other experimental settings were consistent with the single-step prediction experiments.

4.3.3.   Single-step prediction results and discussion

To validate the effectiveness and robustness of the proposed method, we conducted experiments on eight stocks across various sectors, including finance, technology, agriculture, and industry. The LSTM model and the attention-based LSTM model, both commonly used for time series prediction, were employed as comparison methods. The performance of each method was evaluated using MAPE, RMSE, and MAE. For ease of analysis, the experimental results are presented in Table 2. Observing the average values of 8 stocks, we can see that the CNN-Trans-SSP method achieves the best results on all three indicators (0.66 in MAPE, 8.75 in RMSE and 5.90 in MAE), compared to LSTM (1.20, 16.45, and 12.46), attention-based LSTM (0.97, 12.71, and 9.47) and MLP-Trans-SPP (1.04, 13.88, and 8.08). In the term of MAPE, our proposed CNN-Trans-SSP decreased the error by 32% compared to attention-based LSTM and by 45% compared to LSTM. Compared to another transformer model (MLP-Trans-SPP), CNN-Trans-SSP improved by approximately 36.8%. In terms of individual stock prediction analysis, CNN-Trans-SSP model outperform attention-based LSTM, LSTM and MLP-Trans-SPP on all the metrics in the seven stocks, except for one stock (LHT). The performance of MLP-Trans-SPP lies between that of LSTM and A-LSTM. Among all the experimental results, LSTM achieved the worst results.

Table 2.  Comparison of experimental results for single-step prediction.

Metrics	Methods	Avg	PAB	CB	TC	IG	DS	LHT	CHI	XCMG
MAPE(%)$\downarrow$	LSTM	1.20	0.89	1.94	0.95	0.93	1.05	0.72	1.29	1.82
	ALSTM	0.97	0.82	1.53	0.72	0.56	0.81	0.41	1.31	1.62
	MTSP	1.04	0.94	1.56	1.01	0.49	0.86	0.93	1.53	1.03
	CTSP	0.66	0.38	1.37	0.53	0.24	0.34	0.47	1.01	0.93
RMSE(e-2)$\downarrow$	LSTM	16.45	18.67	11.21	13.74	33.87	19.39	17.15	7.03	10.51
	ALSTM	12.71	12.36	9.67	9.72	17.66	21.26	12.75	8.37	9.85
	MTSP	13.88	18.41	11.95	13.51	12.53	16.44	18.82	8.93	10.46
	CTSP	8.75	9.17	9.01	9.08	8.81	9.58	9.46	6.27	8.63
MAE(e-2)$\downarrow$	LSTM	12.46	12.83	6.46	7.93	26.61	18.26	12.45	5.62	9.54
	ALSTM	9.47	11.59	6.09	5.93	15.93	14.46	7.26	5.93	8.57
	MTSP	8.08	10.21	6.39	6.22	7.13	10.31	12.61	5.32	6.47
	CTSP	5.90	5.59	5.53	4.59	7.37	6.12	8.02	4.51	5.41
Note: CTSP is the abbreviation for the CNN-Trans-SPP. ALSTM is the abbreviation for attention-based LSTM. MTSP is the abbreviation for MLP-Trans-SPP. Avg represents the average value of the eight stocks.

---

 | Show Table

DownLoad: CSV

To provide a more intuitive comparison of the performance of various methods, we plot the first 100 predicted values as shown in Figure 3. From the Figure 3, especially in subgraphs (a), (b), (e), and (h), we can observe that the brown dashed line (yielded by LSTM) and blue dashed line (yielded by MLP-Trans-SSP) deviate significantly from the black line (target). Most of the red dashed lines (yielded by CNN-Trans-SSP) overlap with the black line or fluctuate near the black line. From subgraphs (d) and (f), it can be seen that all experimental methods performed well on these two stocks (IG, LHT), almost consistent with the target.

Figure 3.  Charts of experimental results for single-step prediction.

DownLoad: Full-Size Img PowerPoint

For all the stocks, CNN-Trans-SSP exhibits good robustness and high performance.

4.3.4.   Multi-step prediction results and discussion

To gain insights into the fluctuation trends of stock prices, it is essential to predict prices over an extended period. Therefore, we implemented a multi-step prediction approach and evaluated its performance. We also compared the performance of CNN-Trans-SSP, MLP-Trans-SPP, attention-based LSTM, and LSTM using MAPE, RMSE, and MAE as metrics. The detailed experimental results are presented in Table 3. Observing the average values of 8 stocks, we can see that the CNN-Trans-SSP method achieves the best results on all three indicators (0.99% in MAPE, 13.50 in RMSE, and 9.83 in MAE), compared to LSTM (1.21%, 17.31, and 12.75), attention-based LSTM (1.37%, 20.34, and 14.92) and MLP-Trans-SPP (1.28%, 17.99, and 11.44). In the term of MAPE, our proposed CNN-Trans-SSP decreased the error by 18% compared to attention-based LSTM and by 28% compared to LSTM. Similarly, CNN-Trans-SPP improved the prediction performance over MLP-Trans-SPP by approximately 22.8%. Although multi-step prediction does not improve as much as single step prediction, CNN-Trans-SPP outperforms other methods in all metrics.

Table 3.  Comparison of experimental results for multi-step prediction.

Metrics	Methods	Avg	PAB	CB	TC	IG	DS	LHT	CHI	XCMG
MAPE(%)$\downarrow$	LSTM	1.37	1.79	1.93	1.25	0.68	1.51	0.82	1.37	1.58
	ALSTM	1.20	1.46	1.86	1.09	0.62	1.05	0.85	1.59	1.13
	MTSP	1.28	1.61	2.38	1.23	0.51	1.29	0.81	1.41	1.03
	CTSP	0.99	0.97	1.89	0.82	0.49	0.71	0.69	1.38	0.98
RMSE(e-2)$\downarrow$	LSTM	20.34	38.85	12.49	16.06	28.71	33.61	16.23	6.19	10.61
	ALSTM	17.31	33.25	11.09	12.61	18.79	25.81	20.52	7.79	8.65
	MTSP	17.99	35.41	15.03	15.72	16.69	25.58	16.72	9.33	9.43
	CTSP	13.50	22.05	11.62	9.32	15.31	16.93	17.59	7.52	7.64
MAE(e-2)$\downarrow$	LSTM	14.91	26.21	7.83	10.31	19.86	26.65	14.11	5.78	8.59
	ALSTM	12.75	21.44	7.64	8.73	17.64	18.63	14.83	6.82	6.28
	MTSP	11.44	20.61	8.04	6.31	14.35	15.17	14.32	6.42	6.31
	CTSP	9.83	14.29	7.81	6.52	13.91	12.56	12.08	5.93	5.54
Note: CTSP is the abbreviation for the CNN-Trans-SPP. ALSTM is the abbreviation for attention-based LSTM. MTSP is the abbreviation for MLP-Trans-SPP. Avg represents the average value of the eight stocks.

---

 | Show Table

DownLoad: CSV

To compare the performance of various methods more intuitively for multi-step prediction, we also plot the first 100 predicted values as shown in Figure 4. Compared with Figure 3, all the methods have significant fluctuations, as shown in Figure 4(a). Observing Figure 4 (c), (e), and (h), we can see that the red dashed line is still superior to the other lines. All experimental methods perform well on these two stocks (IG, LHT), almost consistent with the target. We can draw a consistent conclusion with the Table 3.

Figure 4.  Charts of experimental results for multi-step prediction.

DownLoad: Full-Size Img PowerPoint

4.3.5.   Ablation experiments

Choices of the input layer architecture. We explore whether the CNN-based input layer has advantages over a linear layer by training and testing two alternative variants: MLP-Trans-SPP and CNN-Trans-SSP. As shown in Figure 5, CNN-Trans-SSP model outperforms the MLP-Trans-SPP model in the term of MAPE, conducting on all the selected stocks. This means that one-dimensional convolution can better capture features than MLP in stock price prediction.

Figure 5.  Comparison of CNN and MLP in term of MAPE.

DownLoad: Full-Size Img PowerPoint

Effect of the multi-head attention mechanism.The multi-head attention mechanism can learn different features from various perspectives, thereby enhancing the ability of model expression. Figure 6 shows the influence of the number of heads in term of MAPE. It can be observed that the impact of the number of heads varies for each stock. The model achieves its best performance by utilizing 4 heads, for Inspur Group (IG) and Denghai Seeds (DS). Meanwhile, the model achieves the best performance by utilizing 16 heads for China Bank (CB). Overall, the model exhibits relatively stable performance for all the stocks by utilizing 8 heads. This is likely because the 16-head attention mechanism is able to capture more high-frequency information while neglecting low-frequency information. In contrast, the 4-head attention mechanism has a better capability for capturing low-frequency information but is insufficient for high-frequency information. Thereby, we adopt an 8-head attention mechanism in our experiments.

Figure 6.  Comparison of different numbers of heads.

DownLoad: Full-Size Img PowerPoint

Effect of the embedding dimension. We further investigated the impact of varying embedding dimensions on model performance. Experiments were conducted on all stocks using three different embedding dimensions: 128,512, and 1024. The results of these experiments are presented in Figure 7. The conclusion is different from our understanding that higher dimensions can bring better results. The model can achieve stable and good performance by utilizing 512 dimensions. This may be because a small model is unable to capture more useful information through high embedding dimensions.

Figure 7.  Comparison of different embedding dimensions.

DownLoad: Full-Size Img PowerPoint

Effect of the transformer blocks number in the architecture. The number of transformer blocks is a critical factor influencing the architecture of the transformer model. We conducted experiments with different layer settings: 1, 3, 5, 8, and 12. The results, displayed in Figure 8, reveal that the impact of the number of layers varies across different stocks. To provide a comprehensive evaluation, we assessed each model's performance based on the average MAPE values across all stocks. The black solid dots in Figure 8 represent these average MAPE values for each transformer configuration. Notably, the transformer model with 3 layers demonstrated superior performance compared to others. This is likely because our dataset is small, which leads to overfitting in the multi-layer transformer model and prevents it from achieving the desired results. Consequently, we focused on the transformer model with 3 layers in our subsequent experiments.

Figure 8.  Comparison of different transformer layers.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

In this paper, we propose a hybrid model based on CNN and transformer architectures for stock price prediction. The model leverages CNN to capture local features and the transformer to extract periodic global features. We evaluated the model on eight stocks across four major sectors, and the results demonstrate its superior prediction performance. Future work will focus on exploring pre-training techniques in stock price prediction to further enhance accuracy.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported in part by the National Natural Science Foundation of China (grant No. 62273212), National Social Science Fund Project of China (grant No. 17BGL058), Shandong Province Natural Science Foundation (grant No. ZR2022MG045).

Conflict of interest

The authors declare there is no conflicts of interest.