An efficient modified HS conjugate gradient algorithm in machine learning

1.   Introduction

Solving systems of nonlinear equations is an important part of optimization theory and algorithms and is essential to applications in machine learning, artificial intelligence, economic planning, and other important fields. The theoretical study of algorithms for nonlinear systems of equations is an important research topic in the fields of computational mathematics, operations research and optimal control, and numerical algebra. As early as the 1970s, the monographs Orrega ^[1] and Rheinboldt ^[2] had done systematic research on nonlinear systems of equations in terms of theory and solutions.

An early and very famous method was the Newtonian method ^[3]. It has the advantage that the algorithm converges quadratically when the initial point chosen is close to the minima; however, Newton's method does not necessarily converge when the initial point is away from the minima, and Newton's method requires the computation and storage of Jacobian matrices. So a wide range of researchers have built proposed quasi-Newtonian methods ^[4,5]. Such algorithms utilize approximate Jacobian matrices, inheriting the fast convergence of Newton's algorithm. In addition, methods for solving problems with linear equations are the Gaussian-Newton method, Levenberg-Marquardt algorithm, and their various modified forms ^[6,7,8]. The above methods necessitate computing and banking Jacobian matrices or approximate Jacobian matrices for each iteration step. The nonlinear conjugate gradient method belongs to the classical computational methods in the first-order optimization methods, which has the characteristics of simple structure, small storage, and low computational complexity, and thus has been widely studied by the optimization community ^{[9,10,11,12,13]}. Derivative-free algorithms are one of the popular algorithms for solving large-scale nonlinear systems of equations; they utilize the hyperplane projection technique ^[14] with a structure of first-order optimization methods, which have an R-linear convergence speed under appropriate conditions. These algorithms have a simple structure, a small amount of storage, a low computational complexity, and they do not require derivative information, thus they are favored by a wide range of researchers.

To ensure the descent of search direction, adjusting search direction structure becomes another important way to study the nonlinear conjugate gradient method. Yuan et al. ^[15] proposed a further improved weak Wolfe-Powell line-search and proved the method's global convergence in determining average functions given appropriate conditions. ^[16] proposed the adaptive scaled damped BFGS method (SDBFGS) for solving gradient non-Lipschitz non-convex objective functions. The above approach is attractive because the algorithm has strong self-correcting properties for large eigenvalues. In recent years, under influence from ^[17], some 1st-order optimization methods exemplified by conjugate gradient (CG) techniques are widely accepted to solve large-scale unconstrained optimization projects and are straightforward and low-memory ^{[9,10,11,12,13]}. These extensions, together with the freshly elaborated techniques, are permutations of renowned conjugate gradient algorithms, another key numerical tool for unconstrained optimization ^{[18,19,20,21]}.

The three-term conjugate gradient method ^[22] is considered to have tantalizing numerical capabilities and good theoretical properties. Yuan ^[23] presented an adaptive three-term Polak-Ribière-Polyak (PRP) method for non-convex functions and non-Lipschitz continuous functions with gradient. The efficient conjugate gradient algorithm is notorious for requiring both rapid convergence and high precision. ^[24] proposed a mixed inertia spectral conjugate gradient projection method for solving constrained nonlinear monotone equations, which is superior in solving large-scale equations and recovering blurred images contaminated by Gaussian noise. ^[25] described two families of self-tuning spectral hybrid DL conjugate gradient methods. The search directions of methods are improved by integrating negative spectral gradients and a final search direction with a convex combinatorial structure. ^[26] proposed a biased stochastic conjugate gradient (BSCG) algorithm with adaptive step size that combines the stochastic recursive gradient method (SARAH) and the improved Barzilai-Borwein (BB) technique into a typical stochastic gradient algorithm. ^[27] applied an improved triple conjugate gradient method and linear search technique to machine learning. The same convergence speed as stochastic conjugate gradient algorithm (SCGA) is obtained under weaker conditional assumptions.

The idea of this paper is to combine family weak conjugate gradient methods proposed in ^[28] with a new parametric formulation of the HS conjugate gradient algorithm proposed in ^[29]. An efficient HS conjugate gradient method (EHSCG) is proposed and used for image restoration problems and machine learning. Basic characterization of the algorithm is given below:

● The new algorithms have decreasing and trust-region properties requiring no extras.

● They converge globally in well-suited circumstances.

● The new algorithms can solve image restoration, nonlinear monotone equations, and machine learning issues.

In Section 2, we present procedures for solving nonlinear equation models and attest to the related properties. In Section 3, global convergence of the algorithm is proved using the weak Wolfe-Powell line-research condition under normal conditions for non-convex functions. In Section 4, we demonstrate the implementation of the algorithms toward image restoration and machine learning tasks and nonlinear monotone equations.

2.   Algorithm

2.1.   Motivation of the algorithm

Consider the following nonlinear model:

where $g:\Re^n\rightarrow \Re^n$ is a continuously differentiable monotone function, including $x\in \Re^n$. $g(x)$ characterization suggests that the inequality is true:

Scholars have come up with a number of interesting theories about this model.

To solve this optimization problem, we typically have iteration $x_{k+1} = x_k+\alpha_kd_k$, which stipulates that symbol $x_k$ signifies the iteration point, $x_{k+1}$ is the following point, $\alpha_k$ is the step length, and $d_k$ is the current direction, which is framed as below:

In ^[14] covered projection techniques to find large-scale nonlinear equation systems, noted that projection technology is strictly coupled to direction and step size. In particular, hyperplane and projection technologies were leveraged to obtain a formulation for further iteration point:

where $w_k = x_k+\alpha_kd_k$.

Furthermore, a linear search solution was presented within ^[30] to resolve step length $\alpha_k$ in iteration sequencing as follows:

where step length $\alpha_k = \max\left\{\tilde{q}, \tilde{q}\dot{t}, \tilde{q}\dot{t}^2...\right\}$, and $\tilde{q} > 0$, $\dot{t}\in(0, 1)$, $\varpi > 0$.

In ^[28], a modified search direction is followed,

where $d_k$ is defined in (2.3), and $r_{k+1}$ is designated as follows:

The authors show that it can be equated with the traditional HS conjugate gradient method under the conjugation condition. They executed numerous tests that illustrated the superiority of the formulation in tackling large-scale optimization issues.

Yuan et al. ^[29] updated the parametric formulation with the following HS conjugate gradient algorithm:

where $y_{k-1} = g_{k}-g_{k-1}$, $\tau_{1, 2, 3}\geq0$. The authors prove their methods fulfill an adequate descent condition by converging globally.

Inspired by (2.6) and (2.7), considering both the excellent theoretical and numerical performance of the two algorithms, we obtain the equation below:

where $\hslash_k = \sqrt{\tau_1^2\|g_{k}\|^2+\frac{(|g_{k}^Ty_{k-1}|\|d_{k-1}\|-|d_{k-1}^Tg_{k}|\|y_{k-1}\|)^2}{\max\{\tau_2\|d_{k-1}\|\|y_{k-1}\|, \tau_3|d_{k-1}^Ty_{k-1}|\}^2}}$.

On account of the above derivation, eventually we acquire the improved $d_{k+1}$ formulation of this paper:

where $\hslash_{k+1} = \sqrt{\tau_1^2\|g_{k+1}\|^2+\frac{(|g_{k+1}^Ty_k|\|d_k\|-|d_k^Tg_{k+1}|\|y_k\|)^2}{\max\{\tau_2\|d_k\|\|y_k\|, \tau_3|d_k^Ty_k|\}^2}}$, $y_k = g_{k+1}-g_k$, $\nu_1 = \vartheta\tau_1$, $\nu_2 = \frac{\tau_2}{\vartheta}$, $\nu_3 = \frac{\tau_3}{\vartheta}$, and $\vartheta > 0$, $\nu_i > 0$, and $\tau_i > 0, i = 1, 2, 3$. Based on (2.8), combined with line search (2.5), the sufficient descent characterization and trust region of the algorithm are provided. Equally the global convergence of the algorithm can be certified. Meanwhile, numerical results also prove the effectiveness and feasibility of the algorithm.

2.2.   Convergence analysis

Assumption 2.1. (i) The problem's solution set is not $\varnothing$. (ii) Gradient $g(x)$ is Lipschitz continuous, and this implies that the following inequality holds: $\exists L > 0$, s.t.

This assumption implies $\exists\; \omega\in \mathbb{C} \; s.t.$

Theorem 2.1. If $d_k$ satisfies Eq (2.8), then

(1) proposed descent:

and (2) trust domain:

Proof. A remarkably similar proof procedure has been granted in Yuan's work in ^[28] and will not be reiterated for here. □

Lemma 2.2. If Assumption 2.1 holds and the objective function monotones, the iterative series $\{x_k\}$ is yielded by Algorithm 1, and point $x^{\star}$ satisfies the condition $g(x^{\star}) = 0$. Taking it a step further, if the series ${x_k}$ is infinite, then

Proof. A detailed proof procedure of it is available in ^[14]. □

Theorem 2.3. If Assumption 2.1 holds, Algorithm 1 produces a finite series of step iterations $\{\alpha_{k}\}$ during the iteration from an active point to the newer one.

Proof. This conclusion is supported by contradiction. Assume the indication set $\varphi = N\cup{\{0\}}$, take any $k \in \varphi$, and consider the iteration of $x_k$. Assume that the step size satisfying the line search does not occur; that is, there occurs a step size such that $\alpha^{\star} = \tilde{q}\dot{t}^a$ satisfies:

where $\mathring{g} = g(x_k+\alpha^{\star}d_k)$. Referring to the previous (2.9) and (2.14), we have

By (2.9) and (2.10), then

Further we obtain that

The above inequality shows that the step size $\alpha^{\star}$ is bounded. □

Theorem 2.4. If Assumption 2.1 stands, Algorithm 1 yields $\{\alpha_k\}$, $\{d_k\}$, $\{x_k\}$, {and} $\{g_k\}$, and then $\liminf_{k\to\infty}\|g_k\| = 0$.

Proof. This theorem is still proved by the converse method. We denote the indicator set $\varphi = N\cup{\{0\}}$, and set $k\in\varphi$. According to Assumption 2.1, assume that $\exists\; \varrho, \; n_0 > 0 \; s.t.$

where $\varrho$ is a constant and $n_0$ is an index. According to (2.11) and (2.10), we have

Consider the Eq (2.11) with (2.12), and we have

It can be concluded that direction $d_{k+1}$ is bounded, we suppose that $\lim_{k\to\infty}d_k = d^{\star}$, and follow (2.13) with the Theorem 2.3 iteration points $\lim_{k\to\infty}x_k = x^{\star}$. Step size $\alpha_{k}$ is bounded, and we have

We obtain that the following inequality,

Both parts of the given inequality take the limit, the one has

Let $k$ tend to infinity, $g_{k+1}^Td_{k+1} = -(1+\vartheta\frac{\|g_{k+1}\|}{\hslash_{k+1}})\|g_{k+1}\|^2$, and each side of

which implies

but this contradicts (2.15). Thus, the conclusion of the theorem holds. □

3.   Unconstrained optimization problems

We apply (2.8) to the massive unconstrained optimization problem. Consider the issues below:

where $f:\Re^n\rightarrow \Re$ is a continuously differentiable function. Set $\nabla f(x) = \digamma(x)$.

Motivated by the description in Section 2, the following formula for $d_{k}$ is proposed:

where $\hslash_{k} = \sqrt{\tau_1^2\|\digamma_{k}\|^2+\frac{(|\digamma^T_{k}\hat{y}_{k-1}|\|d_{k-1}\|-|d_{k-1}^T\digamma_{k}|\|\hat{y}_{k-1}\|)^2}{\max\{\tau_2\|d_{k-1}\|\|\hat{y}_{k-1}\|, \tau_3|d_{k-1}^T\hat{y}_{k-1}|\}^2}}$, $\hat{y}_k = \digamma_{k+1}-\digamma_k$, $\nu_1 = \vartheta\tau_1$, $\nu_2 = \frac{\tau_2}{\vartheta}$, $\nu_3 = \frac{\tau_3}{\vartheta}$, $\vartheta > 0$, and $\tau_i > 0, i = 1, 2, 3$. Analogous to the targeted algorithm in Section 2, $d_{k}$ bears the following traits:

and

where $\vartheta > 0$ is a constant. The proofs of the above traits have been given in Section 2 and will not be repeated in this section.

This section presents the algorithm and global convergence thesis.

Assumption 3.1. (i) The level set $\Theta = \{x|f(x)\leq f(x_0)\}$ bounds.

(ii) $f(x)\in C^2$ bounds below and Lipschitz continues, which implicates that there exists constant $L$ higher than zero so that

Theorem 3.1. If Assumption 3.1 holds, Algorithm 2 creates $\{x_k\}$, $\{\alpha_k\}$, $\{d_k\}$, and $\{\digamma_k\}$, and then

Proof. We will establish this through counterfactuals. Assuming that the original theorem does not hold, and we will have the following conclusion: an existence of a constant $\varepsilon^*$ larger than zero, $\forall k\geq k^* > 0 \; s.t.$

By the decreasing trait (3.3) and line search method (3.5), then

Consequently, let $k$ range from 0 to $\infty$, and then

where the inequality on the right side results from Assumption 3.1(ⅱ). Significantly, Eq (3.9) expresses that

Through the linear search method (3.6) with Assumption 3.1, then

In conclusion, we have the fact that

where these two inequalities are given from (2.12). Hence we obtain (3.8). The proof is finalized. □

4.   Numerical results

All methods are encoded in MATLAB R2021b running on a PC with a Windows 10 operating system with an Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz 1.80 GHz.

4.1.   Monotone linear equations

We compare Algorithm 1 with the modified HS method ^[29], three-term PRP method ^[31], and traditional PRP method ^[21,32]. The termination conditions for each of the eleven test questions are

The parameters in Algorithm 1 are chosen as: $\varpi = 0.01$, $\vartheta = 0.8, \; \tilde{q} = 1$; $\dot{t} = 0.5$, $\nu_1 = 1.8, \nu_2 = 3000$, and $\nu_3 = 1000$. We list those problems from ^[33] here to preserve the neutrality of this paper. The corresponding problems with a matching initial point $x_0$ are tabulated here:

Problem 4.1.. Exponential function 1:

point $x_0 = (\frac{s}{s-1}, \frac{s}{s-1}..., \frac{s}{s-1}, )^T$.

Problem 4.2. Singular function:

point $x_0 = (1, 1..., 1)^T$.

Problem 4.3.

point $x_0 = (1, 1..., 1)^T$.

Problem 4.4. Trigexp function:

point $x_0 = (0, 0..., 0)^T$.

Problem 4.5.

point $x_0 = (\frac{1}{s}, \frac{2}{s}..., \frac{s}{s})^T$.

Problem 4.6. Penalty I function:

point $x_0 = (\frac{1}{3}, \frac{1}{3}..., \frac{1}{3})^T$.

Problem 4.7. Variable dimensioned function:

point $x_0 = (1-\frac{1}{s}, 1-\frac{2}{s}..., 1-\frac{s}{s})^T$.

Problem 4.8. Tridiagonal system:

point $x_0 = (12, 12..., 12)^T$.

Problem 4.9. Five-diagonal system:

point $x_0 = (-2, -2..., -2)^T$.

Problem 4.10. Seven-diagonal system:

point $x_0 = (-3, -3..., -3)^T$.

Problem 4.11. Troesch problem:

point $x_0 = (0, 0..., 0)^T$.

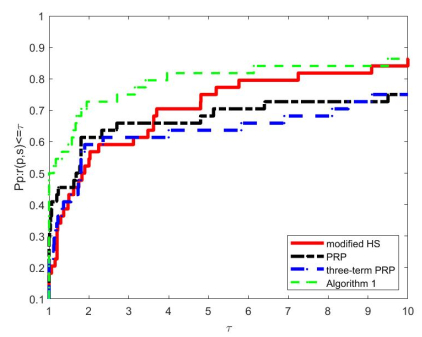
Per issue, four dimensions of 1000, 5000, 10,000 and 50,000 were considered. In order to provide a graphical and well-rounded comparison of these treatments, this paper utilizes the performance curves of ^[34], which have a large resource for messages on both efficiencies and soundness. We graphed testing issue scores $P$ individually, where the measure differs from the corresponding best method by a factor of $\tau$. The performance curves are depicted in Figures 1–3, thereafter. The numerical consequences are tabulated in Table 1, where "Dim" denotes dimension and $\|g_k\|$ denotes the final value.

As can be seen from Figure 1, Algorithm 1 is the most efficient in terms of the sense of the number of iterations, solving $50\%$ of the problem with the least number of iterations. From Figure 2, it can be seen that the most efficient method in the sense of the number of function evaluations is Algorithm 1, which solves $75\%$ of the problem with the minimum number of function evaluations. Figure 3 shows that Algorithm 1 is also the most efficient algorithm in terms of CPU time considerations.

It can be seen that Algorithm 1 fared splendidly in dealing with large-scale constrained monotone equations. Conclusively, numerical investigations indicate that the suggested algorithm constitutes an effective vehicle for solving systems of convex constrained monotone equations.

4.2.   Unconstrained optimization

Numerical outcomes with the proposed Algorithm 2 and modified HS method ^[29], three-term PRP method ^[31], and conventional PRP method ^[21,32] are reported separately. The fifty problems for the experiment were taken from ^[35], and the initial points for every question have been given as shown in Table 2. All algorithms use the weak Wolfe-Powell line-search technique. Each test question's termination conditions are

or

The parameters in Algorithm 2 are chosen as: $\zeta = 0.5, \; \xi = 0.95$, $\nu_1 = 2, \nu_2 = 30,000$, and $\nu_3 = 1000$. For each problem, we considered three dimensions of 30,000, 12,000 and 300,000. The consumed performance curves are shown in Figures 4–6.

4.3.   Image restoration

The image restoration problems were solved by using algorithms. It is well known that in bio-engineering, medicine, and other fields of the science and engineering, image restoration techniques play a pivotal role. One of common image degradation models is defined by the following:

where $\upsilon\in R^{m_1}$ is the observation, $\varXi$ is the linear function of order $m_1\times m_2$, and $\iota$ is a constant greater than zero.

The regularized model (4.1) has attracted much concern, and several scholars have proposed various iterative methods to deal with it ^[36,37,38].

Figueiredo ^[39] developed a gradient-based projection program by reformulating (4.1) as a constrained quadratic program. The reformulation in Figueiredo et al. is by following: split vector $x$ into two pieces, i.e., $x = s-t$, where $s_i = (x_i)_+$, $t_i = (-x_i)_-$, and $(\bullet)_+ = \max\{0, \bullet\}$. Then (4.1) is transformed into

Further, Xiao et al. ^[40] found (4.2) to be equivocated to the following system on nonlinear equations:

Pang ^[41] proved that $H$ satisfies (2.9), while Xiao ^[40] proved that it satisfies (2.2) too.

Codes' stop condition

or

In the experiments, "Man", " Baboon", "colorcheckertestimage", and "car" are the tested images. Comparing Algorithm 1, modified HS ^[29], three-term PRP ^[31], and NPRP2 ^[42], the four algorithms are not effective at adding $30\%, 70\%$ to the noise. The parameters in Algorithm 1 are chosen as: $\varpi = 0.01$, $\vartheta = 0.8, \; \tilde{q} = 1$, $\dot{t} = 0.5$, $\nu_1 = 2.2, \nu_2 = 3000$, and $\nu_3 = 1200$. The time taken for each algorithm is summarized in Tables 3 and 4. From Tables 3 and 4, it can be seen that CPU time for both contrastive and color images processed with Algorithm 1 is less than the time used by the other algorithms, which shows that the algorithms proposed in this paper are more advantageous in dealing with grey image and color image restoration problems.

Figures 7 and 8 show that Algorithm 1 has performed well in tackling the gray image restoration. Visualizing the outcomes of color, Figures 9 and 10 are given and from the results, it is clear that the algorithm of this paper is more competitive in dealing with color image restoration. In image restoration experiments, we usually use the PSNR value and SSIM value to estimate the quality of the processed image. The higher the PSNR value, the less distorted the image is. The higher the SSIM value, the better the image setup. When two mirrors are identical, the SSIM value is 1. As can be seen from Figures 9 and 10, the SSIM value obtained by Algorithm 1 is relatively small compared to the traditional algorithm, and the image restoration effect is not as good as the traditional algorithm. This aspect will be investigated in the future.

4.4.   Machine learning

We now embed the improved HS method into a stochastic large subspace algorithm ^[43] by replacing its search direction with (2.8), thus building an improved HS algorithm based on the stochastic large subspace and variance-reducing SCGN-based algorithms (called mSCGN and mSDSCGN). Next, we test and compare the stochastic gradient descent algorithm (SGD) ^[44] and the STOCHASTIC VARIANCE GRADIENT REDUCTION (SVRG) ^[45] on the following two learning models:

(ⅰ) Nonconvex SVM model with a sigmoid loss function:

where $f_s(x) = 1-tanh(\omega_s < x, \varpi_s > )$, $\varpi \in \Re$, $\omega\in\{-1, 1\}$ signify feature vectors and the corresponding labels, respectively. Support vector machine models were implemented in different areas for pattern recognition, currently focusing on information categorization, encompassing text and images.

(ⅱ) Nonconvex regularized ERM model with a nonconvex sigmoid loss function:

where $f_s(x) = 1/\{1+exp(\epsilon_s\varepsilon_s^Tx)\}$, $\epsilon_s \in \{-1, 1\}$ is target value of the $s$-th sample, $\varepsilon_s \in \Re^d$ is the eigenvector of the $s$-th sample, and $\lambda > 0$ is the regularization parameter. Binary classification models are instrumental in practical problems. While a non-convex ERM model concentrates on minimizing classification inaccuracy, the $s$-type function is also exhibited to be usually superior to alternative loss functions. Accordingly, nonconvex ERM models with s-type loss functions are valuable for mathematical modeling.

The parameters in mSCGN and mSDSCGN are chosen as: $\nu_1 = 3.8, \nu_2 = 300$, and $\nu_3 = 100$. The dataset comes from https://www.csie.ntu.edu.twcjlin/libsvmtools/datasets/. All algorithms were executed on three large datasets, with the specific details of the datasets are shown in Table 5. In all experiments, the regularization was chosen to be $\lambda = 10^{-5}$ and a similar batch size $m$ was used in each iteration. Gradient $\nabla f(x)$ and the Hessian matrix $\nabla^2 f(x)$ are estimated by:

where $\sigma = 10^{-4}$ and $e_s$ is the $s$-th unit-vector. Let the regularization factor $\lambda$ of the learning model be $10^{-4}$, and the convergence result of the algorithms is shown in Figures 11 and 12. In this experiment, the largest count for internal iterations is 30. In principle, the lower the value of the curve, the better convergence in the corresponding algorithm.

The different algorithms' behavior is revealed by plotting the curve of function values over the iteration. Figure 11 illustrates the behavior of mSCGN and SGD at solving (4.4) and (4.5) with alternative decreasing steps. As verified from Figure 11, both algorithms managed to tackle the models. The function values decline at a greater rate initially and incrementally remain constant. Notice that when the mSCGN algorithm and the SGD algorithm share the same step-size on the datasets, the former decays the function value firmer. This reveals that the algorithm herein designed is well executed for having sufficient descent and trust domain capabilities. Observe that for mSCGN, $\alpha_k = 10k^{-0.9}$ converges quicker. Our algorithm exhibits superiority at appropriate step sizes, and experimental results perform better at larger decreasing step sizes.

Figure 12 illustrates the behavior of mSDSCGN and SVRG for solving (4.4) and (4.5) at separate constant step sizes. Analyzing Figure 12, it is obvious that even though the SVRG algorithm uses the best step size, SVRG does not perform as well as mSDSCGN on all three datasets. We observed that of those step sizes, 0.04 is optimally suited toward mSDSCGN. Overall, our algorithm shows more promise and efficiency than others. Based on the analysis of the results, one can conclude that our suggested method is useful for machine learning.

5.   Conclusions

We propose a modified HS conjugate gradient method with the following characteristics: 1) Fulfills descent and trust-region features. 2) A particular method's global convergence for the non-convex functions can be easily established. 3) The image restoration, machine learning issues, and nonlinear monotone equations experiments were tested and the outcomes indicated that the algorithms have promising numerical characterizations for tackling these issues.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

This work is supported by the Guangxi Science and Technology Base and Talent Project (Grant No. AD22080047), the National Natural Science Foundation of Guangxi Province (Grant No. 2023GXNFSBA026063), the major talent project of Guangxi (GXR-6BG242404), the Bagui Scholars Program of Guangxi, and the 2024 Graduate Innovative Programs Establishment (Grant No. ZX01030031124006). We are sincerely grateful to the editors and reviewers for their valuable comments, which have further enhanced this paper.

Conflict of interest

The authors declare there are no conflicts of interest.