Some identities of degenerate higher-order Daehee polynomials based on $\lambda$-umbral calculus

1.   Introduction

Special polynomials play a significantly important role in the development of several branches of mathematics, engineering, and physics by providing us with useful identities and properties. The study of special polynomials provides many useful identities, their relations, and representations associated with special numbers and polynomials. One of the powerful tools in this study is to investigate their generating functions ^[1,2] and connections^[3,4,5,6] using the umbral calculus ^[7]. Furthermore, to better understand generating functions in special polynomials, the degenerate type of special polynomials has been extensively studied in many areas such as probability theory, fuzzy theory, connection problems, and other combinatorial theories in recent years by many mathematicians ^[8,9,10,11]. Since the introduction of degenerate versions of special polynomials and numbers by Carlitz ^[12], many researchers have been interested in the relationships between them. In addition, the degenerate version of umbral calculus, called $\lambda$-umbral calculus, plays a very powerful role in studying the relationships between degenerate versions of special polynomials and numbers. Recently, the Daehee polynomials and numbers were originally introduced as a new type of special polynomials by Kim and Kim ^[13] and thereafter their related properties and relationships with other polynomials have been extensively studied.

In this study, we derive the formulas expressing degenerate higher-order Daehee polynomials in terms of the degenerate versions of other special polynomials by making use of $\lambda$-umbral calculus. These formulas provide the degenerate Daehee polynomials by taking $r = 1$ and the Daehee polynomials by letting $\lambda\to0$. We first review the $\lambda$-analogue of umbral calculus: a class of $\lambda$-linear functionals on the polynomials, $\lambda$-differential operators based on the family of $\lambda$-linear functionals, and also $\lambda$-Sheffer sequences. See ^[14] and the references therein for more details on these contents.

The rest of this section briefly recalls some necessary notations and definitions that are needed throughout this paper. Throughout this paper, we assume that $\lambda \in \mathbb{R}\backslash \{0\}$ for simplicity.

The degenerate exponential function $e_{\lambda}^x(t)$ is defined by

where $(x)_{n, \lambda}$ is a $\lambda$-analogue of the falling factorial sequence which is given by

Also, the degenerate logarithm function is given by $\log_\lambda (t): = \frac{1}{\lambda}(t^\lambda-1)$, which is the compositional inverse of $e_\lambda (t)$, i.e.,

In this study, we consider the degenerate higher-order Daehee polynomials $D_{n, \lambda}^{(r)} (x)$ which are given by the generating function to be

Especially, we call $D_{n, \lambda} (x): = D_{n, \lambda}^{(1)} (x)$ the degenerate Daehee polynomials when $r = 1$ and $D_{n, \lambda}: = D_{n, \lambda}(0)$ the degenerate Daehee numbers when $x = 0$.

The degenerate Stirling numbers of the first kind $S_{1, \lambda}(n, m)$ and the second kind $S_{2, \lambda}(n, m)$ are respectively given by

and

Note that the falling factorial sequence $(t)_{n}$ is given by

which provides the relation with the $\lambda$-analogue of the falling factorial sequence such as

The main contribution of this paper is to provide various representations of the degenerate higher-order Daehee polynomials and numbers using $\lambda$-umbral calculus in terms of other well-known special polynomials and numbers. In more detail, we derive formulas for the $n$-th order of degenerate Daehee polynomials with the degenerate falling factorial polynomials, the degenerate type 2 Bernoulli polynomials, the degenerate Bernoulli polynomials, the degenerate Euler polynomials, the degenerate Mittag-Leffer polynomials, the degenerate Bell polynomials, and the degenerate Frobenius-Euler polynomials (see Theorems 2.1–2.7) as well as their inversion formulas. Therefore, we see that this technique enables us to represent various well-known polynomials in terms of degenerate higher-order Daehee polynomials and vice versa as a classical connection problem. In addition, to confirm the formulas, we present computational results between the degenerate higher-order Daehee polynomials and the degenerate Bernoulli polynomials for fixed variables. Moreover, we investigate the pattern of the root distribution of the polynomials.

2.   Representations of degenerate higher-order Daehee polynomials

Now, we provide brief review of $\lambda$-umbral calculus: Let $\mathbb{P}$ be the algebra of polynomials in $t$ over $\mathbb{C}$, i.e.,

and let $\mathcal{F}$ be the algebra of formal power series in $t$ over the field $\mathbb{C}$ of complex numbers

Then, the $\lambda$-linear functional $\langle f(t)| \cdot\rangle_{\lambda}$ on $\mathbb{P}$ for $f(t) = \sum_{n = 0}^\infty a_n \frac{t^n}{n!}\in \mathcal{F}$ is given by

and it satisfies

where $\delta_{n, k}$ is the Kronecker delta.

Note that the order of the formal power series for a nontrivial $f(t)$, $o(f(t))$, is represented by the smallest integer $k$ for which $a_k$ does not vanish. Especially, we call $f(t)$ a delta series when $o(f(t)) = 1$, and also we say $f(t)$ an invertible series when $o(f(t)) = 0$, (see ^[1,7,14] for details).

For a non-negative integer order $k$, the $\lambda$-differential operator $(t^k)_{\lambda}$ on $\mathbb{P}$ is defined by

In general, for $f(t) = \sum_{k = 0}^\infty a_k \frac{t^k}{k!}\in \mathcal{F}$, the $\lambda$-differential operator $\big(f(t)\big)_{\lambda}$ is satisfied with

Or equivalently, one can express $\big(f(t)\big)_{\lambda}$ as

For a delta series $f(t)$ and an invertible series $g(t)$, i.e., $o\big(f(t)\big) = 1$ and $o\big(g(t)\big) = 0$, there exists a unique sequence ${p}_{n, \lambda}(x)$ of polynomials $deg\big({p}_{n, \lambda}(x)\big) = n$ satisfying the orthogonality condition

Here, ${p}_{n, \lambda}(x)$ is called the $\lambda$-Sheffer sequence for $\big(g(t), f(t)\big)$ denoted by ${p}_{n, \lambda}(x)\sim \big(g(t), f(t)\big)_{\lambda}$.

We recall that ${p}_{n, \lambda}(x) \sim \left(g(t), f(t)\right)_{\lambda}$ if and only if

Here $\bar{f}(t)$ represents the compositional inverse of $f(t)$, i.e., $f\left(\bar{f}(t)\right) = \bar{f}\left(f(t)\right) = t$.

For given a pair of $\lambda$-Sheffer sequences ${p}_{n, \lambda}(x)\sim \big(g(t), f(t)\big)_{\lambda}$ and ${q}_{n, \lambda}(x)\sim \big(h(t), \ell(t)\big)_{\lambda}$, we have the relation:

where ${\mu}_{n, k}$ is obtained by

Likewise, if ${q}_{n, \lambda}(x)$ is expressed in terms of $p_{n, \lambda}(x)$ as

then ${\nu}_{n, k}$ can be obtained by

It is easily shown that for $f(t), g(t)\in\mathcal{F}$ and $p(x)\in\mathbb{P}$,

We also note that from $(x)_{n, \lambda}\sim(1, t)_\lambda$, any $\lambda$-Sheffer sequence ${p}_{n, \lambda}(x)\sim \left(g(t), f(t)\right)_{\lambda}$ is represented by

Now, we want to present representations of the degenerate higher-order Daehee polynomials $D_{n, \lambda}^{(r)} (x)$ by using the algebraic properties of $\lambda$-Sheffer sequences.

From (1.3), we have that $\sum_{n = 0}^{\infty} D_{n, \lambda}^{(r)} (x)\frac{t^n}{n!} = \left(\frac{\log_\lambda (1+t)}{t}\right)^{r} e_\lambda ^x \left(\log_\lambda (1+t)\right)$, so that we consider $f(t) = e_\lambda(t)-1, \bar{f}(t) = \log_\lambda(1+t),$ and $g(t) = \frac{e_\lambda(t)-1}{t}$ in the view of (2.6) to obtain

If we let $p_{n, \lambda}(x) = \sum_{\ell = 0}^{n} \mu_\ell D_{\ell, \lambda}^{(r)}(x)$, then, by using (2.5) we have

which implies

Thus, for $p_{n, \lambda}(x)\in \mathbb{P}$ we have

Then, the formula between $D_{n, \lambda}^{(r)} (x)$ and $(x)_{n, \lambda}$ is obtained.

Theorem 2.1. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, we have

Reversely, we have the inversion formula given by

Proof. Let $D_{n, \lambda}^{(r)}(x) = \sum_{k = 0}^n \mu_{n, k} (x)_{k, \lambda}$. Then, by (1.4), (2.3), and (2.9), we can obtain

which shows the first formula.

For the inversion formula, we first note that

which implies

Now, let $(x)_{n, \lambda} = \sum_{k = 0}^\infty \nu_{n, k} D_{k, \lambda}^{(r)} (x)$. Then, from (1.5), (2.7), and (2.11), $\nu_k$ satisfies

which shows the second result.

Next, we consider the degenerate Bernoulli polynomials $\beta_{n, \lambda}(x)$, which is defined by the generating function to be

Then, the connection formulas between $D_{n, \lambda}^{(r)}(x)$ and $\beta_{n, \lambda}(x)$ are as follows.

Theorem 2.2. For $n\in\mathbb{N}\cup \{0\}$, we have

As the inversion formula, we have

and

Proof. First, note that $\beta_{n, \lambda}(x)$ is the $\lambda$-Sheffer sequence for

Let us consider $D_{\ell, \lambda}^{(r)}(x) = \sum\limits_{k = 0}^n \mu_{n, k} \beta_{k, \lambda}(x)$. By (1.4), (2.9), (2.10) and (2.12), we obtain

which implies the first formula.

To find the inversion formula, we first note that from (1.1) for $r > 1$

Thus, by (2.2) and (2.13)

Now, if we consider $\beta_{n, \lambda}(x) = \sum\limits_{k = 0}^\infty \nu_{n, k} D_{k, \lambda}^{(r)} (x)$, then by (1.5), (2.7), and (2.14), $\nu_{n, k}$ satisfies

which provides the formula.

Next, we consider the degenerate type 2 Bernoulli polynomials $b_{n, \lambda}(x)$, which are defined by the generating functions to be

Note that $b_{n, \lambda}(x)$ satisfies

Then, we can have the following relation between $D_{n, \lambda}^{(r)}(x)$ and $b_{n, \lambda}(x)$.

Theorem 2.3. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, we have

For the inversion formula, we have

and

Proof. Let us consider $D_{n, \lambda}^{(r)}(x) = \sum_{k = 0}^n \mu_{n, k} b_{k, \lambda}(x)$. By (1.4), (2.9), (2.10), and (2.15), we get

From (2.3), it is noted that

By applying the note (2.17) in (2.16), we have

To find the inversion formula, let us consider $b_{n, \lambda}(x) = \sum_{k = 0}^\infty \nu_{n, k} D_{k, \lambda}^{(r)} (x)$. From (1.5), (2.7), and (2.15), $\nu_{n, k}$ satisfies

Since $\frac{e_\lambda^x (t)-1}{t} = \sum_{n = 0}^\infty\frac{(x)_{n+1, \lambda}}{n+1} \frac{t^n}{n!}$, we have that for $r > 1$

Then, (2.19) implies that for $r > 1$

where $\mathcal{E}_{n, \lambda}(x)$ are the type 2 degenerate Euler polynomials defined by the following generating function

Here we call $\mathcal{E}_{n, \lambda}: = \mathcal{E}_{n, \lambda}(0)$ the type 2 degenerate Euler numbers if $x = 0$. Thus, for $m = n-\ell+r-1$ in (2.20) for $r > 1$

and

which provides the inversion formula with (2.18).

We consider the degenerate Euler polynomials $\mathcal{E}_{k, \lambda}$ that is defined by the generating function to be

which satisfies that

Then, the representation formula between $D_{n, \lambda}^{(r)}(x)$ and $\mathcal{E}_{n, \lambda}(x)$ holds true.

Theorem 2.4. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, we have

As the inversion formula, we have

Proof. Let $D^{(r)}_{n, \lambda}(x) = \sum_{k = 0}^n \mu_{n, k} \mathcal{E}_{k, \lambda}$. Then, By (1.4), (2.9), (2.10), and (2.22), we can obtain

where

and

Therefore, combining (2.24) and (2.25) to (2.23), we have

To find the inversion formula, let $\mathcal{E}_{n, \lambda}(x) = \sum_{k = 0}^\infty \nu_{n, k} D^{(r)}_{k, \lambda} (x)$, where $\nu_{n, k}$ satisfies

We note that

and

Thus,

Combining (2.27) to (2.26) gives

The degenerate Mittag-Leffer polynomials $M_{n, \lambda}(x)$ are given by the generating function to be

It is noted that

Then, we have the representation formulas between $D_{n, \lambda}^{(r)}(x)$ and $M_{n, \lambda}(x)$.

Theorem 2.5. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, we have

As the inversion formula, we have

where $K_n(x\vert\lambda)$ are the Korobov polynomials of the first kind given by the generating function

In particular, when $x = 0$ $K_n(\lambda): = K_n(0|\lambda)$ are called Korobov numbers of the first kind, that is,

Proof. Let $D^{(r)}_{\ell, \lambda}(x) = \sum_{k = 0}^n \mu_{n, k} M_{k, \lambda}$. Then, by (1.4), (2.9), (2.10), and (2.28), we can obtain

where

Thus,

To find the inversion formula, let $M_{n, \lambda}(x) = \sum_{k = 0}^\infty \nu_{n, k} D^{(r)}_{k, \lambda} (x)$, where

where

Thus,

Next, let us consider the degenerate Bell polynomials $Bel_{n, \lambda}(x)$, which are defined by the generating function to be

Note that $Bel_{n, \lambda}(x)$ are the $\lambda$-Sheffer sequences of

which satisfies that

Then, we have the representation formulas between $D_{n, \lambda}^{(r)}(x)$ and $Bel_{n, \lambda}(x)$.

Theorem 2.6. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, it holds:

Also the inversion formula are established

Proof. Let $D^{(r)}_{\ell, \lambda}(x) = \sum_{k = 0}^n \mu_{n, k} Bel_{k, \lambda}(x)$. Then, by (1.4), (2.9), (2.10), and (2.30), we can obtain

To find the inversion formula, let $Bel_{n, \lambda}(x) = \sum_{k = 0}^n\nu_{n, k} D^{(r)}_{k, \lambda} (x)$, then $\nu_{n, k}$ satisfies

where

Therefore, we have

The degenerate Frobenius-Euler polynomials $h^{(\alpha)}_{n, \lambda}(x|u)$ of order $\alpha$ are defined by the generating function as

When $x = 0$, $h^{(\alpha)}_{n, \lambda}(u): = h^{(\alpha)}_{n, \lambda}(0|u)$ are called the degenerate Frobenius-Euler numbers.

We note that $h^{(\alpha)}_{n, \lambda}(x|u)$ satisfy

Then, we have the representation formulas between $D_{n, \lambda}^{(r)}(x)$ and $h^{(\alpha)}_{n, \lambda}(x|u)$.

Theorem 2.7. For $n\in\mathbb{N}\cup \{0\}$ and $r\in\mathbb{N}$, the representation holds:

As the inversion formula, we have

Proof. Let $D^{(r)}_{n, \lambda}(x) = \sum_{k = 0}^n\mu_{n, k} h^{(\alpha)}_{k, \lambda}(x\vert u).$ By (1.4), (2.9), (2.10), and (2.31), we have

which implies the first formula.

Conversely, we assume that $h^{(\alpha)}_{n, \lambda}(x|u) = \sum_{k = 0}^n nu_{n, k}D^{(r)}_{k, \lambda}(x).$ Then, $\nu_{n, k}$ satisfies

which shows the second assertion.

3.   Illustrations of formulas

3.1.   Distribution of roots of the polynomials

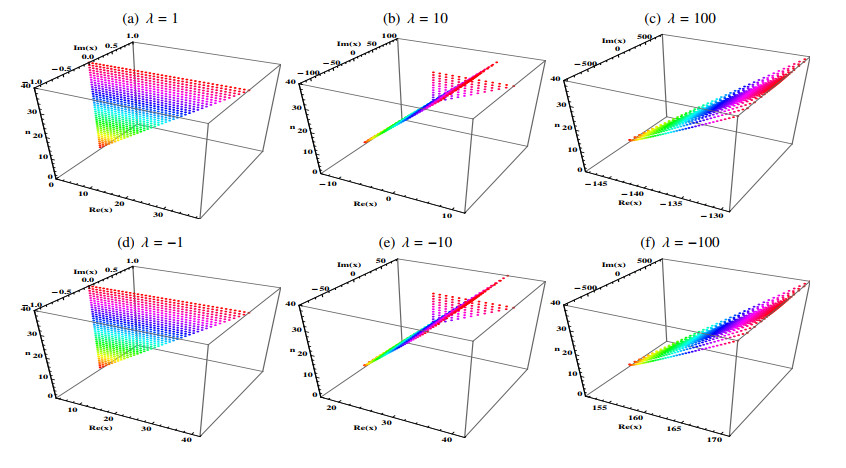
In this subsection, we present the pattern of the zeros of the polynomials. The understanding of patterns of zeros of degenerate polynomials can provide useful information about the original polynomials which can be obtained as limit of $\lambda$ approaches zero. For example, the first three consecutive degenerate higher-order Daehee polynomials of degree $r$ are given by

which approach to the higher-order Daehee polynomials of degree $r$ as $\lambda\to 0$. We observe the patterns of roots by the changing parameters $\lambda$ and $r$ on the polynomials. In order to do this, we fix the degree of the polynomials as $n = 40$, and compute the roots of $D^{(r)}_{40, \lambda}(x)$ with fixed $r = 3$ and six different parameters $\lambda = \pm 1$, $\pm 10$, $\pm 100$ with the help of the Mathematica tool. The results are displayed in Figure 1. Next, we increase the degree of the polynomials and investigate the distribution of the roots of the polynomials.

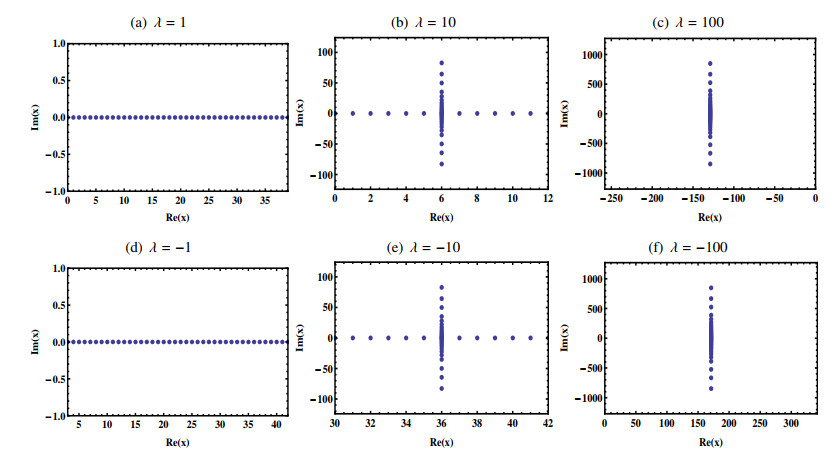
For further investigation, we computed the roots of the polynomials by increasing the degree $n$ of polynomials from $1$ to $40$ in Figure 2.

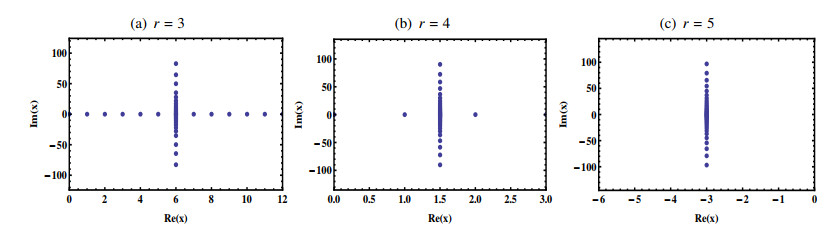
Finally, we investigated the distribution of the roots of $D^{(r)}_{40, \lambda}(x)$ with a fixed $\lambda = 10$ and three different parameters $r = 3$, $4$, $5$ and the results were displayed in Figure 3.

3.2.   Examples of formulas

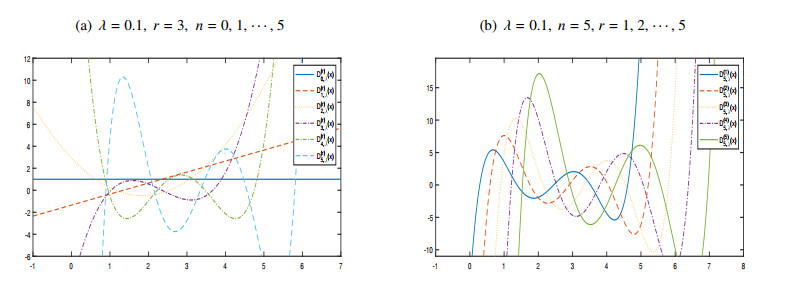
In this subsection, we provide the explicit formulas presented in Theorem 2.2 that show the representations of the degenerate higher-order Daehee polynomials in terms of the degenerate Bernoulli polynomials and vice versa. To better understand, we present the graphs of $D^{(r)}_{n, \lambda}(x)$ with $\lambda = 0.1$ and $r = 3$ for $n = 0$, $1$, $\cdots$, $5$ and of $D^{(r)}_{n, \lambda}(x)$ with $\lambda = 0.1$ for various orders $r = 1$, $2$, $\cdots$, $5$ in Figure 4.

Next, we compute the combinatorial results of $\mu_{n, k}$ and $\nu_{n, k}$ presented in the proof of Theorem 2.2 to confirm the connection formulas presented. To do this, we compute $D^{(r)}_{n, \lambda}(x)$ and ${\beta_{n, \lambda}}(x)$ for $r = 3$, $\lambda = 0.1$, and $n = 0$, $1$, $\cdots$, $5$ and expand them using the coefficients $\mu_{n, k}$ and $\nu_{n, k}$ which are computed with two decimal place accuracy. The expressions presented confirm the results of Theorem 2.2.

The degenerate higher-order Daehee polynomials $D^{(r)}_{n, \lambda}(x)$ with $\lambda = 0.1$, $r = 3$ for $n = 1$, $2$, $\cdots$, $5$ are expressed in terms of ${\beta_{n, \lambda}}(x)$ as follows:

Conversely, the degenerate Bernoulli polynomials ${\beta_{n, \lambda}}(x)$ with $\lambda = 0.1$, $r = 3$ for $n = 1$, $2$, $\cdots$, $5$ are represented in terms of $D^{(r)}_{n, \lambda}(x)$:

4.   Conclusions

The study of special polynomials provides useful tools in differential equations, fuzzy theory, probability, orthogonal polynomials, and special functions and numbers. These researches are conducted using various tools, including generating functions, $p$-adic analysis, combinatorial methods, and umbral calculus. Recently, degenerate versions of special polynomials and numbers have been investigated using $\lambda$-analogues of these methods, and their arithmetical and combinatorial properties and relations have been studied by several mathematicians. These degenerate versions of special polynomials and numbers have been applied in differential equations and probability theories, providing new applications. In this paper, we explore the connection problems between the degenerate higher-order Daehee polynomials and other degenerate types of special polynomials. We present explicit formulas for representations with the help of umbral calculus and vice versa. In addition, we illustrate the results with some explicit examples. In order to better understanding the polynomials, the distribution of roots are presented.

Conflict of interest

The authors declare there is no conflict of interest.