1.
Introduction
1.1. Epidemiological information about SARS-CoV-2
Coronaviruses belong to the Coronaviridae family. The Coronaviridae is sub-divided into four groups of coronaviruses; α-Coronavirus, β-Coronavirus, γ- Coronavirus, and δ-Coronavirus [1]. These viruses were not seen as attractive research in applied sciences since they were not highly pathogenic to humans until the outbreak of SARS-CoV in 2003 and MERS-CoV in 2012. Both viruses were transmitted directly from civets and dromedary camels (intermediate hosts) to the human hosts, respectively, and they showed the same natural host of bats in the epidemic spread [2,3]. These viruses appeared in endemic behaviors, and therefore the related studies were restricted to some areas such as medicine and biology and rarely discussed in applied mathematics [4,5].
In 2003, the world experienced a type of coronavirus in China known as SARS-CoV. This virus was transmitted to humans through intermediate hosts such as market civets. After that, people met another similar infection in the Middle East region in 2012, known as MERS-CoV, which spilled over to dromedary camels. These viruses showed severe respiratory syndromes in humans, including fever, dizziness, and cough [6,7,8]. However, all the coronaviruses mentioned above were endemic in the human populations causing 15-30 percent of respiratory tract infections each year. In December 2019, a virus of the Coronaviridae was announced in China-Wuhan. The spread was reported from the fish market in Wuhan, considering reptilians as intermediate hosts and bats as a natural host. A scenario was designed that the spread started in Wuhan's local fish market, where the people used to buy bats. Another scenario in the community was that the virus spread from the laboratory in Wuhan-China. WHO designated this new virus as COVID-19. Studies have shown that COVID-19 was characterized by two members of β-coronavirus; the human-origin coronavirus (SARS-CoV Tor2) and bat-origin coronavirus (bat-SL-CoVZC45) [9]. A virus that was expected to show similar epidemic behavior like SARS or MERS reached a pandemic stage and still exists in 2022.
1.2. The pandemic spread of COVID-19 and the fear of the community
The world faced many forms of pandemic diseases that changed the life of humans, the environment, and history; for example, plague in the 14th century, the first cholera pandemic recorded in 1817, the Spanish flu that started in 1918. However, nobody expected a change in our life in the fourth industrial revolution based on fear and worry about the future. To remind how the virus spillover, we returned to December 2019, when the world noticed a coronavirus appeared again in China. However, since 2003, SARS-CoV showed an endemic form. Nevertheless, the community was unaware of the consequences of the virustill March 16th, 2020, when the WHO upgraded the status of COVID-19 from epidemic to pandemic.
Several fundamental protections such as quarantines, culling, heavy travel restrictions, and social distancing were applied to the community [10]. In addition, health institutions and organizations took high responsibilities to engage the public with healthy practices such as hand washing, keeping social distance, and staying at home during the lockdown period. Simultaneously, the governments started to collaborate with the WHO. Furthermore, the media played a significant role in informing the civilians about the infection rates, the necessary health protections, and lockdown announcements from the government. Besides this, the internet spreads many unuseful (unrealistic) information. As a result, people started to create illusions related to the virus, which led to a fear effect in the community. The mutated forms of the viruses, such as the delta or omicron, emphasize that the virus continues to transmit the disease with a high transmission rate of R. Therefore, the discussion in the community and social networks will continue [1,9].
Until January 4th, 2022, the number of infections increased to 293,078,911 cases with 5,467,761 deaths and 255,480,149 recovered. The USA shows the highest infection rate with 57,131,187, India with 34,960,261 infections, and Brazil hits 22,305,078 total cases. On the other side, an infection that started in China reached 102,841 infections, whose population is almost 1,439,323,776 [10]. Interestingly, a spread in China (Wuhan) did not show similar outbreaks and fatalities reported in Europe, the USA, or other counties. Additionally, the mutated form on the protein spike of the virus is recorded mainly in Europe, the USA, India, and South Africa, which increased the mortality rate more than before.
Our study wants to emphasize the fear effect spread through the media and associations to humans indifferent, uncertain, and sometimes confusing information about the virus, vaccines, and protection rules. Considering the psychological effect such as anxiety, fear, or worry, it is shown among the students in China that there is a positive statistical correlation between the epidemiological spread and psychological health [11].
We can transform an experimental study from the predator-prey model to our case by defining the virus as a predator and the civilians as prey. This biological interpretation showed that the fear of the community to the virus (predation fears) itself could reduce the prey growth rate (psychological effect) by 40% [12], which means that the immune system becomes weak. Finally, many studies in medicine started in their research on the psycho-social impact of COVID-19, which emphasizes the danger during the pandemic stage and beyond [13,14,15,16]. However, unfortunately, uncertain information about the virus, the spread, mutation, and the vaccines expedite a fear of the present and future. Therefore, we want to analyze and formulate an essential research topic to distinguish between "controlling the spread" with various mechanisms and "the community's fear" during the lockdown period. Beyond that, we want to analyze the psychological pressure on civilians. Significantly, one should realize that the changes in the "normal life" and several waves of lockdowns lead to psychological breakdowns and thus allow the community to ask what the "new normal life" was and the significant reset of our life in the fourth industrial revolution.
2.
Mathematical model
It has been seen that many biological and medical phenomena can be characterized via mathematical models. Specifically, some mathematical models analyze biological and environmental phenomena such as infections, treatments, or diseases [17,18,19,20]. However, the study of these phenomena has been restricted to models of ODEs.
The nonlocal property of fractional-order models depends on the current state and its previous historical states [21]. The transformation of an integer-order model into a fractional-order model needs to be precise with respect to the order of differentiation α. However, a slight change in α may causes a significant change in the behavior of the solutions [22]. Fractional-order differential equations can model complex biological phenomena with non-linear behavior and long-term memory, which cannot be represented mathematically by integer-order differential equations (IDEs) [23,24]. For example, Bozkurt [25] established the glioblastoma multiforme (GBM)–immune system (IS) interaction using a fractional-order differential equation system to include the delay time (memory effect) [25]. Besides this, some vital studies that include the reliability analysis of uncertain fractional-order dynamical systems and other fundamental studies see [26,27,28,29,30]. Thus, it is preferred to use FDEs in biological models since they are relevant to memory and hereditary systems [31,32,33,34,35,36,37,38,39,40,41].
Moreover, the experimental study of Elliott et al. [42] on Drosophila melanogaster as prey and mantid as their predator was necessary proof that the reproductive performance of drosophila decreases in the presence of mantid at low population density. This experiment was the critical evidence for the Allee effect due to the fear, which refers to the positive association among the species density and its per-capita growth rate at low density [43]. From the environmental perspective of the infection during the corona period, each community shows a threshold density that enables the government for a long-term lockdown. Therefore, we incorporate a strong Allee effect into our system to analyze the stabilization under specific conditions.
This paper established a SEIQRS+D model that describes the pandemic infection. The virus is located in the human body and continues to transmit the disease from human to human. The system is divided into six-compartments. S(t) shows the susceptible class that does not have any resistance to COVID-19. E(t) is the exposed compartment that has been infected, but since the virus is in the incubation period, they carry and transmit the virus without showing any symptoms. The I(t) compartment is the infected group determined as COVID-19 positive, and Q(t) shows the isolated class under the quarantine. R(t) is the recovered compartment, while D(t) means only the death class. We assume that the recovered class can return to the susceptible class since there is no permanent protection against the virus. Thus, we establish the model considering two types of fear during the movement from one compartment to the other one; the fear of the susceptible class to be infected and the fear of the individuals under quarantine and who are scared about the daily updated death rates. Therefore, in the system, α1 and α2 denote the level of the fear "to get infected" and "the death from COVID-19". From a biological point of view,
can be reasonably assumed to satisfy the following statements;
Fear from infection COVID-19
➢ f1(0,I)=1; if there is no fear of the infection, the susceptible class does not have the psychological pressure.
➢ f1(α1,0)=1; if the virus disappears, the fear and the psychological effect disappear on the susceptible class.
➢ limα1→∞f1(α1,I)=0; if the virus's fear continues to expand more for a long-term period, then the "mentally healthy" susceptible class decreases to extinct.
➢ limI→∞f1(α1,I)=0; if the virus stays for a long-term period in a pandemic spread, the susceptible non-infected decreases to extinct.
➢ ∂f1(α1,I)∂α1<0; if the fear effect increases, the offspring might be affected, and thus it decreases.
➢ ∂f1(α1,I)∂I<0; if the infection increases, the offspring might be affected, and thus it decreases.
Fear from the death of COVID-19
➢ f2(0,D)=1; if there is no fear of death from COVID-19, then the individuals under quarantine do not have the psychological pressure.
➢ f2(α2,0)=1; if the death from COVID-19 decreases or extinct, then the fear and the psychological effect disappear on the individuals in the quarantine compartment.
➢ limα2→∞f2(α2,D)=0; if the fear of death from COVID-19 increases and expands more for a long-term period, then the "mental health" class would become extinct.
➢ limD→∞f2(α2,D)=0; if the death rate from COVID-19 increases in daily records, the quarantine compartment decreases to extinct because of death.
➢ ∂f2(α2,D)∂α2<0; if the fear effect increases, the carrying capacity of the compartment under quarantine decreases.
➢ ∂f2(α2,D)∂D<0; if the death rate from COVID-19 increases, the compartment's carrying capacity under quarantine decreases.
Thus, the mathematical model is modeled as follows;
and
where the parameters are positive real numbers, 0<α≤1, Dα denotes the Caputo derivative and (S,E,I,Q,R,D)∈R6+.
The susceptible S(t) comprises individuals who have not contacted any infected person but can get infected from COVID-19 infected people. S(t) can get infected through E(t), who do not know they are infected.r is the growth rate of S(t), while ρ is the Allee threshold (0<ρ<K1) and K1 shows the carrying capacity of S(t). Λ1 denotes the recruitment rate of the susceptible class and α1 is the fear of the susceptible class to getting infected. The susceptible class lost their population density following contacts with E(t) at a rate of β1 and with I(t) at a rate of β2. η shows natural death rate of the susceptible class S(t). From the recovered class, a rate of δ2 returns to the susceptible class since there is still no permanent treatment and protection to COVID-19.
The E(t) class does not know that they have COVID-19 because of the late appeared symptoms of the infection. Λ2 denotes the current density of the exposed class. This compartment decreases following the health rules in doing PCR tests regularly before traveling or for work with a screening rate θ. Another stage during the epidemiological cases is that after being informed by the health organizations about the virus, the individuals become aware of the virus' symptoms with a rate of ε1 so that the class moves to the infected compartment I(t). Another vital piece of information about this compartment is that the individual can be the silent transmitter of COVID-19, as mentioned in the article of Harvard Medical School [44]. This is why all compartments need to permanently follow the health protection rules since the community also shows individuals who have the virus but do not show the symptoms at all. The intermediate transmitters, known as the silent transmitters, can recover without recognizing that they were infected from COVID-19. According to this essential study of [44], we show the recovery rate of E(t) to R(t) as δ1. η denotes the natural death in this compartment.
I(t) is the infected COVID-19 class. The population of this class increases with β1ε1 who noticed in the exposed class from the symptoms that they are infected. Another parametric increase comes from the screening rate θ when the test shows COVID-19 positive. We assume that the individuals are aware to inform the health organizations when they feel the infection symptoms. From the infected compartment, a rate of γ1 moves to be hospitalized or to stay at home under quarantine.
The Q(t) compartment shows a fear effect α2 of the daily recorded death rates . The population density of the compartment increases with γ1I(t) who show mainly severe symptoms and are hospitalized under quarantine. γ2 is the rate of recovered individuals during the quarantine period that changes the class from Q(t) to R(t). In both compartments, the infected and the quarantined classes, we expect two types of recorded deaths; natural death and death from COVID-19.
The R(t) compartment shows the class of recovered individuals. γ2Q(t) is the increase of the compartment that is expected from class Q(t) after successful treatment, the density of this class decreases with a rate of δ2 to the susceptible class, which means that one can get infected again. The recovered class shows only the natural death of a rate η.
The most discussed part in the community was the case of "death from COVID-19" and "death with COVID-19". To distinguish this case in the compartment of D(t), the death of the infected population is subtracted from death who died from other symptoms during the infection that affects the immune system, which is denoted as μ1; this means D(t) denotes only the group that died from corona itself.
This study focuses mainly on five essential and sensitive parameters. These are; α1, the fear being infected, α2, the fear to die from COVID-19, θ, the rate of screening, ε1, the rate of awareness and γ2, rate of recovering from successful treatment. In this work, we want to distinguish between "the psychological fear effect" caused by different networks and "get aware" of living in the pandemic stage. Without any confusion, specific information from professional institutions would make civilians aware and not scared of the virus. Getting used to living in this pandemic spread and taking the necessary actions can be explained without terrifying people. Professional and quick response screening tests would reach successful movements between the compartments.
Definition 2.1. [45] Given a function φ(t), the fractional integral with order α>0 is provided by Abdel's formula as
Definition 2.2. [45] Let φ:R+→R be a continuous function. The Caputo fractional derivative of order α∈(n−1,n), where n is a positive integer is defined as
When =n, the derivatives are defined to be the usual nth order derivatives.
Definition 2.3. [46] The Mittag-Leffler function of one variable is
The parametric description is given as in Table 1.
3.
The existence and uniqueness of the solutions in the system
For the biological validity of the system, we need to show that for all non-negative initial values, the solutions of the system (2.1) remain non-negative. Thus, our study in this section includes proving that the domain is positive and that the IVP system has a unique solution in R6+. Denote R6+={M∈R6:M≥0} and let M(t)=(S(t),E(t),I(t),Q(t),R(t),D(t))T. We want to show that the domain R6+ is positively invariant following the lemma in [47,48], and the technique of [49].
Lemma 3.1. [47] (Generalized mean value theorem) Let f(x)∈C[a,b] and Dαf(x)∈C[a,b] for 0<α≤1, then we have
with 0≤ξ≤x, ∀x∈(a,b].
Lemma 3.2. [48] Suppose f(x)∈C[0,b] and Dαf(x)∈C[0,b] for 0<α≤1. Then, from Lemma 3.1. we have the following statements.
(ⅰ) f is non-decreasing if Dαf(x)≥0, ∀x∈(0,b).
(ⅱ) f is non-increasing if Dαf(x)≤0, ∀x∈[0,b].
Theorem 3.1. The solution of the IVP in (2.1) and (2.2) is unique, and the solutions are in R6+.
Proof. From Lemma 3.1 and Lemma 3.2, we want to show the existence and uniqueness of (2.1) and (2.2) in (0,∞) using the technique in [49]. Notice that
on each hyperplane bounding the nonnegative orthant. Hence, the domain R6+ is positively invariant. This completes the proof.
4.
Equilibria and local stability analysis
This section defines at first two equilibria: the disease-free equilibrium point and the co-existing, namely the positive equilibrium point of system (2.1). After that, we analyze the local stability criteria of the system (2.1) around each equilibrium point based on specific conditions.
4.1. Equilibria points
Let us rewrite the system
To analyze the stability of (4.1), we perturb the equilibrium points by εi(t)>0,i=1,2,3,4,5,6, that is
Thus, we have
and
We use the property of equilibrium point that
and therefore, a linearized system about the equilibrium point is obtained, such as
where V=(ε1(t),ε2(t),ε3(t),ε4(t),ε5(t),ε6(t)). Furthermore, J is the Jacobian matrix at the equilibrium point. Moreover, we have W−1JW=C such that C is the diagonal matrix of λi(i=1,2,3,4,5,6) and W shows the eigenvectors of J. Thus, we have
and the solutions are given by Mittag-Leffler functions such as
and
Considering the study of Matington [50] and Zeng et al. [51], where they proved the stability criteria using the Mittag-Leffler functions, we can say that if |arg(λi)|>απ2(i=1,2,3,4,5,6), then ψi(i=1,2,3,4,5,6) are decreasing and therefore, εi(i=1,2,3,4,5,6) are decreasing. In other words, let the solution V=(ε1(t),ε2(t),ε3(t),ε4(t),ε5(t),ε6(t)) of (4.4) exist. If the solution of (4.4) is increasing, then the equilibrium point (−S,−E,−I,−Q,−R,−D) of the system is unstable. Similarly, if the solution of (4.4) is decreasing, then the equilibrium point (−S,−E,−I,−Q,−R,−D) is locally asymptotically stable.
Our study focuses on two equilibrium points; the disease-free equilibrium point and the co-existing equilibrium point. These are given as follows;
Disease-free equilibrium point: χ1=(−S1,0,0,0,0,0), where for the disease free cubic equation
holds for the Allee threshold and the carrying capacity such as
Co-existing (positive) equilibrium point: χ2=(−S2,−E2,−I2,−Q2,−R2,−D2).
4.2. Local stability analysis of the disease-free and co-existing equilibrium points
In this part, we assume that the civilians show total awareness of the virus, ε1=1. Thus, we aim to focus mainly on the screening effect and the fear through different networks in spreading uncertain information about the pandemic case worldwide. We want to know the psychological effect on humans during epidemiological existence.
The Jacobian matrix of the disease-free point χ1=(−S1,0,0,0,0,0) is given by
where
a11=−ρr−η−3rK1−S12+2r(1+ρK1)−S1, a12=−β1−S1, a13=−S1{−α1r(1−−S1K1)(−S1−ρ)−β2}, a15=δ2, a22=β1(1−ε1)−S1−(θ+η+δ1), a32=β1−S1+θ,a33=β2−S1−(γ1+η+μ), a43=γ1,a44=1−(η+μ+γ2),a52=δ1, a54=γ2,a55=−η−δ2, a63=a64=μ and a66=−μ1.
Thus, the Eq (4.1) around the disease-free equilibrium point χ1 is given by
Theorem 4.1. Let χ1 be the disease-free equilibrium point of system (4.1) and assume that η+μ+γ2>1. Then χ1 is stable local asymptotic if and only if
Proof. From (4.9), it follows that
(ⅰ) λ1=−ρr−η−3rK1−S12+2r(1+ρK1)−S1<0, if −S1>2(K1+ρ)3, which holds (4.7).
(ⅱ) λ2=−(θ+η+δ1)<0.
(ⅲ) λ3=β2−S1−(γ1+η+μ)<0, if −S1<γ1+η+μβ2.
(ⅳ) λ4=1−(η+μ+γ2)<0, if η+μ+γ2>1.
(ⅴ) λ5=−η−δ2<0.
(ⅵ) λ6=−μ1<0.
Remark 4.1. Theorem 4.1 shows the essential steps to transform the epidemiological phenomena into a disease-free case. The awareness of the civilians, given as ε1, has been assumed as ε1=1, which means aware with sufficient information from leading pandemic institutions without any confusion to minimize the spread of infection. This awareness applies the rules like keeping social distance from individuals, wearing a mask, etc... The next essential step is to avoid contact with infected individuals and continue using health practices. Professional and quick response tools, including PCR tests at home, would also decrease the exposed compartment. Another sequential step is successful treatment responses to move from the quarantine compartment to the recovery compartment. The equilibrium point of the susceptible class shows the balance of the Allee threshold and the carrying capacity that does not deliver any form of fear effect.
Thus, we summarize the remark of Theorem 4.1. in emphasizing that the disease-free stability criteria exist in some primary parametric forms, such as the screening rate supported by rapid isolation mechanisms, successful treatment, and the infection's awareness.
The Jacobian matrix of the co-existing equilibrium point χ2=(−S2,−E2,−I2,−Q2,−R2,−D2) is given as
where
a11=r(2−S2−3−S22K1+2p−S2K1−p)⋅11+α1−I2−β1−E2−β2−I2−η, a12=−β1−S2, a13=−α1−S2r(1−−S2K1)(−S2−p)⋅1(1+α1−I2)2−β2−S2, a15=δ2,a22=−(θ+η+δ1), a31=β1−E2+β2−I2, a32=β1−S2+θ,a33=β2−S2−(γ1+η+μ),a43=γ1, a44=11+α2−D2−(η+μ+γ2),a46=−α2−Q2(1+α2−D2)2, a52=δ1 a54=γ2,a55=−η−δ2, a63=a64=μ and a66=−μ1.
From the Jacobian matrix in (4.11), we obtain
where we have λ2=−(θ+η+δ1)<0 and λ5=−η−δ2<0. In addition, since we want to focus on the psychological fear effect for the co-existing equilibrium point, we assume that there is no permanent treatment of γ2. This happened precisely when the treatments were in discussion, and some social networks spread wrong information that people can have chronic diseases in the future from those treatments. To understand the individuals fear to get infected and the death from the corona is now more precisely formulated as a characteristic equation that is based on two quadratic equations;
which shows a basic reproduction number of R01=a46a64a44a66. This has an equation of a form such as
Considering the characteristic Eq (4.12) again, we want to incorporate a second reproductive number R02=a13a31a11a33, which belongs to the susceptible and infected compartments, which is
Theorem 4.2. Let χ2 be the positive equilibrium point of the system (4.1) and assume that R01<1 and R02<1. Moreover, let the conditions η+μ+μ1<1, β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p and −S2−−I2−E2>β1β2 hold. If
and
where γ1+η+μβ2<−S2<(K1+p)+√(K1−p)2+K1p3. Then the roots of (4.12) are real or complex conjugates with negative real parts and |arg(λi)|>απ2 (i=1,2,3,4),α∈(0,1) is equivalent to the Routh-Hurwitz Criteria. This implies that χ2 is locally asymptotically stable.
Proof. Let us consider at first the isolated (under quarantine) and the death compartment, where
From (4.18), we have
where R01<1 and η+μ<1. Moreover, computations show that
if
where η+μ+μ1<1. From both (4.19) and (4.21), we obtain
Considering now the discriminant of the characteristic equation of the S−I compartments, we have
if R02<1 and the following statements hold;
and
where
From (4.24) and (2.25), we have β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p such that
Furthermore, we get that
if
From both (4.26) and (4.27), we get at the end that
where −S2−−I2−E2>β1β2. This completes the proof.
Remark 4.2. In the local stability of the co-existing equilibrium point, we assumed that the recognition of the infection is high enough such that ε1=1. To keep the co-existing equilibrium point under control, the major work on stability is on the screening rate, the quick recovery of the exposed compartment, and the movement from the recovery to the susceptible class. Theorem 4.2. shows that the Allee threshold and the carrying capacity of the susceptible class are mainly affected by the interaction of the S−I compartments. Permanent health practices, wearing masks, and keeping social distance can avoid or minimize contact with an infected individual, raising the susceptible compartment's carrying capacity and Allee threshold. We noticed in Theorem 4.2. that the fear of death from the corona is mainly related to distinguishing whether the recorded deaths are from corona or with corona. On the other side, the fear α1 to get infected exists mainly related to the information of silent transmitters and transmitters without recognition.
Theorem 4.3. Let χ2 be the co-existing equilibrium point of system (4.1) and assume that R01=1 and R02=1. Moreover, suppose that η+μ+μ1<1 and −S2−−I2−E2>β1β2. If
and
where −S2<(K1+p)+√(K1−p)2+K1p3. Then the characteristic equation shows some non-negative eigenvalues such that |arg(λ∗)|=0<απ2, where α∈(0,1). Thus the equilibrium point χ2 is unstable.
Proof. Let R01=1. Then we have Δ1=(a44+a66)2>0. Furthermore,
if
where η+μ+μ1<1.
On the other side, since R02=1, we obtain Δ1=(a11+a33)2>0. We have
if
and
where −S2−−I2−E2>β1β2. This completes the proof.
Remark 4.3. Theorem 4.3 considers the co-existing equilibrium point's unstable (uncontrollable) case. The basic reproduction numbers are assumed as R01=1 and R02=1. The reproduction numbers are based on the fear parameters and the compartments of I and D, respectively. The uncontrolled case can exist if the screening rate is low or insufficient, such as it cannot detect the silent spreaders. These infected individuals can continue to transmit the infection to the susceptible class with a rate of β1 and β2. The increase of the infected compartments (exposed and COVID-19 detected classes) decreases the susceptible density, which leads to a fear of mental health problems of the susceptible class. From the reproduction number R01, it can be seen that the fear of dying from corona, which is given as α2 is based on the density of the isolated compartment.
Theorem 4.4. Let χ2 be the co-existing equilibrium point of system (4.1). Assume that η+μ+μ1<1, −S2−−I2−E2>β1β2 and β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p. Let the basic reproduction numbers be
and
such that
α1< 1−I2{r(2K1−S2−3−S22+2p−S2−K1p)K1(β1−E2+β2−I2−β2−S2+(γ1+2η+μ))−1} and α2<1−D2(1η+μ+μ1−1), where γ1+η+μβ2<−S2<(K1+p)+√(K1−p)2+K1p3. Then the eigenvalues of (4.14) and (4.15) show complex conjugate, which implies that the S−I and Q−D interaction has an asymptotic stable behavior such that
and
Proof. Let us consider the isolated (under quarantine) and death compartment where
From (4.37), we have
where
Furthermore, computations show that from (4.39), we have a44+a66>0. This completes the proof of the Q−D interaction.
Considering now the discriminant of the characteristic equation includes the interaction of the S−I compartments
we obtain
where
Furthermore, we get that
if
where −S2−−I2−E2>β1β2.
Remark 4.4. In Theorem 4.4. we proved that the characteristic equations' eigenvalues in (4.14) and (4.15) show complex eigenvalues under specific conditions. In this scenario, the recovery rate is limited or takes a long time to move from the recovery compartment to the susceptible compartment. The basic reproduction number of both R01>1 and R02>1. While the transmission rate is more significant than one, the susceptible class knows that the transmission risk is high from the infected compartment that does not apply the permanent rules. Thus, the fear of getting infected α1 exists and depends on the carrying capacity, the threshold of the susceptible class, and the infectional transmissions from the silent spreaders and the known infected compartments. The fear to die from corona, which is denoted as α2, shows an upper bound according to the parameters of death from corona and death with corona. Thus both parameters, μ and μ1 should be clarified cristal to avoid any confusion in the human mind.
Theorem 4.5. Let χ2 be the co-existing equilibrium point of system (4.1). Assume that η+μ+μ1<1, −S2−−I2−E2>β1β2 and β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p. Let the basic reproduction numbers be
such that
and
1−D2(1η+μ+μ1−1)<α2<1−D2(1η+μ−1) and α1>1−I2{r(2K1−S2−3−S22+2p−S2−K1p)K1(β1−E2+β2−I2−β2−S2+(γ1+2η+μ))−1}, where
γ1+η+μβ2<−S2<(K1+p)+√(K1−p)2+K1p3 for β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p.
Then the S−I and Q−D compartments are asymptotic stable such that
and
Proof. From
we have
where
Furthermore, we have
if
From (4.48) and (4.50), we obtain
Considering now the discriminant of the characteristic equation includes the interaction of the S−I compartments
we obtain
where γ1+η+μβ2<−S2<(K1+p)+√(K1−p)2+K1p3 for β2>3(γ1+η+μ)(K1+p)+√(K1−p)2+K1p.
Moreover, we get that
if
where −S2−−I2−E2>β1β2.
Remark 4.5. In Theorem 4.5. we show that both fears, α1 and α2 are restricted to a bounded interval. The fear effect α2 recognizes the difference between "the death from corona" and "with corona", which keeps the compartments stable. However, the transmission of the exposed and the infected compartments still exist. The fear in α1 focus on the parametric changes of the carrying capacity of the susceptible class, the Allee threshold, and the infectional rates.
5.
Some numerical simulations by using MATLAB 2019
Finally, in this section, we want to illustrate the fear effect of α1 and α2 in using MATLAB 2019. On the other side, we consider the effect of the parameters such as screening, recovering from the infection, and the death rates of infected people who die from different symptoms. Here we discuss and show the psychological pressure on humans spread through different organisations and networks. We determine the initial conditions of system (4.1) as S(0)=2000,E(0)=80,I(0)=40, Q(0)=30,R(0)=10,D(0)=2, and the values of the parameters are given in Table 2.
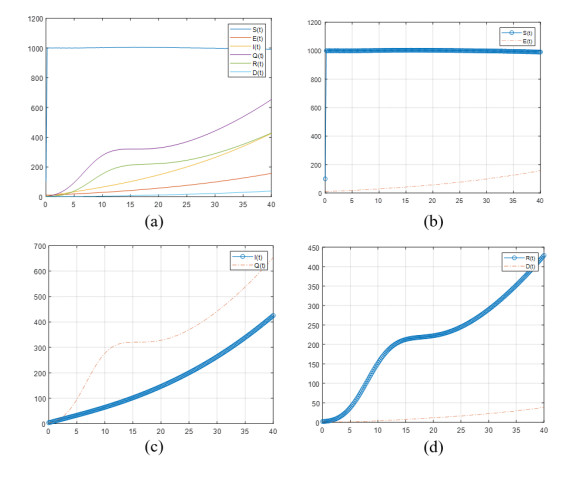
Figure 1 shows a case when the awareness in the community is 60%. The screening exists 20%, and that is why the community is scared from the infection, α1=α2=0.5, since also there is no permanent treatment. We choose in this simulation the recovery due to the treatment as γ2=0.4. According to the graphs, we can notice that the susceptible class reaches a carrying capacity because of the existing treatment and the community awareness. The recovery and the quarantine compartments increase smoothly due to the increase of the infected groups. Here we can see that while the fear exists, the awareness of the community can still keep the carrying capacity of the susceptible compartment stable.
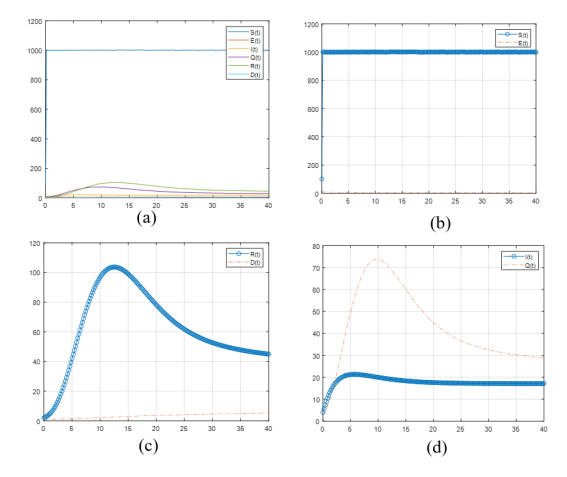
In the theoretical study, we also discuss the case of total awareness, that is, ε1=1. We prove that there is a negative relation between the recognition of the virus and the fear effect. In other words, in full awareness, the fear of getting infected decreases, and as a result, the fear of death from corona decreases. In Figure 2, the fear parameters are chosen α1=α2=0.2. However, as discussed above, we still assume that the screening and treatment rates are low. The below graphs show that full awareness of the community to keep permanent health practices and not to be confused from any distorted information spread through some networks decreases the infection to an endemic stage.
In Figure 3, we increase the screening rate and show that this stabilizes the susceptible class, and from early detections of the infections, the quarantine period can start on time. As a result, Figure 3(a)–(d) shows a successful reduction of the epidemiological case.
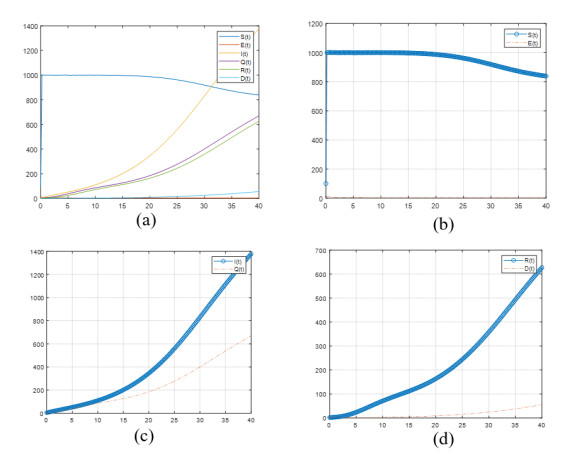
Our main theoretical study was related to open discussions in social networks about whether treatment problems are helpful or successful. Even this discussion increased the fear of the susceptible and infected compartments. In addition, some people stopped using the medicines or avoided taking the vaccine. Figure 4 shows the change of the above graph related to the increase of fear and decrease of treatment. Reducing the treatment process even to 10% shows a constant pandemic spread for a long-term period. We increased the screening test in this scenario; however, this would only help detect and reduce the silent spreaders.
6.
Conclusions
This study constructed a mathematical SEIQRS+D model to discuss the community's fear of considering unstable information through social networks. We want to show the difference between "to keep the community aware" and "let the community be scared".
It is evident that everyone's life almost changed due to the pandemic. People worked for a long time at home; students attended classes online. People talked in social distances and behind masks for more than two years. The new life affects the psychology of humans; however, the adaptation to this new life needs a professional guide from leading organizations. During the pandemic stage, many social networks and media used this environmental phenomenon as trend discussions and did not clarify the situation. This study aims to analyze what would happen when we do not focus on recognition and improvements in medicine rather than concentrating on distorted information. The results show that the epidemiological stage would continue to stay long.
We conclude that permanent health care regulations are essential to stabilize the community's recognition of the virus COVID-19. However, as necessary as the awareness, we also emphasize on reaching clear information about screening tools and treatment processes. The pandemic should not create unrealistic stories that affect mental health during this challenging event.
Conflict of interest
The author declares that no competing financial interests or personal relationships could have influenced the work reported in this paper.









 DownLoad:
DownLoad: