1.
Introduction
1.1. An H-space and a co-H-space
An H-space (or a Hopf space) was named after Heinz Hopf [1] as the Eckmann-Hilton dual of a co-H-space (or a co-Hopf space); it is a pointed topological space with a homotopy multiplication for an H-space and a homotopy comultiplication for a co-H-space [2]. An H-space with a multiplication and a co-H-space with a comultiplication play a pivotal role in classical homotopy theory; see [3] for the relationship between coarse homotopy groups and classical homotopy groups, [4] for the bounding size of homotopy groups of the odd dimensional spheres, [5] for the exponents of the total Cohen groups [J(Sr),Ω(Y)], and [6] for digital smash products.
In general, there are many homotopy comultiplications on a co-H-space X with many distinctive properties, therefore, the calculation of the cardinality of the set C(X) of homotopy comultiplications as a subset of the set (or group) [X,X∨X] of homotopy classes of base point preserving continuous maps from a co-H-space X to the wedge product X∨X is complicated; see [7,8,9].
An exploration of homotopy comultiplications on the wedge product of circles and the wedge sum of two Moore spaces was conducted using the methods of group theory in [10] and homological algebra in [11], respectively; see [12,13] for some rational results for finite 1-connected co-H-spaces, [14] for the cardinality of comultiplications on a suspension of a space, and [15,16,17,18,19,20,21,22] for digital versions of H-spaces and co-H-spaces. From the equivariant homotopy theoretic viewpoint, an explicit expression of the behavior of the local cohomology spectral sequence graded on the representation ring was developed with many pictures in [23]. The study of homotopy comultiplications and the same n-type structures of co-H-spaces with standard comultiplications has been developed by several authors; see [24,25,26,27,28,29,30].
1.2. Localization
The localization of a space or a spectrum at some prime numbers is a homotopical analogue of the notion of the localization of a commutative ring or a module, specifically the ring Z of integers at a set of prime numbers. In addition, a nilpotent CW-complex can be topologically (or homotopically) localized at a prime similar to the localization for a commutative ring at a prime.
The concept of localization of a nilpotent CW-space in homotopy theory was explicitly formulated by Sullivan [31]. In fact, there are many types of localization theories in mathematics and the sciences such as localization of a category, localization of a ring and a module, localization of a topological space and so on; see [32] for the standard reference. Regarding non-nilpotent spaces, there are multiple inequivalent definitions of localization [33].
1.3. Sphere and Moore space
The m-sphere Sm, m≥2 is known to have a unique comultiplication φ:Sm→Sm∨Sm and φ=i1+i2, where i1,i2:Sm→Sm∨Sm are the inclusion maps and + denotes the sum of two maps coming from the standard (or suspension) comultiplication φ on Sm; see [24,Proposition 3.1].
Given an abelian group G and an integer n≥1, a CW-complex X is uniquely determined up to homotopy such that the reduced homology satisfies the following:
The CW-space having the same homotopy type of X is said to be a Moore space M(G,n) of type (G,n). A Moore space is the homology analogue of the Eilenberg-MacLane space of homotopy theory; they are dual notions with one another.
In general, detecting the cardinality of the set C(X)⊆[X;X∨X] of all homotopy classes of homotopy comultiplications on X is difficult. As a particular example, it was shown in [34] that the set of homotopy comultiplications C(M(G,2)) is in one-one correspondence with the group Ext(G,G⊗G) set-theoretically, and that if n≥3, then C(M(G,n)) is the set consisting of only one element as the homotopy class of the standard comultiplication; that is, all homotopy comultiplications on the Moore space M(G,n) are homotopic.
1.4. Goal and organization
Regarding the aforementioned statements, there is a question: How can the structure of homotopy comultiplications of the localization of a wedge of the sphere and the Moore space be developed? In the current study, we provide an answer to this question and, in particular, we examine the structure of the set of all comultiplications up to homotopy on the localization L(p) of a wedge L:=Sm∨M(G,n) of the homotopy spheres and the Moore spaces, where G is an abelian group and 2≤m<n.
The paper is organized as follows: In Section 2, we describe the pivotal ideas of homotopy comultiplications and the localized counterparts of Hilton-Milnor formulae. In Section 3, we explore the fundamental concepts of the types of homotopy comultiplications on the localization L(p) of a wedge L:=Sm∨M(G,n) of the homotopy spheres and the Moore spaces of type (G,n). In Section 4, we provide examples for determining the homotopy phenomena of homotopy comultiplications on L(p) for a prime p. In this article, we mostly use '≃' and '≅' for a homotopy relation and an isomorphism between homotopy groups, respectively.
2.
Preliminaries
A pair (X,ψ) consisting of a pointed space X:=(X,x0) and a base point preserving continuous map ψ:X→X∨X is called a co-H-space if π1∘ψ≃1X and π2∘ψ≃1X, where 1X is the identity map of X and π1,π2:X∨X→X are the first and second projections, respectively. In the current case, the map ψ:X→X∨X is called a homotopy comultiplication on X. A co-H-space with a homotopy comultiplication is an Eckmann-Hilton dual notion of an H-space with a homotopy multiplication; see [9], [35] and [36]. The pair (X,ψ) is known to be a co-H-space if the composite
is homotopic to the diagonal map Δ:X→X×X.
Let X:=Sm1∨Sm2∨⋯∨Smk be a wedge of spheres, and let the canonical inclusion maps αj:Smj→X,j=1,2,…,k be the basic Whitehead products of weight n=1 which are ordered by α1<α2<⋯<αk. Using mathematical induction on n as a positive integer, we can provide a concrete definition of the basic Whitehead products w1,w2,…,ws,… of weight n≥2 and the heights hws of the basic Whitehead products ws,s=1,2,…; see {[7,8,37,38] for more details.
Hilton's formula [39] is shown as follows.
Theorem 2.1. Let hws,s=1,2,3,… be the heights of the basic Whitehead products
of a wedge of spheresX=Sm1∨Sm2∨⋯∨Smk.Then, for all n, we have
Here, the isomorphismξ:⨁∞s=1πn(Shws)→πn(X)is given by the homomorphism between homotopy groups
induced by the basic Whitehead products ws,s=1,2,3,….
We can see that, for each positive integer n, the direct sum in (2.1) is finite because the heights hws of the basic Whitehead products ws,s=1,2,3,… go to infinity as the positive integer 's' becomes large enough that the nth homotopy groups are trivial; that is,
for a sufficiently large number of positive integers 's'.
Hilton's formula was generalized by Milnor [40] as follows:
Theorem 2.2. If A and B are connected CW-complexes, then there is a homotopy equivalence
Proof. See [40] for more details.
In commutative algebra and algebraic geometry, a localization is a formal method for introduction of the denominators to a given ring or module as the field of fractions. In topology, the localization of a nilpotent CW-space was introduced by Sullivan [31] who stated that a nilpotent CW-complex can be topologically (or homotopically) localized at a prime similar to the localization of a ring or an R-module at a prime, where R is a commutative ring with identity.
Let P be a collection of prime numbers which may be the empty set ϕ. A group G is then said to be a P-local group if the rth power map
defined by
is a bijection as sets for all r∈Pc, the complement of P. In the topological sense, a nilpotent CW-complex X is said to be P-local if the nth homotopy group πn(X), n≥1, is a P-local group; see {[31,41] for the localization of a nilpotent CW-space similar to the localization of a ring at a prime number.
As usual, the localization of a nilpotent CW-space X at a collection P of prime numbers is denoted as XP, and similarly, as a special case P={p} (resp. P=ϕ), the localization (resp. the rationalization) of a nilpotent CW-space X at a prime number p (resp. the empty set ϕ) is denoted as X(p) (resp. XQ).
3.
Homotopy comultiplications on localizations
In this section, we examine the structure of all the homotopy comultiplications of the localization L(p) of a wedge L:=Sm∨M(G,n) of the homotopy spheres and the Moore spaces, where G is an abelian group and 2≤m<n. It is noted that the localization of a nilpotent CW-space is uniquely determined up to homotopy using the classical Whitehead theorem.
3.1. Localized Hilton-Milnor formulae
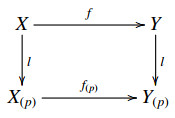
Let X be a nilpotent CW-space and X(p) the localization of X at a prime number p. It is well known that if f:X→Y is a base point preserving continuous map between nilpotent CW-spaces, then there exists a unique map
such that the following diagram
is commutative in the homotopy category of nilpotent CW-spaces, where l:X→X(p) is a p-localizing map. Similarly for the category of nilpotent groups and group homomorphisms.
We can see that the localization of any simply connected co-H-space with a homotopy comultiplication preserves the structure of the co-H-space with the localization of a homotopy comultiplication in the category of simply connected CW-spaces; that is, if X is a simply connected co-H-space, then the localization X(p) of X at a prime p is also a simply connected co-H-space.
We examine the localized counterparts of Hilton-Milnor formulae described in Theorems 2.1 and 2.2 of Section 2 as follows; see also [42,Theorem 2].
Proposition 3.1. Let X(p) be the localization of the wedge sum of spheres X:=Sm1∨Sm2∨⋯∨Smk at a prime p. Then, for all n, we have an isomorphism
where hws is the height of the basic Whitehead product ws for all s≥1. More generally,
for any nilpotent CW-complex W.
Proof. It should be noted that the localization preserves the wedge product in the pointed homotopy category of pointed nilpotent CW-complexes in the following sense:
Because the localizations of abelian groups commute with finite direct sums, by Theorem 2.1, we have the first Eq (3.1) as follows:
where Z(p) is the localization of the ring Z of integers at the prime p.
Milnor's Theorem 2.2 asserts that the second Eq (3.2) holds.
The localization Z(p) of the ring Z of integers at the singleton set {p} should not conflict with the other common usage Zp=Z/pZ, the group of integers modulo p, with the similar notation.
3.2. Localization of a wedge of spheres and Moore spaces
Let G be an abelian group and n a positive integer. As mentioned previously, a Moore space M(G,n) is uniquely determined up to homotopy; that is, any two Moore spaces of type (G,n) have the same homotopy type. We note that the Moore space M(G,n) is simply-connected for n≥2. We can see that the Moore space M(G,n) has only one homotopy comultiplication as the standard (or suspension) comultiplication for n≥3.
Explicitly, if G=Zp, the group of integers modulo p, then the Moore space M(Zp,n) is a CW-complex with a cell structure as follows:
where p:Sn→Sn is the degree p-map; that is, M(Zp,n) is the sphere Sn with an (n+1)-cell en+1 attached by the map p:Sn→Sn of degree p. More generally, the Moore space M(T,n) can also be constructed for a finite abelian group
where
● p1,p2,…,pk are (not necessarily distinct) prime numbers;
● s1,s2,…,sk are (not necessarily distinct) positive integers; and
● Zpisi is the group of integers modulo pisi for i=1,2,…,k.
The fundamental theorem of a finitely generated abelian group G asserts that it can be decomposed as
where F is a free abelian group of finite rank r as a free Z-module, and T is a torsion subgroup of G as in (3.3).
Notation. The following notation is used throughout this paper.
● G is a finitely generated abelian group decomposed as in (3.4); that is,
● L:=Sm∨M(G,n), where 2≤m<n.
● α:Sm→L is the map sending x to (x,y0), where y0 is the base point of M(G,n).
● β:M(G,n)→L is the map sending y to (x0,y), where x0 is the base point of Sm.
● j1:Sm→Sm∨Sm is the map sending s to (s,s0), where s0 is the base point of Sm.
● j2:Sm→Sm∨Sm is the map sending s to (s0,s), where s0 is the base point of Sm.
● ι1:L→L∨L are the map sending x to (x,x0), where x0 is the base point of L.
● ι2:L→L∨L are the map sending x to (x0,x), where x0 is the base point of L.
● π1,π2:L∨L→L are the first and second projections, respectively.
● p is a prime number.
● X(p) indicates the localization of a nilpotent CW-space (or a simply connected CW-space) X.
● f(p):X(p)→Y(p) is the p-localization of a map f:X→Y between connected nilpotent CW-spaces (or simply connected CW-spaces).
● C(L)⊆[L;L∨L] is the set of all homotopy classes of homotopy comultiplications on a simply connected CW-space L:=Sm∨M(G,n), or its localizations.
We now determine the homotopy classes of all the homotopy comultiplications on the p-localization L(p):=Sm(p)∨M(G,n)(p) of L at a prime p as follows.
Proposition 3.2. Let G=F⊕T be a finitely generated abelian group decomposed as in (3.5), and let L(p):=Sm(p)∨M(G,n)(p) with 2≤m<n. If p and pi are relatively prime for all i=1,2,…,k, then any homotopy comultiplication
has the following type
for some homotopy class
such that
for all t=1,2,…,r. Here,
● the first addition in (3.6) is the homotopy addition in the homotopy group;
● the second and third additions in (3.6) are originated from the suspension structures on the Moore spaces M(Zt,n)≃ΣM(Zt,n−1) with Zt=Z for all t=1,2,…,r;
● π1(p),π1(p):L(p)∨L(p)→L(p) are the first and second projections which are the localizations of the first and second projections π1,π2:L∨L→L, respectively; and
● r is the rank of the free Z-module F.
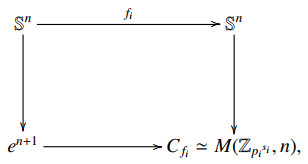
Proof. It should be noted that the Moore space M(Zpisi,n) is the mapping cone Cfi of the map
of degree pisi for each i=1,2,…,k; that is, the Moore space M(Zpisi,n) can be obtained as the homotopy pushout:
where the vertical maps are inclusions and en+1 is the unit ball in dimension n+1 as the (n+1)-cell.
Therefore, the cell structure of M(Zpisi,n) has the form of
for each i=1,2,…,k. More generally, the Moore space M(G,n) has the CW-decomposition as follows:
Because (p,pi)=1 for all i=1,2,…,k, we observe that the p-localizing map
is invertible for all i=1,2,…,k; that is, it has the unique inverse map. Therefore, the p-localization M(Zpisi,n)(p) of the Moore space has the homotopy type of a one point set for all i=1,2,…,k. Indeed, we have
for all i=1,2,…,k. Because the localization of a connected nilpotent CW-space preserves the wedge product, we have
Because the localization L(p) of L at a prime p has the CW-structure, the Cellular Approximation Theorem [43,page 77] asserts that the base point preserving continuous map
is homotopic to a cellular map
that is,
Because the m-sphere Sm,m≥2 has the unique comultiplication structure as the standard (or suspension) comultiplication, we can see that the cellular map ψ(c) and the convolution product induce a unique homotopy comultiplication
on the p-local m-sphere Sm(p), where the addition + is the suspension addition originated from the suspension of the the p-local (m−1)-sphere; that is,
Therefore, the following commutative diagram
asserts that
This proves the first line of (3.6).
Using the suspension structure on the p-localization
of the Moore space M(G,n), we define a homotopy class
by
where Zt=Z for all t=1,2,…,r, and the binary operations are originated from the suspension structure on the p-localization M(Zt,n)(p) of the Moore space as in (3.7) for all t=1,2,…,r. Note that the set [M(Z,n)(p),L(p)∨L(p)] of homotopy classes of continuous maps from M(Z,n)(p) to L(p)∨L(p) under the binary operation induced by the suspension comultiplication is an abelian group. We now obtain
up to homotopy for all t=1,2,…,r and, similarly, π2(p)∘Qt is also the identity element as the homotopy class in [M(Zt,n)(p),L(p)] for all t=1,2,…,r, as required.
Remark 3.3. The relation between the wedge product of pointed CW-spaces and the direct sum of homotopy groups demonstrates that the homotopy element Qt:M(Zt,n)(p)→L(p)∨L(p) of [M(Zt,n)(p),L(p)∨L(p)] for all t=1,2,…,r in (3.6) can lead to the homotopy class expressed as
where Zt=Z for all t=1,2,…,r. In addition, if the image of Q:M(G,n)(p)→L(p)∨L(p) under the homomorphisms
induced by the the first and second projections π1(p),π2(p):L(p)∨L(p)→L(p) is the identity element, then we can see that the map
given by the Eq (3.6) is a homotopy comultiplication on L(p).
Definition 3.4. The homotopy class
in Proposition 3.2 and Remark 3.3 is said to be a homotopy perturbation of the homotopy comultiplication ψ:L(p)→L(p)∨L(p).
Lemma 3.5. Let Q=(Q1,Q2,…,Qt,…,Qr) be a homotopy perturbation of the homotopy comultiplication ψ:L(p)→L(p)∨L(p) in Proposition 3.2 such that
We can then construct a unique homotopy element R of [M(G,n)(p),Sm(p)∨Sm(p)] satisfying
and
where q1(p),q2(p):Sm(p)∨Sm(p)→Sm(p) are the first and second projections, respectively.
Proof. The cofibration sequence is considered as follows:
where q(p):L(p)→M(G,n)(p) is the projection. Let
and
be the inclusion maps. We can then see that the following diagram
is strictly commutative. Here, i♯,j♯ and l♯ are group homomorphisms between homotopy groups induced by inclusion maps i,j and k, respectively. Because the localization L(p)∨L(p) of L∨L at a prime p is (m−1)-connected and M(G,n)(p)∨M(G,n)(p) is (n−1)-connected, by the Blakers-Massey Theorem (see [44,page 48] and [43,page 368]), the first line in the commutative diagram (3.8) shown above is an exact sequence of homotopy groups.
If Q=(Q1,Q2,…,Qt,…,Qr) is a homotopy element of [M(G,n)(p),L(p)∨L(p)] satisfying that
then j♯(Q) is the identity element of [M(G,n)(p),L(p)×L(p)]. Therefore, we have
The Cellular Approximation Theorem [43,page 77] asserts that k♯ is a group monomorphism, we thus have
Since
is a monomorphism between homotopy groups, the exactness of the first line of the commutative diagram (3.8) shown above indicates that there is a uniquely determined homotopy class R in the group [M(G,n)(p),Sm(p)∨Sm(p)] such that
The commutative diagram (3.8) shows that
This implies that i♯(R) is the identity element of [M(G,n)(p),Sm(p)×Sm(p)] because the homomorphism (α(p)×α(p))♯ is a group monomorphism between homotopy groups. Therefore, we have
as required.
Remark 3.6. In Lemma 3.5, the homotopy class R of [M(G,n)(p),Sm(p)∨Sm(p)] can be displayed as
where Rt is the homotopy class of [M(Zt,n)(p),Sm(p)∨Sm(p)] with Zt=Z for all t=1,2,…,r.
Note that if
is the p-localizing map, then the homomorphism
induced by 'l' is an isomorphism of homotopy groups.
The functorial property of the localization of base point preserving continuous maps between simply connected CW-spaces asserts that the localization of the Whitehead product is equal to the generalized Whitehead product of localizations, e.g.,
where the right-hand side of (3.9) is the generalized Whitehead product in the sense of Arkowitz [45,Definition 2.2].
Example 3.7. Let γ:M(Z,n)(p)→S3m−2(p) be the homotopy class of a base point preserving continuous map. We define an element Qt, t=1,2,…,r of [M(Zt,n)(p),L(p)∨L(p)]
as the composition
of continuous maps; that is,
where Zt=Z for all t=1,2,…,r and [j1,[j1,j2]](p) is the localization of the Whitehead product [j1,[j1,j2]]. It can be shown that ψQ:L(p)→L(p)∨L(p) given by
with Zt=Z for all t=1,2,…,r is a homotopy comultiplication whose homotopy perturbation is the homotopy class Q=(Q1,Q2,…,Qt,…,Qr). Indeed, we can see that
for all t=1,2,…,r.
To examine the pivotal property of homotopy comultiplications on the wedge product of the homotopy spheres and the Moore spaces, all of the possible homotopy perturbations should be studied in order to investigate homotopy comultiplications. This raises a question: Is there a general method for construction of the homotopy perturbation of a homotopy comultiplication on the localizations of a wedge of the homotopy spheres and the Moore spaces? The following theorem provides an answer to this query.
Let
be the first and second inclusion maps, respectively. Let w1,w2,…,ws,… be the generalized basic Whitehead products and let hws be the height of ws for each s=1,2,3,…. We then have the following.
Theorem 3.8. Let L:=Sm∨M(G,n) with 2≤m<n, where G=F⊕T is a finitely generated abelian group decomposed as in (3.4) and (3.5) such that p and pi are relatively prime for all i=1,2,…,k. Then, every comultiplication ψ:L(p)→L(p)∨L(p) can be expressed as follows:
Here,
● Qt=(α(p)∨α(p))♯(∑∞s=3ws∘vs) for all t=1,2,…,r;
● ws is the sth generalized Whitehead product consisting of at least one homotopy class j1(p) and at least one homotopy class j2(p) as a factor, localized at p; and
● vs is any homotopy class in the homotopy group [M(Z,n)(p),Shws(p)] for s=3,4,5,….
Proof. It should be noted that
and the expression of Qt is independent of the choice of t=1,2,…,r. By using Proposition 3.2, Remark 3.3 and Lemma 3.5, we observe that every homotopy comultiplication ψ:L(p)→L(p)∨L(p) has the form of (3.10) satisfying that
for all t=1,2,…,r. Using Proposition 3.1, we obtain
We note that
In addition, for any homotopy class
in the homotopy group [M(Z,n)(p),L(p)∨L(p)], Lemma 3.5 demonstrates that there exists a uniquely determined homotopy class
such that
and
for all t=1,2,…,r. The Proposition 3.1 states that the homotopy class Rt can be expressed uniquely as
in the homotopy group [M(Z,n)(p),Sm(p)∨Sm(p)] for all t=1,2,…,r. Here,
● v1 and v2 are homotopy elements in [M(Z,n)(p),Sm(p)]≅[Sn(p),Sm(p)]≅πn(Sm(p));
● vs is any homotopy element in [M(Z,n)(p),Shws(p)] for all integers s≥3; and
● ws is the generalized basic Whitehead product for all integers s≥3.
We recall that
and
and that all of the generalized Whitehead products ws consist of at least one homotopy class
and at least one homotopy class
as the localizations of the basic Whitehead products for all s=3,4,5,…. For example,
● w3=[j1(p),j2(p)];
● w4=[j1(p),[j1(p),j2(p)]];
● w5=[j2(p),[j1(p),j2(p)]];
● w6=[j1(p),[j1(p),[j1(p),j2(p)]]];
● w7=[j2(p),[j1(p),[j1(p),j2(p)]]] and so on.
We now have
and
up to homotopy for all t=1,2,…,r so that v1 and v2 are the trivial (identity) elements of πn(Sm(p)), where 0 is the trivial homotopy element of the homotopy group, as required.
We now present a method for calculating the cardinality of the set consisting of homotopy comultiplications via homotopy perturbations on the localization of the wedge product of the homotopy spheres and the Moore spaces as follows.
Corollary 3.9. Under the hypotheses of Theorem 3.8, the number of homotopy comultiplications on the homotopy localization L(p) of L:=Sm∨M(G,n) at a prime p is
where |X| is the cardinality of a set X.
Proof. By Theorem 3.8, we have the proof.
The aforementioned results raise the following question: What will happen if the prime number p is equal to one of the pi's for i=1,2,…,k? The following gives an answer to this query.
Theorem 3.10. Let L:=Sm∨M(G,n) with 2≤m<n, where G=F⊕T is a finitely generated abelian group decomposed as in (3.4) and (3.5) such that the prime p is equal to one (or more) of the primes p1,p2,…,pk which are not necessarily distinct prime numbers. Then, every comultiplication ψ:L(p)→L(p)∨L(p) can be expressed as follows:
Here,
● QT is the homotopy class in the homotopy group [M(T(p),n),L(p)∨L(p)] given by (α(p)∨α(p))♯(∑∞s=3ws∘xs);
● xs is any homotopy class in [M(T(p),n),Shws(p)] for s=3,4,5,…;
● T(p) is the localization of the torsion subgroup T of G=F⊕T at the prime p; and
● other notations are the same as in Theorem 3.8.
Proof. Since the prime number p equals one (or more) of the primes p1,p2,…,pk which are not necessarily distinct prime numbers, we see that the p-localization T(p) of the torsion part T of G=F⊕T is nontrivial finite group whose order is the power of p. Thus, the localization M(T(p),n) of the Moore space at the prime p is not contractible so that the homotopy perturbation part corresponding to this localized Moore space should be added, namely,
as one of the coordinate of the homotopy perturbation
of the homotopy comultiplication ψ:L(p)→L(p)∨L(p). Now argue as for Theorem 3.8.
More generally, we now calculate the number of homotopy comultiplications on the homotopy localization L(p) of L:=Sm∨M(G,n) at a prime p as follows.
Corollary 3.11. Under the hypotheses of Theorem 3.10, the number of homotopy comultiplications on the homotopy localization L(p) of L:=Sm∨M(G,n) at a prime p is
where |X| is the cardinality of a set X.
Proof. By Theorem 3.10, we have the proof.
Note that if p and pi are relatively prime for all i=1,2,…,k, then the last term of (3.15) should be wiped out due to Theorem 3.8 being the formula (3.13) in the computation of the number of homotopy comultiplications on L(p) because the p-localization T(p) of the torsion part T of G=F⊕T is a trivial group so that the localization M(T(p),n) of the Moore space at the prime p is a one-point space up to homotopy.
4.
Examples
In this section, we provide a list of examples for development of the structure of homotopy comultiplications on the localization L(p) (or the rationalization LQ) of a wedge of the homotopy spheres and the Moore spaces L:=Sm∨M(G,n), where 2≤m<n.
In Tables 1 and 2,
● C(L(p)) is the set (or group) consisting of all the homotopy comultiplications on the localization L(p) of L at a prime p.
● Each group (or ring) in the last columns in Tables 1 and 2 is in one-to-one correspondence with the set C(L(p)); that is, they are of the same cardinality.
● '1' is the trivial group.
● Zn is the group of integers modulo n.
● Z(p) is the p-localization of the ring of integers.
● ϕ is the empty set, and C(L(p))=C(LQ) in this case.
Proof. For a finite group case, if L:=S4∨M(Z2⊕Z5⊕Z22,6), we then have
Therefore, by [24,Propostion 3.1], we can see that the group of homotopy comultiplications on L(13) is the trivial group; that is, the set C(L(13)) of homotopy comultiplications of L(13) is a set consisting of only one homotopy class of the standard comultiplication on S4(13).
In the case of an infinite group, if L:=S4∨M(Z⊕Z⊕Z5,9), we then obtain
Theorem 3.8 and Corollary 3.9 assert that the cardinality |C(L(2))| of the set C(L(2)) of homotopy comultiplications on L(2) is
Similarly, the remaining portions would be proved by the previous results and the various formulas in algebraic topology such as the universal coefficient theorem in cohomology, the Hopf-Whitney theorem [43,page 244], the cellular approximation theorem, the cohomotopy group, and the homotopy group of spheres [46].
5.
Conclusions
A co-H-space with a comultiplication as the Eckmann-Hilton dual of an H-space with a multiplication plays a pivotal role in classical homotopy theory. In general, there are many homotopy comultiplications on a co-H-space with many distinctive properties. The localization of a nilpotent CW-space or a spectrum at a collection of prime numbers is a homotopical analogue of the localization of a commutative ring or a module, specifically the ring Z of integers at a collection of prime numbers.
In this paper, we have described the pivotal ideas of homotopy comultiplications on co-H-spaces and the localized counterparts of Hilton-Milnor formulae. This study focused on the structure of homotopy comultiplications on the localization L(p) of a wedge L:=Sm∨M(G,n) of the homotopy spheres Sm and the Moore spaces M(G,n), where G is an abelian group and 2≤m<n. We have provided examples for determining the homotopy phenomena of homotopy comultiplications on L(p) for a prime p.
We hope that our methods will be used to study the advantages of co-H-spaces along with various homotopy comultiplications and will be valuable in the field of computational topology. We also hope that the results will be applied to the concepts of algebra comultiplications with many kinds of perturbations on the algebraic objects in many areas of algebra as well as algebraic topology.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2018R1A2B6004407). The author is very grateful to the anonymous referees for a careful reading and many helpful suggestions that improved the quality of this paper.
Conflict of interest
The author declares there is no conflicts of interest.









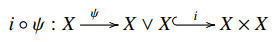

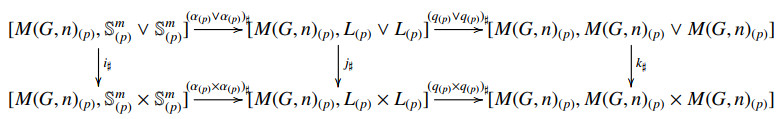
 DownLoad:
DownLoad:


