$\bar{\partial}$-equation look at analytic Hilbert's zero-locus theorem

1.   Description of Theorem 1.1

As one of the fundamentals of algebraic-complex geometry, the analytic Hilbert's Nullstellensatz (either theorem of zeros or zero-locus theorem) ^[1] on the finite complex plane $\mathbb C$ asserts that for finitely many analytic polynomials $\{p_j\}_{j = 1}^n$ without common zeros in $\mathbb C$,

This celebrated principle has been improved and extended for more than a century; see e.g., Hermann ^[2], Masser-Wüstholz ^[3], Brownawell ^[4], Kollár ^[5], and Kwon-Neryanun-Trent ^[6] whose Lemma 1.4 especially indicates that an entire function $Y$ is a polynomial on $\mathbb C$ if and only if $\lim_{|z|\to\infty}|z|^{-m}{|Y(z)|} = 0$ for some positive integer $m$.

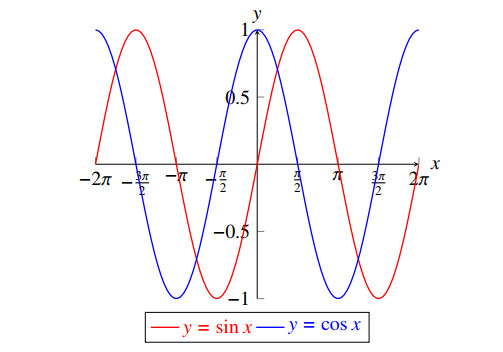
Meanwhile, in complex trigonometry, the Pythagorean Identity on $\mathbb C$ states that

and $\sin z$ & $\cos z$ have no common zero as graphically shown below

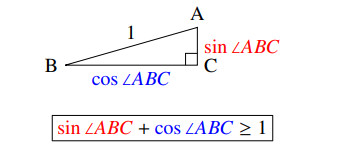
Although the entire functions $\sin z$ & $\cos z$ are not analytic polynomials, they can be appropriately approximated by analytic polynomials and satisfy:

where this last inequality is geometric due to the basic fact that the sum of the lengths of the adjacent & opposite sides $BC$ & $CA$ is not less than the length of the hypotenuse $AB$ in the right triangle $\triangle{ABC}$ drawn below

The previous two-fold observation actually inspires us to extend the analytic Hilbert's Nullstellensatz to some entire function spaces.

For $\alpha > 0$, let $\mathcal F_{\alpha}^2$ be the Fock-Hilbert space of all $L^2(\lambda_\alpha)$-integrable entire functions (or analytic functions on $\mathbb C$) with the inner product

where

Moreover, for a nonnegative integer $m$, let $\mathcal{F}^2_{\alpha, m}$ be the quadratic $m$-order Fock-Sobolev space of all entire functions obeying

Evidently,

see also Zhu's book ^[7] for more information.

Since all analytic polynomials are dense in $\mathcal{F}^2_{\alpha, m}$, as a somewhat unexpected variant of Eqs (1) and (2) we discover the following corona-type principle.

Theorem 1.1. Let

If $g$ is an entire function with

then

Especially, if

then

2.   Demonstration of Theorem 1.1

For $\alpha\in (0, \infty)$, let

Then some elementary calculations derive the following four formulae:

Consequently,

Moreover, a modification of Cho-Zhu's statement on [8, p. 2496] gives the following pointwise estimation

Lemma 2.1. For

let $\phi:\mathbb C\to \mathbb R\ \ \& \ \ g:\mathbb C\to\mathbb C$ be $C^2$-smooth with

$\rm(i)$ Weighted $(L^p, \bar{\partial})$-estimation - not only for a given function $f$ on $\mathbb C$ there exists a weak solution $u\in L^p(e^{-2\phi})$ to $\bar{\partial}u = f$ in the sense of

if and only if

but also Eq $(4)$ holds for all $f\in L^p\big((\Delta(2\phi)e^{2\phi})^{-1}\big)$ if and only if

$\rm(ii)$ Uniqueness up to entire $L^p(e^{-2\phi})$-functions - arbitrary two solutions in (i) differ by a function $h\in A ^p(e^{-2\phi})$ with

$\rm(iii)$ Weighted $(L^p, \bar{\partial})$-Poincaré inequality - if $u\in C^1$ satisfies (i) above and the $L^p(e^{-2\phi})$-minimality below

then

and consequently, if $u\in C^1$ enjoys the case $p = 2$ of (i) and the $L^2(e^{-2\phi})$-orthogonality

then Eq $(7)$ holds for $p = 2$.

$\rm (iv)$ Weighted $(L^2, \bar{\partial})$-estimation is always available.

$\rm (v)$ Uniqueness - if

then the solution in (iv) is unique.

Proof. (i) This part is motivated by Berndtsson's [9, Theorems 2–3]. But, the argument comes from an adjustment of the case $p = 2$ presented in Berndtsson's [10, Proposition 1.1].

Suppose that for a given function $f$ on $\mathbb C$ there exists a weak solution $u\in L^p(e^{-2\phi})$ to $\bar{\partial}u = f$ in the sense of Eq (3). Then the Hölder inequality derives

Hence Eq (4) holds for the previous function $f$. Conversely, if Eq (4) is valid for a given function $f$ on $\mathbb C$, then

is a subspace of $L^{p'}(e^{-2\phi})$, and hence the given function $f$ induces the following bounded antilinear functional on $S_\phi$:

This, along with the Hahn-Banach extension theorem, ensures an extension of ${\rm L}_f$ from $S_\phi$ to $L^{p'}(e^{-2\phi})$. Consequently, the Riesz-type representation theorem for the dual of $L^{p'}(e^{-2\phi})$ produces a function

such that

Upon taking $G = \bar{\partial}^\ast_{2\phi} g$, we find that the last function $u\in L^p(e^{-2\phi})$ is a weak solution to $\bar{\partial}u = f$ in the sense of Eq (3).

Moreover, if Eq (4) holds for all $f\in L^p\big((\Delta(2\phi)e^{2\phi})^{-1}\big)$, then an application of the duality

under the pairing

derives Eq (5). Evidently, if Eq (5) holds, then $\langle f, g\rangle_{2\phi}$ deduces that Eq (4) is valid for all $f\in L^p\big((\Delta(2\phi)e^{2\phi})^{-1}\big)$.

As an aside of the preceding demonstration, we achieve that for any $f\in L^p\big((\Delta(2\phi)e^{2\phi})^{-1}\big)$ there exists a weak solution $u\in L^p(e^{-2\phi})$ of $\bar{\partial}u = f$ with

if and only if Eq (5) holds.

(ii) This follows from the fact that $\bar{\partial}u = 0$ if and only if $u$ is analytic.

(iii) This comes from a modification of the argument for Berndtsson's [10, Corollary 1.4]. Indeed, without loss of generality, we may assume

Now, the verification of (i) ensures that

has a weak solution $v$ enjoying the inequality

Note that (ii) produces a function $h_\dagger\in A ^p(e^{-2\phi})$ such that $v = u+h_\dagger$. So Eqs (6) & (10) imply

as desired in Eq (7).

Especially, if Eq (8) is valid, then a combination of

and the closedness of $A ^2(e^{-2\phi})$ in $L^2(e^{-2\phi})$ yields a function $h_\ddagger\in A ^2(e^{-2\phi})$ such that

Upon noticing $\bar{\partial}(v+h_\ddagger-u) = 0$, we obtain

As a consequence, $u$ is the $L^2(e^{-2\phi})$-minimal solution to $\bar{\partial}v = \bar{\partial}u$. Thus, the weighted $(L^2, \bar{\partial})$-Poincaré inequality follows from the first inequality of Eq (11) and the case $p = 2$ of Eq (10).

Here it is appropriate to mention that as shown in [10, Theorem 3.3] the case $p = 2$ of Eq (10) can be used to establish the following Brunn-Minkowski-type concavity: if $\mathbb D$ is a convex open subset of the $(n+1)$-dimesnional Euclidean space $\mathbb R^n\times(-\infty, \infty)$ and ${\mathbb D}_t = \{x: (x, t)\in \mathbb{D}\}$ then the Lebesgue measure ${\rm M}_n(\mathbb{D}_t)$ satisfies $\partial^2_t\log {\rm M}_n(\mathbb{D}_t)\le 0$ - i.e., - the function $t\mapsto \log {\rm M}_n(\mathbb{D}_t)$ is concave - in particular - so is $t\mapsto \log {\rm A}(\mathbb{D}_t) = \log {\rm M}_2(\mathbb{D}_t)$.

(iv) This is a minor variant of [11, Theorem 1.1] - the well-known Hörmander $L^2$-estimate for the $\bar{\partial}$-equation presented in ^[12]. In fact, given $f\in L^2\big(\big({e^{2\phi}\Delta(2\phi)}\big)^{-1}\big)$ the basic identity (cf. [10, Proposition 1.2])

ensures the second iff-condition of (i) with $p = 2$

thereby reaching the existence of a weak solution $u$ to $\bar{\partial}u = f$ with

(v) Such a uniqueness is newly induced by Eq (1). Yet, its proof is similar to the argument for Hedenmalm's curvature-orientated uniqueness of the $\bar{\partial}$-equation in [11, Theorem 1.4]. As a matter of fact, if $u_1\, \& \, u_2$ are two solutions in (iv), then $u_1-u_2$ is an entire function on $\mathbb C$ due to (ii), and hence $\log|u_1-u_2|$ is subharmonic on $\mathbb C$. This, plus Eq (2), deduces

and so that

is subharmonic on $\mathbb C$. Now, for any

a combination of Eq (9), the mean-value-inequality for the subharmonic function $|u_1-u_2|e^{\phi}$ and the Cauchy-Schwarz inequality derives

Letting $r\to\infty$ in the last estimation gives

Since $z_0$ is arbitrary, the last equality ensures $u_1 = u_2$ on $\mathbb C$.

Argument for Theorem 1.1. Clearly, if $g\equiv 1$ in (3)–(4), then (5)$\Longrightarrow$(6) follows from Eq (3)$\Longrightarrow$(4) which is verified as below.

Suppose that (3) is valid. Let

If $b_{j, k}$ is a function solving pointwisely the $\bar\partial$-equation

then each

is an entire function enjoying

and hence the equation in (4) is met.

Thanks to the smoothness of $f_1, ..., f_n, g$, Lemma 2.1(iv) with

produces a function $b_{j, k}$ such that (12) holds pointwisely with

In order to achieve $g_j\in\mathcal{F}^2_{2m\alpha, 1}$ in (4), in the sequel we employ (12)–(13) to prove

$\rhd$ It is easy to get

In the above and below, $X\lesssim Y$ stands for $X\le cY$ for a positive constant $c$.

For the case $m = 1$, we utilize Eqs (1) & (3) to derive

For the case $m > 1$, we utilize Eq (1) - the Hölder inequality - Eq (3) to derive

In summary, we always have

Now, a straightforward computation gives

As evaluated in ^[13,14], we have

thereby producing

Clearly, we get

whence verifying the first inequality of (15).

$\rhd$ According to Lemma 2.1(i), there exists $b_{j, k}$ classically resolving (12) with (14), and consequently, a combination of Eqs (1) & (17) yields

Since the comparable constants in (18) are independent of $\{j, k\}$, the formula (13), along with (16) & (18), validates the second inequality of (15).

Acknowledgements

XL was supported by NNSF of China (#12171150; #11771139) & NSF of Zhejiang Province (LY20A010008); JX was supported by NSERC of Canada (#202979) & MUN's SBM-Fund (#214311); CY was supported by NNSF of China (#11501415).

Conflict of interest

The authors declare there is no conflict of interest.