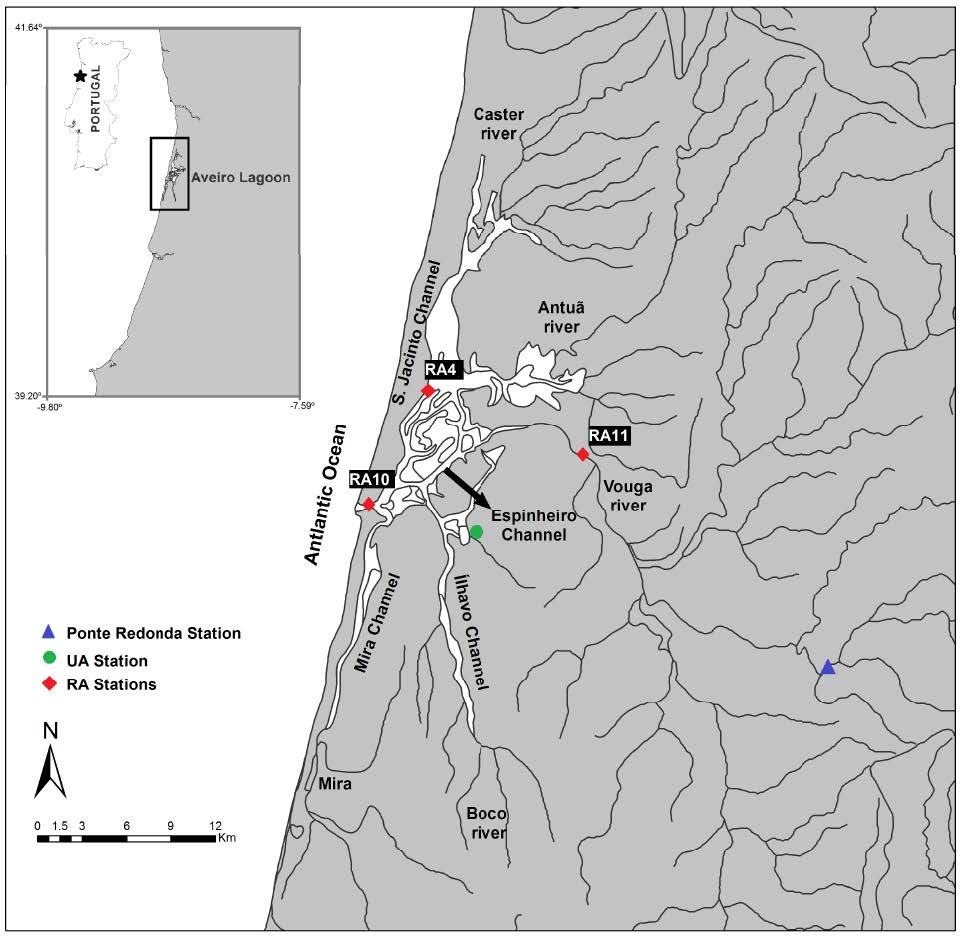
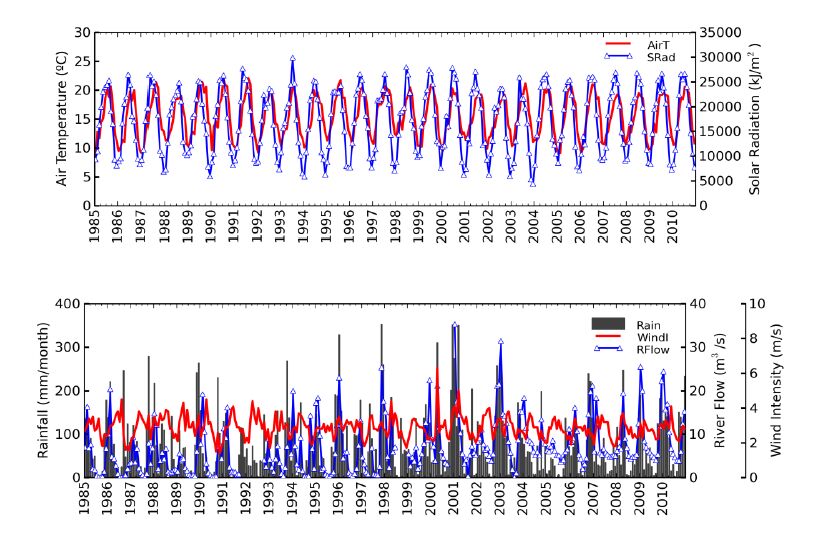
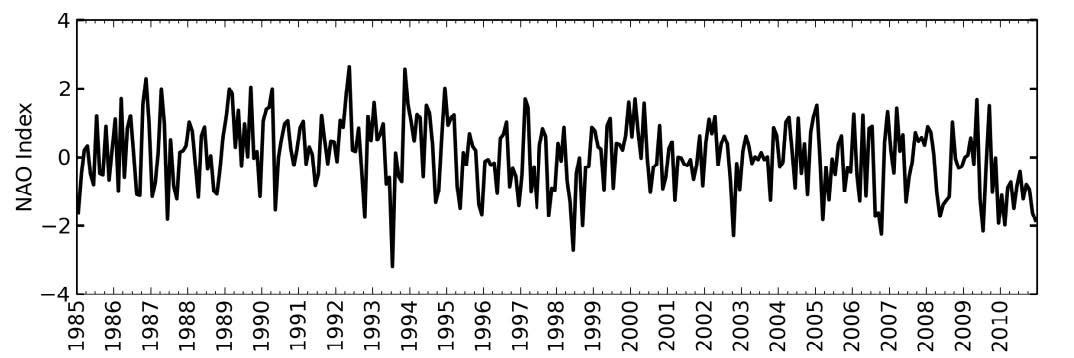
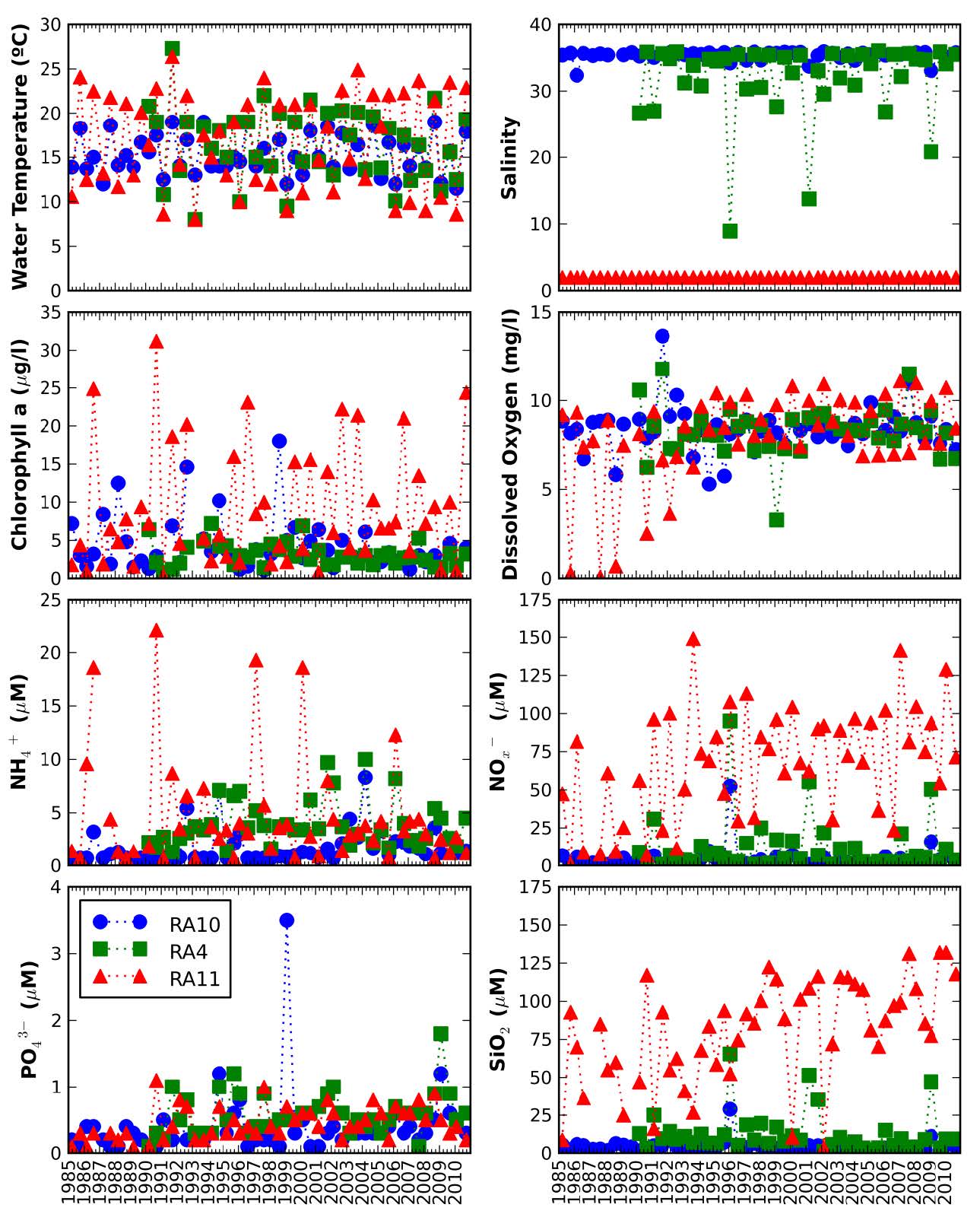
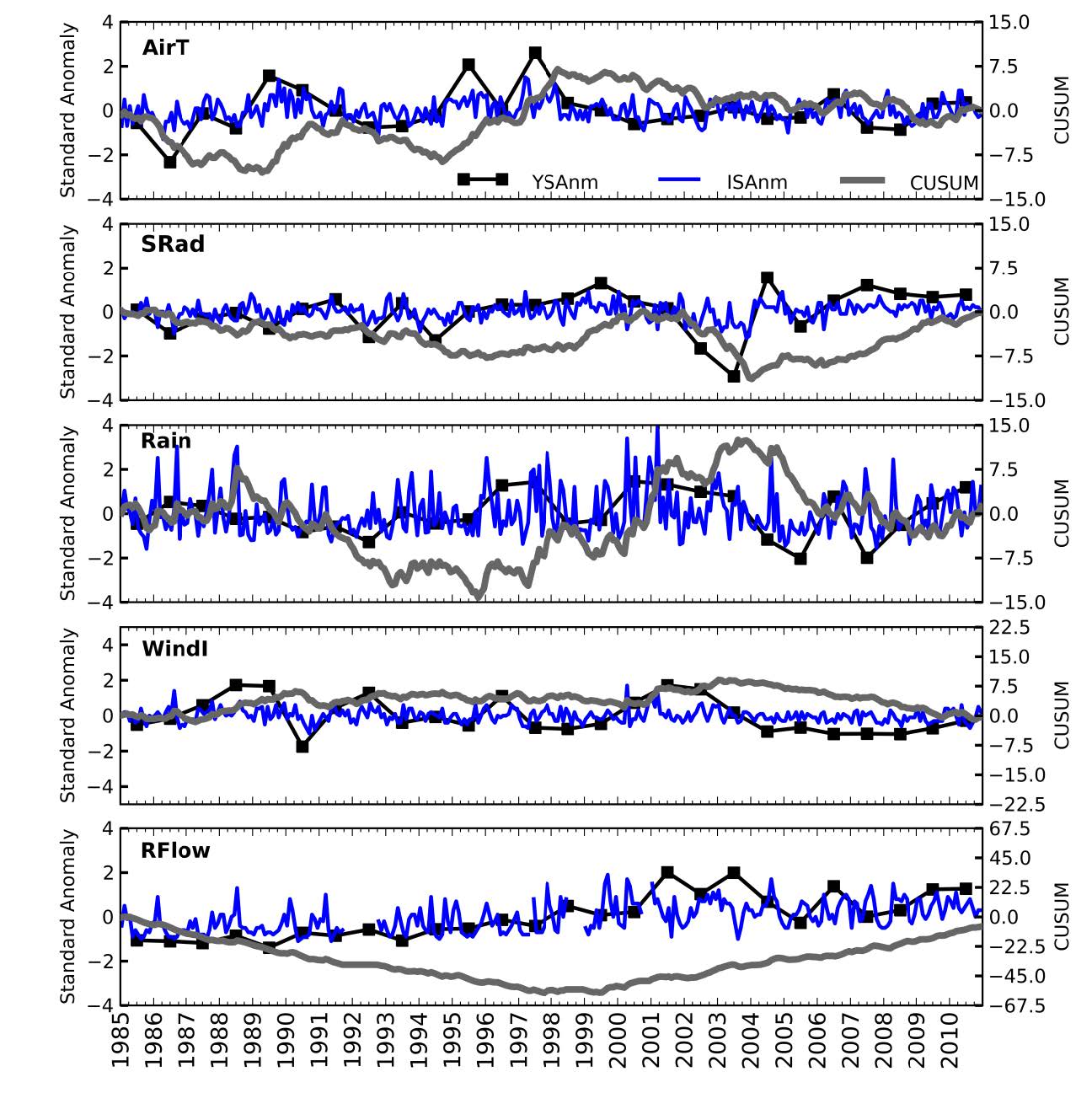
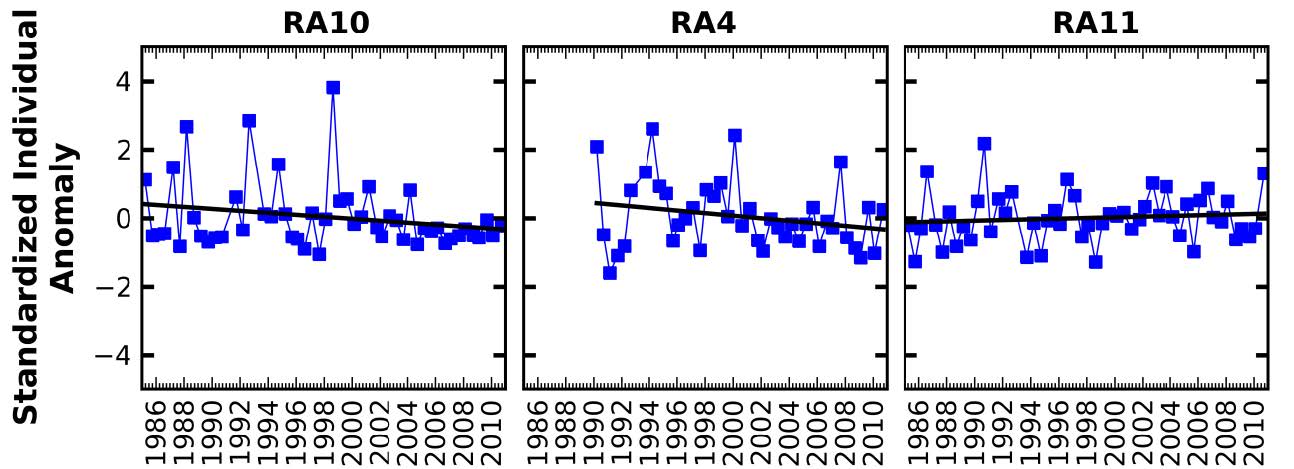
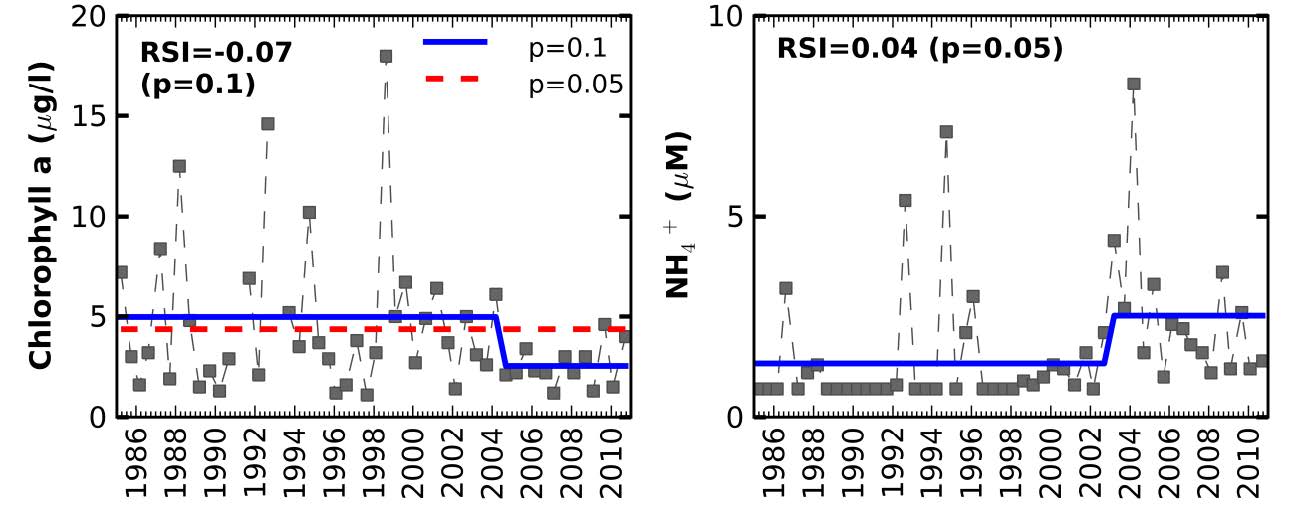
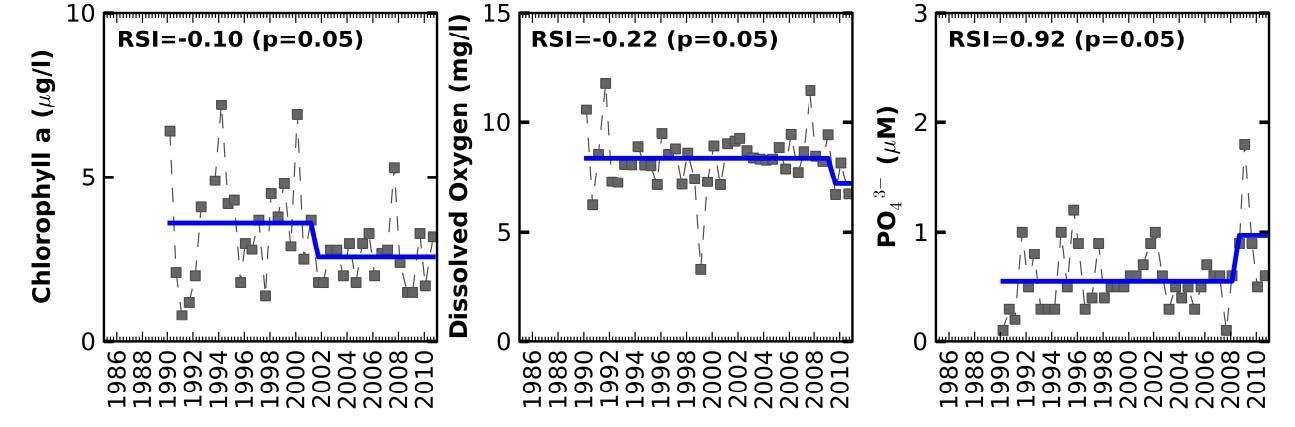
Understanding the natural variability of coastal ecosystems, and in particular distinguishing between the natural fluctuations and the ones that are caused by anthropogenic interventions and long-term climatic variability, is a major concern for establishing adequate management and adaptation strategies. The Aveiro lagoon, a shallow coastal lagoon (Portugal), holds one of the largest saltmarshes and saltpans in Europe and is a very important ecosystem from both economic and ecological viewpoints, making the protection of its water masses a requirement. To better understand the variability of its ecosystem, the factors controlling seasonal, inter-annual and long-term variability of the water quality in the Aveiro lagoon were thus analyzed. The statistical analysis was based on a set of climatic, hydrological and water quality observations undertaken between 1985 and 2010. Seasonal variations were mostly related with the seasonal variation of the main climatic and hydrological drivers, while long-term shifts were typically driven by the anthropogenic interventions in the lagoon. After the adoption of secondary treatment for industrial effluents on 1992, a recovery from hypoxia conditions occurred in the upstream area of the lagoon. After 2000 lower concentrations of silicates occurred downstream, and may also derive from some anthropogenic modifications (e.g., shunting of river water to the sewage system, deepening of the inlet) that may have affected the physical dynamics. In the downstream area of the lagoon, chlorophyll a presented a downward trend between 1985 and 2010 and lower concentrations after 2000, which were probably associated with the lower concentrations of silicates. Results from the data analysis showed that the seasonal, inter-annual and long-term trends observed in the Aveiro lagoon depend on the influence of both anthropogenic and climate drivers, putting in evidence the need to combine these different drivers when evaluating and developing management strategies for estuarine ecosystems.
To Giuseppe Mingione, on the occasion of his 50th birthday, with regard and admiration.
1.
Introduction
The aim of this paper is to study a nonlinear and noncoercive parabolic variational inequality with constraint and homogeneous Dirichlet boundary condition. The Lewy-Stampacchia inequality associated with it is addressed. After the first results of H. Lewy and G. Stampacchia [19] concerning inequalities in the context of superharmonic problems, there is by now a large literature concerning the theory of elliptic obstacle problems as well as of elliptic variational inequalities. We refer to [3,16,25] for a classical overview. For a more recent treatment related to nonlinear elliptic operators see also [23]. The obstacle problem for nonlocal and nonlinear operators has been cosidered in [17,26]. An abstract and general version of the Lewy-Stampacchia inequality is given in [13]. Concerning the parabolic case, first existence results related to problems with time independent obstacles have been treated in [20] in the linear case and in [5] for the more general parabolic problems. The case of obstacles functions regular in time has been considered in [2,5]. Existence and regularity theory for solutions of parabolic inequalities involving degenerate operators in divergence form have been established in [4,18]. More recently in [15], the Authors prove Lewy-Stampacchia inequality for parabolic problems related to pseudomonotone type operators. In this paper we study a variational parabolic inequality for noncoercive operators that present singularities in the coeffcients of the lower order terms in the same spirit of [9,12,14].
Let us state the functional setting and the assumptions on the data.
Let Ω⊂RN, N⩾2, be a bounded open Lipschitz domain and let ΩT:=Ω×(0,T) be the parabolic cylinder over Ω of height T>0. We shall denote by ∇v and ∂tv (or vt) the spatial gradient and the time derivative of a function v respectively. We consider the class
where
and p′ is the conjugate exponent of p, i.e., 1p+1p′=1. In (1.1), Lp(0,T,W1,p0(Ω)) and Lp′(0,T,W−1,p′(Ω)) denote parabolic Banach spaces defined according to (2.7).
Given a measurable function ψ:ΩT∪Ω×{0}→R, we are interested in finding functions u:ΩT→R in the convex subset Kψ(ΩT) of Wp(0,T) defined as
and satisfying the following variational inequality
where
and ⟨⋅,⋅⟩ denotes the duality between W−1,p′(Ω) and W1,p0(Ω). The vector field
is a Carathéodory function, i.e., A measurable w.r.t. (x,t)∈ΩT for all (u,ξ)∈R×RN and continuous w.r.t. (u,ξ)∈R×RN for a.e.
(x,t)∈ΩT, and such that for a.e. (x,t)∈ΩT and for any u∈R and ξ,η∈RN,
hold true. Here α,β are positive constants, while H, K, b and ˜b are nonnegative measurable functions defined on ΩT such that H∈L1(ΩT), K∈Lp′(ΩT) and
where LN,∞(Ω) is the Marcinkiewicz space. For definitions of LN,∞(Ω) and L∞(0,T,LN,∞(Ω)) see Sections 2.2 and 2.3, respectively.
We assume that the obstacle function fulfills
For
we impose the following compatibility condition
In the following, we will refer to a function u∈Kψ(ΩT) satisfying (1.3) and such that u(⋅,0)=u0 as a solution to the variational inequality in the strong form with initial value u0.
Under previous assumptions the existence of a solution in the weak form can be proved, see [12]. However the existence of a solution in the sense stated above is not guaranteed even in simpler cases. Then we assume that the source term and the obstacle function are such that
Here Lp′(0,T,W−1,p′(Ω))+ denotes the non-negative elements of Lp′(0,T,W−1,p′(Ω)). Following the terminology of [7] or [15], (1.15) is equivalent to say that g is an element of the order dual Lp(0,T,W1,p0(Ω))∗ defined as
Then, our main result reads as follows
Theorem 1.1. Let (1.2) and (1.4)–(1.15) be in charge. Assume further that
where SN,p=ω−1/NNpN−p and ωN denotes the measure of the unit ball of RN. Then, there exists at least a solution u∈Kψ(ΩT) of the strong form of the variational inequality (1.3) satisfying u(⋅,0)=u0. Moreover, the following Lewy-Stampacchia inequality holds
In (1.16), Db denotes the distance of b from L∞(ΩT) in the space L∞(0,T,LN,∞(Ω)) defined in (2.8) below.
Assumptions (1.8) on the coefficients of the lower order terms allow us to consider diffusion models in which the boundedness of the convective field with respect to the spatial variable is too restrictive (see [8]). The corresponding bounded case has been treated in [15].
We discuss condition (1.16) through an example. It's easy to verify that the operator
satisfies (1.5)–(1.8). According to (2.2) and (2.3) below, we get that
and so (1.16) holds true whenever γ is small enough. On the other hand, we notice that (1.16) does not imply smallness of the norm of the coefficient b. Indeed
for a constant C independent of γ.
Theorem 1.1 also applies in the case b and ˜b lie in a functional subspace of weak–LN in which bounded functions are dense. For more details see also [10]. For other examples of operators satisfying conditions above we refer to [12].
We remark that for f,ψt,div A(x,t,ψ,∇ψ)∈Lp′(ΩT) condition (1.15) is satisfied. Then, Theorem 1.1 is comparable with the existence result of Lemma 3.1 in [4]. In order to prove our result, we consider a sequence of suitable penalization problems for which an existence result holds true (see [12]). Then we are able to construct a solution u to (1.3) as limit of solutions of such problems despite the presence of unbounded coefficients in the lower order terms.
2.
Preliminary results
In this section we provide the notation and several preliminary results that will be fundamental in the sequel.
2.1. Notation
The symbol C (or C1,C2,…) will denote positive constant, possibly varying from line to line. For the dependence of C upon parameters, we will simply write C=C(⋅,…,⋅). The positive and the negative part of a real number z will be denoted by z+ and z−, respectively, and are defined by z+:=max{z,0} and z−:=−min{z,0}. Given z1,z2∈R, we often use the notation z1∧z2 and z1∨z2 in place of min{z1,z2} and max{z1,z2} respectively.
2.2. Lorentz spaces
Let Ω be a bounded domain in RN. For any 1<p<∞ and 1≤q<∞, the Lorentz space Lp,q(Ω) is the set of real measurable functions f on Ω such that
Here λf(k):=|{x∈Ω:|f(x)|>k}| is the distribution function of f. When p=q, the Lorentz space Lp,p(Ω) coincides with the Lebesgue space Lp(Ω). When q=∞, the space Lp,∞(Ω) is the set of measurable functions f on Ω such that
This set coincides with the Marcinkiewicz space weak-Lp(Ω). The expressions above do not define a norm in Lp,q or Lp,∞ respectively, in fact triangle inequality generally fails. Nevertheless, they are equivalent to a norm, which make Lp,q(Ω) and Lp,∞(Ω) Banach spaces when endowed with them. An important role in the potential theory is played by these spaces as pointed out in [22].
For 1≤q<p<r≤∞, the following inclusions hold
For 1<p<∞, 1≤q≤∞ and 1p+1p′=1, 1q+1q′=1, if f∈Lp,q(Ω), g∈Lp′,q′(Ω) we have the Hölder–type inequality
Since L∞(Ω) is not dense in Lp,∞(Ω), for f∈Lp,∞(Ω) in [6] the Authors stated the following
As already observed in [10,11], we have
and
where, for all m>0, Tm is the truncation operator at levels ±m, i.e.,
Another useful estimate is provided by the following sort of triangle inequality
which holds true for f,g∈Lp,∞(Ω) and ε>0.
For 1≤q<∞, any function in Lp,q(Ω) has zero distance to L∞(Ω). Indeed, L∞(Ω) is dense in Lp,q(Ω), the latter being continuously embedded into Lp,∞(Ω).
Assuming that 0∈Ω, b(x)=γ/|x| belongs to LN,∞(Ω), γ>0. For this function, we have
The Sobolev embedding theorem in Lorentz spaces [1,24] reads as
Theorem 2.1. Let us assume that 1<p<N, 1≤q≤p, then every function u∈W1,10(Ω) verifying |∇u|∈Lp,q(Ω) actually belongs to Lp∗,q(Ω), where p∗:=NpN−p is the Sobolev conjugate exponent of p and
where SN,p is the Sobolev constant given by SN,p=ω−1/NNpN−p.
2.3. Parabolic spaces
Let T>0 and X be a Banach space endowed with a norm ‖⋅‖X. Then, the space Lp(0,T,X) is defined as the class of all measurable functions u:[0,T]→X such that
whenever 1≤p<∞, and
for p=∞. The space C0([0,T],X) represents the class of all continuous functions u:[0,T]→X with the norm
We essentially consider the case where X is either a Lorentz space or Sobolev space W1,p0(Ω). This space will be equipped with the norm ‖g‖W1,p0(Ω):=‖∇g‖Lp(Ω) for g∈W1,p0(Ω).
For f∈L∞(0,T,Lp,∞(Ω)) we define
and as in (2.3) we find
In the class Wp(0,T) defined in (1.1) and equipped with the norm
the following inclusion holds (see [27,Chapter III, page 106]).
Lemma 2.2. Let p>2N/(N+2). Then Wp(0,T) is contained into the space C0([0,T],L2(Ω)) and any function u∈Wp(0,T) satisfies
for some constant C>0.
Moreover, the function t∈[0,T]↦‖u(⋅,t)‖2L2(Ω) is absolutely continuous and
The compactness result due to Aubin–Lions reads as follows.
Lemma 2.3. Let X0,X,X1 be Banach spaces with X0 and X1 reflexive. Assume that X0 is compactly embedded into X and X is continuously embedded into X1. For 1<p,q<∞ let
Then W is compactly embedded into Lp(0,T,X).
As an example, we choose q=p′, X0=W1,p0(Ω), X1=W−1,p′(Ω) and X=Lp(Ω) if p≥2 or X=L2(Ω) for 2NN+2<p<2. Therefore, we deduce
Lemma 2.4. If p>2N/(N+2) then Wp(0,T) is compactly embedded into Lp(ΩT) and into L2(ΩT).
3.
A penalized problem
Let δ>0. We introduce the following initial–boundary value problem
where
Moreover, in this section we assume that
We introduce the notation
By the elementary inequality
and recalling (1.5), (1.6) and (1.7), we easily deduce
for a.e. (x,t)∈ΩT and for any u∈R and ξ,η∈RN.
For u0∈L2(Ω) and f∈Lp′(0,T,W−1,p′(Ω)), a solution to problem (3.1) is a function
such that
for every φ∈C∞(ˉΩT) such that suppφ⊂[0,T)×Ω.
By using the elementary inequality
and Young inequality we see that
Hence, by Theorem 4.2 and Remark 4.5 in [12] we get the following existence result.
Proposition 3.1. Let (1.2), (1.4)–(1.16) and (3.2) be in charge. For every fixed δ>0, problem (3.1) admits a solution uδ∈C0([0,T],L2(Ω))∩Lp(0,T,W1,p0(Ω)).
The arguments of [12] lead to some estimates for the sequence {uδ}δ>0. We propose here a proof that carefully keeps trace of the constants in the estimates.
Lemma 3.2. Let (1.2), (1.4)–(1.16) and (3.2) be in charge. Any solution uδ∈C0([0,T],L2(Ω))∩Lp(0,T,W1,p0(Ω)) to problem (3.1) satisfies the following estimate
Proof. We fix t∈(0,T) and we set Ωt:=Ω×(0,t). We choose φ:=T1(uδ)χ(0,t) as a test function. If we let Φ(z):=∫z0T1(ζ)dζ for z∈R, we have
Assumption (3.2) implies that [(ψ−uδ)+]q−1T1(uδ)⩽0 a.e. in ΩT, so we have
By (1.5) and (1.7) we deduce
Now, as 0⩽Φ(z)⩽z22 for all z∈R, we have
By Hölder and Young inequality we get
Finally, by (3.3)
Gathering (3.6), (3.7), and (3.8) and using Hölder inequality, by (3.5) we have
where
It is easily seen that
and so
We fix t∈(0,T) and choose φ:=uδχ(0,t) as a test function in (3.1). Again, assumption (3.2) implies that [(ψ−uδ)+]q−1uδ⩽0 a.e. in ΩT, then
By Young inequality for ε>0
Then, by (1.5) we further have
For m>0 to be chosen later, we have from (3.3)
We estimate separately the two terms in the right–hand side of (3.12). For k>1 fixed, we obtain
Now we apply Hölder inequality (2.1), estimates (2.6) and (3.10) to get
where M0 is the constant in (3.9). On the other hand, using again Hölder inequality (2.1) and estimate (2.6)
we have
Inserting (3.13), (3.14) and (3.15) into (3.12) we obtain
Observe that (3.11) and (3.16) imply
Now we choose m>0 so large to guarantee
The existence of such a value of m is a direct consequence of (1.16) and the characterization of distance in (2.9). It is also clear that m is a positive constant depending only on b, N, p and α. So we get
for some α1=α1(b,N,p,α). We may also choose ε=α12. Then the latter relation becomes
We choose k=M0(α14C2)N/p so that C2(M0k)p/N=α14 and therefore
Taking into account the definition of M0, the latter leads to the estimate (3.4).
Lemma 3.3. Let (1.2), (1.4)–(1.16) and (3.2) be in charge. Assume further that g− defined in (1.15) is such that
Then, for every δ>0, every solution uδ of problem (3.1) satisfies
Moreover, there exists a positive constant C depending only on the data and independent on δ such that
Proof. We use the function ϕ=(ψ−uδ)+ as a test function in the equation of Problem (3.1). Then, we get
Recalling (1.15), this implies
By (1.14) we observe that
hence, by (1.6) we get
Then, using Hölder inequality and dividing both sides of the inequality by ‖(ψ−uδ)+)‖Lq((ΩT) we obtain (3.18). To obtain (3.19) we fix φ∈Lp(0,T;W1,p0(Ω)) and then we observe that
At this point we observe that the definition of q and Holder inequality imply
Finally, using (3.18) and Poncaré inequality slicewise, we conclude that
where C is a positive constant independent of δ. This immediately leads to (3.19).
4.
Proof of main result
We proceed step by step. We first prove the result under regularity assumptions on g and sign conditon (3.2) on the obstacle function ψ. Then we address the general case.
Proposition 4.1. Let (1.2), (1.4)–(1.16), (3.2) and (3.17) be in charge. There exists at least solution u∈Kψ(ΩT) to the variational inequality (1.3) such that u(⋅,0)=u0 in Ω and satisfying the following estimate
Proof. By Proposition 3.1, for every δ>0 there exists a solution uδ∈C0([0,T],L2(Ω))∩Lp(0,T,W1,p0(Ω)) to problem (3.1) satisfying (3.4). Hence we have that, by Lemma 3.3 and Lemma 2.2, there exists u∈C0([0,T],L2(Ω))∩Lp(0,T,W1,p0(Ω)) such that
as δ→0+. By semicontinuity, (3.4) implies (4.1)
We claim that the limit function u solves the variational inequality (1.3) in the strong form.
It is immediate to check that
Indeed, (4.4) holds since uδ(⋅,0)=u0 a.e. in Ω for every δ>0. On the other hand, if we pass to the limit as δ→0+ in (3.18) and take into account (4.2) we have ‖(u−ψ)−‖L2∧p(ΩT)=0 which clearly implies (4.5).
Our next goal is to prove that
as δ→0+. We test the penalized equation by T1(uδ−u) and since condition (4.5) implies
we get the following inequality
If we set Φ(z):=∫z0T1(ζ)dζ, by (4.4) we obtain
Because of (4.3), the latter term in the last inequality vanishes in the limit as δ→0. So, as Φ is nonnegative, we get
Again by (4.3), the right hand side of (4.7) vanishes in the limit as δ→0, and so (4.7) implies
By (1.7), (3.2) and (3.3) we have
therefore, by the dominated convergence theorem and by (4.2), we get
Combining (4.8) and (4.9) and by (1.6) we get
Using again (1.6), relation (4.10) gives
and so by (4.2) we get
as δ→0. By Lemma 3.1 in [21] we deduce that (4.6) holds.
We let v∈Kψ(ΩT). It is clear that [(ψ−uδ)+]q−1Tλ(uδ−v)⩽0 a.e. in ΩT and for every λ>0. For this reason, if we use Tλ(uδ−v) as a test function in (3.1) we deduce
We set Φλ(z):=∫z0Tλ(ζ)dζ and we have
We observe that Lemma 2.2 applies because of (3.4) and (3.19), so
This convergence and the Lipschitz continuity of Φλ gives Φλ(uδ−v)(⋅,T)⇀Φλ(u−v)(⋅,T) weakly in L2(Ω), then
On the other hand, by Fatou lemma, we are able to pass to the limit as δ→0 in the third term on the left–hand side of (4.11). Indeed, for this term we know by the monotonicity condition (1.6) that the integrand is nonnegative and we have already observed that uδ and ∇uδ converge a.e. according to (4.2) and (4.6) respectively. We only need to handle the term
This can be done arguing similarly as for the case λ=1. By (1.7) we have
By (4.2) and (4.5) we obtain A(x,t,uδ∨ψ,∇v)→A(x,t,u,∇v) a.e. in ΩT, Therefore, by the dominated convergence theorem, A(x,t,uδ∨ψ,∇v)→A(x,t,u,∇v) strongly in Lp′(ΩT,RN), and this yields
Taking into account the latter relation and also (4.12) and (4.13), we can now pass to the limit as δ→0 in (4.11) and obtain
Since
and also observing that
we conclude that (1.3) holds.
Next result shows that a Lewy–Stampacchia inequality can be derived under some suitable assuption, that we are going to remove later.
Proposition 4.2. Let (1.2), (1.4)–(1.16), (3.2) and (3.17) be in charge. If we also assume that
the solution u of the obstacle problem constructed in Proposition 4.1 satisfies the Lewy–Stampacchia inequality (1.17).
Proof. We define
For k⩾1 we also define
Thanks to Lemma 4.3 in [15] we are able to test (3.1) by Ψk(x,s,uδ−ψ)χ(0,t) for t∈(0,T), obtaining
By (1.14) we have
We also have
So, taking into account (4.14), we have
We remark that
Since we have {g−−1δηk((uδ−ψ)−)<0}⊂{uδ<ψ} then
By (1.6) it follows that
Hence, we deduce from (4.15)
Now, we pass to the limit as k→∞. In particular, by using the monotone convergence theorem, we have
and also
We gather the previous relations, and (since t∈(0,T) is arbitrary) we get
Since it is clear that
we obtain
Observing that (4.2), (4.5) and (4.6) hold, then
as δ→0. By (1.7), (3.2) and (3.4), Fδ is also bounded in Lp′(ΩT), hence Fδ⇀0 in Lp′(ΩT). We deduce
By (4.16) we obtain
Hence we have
and so
Similarly, rewriting (3.1) as follows
then
and the proof is completed.
Next result provides the one of Theorem 1.1 under the assumption (3.2) but removing condition (3.17).
Proposition 4.3. Let (1.2), (1.4)–(1.16) and (3.2) be in charge. There exists at least solution u∈Kψ(ΩT) to the variational inequality (1.3) satisfying u(⋅,0)=u0 in Ω, the estimate (4.1) and the Lewy–Stampacchia inequality (1.17).
Proof. We know that
where g± are nonnegative elements of Lp′(0,T,W−1,p′(Ω)). By using a regularization procedure, due to [7] Lemma p. 593, and Lemma 4.1 in [15], we find a sequence {g−n}n∈N of nonnegative functions such that
and
We define
It is clear that
as n→∞. Due to the regularity assumptions on g−n, we get the existence of un∈Kψ(ΩT) with un(⋅,0)=u0 in Ω such that for every v∈Kψ(ΩT) we have
Moreover, the subsequent estimate holds
and the following Lewy-Stampacchia inequality holds
Since the sequence {fn}n∈N is strongly converging (and hence bounded) in Lp′(0,T,W−1,p′(Ω)), we obtain
for some positive constant C independent of n. Moreover, the Lewy–Stampacchia inequality (4.18) implies a uniform bound of this kind
again for some positive constant C independent of n. Therefore, there exists u∈C0([0,T],L2(Ω))∩Lp(0,T,W1,p0(Ω)) with u(⋅,0)=u0 in Ω such that
as n→∞. Obviously (4.19) implies u⩾ψ a.e. in ΩT. If we summarize, we have u∈Kψ(ΩT) and then vn:=un−T1(un−u)∈Kψ(ΩT). Hence, we use vn as a test function in (4.17) and, arguing as in the proof of Proposition 4.1, we obtain
as n→∞. For fixed λ>0 and v∈Kψ(ΩT) we also have vn,λ:=un−Tλ(un−v)∈Kψ(ΩT). Arguing again as in the proof of Proposition 4.1, we get (1.3) passing to the limit (first as n→∞ and then as λ→∞) in the inequality obtained by testing (4.17) by vn,λ.
Finally, we remove condition (3.2), i.e., we are able to prove Theorem 1.1.
Proof of Theorem 1.1. The convex set Kψ(ΩT) is nonempty and one can find w∈Kψ(ΩT) such that w(⋅,0)=ψ(⋅,0) in Ω (see for details Remark 2.1 in [15]). Let us define
Hence ˆf∈Lp′(0,T,W−1,p′(Ω)) and ˆψ and ψ share the same trace on ∂Ω×(0,T). Therefore, one can conclude
Moreover, the vector field ˆA enjoys similar properties as A. This is trivial for conditions (1.6) and (1.7). As in [12], properties of A and Young inequality, we have for ε>0
with a suitable H1∈L1(ΩT). Moreover, as an elementary consequence of the convexity of ||p, for 0<ϑ<1 we find a constant C=C(ϑ,p)>0 such that
Hence, we get coercivity condition for ˆA:
where we set
and denoted by ˆH a suitable nonnegative function in L1(ΩT). Obviously, we can make ˆα arbitrarily close to α, by choosing ε close to 0 and ϑ close to 1. Using inequality (2.5) for b and ˜b in place of f and g, respectively, we can easily show that also Dˆb is arbitrarily close to Db, again by choosing ε close to 0 and ϑ close to 1. Indeed, we have
By (1.16) we can also have
We observe that
We can apply Proposition 4.3 for the operator ˆA. Therefore, we obtain the existence of a function ˆu∈Kˆψ(ΩT) such that
and the following parabolic variational inequality
holds true for every admissible function ˆv∈Kˆψ(ΩT). Since any v∈Kψ(ΩT) can be rewritten as v=ˆv+w for some ˆv∈Kˆψ(ΩT), by (4.20), by the definitions of ˆA, ˆf and ˆψ, we see that the variational inequality (1.3) holds true with u:=ˆu+w and for any admissible function v∈Kψ(ΩT). The fact that u∈Kψ(ΩT) and u(⋅,0)=u0 in Ω is obvious, and this concludes the proof.
Acknowledgments
The authors are members of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). F. Farroni also acknowledges support by project Starplus 2020 Unina Linea 1 "New challenges in the variational modeling of continuum mechanics'' from the University of Naples Federico II and Compagnia di San Paolo. G. Zecca also acknowledges support by Progetto FRA 2022 "Groundwork and OptimizAtion Problems in Transport'' from the University of Naples Federico II.
Conflict of interest
The authors declare no conflict of interest.














 DownLoad:
DownLoad: