1D electrochemical model of lithium-ion battery for a sizing methodology of thermal power plant integrated storage system

Nomenclature

Acronym: BESS: Battery Energy Storage System; BOL: Beginning Of Life; DOD: Depth Of Discharge; EFR: Enhanced Frequency Response; GE: General Electric; LFP: Lithium Iron Phosphate; LTO: Lithium Titanate Oxide; NMC: Nickel Manganese Cobalt; OCV: Open Circuit Voltage; PDE: Partial Differential Equation; PI-BESS: Plant Integrated Battery Energy Storage System; SOC: State Of Charge; SPM: Single Particle Model; SPM-1E: Single Particle Model with single Electrode; TSO: Transmission System Operators

Latin letters: ${A}_{cell}$: cell active surface; ${a}_{s}$: active surface per volume unit; ${C}_{s}$: concentration of lithium inserted in the electrode active particles; ${D}_{s}$: solid diffusion coefficient; ${F}_{surf}$: solid diffusion transfer function; $F$: faraday’s constant; ${I}_{cell}$: cell current; ${I}_{0}$: exchange current; ${j}^{Li}$: volume rate of Li⁺ current generation; ${Q}_{cell}$: cell capacity; ${r}_{\mathrm{\Omega }}$: global ohmic resistance of the cell; ${R}_{s}$: particle radius; $U$: electrode equilibrium potentials; ${U}_{cell}$: cell open circuit voltage or cell e.m.f.; ${U}_{T}$: thermal voltage ${U}_{T} = RT/F$ (R: gas constant, F: Faraday’s constant, T: temperature); ${V}_{cell}$: cell Voltage; $y$: insertion rate calculated with the ratio between ${C}_{s}$ and ${C}_{smax}$ in solid phase

Greek letters: $\delta$: thickness of the considered electrode; ${\epsilon }_{s}$: active material volume fraction; ${\eta }_{e}$: electrolyte overvoltages of the cell; ${\eta }_{\kappa }$: kinetic overvoltages of the cell; ${\eta }_{s}$: electronic overvoltages of the cell; ${\eta }_{\mathrm{\Omega }}$: global ohmic overvoltages of the cell; ${\phi }_{s}$: flux density of lithium in the particle; ${\tau }_{s}$: solid diffusion time constant

Superscripts and subscripts: $cell$: battery cell; $max$: maximum; $mean$: average value; $neg$: negative electrode; $pos$: positive electrode; $sep$: separator; $surf$: surface of the active material; $\infty$: infinite

1.   Introduction

Changes in the electricity generation mix of all European countries are pushing Transmission System Operators (TSO) to technically and commercially modify the mechanisms that ensure the operation of European’s interconnected continental grids. Using the flexibility sources to stabilize the grid is a mix of longterm solutions, such as grid infrastructures and generation units, and shortterm solutions, such as energy storage systems. Power plants are originally designed and built for an optimized operation at base load (which is the maximum power output of the power plant considering the maximum flame temperature, the ambient temperature, etc.). However, the generators are pushed today by TSO to provide more reserve capacity and more flexibility. To meet these challenges, thermal power plant manufacturers, e.g., General Electric, start several years ago to evaluate the benefits of integrating energy storage systems in power plants ^[1,2]. Besides, the Battery Energy Storage System (BESS) becomes more attractive with the drop of the battery cost either for Plant Integrated Battery Energy Storage System (PIBESS) or for standalone BESS which are connected to the electrical grid ^[3]. The description of the achievable services by the systems can be found in ^[3] for the standalone system or in ^[4,5] for the hybrid system. It mainly concerns the grid ancillary services or the enhancement of the operability. Due to its location inside the plant, the PIBESS is limited to the transmission grid services. However, this connection can propose other service opportunities as for the black start by increasing the reliability. The economic benefit of the solution is hard to calculate with the nonexistent ancillary services market for this hybridization. For instance, the only European grid code which introduced battery services is the UK in 2016 with the Enhanced Frequency Response (EFR) ^[6]. Obviously, the system will be cost-effective by performing multiple services, reducing the initial system cost and optimizing the battery control (aging, recharge, storage, etc.).

This work proposes a methodology for the sizing of the PIBESS to reduce the costs and increase the benefit of an integrated storage system through analytical optimization. As stated in ^[7], several existing methods are trying to optimize different indicators. This review gives us a good overview of common sizing techniques and indicators. The present paper will focus on one financial indicator, such as the return on investment, and one requirement indicator, such as enough reliability. The sizing method uses an analytical approach and is inspired by ^[8], which described two phases. The first is an analysis of meteorological data (more probabilistic approach). Then, in the second phase, an iteration loop has been computed to size the equipment. It integrates the equipment efficiency and the battery aging according to the set point and usage. Compared to this article, the methodology proposed here focuses on the second phase and integrates a more accurate electrical model of the Li-ion battery. Besides, ^[9] explains that a thermal model can be added for better precision of the cell performance and linked with the aging and electrical model as achieved in ^[10]. The objective function of the PIBESS methodology is to minimize the number of cells while meeting the grid code requirements. No Pareto front, as used in ^[11], is obtained since the second indicator is mandatory.

In this work, a system approach is needed for the battery model, in order to enable implementation in standard electrical engineering software (Saber, Matlab/Simulink, etc.) for analysis, identification, sizing, and online diagnosis. In our case, the battery model is intended to be implemented in the GE Power real-time simulator. The objective of this simulator is to create, modify, and optimize the control of the whole hybrid power plant. Therefore, the requirement for the storage system is a quite reduced-order model, configurable with supplier datasheet, with good accuracy on battery voltage and state of charge (>95%) and a fastcomputational time.

In electrical engineering, battery models are often based on equivalent electrical circuits. These models, referred as ECM (Equivalent Circuit Models), aim to represent the battery voltage behavior by means of electrical components. They usually consist of a series association of a voltage source standing for the battery open circuit voltage (OCV), an internal resistor reflecting the battery “high frequency” voltage response, and some parallel resistor-capacitor (RC) networks with different time constants, which account for the various battery internal phenomena, such as electrochemical kinetics, ion transport in the electrolyte, and mass transport within the electrode active materials ^[12]. The OCV source is related to the device state-of-charge (SOC), and other components are generally considered to be temperature, current and SOC dependent. The meaning of ‘high frequency’ mainly depends on the model order, and on the resolution time step. First order model, known as Thevenin model, is often used for SOC estimation and prediction, as in ^[13,14]. However, its single time constant makes it difficult to take into account both overvoltage due to ion transport, and OCV transient due to mass diffusion within electrode active particles. Accuracy and physical meaning can of course be enhanced by increasing the model order, as demonstrated in ^[15], in which first, second and third order models are compared. To avoid too high order models, another way to proceed consists in making use of specific elements, for a better description of diffusion process than the one provided by RC network. In ^[16], a fractional-order model is considered, involving constant phase elements instead of capacitors. In ^[17], both ion and mass transports are described by means of transmission lines, which enables high accuracy over a wide range of time, from one millisecond to several hundred of seconds. However, as representative of battery voltage behavior as ECM can be, this kind of global models can hardly account for battery limitations due to local phenomena, especially mass diffusion in solid phase that restricts the energy performances of the battery. Moreover, as can be seen in ^[15,17], accurate ECM requires a heavy characterization procedure for parameter extraction versus temperature, current and SOC, which is contrary to our purpose to make maximum use of the manufacturer’s data.

The main physics of lithium-ion batteries is governed by the following key processes: lithium diffusion within electrode active materials, electron conduction in electrodes, ion migration and diffusion within the electrolyte, and electrochemical kinetics of lithium insertion/de-insertion at electrode/electrolyte interface. The slow kinetics of some of these phenomena, especially the lithium transport in solid phase, limits performances of lithium-ion batteries, particularly in terms of high current regimes, as demonstrated in ^[18]. Moreover, as porous insertion electrodes are involved, these key processes are strongly coupled, which leads to inhomogeneous inner reactions inside the battery, and can give rise to unexpected local effects, such as lithium plating (metal lithium deposition at the negative electrode surface, close to the electrode/separator interface) ^[19]. Electrochemical models have been developed in order to describe locally the physics of lithium-ion cell operation, through coupled partial differential equations (PDE) involving space and time. Earlier significant works ^[20,21] led to an isothermal and pseudo-two dimensional (P2D) formulation, known presently as Newman’s model. Originally dedicated to a metal lithium cell ^[20], this P2D formulation was extended to dual lithium ion insertion cells ^[21], and more recently improved by introducing thermal heat transfer within the cell, temperature dependent parameters and electrothermal coupling ^[22,23]. Electrochemical lithium-ion battery models are knowledge models, close to the battery inner physics. As a result, they are obviously of great accuracy, and enable a deep understanding of battery internal limitations. However, they are hardly usable in a system approach, such as the one which is considered in the present article, and for which a battery model easy to handle is needed. Futhermore, electrochemical models require quite confidential parameters linked to the physical properties, the geometry and the quantity of the materials used for the battery cell design, parameters which are not available in manufacturer’s public data.

Nevertheless, the modeling principles and purposes associated with electrochemical models were extended in the last decade to models dedicated to system state estimation and diagnosis. The most popular approach is called ‘Single Particle Model’ (SPM), which is thoroughly presented in ^[24]. Derived from Newman’s model, the SPM is based on a simplifying assumption, according to which the lithium insertion or de-insertion reaction is supposed to be homogeneous along the electrode. Consequently, the electrode active particles can be reduced to an equivalent single particle, which results in decoupling lithium solid diffusion in active particles from mass and charge transports within the electrolyte, and enables therefore direct resolution of the solid diffusion PDE. More and more articles testify the growing interest of the automatic and control science community for the design of state observers based on this reduced electrochemical model. In ^[24], an extended Kalman filter is used for both SOC and surface insertion rate estimations. Nonlinear robust observer technics associated with SPM are investigated in ^[25,26]. In three previous works, the solid diffusion PDE is transformed into an ordinary differential equation (ODE) by means the finite difference method, prior to observer design. On the contrary, some studies as in ^[27] aim to directly design PDE-based observers. We could have chosen the standard SPM in this work. Nevertheless, in addition to manufacturer’s data, the presence of two electrodes imposes further characterization tests, such as the incremental capacity analysis or the differential voltage analysis, in order to extract both electrode parameters.

As our aim is to rely as much as possible on supplier datasheet for parameter extraction, the lithium-ion battery model proposed in this article called SPM-1E model (‘1E’ stands for ‘one electrode’), is a simplification of the SPM model, reduced to one electrode. The solid diffusion PDE is solved in Laplace domain and treated by means of Padé approximation, which enables to combine high level of accuracy and fast computation in the evaluation of surface insertion rate and OCV, compared to finite difference method ^[28]. To avoid the use of formal computation software for the calculation of Padé coefficients, a mathematical algorithm based on series developments is proposed and will be detailed. So, the main contributions of this paper are the development, the validation, and the implementation, in a sizing methodology, of a simplified electrochemical model configurable with the supplier datasheet. This work allows us to expedite the sizing of a Battery Energy Storage System with an affordable accuracy (around 95%) on the power and energy, and by restricting the input data to the supplier discharge curves.

The paper is organized in six sections which are as follows. Section 2 deals with the description of the SPM-1E model. In Section 3, the model parameters will be extracted for three types of lithium-ion cell (LTO, LFP and NMC). In section 4, experimental tests are carried out to validate the accuracy of the proposed model. In section 5, the model is applied in a sizing methodology to optimize the design of a battery energy storage regarding three different scenarios often encountered by power plant owner. Conclusion is presented in Section 6.

2.   SPM-1E model

The principle of the lithium-ion battery, named ‘rocking chair’, is to de-insert lithium ions from the first electrode structure, and to insert them into the second electrode structure. This operation is governed by transport processes, such as lithium solid diffusion within electrode active particles, lithium-ion diffusion and migration in the electrolyte, and electron conduction in electrodes. In particular, lithium solid diffusion within electrode active particles is the main limiting process, as regard to fast charging notably. It introduces large time constants (several hundred seconds, up to a few thousand seconds), has, therefore, a great influence on the cell voltage, and is responsible for relaxation phenomenon. In Newman’s electrochemical model, it is usually described through a 1D spherical diffusion PDE, with a boundary condition depending on the location variable within the electrode.

The SPM assumption reduces all active particles of an electrode to an equivalent single particle. This results for each electrode in a constant volume rate of current generation, being proportional to the cell current, which enables to decouple lithium solid diffusion in electrode particles from transport processes within the electrolyte. As demonstrated in ^[24], the cell voltage can be written as:

in this relation, subscripts pos, neg and sep stand for positive electrode, negative electrode, and separator, respectively. The electrode insertion rate y is the ratio between the lithium concentration ${C}_{s}$ in solid-phase (concentration of lithium inserted in the electrode active particles) and the maximum lithium concentration ${C}_{smax}$ in solid-phase:

electrode equilibrium potentials are denoted U and depend on the electrode insertion rate ${y}_{surf}$ at the solid-phase/electrolyte phase interface (i.e., at active particle surface). All cell overvoltages are represented by the symbol $\eta$, with the subscript $\kappa$ for kinetic overvoltages, the subscript $s$ for electronic overvoltages, and the subscript e for electrolyte overvoltages. In Eq 1, overvoltages are all of the same sign as the cell current ${I}_{cell}$, in generator convention (${I}_{cell}$ > 0 in discharge regime). They depend on cell physical properties (cell active area, electrode or separator thicknesses, active particle radii, volume fractions of solid and electrolyte phases, exchange current densities, electronic and ionic conductivities), and also on cell current.

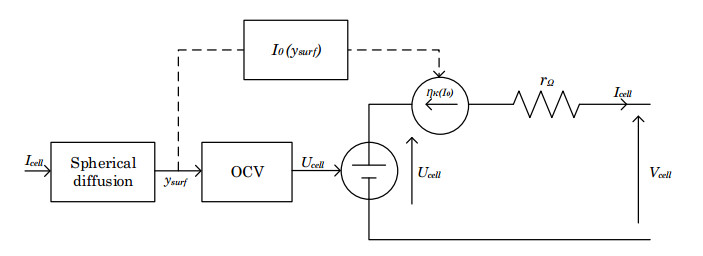
The model reduction introduced by the SPM assumption clearly enables easy handling and fast computation. However, this formulation still involves two electrodes, so that the parameter extraction associated with the SPM model is quite difficult for a common battery user, for whom only the supplier datasheets are generally available. The main objectives of the model proposed in this article are (ⅰ): include lithium solid diffusion and associated limitations, (ⅱ): extract parameters using only the information contained in the supplier curve. This model, called SPM-1E model and depicted in Figure 1, is based on the single electrode assumption, which forces to merge terms of same type in Eq 1: OCV (${U}_{pos}$ and ${U}_{neg}$), kinetic overvoltages (${\eta }_{\kappa, pos}$ and ${\eta }_{\kappa, neg}$), and ohmic overvoltages proportional to cell current (${\eta }_{s, pos}$, ${\eta }_{e, pos}$, ${\eta }_{s, neg}$, ${\eta }_{e, neg}$, and ${\eta }_{e, sep}$). The cell voltage is then simplified in:

where ${U}_{cell}$ is the cell open circuit voltage (OCV) and depends on solid diffusion dynamics, ${\eta }_{\kappa }$ is a global kinetic overvoltage, and ${\eta }_{\mathrm{\Omega }}$ is a global ohmic overvoltage. As for Newman’s or SPM models, lithium transport in the solid phase is treated by means of a 1D spherical diffusion PDE. The latter is solved in the Laplace domain and is evaluated using Padé approximation. Kinetic and ohmic overvoltages are modeled by Butler-Volmer’s law and Ohm’s law, respectively. Mathematical developments associated with our SPM-1E model formulation and parameter extraction procedure are detailed in the following sub-sections.

2.1.   Spherical diffusion transfer function

Lithium transport in active material particles constituting the electrode solid phase is assumed to be purely diffusive. Then, it is governed in a 1D approach, as described in ^[18]:

where ${C}_{s}$ is the lithium concentration in the particle, ${\phi }_{s}$ is the flux density of lithium in the particle, r stands for the radial coordinate, t is the time, and ${D}_{s}$ represents the solid diffusion coefficient. Boundary conditions at the particle center (r = 0) and at particle surface (r = ${R}_{s}$, ${R}_{s}$ being the particle radius) are of Neumann type:

with F the Faraday’s constant (unit: C.mol^-1), ${j}^{Li}$ the volume rate of Li⁺ current generation (unit: A.m^-3), and ${a}_{s}$ the active surface per volume unit (unit: m^-1), which can be expressed versus the particle radius ${R}_{s}$ and the active material volume fraction ${\epsilon }_{s}$ as:

under the assumption of a constant diffusion coefficient ${D}_{s}$, the form of the PDE that controls the lithium transport equation in the solid phase can be simplified in the following:

Then, considering a uniform initial profile of lithium concentration in the solid phase (${C}_{s}\left(0, r\right) = {C}_{s0}$), which is simply obtained by taking the initial instant during a total relaxation phase (no cell current, no lithium flux density within the particle), Laplace transform of Eq 7 leads to:

where $s$ is the Laplace variable, and ${{\tilde C}_{s}}\left(\mathrm{s}, \mathrm{r}\right)$ is the Laplace transform of ${C}_{s}\left(t, r\right)-{C}_{s0}$. Using boundary conditions given in Eq 5, the solution of Eq 8, which represents the transfer function in the Laplace domain defining the lithium concentration variation ${{\tilde C}_{s}}\left(\mathrm{s}, \mathrm{r}\right)$ in response to an input excitation ${j}^{Li}\left(s\right)$, is:

In particular, the lithium concentration at the solid phase/electrolyte phase interface is required for the calculation of electrode equilibrium potentials. This concentration is obtained at r = ${ R}_{s}$ in Eq 10, which leads to:

One will meet this result in ^[29], expressed using exponential function in ^[28], and formulated as a harmonic impedance in ^[30]. Then, considering the electrode maximum lithium concentration ${C}_{smax}$ in a solid-phase, the lithium insertion rate variation at particle surface can be expressed as:

At last, it is interesting to notice that the solid diffusion transfer function ${F}_{surf}\left(s\right)$ is equivalent to 1/s when s = 0. In other words, the transfer function behaves as a pure integrator in long terms.

2.2.   Padé approximation

As previously described in previous works, such as ^[28,31,32], the transcendental transfer function given by Eq 10 can be approximated using the Padé method. It consists in approaching ${F}_{surf}\left(s\right)$ by a polynomial rational fraction as follows:

where n is the order of polynomials N and D. The gain K is the limit value of ${s.F}_{surf}\left(s\right)$ in s = 0 (i.e., in long terms), it is, therefore, equal to 1. The 2n other coefficients are determined by solving the following 2n-equation system:

2.2.1.   Successive derivative values of $s.{F}_{surf}\left(s\right)$ in s = 0

The main resolution issue with such a system lies in the calculation of all the k^th derivative values of $s.{F}_{surf}\left(s\right)$ in s = 0. Generally, articles dealing with Padé approximation of the transfer function associated with 1D spherical diffusion give, as in ^[28], explicit details about Padé coefficients up to only the 4^th-order. We propose hereafter a mathematical method based on series developments, which enables to quickly calculate Padé coefficients whatever the approximation order, without formal computation software or any other specific mathematical tool. Let H_k be the k^th derivative value of $s.{F}_{surf}\left(s\right)$ in s = 0:

The calculation of H_k can be quite easily handled by considering series developments of hyperbolic sine and cosine. An equivalent expression for ${F}_{surf}$ can then be formulated as follows:

Then, by writing:

it can be established:

with the following definition for the coefficients $Z\left(k, j\right)$:

in regard to the general form of the coefficients of Ak and Bk (see Eq 15), it can be noticed that H_k (i.e., the k^th derivative value of $s.{F}_{surf}\left(s\right)$ for s = 0) is proportional to ${\tau }_{s}^{k}$.

2.2.2.   Determination of the approximate transfer function

The calculation of the approximate transfer function can be achieved in the same way. It results in the following 2n-equation linear system:

We give in the following equation the general matrix form of this linear system for n = 3 (i.e., for a 4-order approximate transfer function), and in Table 1 the resulting coefficients up to n = 3 are detailed. Note that the 1-order Pade approximate transfer function is reduced to the pure integrator included within ${F}_{surf}$.

2.2.3.   Comparison between exact and approximate transfer functions

Integrating Eq 9 over the spherical particle volume leads to:

The left hand of this equation represents the volume mean value of lithium concentration within the active particle, and the right member is, as expected, a pure integration of the input constraint at the particle surface. As a result, the volume mean value of lithium insertion rate variation within the active particle is given in the Laplace domain by:

As mentioned before, this quantity represents the long-term response behavior of the spherical diffusion transfer function. It can be easily established that regardless of the order it is also the case of the Padé approximate transfer function. Moreover, by using Eq 15 for the expression of ${F}_{surf}$, one can demonstrate that the real part of ${F}_{surf}$ converges towards ${A}_{1}-{B}_{1}$ at low frequency. Similarly, using Eq 12 enables to show that the real part of the Padé approximate transfer function converges towards ${a}_{1}-{b}_{1}$ at low frequency (if n ≥ 1). Thus, in any case, the limit values of all transfer function real parts in $\omega$ = 0 are equal to H₁, which can be written as follows:

with $\omega$ the pulsation, and i the pure imaginary number of module 1 (${i}^{2} = -1$). As a conclusion, the long-term asymptotic response ${y}_{surf, \mathrm{\infty }}$ of the spherical diffusion to an input step occurring at t = 0 is:

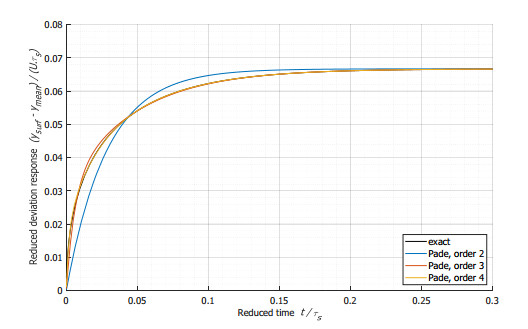
where U is the input step amplitude, and ${y}_{0}$ is the initial insertion rate. We compare in Figure 2 step deviation responses $∆{y}_{surf} = {y}_{surf}-{y}_{mean}$ of the spherical solid diffusion. Curves are reduced in amplitude by the scale factor ${\tau }_{s}.U$(U being the step amplitude), and are drawn versus reduced time $t/{\tau }_{s}$. The exact response (in black) has been computed by means of a finite element resolution method. Its 99.9% time response, above which this transfer function behaves as a pure integrator, is about ${\tau }_{s}/3$. As can be expected from the manner in which the Padé coefficients are determined (in s = 0, i.e., under long-term conditions), short-term responses of the Padé approximate transfer functions are quite inaccurate. Nevertheless, this “short-term” notion hugely depends on the approximation order. Hence, for the 2-order approximation function, the time above which the relative error between approximate and exact responses becomes lower than 0.5% is about $0.22\mathrm{*}{\tau }_{s}$. This characteristic time is reduced to $0.01\mathrm{*}{\tau }_{s}$ for the 4-order approximation function, and to $0.003\mathrm{*}{\tau }_{s}$ for the 6-order approximation function.

2.2.4.   Application to SPM models

In generator convention (${I}_{cell}>0$ in discharge regime), the sign of the volume rate of Li⁺ current generation ${j}^{Li}$ is the same as ${I}_{cell}$ sign for the negative electrode, and the opposite of ${I}_{cell}$ sign for the positive electrode. As previously mentioned, the SPM assumption results in a constant ${j}^{Li}$, which can be proportionally expressed versus cell current as follows:

where ${A}_{cell}$ is the cell active surface, and $\delta$ is the thickness of the considered electrode. Then, considering the electrode maximum lithium concentration ${C}_{smax}$ in the solid phase, and the related electrode capacity ${Q}_{max} = {\epsilon }_{s}.{A}_{cell}.\delta.{C}_{smax}.F/3600$ (unit Ah), the lithium insertion rate variation at particle surface can be expressed as:

For our SPM-1E model, we will consider the negative electrode convention, and the cell capacity ${Q}_{cell}$ instead of electrode capacities, which are not specified in the manufacturer datasheet. The equivalent insertion rate ${y}_{surf}$ is then the state of charge at particle surface (as well as ${y}_{mean}$ is the cell state of charge), and its variation versus current is:

2.3.   Model parameters extraction

Our 1-electrode SPM model (see Eq 3 and Figure 1) requires five parameters. All electronic and electrolytic voltage drops are modeled according to the Ohm’s law, and lumped into a single ohmic resistance ${r}_{\mathrm{\Omega }}$:

Kinetic overvoltages are defined through the Butler-Volmer’s law, by means of an exchange current ${I}_{0}$, as shown below:

where ${U}_{T}$ is the thermal voltage $RT/F$ (R: gas constant, F: Faraday’s constant, T: temperature). Finally, the cell instantaneous OCV is computed using on one hand the spherical diffusion transfer function that requires a solid diffusion time constant ${\tau }_{s}$ and a cell capacity ${Q}_{cell}$, and on the other hand a curve defining the cell OCV versus surface insertion rate.

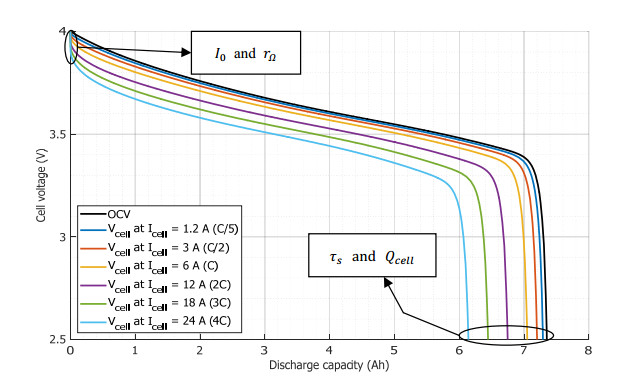
The aim of the parameter extraction procedure detailed hereafter is to use only the of constant current discharge characteristics provided in manufacturer’s datasheet, as shown in Figure 3 and computed using K. Smith and C.-Y. Wang data ^[18]. The two overvoltage parameters can be identified at the beginning of the discharge (allowing no voltage decrease due to OCV variation), by measuring the ‘sudden’ voltage drops linked to the application of the discharge current. For both spherical diffusion parameters, the end of the discharge zone is used, where the useful capacity of the device for the considered current can be measured. Since the curves are almost vertical, there is no need to correct them by adding their initial voltage drop.

Overvoltage parameters ${I}_{0}$ and ${r}_{\mathrm{\Omega }}$ can be identified on two constant current discharge curves, one at ${I}_{cell1}$, the other at ${I}_{cell2}$. These currents should be chosen as far as possible to obtain a correct cell overvoltages representation in a wide current range. Then, the following non-linear system should be solved, for example by means of an iterative method:

Of course, more than two discharge curves can be used, and the parameters can be determined by means of an optimization algorithm, such as the least-squares method.

The spherical diffusion parameters are extracted from the end of discharge data. In this area, the cell usable capacity for a given discharge current can be easily identified. Moreover, the end of discharge is often obtained at a time greater than the characteristic time (as previously mentioned, about ${\tau }_{s}/3$ for a spherical diffusion) above which the diffusion phenomenon has reached its linear asymptotic evolution given by Eq 24. So, under this assumption and as far as the end of discharge is defined by ${y}_{surf} = 0$, the difference between ${Q}_{u1}$ and ${Q}_{u2}$, cell usable capacities (in Ah) for discharge currents ${I}_{cell1}$ and ${I}_{cell2}$ respectively, is given by:

which enables the determination of the solid diffusion time constant ${\tau }_{s}$. Then, the cell capacity ${Q}_{cell}$ can be identified by using Eq 24, this yields:

which supposes that the cell is initially fully charged (${y}_{0}$ = 1). As previously stated for overvoltage parameters, the two chosen discharge currents should be as far as possible to correctly represent the cell diffusion limits in a wide current range. However, this choice must result in a diffusion time constant consistent with the assumption about the diffusion regime, which is supposed to have reached its asymptotic evolution during the two chosen discharge characteristics.

Finally, by running the solid diffusion model and adding ohmic and kinetic overvoltages to the voltage curve obtained during a constant current discharge, the OCV can be extracted (the black curve added in Figure 3, together with typical discharge curves) as a function of insertion rate (i.e., the state of charge). For this purpose, a low C-rate discharge curve should be preferred. In the case of a very weak C-rate, one can even consider the voltage curve without overvoltage correction.

3.   Configuration of the model for LTO 40 Ah cell

An LTO cell of 40 Ah capacity is used to illustrate the configuration method. The datasheet is detailed in Table 2 and the discharge curves are obtained on a test bench, using a climatic chamber for cell temperature setting. A Tektronix TDS5034B oscilloscope is used for cell voltage acquisition, and an H & H NL1V8C80 electronic load is used for discharge current control. Constant current discharge curves at 20 ℃ are shown in Figure 4.

Diffusion parameters ${\tau }_{s}$ and ${Q}_{cell}$:

Considering 80 A and 1 A discharge curves, associated usable capacities are ${Q}_{u1}$ = 39.61 Ah and ${Q}_{u2}$ = 43.14 Ah, respectively. According to Eqs 31 and 32, these leads to:

Discharge durations are 1782 s at 80 A, and greater at 1 A, both of which are greater than ${\tau }_{s}/3 = 804 s$.

Determination of the OCV:

In the case of LTO or LFP cells, for which OCV greatly varies close to SoC = 1, the identification of overvoltage parameters at the very beginning of the discharge may be quite an issue. In this case, it is simpler to directly consider a low C-rate discharge curve as OCV, and to run the solid diffusion model with previously extracted parameters ${Q}_{cell}$ and ${\tau }_{s}$, to evaluate the corresponding surface insertion rate ${y}_{surf}$. We proceeded this way for the present LTO 40 Ah cell, by using the C/40 discharge curve.

Overvoltage parameters:

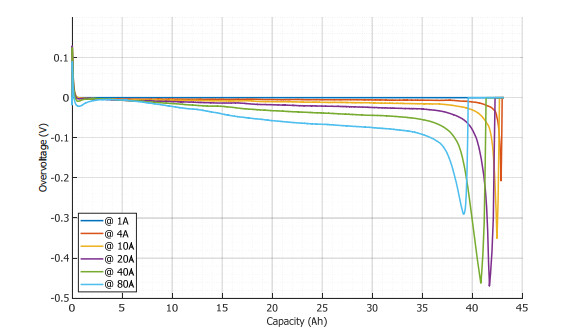
The overvoltage parameters need to be acquired with the immediate voltage drop of the cell. Indeed, the ohmic and the charge transfer voltage losses appear in the first seconds and are modeled with immediate loss in our SPM-1E model. Figure 5 shows the voltage drops resulting from the difference between the cell OCV including the lithium diffusion, and the measured cell voltage ${V}_{cell}$. As it can be seen for the LTO cell, the difference has an important variation from 10 mV to 470 mV for the same discharge current. In other words, the voltage drop is not constant due to the variation of the exchange current ${I}_{0}$ in Eq 30. Indeed, the assumption made so far is a constant kinetic voltage drop and a constant exchange current, which is actually a function of the lithium concentration. This depends on the Li-ion technology, for instance, the same test on LFP cells shows less overvoltage variation (from 7 mV to 80 mV). The important point in the model is to have an accurate voltage drop depending on the current and the state of charge. Later in the document, a comparison between two models (with constant ${I}_{0}$ and with ${I}_{0} = f\left({C}_{s}\right)$) is developed.

The choice of the voltage drops is difficult due to the huge variation, a mean value such as at 30 Ah can be considered as a correct choice:

Using the previous equation system, the parameters found by iteration are ${I}_{0} = 44 A$ and ${r}_{\mathrm{\Omega }} = 74 \mu \mathrm{\Omega }$.

Exchange current function:

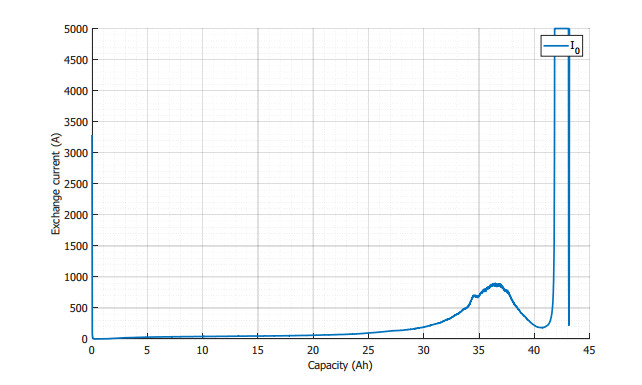
The assumption made so far is a constant kinetic voltage drop and a constant exchange current ${I}_{0}$. However, the exchange current is a function of the lithium concentration. The improvement proposed is to extract the function ${I}_{0} = f\left({C}_{s}\right)$ drawn in Figure 6 and to implement it in the model as depicted in Figure 7. For the extraction, the Eq 30 need to be inverted to separate the exchange current from the other parameters:

A high limit of ${I}_{0}$ is set for incoherent values, for instance at ${I}_{0} = 5000 A$ in the case of the LTO cell.

The enhanced model is presented in Figure 7 and uses the function ${I}_{0} = f\left({C}_{s}\right)$ to modulate the kinetic overvoltage of the cell.

4.   Model assessment

The model will be assessed on three new commercial cells indexed in the next table. The tests are carried out in a climatic chamber at 20 ℃ with a Tektronix TDS5034B oscilloscope, a current probe TCP303 associated with an amplifier TCPA300. The cells are charged each time with the same electrical source (Höcherl & Hackl NL Series) to be in the same initial condition for each test.

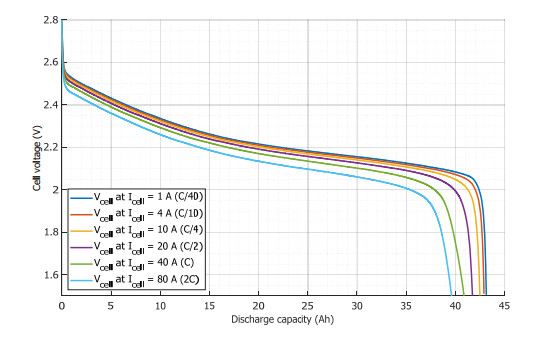
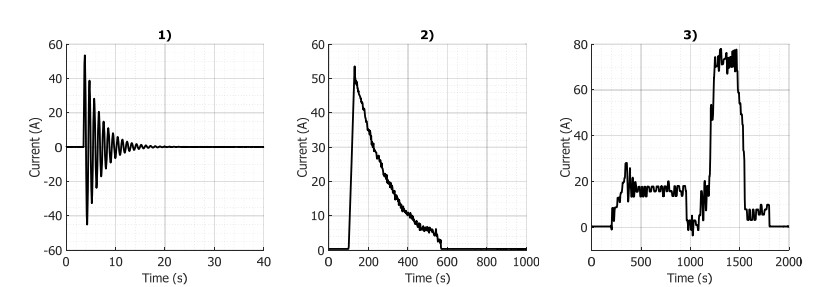
It may be noticed in Figure 4 that the experimental curves have a capacity fade not proportional to the discharge current. This behavior can be explained with the limiting electrode at the end of the discharge. For instance, the capacity difference between C/4 and C/2 is around 0.76 Ah, between C/2 and C is 0.86 Ah and between C and 2 C is 1.26 Ah. At low (respectively high) current the limiting electrode is the negative one (respectively positive), which gives a different behavior. This may be due to the non-linearity of the solid diffusion coefficient, ${D}_{s}$ which depends on lithium concentration. The SPM-1E model cannot logically integrate the behavior of the two electrodes. The assessment of the SPM-1E model is achieved on a current interval as large as possible, to describe the low and high current, as well as on three hybrid profile discharge curves (Figure 8). The small-signal stability concerns the control of reactive power throughout small disturbances on the grid. The frequency response concerns the control of active power throughout frequency variation. The pattern used for the test is the case when the power plant produces a hybrid frequency response. The black start relates to the capability of a power plant to start from its own means, and to connect to the dead grid to re-energize it. Only the Load Commutated Inverter power consumption is used for the test without permanent auxiliary loads. All services (profile, connection, hybridization, etc.) are detailed in previous work ^[4,5]. The profiles are adapted in term of power or energy according to the battery capabilities.

4.1.   Constant current comparison

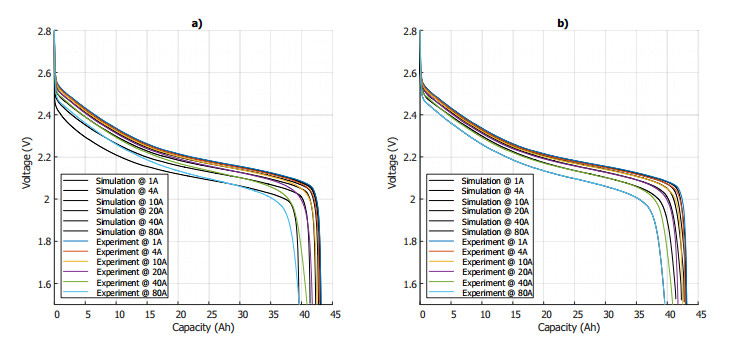
The parameters are calculated in the previous section for the LTO cell. A large range of current is chosen to assess the accuracy of the model. The comparison points are the capacity and the max voltage difference. Both the model with ${I}_{0}$ constant and the model with ${I}_{0}$ variable are assessed. Figure 9 plots the curves simulated with the model (in black) and the voltage curves measured on the test bench (in color). The left screen compares the first model with a constant exchange current (${I}_{0} = constant$) and the right screen compares the improved model (${I}_{0} = f\left({C}_{s}\right)$).

The comparison between the experiment and simulation exhibits quite good agreement on the energy estimation. However the curves still show some issues on the voltage. This can be linked to several points:

● Firstly, the OCV determination due to the specific shape of the OCV at low current which does not fit correctly at higher current

● Secondly, the non-constant voltage losses between discharge start and end can be corrected by model enhancement (${I}_{0} = f\left({C}_{s}\right)$)

● Finally, the non-proportionality of the capacity fade, indeed, the error at the end of the discharge is caused by the convergence towards two different capacity points for the same current discharge (one from the simulation and the other from the experiment)

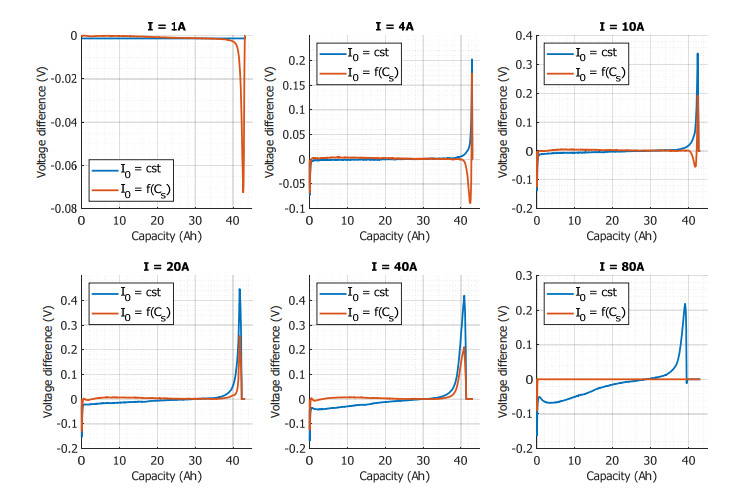
The error between the simulation and the experiment is illustrated in Table 3. It is important to notice that the maximum error in the capacity fade is around 1.3%. In other words, the model accuracy is sufficient for the detailed sizing of the PI-BESS. However, the error on the voltage may appear important. This error occurs due to the non-proportionality of the capacity fade and only at the end of the discharge (see Figure 10). Apart from the end of the discharge, the model has good accuracy with a maximum error of 2.8%.

Figure 10 shows the voltage difference between the simulation and the experiment during the discharge at different currents. The overall shape of all subplot shows a peak error at the end of the discharge, which is much higher than the average error during the discharge.

Concerning the other types of lithium-ion cell tested, the NMC technology have quite similar trend than the LTO cell with the same issues and the same solution. The maximum voltage error is around 13% and the maximum energy error is less than 5%. However, the LFP technology has better results. The variation of the exchange current ${I}_{0}$ is not important (from 10A to 40A) and allows a good fitting with the experimental tests for both models. The maximum voltage error is less than 6% and the maximum energy error is around 1%.

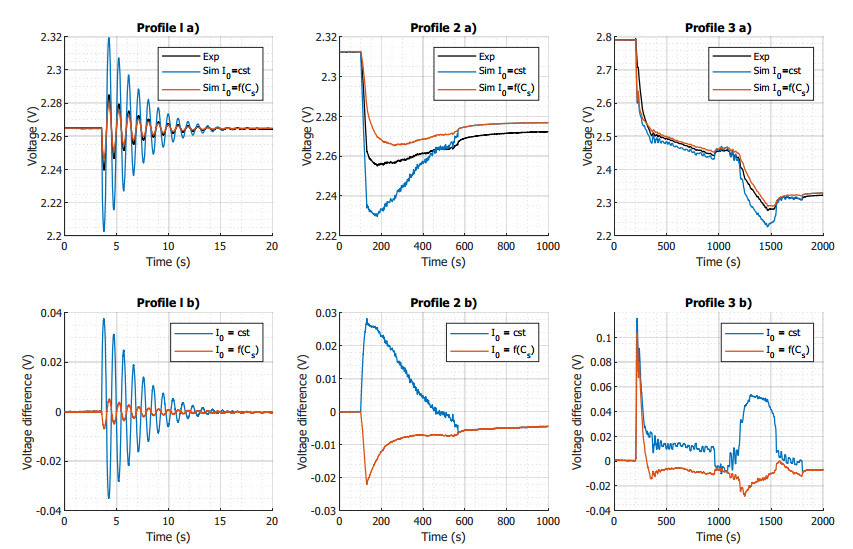
4.2.   Profile comparison

It can be noticed in Figure 11 that the behaviour of the simulation is similar to the experiment. A comparison with profiles gives better results than the previous section because they are performed at a non-zero SoC. In fact, by avoiding the end-of-discharge areas, the model shows good results. The willingness to perform these tests at an SoC similar to the real case seems logical for a sizing. A 50% SoC is chosen for profiles 1 and 2, while a 100% SoC is used for profile 3. Table 5 shows the maximum difference in the voltage and in the capacity. The voltage difference observed at the final state result in a slightly false estimation of the cell capacity, but the accuracy is still around 0.2% for both models. The maximum voltage difference is around 100mV achieved on the 3^rd profile at the beginning of the test. As can be seen from Figure 11, the maximum error is reached in almost all cases at high currents (greater than 50 A) and remains less than 5%.

Identically to the constant current comparison, the profile comparison shows enough accuracy for the PI-BESS applications. The causes of the error observed in this section have been already pointed out in the previous section. The results obtained perform as expected.

5.   Sizing methodology

The SPM-1E model should be used for the detailed design. The analytical methodology presented will focus on the sizing of the battery cells by integrating the cables, the transformers and the converter losses. An aging model or aging curves are also needed for better accuracy of the sizing. The choice of standard aging curves has been made in this work. Of course, more detailed aging model can be integrated to have more accurate results. Finally, ^[9] explains that a thermal model can be added for better accuracy of the cell performance and linked with the aging and electrical model. However, no thermal model is added to the sizing methodology due to the constant temperature assumption made in the SPM-1E model.

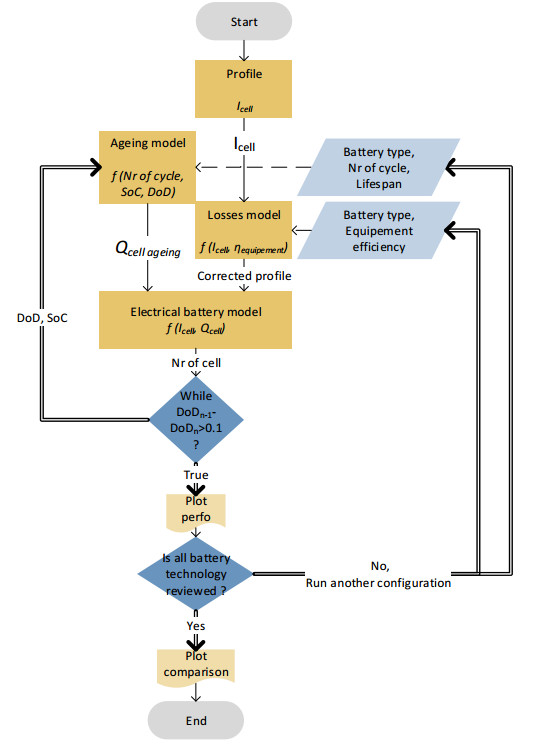
As explained in ^[7], the optimization of the detailed sizing can be achieved by defining performance indicators. The indicators used in this method are a financial indicator, the BESS cost and a technical indicator quantified by binary variable, whether the battery system meets the requirement or not. The financial indicator will focus on the minimization of the cost and thus of the number of cells. Concerning the technical indicator, the aim is to provide the power to ensure the desired profile. For instance, the electrical grid requirement to provide black start service with a storage system is to have enough energy to repeat three times the procedure. In that case, the methodology, presented in Figure 12, will have in input three times the standard black start profile (technical indicator) and the output of the methodology will optimize the minimum energy and power to pass the profile (financial indicator). The other indicators as the safety, the weight and the volume do not have a key role due to the stationary nature of the application.

The flow chart of the methodology is shown in Figure 12. It accepts as the only input the profile corrected for energy conversion and transmission losses. The other parameters, which are variable during optimization, are aged capacity, as a function of SoC and DoD, minimized cell number, cell technology, and system efficiency. It is possible to add constraints on cell voltage to adapt to suppliers “pick and drop” solutions or on the physical limits of the equipment (voltage, current, power, etc.). The output data of the methodology are the number of cells, the optimal SoC, the expected DoD, the expected lifetime, and the energy-power couple of the battery system calculated using the C-rate of the cell.

The sizing methodology includes two iteration loops. The outer loop (right side) changes equipment parameters, as battery characteristics, and battery power output. This loop is activated only to compare different technologies (NMC, LFP, LTO, etc) or different connections by modifying the losses and efficiency of the storage system. The common point of each comparison is only the input profile. The inner loop (left side) optimizes the size of the battery, increasing or reducing the number of elements. The first steps of the inner loop must estimate the capacity fade during the desired service life with the aging model. The calendar aging is calculated using the SoC parameter returned by the electrical model and the cyclic aging is calculated based on the frequency of the service use, i.e. once a week. These aging factors are calculated by fitting the supplier’s datasheet to a simple aging model as described in ^[33]. The impaired cell capacity and the corrected profile are the inputs of the SPM-1E model as described previously. The electrical model is run to optimize the number of cells and to calculate the optimized SoC or DoD. The algorithm iteration is stopped when DoD change (Depth of Discharge) is less than 0.1%. The benefit of using this method is that it takes into account the system’s capabilities at different currents and lifetimes, and it allows the average values provided by the supplier in the datasheet to be dispensed with. It also allows a better fitting of the cell and facilitates the comparison of different cell technologies (NMC, LFP, LTO) and cell types (energy or power).

The flow chart of the sizing methodology is introduced below:

This methodology is run for the black start service and the results are compared in Table 6 and also in the Figure 13:

The sizing methodology shows that the NMC cell is the best choice in terms of costs and technical performances. The results for the other profiles are different due to the medium energy-power nature of the NMC cell and the power behavior of the profiles.

In a nutshell, the Li-ion battery sizing of a 10 MW black start (as shown in Figure 13) converges towards three solutions:

● A storage system with an LFP cell of 5.5 MWh and 30 MW. The power limiting system will be the power converter around 10 MW (maximum power of the profile). The battery will be loaded around 95% of SoC and will discharge entirely each time (at the end of the three-consecutive black start profiles). The lifespan is around 10 years for a cost of about ＄2 M.

● A storage system with an LTO cell of 5.5 MWh and 55 MW. The power limiting system will be the power converter around 10 MW (maximum power of the profile). The battery will be loaded around 98% of SoC and will discharge entirely each time. The lifespan is around 10 years for a cost of about ＄1.9 M.

● A storage system with an NMC cell of 5.5 MWh and 27.5 MW. The power limiting system will be the power converter around 10 MW (maximum power of the profile). The battery will be loaded around 92% of SoC and will discharge around 87%. The lifespan is around 10 years for a cost of about ＄1.8 M.

6.   Conclusions

The equations described by Newman 25 years ago are the basis of the new electrochemical model SPM-1E. This model is also inspired by the single-particle model which describes the average behaviour of the electrodes. The clearly described SPM-1E model can be configured through the supplier’s constant current discharge curves. The configuration method is explained for each parameter of the model. Moreover, the model assessment is conducted on three types of cells, i.e. the LTO, the NMC and the LFP technologies. It exposes some modelling issues, mainly on the voltage cell at the end of the charge and the discharge. On the one hand, these issues are related to the assumptions, on the other hand, it also originate from the nature of the Newman model. However, the accuracy of the model is still convenient for a battery sizing or an electrical simulation.

Taking into account the performance and aging of the cell, equipment losses, and different technologies, a detailed sizing method is introduced. More precise aging model and losses model must be integrated to improve the sizing results. However, the methodology proposes several battery configurations depending on the battery type and characteristics, PI-BESS profile, minimum lifespan and the system efficiency. Each time, the sizing is optimized according to the arrangement of the supplier cells.

Acknowledgments

This work was supported by FLEXITRANSTORE project and has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 774407.

Conflict of interest

The authors declare no conflict of interest.

Author contributions

FK wrote the manuscript, provided data for Tables 3, 4 and 5 and conducted all the tests on bench, SR created the battery model (section 2 and 3). All authors reviewed the final manuscript.