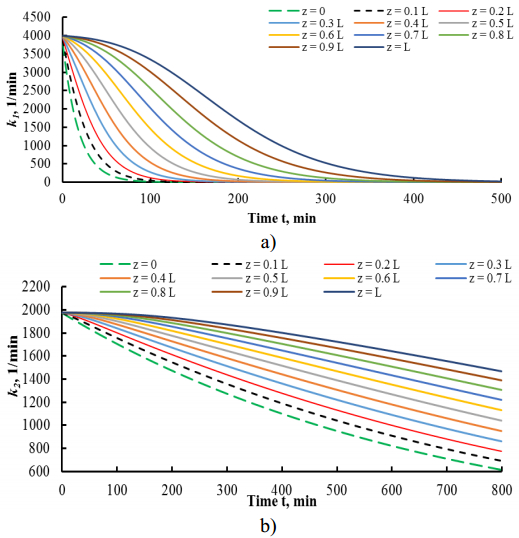
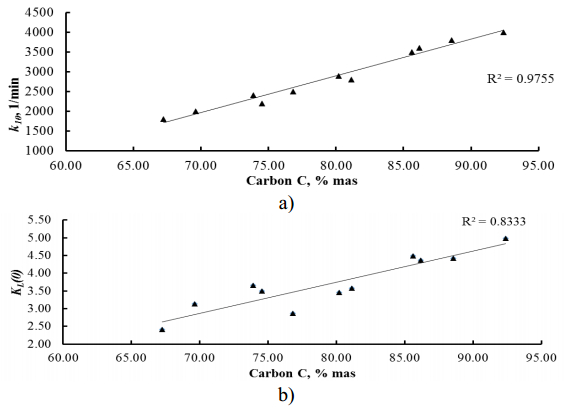
Coals of different rank were studied in order to characterize their activity to ozone decomposition and changes of their properties at interaction with ozone. Effects of coal rank on their reactivity to ozone were described by means of kinetic modeling. To this end, a model was proposed for evaluation of kinetic parameters describing coals activity to ozone. This model considers a case when coals surface properties change during interaction with ozone (deactivation processes). Two types of active sites (zones at the surface that are able to decompose ozone) were introduced in the model differing by their deactivation rates. Activity of sites that are being deactivated at relatively higher rate increases with rank from 2400 1/min for lignite to 4000 1/min for anthracite. Such dependence is related to increase of micropores share in coals structure that grows from lignites to anthracites. Parameter characterizing initial total activity of coals to ozone decomposition also depends on rank by linear trend and vary between 2.40 for lignites up to 4.98 for anthracite. The proposed model could further be used in studies of coals oxidation processes and tendency to destruction under the weathering and oxidation conditions.
1.
Introduction
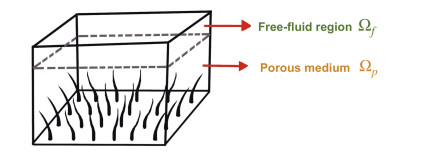
Fluid flow problems have considerable attention from researchers and appear in many applications such as engineering, industry, biomedical sciences and other areas. The fluid flow problems are investigated in both theoretical and applied research, among which is the study of flow through a free-fluid domain and an adjacent porous medium. For example, Basirata et al. [1] studied the CO2 gas flow in a porous medium and free air above it. Oangwatcharaparkan and Wuttanachamsri [2] studied the fluid flow in a periciliary layer (PCL) in the human respiratory system where the mucus layer was on the top of a porous layer. In this research, we focus on fluid flow problems in which the fluid is moved by self-propelled solid phases rather than a pressure gradient. That is, the movement of solids affects the fluid flow whether the fluid is in the same layer as the solid phases or above the solid phases. An example domain that illustrates the regions of interest is represented in Figure 1.
Figure 1 shows a sampling domain consisting of two regions: the layer composed of fluid and self-propelled solid phases, which is considered as a porous medium, Ωp, and a free-fluid region, Ωf, residing on the porous medium. In this study, we consider a macroscopic flow where a bundle of solid phases is considered instead of a single self-propelled solid. The locomotion of solids affects the movement of fluids in the nearby areas. If fluid flows through different domains, then mathematical models are also distinct. That is, the equations for the flow above the porous medium and flow in the porous domain are different.
There are several mathematical models used to describe problems of this type [3,4,5,6,7,8,9,10,11]. Khanafer et al. [3] used Darcy's Law and Brinkman-extended Darcy to investigate the fluid flow inside the hollow fiber bundle of an artificial lung and applied the Navier-Stokes equation for the fluid flow outside the fiber bundle. Ly et al. [4] investigated the problem of fluid flow in coupling a free fluid domain and a porous medium using the Stokes and Darcy equations, respectively. Wuttanachamsri and Schreyer [5] used the Stokes-Brinkman equations to compute the fluid velocities due to the self-propelled solid phases in a three-dimensional domain. Poopra and Wuttanachamsri [6] considered the fluid flow in the periciliary layer (PCL) in human lungs by using the Stokes-Brinkman equations with the Beavers and Joseph boundary condition. Wuttanachamsri [7] used Stokes-Brinkman equations in one dimension with the Stefan problem to estimate the free interface between a porous medium and an adjacent free-fluid region. The well-posedness of the system of the Stokes-Brinkman equations is also provided for both moving or static solid phase [12,13,14,15,16]. For the study of a static solid phase, Ingram [12] applied a finite element discretization to the Brinkman equation and demonstrated that the discretized problem was well-posed. Angot [13] studied the well-posedness of the Stokes-Brinkman and Stokes-Darcy with new jump interface conditions. Chamsri [14] showed the well-posedness of the Stokes-Brinkman model for the case of moving solid phase, while the porosity was assumed to be a constant.
Unlike the usual problems, in this research, we use generalized Stokes-Brinkman equations, where the Brinkman model is developed from the Hybrid Mixture Theory (HMT) [17]. The HMT is a technique for upscaling a multiphase flow by applying an averaging theorem to a microscale equation to obtain a macroscale equation [18,19]. The macroscopic Brinkman equation is distinct from the models in the above literature because it is derived from the conservation of momentum, where the porosity in the equation is considered as a function of space. Therefore, the porosity is subject to a derivative operator, while the porosity in the Brinkman model in the available research is outside the derivative, although the porosity has been used as a function of space. Our model, the macroscopic Brinkman model, can be used for a bundle of self-propelled solid phases instead of a single solid for fluid flow in a porous medium. In addition, we derive the generalized Stokes equation to apply to the incompressible slow flow in the domain of the free-fluid region next to the porous medium. Extra terms appearing in the generalized Stokes and macroscale Brinkman equations aid to match shear stress at the free-fluid/porous-medium interface. Since our model differs from typical Stokes-Brinkman equations in available research, the well-posedness of the generalized Stokes-Brinkman equations in a macroscopic scale when the fluid is moved by self-propelled solid phases is provided, and the permeability in the model is considered as a second-order tensor, not just a constant.
In Section 2, we derive the generalized Stokes-Brinkman equations. In order to present the well-posedness of the discretized form of the mathematical model using a mixed finite element technique, in Section 3, we present the weak formulation of the governing equations as well as the discretized form of the generalized Stokes-Brinkman equations. In Section 4, the continuity and coercivity of linear and bilinear functionals in the discretized system of equations are presented. The well-posedness of the generalized Stokes-Brinkman equations is illustrated in Section 5. The conclusion is drawn in Section 6. The fundamental definitions, theorems and lemmas proved in available literature and books, which are used in the proof of the well-posedness of the discretized equations, are provided in the Appendix.
2.
Generalized Stokes-Brinkman equations
In this section, we present the derivation of our governing equations. For the generalized Stokes equation, we start with the generalized Navier-Stokes equation and then use a nondimensionalization method to obtain the generalized Stokes equation. This is shown in Section 2.1. To derive the Brinkman equation, we begin with a momentum equation obtained from Hybrid Mixture Theory (HMT) [19], an upscaling technique, and then use a nondimensionalization approach to have a macroscopic model in a porous medium, which is illustrated in Section 2.2. We rewrite our governing equations in Section 2.3 in order to summarize and use them in the next sections.
2.1. Derivation of generalized Stokes equation
To obtain the generalized Stokes equation, we start with the generalized Navier-Stokes equation, which is attained from substituting a stress tensor, developed from entropy inequality holding near equilibrium for a viscous fluid, into a momentum equation. The generalized Navier-Stokes equation is [20]
where ρ is density, t is time, u is the velocity, p is pressure, λ is a constant, μ is the dynamic viscosity, and g is gravity. The generalized Navier-Stokes equation, Eq (2.1), is normalized with dimensionless variables, and we get
where the characteristic parameter L is the characteristic length; f is the characteristic frequency; u0 is the characteristic speed; p0 is the reference pressure; g0 is the gravitational acceleration. Multiplying Eq (2.2) by L2μu0 on both sides, we have
Next, we calculate the coefficients in Eq (2.3), where the values of the characteristic variables and other variables in International System (SI) units are shown in Table 1. The characteristic length is the highest length of cilia in the respiratory system [21], the reference f is the frequency of cilia beat in the human respiratory tract [22], the characteristic velocity u0 is the maximum speed of cilia for the effective stroke at temperature 37∘C, the reference pressure p0 is the pressure in the human respiratory tract, which is about one [23], g0 is the Earth's gravity, and ρ and μ are the density of water and dynamic viscosity at 37∘C, respectively. The constant λ is set equal to zero. The values of the coefficients are shown in Table 2.
From Table 2, the coefficients of the first two terms in Eq (2.3) are comparatively small compared with the others. Therefore, the unsteady and nonlinear terms in the equation are neglected, and then Eq (2.3) becomes
In this work, we assume that the velocity u in two dimensions is smooth enough that the order of the derivative can be interchanged, that is, ∂∂x∂u∂y=∂∂y∂u∂x. Then, we obtain
Substituting Eq (2.5) into the second term of Eq (2.4), we have
or
Since the rate of deformation for the liquid phase d=12(∇u+(∇u)T), we rewrite Eq (2.7) as
Notice that if λ=0, then Eq (2.8) becomes
which is the generalized Stokes equation. If the matrix ∇u is symmetric, then Eq (2.9) is the following Stokes equation:
2.2. Derivation of the Brinkman equation
In this section, we show the derivation of the Brinkman equation in a macroscopic scale derived using Hybrid Mixture Theory (HMT). HMT is an upscaling technique used to derive multiphase equations such as the combination of solid and liquid phases. This method uses the averaging theorem to upscale equations from a microscale equation to a macroscale equation [19]. In this study, we focus on developing a model for fluid flow due to the movement of self-propelled solid phases. Here, we follow the procedure provided in [18]. We begin with the multiphase equation upscaled from the conservation of momentum [18] when the porosity is a function, not a constant:
where l and s mean the liquid and solid phases, respectively. The function εl is the porosity, which is a variable in space; dl=0.5(∇ul+(∇ul)T) is the rate of deformation tensor; R is a second-order tensor; ul and us are the velocities of liquid and solid phases, respectively. Substituting R=μεlk−1, where k−1 is the inverse of the permeability tensor, and taking DlulDt=∂ul∂t+ul⋅∇ul into Eq (2.11), subtracting from both sides by p∇εl and dividing by εl on both sides, we have
Then, we normalize Eq (2.12). We use the same characteristic parameters as in the previous subsection. The dimensionless form of Eq (2.12) is
Using the values in Table 1 to calculate the coefficients in Eq (2.13) with the permeability k=10−14 m2 and porosity εl=1, which are the maximum values employed from [24], we obtain the values of the coefficients as illustrated in Table 3.
From the calculation demonstrated in Table 3, we neglect the first two terms in Eq (2.13), the time-dependent and nonlinear terms, because these expressions are significantly small in comparison with others. Therefore, Eq (2.12) becomes
which is called the Brinkman equation in a macroscopic scale. Notice that the macroscale Brinkman equation is distinct from the Brinkman in literature such as in [25],
because our model starts with the momentum equation that the porosity is a function and cannot be moved out of the derivative as a constant, as usually used in research. The porosity in the parentheses in the third term in Eq (2.14) cannot be canceled out with the denominator. Moreover, the first-order derivative of the rate of deformation times the porosity in Eq (2.14) cannot be changed to be the second-order derivative of the velocity as shown in Eq (2.15). It may seem that the difference is not much, but finding the numerical results of Eq (2.14) is more complicated than for Eq (2.15), including the proof of the well-posedness of the equation.
Notice that the Brinkman equation in the macroscopic scale, Eq (2.14), has a good engagement with the generalized Stokes equation, Eq (2.9). Because there are no solid phases in the adjacent free-fluid domain, the porosity becomes one, and the permeability tends to infinity in this region. Therefore, the first term in Eq (2.14) disappears, and then the Brinkman equation, Eq (2.14), becomes generalized Stokes equation, Eq (2.9). Thus, the solutions in these two layers can be matched in the transition zone at the free-fluid/porous-medium interface by using the generalized Stokes-Brinkman model. The mathematical model is summarized in the next section.
2.3. Governing equations
The models for a problem of this kind are summarized in this section. The models in both free-fluid layer and porous medium consist of two unknowns, which are the velocity ul and the pressure p. Therefore, in each region, we need one more equation, which is a continuity equation obtained from conservation of mass. Since a bundle of self-propelled solid phases effects the fluid flow, we employ the continuity equation for two-phase flow in the porous medium derived by HMT [26,27], which is
where f=−˙εl/(1−εl)+∇⋅(εlus) and ˙εl=∂εl/∂t+us⋅∇εl. Let Ω=Ωp∪Ωf be our domain, and ∂Ω is the boundary of the domain. Define the vectors
From Eqs (2.14), (2.16) and (2.17), the system of equations used in domain Ωp is
For the free-fluid domain Ωf, the flow is considered incompressible. Then, the divergence of velocity is zero. Therefore, in domain Ωf, we have the system of equations
Before we prove the well-posedness of the generalized Stokes-Brinkman equations, Eqs (2.18) and (2.19), in the next section we provide the discretized form of the governing equations by using a finite element method.
3.
Discretized model
In this section, we first formulate the weak formulation of the generalized Stokes-Brinkman equations, Eqs (2.18) and (2.19), by using a mixed finite element method. To obtain the weak form of Eq (2.18), we multiply a weight function w∈H10(Ω) and integrate Eq (2.18) over the domain Ω on both sides, and we have
Applying Green's first identity to the second and third terms on the left hand side of Eq (3.1) and using the property that the weight function is zero at the boundary, we have
Substituting dl=0.5[∇(uεl)+(∇(uεl))T] into Eq (3.2), we obtain the weak formulation of Eq (2.18), which is
Similarly, multiplying both sides of Eq (2.19) by another weight function q∈L20(Ω) and integrating both sides, we obtain the weak formulation of Eq (2.19):
The weak formulation of the generalized Stokes-Brinkman equations can be written in linear and bilinear functionals as follows.
Problem 1. The weak form of the generalized Stokes-Brinkman equations is to find u∈H1s(Ω) and p∈L20(Ω) such that
where the linear and bilinear functionals are defined as
where the space H1s(Ω)={w∈H1(Ω):w|∂Ω=s}, and ⟨⋅,⋅⟩ is the duality pairing.
Notice that the space L20(Ω) is used instead of L2(Ω) because the system of Eqs (2.18) and (2.19) demonstrates pressure up to an additive constant; see [28] on page 157 for details. The linear and bilinear functionals in Problem 1 can be written in the form of a linear operator as in Problem 2 (the definition of the linear operator is in the Appendix).
Problem 2. Let A:H10(Ω)→H−1(Ω) and B:H10(Ω)→L20(Ω) be linear operators. Find u∈H1s(Ω), p∈L20(Ω) such that
where
the norm ‖⋅‖H1(Ω) denotes the standard norm on the space H1(Ω), and the function us in f is a bounded continuous function.
Next, we show that the linear and bilinear functionals in Problem 1 are continuous and coercive, and that will be used to prove the existence and uniqueness of the generalized Stokes-Brinkman equations in Section 5.
4.
Continuity and coercivity of linear and bilinear functionals
In this section, we show that the linear and bilinear functionals in Problem 1 are continuous and coercive. These properties are necessary to prove the existence and uniqueness of the governing equations. We first proof the continuity as shown in Theorem 4.1.
Theorem 4.1. The linear functionals c1(w),c2(q) and bilinear functionals a(⋅,⋅), b(⋅,⋅) are continuous. In particular,
where n is the dimensional number, and
Proof. It is obvious that c1(w) and c2(q) are linear functionals, and a(u,w) and b(u,q) are bilinear functionals. Next, we show the continuity of c1(w). Let w∈H1(Ω). Then,
where we apply the definition of norm on the space H−1(Ω), Eq (3.13), at the inequality. The proof of the continuities of c2(q) and b(u,q) has been shown in [16]. Next, we show the continuity of a(u,w) in a two-dimensional domain. Define u=(u1,u2) and w=(w1,w2). Then, from Eq (3.7), we have
where Qa=max{√6μmax1≤i,j≤2|k−1ij|, 2μ‖εl‖H1(Ω)} and the inequality [14]
is applied to the third inequality. For the fifth inequality, we use the fact that ‖⋅‖L2(Ω)≤‖⋅‖H1(Ω), so ‖⋅‖L2(Ω)‖⋅‖H1(Ω)≤1. Therefore, a(u,w) is continuous.
To show that the bilinear form a(⋅,⋅) is coercive, we first proof Lemma 4.2, which will be used in the proof of coercivity presented in Theorem 4.3.
Lemma 4.2. Let w∈H1(Ω). Then,
for some natural number nr.
Proof. Let w∈H1(Ω). Since the porosity εl>0 is a real number, by the Archimedean property, there exists nr∈N such that εl≥1nr. Given W=wεl, then,
where D=12(∇W+(∇W)T) is symmetric with the indicial notation Dij = 12(∂Wi∂xj+∂Wj∂xi). The variable Dij is considered to be a real number for all i,j=1,2, and |V| is the volume of the domain Ω. For the first inequality, we use the fact that the porosity εl≤1. For the second and third inequalities, we apply H¨older's inequality and the triangle inequality, respectively. For the fourth inequality, we apply the spectral norm of a matrix E [29], i.e.,
where σmax(E) represents the largest singular value of a matrix E, and s and m are the dimensional numbers. For the last inequality, we use the Archimedean property [30]. Therefore,
Hence, the proof is complete.
Next, we show the coercivity of the bilinear functional a(⋅,⋅).
Theorem 4.3. The bilinear functional a(⋅,⋅) is coercive, such that
where Qc=min{μQk, μ√|V|n2rK(N−1)2} and Qk is a positive number.
Proof. Let w∈H1(Ω). Then,
where Qc=min{μQk, μ√|V|n2rK(N−1)2}>0. The property [14]
and inequality (4.8) are used in the first inequality. Parallelogram law [31] ∀u,w∈U, ‖u+w‖2+‖u−w‖2=2(‖u‖2+‖w‖2) and the fact that ‖u−w‖2≤‖u‖2+‖w‖2 are applied to the second inequality. Poincarˊe inequality [31] ∃K>0 such that |w|Hm(Ω)≥1K‖w‖Hm(Ω), ∀w∈Hm0(Ω) where m≥0, is applied to the fourth inequality. For the fifth inequality, we apply Archimedean property [30] ∀r∈R, ∃N∈N such that N−1≤r≤N and use the fact that εl is a positive real number. Hence, the proof of the coercivity of the bilinear form a(w,w) is complete.
5.
The existence and uniqueness of the generalized Stokes-Brinkman model
In this section, we provide the proof of the existence and uniqueness of the generalized Stokes-Brinkman equations. Before illustrating the proof of the well-posedness, we present the following proposition.
Proposition 5.1. Let f∈L2(Ω) and s∈H1/2(∂Ω). Then, there exist us∈H1(Ω) and a unique u0∈V⊥ such that
where n is the dimensional number, and β and Qs are positive constants.
Proof. Let f∈L2(Ω), and s∈H1/2(∂Ω). Therefore, there exist us∈H1(Ω), a unique u0∈V⊥⊂H10(Ω) and Qs>0 such that us|∂Ω=s, f−∇⋅us∈L20(Ω), ∇⋅u0=f−∇⋅us,
and there exists β>0 such that
See Lemma A.4 for the details. Next, we show that us+u0 is bounded, as follows.
where the fact that [16] ‖∇⋅ϕ‖L2(Ω)≤√n|ϕ|H1Ω, where n is the dimensional number, is applied to the fourth inequality.
Next, we show the theorem of the well-posedness of the generalized Stokes-Brinkman equations.
Theorem 5.2. Let f∈H−1(Ω), f∈L2(Ω) and s∈H1/2(∂Ω). There exist a unique u∈H1s(Ω) and p∈L20(Ω) satisfying Problem 1. Moreover,
where ˆu=us+u0, β>0, as presented in Proposition 5.1, and Qa and Qc are defined in Theorem 4.1 and Theorem 4.3, respectively.
Proof. Let f∈H−1(Ω), f∈L2(Ω) and s∈H1/2(∂Ω). From Proposition 5.1, we have us∈H1(Ω) and u0∈V⊥⊂H10(Ω) such that us|∂Ω=s and ∇⋅u0=f−∇⋅us. Let ˆu=us+u0 and L(w)=c1(w)−a(ˆu,w) for any w∈V. By adopting the linearity and continuity of c1(⋅) and bilinearity and continuity of a(⋅,⋅) along with the coercivity of a(⋅,⋅), we have that L(⋅) is a linear and continuous function. Then, from the Lax-Milgram theorem, there exists a unique ˜u∈V⊂H10(Ω) such that a(˜u,w)=L(w). Let u=˜u+ˆu. Then,
Therefore, u∈H1s(Ω). Next, we show the uniqueness of u. Since a(˜u,w)=L(w)=c1(w)−a(ˆu,w), by using the bilinear property of a(⋅,⋅), we have
Suppose that u1 and u2 are two such solutions satisfying
Then, substituting w=u1−u2 in Eq (5.7) and subtracting one equation from another equation, we get
where we apply the coercivity of a(⋅,⋅), Theorem 4.3, at the first inequality. Since the constant Qc>0, it implies that ‖u1−u2‖H1(Ω)=0. Then, u1=u2. Therefore, u is unique, satisfying a(u,w)=c1(w), for all w∈V.
Next, we show that u=˜u+us+u0 satisfies the continuity equation. Since ˜u∈V, ∇⋅˜u=0. Then,
where ∇⋅u0=f−∇⋅us is applied at the third equality. Hence, u satisfies the continuity equation.
We prove the existence and uniqueness of p∈L20(Ω). Define L1 such that ⟨L1,w⟩=⟨f,w⟩=c1(w). Then, from Eq (5.6), we have
By the definition of the linear operator, seen in Appendix A, we can rewrite Eq (5.8) in operator notation as A˜u+Aˆu−L1=0. Then, A˜u+Aˆu−L1∈V0, where V0 is the polar set of V; see Appendix A for the definition. Given that B′:L20(Ω)→V0 is an isomorphism grad operator, from Theorem A.2 and the property of isomorphism, there exists a unique p∈L20(Ω) such that B′p=A˜u+Aˆu−L1=Au−L1. Then,
Therefore, there exist a unique u∈H1s(Ω) and p∈L20(Ω) satisfying Problems 1 and 2.
Next, we show the variables u and p are bounded. We first illustrate that ˜u ia bounded. Employing Eq (4.9), we have
where the second inequality is obtained from Theorem 4.1. Dividing both sides of Eq (5.9) by ‖˜u‖H1(Ω) and Qc, we get
Thus,
To show that p is bounded, we first employ Eq (3.5):
where inequalities (4.1) and (4.4) are applied to the inequality. Since
is independent of p, from Eq (A.11),
Rearranging Eq (5.12), we obtain that
Since ‖f‖H−1(Ω)+Qa‖u‖H1(Ω) is independent of w∈H10(Ω),
Therefore,
Hence, the proof of existence and uniqueness of the generalized Stokes-Brinkman equations is complete.
6.
Conclusions
In this research, we focus on the fluid movement in a porous medium induced by self-propelled solid phases and the adjacent free-fluid region. In the porous medium, we employ a macroscale equation derived from an upscaling technique called Hybrid Mixture Theory (HMT) because we consider a bundle of solid phases. Then, we apply a non-dimensionalization scheme to the macroscale equation to obtain the Brinkman equation. Our model is more general than the Brinkman equation in the literature because the porosity in our equation is considered as a function since the beginning of the derivation. Then, our model in the porous medium conserves the reality of the problem. In the free-fluid region, we start with the generalized Navier-Stokes equation and use the non-dimensionalization method to derive the generalized Stokes equation. Our Brinkman and generalized Stokes equations can be matched at the free-fluid/porous-medium interface. We name them as the generalized Stokes-Brinkman equations. We also show that the discretized form of the mathematical model is a well-posed system with the use of a mixed finite element method. The weak formulation of the generalized Stokes-Brinkman equations is rewritten in linear and bilinear functional structures. We show that the bilinear form a(⋅,⋅) is continuous and coercive. Then, we present the well-posedness of the generalized Stokes-Brinkman equations in the last theorem. The system of equations can be useful for more complexity of a real problem in a macroscopic scale than a typical Stokes-Brinkman equation and can be applied to the fluid flow through the regions where fluid is driven by the moving solid phases such as hairlike structures and animal hair. The numerical research will be presented in the next study.
Acknowledgments
This research is supported by RA/TA graduate scholarship from the School of Science, King Mongkut's Institute of Technology Ladkrabang, Thailand, grant number RA/TA-2563-D-003.
Conflict of interest
The authors declare no conflict of interest.
Appendix
A. Fundamental definition and theorems
In this Appendix, we provide notations, definitions, theorems and lemmas used in the proof of the well-posedness of the generalized Stokes-Brinkman equations. They are all presented and proved in [14,32,33,34].
Notations and spaces
In this section, we introduce some notations and spaces used in the proof of the well-posedness of the governing equations [14]. Define
where ⟨⋅,⋅⟩H−1(Ω)×H10(Ω) denotes the duality pairing between H−1(Ω) and H10(Ω). Notice that for n dimension, w∈H1(Ω)n and ∇w∈H1(Ω)n×n. In any case, for the sake of simplicity, we write w∈H1(Ω), and the implication comes from the context of the surrounding sentences.
Next, we provide the fundamental definition, theorems and lemma used in the proof of the existence and uniqueness of Problems 1 and 2 [14,31,32,33,34,35].
Definition A.1. Let u,w∈H1(Ω) and q∈L20(Ω). Define linear operators A:H10(Ω)→H−1(Ω) and B:H10(Ω)→L20(Ω) by
Let B′∈L(L20(Ω);H−1(Ω)) be the dual operator of B. Then,
where the dual spaces of L20(Ω)=(L20(Ω))′ and the dual spaces of H−1(Ω)=(H10(Ω))′.
Theorem A.2. Let Ω be connected. Then,
1. the operator grad is an isomorphism of L20(Ω) onto V0,
2. the operator div is an isomorphism of V⊥ onto L20(Ω).
Therefore, there exists β>0 such that
and for any q∈L20(Ω), there exists a unique u∈V⊥⊂H10(Ω) satisfying
Theorem A.3. There exist positive constants Qt and Qs such that, for each v∈H1(Ω), its trace on ∂Ω belongs to H1/2(∂Ω), and
Conversely, for each given function s∈H1/2(∂Ω), there exists us∈H1(Ω) such that its trace on ∂Ω coincides with s and
Lemma A.4. Suppose that f∈H−1(Ω), f∈L2(Ω) and s∈H1/2(∂Ω). Then, there exist us∈H1(Ω), Qs>0 and β>0 such that
and









 DownLoad:
DownLoad: