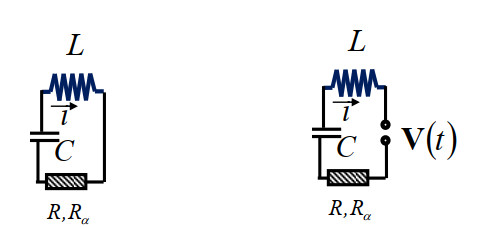Elements of mathematical phenomenology and analogies of electrical and mechanical oscillators of the fractional type with finite number of degrees of freedom of oscillations: linear and nonlinear modes

1.   Introduction

The first ideas about mathematical phenomenology and analogies between electrical and mechanical systems appeared more than one century ago in the works of the famous Serbian mathematician Mihailo Petrović (1868–1943), the founder of the Belgrade and Serbian schools of mathematics between the two world wars. He was a student at the Paris Sorbonne, when Paris was the center of scientific Europe – the hub of scientific and technological innovation. Petrović defended his PhD in mathematics in 1894, before a commission made up of renowned and leading mathematicians of the time, Charles Hermite, Émille Picard and Paul Painlevé. Even as a student, under the influence of his famous professor Henri Poincaré, Petrović acquired a vast knowledge, not only in the field of mathematics, especially in differential equations, but much more widely, which enabled him to write the work Elements of Mathematical Phenomenology on 389 pages ^[1], which remained less known since it was published only in the Serbian language in 1911. One of the last chapters of the book ^[1] refers to analogies of mathematical models, which enable the unification of models of the dynamics of systems of disparate natures and give the possibility of combining research and knowledge from different fields of science on model analogies. Petrović also published a smaller book in French ^[2] on mechanisms common to disparate phenomena, as well as later another book in Serbian on the phenomenological mapping ^[3]. For details, see references ^{[4,5,6,7,8,9,10,11]}. In addition, we mention here another aspect of Petrović's work, which has been presented by Dragović and Goryuchkina ^[12], with Petrović's photo on the cover of this issue of the Bull. Amer. Math. Soc. 57 (2), (2020).

The study of vibrations of linear mechanical systems from an electrical point of view began in the fourth decade of the last century (see paper ^[13] by Firestone from 1933). A comprehensive methodology for obtaining electrical analogues of linear mechanical systems has recently been given in ^[14].

In this paper, we use the original ideas on analogies ^[1,2,3], mathematical, qualitative, and structural ^[15,16,17], as well as the well-known classical models of mechanical and electrical classical models of oscillatory systems. Those analogies are generalized to mechanical and electrical of fractional type, models of oscillatory systems, and systems with a finite number of degrees of freedom of oscillation ^[10,17,18]. We started from the analogy of a mechanical and electrical oscillator, fractional type, with one degree of freedom of oscillation and their elements. In parallel, we considered ordinary homogeneous and inhomogeneous fractional order differential equations as their solutions.

Starting from the 19th century, until today, in the 21st millennium, the theory of fractional calculus on derivatives and differential operators of fractional (non-integer) order has developed rapidly. The driving force behind this rapid development, as in many areas of mathematics, is certainly the wide application of derivatives, differential operators, and fractional (non-integer) order in various areas of natural and technical sciences. With that, the theory of differential equations of fractional order and methods for their approximate solutions, as well as their properties, have been developed (see references ^[19,20,21]).

The main reasons for many successful applications of derivatives and differential operators of the fractional order are the appearance and application of new models of the fractional type with more comprehensive properties and more accurate descriptions than those with integer derivatives and differential operators of integer order. Then, with the differential operators of the fraction order, in research, the entire history of the process, which is described, is included. It means that these differential fractional operators are suitable for describing and modeling both nonlocal and distributive processes and effects, which are often present in natural and technical systems and their processes and dynamics. Differential operators of the fractional order are suitable for determining the dissipative properties of the system, but also the hereditary properties of systems and materials. One of the main reasons for the successful application of the differential operator of fractional order in the constitutive relations of materials, is because with one expression, and by changing the exponent of the fractional order of differentiation, the properties of the material can be described from purely elastic through various dissipative to viscoelastic and viscous properties (cf. ^{[15,16,17,18,22,23]}).

This paper is organized as follows. Basic functions and elements of fractional integrals and derivatives, including history of fractional calculus, as well as the Laplace transform as one of basic tools in this area, are presented in Section 2. Analogous mechanical and electrical elements of the fractional type and their constitutive relations are given in Section 3, and the corresponding mechanical and electrical oscillators with one degree of freedom of oscillation of fractional type are presented in Section 4, including ordinary differential equations of fractional order and their solutions for the case of eigen and forced oscillations of fractional type. Precisely, by applying the direct and the inverse Laplace transformation and the power series expansions, the approximate analytical solutions for eigen oscillations of the fractional type, as well as for forced oscillations, using a convolution integral, are obtained. Fractional type oscillation modes similar to cosine and sine functions were especially analyzed. Such solutions are illustrated graphically in numerical experiments in Section 5. A special class of discrete oscillators of fractional type, with a finite number of degrees of freedom of oscillation and independent eigen-modes and forced modes is considered in Section 6, including a number of theorems on the properties of independent modes of fractional type. Energy analysis of the oscillations on a special class of discrete oscillators of the fractional type, as well as some interesting analogy examples, are given in Sections 7 and 8, respectively. Finally, concluding consideration is presented in Section 9. For some additional interesting results, see ^{[24,25,26,27,28]}.

2.   Basic elements of fractional integrals and derivatives

In this introductory section, we present a brief overview of the basic facts of fractional calculus, i.e., fractional differentiation and fractional integration, including basic tools and some historical background (cf. ^{[29,30,31,32,33]}). For some additional properties of special functions see ^{[34,35,36,37,38]}.

2.1.   Gamma function, Mittag-Leffler function, and hypergeometric functions

One of the basic functions of fractional calculus is Euler's gamma function $\Gamma(z)$, which generalizes the factorial function to non-integer numbers and even complex values in the following way:

For $n\in\mathbb{N}_0$, it is clear that $\Gamma(n+1) = n!$. Two important relations for the gamma function are Euler's reflection formula and Legendre duplication formula,

respectively.

Many functions can be expressed in terms of the so-called (two-parameter) Mittag-Leffler function, defined by

with two positive parameters $\alpha, \beta > 0$. In the case $\beta = 1$, we have the one-parameter Mittag-Leffler function $E_\alpha(z) = E_{\alpha, 1}(z)$. For example, $\mathrm{e}^z = E_{1, 1}(z)$, $(\mathrm{e}^z-1)/z = E_{1, 2}(z)$, $\cosh z = E_{2, 1}(z^2)$, etc. In Wolfram's Mathematica package ^[39], MittagLefflerE is a mathematical function, suitable for both symbolic and numerical manipulation. The problems of the numerical computation of Mittag-Leffler functions and their derivatives, with some applications in fractional calculus, were treated in ^[40,41].

The generalized hypergeometric function $_pF_q$ is defined by

where the Pochhammer symbol $(\lambda)_{\nu}$ is defined by

and $\Gamma(\lambda)$ is the familiar Euler's gamma function given by (2.1). In Wolfram's Mathematica package, the generalized hypergeometric function $_pF_q$ is implemented as HypergeometricPFQ and it is suitable for both symbolic and numerical calculation ^[39]. When $p\leq q$, this series converges for each $z\in{\mathbf C}$. For $p = q +1$, it has a branch cut discontinuity in the complex $z$ plane running from $1$ to $\infty$. For some recent results on this subject, especially on transformations, summations, and other applications, see ^[42,43,44].

In the special case $p = 2$ and $q = 1$, the function $_2F_1(a, b; c;z)$ is the well-known Gauss's hypergeometric function,

This series converges for all $z$ in the unit circle $|z| < 1$. If $\mathrm{Re\, } c > \mathrm{Re\, } a > 0$ there exists the following integral representation

Gauss's hypergeometric function ${}_2F_1(a, b; c;z)$ is a solution of Euler's hypergeometric differential equation

which has three regular singular points: $z = 0, 1, \infty$.

2.2.   The beginnings of fractional calculus

The concept of derivatives and differential operators of fractional orders was introduced almost simultaneously with the development of classical differentials-derivatives and differential operators of integer orders. The symbol ${ \mathrm{d}}^ny/{ \mathrm{d}}x^n = D^ny$ for the $n$-th derivative of a function $y(x)$, where $n$ is a nonnegative integer, was introduced by Leibniz. The first known reference about the possibility of $n$ not being an integer is found in the correspondence of Leibniz and L'Hospital from 1695. L'Hospital asked "What if $n$ be $1/2$?", and Leibniz answered "It will lead to a paradox", but he added: "From this apparent paradox, one day useful consequences will be drawn." Many famous mathematicians of the time mentioned fractional derivatives, e.g., Euler, Lagrange, Laplace, Lacroix, Fourier, Abel, Liouville, Riemann, etc. For a more detailed history, see ^{[29,32,45,46]}.

In 1819, Lacroix [47, pp. 409–410] gave the correct answer to the question of what is the value of the one-half order derivative. Starting with the power function $y = x^m$, where $m$ is a positive integer, he found the $n$th derivative as

Then, changing $m$ by $\alpha$ and $n$ by $\beta$, and taking Legendre's symbol $\Gamma$ as a generalized factorial, he obtained

and formally, for $\alpha = 1/2$ and $y = x$ $(\beta = 1)$, Lacroix concluded that

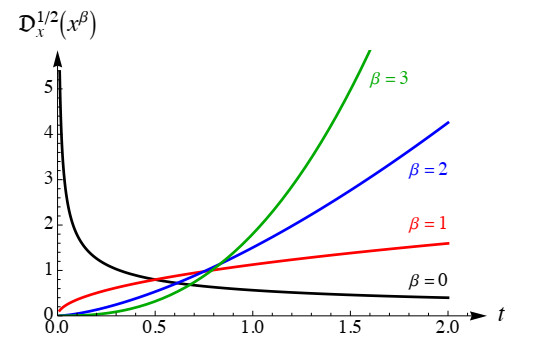
because $\Gamma(2) = 1$ and $\Gamma(3/2) = \sqrt{\pi}/2$. The fractional derivatives $\mathfrak{D}^{1/2}_x[x^\beta]$, defined by (2.2), for $\alpha = 1/2$ and $\beta = 0, 1, 2, 3$, are presented in Figure 1. It is interesting that this approach gives nonzero value for a constant function $y = 1$ $(\beta = 0)$,

While fractional integration usually means the Riemann-Liouville integral, in the case of fractional differentiation there are different definitions. They were mainly introduced due to the coincidence of some properties with those of classical differentiations.

2.3.   Riemann-Liouville fractional integrals

Let $x\in L^1(a, b)$ and $\alpha > 0$. The left and right Riemann-Liouville fractional integrals of order $\alpha$ are defined by

respectively, where $t\in[a, b]$. These integrals exist for almost all $t\in[a, b]$, and also belong to $L^1(a, b)$. Also, for $\alpha = 0$ we can formally define ${}_aI_t^0 [x] = x$, because for functions $x\in C^1[a, b]$ we have $\lim_{\alpha\to0}{}_aI_t^\alpha [x(t)] = x(t)$.

A usual approach for calculating these integrals (2.4) is based on the approximation of the function $x$ by an appropriate function $\tilde x$, so that ${}_aI_t^\alpha [\tilde x(t)]$ and ${}_tI_b^\alpha [\tilde x(t)]$ can be calculated exactly (cf. ^[48,49]). There are many methods of such approximations (or interpolations) by algebraic polynomials, Müntz polynomials ^[50,51,52], splines, etc. (cf. ^{[37,53,54,55]}), as well as several quadrature rules.

Inspired by the papers ^[56,57], Milovanović ^[58] considered certain classes of orthogonal polynomials on the finite intervals and derived the corresponding quadrature formulas of the maximal algebraic degree of precision, which can be successfully applied in numerical calculation of the left and right fractional Riemann-Liouville integrals (2.4) (in particular, see Sections 5 and 6 in ^[58]).

Finally, we mention here that the multiple composition of the left and right fractional Riemann-Liouville integrals was recently introduced by Ciesielski and Blaszczyk ^[59], including analytical and numerical calculations.

In this paper, we use only the left Riemann-Liouville fractional integral, and the phrase "the left" will be omitted. Taking $1-\alpha$ instead of $\alpha$ in (2.4) for the (left) Riemann-Liouville fractional integral ${}_aI_t^{1-\alpha} [x(t)]$, we have the following expression:

2.4.   Fractional derivatives

As we mentioned there are several definitions of fractional derivatives. Similar to (2.4), we define the left and right Riemann-Liouville fractional derivatives of order $\alpha$ $(0\le\alpha < 1)$ by

for $t > a$ and $t < b$, respectively.

In the following, we mainly consider functions on $(0, +\infty)$ and use the (left) Riemann-Liouville fractional derivative, with $a = 0$ and $0\le \alpha < 1$, denoting it as

According to (2.5), we see that, formally, $\mathfrak{D}^\alpha_t[x(t)] = \mathrm{D}\, {}_0I_t^{1-\alpha} [x(t)]$, where $\mathrm{D} = { \mathrm{d}}/{{ \mathrm{d}}t}$.

We note that Lacroix's approach (2.2) coincides with the definition of (2.7).

The previous definition (2.7) can be extended to fractional derivatives of order $\alpha\ge1$, where $n-1\le\alpha < n$ and $n\in\mathbb{N}$, in the following way:

For example, for $1\le\alpha < 2$, (2.8) reduces to

There are also several other definitions of the fractional derivatives (Caputo, Riesz, Marchaud, Grünwald-Letnikov, etc.). We mention here only the so-called Caputo derivative $\mathfrak{D}_\ast^\alpha [x(t)]$ $(t\in[a, b])$ of order $\alpha$ $(0\le\alpha\le1)$, which is defined by (see ^{[35,60,61,62,63]})

where $\dot x(t) = { \mathrm{d}}x(t)/ \mathrm{d} t$. It is introduced in such a way to provide that the Caputo derivative of a constant function is zero. It is well-known that the fractional derivatives of Riemann-Liouville and Caputo type are closely linked by the following relationship:

The operators of fractional derivative $\mathfrak{D}_t^\alpha [x(t)]$ are more complicated than the classical one, and their calculation is also more difficult than in the integer order case. A quadrature method for approximating the fractional derivative of Riemann-Liouville and Caputo type was presented in ^[63], including the corresponding software implementation in Mathematica (for different quadrature formulas see ^[64]). The method is based on nonstandard quadrature processes developed in ^[65]. For other numerical methods see ^{[49,66,67,68]}).

As we mentioned earlier in this paper, we use the Riemann-Liouville fractional derivative $\mathfrak{D}_t^\alpha [x(t)]$, defined by (2.7) or in general by (2.7), where $\alpha$ is a parameter – order of the fractional (non-integer) derivative – and it is determined experimentally depending on the application in certain cases. The time function $x(t)$ represents some independent generalized coordinate.

When $\alpha = 0$ and $\alpha = 1$, then (2.7) and (2.9) give

respectively. This property of the Riemann-Liouville differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of the fractional order $\alpha$ between $0$ and $1$, including its limit values, allows us to define only one expression for both, integer derivatives and derivatives of the fractional order, which is a useful mathematical description in various applications.

The Riemann-Liouville fractional derivative is implemented in Wolfram's Mathematica package ^[39] as FractionalD.

2.5.   Laplace transform

A very useful tool in fractional calculus, especially in fractional differential equations, is the Laplace transform.

Let $x(t)$ be a locally integrable function of a real variable $t$, such that $x(t) = 0$, when $t < 0$. Its Laplace transform is defined by

where $p$ is a complex variable. If this integral is convergent at the point $p_0\in\mathbb{C}$, then it converges absolutely for $p \in\{p\in\mathbb{C}\, |\, \mathrm{Re\, } p > \mathrm{Re\, } p_0\}$ and represents an analytic function $X(p)$. In our consideration we assume that $x(t)$ is an exponentially bounded function, i.e., there exist a positive constant $M$ and a real $\gamma$ such that $|x(t)|\le M { \mathrm{e}}^{\gamma t}$ for all sufficiently large values of $t$.

The inverse Laplace transform is defined by

where $\sigma$ is an appropriate real number chosen so that all singularities of $p\mapsto X(p)$ are to the left of the so-called Bromwich line $\mathrm{Re\, }{p} = \sigma$.

The Duhamel or Laplace convolution of two functions $x(t)$ and $y(t)$ is defined by

Evidently, $(x*y)(t) = (y*x)(t)$. If there exist Laplace transforms ${\cal{L}}[x(t)](p) = X(p)$ and ${\cal{L}}[y(t)](p) = Y(p)$, then the Laplace transform of this convolution is

Laplace transforms of some typical functions are: ${\cal{L}}[t^\alpha](p) = {\Gamma(\alpha+1)}/{p^{\alpha+1}}$ $(\alpha > -1)$, ${\cal{L}}[\mathrm{e}^{\omega t}](p) = {1}/(p-\omega)$, as well as

Suppose that ${\cal{L}}[x(t)](p) = X(p)$. It is easy to see that the Laplace transform of the first derivative of $x(t)$ is given by ${\cal{L}}[\dot{x}(t)] = pX(p)-x(0)$, as well as for the $n$-th derivative

Since the Riemann-Liouville fractional integral ${}_0I_t^\alpha[x(t)]$ $(a = 0)$ of order $\alpha\, (>0)$, defined in (2.4), is a convolution of functions $t^{\alpha-1}/\Gamma(\alpha)$ and $x(t)$, according to (2.10), we get the Laplace transformation of ${}_0I_t^\alpha[x(t)]$ in the form ${\cal{L}}[{}_0I_t^\alpha[x(t)]](p) = X(p)/p^\alpha$.

If $n-1 < \alpha < n$, then formula (2.12) can be generalized as (cf. [29, p. 134])

i.e.,

because $\mathfrak{D}_t^{\alpha+k-n}[x(t)]\bigm|_{t = 0} = \bigl[\mathrm{D}^k\, {}_0I_t^{n-\alpha} [x(t)]\bigr]_{t = 0}$. For $0 < \alpha < 1$ $(n = 1)$, using (2.7), we get

2.6.   Fractional differential equation

In this paper, we refer to the basic ordinary homogeneous differential equation of fractional (non-integer) order

in which $x(t)$ is an independent generalized coordinate, $\omega_0^2$ and $\omega_\alpha^2$ are the coefficients, and $\alpha$ is the fractional order such that $0 < \alpha < 1$.

An analytical solution of this equation (2.14) in the series form can be done (cf. ^[17,22]):

where $x_0$ and $\dot x_0$ are the initial conditions – the initial value of the coordinate $x_0 = x(0)$ and the initial value of the velocity $\dot x_0 = \dot x(0)$ at $t = 0$.

Also, we refer to the corresponding basic abundant nonautonomous (nonhomogeneous) ordinary differential equation of fractional order $\alpha\in(0, 1)$,

whose solution, using the solution (2.15), can be expressed in the following convolution form

Using the generalized hypergeometric function $_1F_2$, a more convenient form of this solution is obtained in §4.2 (Threorem 4.2).

In order to show that the coefficients of the previous fractional differential equations (2.14) and (2.16) have physical meanings, in Section 3 we consider a mechanical oscillator of the fractional type, with one degree of freedom of oscillation in the mode of self-oscillations, that is, forced oscillations. In Section 4, some approximate analytical solutions of these fractional differential equations will be done.

3.   Analogous mechanical and electrical elements of the fractional type and their constitutive relations

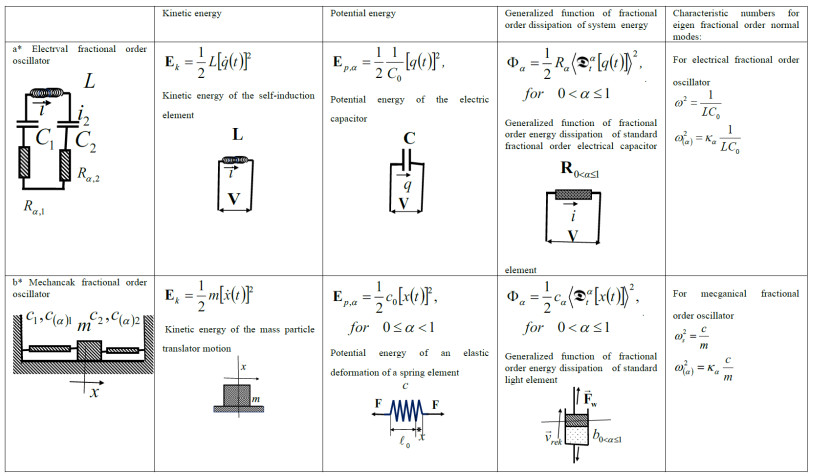
We define a standard light, mechanical element of fractional type, with dissipative properties, by means of a constitutive relation, which contains a differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of fractional order in the form

in which $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ is the differential operator of fractional order, defined by (2.7), $\alpha$ is a real number between $0$ and $1$, determined experimentally, while $c_\alpha$ is a coefficient of fractional properties of the mechanical element of fractional type. $P(t)$ is the resistance force of a fractional type mechanical element to axial deformation – stretching or compression.

When in the previous constitutive relation (3.1) and the differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of fractional order, $\alpha$ as a number between $0$ and $1$ $(0 < \alpha < 1)$ takes the limiting values zero and $1$, then the element becomes classical linear elastic spring or classic linear viscous damper.

For $\alpha = 0$, the application of the differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of fractional order gives the very time function $x(t)$ to which it was applied, so the constitutive relation becomes $P(t) = -c_{\alpha = 0} \mathfrak{D}^{\alpha = 0}_t[x(t)] = -c_{\alpha = 0} x(t) = -c_0 x(t)$. When the exponent $\alpha = 1$, then the application of the differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of fractional order gives the first time derivative of the function to which it is applied, so the constitutive relation, in this case, has the form $P(t) = -c_{\alpha = 1} \mathfrak{D}^{\alpha = 1}_t[x(t)] = -c_{\alpha = 1} \dot{x}(t) = -c_0 \dot{x}(t)$.

This viscous element of the fractional type, schematically represents an absorber in the form of a cylinder, which is filled with a compressible viscous fluid, which is acted upon by a moving piston. It is a fractional type absorber, which is usually connected in parallel with one elastic element (spring) of stiffness. Then, the constitutive relation of such a complex element from the parallel connection of a fractional type element and an elastic element is of the form $P(t) = -\left[c_0x(t)+c_\alpha \mathfrak{D}^\alpha_t[x(t)]\right]$.

A standard electric element of fractional type, with dissipative properties, is defined by means of a constitutive relation, which contains a differential operator of fractional order in the form

where $V(t)$ is the electric voltage, and $q(t)$ is the amount of electricity, while $i(t) = \dot q(t)$ is the electric current and $R_\alpha$ is the coefficient of the fractional properties of the fractional-type electric dissipative element. The exponent $\alpha$ of the fractional differential operator is within the limits of $0 < \alpha\le1$, as well as with the analogous light mechanical element of the fractional type.

For $\alpha = 1$, the previous constitutive relation (3.2) takes the following form $V(t) = -R_{\alpha = 1}\dot{q}(t)$, and represents the classic linear relationship between the electric voltage $V(t)$ and the electric current $i(t) = \dot q(t)$ at the ends of the classic electric resistor. For $\alpha = 0$, the previous constitutive relation (3.2) takes the following form $V(t) = -R_{\alpha = 0}\, q(t) = (1/C_{\alpha = 0})\, q(t)$, where $C_{\alpha = 0} = 1/R_{\alpha = 0}$ represents an additional capacitance of the capacitor.

Here, we have defined two analogous elements of fractional type. One mechanical damping-dissipative viscoelastic element and the other dissipative electrical element, electrical resistor of the fractional type. Now we can define expressions for generalized energy dissipation functions of fractional type: mechanical energy of a mechanical viscoelastic element, as well as electrical energy of an electrical dissipative element – electrical resistor of the fractional type, whose constitutive relations (3.1) and (4.1) we defined using the differential operator $\mathfrak{D}^\alpha_t[\, \cdot\, ]$ of fractional order.

Now, it is easy to supplement the classical list of electromechanical analogies of kinetic parameters of mechanical and electrical systems now by ones of fractional type. The mass $m$ of the mechanical system, which moves at translational velocity $\dot x(t)$, corresponds to the self-inductive element of self-inductance ${L}$, through which electric current $i(t) = \dot q(t)$ flows. Analogous to the kinetic energy ${E}_k = \frac{1}{2}m[\dot{x}(t)]^2$ of the mass $m$, which moves at translational velocity $\dot x(t)$, is the kinetic energy ${E}_k = \frac{1}{2}{L}[\dot{q}(t)]^2$ of the coil of self-inductance, through which the electric current $i(t) = \dot q(t)$ flows. We see that the quantity of electricity $q(t)$ is analogous to the generalized coordinate $x(t)$, and the strength of the electric current $i(t) = \dot q(t)$ to the velocity $\dot x(t)$ (see the second column in Table 1). In the third column of Table 1, the analogous elements are shown: a capacitor of capacitance ${C}$ and a linear elastic spring of stiffness $c$. The potential energy of the spring due to its deformation $x(t)$ is equal to ${E}_{{p}, c} = \frac{1}{2}c[x(t)]^2$, while the corresponding potential capacitor energy is ${E}_{{p}, C} = \frac{1}{2}\frac{1}{{C}}[q(t)]^2$. The generalized mechanical energy dissipation function of a fractional-type mechanical element is $\Phi = \Phi_\alpha = \frac{1}{2}c_\alpha \left[\mathfrak{D}^\alpha_t[x(t)]\right]^2$, while is a generalized function of electrical energy dissipation of the analogous electrical element of the fractional type given by $\Phi = \Phi_\alpha = \frac{1}{2}R_\alpha \left[\mathfrak{D}^\alpha_t[k(t)]\right]^2$ (see the fourth column). The active force ${F}$ and the dissipative force ${F}_v$ in a mechanical system correspond, respectively, to the electrical voltage ${V}$ and the electrical voltage ${V}_v$ at the ends of the fractional-type resistor in the analog electrical system.

4.   Mechanical and electrical oscillators with one degree of freedom of oscillation of fractional type: Ordinary differential equations of fractional order and their approximate analytical solutions for the case of eigen and forced oscillations of fractional type

4.1.   Mechanical oscillators of fractional type

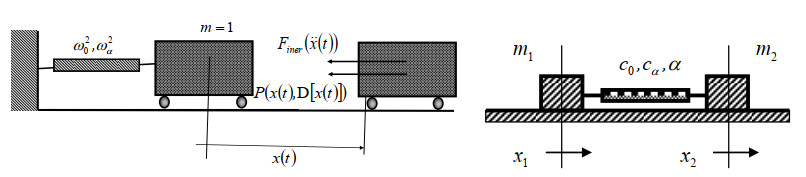
Two mechanical oscillators of the fractional type are shown in Figure 2. The first one, with one degree of freedom of movement and one degree of freedom of oscillation, defined by an independent generalized coordinate $x$, is presented in Figure 2 (left), while the second one with two degrees of freedom of mobility, certain coordinates $x_1$ and $x_2$, and one relative degree of freedom of oscillation determined by an independent generalized coordinate $x = x_2-x_1$ is given also in Figure 2 (right).

A material point of the mass $m = 1$, with translational movement defined by certain independent generalized coordinate $x$, is attached to a fixed wall by a standard light mechanical element of fractional type, with characteristics $\omega_0^2 = c/m$ and $\omega_\alpha^2 = c_\alpha/m$.

Two material points of the masses $m_1$ and $m_2$ bound by a standard light element of fractional type, stiffness $c$ and $c_\alpha$, as a system with two degrees of freedom of mobility and one degree of freedom of oscillation are given in Fig. 2 (right). One material point is in the relation to the other, whose positions are determined by the coordinates $x_1$ and $x_2$. We take into account, for description the independent generalized coordinate in the form $x = x_2-x_1$.

The dynamics of the oscillator of fractional type from Fig. 2 (left) can be described by the ordinary differential equation of fractional order (cf. ^[69,70,71])

or by the following equation, after introducing the notations $\omega_0^2 = c/m$ and $\omega_\alpha^2 = c_\alpha/m$,

Similarly, the dynamics of the system from Fig. 2 (right) can be described by the system of equations (cf. ^[69,70,71])

Multiplying the first equation in (4.3) by $m_2$ and the second one by $m_1$, and then subtracting them, we get

On the other hand, summing the equations in (4.3) leads to $m_2\ddot{x}_2(t)+m_1\ddot{x}_1(t) = 0$, which by integration gives $K = m_2\dot{x}_2(t)+m_1\dot{x}_1(t) = \mathrm{const}$. This means that the entire system, i.e., both masses move with a constant amount of movement.

Introducing a new independent generalized coordinate $x(t) = x_2(t)-x_1(t)$ in Eq. (4.4), which represents the relative displacement of one material point in relation to another, and the notations

this equation becomes

This is completely of the same form as (4.2) and represents the relative oscillations of the fractional type of one material point in relation to another system of the fractional type from Fig. 2 (right), which as a whole moves with a constant linear momentum of movement, as we proved with the equation (2.15). Thus, it is obvious that the solution of the ordinary differential equation of fractional order (4.2) mathematically represents the solution of the equation (4.6), taking into account the corresponding coefficients and the meaning of the independent generalized coordinate and its meaning.

For the limiting cases when $\alpha = 0$ and $\alpha = 1$, we get simple classical cases, which solutions are very well-known. Then, the ordinary differential equations are of the form

and

The analytic solution of the second-order ordinary differential equation (4.7) is given by (cf. ^[69])

while the solution of (4.8) is given by (cf. ^[69])

(for creep cases) or for strong puzzling

In the limit case $\alpha = 1$, when $\omega_0 = \omega_1^2/2$, the solution is given by $x(t) = { \mathrm{e}}^{-\omega_0t}\left(x_0+ {\dot{x}_0\, t}/\omega_0\right)$.

The ordinary differential equation of fractional order (4.2), when $\alpha$ is a real number, $0 < \alpha < 1$, can be solved in the form of power series (2.15), using the Laplace transform (see Subsection 2.5).

Really, applying the Laplace transformation to the ordinary differential equation of fractional order (4.2) and using (2.12) and (2.13), we have ${\cal{L}}[x]\bigl[p^2+\omega_\alpha^2 p^\alpha+\omega_0^2\bigr] = px_0+\dot{x}_0$. Then, the solution ${\cal{L}}[x(t)]$ of this algebraic equation can be expressed in the form

i.e.,

Using the fact that ${\cal{L}}[t^{\alpha-1}](p) = {\Gamma(\alpha)}/{p^{\alpha}}$ $(\alpha > 0)$, by the inverse Laplace transformation ${\cal{L}}^{-1}\bigl[{\cal{L}}[x(t)]\bigr]$ of the previous solution ${\cal{L}}[x(t)]$, given by (4.13), we obtain the required analytical solution of the ordinary homogeneous differential equation of fractional order (4.2), in the form (2.15), i.e.,

The previous expression (4.14) for $x(t)$ can be divided into two own modes $x_\mathrm{likecos}$ and $x_\mathrm{likecos}$, i.e.,

where

These summands are similar to the cosine and sine functions and reduce to them for $\alpha = 0$,

and

4.2.   Cases of external forced oscillations of the fraction type

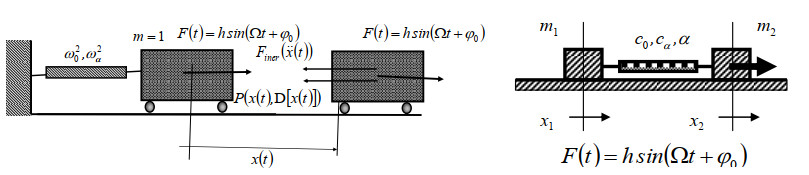
In the event that external forces act on the system, presented as a model in Figure 2 (left or right), we have cases of forced oscillations of the fraction type, with one degree of freedom. Two oscillators of the fractional type that oscillate forcibly, excited by an external single-frequency active force, are shown in Figure 3. The first of them is with one degree of freedom of movement and one degree of freedom of forced oscillation of the fractional type, and defined by an independent generalized coordinate $x$. The second one in Figure 3 is a mechanical model with two degrees of freedom of mobility determined by two coordinates $x_1$ and $x_2$, but with one relative degree of freedom of forced oscillation, determined by an independent generalized coordinate $x = x_2-x_1$.

A material point of mass $m = 1$, with translational movement under the action of an external single frequency force $F(t) = F_0\sin(\Omega t+\varphi_0)$, determined by an independent generalized coordinate $x$ and attached to a fixed wall by a standard light mechanical element of fractional type, with characteristics $c$ and $c_\alpha$ (left in Figure 3). The same figure (right) shows two material points of masses $m_1$ and $m_2$. They are connected by a standard light element of fractional type and stiffness $c$ and $c_\alpha$, as a system with two degrees of freedom of movement and one degree of freedom of oscillation, one material point in relation to the other, subjected to the effect of an external single-frequency force $F(t) = F_0\sin(\Omega t+\varphi_0)$, whose positions are determined by coordinates $x_1$ and $x_2$.

The dynamics of the first oscillator (Figure 3, left) is described by the following ordinary non-homogeneous differential equation of fractional order (cf. ^[69,70,71])

Using the previous notation and $h = F_0/m$, this equation becomes

As before in §4.1, the dynamics of the system from Figure 3 (right) can be described with the same equations (4.3), with the only difference that the second equation is nonhomogeneous, with the right side $F_0\sin(\Omega t+\varphi_0)$. As before, we obtain

and $m_2\ddot{x}_2(t)+m_1\ddot{x}_1(t) = F_0\sin(\Omega t+\varphi_0)$, which gives by integration

from which we conclude that the entire system, mass center of the system with both masses, moves harmonically with an oscillatory linear momentum of movement (harmonically oscillatory impulse of center of system).

By introducing (4.5), $\tilde h = (F_0/m_2)\sin(\Omega t+\varphi_0)$, and the new independent generalized coordinate $x(t) = x_2(t)-x_1(t)$, which represents the relative displacement of one material point in relation to another, we can write the first previously obtained equation (4.19) of fractional order, in the following form

It is a complete form of (4.18) and represents a relatively forced oscillation, of the fractional type, of one material point in relation to another, of the fractional type system (Figure 3, right). The system as a whole moves with a constant amount movement, as he proved with the equation (4.20). Thus, it is obvious that we have here the same ordinary nonhomogeneous differential equation of fractional order (4.21) as the previous one (4.18), with the same solution (2.17). When interpreting the solution, one should only take into account the corresponding coefficients and the meaning of the independent generalized coordinate.

As in §4.1 we use the Laplace transform to get the solution (2.17) of the ordinary nonhomogeneous differential equation of fractional order $\alpha$ $(0 < \alpha < 1)$, given by (4.18) or (4.21). Applying the Laplace transform to (4.18) and using the previous expression (4.12), as well as (2.11) for the Laplace transform of the trigonometric functions, we obtain the following algebraic equation

which the solution can be written in the form

that is, we write the previous expression in the recognizable form of the second term for the convolution integral in the form of the product of two Laplace transforms of the functions, one of which is the Laplace transform of the function $x_{\mathrm{likesin}}(t)$ ("likesin" mode of the fractional-type eigen-oscillators), and the other is the Laplace transform of coercive force $h\sin(\Omega t+\varphi_0)$. This decomposition of ${\cal{L}}[x(t)]$ enables us to recognize terms corresponding to eigen self-oscillation modes of free oscillations ${\cal{L}}[x_{\mathrm{free}}(t)]$ and forced mode ${\cal{L}}[x_{\mathrm{part}}(t)]$, so that we can obtain the corresponding terms in the time domain, because of linearity of the Laplace transforms, ${\cal{L}}[\, \cdot\, ]$ and ${\cal{L}}^{-1}[\, \cdot\, ]$.

For solution (4.15) of the homogenous differential equation (4.2), we denote by $x_{\mathrm{free}}(t)$, i.e.,

where $x_{\mathrm{likecos}}(t)$ and $x_{\mathrm{likesin}}(t)$ are given before by (4.16) and (4.17), respectively. Comparing (4.22) and (4.12), we conclude that the first term in (4.22) corresponds to ${\cal{L}}[x_{\mathrm{free}}(t)]$, and the second one is, in fact, a product of two Laplace transforms of the functions $(1/\dot{x}_0)x_{\mathrm{likesin}}(t)$ and $h\sin(\Omega t+\varphi_0)$, i.e.,

The second addend in (4.22) is, in fact, a product of two Laplace transforms of the functions $(1/\dot{x}_0)x_{\mathrm{likesin}}(t)$ and $h\sin(\Omega t+\varphi_0)$, i.e.,

Therefore, the original $x_{\mathrm{part}}(t)$ is given as the convolution integral of these functions

i.e.,

In this way, we obtain the solution of the ordinary nonhomogeneous differential equation (4.18) of the fractional order $\alpha$ $(0 < \alpha < 1)$, in the form $x(t) = x_{\mathrm{free}}(t)+x_{\mathrm{part}}(t)$, i.e., (2.17).

In the sequel we use the generalized hypergeometric function $_1F_2$ (see Subsection 2.1) to calculate the moments

in an analytic form. That will allow us to obtain a more convenient form of the solution (2.17).

Before, we need the following lemma.

Lemma 4.1. For $\beta > -1$, we have

and

Proof. To prove (4.26), we start with the integral

Since

we conclude that for Pochhammer's symbol the following relation

holds, so that equality (4.28) can be written in the form

because $(1)_\nu = \nu!$. Finally, summing the left and righthand sides of this equality in $\nu$ over $\mathbb{N}_0$, with a justified replacement of the sum and the integral, we get (4.26).

In a similar way, we prove the equality (4.27). □

Theorem 4.2. The solution of the nonhomogeneous differential equation (4.18) of the fractional order $\alpha$ $(0 < \alpha < 1)$ is given by

where the moments $\mu_{k, j}(t, \alpha, \Omega, \varphi_0)$, defined by (4.25), can be expressed in terms of the hypergeometric function ${}_1F_2$ as

Alternatively,

Proof. For $0\le j\le k$, $0 < \alpha < 1$, and putting $\beta = 2k+1-\alpha j$, we start with (4.25), written in the form

By the substitutions $\tau = tx$ and $\Omega\, t = A$, the moments $\mu_{k, j}(t, \alpha, \Omega, \varphi_0)$ reduce to

and after using Lemma 4.1, to (4.29). Using Eq. (4.25) we can obtain the alternative expression (4.30) for the moments $\mu_{k, j}(t, \alpha, \Omega, \varphi_0)$.

Finally, using (4.23), i.e., (4.14), and (4.24), we get the solution of the nonhomogeneous differential equation (4.18) of the fractional order $\alpha$ $(0 < \alpha < 1)$ in the form $x(t) = x_{\mathrm{likecos}}(t)+x_{\mathrm{likesin}}(t)+x_{\mathrm{part}}(t)$, i.e.,

Thus, the theorem is proved. □

Remark 1. The first expression (4.29) has certain numerical advantages, in particular, when $\varphi_0 = 0$. Then, (4.29) reduces only to first term

In that case the third term in (4.31) can be written in the simpler form

where

4.3.   Electrical oscillators of fractional type

Now, we focus our considerations on an electrical oscillator of the fractional type and with one degree of freedom of oscillations (see Figure 4, left), which is analogous to the mechanical oscillator of the fractional type (Figure 2, left) for its own oscillations.

For the model in Figure 4 (left), the expressions for kinetic and potential energy, as well as the generalized energy dissipation function of fractional type, are of the fractional type (cf. ^[16,17]):

where $q(t)$ is the amount of charge in the capacitor in the electric circuit. Kinetic energy $E_{k, L}$ in this electric circuit, originates from the self-inductance coil $L$, through which an electric current flows of the intensity $i(t) = \dot{q}(t)$. Potential energy $E_{p, C}$ originates from the amount of charge $q(t)$ in the capacitor of capacitance $C$. The generalized function of energy dissipation $\Phi$ in an electric circuit is defined by the dissipation of electric energy, which originates from the presence of an electric resistor of fractional type (electric element of fractional type), with dissipation coefficient $R_\alpha$ of fractional type, through which a current of intensity $i(t) = \dot q(t)$ flows.

Now, using the Lagrange differential equation of the second kind for the independent generalized coordinate $q(t)$, we obtain an ordinary autonomous differential equation of fractional order in the form

It can be written in the form (4.2), where $\omega_0^2 = 1/(LC)$ and $\omega_{\alpha}^2 = R_\alpha/L$. The previous ordinary homogeneous differential equation of fractional type can be composed by summing the electric voltages at the ends of the electric circuit elements $V(t) = V_L(t)+V_C(t)+V_\alpha(t) = 0$. The electrical voltages at the ends of individual electrical elements in the electrical circuit are: $V_L(t) = -L\, { \mathrm{d}}i/{ \mathrm{d}}t$ (the self-inductive coil), $V_C(t) = q(t)/C = -1/C\int_0^t i(t)\, { \mathrm{d}}t$ (the capacitor), $V_\alpha(t) = -R_\alpha \mathfrak{D}^\alpha_t[q(t)]$, $0 < \alpha < 1$ (dissipative resistor of fractional type).

The ordinary homogeneous differential equation of fractional type, for this case, is completely identical to the one considered in §4.1 for mechanical systems, as well as their solutions with the corresponding meanings.

4.4.   Case of external periodic excitation

For the model from Figure 4 (right), the expressions for the kinetic $E_{k, L}$ and the potential energy $E_{p, C}$, as well as the generalized function of energy dissipation of the fractional type, $\Phi_\alpha$, we can use all expressions from (4.34), just add a term related to the excitation of the electric circuit by the periodic change of the electric voltage $V(t) = V_0\sin\Omega t$, with the amplitude $V_0$ and the circular frequency $\Omega$.

Using Lagrange's differential equation of the second kind for the independent generalized coordinate $q(t)$, and bearing in mind the external excitation of the electric current by a periodically varying electric voltage $V(t) = V_0\sin\Omega t$, we obtain an ordinary nonautonomous differential equation of fractional order, in the following form

Now, we can write this equation in the form

or in the form of a integro-differential equation, taking $q(t) = \int_0^t i(t)\, { \mathrm{d}}t$.

This fractional differential equation (4.35) can be obtained also by adding the electric voltages at the ends of the electric circuit elements, as in §4.3,

The ordinary nonhomogeneous nonautonomous differential equation of the fractional order (4.35) is mathematically identical to the corresponding equation (4.18) from §4.2. Forced oscillations of fractional type, and all three corresponding modes, two eigen-modes of free oscillations and one forced mode of forced oscillations of fractional type, are defined by analogous solutions obtained in §4.2 (see Eqs. (4.23) and (4.24), as well as Theorem 4.2).

5.   Display of graphics of eigen-modes and forced modes of oscillators of fractional type with one degree of freedom

Taking the first $N+1$ terms (for $k\le N$) in the solution of the nonhomogeneous differential equation (4.18) of the fractional order $\alpha$ $(0 < \alpha < 1)$, we get an analytic approximation of this solution,

with three components, two of eigen-modes and one of the forced mode. According to Theorem 4.2, Remark 1 $(\varphi_0 = 0)$, and Eq. (4.32)), we have

where the coefficients $c_{k, j}(t, \alpha, \Omega)$ are given by (4.33).

In this section, we provide a graphical presentation of these three components for different values of the parameters $\omega_0^2$ and $\omega_{\alpha}^2$, as well as of the values $\Omega$, i.e., circular frequency of the external single-frequency coercive force, which acts to the oscillator of the fractional type (mechanical or electrical). Given that we consider all three components separately, without loss of generality, we can assume that $\varphi_0 = 0$ (as well as $x_0 = 1$, $\dot x_0 = 1$, $h = 1$).

The graphics are in the form of spatial surfaces in the coordinate system of mode elongation, two own modes $x_{\mathrm{likecos}}(t, \alpha)$ and $x_{\mathrm{likesin}}(t, \alpha)$, where $t$ is time and $\alpha$ is the fractional order of derivative in the interval $(0, 1)$. In the second part of this section the corresponding graphics for $x_{\mathrm{part}}(t, \alpha)$ for different values of $\Omega$ are given in a similar way.

5.1.   Graphics of eigen-modes

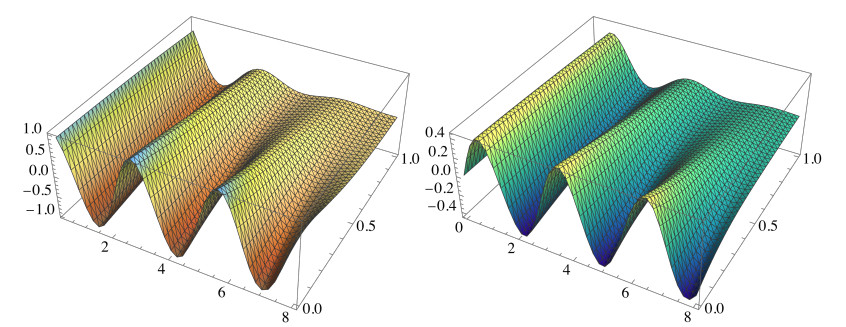
In our numerical examples we take $\omega_\alpha = 1$ and $\omega_0 = 1/2$ or $2$, and consider the domain $D = \bigl\{ (t, \alpha)\ |\ 0 < t < 8, \, 0 < \alpha < 1\bigr\}$. The usual value for the number of terms is $N = 40$. All computations were performed in Mathematica Ver. 14.0 on MacOS Sonoma 14.2.1.

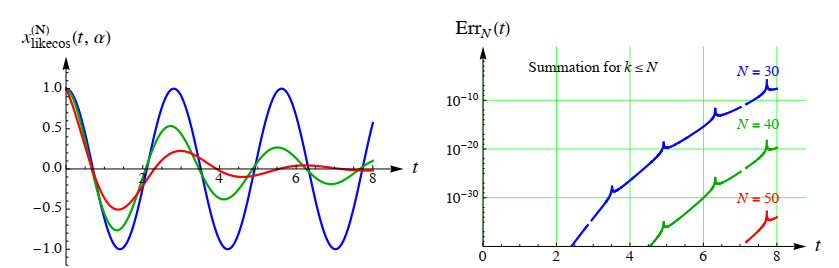
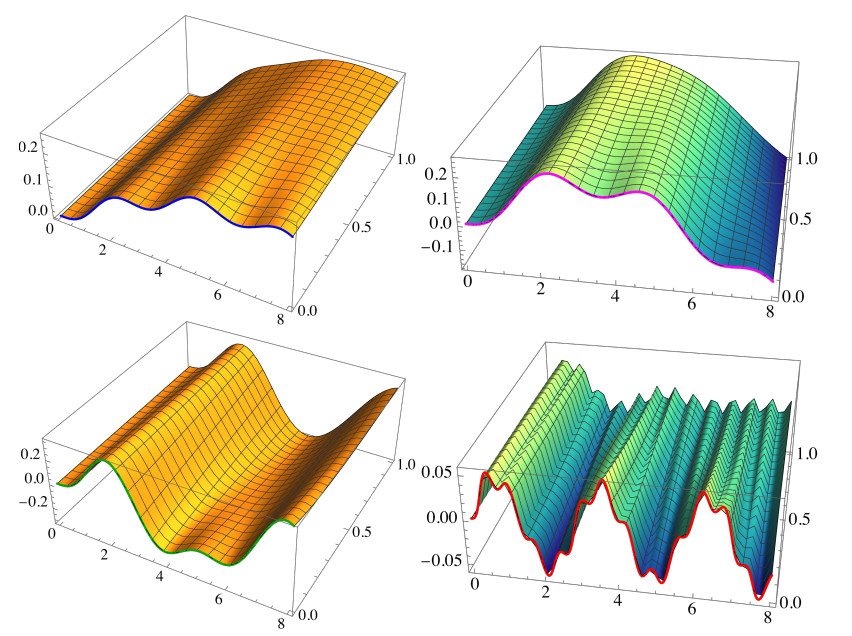
Example 5.1. Here, we consider the approximative solutions $x^{(N)}_{\mathrm{likecos}}(t, \alpha)$ and $x^{(N)}_{\mathrm{likesin}}(t, \alpha)$, given by (5.2) and (5.3), respectively, when $\omega_0 = 2$ and $\omega_\alpha = 1$ (Figure 5). We note that for $\alpha = 0$ on the boundaries of the surface of the eigen-modes, the limit line is the graph of the cosine and sine function. Then, the modes are purely harmonic, because it is a linear differential equation with one of the particular solutions of the form $x_{\mathrm{likecos}}(t, 0) = \cos\left(\widetilde\omega\, t\right)$ (left) and $x_\mathrm{likesin}(t, 0) = \sin\left(\widetilde\omega\, t\right)/\widetilde\omega$ (right), where $\widetilde\omega = \sqrt{\omega_0^2+\omega_{\alpha = 0}^2} = \sqrt{5}\approx 2.23607$. Precisely, in Figure 6 (left) we present the eigen-mode $x^{(N)}_{\mathrm{likecos}}(t, \alpha)$ for some selected values of $\alpha = 0, 1/2, 1$.The effect of the number of terms $N$ in the approximate sum (5.2) on the accuracy of this approximation is shown in Figure 6 (right). Since we have the exact formula for $\alpha = 0$, $x_{\mathrm{likecos}}(t, 0) = \cos\left(\widetilde\omega\, t\right)$, where in our case $\widetilde\omega = \sqrt{\omega_0^2+\omega_{\alpha = 0}^2} = \sqrt{5}$, we have calculated the relative errors in approximations $x^{(N)}_{\mathrm{likecos}}(t, 0)$, taking $N = 30, 40$, and $50$,

Plots of $t\mapsto \mathrm{Err}_N(t)$ in $\log$-scale are shown in Figure 6 (right). It is obvious that the relative error increases with $t$. In our domain $(t < 8)$ for $N = 40$, this relative error is less than $10^{-20}$, which, roughly speaking, we have 20 correct decimal digits in the approximation. This was the main reason for choosing the number of terms in the finite sum.

Behavior of the first derivatives in time of the eigen-modes,

and

are shown in Figure 9. Note that $\dot{x}_{\mathrm{likesin}}^{(N)}(t, \alpha) = x_{\mathrm{likecos}}^{(N)}(t, \alpha)$.

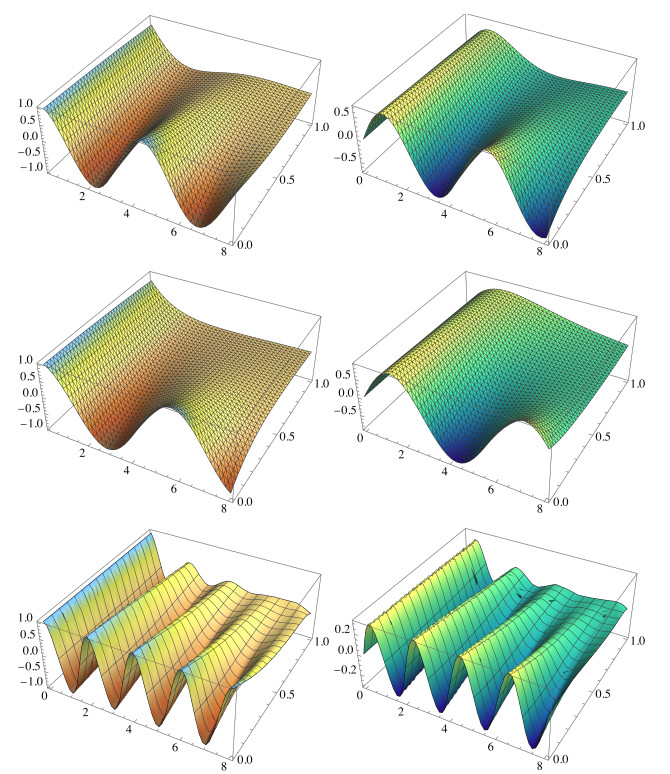
Example 5.2. Here, we give graphics of the corresponding approximative solutions $x^{(N)}_{\mathrm{likecos}}(t, \alpha)$ and $x^{(N)}_{\mathrm{likesin}}(t, \alpha)$ for some different values of $\omega_{\alpha}$ and $\omega_0$.

Three following cases are considered and presented in Figure 8:

● $\omega_{\alpha} = \omega_0 = 1$ (above);

● $\omega_{\alpha} = 1$ and $\omega_0 = 1/2$ (middle);

● $\omega_{\alpha} = 1$ and $\omega_0 = 3$ (below).

5.2.   Graphics of the forced mode

In the sequel, we give the corresponding graphics for approximations of the forced mode $x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$, given by (5.4), for different values of the frequency $\Omega$. Usually, we take $N = 40$.

According to Theorem 4.2 and Remark 1, in our computation we will use Eqs. (4.32) and (4.33), supposing that $\varphi_0 = 0$. For the beginning we want to determine $x_{\mathrm{part}}(t)$ in the case when $\alpha = 0$. Then, using directly (4.24) for $\alpha = 0$, we get

i.e.,

The general solution of the nonhomogeneous differential equation (4.18) (for $\alpha = 0$ and $\varphi_0 = 0$) is given by

i.e.,

which satisfies the conditions $x(0)\bigl|_{\alpha = 0} = x_0$ and $\dot x(0)\bigl|_{\alpha = 0} = \dot{x}_0$. The last equation shows that the first two oscillations in (5.6) are with the eigen frequency $\widetilde\omega = \sqrt{\omega_0^2+\omega_{\alpha = 0}^2}$, and third one is a forced oscillation

with the frequency $\Omega$. Notice that this forced oscillation is always a part of the particular solution $x_{\mathrm{part}}(t)\bigl|_{\alpha = 0}$.

Remark 2. A general case with $\varphi_0\ne0$ can be considered in a similar way. The corresponding expression is a slightly more complicated than (5.5), namely

Remark 3. If in differential equation (4.18), instead of $h\cos(\Omega\, t+\varphi_0)$ the external force $h\sin(\Omega\, t+\varphi_0)$ acts, the corresponding particular solution of this equation, in the case $\alpha = 0$, has the following form:

Taking again $x(t)\bigl|_{\alpha = 0} = x_\mathrm{likecos}(t)\bigl|_{\alpha = 0}+x_\mathrm{likesin}(t)\bigl|_{\alpha = 0}+x_{\mathrm{part}}(t)\bigl|_{\alpha = 0}$, we see that there are three oscillations, two of them with the eigen frequency $\widetilde\omega$ and the third one is a forced oscillation like (5.7), i.e., $x_{\mathrm{forced}}(t) = {h}/\left(\omega_0^2+\omega_{\alpha = 0}^2-\Omega^2\right)\sin (\Omega\, t+\varphi_0)$. For $\varphi_0 = 0$, the last expression becomes much simpler

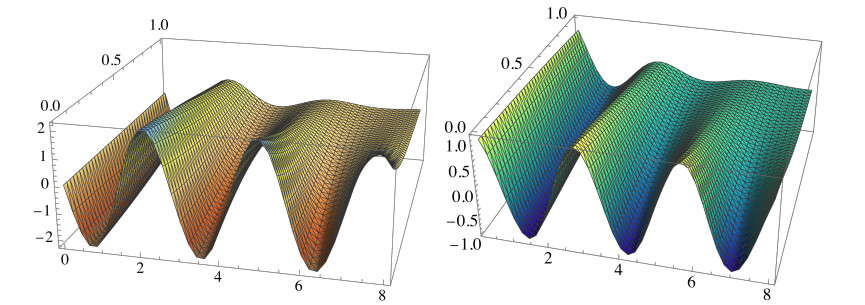
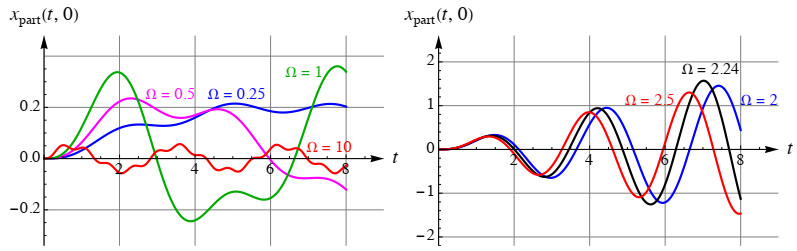
Example 5.3. As before, we take $\omega_{\alpha} = 1$ and $\omega_0 = 2$, as well as $h = 1$. Using Eq. (5.5), we present the graphics $t\mapsto x_{\mathrm{part}}(t, 0)$ for different values of $\Omega$ in Figure 9.

In this oscillatory system of fractional order, with one degree of freedom of forced oscillation (in a mechanical or electrical oscillator), we can observe a different behavior of the particular solution around one specific value of the frequency $\Omega_0$ (see graphics in Figure 9, left and right) in comparison to the cases with lower and higher frequencies and in the same time interval. This value depends on the elements of the system, $\omega_{\alpha}$ and $\omega_0$, and in our case it is $\Omega_0 = \sqrt{\omega_{\alpha}^2+\omega_{\alpha}^2} = \sqrt{5}\approx 2.236$. In the same time interval, for frequency values around $\Omega_0$, this particular solution has the smallest number of whole oscillations, in relation to lower or higher frequencies of external forces on the oscillatory system (mechanical or electrical), when it has a larger number of whole waves.

The corresponding $3D$-graphics of $x_{\mathrm{part}}^{(N)}(t, \alpha)$ in the domain

for the same values of $\Omega$, are presented in Figures 10 and 11. Note that the curves for $\alpha = 0$ (which are shown in Figure 9) are especially highlighted in these 3D-plots. Specifically, in Figure 11 (down) the $3D$-graphic is shown for the frequency $\Omega = 2.24$, viewed from two different positions.

Example 5.4. In this example we consider approximative solution (5.1), i.e.,

of the nonhomogeneous differential equation

of the fractional order $\alpha$ $(0 < \alpha < 1)$. As we have seen, the exact solution of this equation can be developed in the form of a series (see (4.32)–(4.33)).

Taking $x_0 = 0$, $\dot x_0 = 0$, $h = 1$, and $\varphi_0 = 0$, we analyze the approximations $x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$ as functions, defined in the domain $\bigl\{(\Omega, \alpha)\, |\, 0 < \Omega < 10, \ 0 < \alpha < 1\bigr\}$, i.e., functions $(\Omega, \alpha)\mapsto x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$ in two variables $\Omega$ and $\alpha$, for some fixed values of $t$. These approximations are determined by the first $N+1$ terms of the series (see (5.4)).

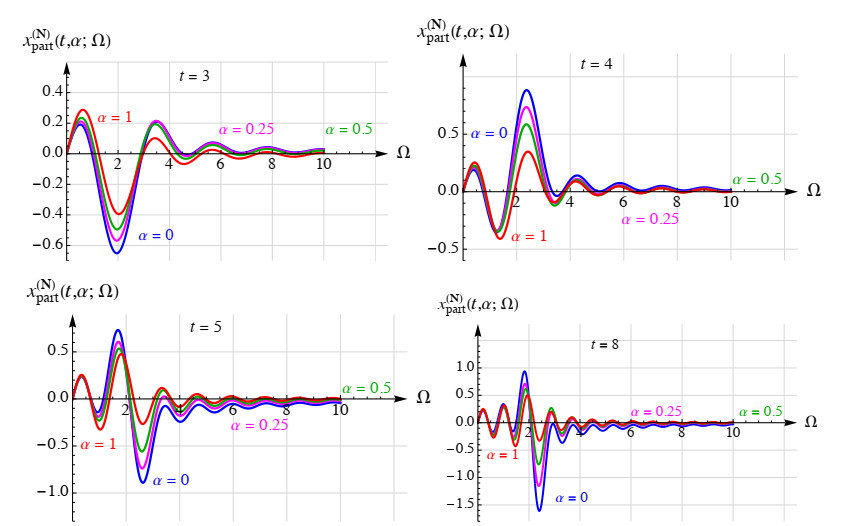
Before this type of observation, we consider one-dimensional functions $\Omega\mapsto x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$, fixing also the values of $\alpha$. This approach is simpler and clearer. We take different values of $\alpha\, ( = 0, 1/4, 1/2, 1)$ and some selected $t = 3, 4, 5, 8$.

The graphics $\Omega \mapsto x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$ are presented in Figure 12. In our calculation of $x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$, for $t = 3$ and $t = 4$, we used $N = 20$; for $t = 5$ we used $N = 30$, and for $= 8$ it was $N = 40$.

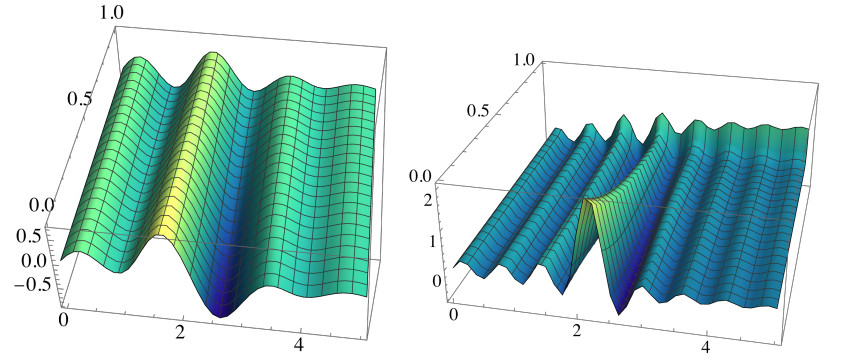
In Figure 13 we present the corresponding $3D$-graphics taking $\alpha$ $(0 < \alpha < 1)$ as a second coordinate. Thus, our $3D$-graphics of the function $(\Omega, \alpha)\mapsto x_{\mathrm{part}}^{(N)}(t, \alpha; \Omega)$ in the domain $\bigl\{(\Omega, \alpha)\, |\, 0 < \Omega < 10, \ 0 < \alpha < 1\bigr\}$ are given for $t = 5$ (left) and $t = 10$ (right). From the both of Figures 12 and 13, we can see that the elongation (amplitude) of the oscillation $x_{\mathrm{part}}(t, \alpha; \Omega)$ increases with increasing time $t$, when $\Omega\to\Omega_0$. This resonant frequency $\Omega_0$, with our parameters is $\Omega_0\approx 2.236$. Then resonance occurs in the system and the system oscillates at its eigen frequency (examples are oscillators in electronic circuits).

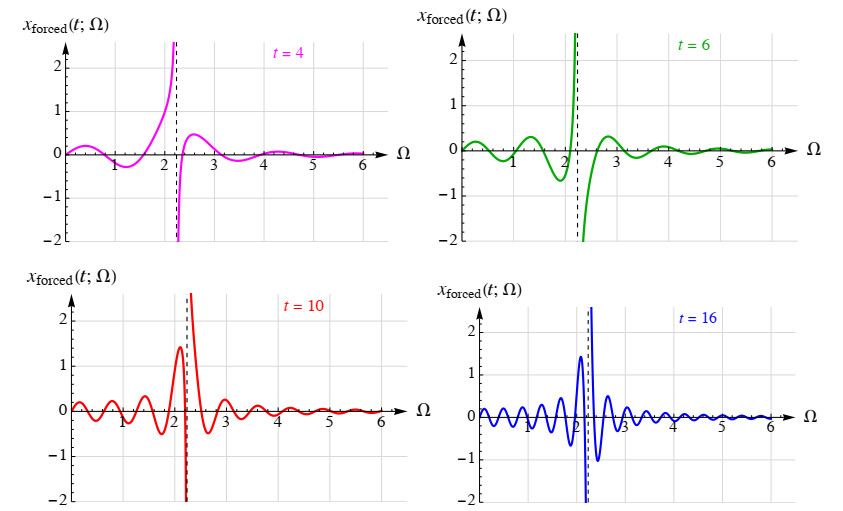
That is much clearer if we consider only the forced oscillation, in notation $x_{\mathrm{forced}}(t, \alpha; \Omega)$, as a part of $x_{\mathrm{part}}(t, \alpha; \Omega)$, which is easy to do only for $\alpha = 0$, namely using

(see Eq. (5.7), as well as Remarks 2 and 3). We get the graphics $\Omega\mapsto x_{\mathrm{forced}}(t, 0;\Omega)$ in Figure 14 for some fixed values of $t$. We can see that

Vertical asymptotes on the graphics are indicated by dashed vertical lines at the point $\Omega = \Omega_0 = \sqrt{5}\approx 2.236$.

For $\alpha\ne0$, it would be very interesting to extract $x_{\mathrm{forced}}(t, \alpha; \Omega)$ or its finite part $x_{\mathrm{forced}}^{(N)}(t, \alpha; \Omega)$ from the general expression (4.32) or (5.4), respectively.

6.   A special class of discrete oscillators of fractional type, with a finite number of degrees of freedom of oscillation and independent eigen-modes and forced modes, of fractional type

In this part, using the matrix method, we describe forced oscillations of the fractional type, under the action of single frequency force, as well as their independent modes, which are realized in one class of discrete system of fractional type, with a finite number $n$ of degrees of freedom of oscillation. We describe the configuration of such a system with a matrix column $\{x\}$, whose elements are independent generalized coordinates $x_k$, $k = 1, 2, \ldots, n$, because their number corresponds to the number of degrees of freedom of oscillation of that discrete system of fraction type.

Such a class of discrete systems of fractional type, with a finite number of degrees of freedom of system $n$, is described by means of three matrices of dimensions $n\times n$, namely: an inertia matrix $A$, a stiffness matrix $C$ and a fractional type property matrix $C_\alpha$. The elements of the inertial matrix $A$ are $a_{kj}$ $(k, j = 1, 2, \ldots, n)$. The coefficients of elasticity, as elements of the stiffness matrix are $c_{kj}$ $(k, j = 1, 2, \ldots, n)$, while the elements of the matrix $C$ are denoted as $c_{\alpha, kj}$ $(k, j = 1, 2, \ldots, n)$, where $0 < \alpha < 1$.

Let the system be acted upon by an external force $Q_1(t) = Q_{01}\sin\Omega t$ on the inertial element $a_{11}$, then we can introduce a column matrix of forced forces in the form of $\{Q_{0, i}\}\sin\Omega t$. We can use all those matrices in the following form: $A = (a_{kj})_{1}^n$, $C = (c_{kj})_{1}^n$, $C_\alpha = (c_{\alpha, kj})_{1}^n$, $0 < \alpha < 1$, and

A system of $n$ ordinary nonhomogeneous differential equations in matrix form, which describe forced oscillations (of the fractional type) of the previously defined class of discrete systems, with $n$ degrees of freedom of oscillation, can be written in the form:

Now, we use a matrix formula for the transformation of the independent generalized coordinates $\{x\}$, with $x_k$, $k = 1, 2, \ldots, n$, to the main coordinates $\{\xi\}$, with $\xi_k$, $k = 1, 2, \ldots, n$, of the studied class of systems of fractional type, in the following form $\{x\} = R\{\xi\}$ (cf. ^[17,23]).

In the previous transformation formula, the matrix $R$ is the modal matrix of the corresponding linear system of equations in the form $R = \left(\left\{ K_{nk}^s(\omega_s^2)\right\}\right) = \left(K_{nk}^s\right)_1^n$, in which the elements $K_{nk}^s(\omega_s^2)$ are determinant cofactors from the frequency equation of the corresponding linear system $f(\omega^2) = \left|C-\omega^2A\right| = \{0\}$.

Using the transformation formula $\{x\} = R\{\xi\}$, we enter the main coordinates $\{\xi_s\}$ $(\xi_s, \ s = 1, 2, \ldots, n)$ into the system of ordinary nonhomogeneous differential equations (6.2) of fractional order, replacing the independent generalized coordinates $\{x\}$ $(x_k, \ k = 1, 2, \ldots, n)$, so that we obtain the following matrix differential equation of fractional order

Then, we multiply the obtained matrix differential equation (6.3) from the left side by the transposed modal matrix $R'$ and introduce the following new notations

For a given external single-frequency force to the system, we have

Taking into account the newly introduced notations, the system of ordinary nonhomogeneous differential equations (6.3) of fractional order can be written in the following matrix form

Since $R' = \left(K_{nk}^s\right)_{1}^n$ we have

For our class of discrete oscillatory systems of the fractional type, the connection between the stiffness matrix and the matrix of the fractional type properties of the system is given by $C_\alpha = \kappa C$. In that relation $\kappa$ is some real number. It is easy to conclude that the matrix differential equation of fractional order (6.4) on the left side contained all three diagonal matrices $\mathfrak{A}$, $\mathfrak{C}_{\alpha}$ and $\mathfrak{C}$.

This indicates to us the fact that this matrix differential equation of fractional order contains a system of mutually independent ordinary nonhomogeneous differential equations of fractional order, such that each of them contains only one principal coordinate $\xi_s$ from the set of principal coordinates of the system $\xi_s$, $s = 1, 2, \ldots, n$. Such equations can be written in the scalar form

By introducing standard notation $\omega_s^2 = {\mathfrak{c}_{ss}}/{\mathfrak{a}_{ss}}$, $\omega_{(\alpha)s}^2 = {\mathfrak{c}_{(\alpha)ss}}/{\mathfrak{a}_{ss}}$, $h_s = {K_{n1s}^s Q_{01}}/{\mathfrak{a}_{ss}}$, $s = 1, 2, \ldots, n$, for each of these independent differential equations

we can state the result on independent forced modes of fractional type for the class of oscillators of systems with a finite number of degrees of free oscillations considered in this section.

Theorem 6.1. The matrix nonhomogeneous nonautonomous differential equation (6.4), i.e.,

contains a system of $n$ independent nonhomogeneous nonautonomous scalar differential equations of fractional order (6.5).

Based on this result, as well as Theorem 4.2 and Remark 1, we can state the following result:

Theorem 6.2. The solution of the system of the equations (6.5) can be expressed for each $s = 1, 2, \ldots, n$ in the form

where $c_{k, j}(t, \alpha, \Omega)$ is defined by (4.33).

The analytic solution (6.6) describes the independent forced modes of a fractional-type oscillator with a finite number $n$ of degrees of freedom of oscillation. As before, this solution contains three terms, the first two of which correspond to their own eigen free oscillations of the fractional type, $\xi_{s, \mathrm{likecos}}(t)$ and $\xi_{s, \mathrm{likesin}}(t)$, while the third one corresponds to the particular solution and originates from external single frequency force, in notation $\xi_{s, \mathrm{part}}(t)$. Therefore, this solution (6.6) can be decomposed as

$s = 1, 2, \ldots, n$, where $\xi_{s, \mathrm{free}}(t) = \xi_{s, \mathrm{likecos}}(t)+\xi_{s, \mathrm{likesin}}(t)$, $s = 1, 2, \ldots, n$, can be done as before in form (4.15)–(4.17). There is no interaction between these forced modes of fractional type, so that they represent independent oscillators, each with one degree of freedom.

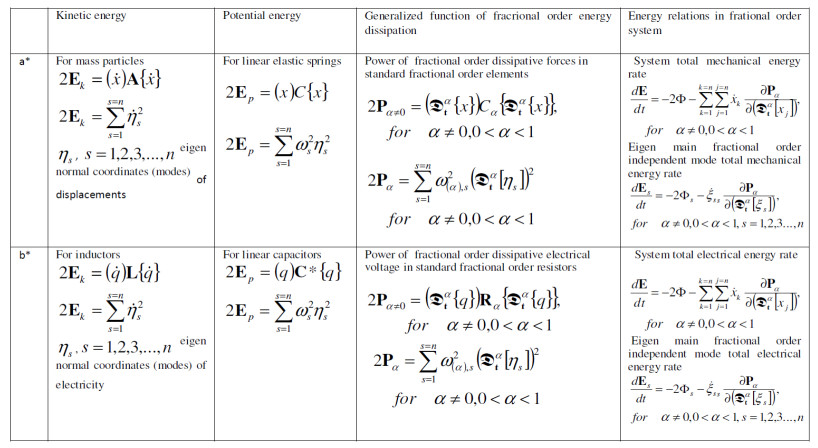
Expressions for kinetic and potential energies, for the generalized function of dissipation (scattering) of the total energy of the system of the fractional type, as well as the relation of change with time of the total energy of the system, are shown by columns in Table 2. Those expressions are shown by type for mechanical and electrical system of the fractional type and with a finite number of freedom of oscillation.

7.   Energy analysis of the oscillations of a special class of discrete oscillators of the fractional type, with a finite number of degrees of freedom of oscillation and independent eigen-modes and forced modes of the fractional type

In this section, we analyze the total mechanical, i.e., electrical energy, which oscillates discrete oscillators of the fraction type, with a finite number of degrees of freedom of oscillation. This special class was analyzed in the previous part, including nonhomogeneous nonautonomous differential equations of fractional order as well as their solutions.

Now we will focus our considerations first on the total dynamic energy of such a fractional-type system, which oscillates over time, and then on its change during oscillation, bearing in mind that it is a dissipative system with fractional-type energy dissipation.

Using the already introduced notations in previous considerations, we write the following expressions for kinetic and potential energies using matrices: $2E_k = (\dot x)A\{\dot x\}$, $2E_p = (x)C\{x\}$, as well as Rayleigh's function of linear dissipation of energy, generalized function of dissipation of system energy of fractional type $2\Phi = (\dot x)B\{\dot x\}$, where $B = (b_{kj})_{k, j}^n$, and $2P_{\alpha\ne0} = \left(\mathfrak{D}^\alpha_t\right)C_\alpha \left\{\mathfrak{D}^\alpha_t\{x\}\right\}$ for $0 < \alpha\le1$.

For $\alpha = 0$ and $\alpha = 1$, we have $2E_{p, \alpha} = 2P_{\alpha = 0} = (x)C_{\alpha = 0}\{x\}$ and $2\Phi = 2P_{\alpha = 1} = (\dot x)C_{\alpha = 1}\{\dot x\}$, respectively.

Extended Lagrange's differential equations in matrix form are (see ^[17])

If we multiply the previous matrix equation on the left side by the matrix-row $(\dot x)$ of derivatives of independent generalized coordinates, we get

Now, we analyze and transform individual terms-products from the previous matrix equation (7.1):

Then, Eq. (7.1) becomes

Since the total energy of the system is $E = E_k+E_p$ we get

This is a new relation and it, in fact, gives a mathematical description of the theorem on the change of the total energy of a fractional type system, with a finite number of degrees of freedom of oscillation. It is valid for any fractional type system, when the system is forced to oscillate. Therefore, relation (7.2) is valid for every system that is in forced oscillation mode.

For a discrete system of fractional type, with a finite number of degrees of freedom of oscillation $n$, defined as in Section 6, with the matrices of order $n$: $A$ (inertia matrix), $C$ (stiffness matrix), and fractional properties matrix $C_\alpha$ for $0 < \alpha < 1$, as well as with a linear damping matrix $B = (b_{kj})_1^n$, we formulate the following result, based on the relation (7.2). Assume that the system is acted upon by an external coercive force $\{Q\}$.

Theorem 7.1. Let $2E_k = (\dot x)A\{\dot x\}$ and $2E_p = (x)C\{x\}$ be expressions for the kinetic and potential energy, as well as $\Phi = \frac{1}{2}(\dot x)B\{\dot x\}$ for Rayleigh's function of linear energy dissipation and let the generalized function of the system energy dissipation of the fractional type be given by $2P_{\alpha\ne0} = \left(\mathfrak{D}^\alpha_t\right)C_\alpha \left\{\mathfrak{D}^\alpha_t\{x\}\right\}$ for $0 < \alpha\le1$.

For such a system the relation (7.2) holds, which gives the relationship of the change in the total energy of the system in time and working power of resisting forces and working power of active forces acting on the system of fractional type.

The relation says (7.2) that the change of the total energy of the system of fractional type in time is equal to the work power of active forces and reduced by the work power of resistive dissipative forces of linear and fractional type.

Further details on these topics can be found in ^[17,72] and the references cited therein.

8.   Analogy examples of mechanical and electrical forced oscillators of fractional type, with a finite number of degrees of oscillation

In this section, we focus our attention to oscillations of fractional type, on two analogous oscillators, one mechanical and the other electric. They oscillate under the action of an external active single-frequency periodic force $F_1(t) = F_0\sin\Omega t$ and the action of a periodic electric voltage $V_1(t) = V_0\sin\Omega t$, respectively.

Here, we present the corresponding systems of nonhomogeneous differential equations of the fractional type, and the dynamics of the observed analogous models and indicate that their mathematical description fully corresponds to those presented in Sections 6 and 7. Therefore, for special numerical values of system parameters, they can be represented graphically by similar surfaces as in Section 5 for main eigen and forced modes of fractional type.

In our examples, we use $n$-order diagonal and symmetric tridiagonal matrices,

and

where the elements outside these diagonals are zero.

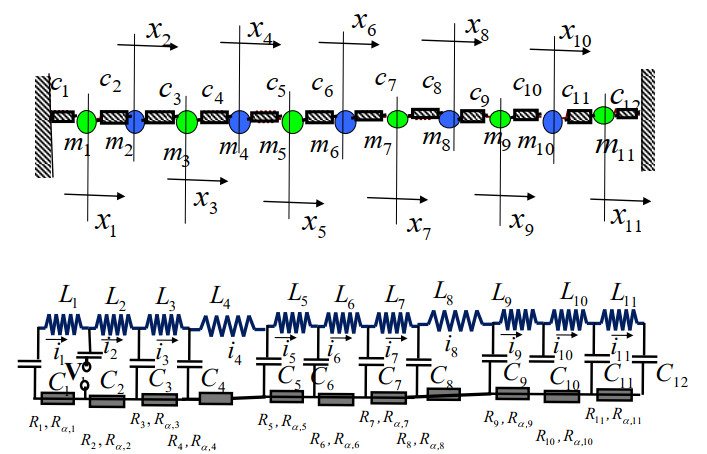
Example 8.1. In Figure 15, two mathematically analogous models of oscillators of the fractional type are shown. One model is of a mechanical chain system, clamped (fixed) on both sides, and the other model is of an electric chain circuit. Both have the same number of degrees of freedom of oscillation, as shown in Figure 15.

For the mechanical oscillatory system of fractional type in Figure 15 (top), the characteristic matrices of order $n = 11$ are: the matrix of inertia coefficients $A = M_{11}$, with the diagonal elements $d_k = m_k$ $(k = 1, 2, \ldots, 11)$ and the tri-diagonal matrix of stiffness $C = J_{11}$, with the elements

The matrix of fractional properties of the chain mechanical system is $C_\alpha = \kappa_\alpha C$, in which $\kappa_\alpha$ is a real number. Since, the first material point of the chain system of fractional type is affected by a coercive force, it can be presented to the matrix form (6.1), so that the matrix ordinary nonhomogeneous nonautonomous differential equation of fractional type for the mechanical chain from Figure 15 (top) is given by (6.2), i.e.,

For the electrical oscillatory system of the fractional type (Figure 15, down), the characteristic matrices are: the matrix of inertia coefficients (self-inductance of the self-induction coils) $A = M_{11}$, with the diagonal elements $d_k = L_k$ $(k = 1, 2, \ldots, 11)$ and the stiffness matrix (capacitance of the capacitor) of the system $C = J_{11}$, with the elements

The number of fractional properties of electrical resistors (of fractional type) of a chain electrical system (circuit) is $C+\alpha = J_{11}$, with elements

as well as $C_\alpha = \kappa_\alpha C$, where $\kappa_\alpha$ is a real number.

As the first electrical sub-circuit of the electrical chain system is affected by the forced electric single frequency voltage, it can be expressed in matrix form

and the corresponding matrix of the ordinary nonhomogeneous nonautonomous differential equation (of fractional order) for the electrical chain system (Figure 15 (down)) is given by

in which the matrix $\{q\}$ is a column of capacitor charges in an electric chain system. This matrix of nonhomogeneous differential equations of fractional order is quite mathematically identical with (8.3) and their properties and solutions are given earlier in Section 6, and the properties of the system are described in Section 7.

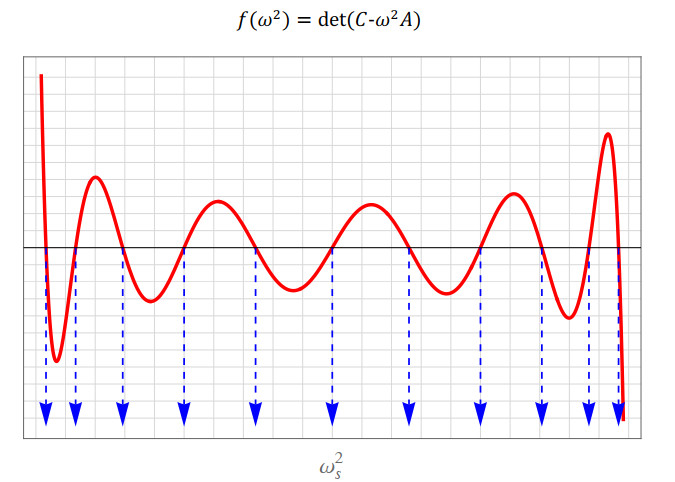
Graphics of the frequency function $f(\omega^2) = \det(C-\omega^2 A)$ of the corresponding linear system is shown in Figure 16, from which the squares of the eigen circular frequencies $\omega_s^2$ $(s = 1, 2, \ldots, 11)$ can be read, and then, for the considered class of systems, the coefficients $\omega_{(\alpha)s}^2 = \kappa_{\alpha, s}\omega_s^2$ $(s = 1, 2, \ldots, 11)$ can be determined. Now, we can describe the oscillations of the forced main independent modes by

Here, we will pay special attention to homogeneous chains. For those chains, using the trigonometric method of Rašković, the squares of the eigen circular frequencies $\omega_s^2$ and $\omega_{(\alpha)s}^2$ can be found as (see ^[69,70,71])

Notice that $\omega_{12-s}^2 = 4c/m-\omega_s^2$, $s = 1, 2, \ldots, 6$. Thus,

Using earlier presented results and the solution from Theorem 6.2, it is easy to describe eleven independent principal forced modes of fractional type. All these eleven independent forced modes of fractional type do not interact with each other. There is no exchange of mechanical energy between them. Each one oscillates with its initial total energy, which changes during the oscillation, and this change is described in detail in ^[17]. Finally, we mention that this example can be extended to an arbitrary number $n$ of independent principal forced modes of fractional type.

Example 8.2. Two mathematical analogous oscillator models of fractional type are shown in Figure 17. One is a model of a mechanical system, with two degrees of freedom of oscillation, and the second one is a model of an electric circuit, containing two elementary electric circuits.

Let us direct our attention to the electric oscillatory system of the fractional type, with two degrees of freedom of oscillation (on the left in Figure 17). For independent generalized coordinates, we adopt quantities of electricity in capacitors $q_1$ and $q_2$. The kinetic parameters of the electric system in Figure 17 are indicated by $L_1, L_2, L_3$ (parameters of self-inductance of self-inductive coils), $C_1, C_2, C_3$ (capacitance of capacitors), $R_{\alpha, 1}$, $R_{\alpha, 2}$, $R_{\alpha, 3}$, $0 < \alpha\le1$ (parameters of fractional properties of electrical dissipative resistors of fractional type). The electrical system is excited by a periodic single-frequency electric voltage $V_1(t) = V_0\sin\Omega\, t$ of the amplitude $V_0$ and the circular frequency $\Omega$, acting through the first independent generalized coordinate $q_1$. The system of ordinary nonhomogeneous nonautonomous differential equations of fractional order, which describe the oscillation of the fractional type of this electrical system, is given in the form

The kinetic and potential energies of this electrical system of fractional type are given by

and Rayleigh's function of linear energy dissipation, as well as the generalized energy dissipation function, which originates from electrical resistors, are given by

and

respectively. The corresponding matrices of this system can be obtained from (8.4) in the form

and

In case there is a connection $C_{0 < \alpha\le 1} = \kappa C$, the fractional-type electric oscillator model belongs to a special class of fractional-type oscillators, which have independent and own modes of free oscillations, as well as the main forced modes of oscillations of forced oscillations of the fractional type system. If there is no previous connection, the electric oscillator has coupled, both natural and forced modes of the fractional type, the mode interaction is present, as well as the transfer of the total energy of one mode to another, which interacts with the energies of other modes, and the system behaves as a nonlinear system.

The frequency function of the system (8.4) has the following form:

After finding two roots $\omega_s^2$ $(s = 1, 2)$ of the quadratic equation $f(\omega^2) = 0$ in $\omega^2$, and also the coefficients $\omega_{(0 < \alpha\le1), s}^2$ $(s = 1, 2)$, we are able to transform the system of equations (8.4) to a system of two independent nonhomogeneous nonautonomous differential equations of fractional order, given by (6.5), and then apply Theorem 6.1 for finding the final two independent eigen-modes of free oscillations of the fractional type, as well as two independent forced motions of the fractional type.

The mechanical analogue of the electric oscillator is shown in Figure 17 (right).

9.   Concluding consideration

The main motives of this article are to explain the elements of mathematical phenomenology through a mathematical, qualitative and structural analogy between mechanical and electrical fractional-type oscillatory systems, to give descriptions of disparate physical processes in both analogous systems, to introduce a resistor of fractional type, as well as to introduce the generalized energy dissipation functions in these two analogous oscillatory systems. This conclusion also extends the field of analogy of the fractional-type system model to oscillatory systems with a complex structure of coupled beams, coupled plates, or coupled membranes.

Table 3 shows one of those extensions of analogies (mathematical, qualitative, and structural), from discrete mechanical and electrical systems with a finite number of degrees of freedom of oscillation to their own time functions, their modes in one of the infinite number of amplitude functions of the form depending on boundary conditions, and the number of coupled deformable bodies (beams, membranes, or plates) distributed by standard light elements of the fractional type in the layer between coupled bodies. The table quite obviously provides a good illustration of the extended structural analogy.

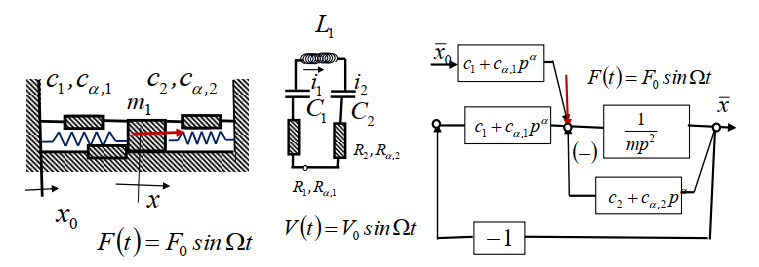
Using an idea from automatic control (see reference ^[73]), we put together a block diagram for controlling system oscillations of fractional type, with one degree of freedom of oscillation, which is presented in Figure 18. It is the basis for modeling the structure and also, the electrical oscillator with one degree of freedom of oscillation, which is analogous to the presented mechanical oscillator. This approach to oscillation control can also be used for modeling structures, as well as oscillation control and systems with multiple degrees of oscillation freedom. Of course, here our focus has not been on these possibilities, but we have only pointed out that the elements of mathematical phenomenology and the corresponding analogues can be used in the modeling of complex structures of mechanical and electrical oscillators with multiple degrees of freedom of oscillation, as well as coupled electromechanical structures of fractional type.

Author contributions

All authors contributed equally and efficiently while preparing this article.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are deeply grateful to the referees for their valuable comments and constructive suggestions for significant improvements of this paper and its better presentation.

The work of G.V. Milovanović was supported in part by the Serbian Academy of Sciences and Arts, Belgrade (Grant No. $\Phi$-96).

Conflict of interest

The authors declare there is no conflict of interest.