1. Introduction
The microcirculation is the collective name for the smallest (<150 µm in diameter) blood vessels in the body. As a first approximation, it consists of blood vessels that are too small to be seen with the naked eye. Microcirculatory vessels are the site of control of tissue perfusion, blood-tissue exchange, and tissue blood volume. Each of these functions can be associated, though not exclusively, with a specific type of microvascular segment: arterioles, capillaries and venules. Arterioles are known as resistance vessels since a major fraction of total blood pressure dissipation occurs across them. Local and extrinsic stimuli (e.g., neural, metabolic, and mechanical) act on the thick muscular wall of arterioles, exerting control over the vessel diameter and modulating the level of local blood flow. The capillaries are the site of major exchange between blood and tissue. Nutrients and other molecules diffuse or are transported across the capillary wall to sustain life of the body's cells. Finally, venules are classified as capacitance vessels because most of the tissue blood volume is localized in these microvessels. Comprehensive, recent reviews on the biological, anatomical and structural aspects of the microcirculation can be found in [1,2,3]. In addition, there exist several review works focused on the microcirculation in specific organs and tissues, see, e.g., [4] for brain, [5] for kidneys, [6] for gastrointestinal organs and [7] for lungs.
Various techniques have been used to obtain a substantial amount of hemodynamic and geometric information about the microcirculation. For example, data has been obtained from studying whole organs both in vivo and in perfused conditions. The results of these studies are averaged quantities that give indirect information about microcirculatory behavior. Modern non-invasive imaging techniques are used to obtain data about normal and diseased states in microcirculation. Imaging techniques—including MRI, imaging with light and sound, optical techniques such as laser Doppler and multispectral imaging—show microvascular structure and provide measures of function via perfusion, oxygenation, or permeability parameters. We refer to [8,9,10] for reviews on these imaging techniques.
The role of theoretical models of the microcirculation has been described previously by Secomb in [11]. In this work, Secomb remarks that mathematical modelers of the microcirculation have pioneered the integration of knowledge across multiple levels of biological organization. He classifies models as phenomenological, qualitative, quantitative, and predictive. In the present review, we will adopt a similar classification for microcirculation models; furthermore, in our model classification we will also highlight the spatial dimension of the models (0D to 3D) and their mathematical features. In Figure 1, we present a schematic illustration of the classification and scale of mathematical models of the microcirculation that are reviewed in this study. Geometrically reduced 0D/1D models are capable of providing very useful information on whole-scale vascular beds or organs (e.g., the brain or kidney), even if they cannot provide a spatially-resolved information. On the other hand, 3D models can capture detailed and patient-specific components of the vascular anatomy, at the price of a rapidly increasing computational cost. The full range of models between 0D and 3D representations offer a balance of information and can be used to study a large spectrum of scales.
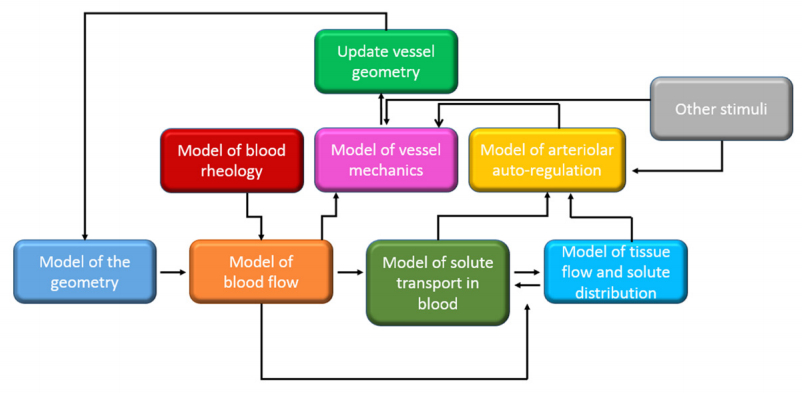
Theoretical modeling of microvascular networks typically involves several steps (see Figure 2). First, the geometry of the network must be specified. In this step, the length and diameter (or cross-sectional shape) of vessels are defined as well as the network connectivity. Next, fluid dynamics and blood rheology models are combined to predict the distribution of flow, pressure, and hematocrit throughout the network. Then, solute transport and delivery to the surrounding tissue is studied along the network. Vessel geometry may vary due to the interaction with the blood flow (fluid-structure problem) or the input of autoregulatory signals. Last, computed solute levels and other stimuli (neural, mechanical) may enter into the model of vessel regulation.
Several review articles address theoretical modeling of the microcirculation (recently, we refer to [12,13,14,15]. But, most of these papers focus on a specific aspect of modeling or on a specific scale of the problem. The aim of this work is to survey the mathematical approaches used broadly to study the microcirculation. Modeling microcirculatory networks requires ad hoc approaches. There are profound differences between modeling large/medium-sized blood vessels (e.g., the aorta, the circle of Willis, the femoral vessels) and modeling microcirculatory vessels. The number of vessels (a few vs. several thousand), vascular radial dimensions (cm vs. microns), the characteristic Reynolds and Womersley numbers (relevant vs. very low), and the role of blood rheology (Newtonian vs. corpuscular fluid models) are just some of the elements that impact the choice of mathematical and numerical models.
The present work is organized as follows. In Section 2 we review the definition of the geometry of microvascular networks and their surrounding tissues; in Section 3 we review models for blood flow when blood is modeled as a continuum or a corpuscular medium; in Section 4 we review models for gaseous solute transport in blood and delivery to tissue; in Section 5 we review models for vessel mechanics and autoregulation; in Section 6 we highlight models of the retinal microcirculation. Finally, in Section 7 we summarize the conclusions of our work and present perspectives on mathematical models in this field.
2. Modeling of Microvascular Networks and the Surrounding Tissue
Microvascular networks are very complex structures, and their complexity is often related to the tissue they are supplying. For example, the mesenteric microcirculation exhibits a fairly regular organization whereas the cerebral microcirculation differs greatly among subjects and within specific parts of the brain. In general, micro-vessels do not form precise arrays in the tissue; rather, their spacing is non-uniform and their pathways are often tortuous [15]. Different mathematical methods are chosen to describe the geometrical features of the different microcirculatory beds, where the degree of complexity included in the model depends on the environment being modeled.
2.1. Modeling of blood vessels
Despite the irregularities in network structure, almost ubiquitously, arterioles and venules are organized in tree-like structures and capillary beds in net-like structures. Arterioles and venules are thus analyzed with distinct models from capillaries. Vessels are generally classified as arterioles/venules or capillaries based on diameter. Within these classifications, vessels are often divided into more specific subclasses with explicit diameter ranges [16,17]. The number of vessels in a certain class or subclass may dictate the type of model used to describe that class. For example, in complex 3D geometries with thousands of vessels, capillaries can be represented in a simplified manner to reduce the computational cost [18,19]. The modeling choice may also reflect the resolution limit of available imaging techniques. Last, but not least, since microvascular beds are the main site of metabolic exchange, it is also important for models to account for the tissue environment in which the microvessels are embedded.
2.1.1. Arteriolar and venular trees
We define two main types of arteriolar and venular tree models: (ⅰ) compartmental models, in which there is no topology (or connectivity) of the vessel branches, and (ⅱ) topological
models, in which a proper, connected, anatomical network is built according to geometrical data. Compartmental models maintain a low number of unknowns and are capable of reproducing the global behavior of the system. The more complex topological models account for the spatial distribution of field variables and the complexity of interactions among vessels in the microcirculatory network.
In the compartmental approach, several authors exploit the analogy of a vascular network with an electric circuit, formed by lumped resistive, capacitive and inductive elements. This reduced modeling approach allows for the inclusion of the microcirculatory network within a more comprehensive system, as in whole brain circulation studies [20,21]. Other compartmental models represent the arteriolar and venular trees as idealized classes of different hierarchy; for example, compartments are defined for large arterioles, small arterioles, capillaries, small venules and large venules [22]. The vessels comprising each compartment are arranged in parallel and are assumed to exhibit identical properties. The compartments are connected in series by conservation laws, so that each flow pathway from the arterial inflow to the venous drainage is equivalent. The functional characteristics of complete vascular beds are then derived, in an averaged sense, from the properties of the individual vessel classes and the number of vessels within each class.
In the topological approach, anatomically-specific geometrical data are used to build the model. Usually, the tissue is represented as a simple volumetric shape (e.g., cube, parallelepiped, cylinder) of linear dimension ranging from a hundred microns to a few millimeters. The main complexity resides in the representation of the embedded vessel network. According to a "topological geometrical" approach, vessel trees are constructed ex-novo using a mathematical algorithm that retains the relevant vascular morphology and topology. Principles of fractal geometry derived from Murray's law have been used in [23,24] to define the diameter of daughter vessels sprouting from a bifurcation. The degree of asymmetry of the network can be controlled via an asymmetry parameter as in [25,26] or using distributions of generation numbers using, for example, the Horton-Strahler approach as in [27,28]. Stochastic growth techniques have been adopted to obtain random graphs (see [1], Ch.1, for a review), including the diffusion limited algorithm used in [29] to obtain a network with a prescribed fractal dimension. In the "topological anatomical" approach, the network geometry (vessel radii and lengths) is extracted from digitized images of experimental measures. A relevant problem is constituted by the reconstruction of the graph connectivity. Generally, a backbone system of vessels is identified (see the procedure detailed in [19]). Semi-automatic or manual techniques are then used to segment the backbone and prune dead-end vessels. In [30], intravital microscopy was used to define the vessel lengths and connection patterns in the mesenteric plexum. Vessel diameters were measured manually at the center of each segment. In [17], raw data were obtained from a multi-diode target camera of rodent mesentery. Network connectivity, topology and diameter distribution were manually reconstructed from the images, and a Bézier approximation was used to enhance the segment tortuosity.
Over time, the resolution limits of various imaging techniques have vastly improved. For example, adaptive optics and ultra-high resolution optical coherence tomography has allowed for ultrahigh 3D resolution (3 × 3 × 3 µm3) to capture data on the smallest capillary vessels. However, details of the smallest capillary vessels have not always been possible to obtain, and thus several models include artificially generated geometrical trees to account for these small vessels. For example, in [31], a 3D model of a 3 × 3 × 3 mm3 portion of the human brain secondary cortex was presented. A backbone of visible large microvessels was reconstructed from high-resolution images, and smaller artificially generated segments were successively added using constructive optimization techniques. In [32], a network was obtained from high-resolution images of the mouse primary somatosensory cortex, ranging from the pial vessels to individual brain cells. In [16], images of the eye fundus were acquired and arteriolar vessels of the retina were segmented. Terminal arterioles with outlet diameter greater than 30 microns were connected with asymmetric structured fractal trees representing smaller vessels. Mixed topological/compartmental models were used by some authors to describe in detail certain portions of the network and, at the same time, represent other portions of the network in a lumped manner. For example, in [33], upstream and downstream portions of an otherwise microvascular anatomically accurate network were modeled by large arteries/veins and large arterioles/venules classes. In [20], lumped arteriolar/venular networks were coupled with more detailed models of larger vessels.
All topological networks are eventually reduced to graphs for computational purposes. The network graph is uniquely described by the node coordinates and by the connectivity matrix. In the latter, the (i, j)-th element is equal to one if node i is connected to node j and zero otherwise, leading to the creation of one ''arc''. A single vessel can be composed of several arcs arranged in cascade or by a single arc. Vessel junctions are nodes at which different vessels are connected to each other. The most frequently adopted type of junction is the bifurcation (see the discussions in [18] and in [34]).
2.1.2. Capillaries
Capillary beds are composed of an extremely large number (>104) of tiny vessels (diameter ranging from 5 to 9 microns). Representations of capillaries using a vessel-by-vessel description are technically feasible but would be restricted to a small tissue region [30,33]. In certain topological geometrical models, capillaries are arranged as a compartment of parallel vessels, as in [23]. However, this representation does not fully describe the real net-like organization of capillaries. To model the net-like structure of capillary beds, some studies use mathematical algorithms to generate coherent capillary meshes. In [17] and [35], the capillary beds were generated on the basis of a Voronoi tessellation. In [27], a concentric circle mesh-like model was proposed to simulate capillaries in the rat retina. In [34], statistical algorithms were used to explore how the structural properties of the capillary bed influence the transport of blood through the human cerebral microvasculature. Sprouting angiogenesis algorithms are often used to generate capillary networks embedded in tumoral tissues (see, e.g., [36,37,38,39]). The network shape is forged by stimuli coming from the tumor itself.
2.2. Tissue
Unlike large blood vessels, microcirculatory vessels are embedded within tissues. This enables communication and mass (fluid, solute) exchange between the parenchymal tissue and these vessels. Several models thus couple a tissue description with the microcirculatory network. In compartmental models, the tissue is described as a well-mixed medium exchanging mass flux with the circulatory network across a lumped boundary. In topological models, the surface of exchange is extended and geometrically characterized. In general, the tissue slab is assumed to have a simple geometrical shape, for example a cylinder or a parallelepiped. The volume of the considered tissue slab may range from a few mm3 to several hundred mm3. There are also more complex representations. For example, in [40], the intricate geometry of lung alveoli is considered, where the capillary plexi surround an assumed spherical tissue region. In [18], the tissue continuum consists of nodes interconnected on a lattice, each node representing a tissue voxel with associated numerical quantities. Some authors introduce separate representations for the interstitial portion of the tissue and the (metabolically active) parenchymal cellular portion, see, e.g., [41].
2.3. Homogenized models: perfused-tissue representations
In some studies, mathematical techniques are used to homogenize the tissue and embedded vessels as single medium. Such techniques are typically employed when describing the capillary-perfused tissue matrix, for which the network of vessels is so dense that the computational cost of addressing each vessel is too high. A simple model of capillary-perfused tissue can be found in [42] where capillaries were represented as distributed sources in the homogeneous tissue. More sophisticated homogenized models give rise to porous media representations. Effective permeability and diffusion coefficients of the matrix were computed via different approaches. For example, in [18], a number of sub-volumes (cells) were identified in the capillary plexum. For each cell, integral quantities such as effective conductance, vascular volume, and surface area were determined via explicit computation. Upscaling technique are successively used to connect the homogenized medium to larger scale vessels. Homogenization techniques are widely used to study blood perfusion in tumoral tissues. The literature in this field is very vast and in this context we limit ourselves to cite the comprehensive review works [43,44,45,46].
In Tables 1 and 2, we compare geometrical descriptions of the microvascular bed for compartmental, topological and homogenized approaches. We do not include purely morphometric studies (for which we refer to [17]) and we limit ourselves to relevant examples of a certain type of model, giving preference, when possible, to 3D models. The Tables in this review provide a comprehensive list of studies that are not all referenced in the article due to space constraints.
Table 1. Geometric description of compartmental models (R = resistive, C = capacitive, L = inductive element in electric analogy).
| Reference |
Species and district |
Microcirculatory compartments |
Other compartments |
Tissue |
| Ye (1993) [47], Arciero (2008) [22], Piechnik (2008) [48], Fantini (2014) [49] |
human |
[47]: arteriole and venule compartments grouped in length classes, capillary compartment; [22]: representative segment model: large/small arterioles and venules and capillaries; [48: different hierarchies of arteriolar/venular vessels {Fantini, 2014 #67]: arteriole, capillary and venule compartments; |
[22]: large inlet/outlet artery/vein |
[47], [49]: lumped tissue compartment |
| Ursino (1998) [50], Spronck (2012) [51], Payne (2006) [52], Diamond (2009) [53], Müller (2014) [54] |
human brain |
[51]: PCA arterioles (R-C); [50]: large and medium/small pial arteries (R-C); [53]: cerebral arterioles and capillaries (R-C); ) [54]:arterioles/capillaries/venules (R-C-L) attached at the terminals of larger vessels; ) [52]: arterial and capillary/venous compartments (R-C) |
[50]: cerebral arteries and veins, CSF; [51]: PCA + venous, [53]: pial arteries/veins, body circulation, CSF, ISF; )
[54]: body circulation, large brain arteries and veins |
- |
| Gutierrez (2004) [55], Vazquez (2008) [56], Barrett (2013) [57] |
[55]: dog limb; [56], [57]: human brain |
[55], [56]: unique vascular compartment; [57]: arteries, capillaries and veins |
|
lumped tissue compartment |
Table 2. Geometric description of topological models (A = anatomical, G = geometrical).
| Reference |
Dimension and district |
Arterioles |
Venules |
Capillaries |
Inlet/Outlet |
Tissue |
| Liu [16] (2009) |
2D human eye |
A + G for smaller vessels |
|
G |
1 main inlet and 12 outlets |
as boundary condition |
| Guibert (2010) [19] |
3D human brain |
A |
A |
G (2D mesh) |
multiple I/Os |
|
| Fang (2008) [58], Reichold (2009) [18], Lorthois (2011) [59], Pan (2014) [30] |
[58], [18]: 3D rat cortex, [59], [52]: 3D human brain; [30]: 2D, rat mesentery |
A |
A |
A |
[18]: pial arteriole, draining venule; [30]: 1 main artery/vein, 30 secondary inputs and 4 secondary outputs |
[58]: 230 × 230 × 450 μm3 region, [18]: 0.23 × 0.23 × 0.45 mm3 region [59]: 1.6 mm3 region |
| Fry (2013) [33] |
3D, hamster cremaster Muscle |
A smaller arterioles + G large arterioles |
A smaller veins +G large veins |
A |
1 main artery and 2 veins, 6 terminal arteries |
3D parallelepiped |
| Gould (2015) [17] |
3D, human brain |
A + G for smaller vessels |
A + G for smaller vessels |
G (Voronoi tessellation) |
1 main artery and 1 main vein |
27 mm3 |
| Boas (2008) [60]. Takahashi (2014) [61] |
[60]: 1D human brain; [61]: 1D |
G |
G |
G |
1 main artery and 1 main vein |
|
| Ganesan (2010) [62] |
3D rat retina |
A |
A |
G (2D mesh) |
6 main arteries and 6 main veins |
|
| Causin (2016) [29] |
3D human retina |
DLA algorithm |
DLA algorithm |
G (equivalent resistance) |
1 main artery and 1 main vein |
1D slabs (250 μm) |
| El-Bouri (2015) [63], Su (2012) [34], Safaeian (2013) [35], Gagnon (2015) [64], Tsoukias (2007) [65], Park (2016)
[66] |
[63], [34], [35], [58]: 3D human brain; [65]: 3D hamster cheek pouch retractor muscle; [64]: 2D brain; |
|
|
G with [34] investigation of different approaches (shortest arc, Gamma distribution, spanning tree); [58]: minimum spanning tree; [35]: Voronoi tessellation; [64]: hexagonal tessellation |
[34]: two outlet and inlet junctions; [35]: twelve inlet and 24 outlet flows; [56]: 1 inflowing arteriole and 3 outflowing venules; [65]: 2 arteriolar inlets and two venous outlets; [66]: multiple I/Os |
[63]: cubes with side from 125 to 625 µm; [34]: cube with side 10 μm; [35]: 0.6 × 0.38 × 0.3 mm3 region; [65]: 100 × 100× 800 mm3 region |
| Gorodnova (2016) [67] |
3D |
G (directed force layout algorithm) |
G (directed force layout algorithm) |
G (fractal) |
1 inlet and multiple outlets |
sphere of radius of 0.6 cm |
3. Modeling the Fluid Dynamics of Blood
Blood is a dense suspension of cells in plasma solvent. Red blood cells (RBCs) are the primary cellular constituent of blood, with a volume fraction (hematocrit, HD) of typically 40–45%. While plasma is a Newtonian fluid, interactions between cells and plasma lead to complex non-Newtonian dynamics. This is especially true in the microcirculation, since vessel dimensions are comparable to cell diameter [13]. Radial migration of the RBCs away from the vessel wall occurs from hydrodynamic interactions, forming a low-hematocrit/cell depleted layer along the vessel wall [68]. This phenomenon is the basis of several important rheological effects observed in vitro and in vivo [17]: (ⅰ) the Fåhraeus effect, which is the apparent reduction in tube hematocrit with respect to discharge hematocrit [69,70]; (ⅱ) the Fåhraeus-Lindqvist effect, which dictates that the apparent viscosity of blood decreases when the vessel diameter is reduced below 1 mm; and (ⅲ) plasma skimming at network bifurcations (also known as the "network Fåhraeus effect"), in which the fraction of the total RBC flow in the mother vessel of a bifurcation that enters one of the daughter branches does not correspond to the fractional blood flow entering that branch, due to the hindrance of the cell depleted layer. Plasma skimming results in a heterogeneous spatial distribution of hematocrit in the network [71].
3.1. Continuum modeling of blood flow
Blood flow in the microcirculation differs substantially from flow in large vessels. In the microcirculation, inertial effects as well as pulsatility are generally neglected (see [72] for exceptions). A large majority of blood flow models applied to the study of networks treat blood as a (multiphase) continuum. In the simplest approach, whole blood flow is described as the flow of a Newtonian fluid governed by the Stokes equations. Poiseuille's law has been traditionally used as a first approximation of such equations. In this context, the volumetric flow Q in the vessel is proportional to the pressure drop ΔP along the vessel and the fourth power of the vessel radius R:
The symbol μ in Eq. 1 is the whole blood viscosity. In comprehensive models of the circulatory system, μ is generally prescribed as a constant [54] (see also [59] for the same choice in a smaller network). More physiologically-relevant expressions for μ have been obtained from empirical equations fitting the Fåhraeus and Fåhraeus-Lindqvist effects to a range of hemodynamic measurements [15]. As reviewed in [73,74], in vitro data were originally used to determine a relationship between effective viscosity, hematocrit and glass-tube diameter. This relationship was subsequently modified based on data that showed a greater in vivo resistance. Specifically, μ corresponds to the concept of bulk ("apparent") viscosity and is formally obtained from experimental data and upon application of the Hagen-Poseuille model as:
Often, the relative value of the apparent viscosity (i.e., normalized with respect to plasma viscosity) is provided. Recently, an improved model of viscosity has been devised by including the effects of the endothelial surface layer (ESL) [74]. Alternative models for the viscosity have been proposed in [75], where an empirical equation for the apparent relative viscosity was derived as a function of hematocrit, and in [23], where an expression for μ as a function of radius was proposed (see also [76]). Further attempts to develop physically consistent constitutive models of blood viewed as a non-Newtonian fluid have led, for example, to the use of the Casson-Quemada model, where the viscosity depends on the shear rate (we refer to [77] for a comparative study of different constitutive equations).
The hematocrit value appearing in the phenomenological relations for the viscosity may be prescribed as in [16] or can be treated as an unknown in the model, as done in [31,62,78]. When the hematocrit is computed, an additional equation for the mass conservation of the continuum fluid representing RBCs must be added to the system, and volume fractions for plasma and RBC phases must be taken into account according to mixture theory [79].
When modeling a network of vessels, an analogy to Kirchhoff's first rule for electrical networks is generally adopted at the vessel bifurcations, where flux and RBC flux mass balances are enforced (see [62] for a detailed discussion of the related numerical procedure); pressure continuity is also usually enforced at bifurcation nodes [60]. Due to the low Reynolds number of the flow in microvessels, the continuity of the static pressure at bifurcations is generally used instead of the continuity of the total (static plus dynamic) pressure (see [80] for a discussion on this issue and [30] for an example where the continuity of the total pressure is considered). In a microvascular network, a proper treatment of plasma skimming at the bifurcations is also needed. Empirical equations have been developed that depend on the flow split in the bifurcation, the vessel diameters, and the discharge hematocrit in the parent vessel in [74,81]. An alternative approach that can be applied to branch points with more than two outflowing segments was proposed in [17]. Another alternative approach has been proposed based on the assumption that the distribution of RBCs in diverging bifurcations satisfy a mathematical principle of optimality [69].
A mathematically rigorous approach for computing blood flow in a vessel stems from the mathematical procedure of averaging the velocity field (approximated by a purely axial component) over the vessel cross section. Namely, introducing a system of cylindrical coordinates (r,θ,z) and assuming that the variables are separable, one sets
where ˉu is the average velocity on the cross section A, such that Q=Aˉu and where fu is a prescribed radial shape function. A typical velocity profile is given by the function [82]
where γ is a bluntness parameter ranging from 2 (parabolic profile) to 9 (plug flow profile). This approach allows for a rigorous asymptotic analysis of the various contributions arising in the balance equations.
To obtain a unique solution for the fluid-dynamic fields in the network, it is necessary to impose (ⅰ) flow or pressure boundary conditions on inflowing and outflowing segments and (ⅱ) hematocrit boundary conditions on inflowing segments. Difficulties may arise when multiple inflows/outflows exist but the corresponding boundary conditions are not all available from experiments. Several approaches have been used to address this issue. The use of literature-based typical values at outflow under the satisfaction of "target constraints" is the basis of the approaches proposed in [83]. A parametric analysis of boundary condition values has been carried out as well in [83] and [59].
An immediate extension of the homogeneous continuum was originally proposed in [84] and further developed in several works. In these approaches, the domain is usually a single cylindrical vessel in which two layers are arranged in a concentric fashion: an external plasma region (denoted here below by 'a') devoid of cells and a core RBC region (denoted here below by 'c'). Each layer is generally supposed to consist of an incompressible Newtonian fluid with constant viscosity (μa in a and μc in c, usually μc>μa). Imposing the balance of mass and momentum in each fluid domain with appropriate interface boundary conditions (continuity of velocity and shear stress are usually enforced [85,86,87]) yields two distinct velocity profiles of the type
|
va=ΔPL14μa(R2−r2),vc=−ΔPL(r∗2−r24μc+R2−r∗24μa)
|
(5)
|
where r* is the (unknown) thickness of the cell depleted layer (see, e.g.,
[88] for a simplified trial-and-error solution procedure to determine its size). The above relations for the core and cell depleted layer velocities have been again generalized to the case of blunted velocity profiles [89]. The overall mass balance of RBCs in the tube is then defined by:
|
QHD=2πR∫0v(r)h(r)rdr,
|
(6)
|
where h(r) is the radial profile of the hematocrit, commonly chosen to be equal to zero in the cell depleted layer and equal to the (unknown) core hematocrit in the RBC layer [86]. Generally, the core hematocrit is assumed to be constant, but polynomial radial profiles [84], [90] have also been proposed. In [91], the RBC core was divided into two domains: an outer region characterized by reduced hematocrit with a constant or linear radial profile and linear variation of viscosity, and a core region with uniform hematocrit concentration and uniform viscosity. To compute the unknown quantities, model closure is performed in the above models using empirical data. For example, in [86], the core viscosity is described as a function of hematocrit via phenomenological equations using the model described in [71] or [92]. In some studies, the Oldroyd-B [93] or Casson [83] models have been used to describe the RBC core phase as a non-Newtonian fluid. In [89], a detailed derivation of the velocity profile in the core region considering a power-law fluid model is carried out.
3.2. Mesoscale modeling of blood flow
While a continuum description of blood is sufficient to obtain flow data for blood viewed as a bulk volume, more detailed studies are needed to consider the corpuscular nature of blood. Studying such details will aid the comparison and analysis of the mechanisms that lead to experimentally observed results of blood rheology. These approaches are known in the specialized literature as "mesoscale models". Here, we limit ourselves to a brief description of the main approaches found in mesoscale models and we refer for additional details to the recent specific reviews by Cristini et al. [68] (till 2005), Secomb et al. [94] (till 2011), AlMomani et al. [95] (till 2012), Ju et al. [96] (till 2015) and Ye et al. [97] (till 2016).
3.2.1. Modeling of the cellular phase
Red blood cells are the most abundant type of cells in blood. An adequate representation of their mechanical and rheological properties requires correct descriptions of the elastic and viscous properties of their membrane, the bending resistance of the membrane, and the difference in viscosity between the external and internal fluids. Deformable RBCs were first modeled with simple elastic models that evolved into hyperelastic models for fully deformable 3D cells. Both discrete and continuum models of the RBC membrane have been proposed. Discrete spring network models have been widely used to model the RBC membrane (see, e.g., [98,99]). A discrete representation of the membrane as a network of viscoelastic springs in combination with bending energy and constraints for surface-area and volume conservation is adopted for example in [100]. The continuum approach treats the whole cell as a homogeneous material represented by appropriate constitutive equations. Several models adopt the Mooney-Rivlin or Skalak constitutive relations, eventually adding bending resistance [101]. More complex constitutive equations, accounting for shear-thinning and viscoelasticity, have also been proposed (see, e.g., [102]). Mixture-type "biphasic models" as well as two-phase models of the cell as a deformable capsule with liquid cytoplasm enclosed by an elastic or viscoelastic membrane have been used to represent the multiphase nature of the cellular components [103,104,105,106,107]).
The number of RBCs being modeled dictates the numerical approach. Ye and colleagues developed a series of papers where a single RBC is considered (see [97] and references therein). This approximation is valid where RBCs move in single-file, namely in capillaries. More realistic simulations of multiple RBCs flowing through vessels with diameter ranging from 10 to 500 microns remains a major challenge. A large population (thousands) of RBCs is necessary to account for cell-cell hydrodynamic interactions in these vessels. Sun et al. [105] used a Lattice-Boltzmann discretization to describe blood flow (plasma with suspended rigid particles) in a 2D channel. In recent years, some authors have proposed the use of hybrid models to describe single cellular components and their interaction in combination with a continuum representation of intra-cellular and extra-cellular processes (see the works by Bessonov and colleagues, e.g., [108]).
A number of studies introduce mathematical models of other cellular components of blood, namely white blood cells and platelets immersed in plasma flow. Complex mechanisms involving these particles, such as coagulation and interactions between different types of cells, have also been studied. We refer to [109,110] for detailed overviews on these aspects. Moreover, we refer to [111] for an overview of the main mathematical models related to blood formation (hematopoiesis), disorders and treatments.
3.2.2. Modeling of the plasma phase
Lattice Boltzmann methods, mesh-free particle methods and dissipative particle dynamics (DPD) have been used to discretize the plasma component of blood. We refer to [112] for a detailed overview of these approaches and discussion of their applicability to problems of different scales.
3.2.3. Modeling of cell-to-cell interactions
RBCs immersed in plasma flow aggregate and form rouleaux due to mutual interactions. The equilibrium configuration and the cell shape are related to the strength of these interactions. Intercellular interactions and cell aggregation have been modeled using a Morse potential [113], according to a ligand-receptor binding model [114,115] or using a theoretical formulation of depletion energy [96].
3.2.4. Modeling of plasma-cell interactions
The motion of the RBC membrane is coupled to the flow of the surrounding plasma, thus yielding a fluid-structure interaction problem. The difficulty of such a problem lies in the fact that RBCs can approach each other very closely, till aggregation. Moving mesh approaches are thus not frequently used, since meshes may face break down. The immersed boundary method has been a popular approach in combination with a fixed Cartesian mesh for the fluid [116]. Mesh-free particle methods have also been used where fluid-structure interactions are dealt with by adding elastic forces to membrane particles (see, e.g., [117], with an application to malaria infection). We refer to [118] for a comprehensive review of the possible numerical approaches in this context.
Table 3. Models of blood flow in concentric regions ("a" = cell depleted layer, "c" = RBC core).
| Reference |
Cell-depleted layer fluid model |
Core layer fluid model |
Hematocrit model |
Viscosity model |
| Sharan [86] (2001) [88] |
Newtonian fluid, Poiseuille flow |
Newtonian fluid, Poiseuille flow |
constant in c, zero in a, relation between tube hematocrit and core hematocrit from Pries' model |
model from Pries |
| Verma (2014) [89], Zaman (2016) [93], Shaw (2014) [119], Sriram (2014) [69], Das (1998) [90] |
Newtonian fluid, Poiseuille flow |
axial flow; [89], [121]: power law fluid; [93]: Oldroyd-B fluid; [119]: Casson fluid with glycocalyx layer; [69], [90]: Quemada fluid |
[89]: constant inc, zero in a, parametric analysis, [93]: no hematocrit; [119]: given constant in c; [69]: constant in c, zero in a; [90]: polynomial expression in c and small value in a. |
[89]: prescribed constant values; Zaman: prescribed relaxation and retardation parameters; [119]: constant in a, Pries model in c; [69]: constant in a, fitted from data in c; [90]: analytic expression function of hematocrit |
| Chebbi (2015) [88] |
Newtonian fluid, Poiseuille flow |
Newtonian fluid, Poiseuille flow |
constant in c, zero in a, plasma skimming model (bifurcation) |
constant value |
3.3. Blood flow in homogenized tissue-perfused models
The idea of explicitly modeling arteriolar and venular trees and using homogenization techniques to describe the capillary-perfused tissue is the focus of several studies. The concept of a capillary-perfused tissue relates to the theory of porous media. Fluid flow in this composite matrix is studied introducing effective permeability and diffusion coefficients. Several approaches have been proposed to compute these quantities, ranging from model unit cells [18] to asymptotic analysis [120]. Double porosity media have also been proposed in this context. In these models, a fracture pore system represents the embedded capillaries while a less permeable matrix pore system represents the interstitial fluid space [40].
4. Models of Gas Transport in Blood and Tissue
The circulatory system is responsible for the transport, delivery and waste removal of gaseous species from blood to every tissue in the body. Oxygen, for example, is delivered to tissue via passive diffusion from blood, so blood must flow within a very short distance of every tissue point in the body. The distance that oxygen can diffuse into tissue is on the order of microns, and thus the circulatory system plays a critical role in transporting blood throughout the body via convection along a network of vessels before reaching the capillaries where the majority of diffusive oxygen exchange occurs. Blood gas transport involves a combination of convection, diffusion, permeation, and/or chemical reactions and takes place over a range of special and temporal scales (see [15,121] for recent physiological reviews). The structural complexity and heterogeneity of the vascular networks of the microcirculation leads to heterogeneity also in tissue oxygenation and consumption. Experimental measures of the impact of such heterogeneity on tissue oxygenation are difficult to obtain, and thus theoretical modeling has served as an essential tool to characterize the physiological implications of such heterogeneity on oxygen delivery to tissue. Numerous theoretical models have been developed to describe the transport of oxygen to tissue by the microcirculation. These models include either steady-state or time-dependent oxygen transport descriptions from single or multiple vessels, as reviewed previously [122,123].
The value of theoretical models in providing a quantitative understanding of organ function at homeostasis and in pathological states such as ischemia and hypoxia has long been recognized. Studies of gas transport from blood to tissue date back to the pioneering work of Krogh [124] in 1919, and were mainly focused on O2 transport. These studies sought certain quantities of interest: (i) tissue O2 extraction fraction (OEF), defined as the weighted average inlet-outlet gas concentration, which is an important indicator of tissue viability; and (ii) (cerebral) metabolic rate of O2 ((C)MRO), which correlates BF and the metabolic rate of O2 consumption. We refer to [125] for a precise definition of these quantities and their inter-correlation. As established more recently, these two definitions are not sufficient for estimating tissue oxygen (gas) levels since the heterogeneity of the microcirculation leads to heterogeneity in gas gradients, chemical interactions among species, and the spatial distribution of gas in tissue. This section reviews models of gas transport in tissue and blood. We do not consider models devoted to the study of BOLD (blood-oxygenation level dependent) signals in medical imaging, for which a vast literature exists. We refer for this topic to [83,126] and references therein.
4.1. Modeling gas transport in tissue
4.1.1. Krogh cylinder model
The Krogh cylinder model [124] defines an array of parallel, evenly spaced oxygen-delivering vessels (e.g., capillaries) that supply oxygen exclusively to tissue cylinders surrounding each vessel. In this model, tissue oxygen consumption is assumed constant, the tissue partial pressure of oxygen (PTO2) at the capillary wall equals the average capillary PO2, axial diffusion of oxygen is neglected, and tissue oxygen solubility and diffusivity are uniform. Eq. 7 gives the partial differential equation for the partial pressure PTi of species i in the cylindrical tissue surrounding a capillary:
|
0=−DTi(1r∂∂r(r∂PTi∂r))+˙RTi,
|
(7)
|
where r is the radial coordinate and DTi and ˙RTi are the constant tissue diffusivity and source/consumption rate (possibly depending on other chemicals), respectively. An explicit solution of Eq. 7 can be found using a Bessel function expansion that gives the radial variation in tissue gas partial pressure as a function of radial distance from the vessel. Although the model includes many simplifications and often does not yield predictions that are consistent with experimental measures, the Krogh model provides an important foundation in the study of oxygen exchange with tissue and has been used and improved upon by several models.
The Krogh model has been extended to include other effects including time-dependent transport [127], PTO2-dependent O2 consumption (e.g., Michaelis-Menten kinetics) [128,129,130], myoglobin-facilitated tissue transport and intravascular resistance to radial oxygen diffusion. Myoglobin (Mb) can bind and release oxygen in the same way as the hemoglobin molecule, and thus movement of myoglobin can increase oxygen diffusion (known as myoglobin facilitation). In several models, the term for total oxygen flux is altered to include the effects of Mb facilitation [131,132,133], and the models predict that this extra term provides tissue with some resistance to hypoxia by increasing oxygen diffusion to low-PO2 regions. Capillary intravascular resistance arises from the PO2 drop between the center of a red blood cell and the capillary wall and has been shown to depend on capillary diameter and red blood cell velocity [78,134]. This factor can also be approximated in models by using a flux boundary condition on tissue PO2 at the outer edge of the capillary wall instead of the continuous PO2 condition of the Krogh model. Detailed reviews about the Krogh model and its applicability in standard and modified formulations are provided in [122,123,135,136].
4.1.2. Compartment models
An alternative, yet related, simplified approach is represented by well-stirred compartment models, in which the tissue is characterized by a single, uniform compartmental concentration/pressure. The compartmental equation in the tissue can be formally obtained from 3D balance equations, performing volume averaging, yielding:
|
VTdˉPTidt=∑mkm(ˉPmi−ˉPTi)+˙RTi,
|
(8)
|
where bars indicate average values, VT is the tissue compartment volume and exchange with other compartments (including blood and a possible subdivision in interstitial and cell phases) with concentration ˉPmi is considered. This procedure and its connection with the Krogh model are outlined in [137].
Recent models of gas delivery adopt a fully spatially-dependent description of the gas content in tissue, where diffusive processes occur due to spatial gradients. In [42], the concept of "capillary-perfused tissue" is introduced, in which the tissue description is enriched with terms representing gas exchange with embedded capillaries. Porous medium approximations of the tissue carried out in [18,138], where a seepage interstitial velocity computed from a Darcy model conveys the gas, are conceptually similar though mathematically more involved.
4.2. Modeling gas transport in blood
A prototype molar balance in blood for a generic gaseous species i is formulated in [139], according to the following partial differential equation:
|
∂CBi∂t+vB⋅∇CBi−DiΔCBi=˙RBi,
|
(9)
|
where vB is the advective blood velocity (consistently computed, see Section 3 or prescribed), DBi the gas diffusion coefficient in blood and ˙RBi the reaction transform rate in blood. The gas content (dissolved component) CBi and its partial pressure PBi are related according to Henry's law CBi/αi. In compartmental approaches, for example [50,55,140], Eq. 9 reduces to
|
∂ˉCBi∂t+Q[ˉCBi,in−ˉCBi,out]+∑mkm(ˉCmi−ˉCBi)=˙RBi
|
(10)
|
In [22,139,141], multiple vessel compartments are considered, and thus Eq.10 also includes the cascade of gas from one vessel hierarchy to the next.
When dealing with a spatially resolved form of Eq. 9, as with blood flow models, a radial gas concentration profile is prescribed via cross-sectional averaging. A mathematical characterization of this procedure can be found for a generic solute in [142] and specifically for O 2 in [29].
In Eq. 9, blood is treated as a single-phase continuum and the i-th gaseous species is characterized by a single partial pressure value. More generally, gases like O2, CO2 and NO are carried in blood in hemoglobin-bounded form and dissolved form. A multi-phase model of blood (plasma dissolved and RBC-bound fractions) is a more suitable choice to represent a wider range of conditions. For example, for oxygen, the total concentration in blood can be written as
|
CO2,tot=αpl,O2Ppl,O2(1−HD,O2)+αRBC,O2PRBC,O2HD+cHb,O2HDS,
|
(11)
|
where the subscript pl indicates the fraction dissolved in plasma and the subscript RBC indicates the fraction dissolved in the RBCs; where HD,02 and (1−HD,02) are the hemoglobin bound and free fractions, respectively; and where cHb,O2 is the hemoglobin carrying capacity for oxygen. Typically, the free part in the plasma and the free part in the RBCs are assumed to be at the same partial pressure, so that Ppl,O2=PRBC,O2=PBO2. Also, local chemical equilibrium is usually assumed for the free and bound fraction of the gas. This introduces a saturation function S=S(PBO2), connecting the partial pressure of free and bound gas fractions. The most common function used to describe saturation is the Hill equation, which supposes a single-step reaction kinetic for O2 binding to Hb. A few models assume non-equilibrium kinetics, as in the Adair equation (see [121] for a complete discussion of this topic). In non-equilibrium conditions, separate balance equations are written for the bound and the dissolved fractions that include reaction terms between the different forms (see [78]).
In smaller vessels like capillaries, continuum-based approaches like the one in Eq. 9 may fail to yield accurate results. Approaches based on discrete modeling of RBCs address this issue. Generally, these models work in the frame of reference of the erythrocyte, which simplifies the numerical treatment of the reaction between oxygen and hemoglobin in RBCs. This idea was first used by [79], who used an analytical model with a cylindrical RBC and the adjacent tissue to compute MTCs. In [143], a model with concentric layers around the capillary for wall, interstitial fluid, and the tissue is presented. Recent contributions from this viewpoint can be found in [144].
Detailed mathematical models of the acid-base chemistry of blood based upon mass action and mass balance equations have been also developed (see, for example, [145]). Transport of other species (e.g., CO2, CO, NO, etc) affects the transport of oxygen and is thus also an important modeling consideration. More precisely, CO2 shifts the hemoglobin-oxygen saturation curve, CO competes with oxygen for binding sites to Hb, and NO inhibits mitochondrial oxygen consumption. Several studies have implemented such multi-species models, for example for oxygen and carbon dioxide [41,146,147,148,149]. Ye et al. [139] developed a compartmental model of oxygen-carbon dioxide transport in the microcirculation that uses a Krogh cylinder approach and accounts for the coupling between oxygen and carbon dioxide transport. The equations for steady-state oxygen-carbon dioxide coupled transport in the microcirculation are given as:
|
Q[ci,g(0)−ci,g(L)]−Ei,g(PBi,g−Pn,g)−Fi,g(Pi,g−Pn−i,g)=0,fori=1,2,…,n−2;g=0,1
|
(12)
|
|
∑n−1j=1Ej,g(Pj,g−Pn,g)+MgVT=0fori=n;g=0,1
|
(13)
|
where ci, g is the average total concentration of gas (g = 0 for oxygen, g = 1 for carbon dioxide) over the vessel cross-section, Mg is the metabolic rate, VT is the tissue volume, Fi is the countercurrent exchange of gas (omitted in the model), Ei is the diffusion conductance, and Pi is the partial pressure in the i-th compartment. The model predicts the distributions of PO2, PCO2, saturation, and pH within the vessel and tissue compartments and includes the Bohr effect and Haldane effect. The effects of the radial variation in PO2 and PCO2 and the difference between the metabolic rates of the vessel wall and tissue are included in the model to improve the accuracy of oxygen and carbon dioxide vessel-tissue conductance predictions. Overall, including the transport of multiple species significantly improves predictions of tissue oxygenation when compared with models including only transport of a single species.
4.3. Modeling blood-tissue gas exchange
Blood-tissue exchange occurs mainly in capillary beds, although arterioles are also sites of important gas exchange in some cases. For example, it has been observed that in the hamster retractor muscle, two-thirds of oxygen is exchanged in the arterioles and the rest in capillaries while cerebral cortical capillaries unload about twice the amount of oxygen to the brain tissue as compared to arterioles [42,150].
4.3.1. Fick's Law models
From a mathematical viewpoint, a straightforward representation of the exchange process prescribes a proportionality relation between gas concentration in different compartments (for example, between venous and tissue concentration [142,151] or between arteriolar and tissue concentration [152]). In these models, the transfer of gas through the vessel wall is defined according to Fick's law:
|
J=ΔN╱Δt=DAΔC╱Δx=LpAΔC
|
(14)
|
where ΔNΔt is the amount of the gas substance exchanged per unit time, D is the diffusion coefficient for the substance through the vessel wall, A is the surface area available for diffusion, ΔC is the concentration difference across the vessel wall (ΔC=CBi−CTi), Δx is the thickness of the vessel wall (~1 μm) and Lp is the permeability of the capillary wall defined as D/Δx [121]. The value CTi can be a given, fixed, parameter or can be computed from a consistently coupled model for tissue as for example in [29,31,58,60].
In some approaches stemming from modifications of the Krogh model, a mass transfer coefficient (MTC) is introduced, defined as MTC=ˉJ¯PBi−PTi, where the bars indicate the average of the quantity per unit area of the vessel wall [123]. The MTC, which can be considered as a permeability of the wall appearing in Eq.(12) [122], relates the PO2 drop from the intravascular space to the O2 flux across the capillary wall. Since the MTC depends on hematocrit, prescribing it introduces the influence of RBC flow on tissue oxygenation. Occasionally, the MTC quantity is expressed as a function of the non-dimensional Nusselt [123] or Sherwood numbers [153].
McGuire and Secomb [132,133] developed a model of oxygen transport to exercising skeletal muscle that is an example of an extended Krogh model that includes the effects of the decline in oxygen content of blood flowing along capillaries, intravascular resistance to oxygen diffusion, and myoglobin-facilitate diffusion. The oxygen consumption rates depend on both convective and diffusive limitations on oxygen deliver when oxygen demand is high.
4.3.2. Green's functions model
Secomb et al. [154,155,156] introduced a steady-state model of oxygen transport in capillary networks and surrounding tissue based a Green's function method (Eqs. 15–17). The model utilizes techniques from potential theory which seek to reduce the number of unknowns needed to represent the oxygen field. Vessels are modeled as discrete oxygen sources, and the tissue regions are considered oxygen sinks; the resulting oxygen concentration at a tissue point is calculated by summing the oxygen fields (called Green's functions) produced by each of the surrounding blood vessels. The tissue is assumed homogeneous with respect to oxygen diffusivity (D) and solubility (α), and Eq. 15 is obtained from the conservation of mass where P is tissue PO2 and M(P) is the tissue consumption rate (usually assumed as a constant value or according to Michaelis-Menten kinetics). The Green's function G(x, xi) is the solution of Eq. 16 and represents the PO2 at a point x resulting from a unit point source at xi. The PO2 is given by Eq. 17 where qi represents the distribution of source strengths. A great benefit of this model is the ability to predict tissue oxygenation for a heterogeneous network of capillaries in three dimensions. The model predicted a much lower minimum tissue PO2 than would be predicted by a corresponding Krogh model.
More detailed descriptions of the blood-tissue gas exchange are considered by some authors. They usually consider a single vessel and partition the vessel wall into three or four layers (endothelium, smooth muscle layer and adventitia). They study gas transport in the radial direction in the vessel according to diffusion-reaction equations solved by Bessel expansions. Such a model is used in [147] in the context of O2-CO2 interaction, in [157,158,159] in the case of NO-O2 interaction, especially when dealing with the NO scavenging mechanism in artificial RBC substitutes, see e.g., [159].
5. Modeling of Passive and Active Regulation of Microvessels
When modeling the regulation of blood flow through a network, there are several forces acting on a vessel wall that should be considered. First, blood flow creates a pressure inside the vessel lumen that distends the vessel. Pressure external to the vessel created from the surrounding fluids, organs, and cytoskeletal structures tends to compress the vessel. The difference between the internal and external pressures is known as transmural pressure. According to the Law of Laplace [160], the circumferential tension generated within the vessel wall exactly balances the transmural pressure so that the diameter of the vessel is maintained.
The tension that is developed within the vessel wall can be divided into two main components: passive tension and active tension. Passive tension is generated by the structural components of the vessel wall such as collagen and elastin fibrils; active tension is generated in the vessel wall due to the contraction of smooth muscle cells. Vasoactive agents interact with the vascular smooth muscle (VSM) of arterioles to cause a change in muscle tone and, consequently, vessel diameter. An increase in VSM tone causes an increase in active tension and thus a constriction of the vessel; a relaxation of VSM cells causes a decrease in active tension and a dilation of the vessel. In this section, different approaches used to model blood flow regulation are reviewed, and the mechanisms to which vessels respond are summarized.
5.1. Wall mechanics models
Several studies have incorporated the passive and active components of wall tension when modeling vessel mechanics (e.g., as in Eq. 18 where T is wall tension). Gonzalez-Fernandez and Ermentrout [161] include passive and active length-tension relationships of smooth muscle in their model to predict the occurrence of vasomotion in small arteries. Passive tension is described in the model by a nonlinear function that includes terms for stiff collagen, compliant elastin fibers, and general vessel wall stiffness. Maximally active tension is represented by a modified Gaussian function. The resulting active tension is assumed to be the product of the maximally active tension and a factor between zero and one determined by intracellular calcium levels. Achakri [162] et al. propose a similar mechanism for the appearance of vasomotion that is dependent on the active behavior of vascular smooth muscle. Circumferential stress in the arterial wall is defined by the sum of passive stress (completely relaxed muscle) and active stress (contracted muscle). The nonlinear function for passive stress is based on experimental measures. The function for active stress reflects length-tension characteristics of muscle, and the level of muscle contraction is assumed to depend on the degree of activation of the contractile proteins, which depends on the concentration of calcium ions in the intracellular space. The rate of change of calcium is assumed to depend on arterial pressure and on endothelial shear stress.
Similar mechanical definitions based on length-tension characteristics described in [161,162] are used in numerous theoretical models of blood flow regulation [22,33,163,164]. In these models, the passive tension is defined as an exponential function of diameter with parameters estimated from several experimental studies giving pressure-diameter curves for vessels with diameters ranging from 40 to 300 μm (Eq. 19). The exponential function represents the observed nonlinear behavior of tension increasing rapidly as diameter increases. A Gaussian function is used to describe the maximally active tension generated by the VSM cells in the vessel wall (Eq. 20). The activation function that determines the level of VSM tone varies between 0 and 1 and is assumed to be a sigmoidal function (Eq. 21) of a stimulus function that depends on linear combinations of various factors (see Section 5.3, Eq. 22)). In the studies that incorporate this description of wall tension the model predictions are compared with experimental data and show a good fit [22,164,165,166].
|
Ttotal=Tpass+ATmaxact
|
(18)
|
|
Tpass=Cpassexp[C′pass(DD0−1)]
|
(19)
|
|
Tmaxact=Cactexp[−(DD0−C′actC″act−1)2]
|
(20)
|
|
Atotal=11+exp[−Stone(Ttotal)]
|
(21)
|
|
Stone=CmyoT−Cshearτwall+C′tone
|
(22)
|
Ursino and colleagues [50,167,168] have employed a similar modeling approach in which the inner radius of a vessel is computed from the equilibrium of forces acting on the vessel wall (Law of Laplace). Wall tension is considered the sum of elastic, smooth muscle, and viscous tensions. Regulatory mechanisms are assumed to act on the smooth muscle tension of resistance vessels (i.e. arterioles). In these models, the relationship between active tension and inner vessel radius depends on an activation factor that represents the degree of smooth muscle contraction in a given vessel. The dynamics of various regulatory mechanisms are implemented using a first-order low-pass filter characterized by a gain function and time constant. This approach developed by Ursino has been adapted in several studies, including the comprehensive model of cerebral blood flow control presented by Banaji et al. [169].
5.2. Mechanistic tube law models
In the absence of branching, a short section of vessel can be considered as a cylindrical compliant tube. One-dimensional blood flow models are obtained by averaging the incompressible Navier-Stokes equations (with constant viscosity) over a vessel cross section given some assumptions about the radial displacement and elastic material properties of the vessel wall. The following first-order, nonlinear hyperbolic system provides the one-dimensional equations for blood flow in elastic vessels:
Table 4. Models of oxygen/gas transport in blood and tissue (HL = Hill's law, MM = Michaelis-Menten, FD = finite differences, FV = finite volumes, FEM = finite elements).
| Reference |
Gas |
Gas transport in blood |
Gas transport in tissue |
Blood-tissue exchange |
Numerical approach |
Target quantities |
| Moschandreou (2011) [42] |
O2(HL) |
bi-phasic mixture with distinction in rich blood core (advection-diffusion) and plasma layer (pure diffusion) in a single arteriole |
Krogh-like model with embedded mass transfer term with capillaries |
continuity |
FD |
perivascular radial and axial O2 perfusion profiles, Sherwood number as a function of saturation and vessel radius |
| Linninger (2013) [31], Beard (2001) [170], Park (2016) [66], Fang (2008) [58], Lucker (2015) [144] |
O2[31], [58]: HL; [170]: Adair; HL, Clark |
unsteady convection for [31], [66]: mono-phasic blood; [170]:biphasic fluid (mixture) in 3D capillary network; [144]: bi-phasic flow in a single capillary with discrete RBCs; |
unsteady diffusion-reaction with [31]: first order metabolism, [170], [144]: MM with myoglobin facilitation, [66]: constant metabolic rate |
[31], [66], [58]: diffusive permeation; [170], [144]: continuity |
[31]: FV; [170]: FD; [58]: FEM |
[31]: blood O2 tension in an arteriole/venule sub-unit, radial O2 profile; [170]: steady-state O2 concentration profiles as a function of O2 consumption, impact of myoglobin; [170]: CMRO and OEF as a function of transit time and BF; [58]:partial pressure of oxygen versus vessel diameter and O2 distribution in tissue; longitudinal O2 profiles, impact of instantaneous hematocrit fluctuations on tissue oxygenation |
| Safaeian (2013) [35] (2013) [178], Jespersen (2012) [171], Lemon (1987) [172], Fry (2013) [33], Goldman (2000) [173], Tsoukias (2007) [65] |
[35], [171], [33]: O2(HL); O2 (Moll); [65]: O2 (HL) + Hb carriers |
steady convection for mono-phasic blood in [171] a single capillary (in collection of capillaries with different transit times) or [33], [173] vessel/capillary network, bi-phasic mixture in [35], [65] anatomical network or [172] single capillary |
[35], [33]: steady diffusion-reaction in 3D volume; [171], [172]: given constant O2 pressure in tissue; [173], [65]: steady diffusion-reaction with myoglobin facilitation |
[35]: pointwise sources; [171], [172], [65]: first order exchange with permeation; [33]: pointwise sources; [173]: hematocrit dependent permeation |
[178], [160]: Green's function method, [172]: FD + FEM; [173], [65]: FD |
tissue O2 pressure distribution for different CMRO and perfusion levels, OEF as a function of BF (comparison with Buxton model); [171]: net O2 extraction as a function of transit time, tissue O2 concentration and capillary arrangement; [172]: O2 profiles in radial and axial directions as a function of chemical equilibrium parameters; [33]: O2 contour curves in tissue slices for different CMRO; [173]: study of geometric factors (shunts, tortuosity) in O2 levels in tissue and axial O2 profiles in capillaries; [65]: PO in the capillaries and O2 in tissue as a function of the Hb substitute |
| Eggleton (2000) [143] |
O2 |
unsteady diffusion in single erythrocytes and plasma in a capillary vessel |
unsteady diffusion-convection in annular muscular region |
FEMs in a frame moving with RBC velocity |
|
radial O2 profile, local mass transfer coefficient for 1s simulated time, MTC |
| Tsoukias (2003) [174], Chen (2007) [138] |
[174]: NO, O2+ NO |
steady diffusion-convection-reaction for [174] capillary with discrete parachute-shaped RBCs, [138] straight arteriole and venule pair; |
[174]: steady diffusion-convection-reaction for 2D tissue and interstitium; [138]: diffusion-convection porous medium perfused by capillaries |
[174]: continuity + (flux continuity with sources); [138]; first order reaction |
[174]: FEM + moving frame for RBCs; [138]: semi-analytic |
[174]: NO contour curves, comparison between discrete cell and continuum model, estimation of intravascular MTC; [138]: NO profiles, effect of capillary-perfused tissue |
| Vazquez (2008) [56], Barrett (2013) [57] |
O2(HL) |
unsteady balance for monophasic blood in [56] in capillary compartment, [57] arteries, capillaries, veins |
unsteady compartmental reaction |
permeation |
ODE solver |
lumped tissue compartment; tissue and vascular O2 as a function of time for different permeability increase; [57]: sensitivity analysis on permeation parameter |
| Reichold (2009)[18] |
generic solute |
unsteady graph-based 1D advection for monophasic fluid with upscaling procedure |
unsteady diffusion-reaction with upscaling |
permeation |
FV |
solute levels in tissue |
|
∂q∂t+∂∂x(αq2A)+Aρ∂p∂x=−f
|
(24)
|
where x is the axial coordinate along the longitudinal axis of the vessel, t is time, A(x, t) is the cross-sectional area of the vessel, q(x, t) is blood flow, p(x, t) is the average internal pressure over a cross section, f(x, t) is the friction force per unit length of the tube, ρ is the fluid density, and α is a coefficient that depends on the velocity profile assumed in the system.
A complete derivation of these equations is provided in [80]. A tube law is implemented to close the system, where the transmural pressure (i.e., the difference between the internal pressure p(x, t) and external pressure pe(x, t)) is a function of cross-sectional area A(x, t) of the vessel and other parameters related to the geometric and mechanical properties of the system such the elasticity and stress-strain response curves for a vessel. Multiple different functions can be used to express this pressure-area relationship. Appropriate choices for such functions and parameters for both arteries and veins are described by Muller et al. They implement this tube law modeling approach when studying cerebral venous flow [20] and when developing a global multiscale model for the human circulation [54].
Similarly, fluid dynamic equations are derived from the continuity equation and momentum equation by Olufsen et al. [25]. In such models, the pressure-area relationship is shown to depend on Young's modulus (E) in the circumferential direction. Young's modulus is assumed to vary based on vessel type to reflect the elastin content of the vessel wall at different points along the arterial tree. For example, since small arteries are stiffer, E is chosen to be a function of vessel radius based on compliance estimates. In this way, the structural components of vessels are incorporated correctly into theoretical models.
5.3. Factors eliciting a vasodilatory response in resistance vessels
The models described in Sections 5.1 and 5.2 describe changes in vessel diameter due to various stimuli. Depending on the tissue and the metabolic conditions, vessels are known to respond to a great multitude of factors, including: pressure (myogenic response), shear stress, ATP concentration (conducted metabolic response), local metabolic factors, carbon dioxide concentration, hormones, neurological stimuli, and tubuloglomerular feedback. For example, in exercising muscle, metabolites from contracting muscle can cause direct vasodilation of resistance arterioles or indirect inhibition of noradrenaline release from nerves to prevent vasoconstriction [175]. Vasodilatory factors also affect vessels to very different extents depending on the size of the vessel. For example, sympathetic innervation is more pronounced in small vessels while the endothelium of large resistance vessels releases dilatory factors like nitric oxide at a much higher rate than small vessels [176]. Responsiveness to pressure (myogenic responsiveness) is expressed more distinctly in smaller vessels than larger vessels in some cases [176]. Despite differences in their reactivity, it has been shown that large and small vessels react in a coordinated manner, which is critical for an appropriate vasodilatory response. Network geometry also plays a role vasoactive responses. For example, the anatomical relationship between pre-and post-capillary vessels allows for the diffusive exchange of substances between these vessels, providing important information about distal tissue regions to proximal vessels in the network [177].
6. Focus: Modeling of the Retinal Circulation
Various modeling techniques described in this article have been applied to understanding the geometry, mechanics and hemodynamics of the retinal microcirculation under both healthy and disease conditions. In this section, the various modeling techniques and methods used to study the retinal circulation are reviewed.
6.1. Anatomic summary
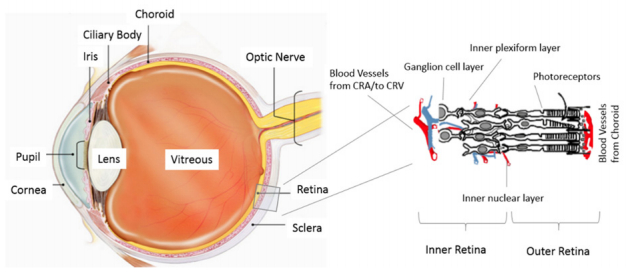
The retina is the sensitive tissue lining the back of the eye. It collects the visual signal and sends it to the brain in the form of a neural signal. These tasks imply high oxygen demands. The retina receives oxygen from two distinct vascular systems [178]: the retinal blood vessels and the choroidal blood vessels (see 3). The first system specifically provides nourishment to the innermost retinal layers, while the choroid choriocapillaris provide nourishment via diffusion to the outermost retinal layers, which are normally avascular. Oxygenated blood is supplied to the retina by the central retinal artery (CRA) which, at the entrance of the optic nerve head, is approximately 170 µm in diameter. The CRA branches into the superior and inferior papillary arteries, which in turn divide again, with each branch supplying roughly a quadrant of the retina. The major branching arteries are approximately 120 mm in diameter. In the posterior retina, the fine arterioles that arise by side-arm branching leave the main arteries and enter the inner plexiform and ganglion cell layers. Only capillaries are found as deep as the inner nuclear layer. The venous system of the retina usually mirrors the arteriolar circulation. De-oxygenated blood is drained from the capillaries into successively larger veins that eventually converge into the central retinal vein (CRV). At the entrance of the optic nerve head, the CRV is approximately 220 µm in diameter.
6.2. Geometric models of blood flow in the retinal circulation
Takahashi et al. [23,61] developed a model of the microvasculature of the human retina using a fractal dichotomous branching structure. The model included arterioles stemming from the CRA, capillaries and venules converging into the CRV. Symmetric as well non-symmetric networks were considered. The model was used to quantify parameters such as blood pressure, blood flow, blood velocity, shear rate, and shear stress as a function of vessel diameter in the retinal microcirculation. Ganesan et al. [27] introduced a more realistic network model of the retinal using confocal microscopy images from a mouse retina to develop a complex network of microvessels that are distributed non-uniformly into multiple distinct retinal layers at varying depths. In the model, capillaries were represented as a circular mesh consisting of concentric rings along which several uniformly distributed nodes represent capillary vessels. The study defined a series of rules that explains the process of connecting the capillary network to arterial and venous networks to provide a complete and comprehensive vascular network of the retinal circulation. The model predicted the non-uniform repartition of blood hematocrit in the retina. In [179], Aletti et al. studied fluid-structure interactions in a 3D network representing the inferior temporal arteriole tree in the human retina. Typical diameters of the network were between 70 µm and 160 µm. They proposed a simplified model that could be used to solve the fluid problem on a fixed domain, where Robin-like boundary conditions represented the effect of the solid wall. In [180], Causin et al. adapted the geometry proposed by Takahashi in [61] to describe the retinal network. Blood flow and pressure drop in each vessel were related through a generalized Ohm's law featuring a conductivity parameter, function of the area and shape of the vascular cross section. The model was used to study the response of the network to different interstitial and outlet pressures (or intraocular pressure, IOP). Phenomena of flow plateau, choking and flow diversion from one branch of the system to the other were predicted.
6.3. Retinal blood flow regulation models
Blood flow is regulated in the retina according to mechanistic responses to intraluminal pressure (myogenic response), shear stress, metabolite concentrations, and neural stimuli. Arciero et al. [22] developed a model that assessed the relative contributions of myogenic, shear, conducted metabolic, and carbon dioxide responses to blood flow in the retina. The model predicted that the metabolic responses were most significant in obtaining autoregulation of flow. This model has served as a foundation upon which more recent models have been developed to combine a mechanistic description of blood flow autoregulation in the retinal microcirculation with the mechanistic models described in Section 3. Arciero et al. [166], Carichino et al. [181] and Cassani et al. [182] have implemented Krogh-type models within a compartmental representation of the retinal microcirculation. These models yield predictions of blood flow that are consistent with experimental measures but do not capture the spatial variation of oxygen levels in retinal tissue. In [29], Causin et al. coupled a wall mechanics model with a model for oxygen transport in the retina and quantified the effects of blood pressure, blood rheology, arterial permeability to oxygen, and tissue oxygen demand on the distribution of oxygen in retinal blood vessels and tissue.
6.4. Models of gas transport in the retinal tissue
Several models have been developed to estimate oxygen profiles in the avascular region of the retina (outer retina). Cringle and colleagues studied (see, e.g., [183,184]) oxygen delivery to the outer retina by 1D reaction-diffusion equations with constant or linear oxygen consumption in the region corresponding to photoreceptor mitochondria. The source of oxygen from choroid (not represented) was modeled as a boundary condition. The inclusion of the inner retinal layers along with the embedded blood sources in the inner retinal layer was proposed by Roos [185]. Oxygen sources were embedded in the inner retina via a prescribed flux term depending on blood convection. The effect of arterial occlusion was investigated, blocking the supply of blood from the inner retina. The results suggested that extreme hyperoxia would be needed to make the choroid capable of supplying oxygen to the entire retina by itself.
One of the difficulties in modeling gas transport in the retina is that important parameters such as the average thickness of the retina, the choroidal tension and the structure of the inner retinal vascularization present relevant intra and inter-species differences. These model parameters are often fit to experimental data. For example, in [186] it was found by linear regression that the most metabolically active region extended from about 75% to 85% of the retinal depth from the vitreous.
Table 5. Summary of blood flow regulation mechanisms in mathematical models of the microcirculation.
| Regulatory mechanism |
Model implementation |
Effect on vessel diameter |
| myogenic response |
[166], [165], [163], [22], [187], [33], [188], [189] |
vasoconstriction |
| shear-dependent response |
[187], [33], [52], [166], [22], [163], [165] |
vasodilation |
| local metabolic response |
[187], [190] |
vasodilation |
| conducted metabolic response |
[166], [22], [163], [33] |
vasodilation |
| CO2 response |
[52], [166] |
vasodilation |
| neural stimuli |
[191], [50], [52] |
Vasoconstriction or vasodilation |
6.5. Mechanistic models in retinal circulation
The vasculature system of the retina is subjected to multiple mechanical forces. Intraocular pressure (IOP) from the anterior chamber of the eye, cerebral spinal fluid (CSF) pressure from the brain and tensions that come from the sclera exert significant biomechanical actions. The role of these actions is especially relevant near the entrance of the optic nerve head (ONH), where the nerve bundles pass through a sieve-like portion of sclera called lamina cribrosa (LC). The LC is also pierced by the CRA and CRV. Several mathematical models have described the mechanical response of the optic nerve head to variations in IOP, scleral tension and CSF pressure and its correlation to pathological conditions, in particular open angle glaucoma (see, e.g.,
[192,193,194,195]). In [196], Harris et al. analyzed the role of mathematical models in assessing how hemodynamic alterations may contribute to open angle glaucoma pathophysiology. A recent model by Guidoboni et al. [197] was used to predict the effects of IOP, CSF pressure, and scleral tension on the deformation of the LC and the resulting effect on the flow of blood through the CRA and CRV. This information was incorporated into a more comprehensive model of the retina that accounts for the compression of the CRA/CRV by the lamina as well as blood flow regulatory mechanisms while IOP and mean arterial pressure (MAP) are varied [198]. The model represents veins as Starling resistors and accounts for venous compressibility. The model predicts that an increase in IOP or decrease in MAP do not have the same effect on ocular perfusion pressure due to the built-in compensatory mechanism in the veins to increase blood pressure in the retinal vasculature. In [199], Causin et al. demonstrated the relationship between stress state in the LC and blood perfusion using a poroelastic material model where blood vessels are viewed as pores in a solid elastic matrix. The model was used to investigate the influence on the distributions of stress, blood volume fraction (or vascular porosity) and blood velocity within the lamina cribrosa due to different levels of IOP and different mechanical constraints at the boundary of the lamina. The model simulations suggest that the degree of fixity of the boundary constraint strongly influences the lamina's response to IOP elevation.
7. Conclusions and Perspectives
It was in 1661 that the physiologist M. Malpighi published the treatise "De pulmonibus observationes anatomicae" where he exposed the results of his observations of frog pulmonary alveoli obtained with a single lens microscope. His studies revealed for the first time the existence of a very fine network of vessels connecting arteries and veins. The importance of this discovery, and all the successive studies opened by it, is major. The microcirculation plays a fundamental role in the homeostasis of the body. Microcirculatory disorders are major contributors to morbidity and mortality. In the past few decades, much progress has been made in the mathematical and computational modeling of these complex systems. Their hierarchical structure includes at least three modeling scales, ranging from the cellular level to the vessel network level. There is a strong coupling of microvessels with the surrounding parenchymal tissue and cells. Feed-forward and feedback interactions have been envisaged [200]. The scenario is thus very complex. On the computational side, the applicability of high performance computing techniques favors large scale simulations, based on 3D anatomic models. This will be a steadily growing trend in future models. However, important gaps must still be filled. For example, to what extent can detailed single vessel simulations be enlarged to a network of thousands of vessels? Is the information from a single RBC tractable (and meaningful) to a much larger scale? What are appropriate upscaling techniques to transfer information between scales? These are only a few aspects that must be considered to advance in this field. Finally, we note that in this study we did not review the fundamental topic of drug delivery. The microcirculation is the ultimate site of exchange of substances/molecules and also functions as an important route for clearance. The delivery of drugs to certain organs can be difficult, such as in the brain due to the tight blood-barrier. Studies and numerical simulations of drug delivery rely on the precise knowledge of microcirculatory mechanisms. A correct representation of these latter is a fundamental background to obtain meaningful results.
Conflict of Interest
The authors declare no conflict of interest in this paper.









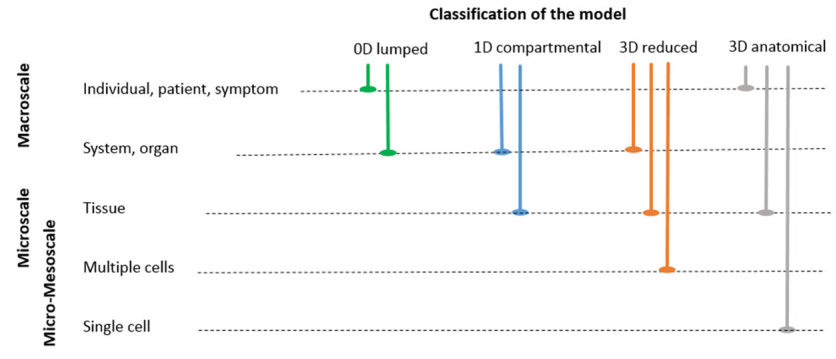
 DownLoad:
DownLoad: