Citation: Stephanie H. DeLuca, Samuel L. DeLuca, Andrew Leaver-Fay, Jens Meiler. RosettaTMH: a method for membrane protein structure elucidation combining EPR distance restraints with assembly of transmembrane helices[J]. AIMS Biophysics, 2016, 3(1): 1-26. doi: 10.3934/biophy.2016.1.1
| [1] | Wei Zhang, Sheng Cao, Jessica L. Martin, Joachim D. Mueller, Louis M. Mansky . Morphology and ultrastructure of retrovirus particles. AIMS Biophysics, 2015, 2(3): 343-369. doi: 10.3934/biophy.2015.3.343 |
| [2] | Thuy Hien Nguyen, Catherine C. Moore, Preston B. Moore, Zhiwei Liu . Molecular dynamics study of homo-oligomeric ion channels: Structures of the surrounding lipids and dynamics of water movement. AIMS Biophysics, 2018, 5(1): 50-76. doi: 10.3934/biophy.2018.1.50 |
| [3] | Katie M. Dunleavy, Eugene Milshteyn, Zachary Sorrentino, Natasha L. Pirman, Zhanglong Liu, Matthew B. Chandler, Peter W. D’Amore, Gail E. Fanucci . Spin-label scanning reveals conformational sensitivity of the bound helical interfaces of IA3. AIMS Biophysics, 2018, 5(3): 166-181. doi: 10.3934/biophy.2018.3.166 |
| [4] | Domenico Lombardo, Pietro Calandra, Maria Teresa Caccamo, Salvatore Magazù, Luigi Pasqua, Mikhail A. Kiselev . Interdisciplinary approaches to the study of biological membranes. AIMS Biophysics, 2020, 7(4): 267-290. doi: 10.3934/biophy.2020020 |
| [5] | Jacques Fantini, Francisco J. Barrantes . How membrane lipids control the 3D structure and function of receptors. AIMS Biophysics, 2018, 5(1): 22-35. doi: 10.3934/biophy.2018.1.22 |
| [6] | Anna Kahler, Heinrich Sticht . A modeling strategy for G-protein coupled receptors. AIMS Biophysics, 2016, 3(2): 211-231. doi: 10.3934/biophy.2016.2.211 |
| [7] | Carsten Sachse . Single-particle based helical reconstruction—how to make the most of real and Fourier space. AIMS Biophysics, 2015, 2(2): 219-244. doi: 10.3934/biophy.2015.2.219 |
| [8] | Mathieu F. M. Cellier . Evolutionary analysis of Slc11 mechanism of proton-coupled metal-ion transmembrane import. AIMS Biophysics, 2016, 3(2): 286-318. doi: 10.3934/biophy.2016.2.286 |
| [9] | Alyssa D. Lokits, Julia Koehler Leman, Kristina E. Kitko, Nathan S. Alexander, Heidi E. Hamm, Jens Meiler . A survey of conformational and energetic changes in G protein signaling. AIMS Biophysics, 2015, 2(4): 630-648. doi: 10.3934/biophy.2015.4.630 |
| [10] | Ateeq Al-Zahrani, Natasha Cant, Vassilis Kargas, Tracy Rimington, Luba Aleksandrov, John R. Riordan, Robert C. Ford . Structure of the cystic fibrosis transmembrane conductance regulator in the inward-facing conformation revealed by single particle electron microscopy. AIMS Biophysics, 2015, 2(2): 131-152. doi: 10.3934/biophy.2015.2.131 |
Approximately one-third of all proteins are integral membrane proteins (MPs) [1,2,3,4], and they comprise more than half of all drug targets due to their prevalence in a wide variety of biological functions [5,6,7,8]. However, of the more than 106,000 proteins with experimentally determined three-dimensional (3D) structures in the Protein Data Bank (PDB) [2,9,10,11,12,13,14], only about 2,300 are MPs [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Further, according to Stephen White’s database of MPs of known structure (http://blanco.biomol.uci.edu/mpstruc/), only approximately 520 unique MP structures have been determined. The disparity between the importance of MPs and the available 3D structures reflects the technical difficulties associated with MP structure determination by X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. To study MPs in their biologically relevant native conformation(s), a membrane mimic must be present during the experiment. While exciting progress in the field of crystallography are observed, such as the use of femto-second crystallography [21,22], robotics [23,24], and antibodies [1,3,4], MP crystallization remains a bottleneck. Limiting factors for solution NMR spectroscopy include line-broadening due to slow tumbling times of large MPs embedded in membrane mimics. Cryo-probes, increasingly powerful NMR magnets, selective labeling, and the development of solid-state NMR techniques [5] are continuously pushing the MP NMR field forward, but challenges remain [9,10,13,14].
Site-directed spin labeling electron paramagnetic resonance (SDSL-EPR) spectroscopy may serve as another means of MP structure determination because it has a number of advantages compared to more traditional methods. For example, proteins can be studied in native-like environments, such as in lipid bicelles or vesicles, and no crystallization is required. Because of the sensitivity of SDSL-EPR relatively small amounts of protein suffice, which is important in the case of MPs that are often difficult to express and purify. As unpaired electrons are only present at the two labeling sites, results are straight-forward to interpret as an error-prone resonance assignment process is omitted, unlike in NMR spectroscopy [8,15,16,17,18,19,20].
However, EPR is not without its disadvantages. Like NMR spectroscopy, structure determination is indirect in that the spectroscopic data are first converted to structural restraints [25,26,27,28]. Also, for distance measurements, SDSL requires the removal of all endogenous reactive cysteines in the protein and the mutation of the residues of interest into cysteines. As a result, in contrast to NMR spectroscopy, only one inter-residue distance can be measured per experiment. This results in low throughput and sparse datasets. In addition, the spin label itself introduces uncertainty, as the distance between the paramagnetic spin labels, which are at the tips of long and flexible side-chains, is measured. This distance then needs to be converted into a structural restraint based on MP backbone coordinates.
There are two principal ways to accomplish this conversion. Explicit approaches such as MMM [29], mtsslWizard [30], PRONOX [31,32], and RosettaEPR [33] model the spin label explicitly. Such programs can predict EPR distances with an accuracy of ~3 Å. Unfortunately, such methods are too slow to be integrated into de novo folding simulations such as RosettaTMH. As a rapid but less precise alternative we also implemented an implicit Knowledge-Based Potential (KBP) into RosettaEPR that computes a likelihood distribution for the Cβ distance based on the observed distance of the unpaired electron in the SDSL-DEER experiment [25,26]. This potential is used in calculations labeled RosettaTMH+EPR in the present manuscript.
In order to aid in MP structure determination, several computational methods have been developed. These methods can be divided into two categories: template-based comparative modeling, and de novo folding. Template-based methods, such has Modeller [34,35,36,37], Rosetta [38,39], SWISS-MODEL [40], and I-TASSER [41,42,43], are commonly used when the structure of a homologous protein exists. Template-based modeling methods are so named because they require a structural template onto which a target sequence can be threaded. For the sequence in question, a template structure, whether it is a sequence homolog or a structure exhibiting the same expected fold, must first be identified. Next, often after performing one or more sequence alignments, the target sequence is threaded onto the 3D coordinates of the template structure, thus replacing the sequence of the template with that of the target [44].
Even though significant advances are being made in the structure determination of additional GPCR or LeuT-fold structures, progress is slow when it comes to the determination of new MP folds. Thus, it is often difficult to identify a suitable template structure for MP comparative modeling because there are a limited number unique MP structures available in the PDB. Additionally, even though templates having a similar fold may exist, it is possible that the sequence homology between the target and the template is too low to be confidently detected. For example, of the more than 20 experimentally determined structures of G-protein coupled receptors (GPCRs), the majority are of class A, or class 1 (http://gpcr.scripps.edu/index.html) [45], even though there are five or six classes of GPCRs [46]. Similarly, while there are some structures of transporters, such as LeuT [47], vSGLT [48], BetP [49], and GadC [50], MPs having the LeuT fold perform a large variety of functions, show significant divergence in sequence, and can belong to a number of different protein superfamilies [51]. While comparative modeling based on an evolutionarily distant template can be useful for hypothesis generation, especially when combined with experimental methods in an iterative fashion [52], de novo structure prediction of MPs is needed in the absence of a structural template. Additionally, de novo folding methods allow for an unbiased exploration of the conformational space and can be used to complement comparative modeling in case of low similarity between template and target.
Compared to template-based MP modeling methods, there are only a handful of tools for de novo folding of MPs. RosettaMembrane was introduced in 2006 [53] and was later expanded to include full-atom scoring potentials [54]. Its structure prediction capabilities were limited to MPs of fewer than 150 amino acids. The addition of limited helix-helix contact restraints derived from sequence conservation allowed for accurate modeling of larger MPs - in four of twelve test cases models superimposable below a RMSD of 4 Å were observed [55]. One limitation was that this method could only account for one restraint at a time. Furthermore, the utility of RosettaMembrane in its current state is limited. For technical reasons that originate in the RosettaMembrane code base, it is not possible to de novo fold MPs with multiple restraints, such as those obtained from NMR and EPR.
Other methods to predict MP structure, such as FILM3, exhibit mild success for predicting large MPs, but they rely on correlated mutational information to score MP models. Of 71 MP sequences, FILM3 was able to correctly predict 100% of inter-helix contacts for 17 proteins. Upon comparison with two-dimensional slices of the experimental structures, 9 predicted structures had the correct fold [56,57]. EVfold_membrane is also a promising method for MP structure determination but also relies on information from evolutionary covariation [58]. BCL::MP-Fold, on the other hand, is independent of contacts predicted from correlated mutations. It reduces the conformational search space by assembling secondary structure elements (SSEs) combined with knowledge-based potentials (KBPs) to assess model quality [59]. The disadvantage of BCL-generated models is the lack of inter-helix loop regions. Additionally, it under-predicts secondary structural features often present in MPs, such as helical kinks because models are comprised of idealized α-helices.
We have developed RosettaTMH to address the size limitation of other reported MP de novo folding methods. RosettaTMH assembles MP folds via rigid body perturbations of transmembrane helices (TMHs). However, unlike BCL::MP-Fold, 3- and 9-amino acid fragment insertions, as used in the traditional Rosetta de novo folding algorithm [53,55,60], are used to more thoroughly sample helical orientations and introduce bends and kinks. Throughout the de novo folding process, RosettaMembrane’s MP-specific scoring functions are used [53,54]. RosettaTMH can be combined with multiple experimental restraints, such as inter-residue distance information from EPR, which is an advantage compared to previously published RosettaMembrane folding protocols. This additional feature allows for improved sampling of native-like folds that are in agreement with empirical information.
RosettaTMH was benchmarked on 34 MPs of known structure. It was compared to the original RosettaMembrane folding algorithm, “MembraneAbinitio” [53,55] and the traditional fragment assembly-only method used for folding soluble proteins in Rosetta, “ExtendedChain” [61] but using the RosettaMembrane scoring function. In order to assess the performance of combining RosettaTMH with experimentally obtained structural data, EPR distance restraints were simulated for all MPs in the benchmark set. The purpose of the benchmark was to determine if these restraints increase the sampling of native-like MP folds. The simulated distance restraints were generated using the BioChemical Library (BCL, www.meilerlab.org) and the restraint-picking algorithm introduced by Kazmier, et al. [62]. We show that, by implementing the ability to fold MPs with structural restraints, native-like folds can be obtained for 30 MPs in the benchmark set. For the purpose of this manuscript we define a native-like fold as having a RMSD100SSE value smaller than 8 Å (read below).
The RosettaTMH MP folding algorithm differs significantly from both the Rosetta folding algorithm for soluble proteins, “ExtendedChain” [61], as well as the published RosettaMembrane folding protocols [53,55]. The primary difference is that RosettaTMH allows for potentially enhanced sampling of MP folds by treating TMHs as rigid bodies. Each TMH can be rotated, translated, or transformed as an independent entity. In order to implement this new algorithm in the overall Rosetta folding framework, the model’s fold tree was modified. The fold tree of a protein model is a directed acyclic graph representing the connectivity of the model in internal coordinate space. This connectivity is distinct from chemical connectivity and enables Rosetta to rapidly move large sections of the protein independently [63,64]. In the case of a helical MP, a radial, or star-shaped, fold tree is used; therefore, the center of mass (CoM) of each TMH is connected to a central node (Figure 1).
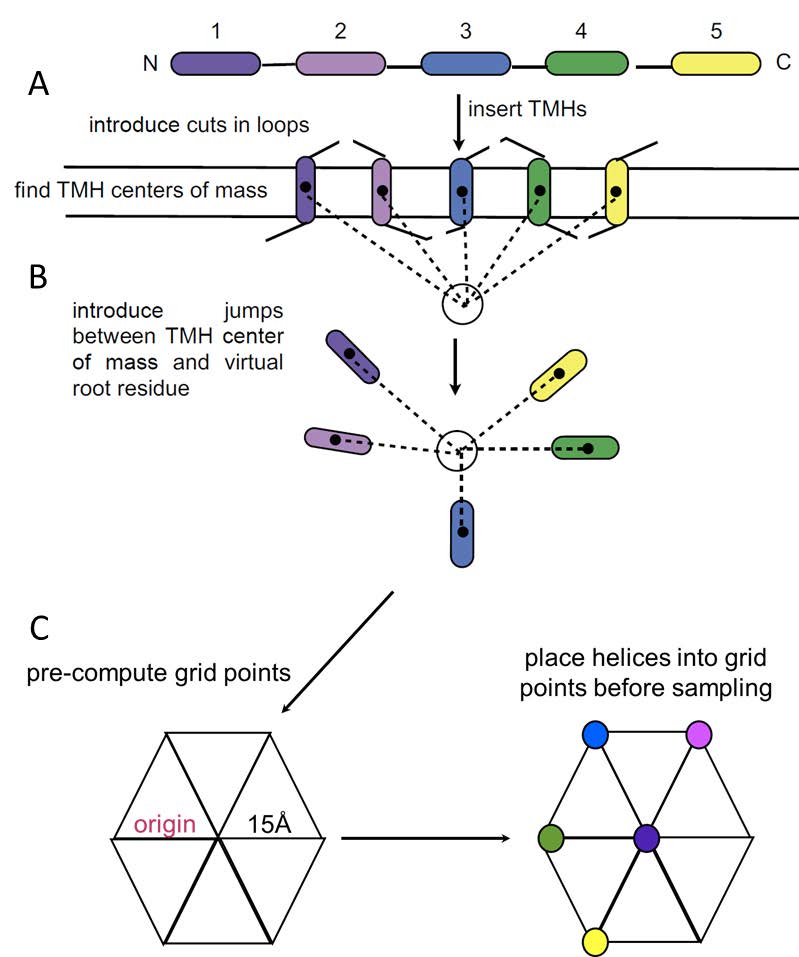 Figure 1. Generation of membrane protein fold tree in RosettaTMH and initial placement of transmembrane helices This schematic outlines how RosettaTMH generates a radial fold tree for a 5-TMH MP. In preparation for generating the fold tree (A), the primary sequence of the protein is read in and used to create an idealized α-TMH. RosettaTMH utilizes user-defined TMH definitions to divide the idealized TMH and insert each individual TMH into the implicit membrane. It then calculates each TMH’s center of mass (CoM). (B) The CoMs connect the TMHs to a central root residue (open circle) in internal coordinate space. (C) A hexagonal grid is computed, such that the vertices are aligned along the membrane center plane and are 15 Å away from one another and from the origin. Then, for each grid point, a TMH is chosen randomly, and the TMH is transformed to that grid point such that its CoM is aligned with the origin. The hexagonal grid can be expanded as needed, depending on the number of TMHs in the protein.
Figure 1. Generation of membrane protein fold tree in RosettaTMH and initial placement of transmembrane helices This schematic outlines how RosettaTMH generates a radial fold tree for a 5-TMH MP. In preparation for generating the fold tree (A), the primary sequence of the protein is read in and used to create an idealized α-TMH. RosettaTMH utilizes user-defined TMH definitions to divide the idealized TMH and insert each individual TMH into the implicit membrane. It then calculates each TMH’s center of mass (CoM). (B) The CoMs connect the TMHs to a central root residue (open circle) in internal coordinate space. (C) A hexagonal grid is computed, such that the vertices are aligned along the membrane center plane and are 15 Å away from one another and from the origin. Then, for each grid point, a TMH is chosen randomly, and the TMH is transformed to that grid point such that its CoM is aligned with the origin. The hexagonal grid can be expanded as needed, depending on the number of TMHs in the protein.
Before de novo folding begins, each TMH is inserted into the implicit RosettaMembrane environment [53]. The CoM of each TMH is set at the membrane center, and the helices are aligned to the membrane normal such that each TMH is antiparallel to its sequential neighbors. The helices are arranged in a hexagonal grid and are initially separated from each other by 15 Å. The starting fold of the model is randomized; that is, the arrangement of helices in the hexagonal grid is different for each starting model (Figure 1).
The pre-processing and de novo folding stages of RosettaTMH are summarized in Figure 2.
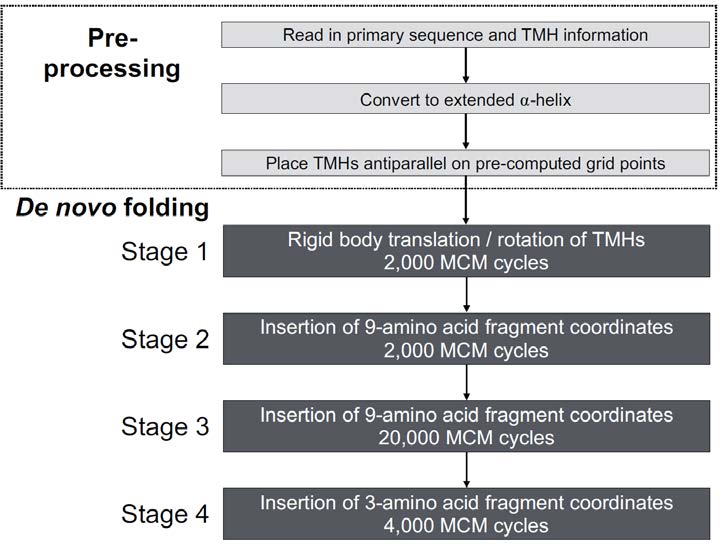 Figure 2. Outline of stages for RosettaTMH de novo folding This flowchart summarizes the process of de novo folding with RosettaTMH, including the pre-processing that takes place prior to Monte Carlo Metropolis (MCM) sampling.
Figure 2. Outline of stages for RosettaTMH de novo folding This flowchart summarizes the process of de novo folding with RosettaTMH, including the pre-processing that takes place prior to Monte Carlo Metropolis (MCM) sampling.
Folding begins after the initialization of the model. The first stage of de novo folding consists entirely of rigid body transformations [53] performed in a Monte Carlo Metropolis (MCM) fashion [65,66]. For each MCM move, the TMH is allowed to either rotate by up to 0.1° about any axis or translate up to 0.5 Å in any direction from its current position. The conformation resulting from each transformation is scored according to the RosettaMembrane centroid-based scoring function. Stage 1 of folding consists of 2,000 MCM moves, and the RG and RosettaMembrane-specific “density” term are turned on [53]. These scoring terms aid in improving the compactness of the model. After the first stage, the model undergoes 9- and 3-amino acid fragment insertions using a protocol analogous to the one used for soluble proteins [53,61]. Briefly, in Stage 2,2,000 MCM cycles are performed, during which 9mer fragments are inserted onto the helical protein backbone. The density scoring term is turned off, and residue pairing, membrane environment, and membrane-specific penalties are added [53,54]. The density term is re-introduced in Stage 3, which consists of 10 inner cycles; during these inner cycles, the scoring function can be alternated if desired. However, for MPs, the scoring function is the same for each of two inner cycle sub-stages. Each sub-stage consists of 2,000 MCM cycles for inserting 9mer fragments, resulting in a total of 20,000 fragment insertions. Finally, the density term is up-weighted in Stage 4, and 4,000 MCM cycles of 3mer fragment insertions are performed. Note, that we omitted construction of loops between TMHs as we wanted to test the TMH folding protocol. An inter-helix distance score ensures that TMHs are close enough to allow for construction of loops (red below).
The 34-protein benchmarking set exhibits a wide range of sizes and topological complexity. The number of EPR distance restraints simulated was computed as
| #restraints=0.2×#aaTMH |
Ten sets of EPR distance restraints were generated for each protein for the 34-MP benchmark. This was done to avoid bias resulting from using any single restraint set. The restraint selection algorithm developed by Kazmier, et al. [62] was employed. The algorithm optimizes the information content of the restraint set by maximizing the sequence separation between spin labeling sites. At the same time, the algorithm finds restraint sets that link all pairs of SSEs in the protein and excludes positions that are likely buried and unlikely to be labeled without disruption of the tertiary structure. In order to convert the resulting restraint sets to EPR-like distance restraints for testing during de novo folding, the Euclidian distances between the specified residues were determined from the MP experimental structures. Next, a spin label uncertainty was added to each distance, based on the cone model-based spin label statistics generated for the RosettaEPR KBP [26]. These statistics were generated by placing a pseudo-spin label in the form of a right-angle cone (based on methanethiosulfonate, or MTS) on exposed residue pairs in a database of over 3,500 proteins. The frequency of observed values for the calculated difference between spin label distance and Cβ distance (dSL-dCβ) were collected in a histogram, which was shown to match relatively well to experimentally determined dSL-dCβ values for T4-lysozyme and αA-crystallin. This histogram of spin label statistics quantifies the expected uncertainty associated with EPR distances measured on proteins spin labeled with MTS.
The EPR distances for the residue pairs were simulated as described in the previous section. Preliminary benchmarking indicated that the EPR score used for the folding of T4-lysozyme [26] was insufficient to improve MP model quality of large MPs, such as rhodopsin. Instead, it was determined that a two-component scoring term was needed.
The modified EPR restraint potential for folding MPs consists of an energetic bonus derived from the aforementioned cone model statistics. Indeed, this energetic bonus is the same KBP used in the de novo folding of T4-lysozyme [26]. However, in addition to the KBP energetic bonus, the EPR restraint score contains an energetic penalty characterized by the equation:
| f(x)={(x−lb)2forx<lb0forlb≤x≤ub(x−ub)2forub<x≤ub+rswitchx−ub−rswitch+rswitch2forx>ub+rswitch |
The weight of each EPR scoring term component was optimized separately. One thousand models of each of 9 proteins indicated in Table 1 were folded using RosettaTMH for each EPR restraint weighting scheme. Combinations of the weights for both components of the scoring term were systematically tested in a grid search. For each protein and each of 49 weighting schemes, the percentage of models having RMSD100SSE < 8 Å was computed, and the average of these values across the 9 proteins are reported in Table S1. The RMSD100SSE is defined as:
| RMSD100SSE=RMSD_SSE/(1+ln√N/100) |
| enrichment=TPTP+FP×P+NP |
| PDB | Chain | Domain | # Res | # TMH | Contact Order | # Restraints |
| 3SYO | 76–197 | 122 | 2 | 14.4 | 12 | |
| 2BG9 | A | 211–301 | 91 | 3 | 6.9 | 16 |
| 1J4N | 4–119 | 116 | 3 | 15.2 | 17 | |
| 2KSF | 396–502 | 107 | 4 | 11.9 | 13 | |
| 1PY6 (1PY7)a | 77–199 | 123 | 4 | 13.3 | 20 | |
| 2PNO | A | 2–131 | 130 | 4 | 13.6 | 22 |
| 2BL2 | 12–156 | 145 | 4 | 20.7 | 25 | |
| 2K73 | 1–164 | 164 | 4 | 15.5 | 19 | |
| 2ZW3 | A | 2–217 | 216 | 4 | 25.7 | 24 |
| 1IWG | 336–498 | 163 | 5 | 17.4 | 26 | |
| 1RHZ | A | 23–188 | 166 | 5 | 19.8 | 21 |
| 2YVX | A | 284–471 | 188 | 5 | 20.6 | 26 |
| 1OCC | C | 71–261 | 191 | 5 | 24.1 | 29 |
| 4A2N | 1–192 | 192 | 5 | 22.4 | 24 | |
| 1KPL | 31–233 | 203 | 5 | 23.4 | 31 | |
| 2BS2 | C | 21–237 | 217 | 5 | 17.5 | 29 |
| 3P5N | 10–188 | 179 | 6 | 17.9 | 22 | |
| 2IC8 | 91–272 | 182 | 6 | 17.9 | 23 | |
| 1PV6 | 1–190 | 189 | 6 | 28.3 | 33 | |
| 2NR9 | 4–195 | 192 | 6 | 17.6 | 24 | |
| 1OKCb | 2–293 | 292 | 6 | 25.8 | 34 | |
| 3B60b | A | 10–328 | 319 | 6 | 25.7 | 52 |
| 2KSY | 1–223 | 223 | 7 | 20.1 | 37 | |
| 1PY6b | 5–231 | 227 | 7 | 25.2 | 36 | |
| 3KCU | 29–280 | 252 | 7 | 29.7 | 33 | |
| 1FX8b | 6–259 | 254 | 7 | 28.6 | 38 | |
| 1U19b | 33–310 | 278 | 7 | 25.0 | 41 | |
| 3KJ6 | A | 35–346 | 311 | 7 | 39.5 | 31 |
| 3HD6b | 6–448 | 403 | 12 | 43.6 | 59 | |
| 3GIAb | 3–435 | 433 | 12 | 62.5 | 64 | |
| 3O0Rb | B | 10–458 | 449 | 12 | 30.6 | 69 |
| 3HFXb | 12–504 | 493 | 12 | 68.0 | 63 | |
| 2XUT | A | 13–500 | 488 | 14 | 42.8 | 71 |
| 2XQ2 | A | 9–573 | 565 | 15 | 71.8 | 79 |
| a Referred to as 1PY7 in this publication | ||||||
| b These proteins were used in RosettaTMH parameter optimization | ||||||
During EPR restraint weight optimization, the Rosetta radius of gyration (RG) scoring term was used with a weight of 4.25. Each restraint was scored independently, and the sum of individual restraint scores constitutes the total raw restraint score. The total restraint score was multiplied by a normalization factor that is equal to:
| weightcst=log(#cst)#cst×#aa |
| cst_scoreweighted=average(cst_scoreweighted)×log(#cst)×#aa |
The generation of input files for this benchmark, except for the simulated restraints, is described in the work by Weiner, et al. on BCL::MP-Fold [59]. Briefly, the primary sequence of each protein listed in Table 1 was used to generate 3- and 9-amino acid fragment files required for de novo folding in Rosetta. The Rosetta spanfiles containing the TMH definitions were obtained by using predictions from OCTOPUS [71]. Rosetta lipophilicity files were also generated for each protein using the LIPS algorithm [72]. Five thousand models were folded from the primary sequence, using TMH information and the RosettaMembrane centroid-based scoring function [53]. When multiple EPR restraint sets were used, the number of total models generated per restraint set was equal to the total number of models generated divided by the number of different restraint sets (i.e., 10 sets of 500 models for each protein).
All computations were performed using the Vanderbilt University Advanced Computing Cluster for Research and Education (ACCRE) on a combination of AMD Opteron and Intel Nehalem processor nodes or the Vanderbilt University Center for Structural Biology computing cluster on a variety of x86 computing processors.
The RosettaTMH source code is available in the Rosetta master branch, which is available to developers in the RosettaCommons via https://github.com/RosettaCommons. Rosetta revision numbers d592380 and d7b5a70 were used for RosettaTMH parameter optimization and benchmarking, respectively. The software licenses and the complete protocol capture for this work is available from the RosettaCommons (www.rosettacommons.org), as well as in the Supplemental Information. Information for obtaining software licenses for the BioChemical Library is available at www.meilerlab.org/bclcommons.
Thirty-four α-helical MPs and MP subunits of known structure were chosen to test the RosettaTMH folding algorithm (Table 1). Nine of these proteins (underlined) were used for the initial testing and parameter optimization of the RosettaTMH protocol. These nine proteins were chosen because we wanted to design a method that would be primarily used for folding larger, complex MPs. While many MPs are oligomers, the present benchmarks includes only monomeric MPs or protomeric subunits of oligomeric MPs. Folding as well as EPR labeling strategies need to be adapted when moving to oligomeric MPs which is a focus of ongoing research but beyond the scope of this initial manuscript.
De novo folding of soluble proteins with EPR restraints in Rosetta had been optimized previously [25,26]. However, it was found that, for MPs, a quadratic penalty was needed in addition to the EPR KBP energetic bonus to sufficiently improve conformational sampling of native-like folds where a ‘native-like’ fold is defined as having a RMSD100SSE value smaller than 8 Å. The EPR KBP and the quadratic penalty were weighted equally. The enrichment for folding was 2.93 (Table S2). RMSD100SSE and enrichment are defined in Materials and Methods.
As expected, the enrichment for de novo folding with EPR restraints was generally lower than folding with no restraints. This is because the number of false positives, or low-scoring, high-RMSD models, was higher when folding with simulated restraints. This is perhaps due to the higher promiscuity of the EPR restraints, which are broader than distance restraints resulting from NMR nuclear Overhauser effects (NOEs). Therefore, models that fulfill the simulated restraints and are lower-scoring have not always native-like fold. This phenomenon is generally observed across all 34 benchmarked MPs as well (Table S3).
In order to assess the overall sampling capability of each folding protocol, we computed the percentage of models having an RMSD100SSE < 8 Å (FractionRMSD<8 Å, Table 2), which serves as a cutoff for determining if models have the correct fold. We also report the best RMSD100SSE (RMSD1st RMSD) obtained for each method and the mean RMSD100SSE of the five lowest-scoring models (RMSDtop5 score). As was observed with T4-lysozyme [25,26], the addition of EPR restraints increases the likelihood of obtaining the correct MP fold for both RosettaTMH and ExtendedChain. When looking at FractionRMSD<8 Å, followed by the RMSD10% RMSD and RMSDtop5 score, RosettaTMH performs better than ExtendedChain for 11 of 34 proteins, including the 6 largest proteins. Further, when compared to other Rosetta MP folding methods, RosettaTMH+EPR obtains the highest percentage of correctly folded models for 3 of the 13 medium-sized proteins, 2 of the 8 large proteins, and 3 of the 6 very large proteins. Interestingly, ExtendedChain+EPR performs best for de novo folding of medium-sized proteins (Table 2).
| RMSDtop5 score | RMSD1st RMSD | FractionRMSD<8 Å | |||||||||||||
| average RMSD100SSE to experimental structure of the top five models by score | lowest RMSD100SSE to experimental structure | percentage of models with a RMSD100SSE better than 8 Å | |||||||||||||
| PDB | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR |
| 3SYO | 11.0 | 11.8 | 12.3 | 12.6 | 12.4 | 7.1 | 7.2 | 8.5 | 6.4 | 8.0 | 0 | 0 | 0 | 0 | 0 |
| 2BG9 | 6.3 | 9.7 | 9.1 | 12.5 | 8.4 | 4.0 | 4.2 | 4.6 | 5.7 | 4.3 | 0 | 23 | 30 | 2 | 25 |
| 1J4N | 9.7 | 7.8 | 8.0 | 12.9 | 11.3 | 5.0 | 4.7 | 4.4 | 6.7 | 7.4 | 13 | 14 | 28 | 0 | 1 |
| 2KSF | 8.0 | 9.1 | 10.0 | 9.4 | 10.6 | 5.2 | 5.7 | 5.9 | 5.0 | 5.8 | 21 | 10 | 15 | 1 | 9 |
| 1PY7 | 4.9 | 6.1 | 4.2 | 11.1 | 7.7 | 2.2 | 2.4 | 2.5 | 5.6 | 4.5 | 66 | 67 | 58 | 1 | 23 |
| 2PNO | 7.6 | 8.7 | 7.0 | 12.3 | 8.4 | 3.0 | 3.2 | 3.3 | 7.5 | 5.5 | 29 | 21 | 47 | 0 | 11 |
| 2BL2 | 6.1 | 5.5 | 4.7 | 11.5 | 7.0 | 2.4 | 2.5 | 2.8 | 5.5 | 4.0 | 71 | 55 | 68 | 0 | 39 |
| 2K73 | 9.7 | 10.2 | 10.2 | 12.7 | 10.9 | 5.9 | 4.8 | 6.8 | 7.9 | 6.7 | 2 | 1 | 1 | 0 | 2 |
| 2ZW3 | 13.1 | 12.9 | 13.0 | 16.0 | 13.2 | 8.7 | 9.9 | 10.5 | 10.1 | 9.8 | 0 | 0 | 0 | 0 | 0 |
| 1IWG | 7.3 | 9.1 | 7.3 | 12.9 | 8.4 | 5.0 | 5.5 | 4.4 | 8.1 | 5.9 | 16 | 4 | 48 | 0 | 13 |
| 1RHZ | 10.1 | 10.7 | 8.8 | 11.6 | 11.5 | 6.1 | 6.6 | 6.1 | 8.5 | 7.7 | 1 | 1 | 10 | 0 | 1 |
| 2YVX | 9.2 | 9.0 | 7.9 | 14.7 | 9.0 | 5.9 | 6.0 | 5.1 | 8.2 | 6.7 | 5 | 1 | 20 | 0 | 6 |
| 1OCC | 11.3 | 10.4 | 10.4 | 13.1 | 8.4 | 6.7 | 7.0 | 7.2 | 7.9 | 5.4 | 1 | 0 | 1 | 0 | 17 |
| 4A2N | 8.4 | 9.2 | 9.4 | 11.2 | 10.5 | 5.4 | 6.2 | 6.3 | 7.8 | 7.2 | 4 | 1 | 6 | 0 | 2 |
| 1KPL | 13.2 | 14.4 | 11.8 | 15.1 | 12.7 | 10.0 | 10.7 | 7.9 | 11.1 | 9.5 | 0 | 0 | 1 | 0 | 0 |
| 2BS2 | 10.0 | 9.7 | 10.0 | 13.5 | 10.1 | 6.1 | 5.3 | 5.8 | 8.8 | 6.9 | 1 | 1 | 6 | 0 | 3 |
| 3P5N | 9.5 | 10.4 | 9.5 | 12.6 | 11.7 | 5.3 | 6.0 | 6.9 | 9.5 | 9.0 | 2 | 1 | 2 | 0 | 0 |
| 2IC8 | 9.1 | 9.4 | 9.1 | 11.5 | 10.2 | 5.3 | 5.0 | 6.1 | 8.7 | 7.1 | 4 | 1 | 5 | 0 | 1 |
| 1PV6 | 10.4 | 10.1 | 8.1 | 11.5 | 8.1 | 5.7 | 6.4 | 5.1 | 8.0 | 5.4 | 4 | 1 | 18 | 0 | 15 |
| 2NR9 | 10.2 | 10.9 | 9.8 | 12.2 | 11.3 | 5.8 | 6.9 | 6.3 | 8.6 | 7.4 | 2 | 0 | 3 | 0 | 1 |
| 1OKC | 12.3 | 12.5 | 13.1 | 12.6 | 11.9 | 9.0 | 10.8 | 8.9 | 9.2 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 3B60f | 9.8 | 9.7 | 6.3 | 13.7 | 9.7 | 6.3 | 6.1 | 4.1 | 9.2 | 6.0 | 2 | 1 | 38 | 0 | 10 |
| 2KSY | 8.9 | 8.4 | 6.8 | 12.8 | 8.5 | 3.9 | 4.2 | 4.5 | 7.7 | 5.1 | 30 | 15 | 28 | 0 | 19 |
| 1PY6f | 8.0 | 8.5 | 8.2 | 12.2 | 7.9 | 3.9 | 5.1 | 5.2 | 7.8 | 5.2 | 27 | 9 | 15 | 0 | 18 |
| 3KCU | 10.6 | 10.3 | 9.9 | 11.9 | 10.8 | 6.3 | 6.9 | 6.4 | 9.7 | 7.9 | 1 | 0 | 2 | 0 | 0 |
| 1FX8f | 10.7 | 11.3 | 10.5 | 12.4 | 10.4 | 7.8 | 8.3 | 7.7 | 8.4 | 8.0 | 0 | 0 | 1 | 0 | 0 |
| 1U19f | 12.7 | 14.6 | 11.8 | 12.4 | 8.7 | 9.2 | 11.4 | 8.4 | 8.7 | 6.1 | 0 | 0 | 0 | 0 | 7 |
| 3KJ6 | 14.6 | 15.2 | 15.5 | 15.6 | 15.3 | 11.5 | 12.1 | 12.0 | 12.4 | 12.7 | 0 | 0 | 0 | 0 | 0 |
| 3HD6f | 10.6 | 16.0 | 12.0 | 13.2 | 10.9 | 7.5 | 12.4 | 9.1 | 10.3 | 8.5 | 0 | 0 | 0 | 0 | 0 |
| 3GIAf | 14.1 | 25.5 | 13.9 | 14.2 | 12.0 | 11.8 | 17.2 | 9.2 | 11.6 | 9.5 | 0 | 0 | 0 | 0 | 0 |
| 3O0Rf | 10.1 | 24.0 | 11.2 | 13.0 | 10.0 | 6.4 | 18.6 | 7.6 | 8.9 | 6.5 | 2 | 0 | 1 | 0 | 4 |
| 3HFXf | 13.5 | 29.9 | 13.5 | 13.1 | 11.6 | 10.0 | 22.2 | 10.2 | 10.6 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 2XUT | 14.3 | 25.1 | 15.1 | 16.2 | 15.0 | 12.4 | 20.2 | 12.6 | 14.6 | 12.9 | 0 | 0 | 0 | 0 | 0 |
| 2XQ2 | 15.8 | 35.9 | 16.0 | 16.6 | 15.7 | 13.6 | 25.5 | 12.9 | 14.8 | 13.7 | 0 | 0 | 0 | 0 | 0 |
| mean | 10.3 | 13.0 | 10.1 | 13.0 | 10.6 | 6.8 | 8.7 | 6.9 | 8.8 | 7.5 | 10 | 7 | 13 | 0 | 7 |
| stddev. | 2.6 | 7.0 | 2.9 | 13.0 | 10.6 | 2.8 | 5.8 | 2.7 | 2.2 | 2.4 | 18 | 15 | 19 | 0 | 10 |
A representative subset of 7 proteins was chosen from the 34-protein benchmark set for further RMSD100SSE analysis. For each protein and for each folding method, the RMSD100SSE values were sorted from lowest to highest, and the top 5% of models by RMSD100SSE were selected. Next, RMSD100SSE vs. RMSD100SSE plots comparing RosettaTMH and RosettaTMH+EPR with the other Rosetta MP folding methods were generated. This analysis clarifies a few key conclusions concerning RosettaTMH. First, when no EPR restraints are used, MembraneAbinitio and ExtendedChain outperform RosettaTMH for small- or medium-sized MPs. Second, RosettaTMH+EPR samples more lower-RMSD conformations for larger MPs when compared to RosettaTMH and ExtendedChain (distance restraints cannot be used with MembraneAbinitio). Finally, RosettaTMH performance is comparable to MembraneAbinitio and ExtendedChain for 3HFX and 1FX8, respectively, while RosettaTMH+EPR and ExtendedChain+EPR are comparable when folding 1FX8 (Figure 3).
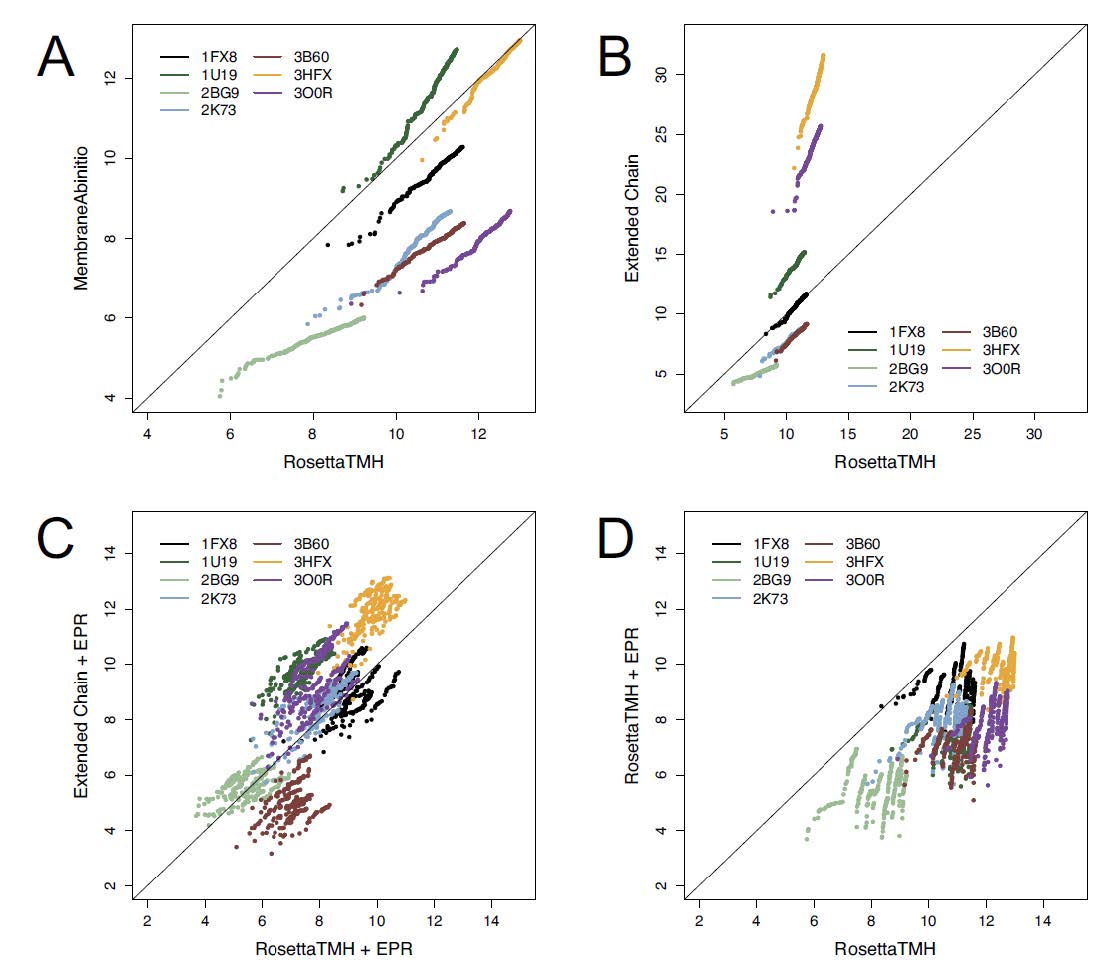 Figure 3. Sampling performance for de novo folding with RosettaTMH compared to other folding methods. For each panel, the RMSD100SSE of the top 5% of models by RMSD100SSE were selected for 7 proteins. A) MembraneAvinitio vs. RosettaTMH, B) Folding from an extended chain vs. RosettaTMH, C) Folding from an extended chain with EPR restraints vs. RosettaTMH with EPR restraints, D) RosettaTMH with EPR restraints vs. RosettaTMH (without EPR restraints).
Figure 3. Sampling performance for de novo folding with RosettaTMH compared to other folding methods. For each panel, the RMSD100SSE of the top 5% of models by RMSD100SSE were selected for 7 proteins. A) MembraneAvinitio vs. RosettaTMH, B) Folding from an extended chain vs. RosettaTMH, C) Folding from an extended chain with EPR restraints vs. RosettaTMH with EPR restraints, D) RosettaTMH with EPR restraints vs. RosettaTMH (without EPR restraints).
The MembraneAbinitio folding algorithm was first benchmarked on a dataset of relatively small proteins and performed best with small helical bundles [53]. However, it was found that MPs having more complex folds posed a much more difficult challenge, one which folding with experimental restraints and/or a new sampling algorithm could possibly address. Further, the addition of the RosettaEPR distance restraint potential improves sampling of native-like folds significantly. This appears to be primarily due to the influence of the EPR restraints, as folding with ExtendedChain+EPR also increases sampling efficiency to include the correct fold. In order to test this hypothesis, rhodopsin (PDB ID: 1U19 [73]) was selected for an in-depth analysis of the relationship between the number of EPR restraints and overall conformational sampling ability.
Rhodopsin was folded using all of the Rosetta methods listed in Table 2. However, for RosettaTMH+EPR and ExtendedChain+EPR, multiple sets of models were generated based on whether 0, 10, 20, 40, 80, or 160 simulated EPR distance restraints were used. Unlike in the 34-protein benchmark, only one EPR restraint set for each scenario was generated, and 1,000 models were folded for each case. Box-and-whisker plots of the resulting RMSD100SSE distributions are displayed in Figure 4. When no restraints are used, MembraneAbinitio and folding from an extended chain perform similarly, while RosettaTMH generally appears to generate lower-RMSD models. When using 10 restraints, RosettaTMH+EPR and ExtendedChain+EPR exhibit similar median RMSD100SSE values, but RosettaTMH+EPR samples a wider range of conformations. However, when 20 or more restraints are used, RosettaTMH+EPR is consistently better in sampling the correct fold. As expected, the number of outliers correlates inversely with the number of restraints.
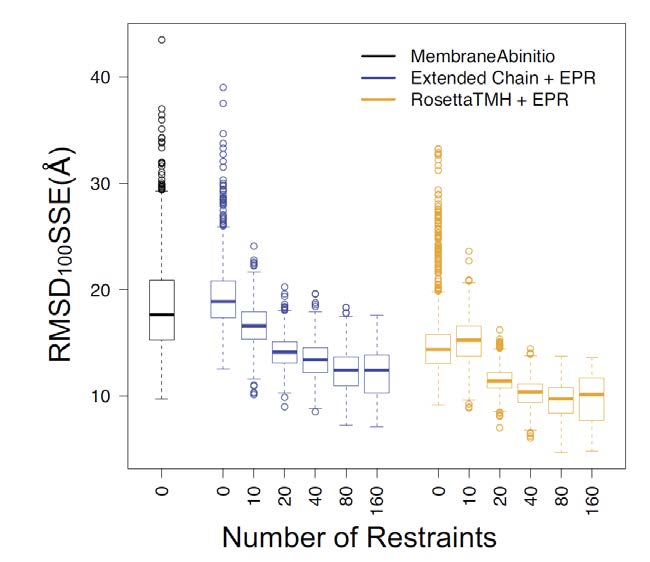 Figure 4. Sampling performance of RosettaTMH with various EPR restraint set sizes for folding rhodopsin Box-and-whisker plot indicating the breadth of model accuracy obtained for folding rhodopsin with RosettaTMH with 10, 20, 40, 80 and 160 simulated EPR distance restraints. The thick line indicates the median RMSD100SSE obtained, while the boxes indicate the interquartile range. The highest and lowest RMSD100SSE values, excluding outliers, are indicated by the “whiskers, ” and outliers are shown as open circles.
Figure 4. Sampling performance of RosettaTMH with various EPR restraint set sizes for folding rhodopsin Box-and-whisker plot indicating the breadth of model accuracy obtained for folding rhodopsin with RosettaTMH with 10, 20, 40, 80 and 160 simulated EPR distance restraints. The thick line indicates the median RMSD100SSE obtained, while the boxes indicate the interquartile range. The highest and lowest RMSD100SSE values, excluding outliers, are indicated by the “whiskers, ” and outliers are shown as open circles.
In addition to studying the overall performance of RosettaTMH with and without EPR restraints, the ability of the protocol to sample MP folds during each stage of folding (see Figure 2) was also analyzed. As with the above experiment, rhodopsin was chosen as an example protein, and only one set of 41 optimally weighted restraints was used. For each folding method, 1,000 individual trajectories were run, and the conformations before folding began and after each stage of folding were output. Then, similar to in Figure 4, the RMSD100SSE distributions for each folding stage were plotted. The first step in the Rosetta MembraneAbinitio folding algorithm (Stage 0), samples a single, high scoring, extended-chain conformation. For MembraneAbinitio and ExtendedChain, model quality significantly improves from initiation to Stage 1 and then from Stage 1 to Stage 2. In contrast, RosettaTMH-generated model accuracy decreases during Stage 1 of folding. That is, the rigid body sampling causes the quality of rhodopsin models to decrease. The RMSD100SSE values do not improve significantly for Stages 2-4 when no restraints are used. When EPR restraints are used, the models’ accuracy improves from Stage 1 to Stage 2 but does not change significantly after Stage 2. This was also observed for ExtendedChain+EPR.
RosettaTMH assembles MP folds by breaking up the proteins into individual TMHs and allowing the helices to move as independent rigid bodies. The resulting arrangements could result in distances between subsequent SSEs that cannot be connected by a loop. In order to determine if the SSEs can be connected by loops, the Euclidian distance between subsequent SSEs was measured for all 34 native MPs, as well as for the 5,000 models for all 34 benchmark MPs folded with and without EPR restraints. For each protein, the percentage of models in which all loops could be theoretically or realistically closed was determined. The maximum Euclidian distance theoretically possible (“Maximum Possible”) was computed as:
| MaximumPossible=(3.8∗(LoopLength−1)) |
Generally speaking, RosettaTMH, either with and without EPR restraints, fails to reflect the dependence of Euclidean distance from loop length accurately. Indeed, every protein had at least five models in which all inter-helix distances can theoretically be spanned by a loop, but only a small percentage - if any - exhibit native-like inter-helix distances. Unsurprisingly, the addition of EPR restraints did improve the possibility of generating models with closeable loops in the majority of cases. However, for the very large MPs, no models exhibited native-like loop distances, and of the large MPs, only 0.04% of 1FX8 models had this characteristic, even when restraints were used (S4 Table).
Based on the analysis presented in this work, we have developed a proximate guide for choosing which Rosetta MP modeling protocol to use based on the protein of interest (Figure S2). First, de novo folding should ideally be used only when there is no protein of ≥ 30% sequence homology for which there is a structure available. Next, Rosetta is currently only capable of de novo folding primarily helical MPs. If the protein of interest has fewer than 200 residues, we recommend folding with MembraneAbinitio (no restraints) or from an extended chain (with restraints). However, if the protein is large and relatively complex, MembraneAbinitio is recommended. Finally, RosettaTMH would be suitable for folding large MPs if experimental restraints, such as those from EPR or NMR, are available.
We are introducing a new de novo folding algorithm for MPs. This initial implementation is already on par with other methods for folding large MPs within Rosetta. It has some advantages: One advantage is that experimental restraints can be incorporated, a feature that earlier folding protocols lacked. We illustrate this feature using simulated EPR distance restraints. The second advantage is the very short run time and an observed tendency to work better for large MPs.
The results in Table 2 and Figure 3-5 indicate that, for large and very large MPs, the conformational search space of MP structures must be limited in order to obtain de novo-folded models with native-like folds. The MembraneAbinitio protocol attempts to accomplish this by folding MPs “from the inside out.” That is, a TMH in the middle of the protein sequence is inserted into the implicit membrane environment first. Next, either TMHs N- or C-terminal to the initially inserted TMH are folded into the membrane via fragment-based assembly, beginning with the TMH adjacent to the starting TMH. Then, the TMHs on the other side (in terms of sequence) are folded in the same manner [53].
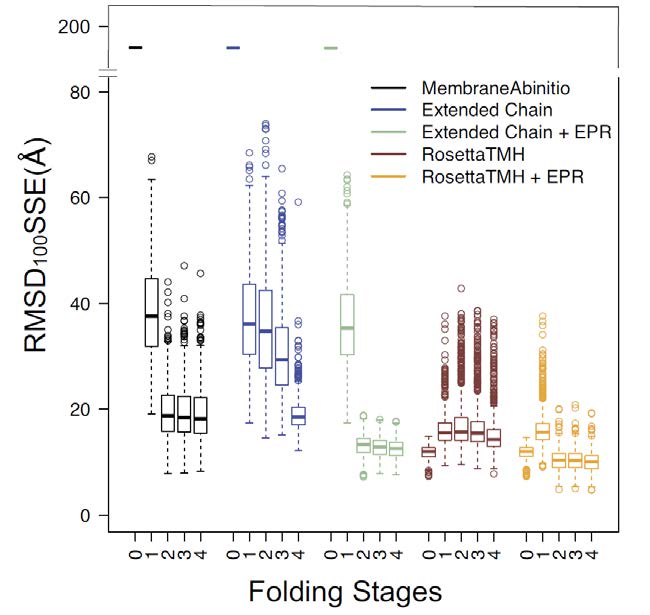 Figure 5. Sampling performance of various Rosetta methods during each stage of de novo folding using rhodopsin as an example. Box-and-whisker plot indicating the breadth of model accuracy obtained during each stage of folding with MembraneAbinitio, folding from an extended chain with and without EPR restraints, and folding with RosettaTMH with and without restraints. The thick line indicates the median RMSD100SSE obtained, while the boxes indicate the interquartile range. The highest and lowest RMSD100SSE values, excluding outliers, are indicated by the “whiskers, ” and outliers are shown as open circles.
Figure 5. Sampling performance of various Rosetta methods during each stage of de novo folding using rhodopsin as an example. Box-and-whisker plot indicating the breadth of model accuracy obtained during each stage of folding with MembraneAbinitio, folding from an extended chain with and without EPR restraints, and folding with RosettaTMH with and without restraints. The thick line indicates the median RMSD100SSE obtained, while the boxes indicate the interquartile range. The highest and lowest RMSD100SSE values, excluding outliers, are indicated by the “whiskers, ” and outliers are shown as open circles.
While MembraneAbinitio was able to generate models with RMSD100SSE < 8 Å for over 26 of the 34 proteins tested. For the remaining 8 cases in which no correctly folded models were obtained, the addition of EPR restraints did enable other folding protocols to do so (Table 2). Indeed, for majority of benchmarked proteins, the MembraneAbinitio protocol performs better than either RosettaTMH or folding from an extended chain when EPR restraints are not used. However, when EPR restraints were used, the additional restraints often resulted in more models having the correct fold. This is important because MembraneAbinitio, unlike RosettaTMH, cannot take EPR restraints into account.
Therefore, for MPs of more than 4 TMHs and 145 residues, it is advantageous to include structural restraints, such as those available from NMR, EPR, etc. If one does employ such restraints, the traditional folding method, ExtendedChain, appears to be better suited for medium-sized MPs. On the other hand, when looking at MsbA (3B60), rhodopsin (1U19), and nitric oxide reductase (3O0R), RosettaTMH shows promise for de novo folding larger MPs, such as GPCRs, channels, and transporters (Table 2).
Even though Rosetta is now capable of folding MPs that have the correct fold and is sometimes able to recover intra-helical features, these models are not yet accurate enough to be used as the input to full-atom refinement using the RosettaMembrane all-atom scoring functions [54]. Typically, models of approximately 2.0 Å RMSD100SSE relative to the native structure are required in order to successfully obtain atomic detail information [74].
Based on the information in Figure 5, one next step in protocol optimization would be to forego the rigid body sampling in Stage 1 of RosettaTMH folding. It is expected that the initial set of rigid body transformations result in less viable MP conformations (e.g., TMH out of the membrane, lying too orthogonal to the membrane normal, or too far apart in 3D space). The fragment insertions in Stages 2-4 are then not able to recover the correct fold. This is supported by the lowest-RMSD models displayed in Figure 6 and the data in Table S4, which show that there is a general lack of inter-helical packing and native-like placement that is not remedied by fragment insertions. Not surprisingly, the addition of EPR restraints assists in improving packing and in the recovery of helical features (Figure 6).
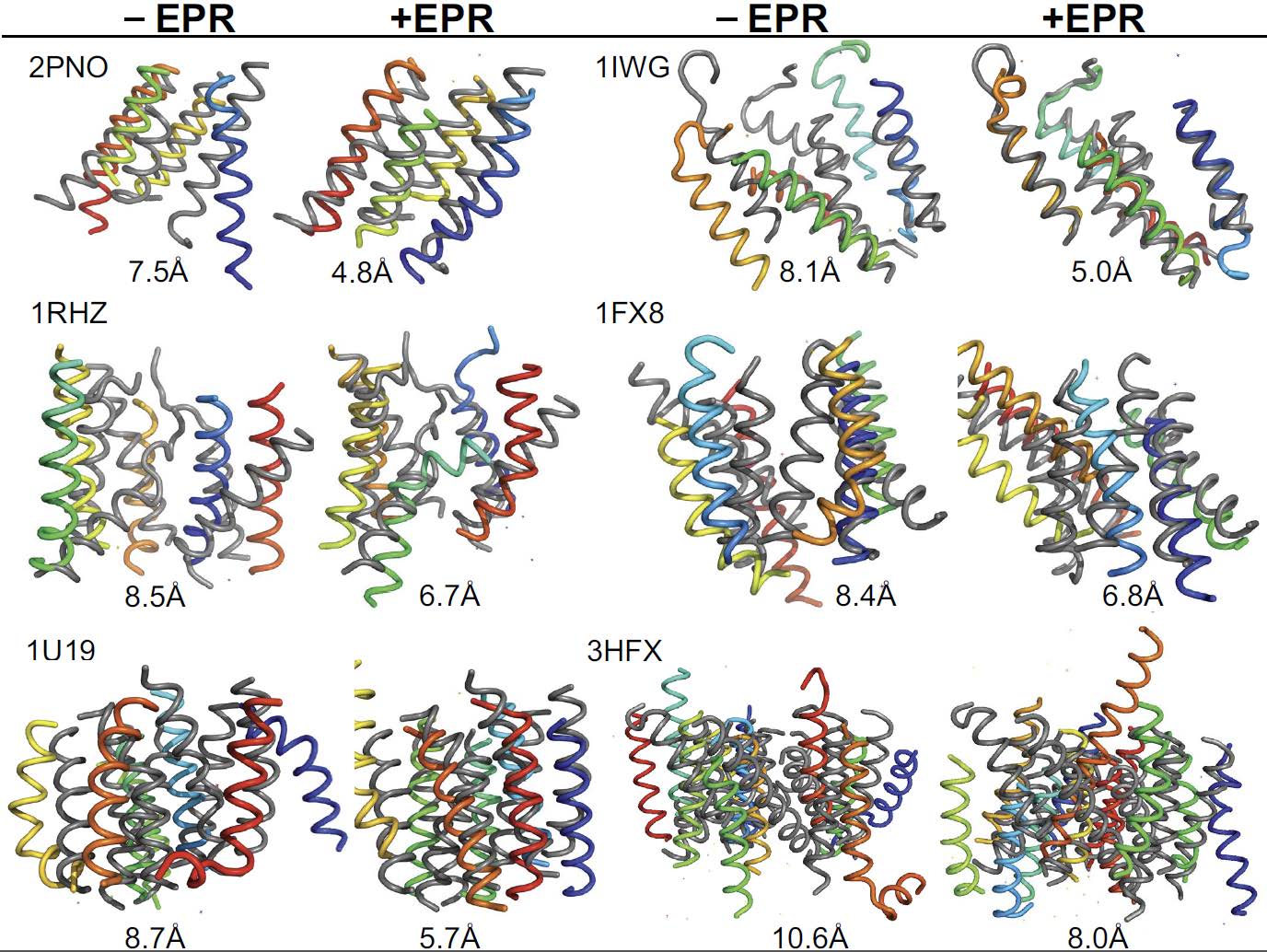 Figure 6. Most accurate model resulting from RosettaTMH folding for six proteins. The most accurate models obtained from folding with RosettaTMH without EPR restraints (left model) and with EPR restraints (right model) are colored in rainbow. The native structures are colored in gray. The RMSD100SSE of the model compared to native is reported in angstroms.
Figure 6. Most accurate model resulting from RosettaTMH folding for six proteins. The most accurate models obtained from folding with RosettaTMH without EPR restraints (left model) and with EPR restraints (right model) are colored in rainbow. The native structures are colored in gray. The RMSD100SSE of the model compared to native is reported in angstroms.
In order to create a radial fold tree for each model, the original simple fold tree must be “cut” to maintain the data structure’s acyclic nature. For folding with RosettaTMH, these cutpoints are chosen within the MP loops (Figure 1). However, now that the TMHs can move independently from one another, another external force must be applied to keep the TMHs in relatively close proximity, as they will otherwise drift apart and not exhibit native-like packing (Figure S2 and 6, Table S4). One approach is to integrate a loophash filter, which would ensure that TMHs that would normally be connected by a loop remain close enough in Cartesian space such that the inter-helical loop can be successfully rebuilt at a later stage.
The loophash filter is based on work published by Tyka, Jung, and Baker [75]. In the protocol introduced by the authors, the loophash algorithm allows for extremely fast rebuilding of protein segments by rapidly determining if a loop of a given sequence length can span the distance defined by two endpoints. A hash lookup table is generated for a loop of a given sequence length, and the hashes in the table refer to specific protein segments found in a database of non-homologous proteins of known structure. In addition to the loophash, or loop closure, filter, the implementation of a loop distance KBP, such as that used by BCL::Fold [76,77] could also be beneficial. While the loop closure filter would assist in ruling out models where TMHs could not theoretically be connected, and the loop distance KBP would provide an energetic incentive to place TMHs in more native-like conformations.
The RosettaTMH folding protocol appears to be a more rapid means of folding MPs than MembraneAbinitio and fragment-based assembly alone (Figure S3). This is probably a result of the lack of fragment insertions, and thus recalculation of torsion angles, during the first stage of folding. However, this decreased amount of fragment insertion may be the cause of the generation of lower-quality models. In any case, the significant speedup in model production allows for the generation of many more models. This increased sampling speed may be beneficial for obtaining higher quality models of large MPs when using a more optimized RosettaTMH protocol.
RosettaTMH is a new de novo folding protocol that assembles MP folds from the rigid body movements of TMHs, followed by peptide fragment insertions. This approach, along with the significantly decreased time required to fold models, allows for increased sampling of conformational space, which is important for the structure prediction of more complex proteins, such as GPCRs, transporters, and channels. RosettaTMH, unlike MembraneAbinitio, allows for the folding of MPs with experimental restraints. Further, while the new folding protocol alone improves sampling, the addition of experimental restraints may be necessary to obtain native-like folds, which is especially important for determination of MPs for which there is no structural template.
J.M. and S.H.D. conceived the RosettaTMH modeling protocol for use within the Rosetta. S.H.D. was primarily responsible for the implementation and testing of it. S.H.D. created the first version of this manuscript including tables and figures. S.L.D. was involved in the implementation of RosettaTMH within the Rosetta framework, as well as merging the RosettaTMH source code with the publicly released version of Rosetta. A.L.F. performed thorough testing of the RosettaTMH Protocol Capture and provided feedback to S.H.D. J.M. supervised the project and finalized the manuscript.
The authors would like to thank Drs. Frank DiMaio, Steven Lewis, and other members of the RosettaCommons for their assistance in the development of RosettaTMH. Axel Fischer was also very helpful in providing protocols on simulating EPR distance restraints in the BCL, and Dr. Brian Weiner provided many of the Rosetta-ready input files for the benchmark set.
Table S1: Percentage of correctly folded models obtained for folding 1,000 models of 9 membrane proteins with RosettaTMH using a variety of restraint score weighting schemes
Table S2: Enrichment obtained for folding 1,000 models of 9 membrane proteins with RosettaTMH using a variety of restraint score weighting schemes
Table S3: Enrichment obtained for folding 5,000 models of 34 membrane proteins with and without simulated EPR distance restraints
Table S4: RosettaTMH ability to generate models with loops that can or are likely to be closeable
Figure S1: Percentage of models with closeable loops generated by RosettaTMH
Figure S2: General guidelines for membrane protein modeling in Rosetta
Figure S3: Average time required for de novo folding
Protocol: Protocol Capture for the work presented
| [1] |
Krishnamurthy H, Gouaux E (2012) X-ray structures of LeuT in substrate-free outward-open and apo inward-open states. Nature 481: 469–474. doi: 10.1038/nature10737

|
| [2] | Sanders CR, Sonnichsen F (2006) Solution NMR of membrane proteins: practice and challenges. Magn Reson Chem 44 Spec No: S24–40. |
| [3] |
Horst R, Stanczak P, Stevens RC, et al. (2013) beta2-Adrenergic receptor solutions for structural biology analyzed with microscale NMR diffusion measurements. Angew Chem Int Ed Engl 52: 331–335. doi: 10.1002/anie.201205474

|
| [4] |
Chun E, Thompson AA, Liu W, et al. (2012) Fusion partner toolchest for the stabilization and crystallization of G protein-coupled receptors. Structure 20: 967–976. doi: 10.1016/j.str.2012.04.010

|
| [5] |
Baker LA, Baldus M (2014) Characterization of membrane protein function by solid-state NMR spectroscopy. Curr Opin Struct Biol 27: 48–55. doi: 10.1016/j.sbi.2014.03.009

|
| [6] |
Hopkins AL, Groom CR (2002) The druggable genome. Nat Rev Drug Discov 1: 727–730. doi: 10.1038/nrd892

|
| [7] |
Overington JP, Al-Lazikani B, Hopkins AL (2006) How many drug targets are there? Nat Rev Drug Discov 5: 993–996. doi: 10.1038/nrd2199

|
| [8] |
Bakheet TM, Doig AJ (2009) Properties and identification of human protein drug targets. Bioinformatics 25: 451–457. doi: 10.1093/bioinformatics/btp002

|
| [9] |
Maslennikov I, Choe S (2013) Advances in NMR structures of integral membrane proteins. Curr Opin Struct Biol 23: 555–562. doi: 10.1016/j.sbi.2013.05.002

|
| [10] |
Klammt C, Maslennikov I, Bayrhuber M, et al. (2012) Facile backbone structure determination of human membrane proteins by NMR spectroscopy. Nat Methods 9: 834–839. doi: 10.1038/nmeth.2033

|
| [11] |
Berman HM, Battistuz T, Bhat TN, et al. (2002) The Protein Data Bank. Acta Crystallogr D Biol Crystallogr 58: 899–907. doi: 10.1107/S0907444902003451

|
| [12] |
Berman HM, Westbrook J, Feng Z, et al. (2000) The Protein Data Bank. Nucleic Acids Res 28: 235–242. doi: 10.1093/nar/28.1.235

|
| [13] |
Tang M, Comellas G, Rienstra CM (2013) Advanced solid-state NMR approaches for structure determination of membrane proteins and amyloid fibrils. Acc Chem Res 46: 2080–2088. doi: 10.1021/ar4000168

|
| [14] |
Ni QZ, Daviso E, Can TV, et al. (2013) High frequency dynamic nuclear polarization. Acc Chem Res 46: 1933–1941. doi: 10.1021/ar300348n

|
| [15] |
Zou P, McHaourab HS (2010) Increased sensitivity and extended range of distance measurements in spin-labeled membrane proteins: Q-band double electron-electron resonance and nanoscale bilayers. Biophys J 98: L18–20. doi: 10.1016/j.bpj.2009.12.4193

|
| [16] |
Mchaourab HS, Steed PR, Kazmier K (2011) Toward the fourth dimension of membrane protein structure: insight into dynamics from spin-labeling EPR spectroscopy. Structure 19: 1549–1561. doi: 10.1016/j.str.2011.10.009

|
| [17] |
Tusnady GE, Dosztanyi Z, Simon I (2004) Transmembrane proteins in the Protein Data Bank: identification and classification. Bioinformatics 20: 2964–2972. doi: 10.1093/bioinformatics/bth340

|
| [18] | Mchaourab HS, Lietzow MA, Hideg K, et al. (1996) Motion of spin-labeled side chains in T4 lysozyme. Correlation with protein structure and dynamics. Biochemistry 35: 7692–7704. |
| [19] |
Hubbell WL, McHaourab HS, Altenbach C, et al. (1996) Watching proteins move using site-directed spin labeling. Structure 4: 779–783. doi: 10.1016/S0969-2126(96)00085-8

|
| [20] |
Fanucci GE, Cafiso DS (2006) Recent advances and applications of site-directed spin labeling. Curr Opin Struct Biol 16: 644–653. doi: 10.1016/j.sbi.2006.08.008

|
| [21] | Weierstall U, James D, Wang C, et al. (2014) Lipidic cubic phase injector facilitates membrane protein serial femtosecond crystallography. Nat Commun 5: 3309. |
| [22] |
Liu W, Wacker D, Gati C, et al. (2013) Serial femtosecond crystallography of G protein-coupled receptors. Science 342: 1521–1524. doi: 10.1126/science.1244142

|
| [23] | Li D, Boland C, Walsh K, et al. (2012) Use of a robot for high-throughput crystallization of membrane proteins in lipidic mesophases. J Vis Exp: e4000. |
| [24] | Li D, Boland C, Aragao D, et al. (2012) Harvesting and cryo-cooling crystals of membrane proteins grown in lipidic mesophases for structure determination by macromolecular crystallography. J Vis Exp: e4001. |
| [25] |
Alexander N, Al-Mestarihi A, Bortolus M, et al. (2008) De novo high-resolution protein structure determination from sparse spin-labeling EPR data. Structure 16: 181–195. doi: 10.1016/j.str.2007.11.015

|
| [26] |
Hirst SJ, Alexander N, Mchaourab HS, et al. (2011) RosettaEPR: an integrated tool for protein structure determination from sparse EPR data. J Struct Biol 173: 506–514. doi: 10.1016/j.jsb.2010.10.013

|
| [27] |
Islam SM, Stein RA, McHaourab HS, et al. (2013) Structural refinement from restrained-ensemble simulations based on EPR/DEER data: application to T4 lysozyme. J Phys Chem B 117: 4740–4754. doi: 10.1021/jp311723a

|
| [28] |
Fischer AW, Alexander NS, Woetzel N, et al. (2015) BCL::MP-Fold: Membrane protein structure prediction guided by EPR restraints. Proteins 83: 1947–1962. doi: 10.1002/prot.24801

|
| [29] |
Jeschke G, Chechik V, Ionita P, et al. (2006) DeerAnalysis2006 - a comprehensive software package for analyzing pulsed ELDOR data. Appl Magn Reson 30: 473–498. doi: 10.1007/BF03166213

|
| [30] |
Hagelueken G, Ward R, Naismith JH, et al. (2012) MtsslWizard: In Silico Spin-Labeling and Generation of Distance Distributions in PyMOL. Appl Magn Reson 42: 377–391. doi: 10.1007/s00723-012-0314-0

|
| [31] |
Beasley KN, Sutch BT, Hatmal MM, et al. (2015) Computer Modeling of Spin Labels: NASNOX, PRONOX, and ALLNOX. Methods Enzymol 563: 569–593. doi: 10.1016/bs.mie.2015.07.021

|
| [32] |
Hatmal MM, Li Y, Hegde BG, et al. (2012) Computer modeling of nitroxide spin labels on proteins. Biopolymers 97: 35–44. doi: 10.1002/bip.21699

|
| [33] |
Alexander NS, Stein RA, Koteiche HA, et al. (2013) RosettaEPR: Rotamer Library for Spin Label Structure and Dynamics. PLoS One 8: e72851. doi: 10.1371/journal.pone.0072851

|
| [34] |
Sali A, Blundell TL (1993) Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol 234: 779–815. doi: 10.1006/jmbi.1993.1626

|
| [35] |
Fiser A, Sali A (2003) Modeller: generation and refinement of homology-based protein structure models. Methods Enzymol 374: 461–491. doi: 10.1016/S0076-6879(03)74020-8

|
| [36] |
Webb B, Sali A (2014) Protein structure modeling with MODELLER. Methods Mol Biol 1137: 1–15. doi: 10.1007/978-1-4939-0366-5_1

|
| [37] | Webb B, Sali A (2014) Comparative protein structure modeling using MODELLER. Curr Protoc Bioinformatics 47: 5.6.1–5.6.32. |
| [38] |
Rohl CA, Strauss CEM, Chivian D, et al. (2004) Modeling structurally variable regions in homologous proteins with rosetta. Proteins 55: 656–677. doi: 10.1002/prot.10629

|
| [39] |
Misura KM, Chivian D, Rohl CA, et al. (2006) Physically realistic homology models built with ROSETTA can be more accurate than their templates. Proc Natl Acad Sci U S A 103: 5361–5366. doi: 10.1073/pnas.0509355103

|
| [40] |
Schwede T, Kopp J, Guex N, et al. (2003) SWISS-MODEL: An automated protein homology-modeling server. Nucleic Acids Res 31: 3381–3385. doi: 10.1093/nar/gkg520

|
| [41] | Zhang Y (2009) I-TASSER: fully automated protein structure prediction in CASP8. Proteins 77 Suppl 9: 100–113. |
| [42] |
Zhang Y (2008) I-TASSER server for protein 3D structure prediction. BMC Bioinformatics 9: 40. doi: 10.1186/1471-2105-9-40

|
| [43] |
Roy A, Kucukural A, Zhang Y (2010) I-TASSER: a unified platform for automated protein structure and function prediction. Nat Protoc 5: 725–738. doi: 10.1038/nprot.2010.5

|
| [44] |
Combs SA, Deluca SL, Deluca SH, et al. (2013) Small-molecule ligand docking into comparative models with Rosetta. Nat Protoc 8: 1277–1298. doi: 10.1038/nprot.2013.074

|
| [45] | Stevens RC, Cherezov V, Katritch V, et al. (2013) The GPCR Network: a large-scale collaboration to determine human GPCR structure and function. Nat Rev Drug Discov 12: 25–34. |
| [46] |
Kroeze WK, Sheffler DJ, Roth BL (2003) G-protein-coupled receptors at a glance. J Cell Sci 116: 4867–4869. doi: 10.1242/jcs.00902

|
| [47] |
Yamashita A, Singh SK, Kawate T, et al. (2005) Crystal structure of a bacterial homologue of Na+/Cl--dependent neurotransmitter transporters. Nature 437: 215–223. doi: 10.1038/nature03978

|
| [48] |
Faham S, Watanabe A, Besserer GM, et al. (2008) The crystal structure of a sodium galactose transporter reveals mechanistic insights into Na+/sugar symport. Science 321: 810–814. doi: 10.1126/science.1160406

|
| [49] |
Perez C, Koshy C, Yildiz O, et al. (2012) Alternating-access mechanism in conformationally asymmetric trimers of the betaine transporter BetP. Nature 490: 126–130. doi: 10.1038/nature11403

|
| [50] |
Ma D, Lu P, Yan C, et al. (2012) Structure and mechanism of a glutamate-GABA antiporter. Nature 483: 632–636. doi: 10.1038/nature10917

|
| [51] |
Kazmier K, Sharma S, Quick M, et al. (2014) Conformational dynamics of ligand-dependent alternating access in LeuT. Nat Struct Mol Biol 21: 472–479. doi: 10.1038/nsmb.2816

|
| [52] |
Gregory KJ, Nguyen ED, Reiff SD, et al. (2013) Probing the metabotropic glutamate receptor 5 (mGlu(5)) positive allosteric modulator (PAM) binding pocket: discovery of point mutations that engender a "molecular switch" in PAM pharmacology. Mol Pharmacol 83: 991–1006. doi: 10.1124/mol.112.083949

|
| [53] | Yarov-Yarovoy V, Schonbrun J, Baker D (2006) Multipass membrane protein structure prediction using Rosetta. Proteins 62: 1010–1025. |
| [54] |
Barth P, Schonbrun J, Baker D (2007) Toward high-resolution prediction and design of transmembrane helical protein structures. Proc Natl Acad Sci U S A 104: 15682–15687. doi: 10.1073/pnas.0702515104

|
| [55] |
Barth P, Wallner B, Baker D (2009) Prediction of membrane protein structures with complex topologies using limited constraints. Proc Natl Acad Sci U S A 106: 1409–1414. doi: 10.1073/pnas.0808323106

|
| [56] |
Nugent T, Jones DT (2012) Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis. Proc Natl Acad Sci U S A 109: E1540–1547. doi: 10.1073/pnas.1120036109

|
| [57] |
Nugent T, Jones DT (2013) Membrane protein orientation and refinement using a knowledge-based statistical potential. BMC Bioinformatics 14: 276. doi: 10.1186/1471-2105-14-276

|
| [58] |
Hopf TA, Colwell LJ, Sheridan R, et al. (2012) Three-dimensional structures of membrane proteins from genomic sequencing. Cell 149: 1607–1621. doi: 10.1016/j.cell.2012.04.012

|
| [59] |
Weiner BE, Woetzel N, Karakas M, et al. (2013) BCL::MP-fold: folding membrane proteins through assembly of transmembrane helices. Structure 21: 1107–1117. doi: 10.1016/j.str.2013.04.022

|
| [60] |
Simons KT, Kooperberg C, Huang E, et al. (1997) Assembly of Protein Tertiary Structures from Fragments with Similar Local Sequences using Simulated Annealing and Bayesian Scoring Functions. J Mol Biol 268: 209–225. doi: 10.1006/jmbi.1997.0959

|
| [61] |
Rohl CA, Strauss CE, Misura KM, et al. (2004) Protein structure prediction using Rosetta. Methods Enzymol 383: 66–93. doi: 10.1016/S0076-6879(04)83004-0

|
| [62] |
Kazmier K, Alexander NS, Meiler J, et al. (2011) Algorithm for selection of optimized EPR distance restraints for de novo protein structure determination. J Struct Biol 173: 549–557. doi: 10.1016/j.jsb.2010.11.003

|
| [63] |
Dimaio F, Leaver-Fay A, Bradley P, et al. (2011) Modeling symmetric macromolecular structures in rosetta3. PLoS One 6: e20450. doi: 10.1371/journal.pone.0020450

|
| [64] |
Leaver-Fay A, Tyka M, Lewis SM, et al. (2011) ROSETTA3: an object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol 487: 545–574. doi: 10.1016/B978-0-12-381270-4.00019-6

|
| [65] |
Metropolis N, Rosenbluth A, Rosenbluth M, et al. (1953) Equations of state calculations by fast computing machines. J Chem Phys 21: 1087–1091. doi: 10.1063/1.1699114

|
| [66] |
Metropolis NU, Ulam S (1949) The Monte Carlo Method. J Am Stat Assoc 44: 335–341. doi: 10.1080/01621459.1949.10483310

|
| [67] |
Perozo E, Cortes DM, Cuello LG (1999) Structural rearrangements underlying K+-channel activation gating. Science 285: 73–78. doi: 10.1126/science.285.5424.73

|
| [68] |
Liu YS, Sompornpisut P, Perozo E (2001) Structure of the KcsA channel intracellular gate in the open state. Nat Struct Biol 8: 883–887. doi: 10.1038/nsb1001-883

|
| [69] |
Zou P, Mchaourab HS (2009) Alternating Access of the Putative Substrate-Binding Chamber in the ABC Transporter MsbA. J Mol Biol 393: 574–585. doi: 10.1016/j.jmb.2009.08.051

|
| [70] |
Altenbach C, Cai K, Klein-Seetharaman J, et al. (2001) Structure and function in rhodopsin: mapping light-dependent changes in distance between residue 65 in helix TM1 and residues in the sequence 306-319 at the cytoplasmic end of helix TM7 and in helix H8. Biochemistry 40: 15483–15492. doi: 10.1021/bi011546g

|
| [71] |
Viklund H, Elofsson A (2008) OCTOPUS: improving topology prediction by two-track ANN-based preference scores and an extended topological grammar. Bioinformatics 24: 1662–1668. doi: 10.1093/bioinformatics/btn221

|
| [72] |
Adamian L, Liang J (2006) Prediction of transmembrane helix orientation in polytopic membrane proteins. BMC Struct Biol 6: 13. doi: 10.1186/1472-6807-6-13

|
| [73] | Okada T, Sugihara M, Bondar AN, et al. (2004) The retinal conformation and its environment in rhodopsin in light of a new 2.2 A crystal structure. J Mol Biol 342: 571–583. |
| [74] |
Misura KM, Baker D (2005) Progress and challenges in high-resolution refinement of protein structure models. Proteins 59: 15–29. doi: 10.1002/prot.20376

|
| [75] |
Tyka MD, Jung K, Baker D (2012) Efficient sampling of protein conformational space using fast loop building and batch minimization on highly parallel computers. J Comput Chem 33: 2483–2491. doi: 10.1002/jcc.23069

|
| [76] |
Woetzel N, Karakas M, Staritzbichler R, et al. (2012) BCL::Score--knowledge based energy potentials for ranking protein models represented by idealized secondary structure elements. PLoS One 7: e49242. doi: 10.1371/journal.pone.0049242

|
| [77] |
Karakas M, Woetzel N, Staritzbichler R, et al. (2012) BCL::Fold--de novo prediction of complex and large protein topologies by assembly of secondary structure elements. PLoS One 7: e49240. doi: 10.1371/journal.pone.0049240

|
| 1. | Christoph Gmeiner, Georg Dorn, Frédéric H. T. Allain, Gunnar Jeschke, Maxim Yulikov, Spin labelling for integrative structure modelling: a case study of the polypyrimidine-tract binding protein 1 domains in complexes with short RNAs, 2017, 19, 1463-9076, 28360, 10.1039/C7CP05822E |
| PDB | Chain | Domain | # Res | # TMH | Contact Order | # Restraints |
| 3SYO | 76–197 | 122 | 2 | 14.4 | 12 | |
| 2BG9 | A | 211–301 | 91 | 3 | 6.9 | 16 |
| 1J4N | 4–119 | 116 | 3 | 15.2 | 17 | |
| 2KSF | 396–502 | 107 | 4 | 11.9 | 13 | |
| 1PY6 (1PY7)a | 77–199 | 123 | 4 | 13.3 | 20 | |
| 2PNO | A | 2–131 | 130 | 4 | 13.6 | 22 |
| 2BL2 | 12–156 | 145 | 4 | 20.7 | 25 | |
| 2K73 | 1–164 | 164 | 4 | 15.5 | 19 | |
| 2ZW3 | A | 2–217 | 216 | 4 | 25.7 | 24 |
| 1IWG | 336–498 | 163 | 5 | 17.4 | 26 | |
| 1RHZ | A | 23–188 | 166 | 5 | 19.8 | 21 |
| 2YVX | A | 284–471 | 188 | 5 | 20.6 | 26 |
| 1OCC | C | 71–261 | 191 | 5 | 24.1 | 29 |
| 4A2N | 1–192 | 192 | 5 | 22.4 | 24 | |
| 1KPL | 31–233 | 203 | 5 | 23.4 | 31 | |
| 2BS2 | C | 21–237 | 217 | 5 | 17.5 | 29 |
| 3P5N | 10–188 | 179 | 6 | 17.9 | 22 | |
| 2IC8 | 91–272 | 182 | 6 | 17.9 | 23 | |
| 1PV6 | 1–190 | 189 | 6 | 28.3 | 33 | |
| 2NR9 | 4–195 | 192 | 6 | 17.6 | 24 | |
| 1OKCb | 2–293 | 292 | 6 | 25.8 | 34 | |
| 3B60b | A | 10–328 | 319 | 6 | 25.7 | 52 |
| 2KSY | 1–223 | 223 | 7 | 20.1 | 37 | |
| 1PY6b | 5–231 | 227 | 7 | 25.2 | 36 | |
| 3KCU | 29–280 | 252 | 7 | 29.7 | 33 | |
| 1FX8b | 6–259 | 254 | 7 | 28.6 | 38 | |
| 1U19b | 33–310 | 278 | 7 | 25.0 | 41 | |
| 3KJ6 | A | 35–346 | 311 | 7 | 39.5 | 31 |
| 3HD6b | 6–448 | 403 | 12 | 43.6 | 59 | |
| 3GIAb | 3–435 | 433 | 12 | 62.5 | 64 | |
| 3O0Rb | B | 10–458 | 449 | 12 | 30.6 | 69 |
| 3HFXb | 12–504 | 493 | 12 | 68.0 | 63 | |
| 2XUT | A | 13–500 | 488 | 14 | 42.8 | 71 |
| 2XQ2 | A | 9–573 | 565 | 15 | 71.8 | 79 |
| a Referred to as 1PY7 in this publication | ||||||
| b These proteins were used in RosettaTMH parameter optimization | ||||||
| RMSDtop5 score | RMSD1st RMSD | FractionRMSD<8 Å | |||||||||||||
| average RMSD100SSE to experimental structure of the top five models by score | lowest RMSD100SSE to experimental structure | percentage of models with a RMSD100SSE better than 8 Å | |||||||||||||
| PDB | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR |
| 3SYO | 11.0 | 11.8 | 12.3 | 12.6 | 12.4 | 7.1 | 7.2 | 8.5 | 6.4 | 8.0 | 0 | 0 | 0 | 0 | 0 |
| 2BG9 | 6.3 | 9.7 | 9.1 | 12.5 | 8.4 | 4.0 | 4.2 | 4.6 | 5.7 | 4.3 | 0 | 23 | 30 | 2 | 25 |
| 1J4N | 9.7 | 7.8 | 8.0 | 12.9 | 11.3 | 5.0 | 4.7 | 4.4 | 6.7 | 7.4 | 13 | 14 | 28 | 0 | 1 |
| 2KSF | 8.0 | 9.1 | 10.0 | 9.4 | 10.6 | 5.2 | 5.7 | 5.9 | 5.0 | 5.8 | 21 | 10 | 15 | 1 | 9 |
| 1PY7 | 4.9 | 6.1 | 4.2 | 11.1 | 7.7 | 2.2 | 2.4 | 2.5 | 5.6 | 4.5 | 66 | 67 | 58 | 1 | 23 |
| 2PNO | 7.6 | 8.7 | 7.0 | 12.3 | 8.4 | 3.0 | 3.2 | 3.3 | 7.5 | 5.5 | 29 | 21 | 47 | 0 | 11 |
| 2BL2 | 6.1 | 5.5 | 4.7 | 11.5 | 7.0 | 2.4 | 2.5 | 2.8 | 5.5 | 4.0 | 71 | 55 | 68 | 0 | 39 |
| 2K73 | 9.7 | 10.2 | 10.2 | 12.7 | 10.9 | 5.9 | 4.8 | 6.8 | 7.9 | 6.7 | 2 | 1 | 1 | 0 | 2 |
| 2ZW3 | 13.1 | 12.9 | 13.0 | 16.0 | 13.2 | 8.7 | 9.9 | 10.5 | 10.1 | 9.8 | 0 | 0 | 0 | 0 | 0 |
| 1IWG | 7.3 | 9.1 | 7.3 | 12.9 | 8.4 | 5.0 | 5.5 | 4.4 | 8.1 | 5.9 | 16 | 4 | 48 | 0 | 13 |
| 1RHZ | 10.1 | 10.7 | 8.8 | 11.6 | 11.5 | 6.1 | 6.6 | 6.1 | 8.5 | 7.7 | 1 | 1 | 10 | 0 | 1 |
| 2YVX | 9.2 | 9.0 | 7.9 | 14.7 | 9.0 | 5.9 | 6.0 | 5.1 | 8.2 | 6.7 | 5 | 1 | 20 | 0 | 6 |
| 1OCC | 11.3 | 10.4 | 10.4 | 13.1 | 8.4 | 6.7 | 7.0 | 7.2 | 7.9 | 5.4 | 1 | 0 | 1 | 0 | 17 |
| 4A2N | 8.4 | 9.2 | 9.4 | 11.2 | 10.5 | 5.4 | 6.2 | 6.3 | 7.8 | 7.2 | 4 | 1 | 6 | 0 | 2 |
| 1KPL | 13.2 | 14.4 | 11.8 | 15.1 | 12.7 | 10.0 | 10.7 | 7.9 | 11.1 | 9.5 | 0 | 0 | 1 | 0 | 0 |
| 2BS2 | 10.0 | 9.7 | 10.0 | 13.5 | 10.1 | 6.1 | 5.3 | 5.8 | 8.8 | 6.9 | 1 | 1 | 6 | 0 | 3 |
| 3P5N | 9.5 | 10.4 | 9.5 | 12.6 | 11.7 | 5.3 | 6.0 | 6.9 | 9.5 | 9.0 | 2 | 1 | 2 | 0 | 0 |
| 2IC8 | 9.1 | 9.4 | 9.1 | 11.5 | 10.2 | 5.3 | 5.0 | 6.1 | 8.7 | 7.1 | 4 | 1 | 5 | 0 | 1 |
| 1PV6 | 10.4 | 10.1 | 8.1 | 11.5 | 8.1 | 5.7 | 6.4 | 5.1 | 8.0 | 5.4 | 4 | 1 | 18 | 0 | 15 |
| 2NR9 | 10.2 | 10.9 | 9.8 | 12.2 | 11.3 | 5.8 | 6.9 | 6.3 | 8.6 | 7.4 | 2 | 0 | 3 | 0 | 1 |
| 1OKC | 12.3 | 12.5 | 13.1 | 12.6 | 11.9 | 9.0 | 10.8 | 8.9 | 9.2 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 3B60f | 9.8 | 9.7 | 6.3 | 13.7 | 9.7 | 6.3 | 6.1 | 4.1 | 9.2 | 6.0 | 2 | 1 | 38 | 0 | 10 |
| 2KSY | 8.9 | 8.4 | 6.8 | 12.8 | 8.5 | 3.9 | 4.2 | 4.5 | 7.7 | 5.1 | 30 | 15 | 28 | 0 | 19 |
| 1PY6f | 8.0 | 8.5 | 8.2 | 12.2 | 7.9 | 3.9 | 5.1 | 5.2 | 7.8 | 5.2 | 27 | 9 | 15 | 0 | 18 |
| 3KCU | 10.6 | 10.3 | 9.9 | 11.9 | 10.8 | 6.3 | 6.9 | 6.4 | 9.7 | 7.9 | 1 | 0 | 2 | 0 | 0 |
| 1FX8f | 10.7 | 11.3 | 10.5 | 12.4 | 10.4 | 7.8 | 8.3 | 7.7 | 8.4 | 8.0 | 0 | 0 | 1 | 0 | 0 |
| 1U19f | 12.7 | 14.6 | 11.8 | 12.4 | 8.7 | 9.2 | 11.4 | 8.4 | 8.7 | 6.1 | 0 | 0 | 0 | 0 | 7 |
| 3KJ6 | 14.6 | 15.2 | 15.5 | 15.6 | 15.3 | 11.5 | 12.1 | 12.0 | 12.4 | 12.7 | 0 | 0 | 0 | 0 | 0 |
| 3HD6f | 10.6 | 16.0 | 12.0 | 13.2 | 10.9 | 7.5 | 12.4 | 9.1 | 10.3 | 8.5 | 0 | 0 | 0 | 0 | 0 |
| 3GIAf | 14.1 | 25.5 | 13.9 | 14.2 | 12.0 | 11.8 | 17.2 | 9.2 | 11.6 | 9.5 | 0 | 0 | 0 | 0 | 0 |
| 3O0Rf | 10.1 | 24.0 | 11.2 | 13.0 | 10.0 | 6.4 | 18.6 | 7.6 | 8.9 | 6.5 | 2 | 0 | 1 | 0 | 4 |
| 3HFXf | 13.5 | 29.9 | 13.5 | 13.1 | 11.6 | 10.0 | 22.2 | 10.2 | 10.6 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 2XUT | 14.3 | 25.1 | 15.1 | 16.2 | 15.0 | 12.4 | 20.2 | 12.6 | 14.6 | 12.9 | 0 | 0 | 0 | 0 | 0 |
| 2XQ2 | 15.8 | 35.9 | 16.0 | 16.6 | 15.7 | 13.6 | 25.5 | 12.9 | 14.8 | 13.7 | 0 | 0 | 0 | 0 | 0 |
| mean | 10.3 | 13.0 | 10.1 | 13.0 | 10.6 | 6.8 | 8.7 | 6.9 | 8.8 | 7.5 | 10 | 7 | 13 | 0 | 7 |
| stddev. | 2.6 | 7.0 | 2.9 | 13.0 | 10.6 | 2.8 | 5.8 | 2.7 | 2.2 | 2.4 | 18 | 15 | 19 | 0 | 10 |
| PDB | Chain | Domain | # Res | # TMH | Contact Order | # Restraints |
| 3SYO | 76–197 | 122 | 2 | 14.4 | 12 | |
| 2BG9 | A | 211–301 | 91 | 3 | 6.9 | 16 |
| 1J4N | 4–119 | 116 | 3 | 15.2 | 17 | |
| 2KSF | 396–502 | 107 | 4 | 11.9 | 13 | |
| 1PY6 (1PY7)a | 77–199 | 123 | 4 | 13.3 | 20 | |
| 2PNO | A | 2–131 | 130 | 4 | 13.6 | 22 |
| 2BL2 | 12–156 | 145 | 4 | 20.7 | 25 | |
| 2K73 | 1–164 | 164 | 4 | 15.5 | 19 | |
| 2ZW3 | A | 2–217 | 216 | 4 | 25.7 | 24 |
| 1IWG | 336–498 | 163 | 5 | 17.4 | 26 | |
| 1RHZ | A | 23–188 | 166 | 5 | 19.8 | 21 |
| 2YVX | A | 284–471 | 188 | 5 | 20.6 | 26 |
| 1OCC | C | 71–261 | 191 | 5 | 24.1 | 29 |
| 4A2N | 1–192 | 192 | 5 | 22.4 | 24 | |
| 1KPL | 31–233 | 203 | 5 | 23.4 | 31 | |
| 2BS2 | C | 21–237 | 217 | 5 | 17.5 | 29 |
| 3P5N | 10–188 | 179 | 6 | 17.9 | 22 | |
| 2IC8 | 91–272 | 182 | 6 | 17.9 | 23 | |
| 1PV6 | 1–190 | 189 | 6 | 28.3 | 33 | |
| 2NR9 | 4–195 | 192 | 6 | 17.6 | 24 | |
| 1OKCb | 2–293 | 292 | 6 | 25.8 | 34 | |
| 3B60b | A | 10–328 | 319 | 6 | 25.7 | 52 |
| 2KSY | 1–223 | 223 | 7 | 20.1 | 37 | |
| 1PY6b | 5–231 | 227 | 7 | 25.2 | 36 | |
| 3KCU | 29–280 | 252 | 7 | 29.7 | 33 | |
| 1FX8b | 6–259 | 254 | 7 | 28.6 | 38 | |
| 1U19b | 33–310 | 278 | 7 | 25.0 | 41 | |
| 3KJ6 | A | 35–346 | 311 | 7 | 39.5 | 31 |
| 3HD6b | 6–448 | 403 | 12 | 43.6 | 59 | |
| 3GIAb | 3–435 | 433 | 12 | 62.5 | 64 | |
| 3O0Rb | B | 10–458 | 449 | 12 | 30.6 | 69 |
| 3HFXb | 12–504 | 493 | 12 | 68.0 | 63 | |
| 2XUT | A | 13–500 | 488 | 14 | 42.8 | 71 |
| 2XQ2 | A | 9–573 | 565 | 15 | 71.8 | 79 |
| a Referred to as 1PY7 in this publication | ||||||
| b These proteins were used in RosettaTMH parameter optimization | ||||||
| RMSDtop5 score | RMSD1st RMSD | FractionRMSD<8 Å | |||||||||||||
| average RMSD100SSE to experimental structure of the top five models by score | lowest RMSD100SSE to experimental structure | percentage of models with a RMSD100SSE better than 8 Å | |||||||||||||
| PDB | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR | Membrane Ab Initio | Extended Chain | Extended Chain + EPR | Rosetta TMH | Rosetta TMH + EPR |
| 3SYO | 11.0 | 11.8 | 12.3 | 12.6 | 12.4 | 7.1 | 7.2 | 8.5 | 6.4 | 8.0 | 0 | 0 | 0 | 0 | 0 |
| 2BG9 | 6.3 | 9.7 | 9.1 | 12.5 | 8.4 | 4.0 | 4.2 | 4.6 | 5.7 | 4.3 | 0 | 23 | 30 | 2 | 25 |
| 1J4N | 9.7 | 7.8 | 8.0 | 12.9 | 11.3 | 5.0 | 4.7 | 4.4 | 6.7 | 7.4 | 13 | 14 | 28 | 0 | 1 |
| 2KSF | 8.0 | 9.1 | 10.0 | 9.4 | 10.6 | 5.2 | 5.7 | 5.9 | 5.0 | 5.8 | 21 | 10 | 15 | 1 | 9 |
| 1PY7 | 4.9 | 6.1 | 4.2 | 11.1 | 7.7 | 2.2 | 2.4 | 2.5 | 5.6 | 4.5 | 66 | 67 | 58 | 1 | 23 |
| 2PNO | 7.6 | 8.7 | 7.0 | 12.3 | 8.4 | 3.0 | 3.2 | 3.3 | 7.5 | 5.5 | 29 | 21 | 47 | 0 | 11 |
| 2BL2 | 6.1 | 5.5 | 4.7 | 11.5 | 7.0 | 2.4 | 2.5 | 2.8 | 5.5 | 4.0 | 71 | 55 | 68 | 0 | 39 |
| 2K73 | 9.7 | 10.2 | 10.2 | 12.7 | 10.9 | 5.9 | 4.8 | 6.8 | 7.9 | 6.7 | 2 | 1 | 1 | 0 | 2 |
| 2ZW3 | 13.1 | 12.9 | 13.0 | 16.0 | 13.2 | 8.7 | 9.9 | 10.5 | 10.1 | 9.8 | 0 | 0 | 0 | 0 | 0 |
| 1IWG | 7.3 | 9.1 | 7.3 | 12.9 | 8.4 | 5.0 | 5.5 | 4.4 | 8.1 | 5.9 | 16 | 4 | 48 | 0 | 13 |
| 1RHZ | 10.1 | 10.7 | 8.8 | 11.6 | 11.5 | 6.1 | 6.6 | 6.1 | 8.5 | 7.7 | 1 | 1 | 10 | 0 | 1 |
| 2YVX | 9.2 | 9.0 | 7.9 | 14.7 | 9.0 | 5.9 | 6.0 | 5.1 | 8.2 | 6.7 | 5 | 1 | 20 | 0 | 6 |
| 1OCC | 11.3 | 10.4 | 10.4 | 13.1 | 8.4 | 6.7 | 7.0 | 7.2 | 7.9 | 5.4 | 1 | 0 | 1 | 0 | 17 |
| 4A2N | 8.4 | 9.2 | 9.4 | 11.2 | 10.5 | 5.4 | 6.2 | 6.3 | 7.8 | 7.2 | 4 | 1 | 6 | 0 | 2 |
| 1KPL | 13.2 | 14.4 | 11.8 | 15.1 | 12.7 | 10.0 | 10.7 | 7.9 | 11.1 | 9.5 | 0 | 0 | 1 | 0 | 0 |
| 2BS2 | 10.0 | 9.7 | 10.0 | 13.5 | 10.1 | 6.1 | 5.3 | 5.8 | 8.8 | 6.9 | 1 | 1 | 6 | 0 | 3 |
| 3P5N | 9.5 | 10.4 | 9.5 | 12.6 | 11.7 | 5.3 | 6.0 | 6.9 | 9.5 | 9.0 | 2 | 1 | 2 | 0 | 0 |
| 2IC8 | 9.1 | 9.4 | 9.1 | 11.5 | 10.2 | 5.3 | 5.0 | 6.1 | 8.7 | 7.1 | 4 | 1 | 5 | 0 | 1 |
| 1PV6 | 10.4 | 10.1 | 8.1 | 11.5 | 8.1 | 5.7 | 6.4 | 5.1 | 8.0 | 5.4 | 4 | 1 | 18 | 0 | 15 |
| 2NR9 | 10.2 | 10.9 | 9.8 | 12.2 | 11.3 | 5.8 | 6.9 | 6.3 | 8.6 | 7.4 | 2 | 0 | 3 | 0 | 1 |
| 1OKC | 12.3 | 12.5 | 13.1 | 12.6 | 11.9 | 9.0 | 10.8 | 8.9 | 9.2 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 3B60f | 9.8 | 9.7 | 6.3 | 13.7 | 9.7 | 6.3 | 6.1 | 4.1 | 9.2 | 6.0 | 2 | 1 | 38 | 0 | 10 |
| 2KSY | 8.9 | 8.4 | 6.8 | 12.8 | 8.5 | 3.9 | 4.2 | 4.5 | 7.7 | 5.1 | 30 | 15 | 28 | 0 | 19 |
| 1PY6f | 8.0 | 8.5 | 8.2 | 12.2 | 7.9 | 3.9 | 5.1 | 5.2 | 7.8 | 5.2 | 27 | 9 | 15 | 0 | 18 |
| 3KCU | 10.6 | 10.3 | 9.9 | 11.9 | 10.8 | 6.3 | 6.9 | 6.4 | 9.7 | 7.9 | 1 | 0 | 2 | 0 | 0 |
| 1FX8f | 10.7 | 11.3 | 10.5 | 12.4 | 10.4 | 7.8 | 8.3 | 7.7 | 8.4 | 8.0 | 0 | 0 | 1 | 0 | 0 |
| 1U19f | 12.7 | 14.6 | 11.8 | 12.4 | 8.7 | 9.2 | 11.4 | 8.4 | 8.7 | 6.1 | 0 | 0 | 0 | 0 | 7 |
| 3KJ6 | 14.6 | 15.2 | 15.5 | 15.6 | 15.3 | 11.5 | 12.1 | 12.0 | 12.4 | 12.7 | 0 | 0 | 0 | 0 | 0 |
| 3HD6f | 10.6 | 16.0 | 12.0 | 13.2 | 10.9 | 7.5 | 12.4 | 9.1 | 10.3 | 8.5 | 0 | 0 | 0 | 0 | 0 |
| 3GIAf | 14.1 | 25.5 | 13.9 | 14.2 | 12.0 | 11.8 | 17.2 | 9.2 | 11.6 | 9.5 | 0 | 0 | 0 | 0 | 0 |
| 3O0Rf | 10.1 | 24.0 | 11.2 | 13.0 | 10.0 | 6.4 | 18.6 | 7.6 | 8.9 | 6.5 | 2 | 0 | 1 | 0 | 4 |
| 3HFXf | 13.5 | 29.9 | 13.5 | 13.1 | 11.6 | 10.0 | 22.2 | 10.2 | 10.6 | 8.7 | 0 | 0 | 0 | 0 | 0 |
| 2XUT | 14.3 | 25.1 | 15.1 | 16.2 | 15.0 | 12.4 | 20.2 | 12.6 | 14.6 | 12.9 | 0 | 0 | 0 | 0 | 0 |
| 2XQ2 | 15.8 | 35.9 | 16.0 | 16.6 | 15.7 | 13.6 | 25.5 | 12.9 | 14.8 | 13.7 | 0 | 0 | 0 | 0 | 0 |
| mean | 10.3 | 13.0 | 10.1 | 13.0 | 10.6 | 6.8 | 8.7 | 6.9 | 8.8 | 7.5 | 10 | 7 | 13 | 0 | 7 |
| stddev. | 2.6 | 7.0 | 2.9 | 13.0 | 10.6 | 2.8 | 5.8 | 2.7 | 2.2 | 2.4 | 18 | 15 | 19 | 0 | 10 |