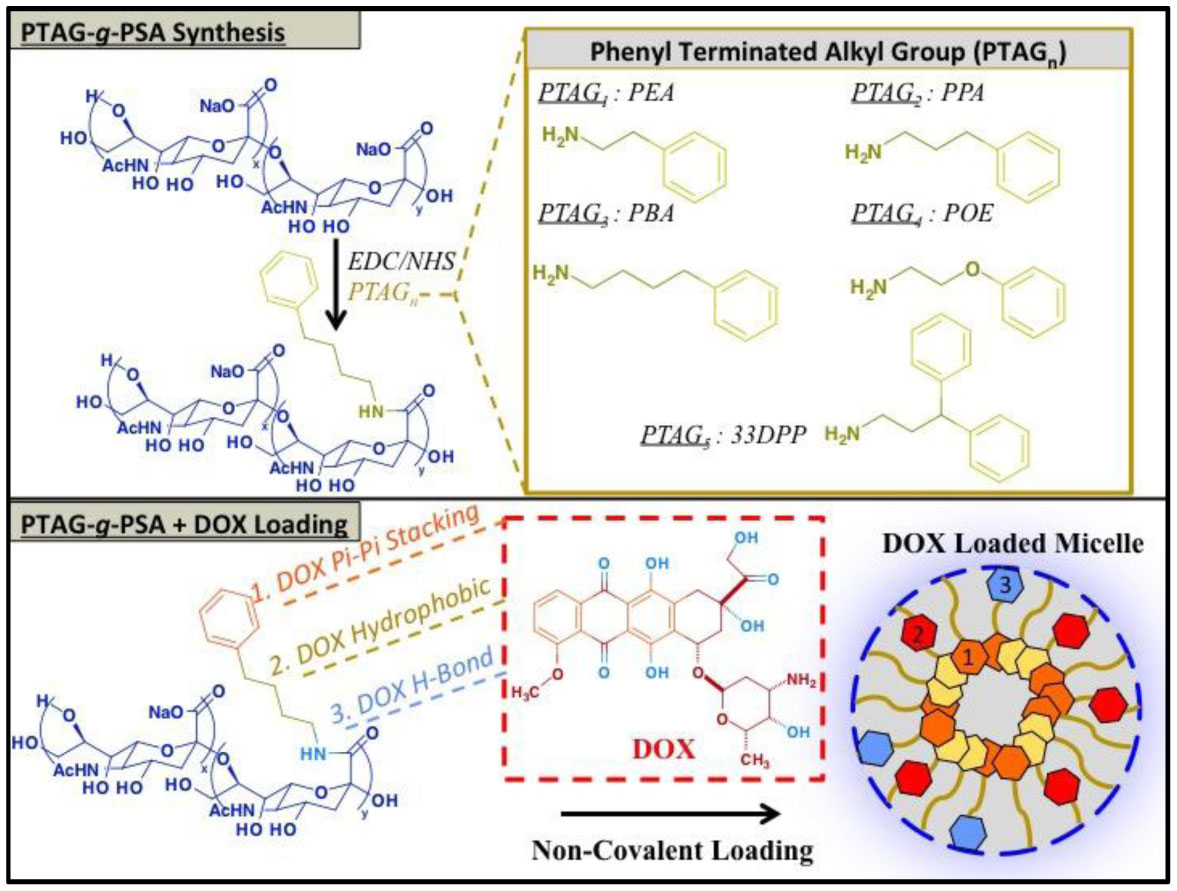
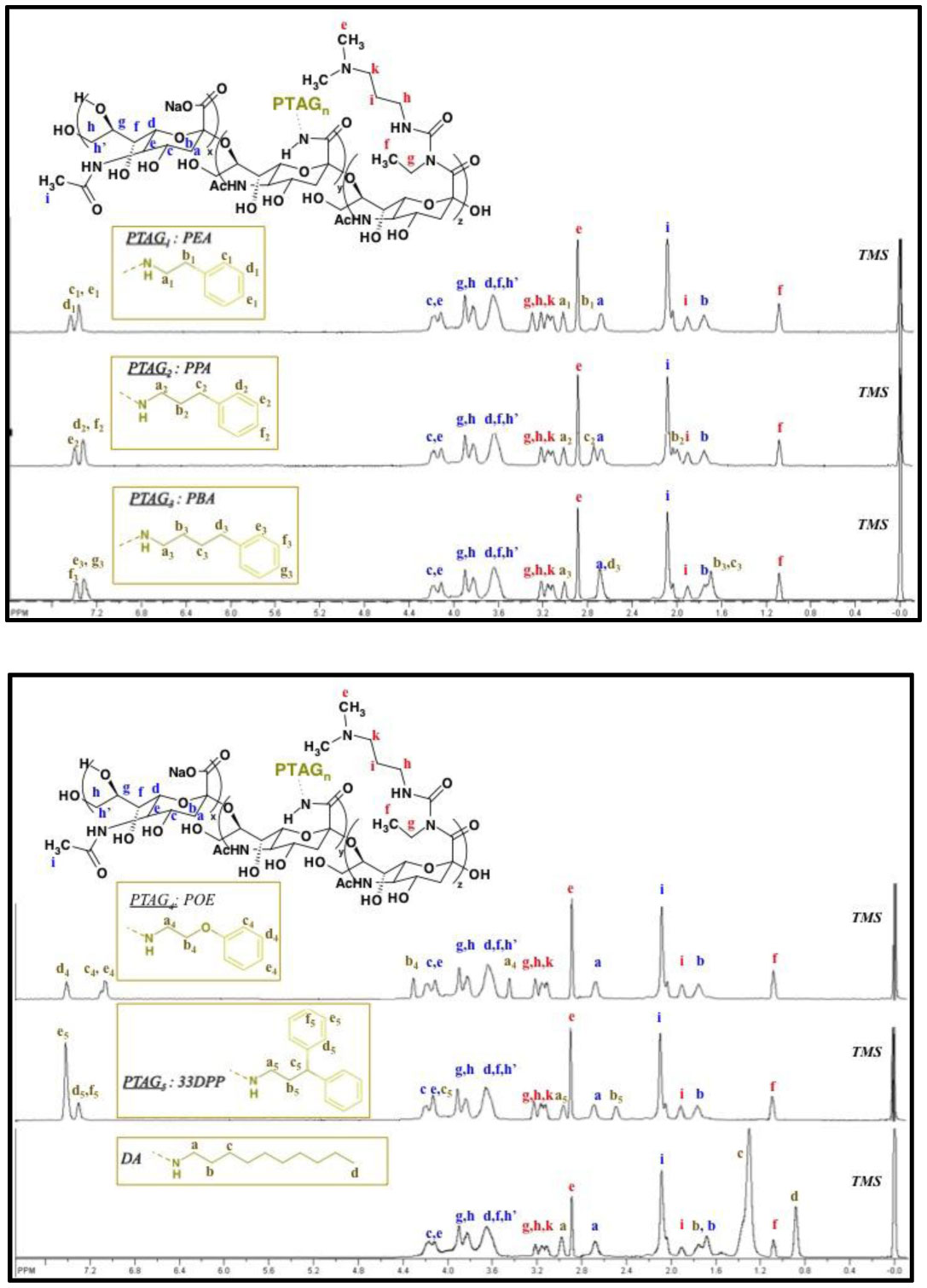
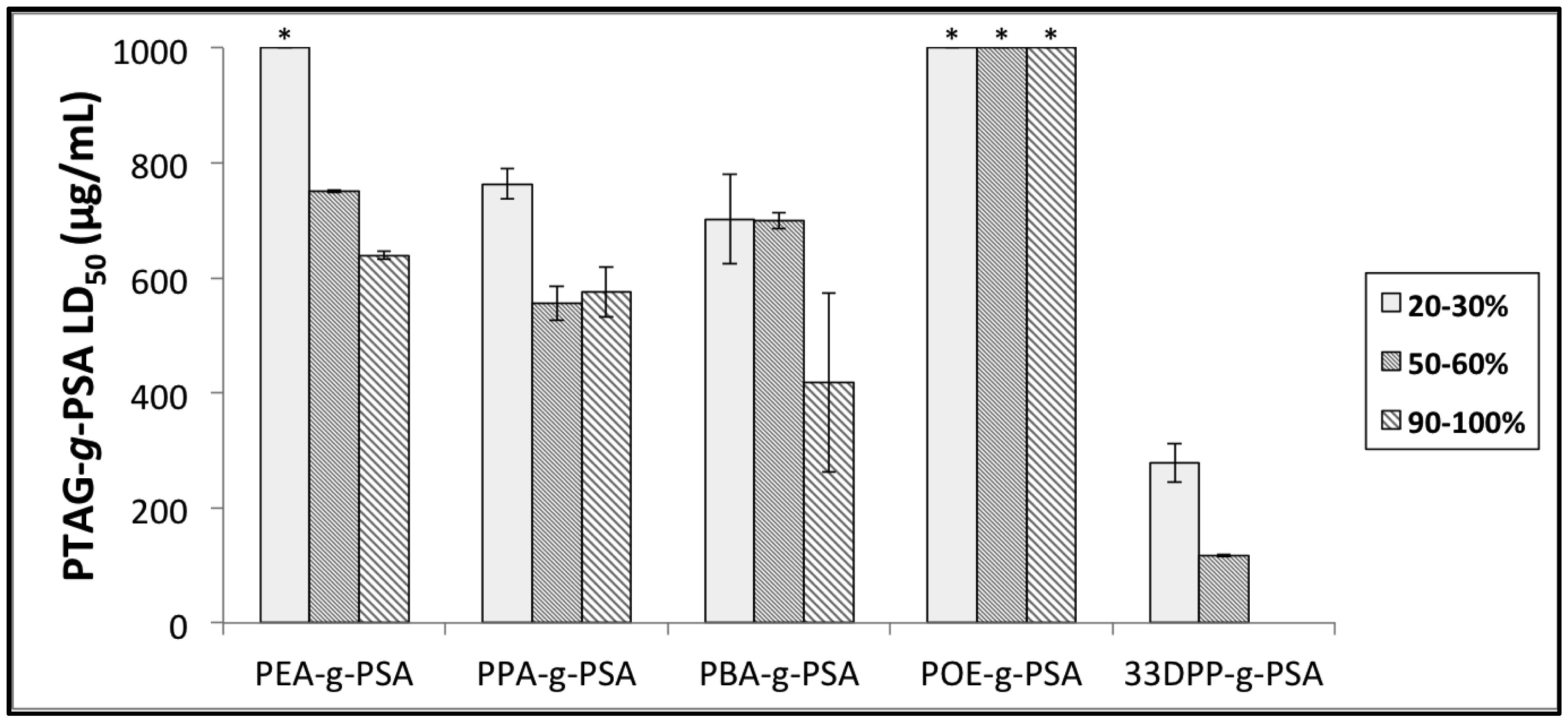
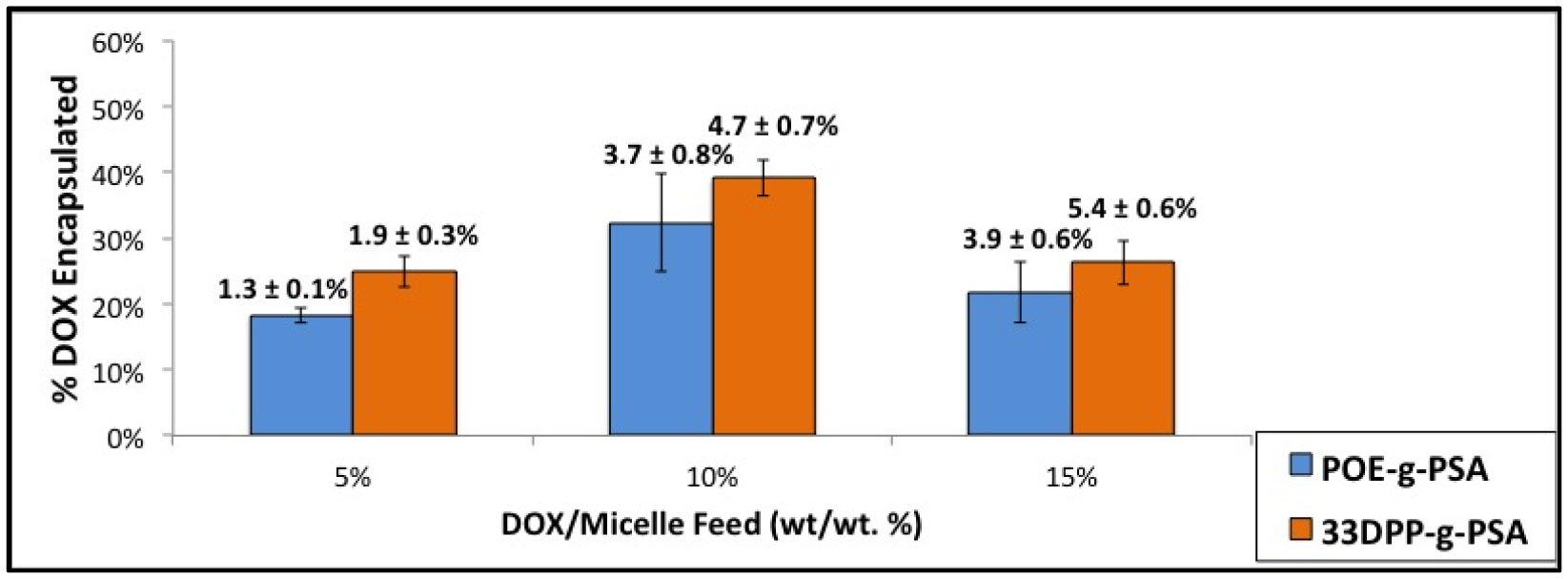
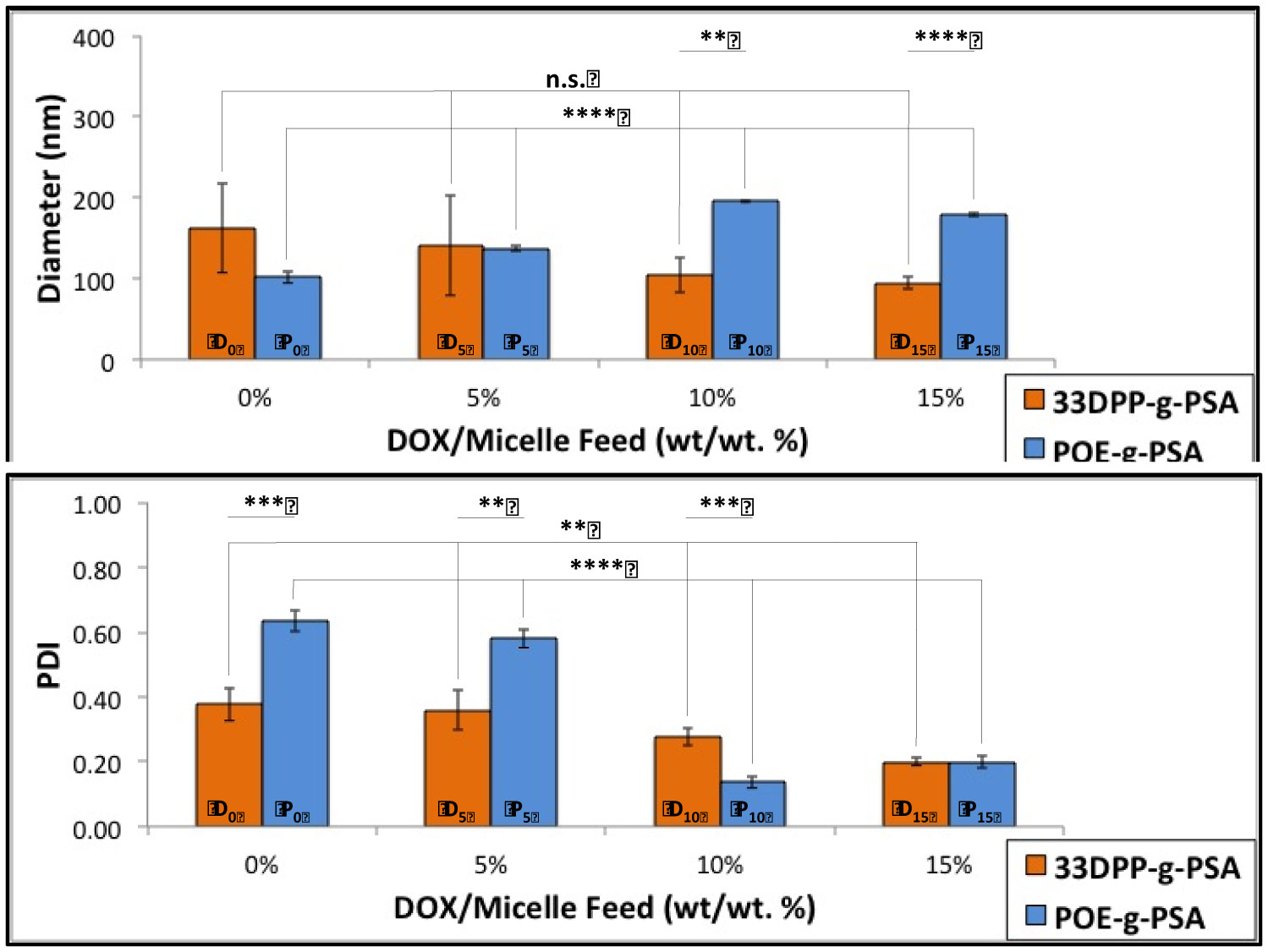
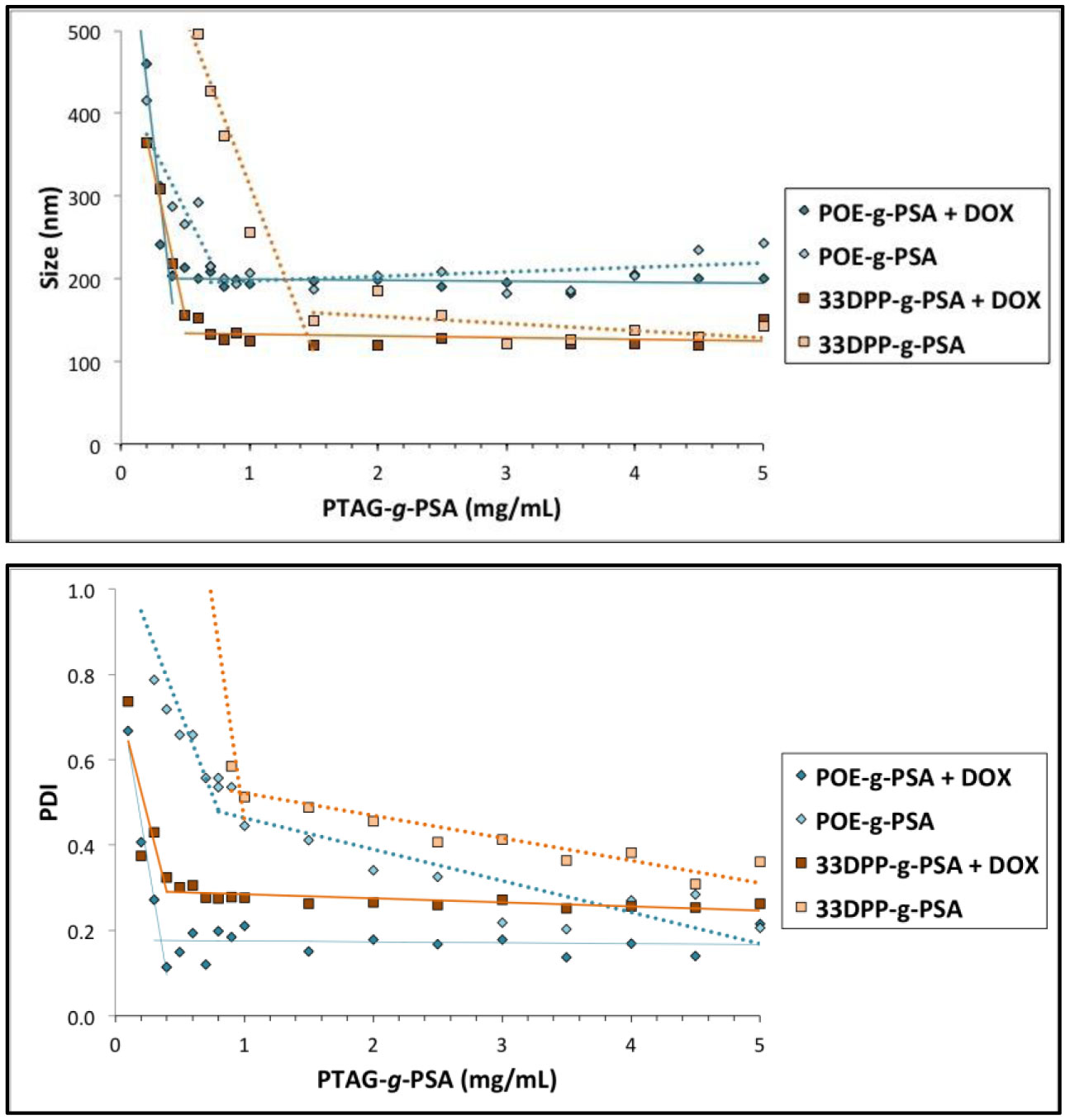
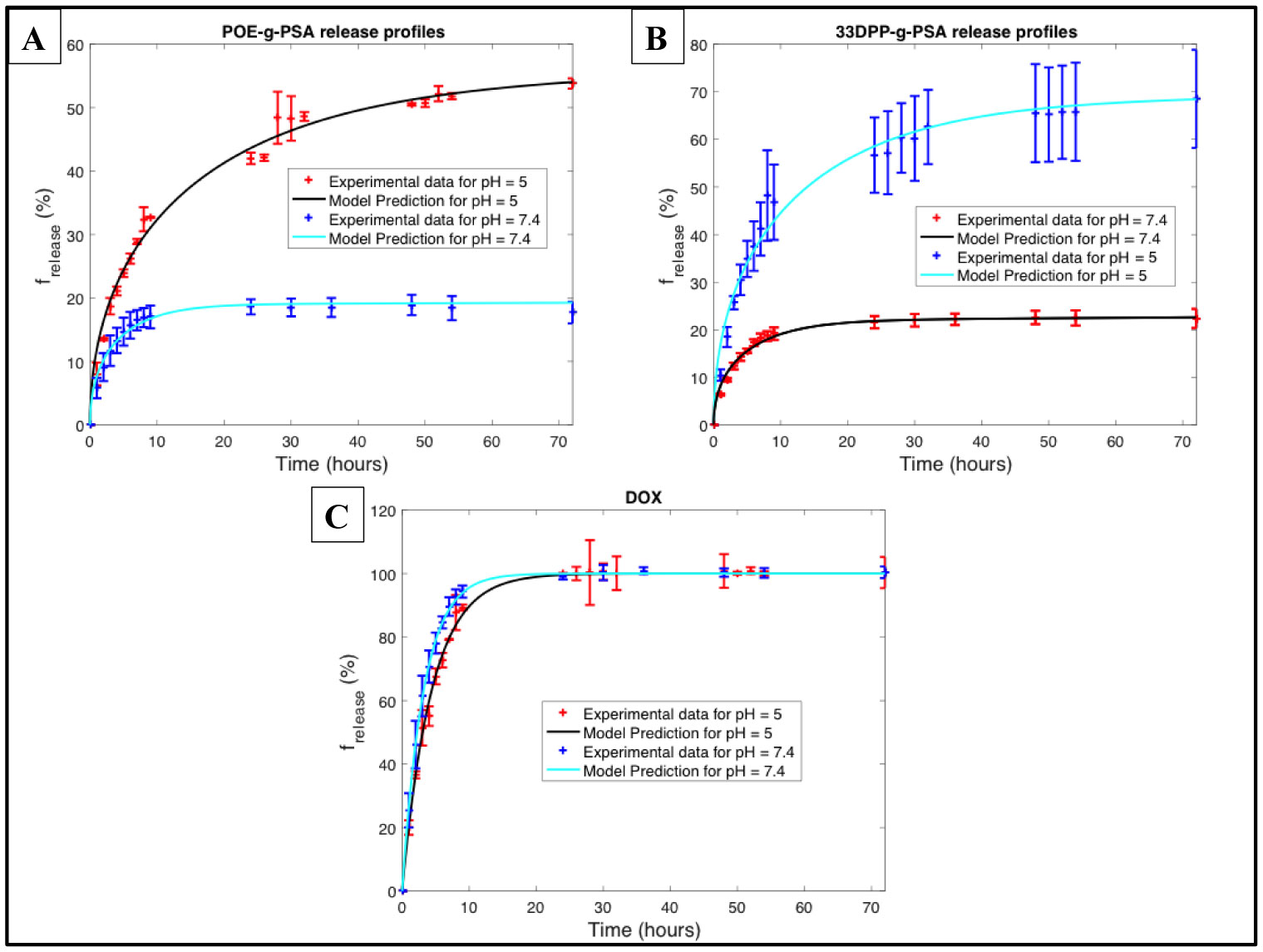
New methods in nanoparticle development have aimed to develop customized carriers suited for specific purposes. Micelles, due to their highly tailorable nature, are prime candidates for this customizable methodology. In order to maximize drug loading and tailor release, groups of the micelle core should be carefully selected in order to exploit inherent interactions between the selected drug and the carrier core. Small variations within the composition of these groups can greatly affect micelle characteristics (e.g., size, stability, loading and release). While covalent bonding of drug-to-carrier has enhanced drug loading, drawbacks include inhibited release and altered drug properties. As a result, drug/carrier non-covalent interactions such as hydrophobic attraction, hydrogen bonding and π-π stacking have all garnered great interest, allowing for both enhanced loading as well as bond dissociation to aid in drug release. Just as important, external composition of these micelles should be suited for specific therapeutic applications. Examples include providing stabilization, enhanced circulation times and site-specific targeting. Poly (sialic acid) (PSA), a naturally occurring polysaccharide, has been shown to exhibit all three of these properties yet remains relatively unexplored in the field of micelle-based cancer drug delivery applications. Here, we have grafted various phenyl-terminated alkyl groups (PTAGs) onto the backbone of PSA (PTAG-g-PSA), each selected in order to exploit a specific non-covalent interaction (hydrophobic attraction, hydrogen bonding and π-π stacking) between the PTAG group and the anthracycline chemotherapeutic doxorubicin (DOX) (Figure 1). Upon aqueous self-assembly, these amphiphiles formed micelles which exhibited variation in size, stability, cytotoxicity and DOX loading/release based upon the PTAG selected. For example, PTAGs selected to exploit either hydrogen bonding or π-π stacking loaded in a similar fashion yet varied greatly in release properties. Therefore, the synergistic effect of these small-scale modifications in core groups selected can greatly effect micelle characteristics and result in highly tailorable carriers.
1.
Introduction
In the relentless battle against infectious diseases, the development and refinement of mathematical models plays a crucial role in understanding the dynamics of epidemics and devising effective control strategies. The complex interplay of various factors, such as population heterogeneity, imperfect interventions, and periodic fluctuations, requires a comprehensive approach to model formulation. The dynamics of infectious diseases is influenced by the interaction between the pathogen and the host population, as well as the effectiveness of the control measures implemented [1]. In real-world scenarios, the implementation of quarantine, isolation, and vaccination strategies is often imperfect due to compliance issues, limited resources, and the emergence of new variants [2]. Understanding the impact of imperfect interventions on epidemic dynamics is crucial to designing robust public health strategies [3]. Imperfect quarantine and isolation can have an impact on the spread of infectious diseases. The use of quarantine and isolation as control measures can lead to the elimination of the disease if its level of effectiveness is sufficiently moderate [4]. However, the effectiveness of these measures may be influenced by other factors. For example, the level of transmission by isolated individuals in hospitals plays an important role in determining the impact of quarantine and isolation [5]. Furthermore, the combined use of quarantine and isolation with a vaccination strategy can further improve disease control and elimination [6]. It is important to note that the impact of quarantine and isolation can vary depending on the specific characteristics of the disease and the population studied.
The periodic nature of many infectious diseases, influenced by seasonal variations, environmental factors, or human behavior, adds an additional layer of complexity to the modeling framework [7,8,9,10]. Periodicity introduces threshold dynamics that govern the stability and persistence of epidemic cycles [11,12]. Investigating the interaction between threshold dynamics and imperfect interventions is essential to understand disease transmission and control. In [13], the authors investigate the dynamical behavior of an SIRVS (susceptible - infected - recovered - vaccinated) epidemic model with time-dependent coefficients and give some new threshold conditions which determine whether or not the disease will go to extinction. In their work, [14] introduces a nonautonomous SIQR (susceptible - infected - quarantine - recovered) model that incorporates time-varying parameters and examines the criteria for eliminating or sustaining infection within this framework. The study defines critical thresholds for the autonomous, asymptotically autonomous and periodic scenarios, along with the general nonautonomous model featuring various forms of disease transmission.
Threshold dynamics in a periodic mathematical model with imperfect interventions have been studied in the context of various infectious diseases. The basic reproduction number ($ \mathcal{R}_0 $) is a key parameter that determines the persistence or extinction of the disease. If $ \mathcal{R}_0 $ is less than one, the disease will gradually disappear, while if $ \mathcal{R}_0 $ is greater than one, the disease will become endemic and persist [15,16,17,18]. The research by Safi et al. [19] examines a nonautonomous SEIRS (susceptible - exposed - infected - recovered) model that incorporates quarantine and isolation measures for a contagious disease. It shows that the disease-free state is globally asymptotically stable if the reproduction ratio is less than one, while the disease persists if the ratio exceeds one. The findings suggest that the introduction of periodicity into the autonomous quarantine/isolation model does not alter the threshold behavior of the system in terms of the elimination or persistence of the disease within the population. In [17], a mathematical model was established that includes a seasonal transmission parameter and a double dose vaccination to examine how measles spreads over time. The basic reproduction number $ \mathcal{R}_0 $ was defined, and its utility as a threshold parameter for global dynamics and the existence of periodic solutions was demonstrated.
In this work, a nonautonomous mathematical model is developed to understand the spread of diseases over time, considering the complexities of periodic epidemic dynamics coupled with imperfections in quarantine, isolation, and vaccination strategies. Our model is based on previous work, specifically those presented in [5,6,17,20,21]. Through a comprehensive exploration of threshold dynamics, the global dynamics of disease transmission is governed by the basic reproduction number ($ \mathcal{R}_0 $). This number serves as a threshold value to determine the extinction or persistence of the disease, as well as the existence of periodic solutions. The following section introduces a comprehensive periodic model encompassing quarantine, isolation, and vaccination, revealing the presence of a disease-free equilibrium. Sections 3 to 6 are dedicated to derive the basic reproduction number ($ \mathcal{R}_0 $) for our model. These sections elucidate that, depending on its value, the disease-free equilibrium will either be globally stable or the disease will persist within the population. In Section 7, we integrate our model with the measles data from Saudi Arabia and Pakistan. Through this collaboration, we estimate various unknown parameters and determine the basic reproduction number. Furthermore, we illustrate the sensitivity of the parameters to the average reproduction number ($ \langle \mathcal{R}_0 \rangle $). Section 8 presents numerical simulations for both scenarios, reinforcing our theoretical findings. Subsequently, we performed numerical evaluations to examine the influence of seasonal contact rate, imperfect quarantine, isolation, imperfect vaccination, and other significant parameters on the transmission dynamics of measles. Section 9 contains our final discussion, summarizing the key findings and insights from the study.
2.
Periodic model formulation
In this study, we consider the division of the total human population, indicated by $ N(t) $, taking into account quarantine for exposed individuals, isolation for those with clinical symptoms of the disease, and vaccination. This partition was designed to analyze the dynamics of disease transmission and includes eight distinct compartments: susceptible ($ S(t) $), individuals who have received the first dose of the vaccine ($ V_{1}(t) $), those who have received the second dose of the vaccine ($ V_{2}(t) $), exposed individuals who are infected but not yet show clinical symptoms of the disease ($ E(t) $), infected individuals who are symptomatic ($ I(t) $), quarantined individuals who are infected but do not display clinical symptoms of the disease ($ Q(t) $), hospitalized individuals ($ H(t) $) and recovered individuals ($ R(t) $).
Quarantine in general involves the isolation of susceptible individuals suspected of exposure to a disease, but in this work, quarantine refers to the removal of newly-infected individuals from contact with the general population [19,22]. This is because quarantine of susceptible individuals is unlikely to significantly impact disease dynamics for large total population sizes, as it only involves newly-infected individuals detected through contact tracing or random testing. Those who remain susceptible at the end of the quarantine period are not included in the $ Q $ class [19,22].
Displayed in Figure 1 is the transition of individuals among compartments, while the model equations are expressed as follows:
where
denotes the time-dependent infection rate and $ N(t) - (1-\varepsilon_1) Q(t) - (1-\varepsilon_2) H(t) = S(t) + V_1(t)+ V_2(t)+ I(t) + \varepsilon_1 Q(t) +\varepsilon_2 H(t) + R(t) $ is the total actively-mixing population.
In the system (2.1), we assume that the effective contact rate $ \beta(t) $ is a continuous, positive $ \omega $-periodic function. The human recruitment rate and the natural death rate are denoted by $ \Lambda $ and $ \mu $, respectively. Susceptible individuals who have received the first dose of the vaccine transition to the vaccinated compartment $ V_1 $ at a rate of $ \theta $. Because the first dose of the disease vaccine is not very effective, people who have had a single dose can contract the disease by coming into contact with infected people at a rate of $ (1-\alpha_1)\lambda(t) $. On the other hand, most people fall into the category of people who have received two doses at a rate of $ \sigma_1 $, as explained in [17,20,23]. Unlike [17,20,23], and in agreement with [24], we assume that the second dose of the vaccine is ineffective in preventing the disease. Individuals with two doses can contract the disease by contact with infected individuals at a rate of $ (1-\alpha_2)\lambda(t) $, while the majority of the population transitions to the recovery class at a rate of $ \sigma_2 $. It is important to note that $ \alpha_1 = 0 $ or $ \alpha_2 = 0 $ indicates a vaccine that offers no protection at all, while $ \alpha_1 = 1 $ or $ \alpha_2 = 1 $ represents a perfect vaccine, with $ 0 < \alpha_1, \alpha_2 < 1 $. Based on the insights of [19], it is important to note that, in the context of this study, the quarantine process usually involves isolating susceptible individuals suspected of exposure to the disease. Specifically, the quarantine class ($ Q $) comprises newly infected (asymptomatic) individuals, with detection usually carried out through contact tracing or random tests. In this study, quarantine specifically refers to the separation of newly infected individuals from the general population. Consequently, individuals who remain susceptible at the end of the quarantine period are not considered to be part of the $ Q $ class. The parameters $ \varepsilon_1 $ and $ \varepsilon_2 $, both of which range from $ 0 $ to $ 1 $, act as modifiers to measure the effectiveness of quarantine and isolation. Perfection is achieved when $ \varepsilon_1 = 0 = \varepsilon_2 $, ensuring that individuals in these categories avoid contact with the general public, thus preventing the transmission of infection. Leaky quarantine is represented by $ 0 < \varepsilon_1, \varepsilon_2 < 1 $. On the contrary, when $ \varepsilon_1 = 1 = \varepsilon_2 $, people in quarantine and isolation are as likely as any other member of the population to interact with the general public. We provide a complete description of the model parameters, which is presented in Table 1.
It is evident that any solution to the system (2.1) that begins with nonnegative initial values will also be nonnegative. Therefore, we will first examine the bounds of the solution of this system.
Define
and let $ \Psi $ be defined as the set
Under this definition, we introduce the following lemma.
Lemma 1. The solution to System (2.1) is both unique and bounded, given the initial value $ X(0) \in X $ defined in (2.2). Moreover, the set $ \Psi $ is compact, positively invariant, and attracts all positive orbits in $ X $.
Proof. Consider $ X_1 = (S, V_1, V_2, E, I, Q, H, N) $. Building upon references [19,25,26], we introduce the functions $ g_1, g_2, g_3 \in (\mathbb{R}^8_+, \mathbb{R}_+) $ defined as follows:
Through a change of variable where $ N = S + V_1 + V_2 + E + I + Q + H + R $ and from (2.3), system (2.1) can be reformulated as follows:
It is evident that $ g_1(X_1) $, $ g_2(X_1) $, and $ g_3(X_1) $ are continuous and globally Lipschitz in $ \mathbb{R}^8_+ $. Applying Theorem 5.2.1 from [27] allows us to establish that, for any $ (S(0), V_1(0), V_2(0), E(0), I(0), Q(0), H(0), N(0)) \in \mathbb{R}^8_+ $, the system (2.4) possesses a unique local nonnegative solution $ (S, V_1, V_2, E, I, Q, H, N) $.
From the total human population $ N(t) $ with a positive initial condition $ X(0) \in \mathbb{R}^{8}_{+} $, we have the equation
indicating that the associated linear differential equation,
has a unique equilibrium $ N^* = \frac{\Lambda}{\mu} $ in $ \mathbb{R}_{+} $. Hence, as $ t \to \infty $, the difference $ |N(t)-N^*| $ tends to zero and $ N^* $ becomes globally attractive in $ \mathbb{R}_{+} $. Additionally, employing the comparison theorem [28] confirms that $ N(t) $ remains bounded. Consequently, the solution of the system (2.1) exists globally over the interval $ [0, \infty) $.
□
The equilibrium without the presence of the disease, known as the disease-free equilibrium in (2.1), can be determined by solving the system below:
Clearly, the solution to (2.5) is the unique disease-free equilibrium of system (2.1), as given by:
where $ S^{*} = \dfrac{\Lambda}{\theta+\mu} $.
3.
Basic reproduction number
For periodic epidemic compartmental models, Bacaër and Guernaou [29] provided a definition of $ \mathcal{R}_0 $ as the spectral radius of an integral operator acting on the space of continuous periodic functions. Later, Wang and Zhao [11] characterized $ \mathcal{R}_0 $ for such models and proved that it serves as a threshold parameter regarding the local stability properties of the disease-free periodic solution. Rebelo et al. [12] studied persistence in epidemiological models in a seasonal environment. Bacaër and Ait Dads [30] gave a more biological explanation of $ \mathcal{R}_0 $ for compartmental epidemic models with periodic parameters. Therefore, the global dynamics of the system is characterized by the basic reproduction number ($ \mathcal{R}_0 $) of periodic compartmental models.
Within this section, we employ the methodology introduced in [11,12,31] to determine the basic reproduction number ($ \mathcal{R}_0 $) for the system (2.1). Define the vector $ \mathcal{H} = (E, I, Q, H, S, V_1, V_2, R)^T $, where $ E $, $ I $, $ Q $, and $ H $ correspond to the infected classes, and $ S $, $ V_1 $, $ V_2 $, and $ R $ denote the uninfected classes with
The nonautonomous equation presented below,
is equivalent to System (2.1). The disease-free equilibrium for (3.1) is $ \mathcal{H}^{*} = \left(0, 0, 0, 0, S^*, V_1^*, V_2^*, R^*\right) $. To start the analysis, we verify that the model (2.1) satisfies the conditions (A1)–(A7) outlined in [11]. Subsequently, we determine the matrix functions $ 4\times 4 $, $ F(t) = \big(\frac{\partial \mathcal{F}_i(t, \mathcal{H}^{*})}{\partial \mathcal{H}_j}\big)_{1 \leqslant i, j \leqslant 4} $, and $ V(t) = \big(\frac{\partial \mathcal{V}_i(t, \mathcal{H}^{*})}{\partial \mathcal{H}_j}\big)_{1 \leqslant i, j \leqslant 4} $ in the following manner:
and
where $ L^* = \frac{S^*+ (1-\alpha_1) V_1^*+ (1-\alpha_2) V_2^*}{N^*} $. Conditions (A1) through (A6) provided in [11] are easily verified, and the disease-free subspace $ \mathcal{H}^{*} $ is linearly asymptotically stable at $ \mathcal{H}_s = (0, 0, 0, 0, S, V_1, V_2, R) \in \mathbb{R}_{+}^{8}. $
Consider $ \mathbf{G}(x, y) $ as a matrix solution to the initial value problem presented below, where $ x\geqslant y $:
where $ I $ is the $ 4 \times 4 $ identity matrix. Thus, $ \mathbf{G}(x, y) $ can easily be calculated as
where
Therefore, the requirement (A7) described in [11] is met, as the matrix $ \mathcal{\varPsi}_{-{V}}(x) $ of (3.2) for $ x \geqslant 0 $ is equivalent to $ \mathbf{G}(x, 0) $. Let $ \mathcal{B}_\omega $ represent the ordered Banach space of $ \omega $-periodic functions from $ \mathbb{R} $ to $ \mathbb{R}^{4} $, equipped with the usual maximum norm $ \|\cdot\|_{\infty} $. Additionally, define $ \mathcal{B}^{+}_\omega := \{\phi \in \mathcal{B}_\omega : \phi(t) \geqslant 0, \ \forall t \in \mathbb{R}\} $ as the positive cone.
Define the linear next-generation operator (NGO) $ \mathcal{K} $, responsible for subsequent infections, which maps $ \mathcal{B}_\omega $ to $ \mathcal{B}_\omega $ as given below:
The basic reproduction number $ \mathcal{R}_0 $ for the model (2.1) can be computed as the spectral radius of $ \mathcal{K} $, denoted as $ \mathcal{R}_0:= \rho(\mathcal{K}). $
In order to calculate an approximate numerical value for $ \mathcal{R}_0 $, as described in [11], we define $ {\varPsi}_{\frac{F}{\lambda}- {V}}(t, \lambda) $ as the fundamental matrix of the linear $ \omega $-periodic equation
where $ \lambda $ is a parameter in the interval $ (0, \infty) $. Additionally, without losing generality, we make the assumption that $ {\varPsi}_{\frac{F}{\lambda}- {V}}(0, \lambda) $ is equivalent to the identity matrix $ I $. It is crucial to keep in mind that $ {\varPsi}_{\frac{F}{\lambda}- {V}}(\omega, \lambda) $ represents the monodromy matrix of the linear $ \omega $-periodic system (3.3).
Theorem 2 ([11], Theorem 2.1]). The following assertions are valid.
(i) If $ \rho({\varPsi}_{\frac{F}{\lambda}- {V}}(\omega, \lambda)) = 1 $ has a positive solution $ \lambda_0 $, then $ \lambda_0 $ is an eigenvalue of operator $ \mathcal{K} $ and, hence, $ \mathcal{R}_0 > 0 $.
(ii) If $ \mathcal{R}_0 > 0 $, then $ \lambda_0 = \mathcal{R}_0 $ is a unique solution of $ \rho({\varPsi}_{\frac{F}{\lambda}- {V}}(\omega, \lambda)) = 1 $.
(iii) $ \mathcal{R}_0 = 0 $ if and only if $ \rho({\varPsi}_{\frac{F}{\lambda}- {V}}(\omega, \lambda)) < 1 $ for all $ \lambda > 0 $.
More details about the numerical method used to compute the basic reproduction number $ \mathcal{R}_0 $ (the spectral radius of the NGO $ \mathcal{K} $) can be found in [32,33].
4.
Stability analysis of the disease-free equilibrium ($ \mathcal{D}_0 $) of system (2.1)
In this section, our objective is to demonstrate the local and global stability of $ \mathcal{D}_0 $ and establish that the disease undergoes extinction when $ \mathcal{R}_0 < 1 $.
Consider $ {\varPsi}_{{F}- {V}}(t) $ as a fundamental matrix of the linear $ \omega $-periodic system $ \mathbf{x'} = [F(t)-V(t)] \mathbf{x} $. Additionally, and without loss of generality, assume that $ \varPsi_{F-V}(0) = I $, representing the identity matrix. It is important to note that $ \varPsi_{F-V}(\omega) $ is the monodromy matrix of the linear $ \omega $-periodic system mentioned above. Now, we recall the following Theorem 2.2 from [11] regarding the local stability of the disease-free equilibrium $ \mathcal{D}_0 $.
Theorem 3 ([11], Theorem 2.2). The following statements are valid:
(i) $ \rho(\varPsi_{F-V}(\omega)) < 1 (>1)\iff \mathcal{R}_0 < 1 (>1) $;
(ii) $ \rho(\varPsi_{F-V}(\omega)) = 1 \iff \mathcal{R}_0 = 1 $.
Building on the preceding discussion, the subsequent theorem delves into the local stability of the disease-free equilibrium $ \mathcal{D}_0 $ of (2.1).
Theorem 4. The disease-free equilibrium $ \mathcal{D}_0 $ is locally asymptotically stable if $ \mathcal{R}_0 < 1 $ and unstable if $ \mathcal{R}_0 > 1 $.
Proof. Consider the Jacobian matrix of (2.1) calculated at $ \mathcal{D}_0 $, represented as
where
and
Referring to [34], the local asymptotic stability of $ \mathcal{D}_0 $ is contingent on two conditions: $ \rho(\mathcal{\varPsi}_{\mathcal{A}_2}(\omega)) < 1 $ and $ \rho(\mathcal{\varPsi}_{F-V}(\omega)) < 1 $. Here, $ \mathcal{A}_2 $ is a constant matrix with negative eigenvalues $ -(\theta+\mu) < 0 $, $ -(\sigma_1+\mu) < 0 $, $ -(\sigma_2+\mu) < 0 $, and $ -\mu < 0 $, so $ \rho(\mathcal{\varPsi}_{\mathcal{A}_2}) < 1 $. The stability of $ \mathcal{D}_0 $ is ultimately determined by $ \rho(\mathcal{\varPsi}_{F-V}(\omega)) $. Therefore, $ \mathcal{D}_0 $ is locally asymptotically stable if $ \rho(\mathcal{\varPsi}_{F-V}(\omega)) < 1 $ and unstable if $ \rho(\mathcal{\varPsi}_{F-V}(\omega)) > 1 $. This completes the proof using Theorem 3.
□
Theorem 5. If $ \mathcal{R}_0 < 1 $, then the disease-free equilibrium $ \mathcal{D}_0 $ of (2.1) is globally asymptotically stable.
Proof. Extending our analysis to local stability in Theorem 4, if $ \mathcal{R}_0 < 1 $, the disease-free equilibrium $ \mathcal{H}^* $ is proven to be locally asymptotically stable. However, to establish global attractiveness, it is essential to confirm the fulfillment of requirements (A1) through (A7) as outlined in [12], discussed in Section 3. Furthermore, note that $ \mathcal{H}^* = \left(0, 0, 0, 0, S^*, V_1^*, V_2^*, R^*\right) $ stands as the unique equilibrium of (3.1) within the set of disease-free states $ \mathcal{H}_s $.
The first three equations of (2.1) yield the following system:
Considering the nonnegativity constraints $ E(t)\geq 0 $, $ I(t)\geq 0 $, $ Q(t)\geq 0 $, and $ H(t)\geq 0 $ established in Lemma 1, we can deduce the following inequalities:
These inequalities imply:
Consequently, for any arbitrary positive $ m $, there exists $ t(m) > 0 $ such that $ S(t) \leq S^* + m $, $ V_1(t) \leq V_1^* + m $, and $ V_2(t) \leq V_2^* + m $ for all $ t > t(m) $.
We define $ q (m):= \min\{\frac{S^* + (1-\alpha_1) V_1^* + (1-\alpha_2) V_2^*}{S^*+m + (1-\alpha_1) (V_1^*+m)+ (1-\alpha_2) (V_2^*+m) } \} $. From the system in (2.1), for $ t > t(m) $, the following inequalities can be derived:
and system (4.1) can be reformulated as
with $ \mathcal{Y}(t) = \left(E(t), I(t), Q(t), H(t)\right) $. In the limit as $ t $ approaches infinity, $ \mathcal{Y}(t) $ tends to zero, signifying the eventual extinction of the disease. Using ([12], Theorem 2), it follows that $ \mathcal{H}^* $ achieves global asymptotic stability (GAS) due to its GAS behavior within the disease-free subspace $ \mathcal{H}_s $. □
5.
Persistence of the infective compartments
In this subsection, we employ the methodology introduced by [12] to showcase the persistence of infective compartments within the system (2.1) when $ \mathcal{R}_0 > 1 $.
Theorem 6. If $ \mathcal{R}_0 > 1 $, the dynamical system described by (2.1) displays persistent behavior regarding the variables $ E $, $ I $, $ Q $, and $ H $.
Proof. Given the persistence of the sum $ E+I+Q $, we can establish the persistence of each infectious variable $ E $, $ I $, and $ Q $, ultimately resulting in the persistence of variable $ H $. Let $ \varepsilon $ be a positive value such that $ \lim\inf_{t\to +\infty} \big(E+I+Q\big)\geqslant m $. Consequently, for large values of $ t $, it can be deduced that $ E \geqslant \frac{m}{3}-I-Q $. Obtaining expressions for $ I' $ and $ Q' $ from the equations in (2.1), we derive the following inequalities:
Consequently, we can infer that
Upon substituting the inequality (5.1) into the equation for $ H' $ in (2.1), we derive the inequality
from which we deduce
Define $ \eta(m):= \max\{\frac{S^* + (1-\alpha_1) V_1^* + (1-\alpha_2) V_2^* }{S^*-4 m + (1-\alpha_1) (V_1^*-4 m)+ (1-\alpha_2) (V_2^*-4 m) } \}. $ For sufficiently large $ t \geq t(m) $, from the equations of (2.1), we have
The system (5.2) can be expressed as
with $ \tilde{\mathcal{Y}}(t) = \left(\tilde{E}(t), \tilde{I}(t), \tilde{Q}(t), \tilde{H}(t)\right) $. Therefore, the assumptions of ([12], Theorem 4) are satisfied, establishing the persistence of the system (2.1) with respect to $ E $, $ I $, $ Q $, and $ H $. □
6.
Existence of positive periodic solutions
Define
and
Consider the Poincaré map $ \mathcal{Q} \colon \mathbb{R}^{8}_+ \rightarrow \mathbb{R}^{8}_+ $ associated with (2.1). Then, for $ q^0 \in \mathbb{R}^{8}_+ $, the map is given by $ \mathcal{Q}(q^0) = u(\omega, q^0) $, where $ u(t, q^0) $ represents the unique solution of (2.1) with the initial condition $ q^0 \in \mathcal{U} $.
Lemma 7. For $ \mathcal{R}_0 > 1 $, there exists $ \chi > 0 $ such that, for any $ X(0) \in \mathcal{U}_0 $ defined in (2.2) with $ \| X(0) -\mathcal{D}_0 \| \leqslant \chi $, the following holds:
Proof. Given $ \mathcal{R}_0 > 1 $, as indicated by Theorem 3, we ascertain $ \rho(\mathcal{\varPsi}_{F-V}(\omega)) > 1 $. Thus, it is possible to choose a sufficiently small $ \zeta > 0 $ to ensure $ \rho(\mathcal{\varPsi}_{F-V-\mathcal{P}_{\zeta}}(\omega)) > 1 $. The matrix function $ \mathcal{P}_{\zeta}(t) $, sized $ 4\times4 $, is defined by
where $ c(t) = \beta(t) (\zeta + (1-\alpha_1)\zeta+ (1-\alpha_2) \zeta) $.
In what follows, we claim
Assume, for the sake of contradiction, that equation (6.1) is false. Then, there exists $ X(0)\in \mathcal{U}_0 $ such that
For simplicity, let us suppose that
Owing to the continuous dependency of the solutions on the initial values, we obtain
Let $ t\geqslant0 $ be expressed as $ t = m\omega + s, $ where $ s \in\left[0, \omega\right) $ and $ m = \big[\frac{t }{\omega}\big] $, representing the largest integer less than or equal to $ \frac{t}{\omega} $. Consequently, we can derive
for all $ t \geqslant 0 $. This inequality implies $ S^* -\zeta \leq S(t) \leq S^* +\zeta $, $ V_1^* -\zeta \leq V_1(t) \leq V_1^* +\zeta $, $ V_2^* -\zeta \leq V_2(t) \leq V_2^* +\zeta $, $ 0\leq E(t) \leq \zeta $, $ 0\leq I(t) \leq \zeta $, $ 0\leq Q(t) \leq \zeta $, and $ 0\leq H(t) \leq \zeta $. Given that $ \| X(0) - \mathcal{D}_0\| \leqslant \chi $, we can derive the following:
where $ b(\zeta) = \frac{S^*-\zeta+ (1-\alpha_1) (V_1^*-\zeta) +(1-\alpha_2) (V_2^*-\zeta)}{N^*} $. To aid our analysis, we consider the following linear system
According to [35, Lemma 1], we can establish the existence of a positive, $ \omega $-periodic function $ p(t) $, making $ (E(t), I(t), Q(t), H(t)) = e^{\xi t} p(t) $ a solution to (6.3), where $ \xi = \frac{1}{\omega} \ln \rho(\mathcal{\varPsi}_{F-V+ \mathcal{P}_{\zeta} }(\omega)) > 0 $. Given that $ \mathcal{R}_0 > 1 $ and $ \rho(\mathcal{\varPsi}_{F-V-\mathcal{P}_{\zeta}}(\omega)) > 1 $, it follows that if $ (E(0), I(t), Q(0), H(0)) > (0, 0, 0, 0) $, then $ (E(t), I(t), Q(t), H(t)) \to \infty $ as $ t\to \infty $. Applying the comparison principle [28, Theorem B.1], we deduce $ E(0) > 0 $, $ I(0) > 0 $, $ Q(0) > 0 $, $ H(0) > 0 $, $ \lim_{t\to \infty} E(t) = \infty $, $ \lim_{t\to \infty} I(t) = \infty $, $ \lim_{t\to \infty} Q(t) = \infty $, and $ \lim_{t\to \infty} H(t) = \infty $. However, this contradicts conditions $ E(t) < \zeta $, $ I(t) < \zeta $, $ Q(t) < \zeta $, $ H(t) < \zeta $, and Eq (6.2). Consequently, Eq (6.1) holds true, and this concludes the proof. □
Theorem 8. For $ \mathcal{R}_0 > 1 $, there exists at least one positive periodic solution to system (2.1).
Proof. To establish the uniform persistence of $ \mathcal{Q} $ with respect to $ (\mathcal{U}_0, \partial \mathcal{U}_0) $, we can apply [36, Theorem 3.1.1]. This, in turn, implies the uniform persistence of the solution to (2.1) with respect to $ (\mathcal{U}_0, \partial \mathcal{U}_0) $. To begin, let us establish that $ \mathcal{U}_0 $ and $ \partial \mathcal{U}_0 $ are positively invariant with respect to the system (2.1). For $ X(0) \in \mathcal{U}_0 $, solving (2.1) for all $ t > 0 $, we obtain
where $ a(t) = S(t) + (1-\alpha_1) V_1(t)+ (1-\alpha_2) V_2(t) $. Therefore, $ \mathcal{U}_0 $ is confirmed as a positively invariant set. Furthermore, considering the positive invariance of $ \mathcal{U} $ and the fact that $ \partial \mathcal{U}_0 $ is relatively closed within $ \mathcal{U} $, we conclude that $ \partial \mathcal{U}_0 $ is also positively invariant. Furthermore, according to Lemma 1, it is established that the system (2.1) is point dissipative.
Let $ M_{\partial} $ be defined as the set of $ \left\lbrace X(0) \in \partial \mathcal{U}_0: \mathcal{Q}^m(X(0))\in \partial \mathcal{U}_0, \ \forall m \geqslant 0 \right\rbrace. $ We aim to establish that
It is evident that $ M_{\partial} $ includes the set $ \big\lbrace \big(S(0), V_1(0), V_2(0), E(0), I(0), Q(0), H(0), R(0)\big) : S > 0, V_1 > 0, V_2 > 0, R > 0 \big\rbrace $. To complete the proof, we need to show that $ M_{\partial} \subset \big\lbrace \big(S, V_1, V_2, 0, 0, 0, 0, R \big) : S > 0, V_1 > 0, V_2 > 0, R > 0 \big\rbrace, $ for any initial condition $ X(0) \in \partial \mathcal{U}_0 $, $ E(n \omega) = 0 $ or $ I(n \omega) = 0 $ or $ Q(n \omega) = 0 $ or $ H(n \omega) = 0 $, for all $ n \geqslant 0 $.
Suppose, for the sake of contradiction, that there exists an integer $ n_1 \geqslant 0 $ such that $ E(n_1 \omega) > 0 $ and $ I(n_1 \omega) > 0 $. Substituting $ t = n_1 \omega $ for the initial time $ t = 0 $ into (6.4)–(6.11), we obtain $ S(t) > 0 $, $ V_1(t) > 0 $, $ V_2(t) > 0 $, $ E(t) > 0 $, $ I(t) > 0 $, $ Q(t) > 0 $, $ H(t) > 0 $, and $ R(t) > 0 $. However, this contradicts the positive invariance of $ \partial \mathcal{U}_0 $.
Establishing weak uniform persistence with respect to $ (\mathcal{U}_0, \partial \mathcal{U}_0) $ is ensured by Lemma 7. The presence of a global attractor for $ \mathcal{Q} $ is guaranteed by Lemma 1. This implies that $ \mathcal{D}_0 $ serves as an isolated invariant set within $ \mathcal{U} $ and $ W^s(\mathcal{D}_0) \cap \mathcal{U}_0 = \emptyset $. All solutions within $ M_\partial $ converge to $ \mathcal{D}_0 $, and it is evident that $ \mathcal{D}_0 $ is acyclic in $ M_\partial $. Applying [36, Theorem 1.3.1 and Remark 1.3.1], we can therefore conclude that $ \mathcal{Q} $ exhibits uniform (strong) persistence with respect to $ (\mathcal{U}_0, \partial \mathcal{U}_0) $. Consequently, there exists an $ \varepsilon > 0 $ such that
for all $ X(0) \in \mathcal{U}_0 $. Invoking [36, Theorem 1.3.6], we determine the existence of a fixed point $ \bar{X}(0) \in \mathcal{U}_0 $ for $ \mathcal{Q} $. Consequently, system (2.1) has at least one periodic solution $ u(t, \bar{X}(0)) $, where $ \bar{X}(0) = (\bar{S}(0), \bar{V}_1(0), \bar{V}_2(0), \bar{E}(0), \bar{I}(0), \bar{Q}(0), \bar{H}(0), \bar{R}(0)) \in \mathcal{U}_0 $. To establish that $ \bar{S}(0) $ is positive, consider the scenario where $ \bar{S}(0) = 0 $. In this case, it is inferred that $ \bar{S}(0) > 0 $ for all $ t > 0 $. However, by exploiting the periodicity of the solution, a contradiction arises with $ \bar{S}(0) = \bar{S}(n \omega) = 0 $. □
7.
Model calibration and sensitivity analysis
In order to verify and strengthen our analytical results, we apply our seasonal compartmental mathematical model to real measles data from two Asian countries. Measles, an infectious disease, presents substantial public health and economic challenges throughout the world. Despite the limitations of testing, quarantine, and isolation measures it has been effective in controlling the spread of diseases [37,38]. These measures play a crucial role in reducing the risk of infection and preventing the future prevalence of the disease. Vaccination is essential for the management of infectious diseases, but many vaccines are imperfect, with partial protective effects and trade-offs between transmission and recovery [37,38]. The efficacy of a vaccine and the population turnover rate play crucial roles in disease eradication. The results of vaccination games depend on factors such as the dynamics of disease transmission, the cost of infection, and the efficacy of the vaccine. It is important to consider the imperfections of vaccines in disease models, especially for diseases with high basic reproduction numbers.
Within this section, our focus turns to investigating the spread of measles as a case study in two different countries: Saudi Arabia from August 2018 to August 2021 and Pakistan from January 2019 to December 2021, as documented by the World Health Organization (WHO) [39], using our established model. The simulation results presented aim to illustrate the performance of our model with periodic parameters in capturing seasonal fluctuation data. With reference to [7,17,40,41,42], we assume that the transmission rate $ \beta(t) $ follows a time-periodic pattern with a period of 12 months. This is mathematically expressed as $ \beta(t) = \beta_0 \cdot \left(a + b \sin\left(c + \frac{2\pi t}{12}\right)\right). $ Here, $ a $ and $ b $ function as adjustable parameters, $ c $ denotes the amplitude of the forcing, and $ \beta_0 $ signifies the baseline value of the time-dependent contact rate.
7.1. Parameters estimation and curve fitting to measles data from Saudi Arabia and Pakistan
The World Bank report on Saudi Arabia [43] in 2021 indicates a total population of $ 36, 408, 820 $ with a life expectancy at birth of $ 77 $ years. This results in a monthly birth rate of approximately $ \Lambda = \mu \times N = 39, 403 $, where $ \mu $ is determined as $ 1/(12 \times 77) $. Similarly, World Bank data for Pakistan [44] reveals a total population of $ 231, 402, 117 $ in 2021, with a life expectancy at birth of $ 66 $ years. Applying the same calculation, the estimated monthly human birth population in Pakistan is approximately $ 292, 174 $, with $ \mu $ calculated as $ 1/(12 \times 66) $. A single administration of the MMR (Measles, Mumps, and Rubella) vaccine demonstrates an efficacy of around 93% in preventing measles, while two doses of the vaccine exhibits an efficacy of approximately 97%, as reported by both the WHO [45] and the Centers for Disease Control and Prevention (CDC) [46]. Consequently, the assumed values for the efficacy of the vaccine are denoted as $ \alpha_1 = 0.93 $ for a single dose and $ \alpha_1 = 0.97 $ for two doses. Applying Latin hypercube sampling alongside the least squares method, we aim to estimate the parameters of the model (2.1) to obtain the optimal fit with the given data. This sampling technique allows for the simultaneous evaluation of variance in multiple parameter values, as outlined in [34].
Fitting our model (2.1) to confirmed measles cases in Saudi Arabia from August 2018 to August 2021 and in Pakistan from January 2019 to December 2021 allowed us to obtain estimates for the parameters of the measles model. Although certain parameter values were drawn from existing literature to inform our initial estimates, the remaining parameters were determined through the process of fitting the model to the observed data.
Figure 2 presents the fit of the model with data on measles (cumulative cases and new cases) from Saudi Arabia between 2018 and 2021, showing a reasonably good fit and a high goodness of fit $ R^2 = 0.95961 $. Using the method established in [32], we numerically estimated the current basic reproduction number as $ \mathcal{R}_0 \approx 0.585887 < 1 $, signifying the extinction of the disease in Saudi Arabia.
On the contrary, Figure 3 shows the fit of the model with Pakistan's measles data between 2019 and 2021, also showing a reasonably good fit and a high goodness of fit $ R^2 = 0.972413 $, indicating its ability to capture key patterns of incidence of measles epidemics during 2019-2021. Once again, we estimate $ \mathcal{R}_0 \approx 4.05938 > 1 $, which reveals the persistence of the disease in Pakistan. This demonstrates that our model (2.1) is capable of reproducing the two types of outcomes observed in the measles epidemic in Asia.
7.2. Sensitivity analysis of the time–average reproduction number
Performing a sensitivity analysis on the basic reproductive number $\mathcal{R}_0$, our aim is to quantify the variations in the parameters of the model given in Eq (2.1). This analysis helps identify parameters that significantly influence both the basic reproduction number and disease transmission dynamics. Given that our main focus lies in determining the basic reproduction number ($ \mathcal{R}_0 $) of the periodic model (2.1), which lacks an explicit expression for $ \mathcal{R}_0 $ defined as the spectral radius of a linear operator, we will employ the following remark to derive a formula for the time–average reproduction number ($ \langle \mathcal{R}_0 \rangle $) of the associated nonautonomous system (see [32] for more details).
Remark 9. In accordance with the notation provided in [32], the integral average of a continuous function $ f(t) $, which exhibits periodicity with a period of $ \omega $, can be defined as $ \langle f \rangle := \frac{1}{\omega} \int_{0}^{\omega} f(t) \, dt. $
By applying the findings derived from the study conducted by [50], we obtain
and
where $ L^* = \frac{S^*+ (1-\alpha_1) V_1^*+ (1-\alpha_2) V_2^*}{N^*} $. Hence, we get
where
The use of sensitivity indices is a common practice in sensitivity analysis, as elucidated in [51]. The normalized forward sensitivity index for a variable concerning a parameter is determined by calculating the ratio between the relative change in the variable and the relative change in the parameter. Specifically, the normalized forward sensitivity index of $ \langle\mathcal{R}_0\rangle $ with respect to a parameter $ x $ is defined as
We conducted a sensitivity analysis for the time-averaged reproduction number $ \langle \mathcal{R}_0 \rangle $, as defined in Eq (7.1). Our investigation, as depicted in Figure 4, reveals that $ \langle \mathcal{R}_0 \rangle $ exhibits heightened sensitivity to variations in the infection rate ($ \langle \beta \rangle $), relative transmissibility ($ \tau $ and $ \tau_e $), and recovery rates ($ \gamma_1 $ and $ \gamma_3 $). Turning our attention to Figure 5, we present the sensitivity indices for $ \langle \mathcal{R}_E \rangle $, $ \langle \mathcal{R}_I \rangle $, $ \langle \mathcal{R}_Q \rangle $, and $ \langle \mathcal{R}_H \rangle $. This visualization allows for a comprehensive understanding of the factors that influence these specific reproduction numbers, providing a nuanced perspective on their sensitivities to parameters such as infection rate, relative transmissibility, and recovery rates.
By setting the time-varying transmission rate to a constant value, $ \beta(t) = \beta_0 $, one can derive a formula for the basic reproduction number of the autonomous version of system (2.1). Referring to (7.1), we obtain
Figure 6 depicts the curves of the basic reproduction number $ \mathcal{R}^a_0 $ of the autonomous version of system (2.1), the time-averaged reproduction number $ \langle \mathcal{R}_0 \rangle $ and the the basic reproduction number $ \mathcal{R}_0 $ plotted in relation to certain parameters of the system (2.1). Specifically, these parameters include the average transmission rate ($ \langle \beta \rangle $), relative transmissibility ($ \tau $ and $ \tau_e $), quarantine rate for exposed individuals ($ \nu_2 $), recovery rate for infectious individuals ($ \gamma_1 $), and vaccine coverage rate ($ \theta $). This visual representation of the curve in relation to these system parameters improves our understanding of how they collectively influence the potential for disease transmission.
The calculations show that $ \mathcal{R}^a_0 > \langle \mathcal{R}_0 \rangle \geq \mathcal{R}_0 $, suggesting that $ \mathcal{R}^a_0 $ and $ \langle \mathcal{R}_0 \rangle $ overestimate the risk of disease transmission. It is worth noting that several papers have addressed the issue of underestimation and overestimation of the average basic reproduction number. For instance, it was demonstrated in [11,17,25] that $ \mathcal{R}_0 > [\mathcal{R}_0] $, whereas in [26], the authors provided an example where $ \mathcal{R}_0 < [\mathcal{R}_0] $. More details can also be found in [11,52].
8.
Numerical simulations
This section is dedicated to presenting numerical simulations. The aim is to both illustrate and validate the theoretical findings discussed earlier. Through these simulations, we provide visual evidence that demonstrates the alignment between our time-periodic model and the observed seasonal fluctuations.
8.1. Extinction and persistence
It is clear from the exposition in Section 4 until Section 6 that the parameter $ \mathcal{R}_0 $ plays a significant role in determining whether the disease will persist in the population, as elucidated by Theorems 5 and 8. Theorem 8 asserts that if $ \mathcal{R}_0 > 1 $, the dynamical system (2.1) possesses a positive $ \omega $-periodic solution. To show the persistence of the disease and the existence of the periodic solution, we set the parameter values as follows: $ a = 0.9 $, $ \beta_0 = 0.312 $, $ b = 8.6 $, $ c = 1.7 $, $ \alpha_1 = 0.93 $, $ \alpha_2 = 0.5 $, $ \gamma_1 = 0.1 $, $ \gamma_2 = 0.3 $, $ \gamma_3 = 0.1 $, $ \delta_1 = 0.0365 $, $ \delta_2 = 0.0465 $, $ \epsilon_1 = 0.523 $, $ \epsilon_2 = 0.474 $, $ \theta = 0.000154 $, $ \kappa_1 = 0.231 $, $ \kappa_2 = 0.203 $, $ \nu_1 = 0.166 $, $ \nu_2 = 0.178 $, $ \sigma_1 = 0.047 $, $ \sigma_2 = 0.028 $, $ \tau_e = 0.556 $, and $ \tau = 0.523 $. To further elaborate on the profound implications of this result, Figures 7–9 offer vivid illustrations of the long-term behavior and the enduring presence of measles, along with the existence of periodic positive solutions when $ \mathcal{R}_0 \approx 1.12776 > 1 $. Consequently, disease compartments not only persist, but also evolve into an endemic state within the population, characterized by recurring annual outbreaks.
Figures 10 and 11 provide visual representations that effectively corroborate the theoretical findings. These findings show that the disease-free equilibrium $ \mathcal{D}_0 $ demonstrates global asymptotic stability when $ \mathcal{R}_0 = 0.474236 < 1 $. As a result, it can be inferred that the disease can be eliminated if $ \mathcal{R}_0 < 1. $
8.2. Examining the impact of imperfect quarantine and isolation
Imperfect quarantine and isolation can significantly impact the spread of measles. It is crucial to acknowledge that the effects of quarantine and isolation can vary based on the specific characteristics of the disease and the population studied. In this study, we investigate the influence of imperfect quarantine and isolation on the spread of measles in Pakistan, using parameter values fitted to the measles data presented in Table 2.
To predict and estimate the impact of quarantine and isolation on future measles outbreaks in Pakistan, simulations were started using parameters fitted up to month 35, with subsequent adjustments. Different values of the quarantine efficacy modification parameter, $ \epsilon_1 $, are illustrated in Figure 12, while the isolation efficacy modification parameter, $ \epsilon_2 $, is shown in Figure 13. The results indicate that the imperfect implementation of quarantine and isolation, particularly when $ \epsilon_2 = 1 = \epsilon_2 $, may lead to a substantial increase in the number of measles infectious populations. On the contrary, the perfect implementation of quarantine with $ \epsilon_1 = 0 $ decreases the number of infectious individuals without causing extinction. Perfect isolation, observed when $ \epsilon_2 = 0 $, leads to a significant decrease in the number of infectious individuals, leading to extinction. These findings underscore the importance of implementing perfect quarantine and isolation measures.
8.3. Examining the impact of imperfect vaccination
The impact of incomplete first- and second-dose vaccination on measles is a significant concern for public health. Incomplete coverage, suboptimal vaccine efficacy, and deviations from recommended dose schedules can undermine the effectiveness of vaccination efforts. As seen in Figure 14, when the vaccination coverage rate ($ \theta $) improves, the impact of the measles epidemic decreases. This can be a challenge to achieve in countries like Pakistan.
While the effectiveness of a vaccine is crucial in managing the spread of diseases, its impact can vary depending on the basic reproduction number of the disease. Diseases with lower basic reproduction numbers may show minimal differences in outcomes between perfect and imperfect vaccines. In contrast, diseases with higher basic reproduction numbers, such as measles, pose greater challenges when faced with an imperfect vaccine. The presence of imperfections in vaccine efficacy can cause increased difficulties in achieving effective disease control measures.
To address the challenge of measles control, the government could prioritize improving the efficacy of vaccines ($ \alpha_1 $ and $ \alpha_2 $), as illustrated in Figures 15 and 16. At the same time, it is crucial to ensure accessibility for individuals in poverty. In particular, achieving a high coverage rate ($ \theta $) for the vaccine, coupled with elevated efficacy rates ($ \alpha_1 $ and $ \alpha_2 $), proves paramount. A higher efficacy rate plays a crucial role in decreasing the number of infectious cases, highlighting its importance in alleviating the impact of the measles epidemic.
9.
Discussion
This study delves into the intricacies of a nonautonomous mathematical model designed to elucidate the transmission dynamics of infectious diseases over time. By incorporating a seasonal transmission parameter and imperfections in quarantine, isolation, and vaccination strategies, the model builds on previous works such as [17,19] to explore threshold dynamics that govern disease persistence or elimination. Through a comprehensive analysis of the basic reproduction number ($ \mathcal{R}_0 $), the research establishes its pivotal role as a threshold parameter, delineating the conditions under which the disease-free equilibrium is globally stable or the disease persists. The complexity of the model lies in its integration of time-dependent coefficients and the interplay of quarantine, isolation, and vaccination measures, allowing a nuanced understanding of the dynamics of the disease. This study differs from [17], which employed a mathematical model with a seasonal transmission parameter and a double-dose vaccination to examine the spread of measles over time, assuming that only the first dose of the vaccine was imperfect. In contrast, our study assumes imperfections in both the first and second doses of the vaccine. Additionally, we incorporate the impact of imperfect interventions, specifically quarantine, isolation, and vaccination.
Using real-world measles data from two Asian countries, our seasonal compartmental mathematical model validates and supports our analytical results. The research focuses on examining measles dynamics in Saudi Arabia and Pakistan, incorporating essential factors such as vaccination, time-varying transmission rates, and imperfections in control strategies. By calibrating the model with real-world data, the dynamics of the disease are successfully captured. Key parameters such as vaccine efficacy ($ \alpha_1 $ and $ \alpha_2 $) and time-dependent transmission rates were crucial to accurately reproduce observed patterns and estimate critical parameters. Numerical simulations highlighted the importance of the basic reproduction number ($ \mathcal{R}_0 $) in determining the persistence of the disease. Measles demonstrated persistence when $ \mathcal{R}_0 > 1 $ and tended toward extinction when $ \mathcal{R}_0 < 1 $. Sensitivity analysis emphasized the importance of effective quarantine, isolation, and vaccination strategies in the control of infectious populations. Our sensitivity analysis of the time-averaged reproduction number, $ \langle \mathcal{R}_0 \rangle $, in a periodic model revealed a significant sensitivity to key parameters such as infection rate, relative transmissibility, and recovery rates. The formula derived for $ \langle \mathcal{R}_0 \rangle $ allowed for a comprehensive understanding of its contributions from exposed, infectious, quarantined, and hospitalized individuals. Visualizations of the sensitivity indices provided information on the influence of specific parameters on different reproduction numbers, helping to prioritize interventions as shown in Figures 4 and 5. The graphical representation of the curves of the basic reproduction number $ \mathcal{R}^a_0 $ of the autonomous model, the time-averaged reproduction number $ \langle \mathcal{R}_0 \rangle $, and the basic reproduction number $ \mathcal{R}_0 $ in relation to the system parameters further improved our understanding of its impact on the potential for disease transmission as shown in Figure 6. In general, this analysis provides valuable information to inform interventions and guide future research in infectious disease modeling.
The numerical simulations conducted in this study serve to validate and illustrate the theoretical insights discussed earlier on the dynamics of measles in a population. The visual evidence presented in Figures 7, 9, 10, and 11 aligns with the theoretical findings, emphasizing the pivotal role of the basic reproduction number ($ \mathcal{R}_0 $) in determining the long-term behavior of measles. When $ \mathcal{R}_0 $ exceeds $ 1 $, the simulations demonstrate the persistence of measles in the population, accompanied by the existence of periodic positive solutions. In contrast, when $ \mathcal{R}_0 $ falls below $ 1 $, the disease-free equilibrium is globally asymptotically stable, leading to the extinction of measles. These results provide valuable information on the conditions under which measles can establish and persist within a population or face elimination. Examining imperfect quarantine, isolation, and vaccination further illuminates the practical implications for disease control. Simulations indicate that the effective implementation of quarantine and isolation measures is crucial to curtailing the spread of measles, highlighting the sensitivity of the model to variations in the parameters of efficacy modification. Furthermore, the impact of imperfect vaccination, considering coverage rates and vaccine efficacy, underscores the importance of these factors in mitigating the burden of measles. These results are important for understanding the variations in the infectious population due to the overestimation/underestimation of the disease transmission risk provided by the basic reproduction numbers of the autonomous system as shown in Figure 6.
Looking forward, future research should explore the long-term impact of vaccination campaigns in dynamic epidemiological landscapes. Incorporating real-time data and refining models based on ongoing observations, considering the time delay between the first and second doses, as well as the time to arrive in the recovered state after receiving the second dose of the vaccine, will improve predictive accuracy. Addressing uncertainties in parameter estimates and evaluating the effectiveness of new vaccines are crucial for future research.
Use of AI tools declaration
The author declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
M.A.I. was supported by the project No. 146210, implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the PD_23 funding scheme, by the National Laboratory for Health Security, RRF-2.3.1-21-2022-00006 and by the project No. 129877, implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the KKP_19 funding scheme. This publication is funded by University of Szeged Open Access Fund (grant number: 6993).
Conflict of interest
The author declares no conflict of interest.










 DownLoad:
DownLoad: