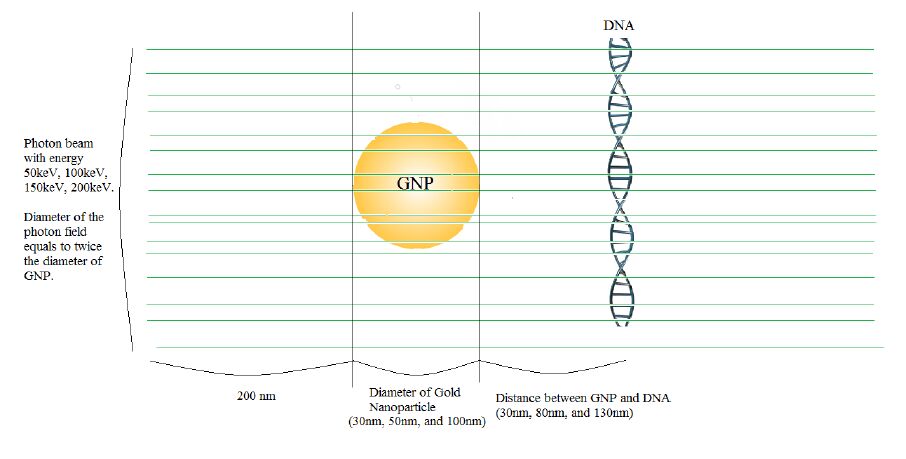
This study investigated the DNA damage due to the dose enhancement of using gold nanoparticles (GNPs) as a radiation sensitizer in radiotherapy. Nanodosimetry of a photon irradiated GNP was performed with Monte Carlo simulations using Geant4-DNA (ver. 10.2) in the nanometer scale. In the simulation model, GNP spheres (with diameters of 30, 50, and 100 nm) and a DNA model were placed in a water cube (1 µm3). The GNPs were irradiated by photon beams with varying energies (50, 100, and 150 keV), which produced secondary electrons, enhancing the dose to the DNA. To investigate the dose enhancement effect at the DNA level, energy deposition to the DNA with and without the GNP were determined in simulations for calculation of the dose enhancement ratio (DER). The distance between the GNP and the DNA molecule was varied to determine its effect on the DER. Monte Carlo results were collected for three variables; GNP size, distances between the GNP and DNA molecule, and the photon beam energy. The DER was found to increase with the size of GNP and decrease with the distance between the GNP and DNA molecule. The largest DER was found to be 3.7 when a GNP (100 nm diameter) was irradiated by a 150 keV photon beam set at 30 nm from the DNA molecule. We conclude that there is significant dependency of the DER on GNP size, distance to the DNA and photon energy and have simulated those relationships.
1.
Introduction
Let A be the class of functions h of the form
where h is analytic in U={z∈C:|z|<1}.
We denote S,S∗ and K the subclasses of A consisting of univalent, starlike and convex functions respectively ([1,2]) and denote P={p:p(0)=1,Rep(z)>0,z∈U}.
An analytic function s:U={z:|z|<1}→C is subordinate to an analytic function t:U→C, if there is a function ν satisfying ν(0)=0and|ν(z)|<1(z∈U), such that s(z)=t(ν(z))(z∈U). Note that s(z)≺t(z). Especially, if t is univalent in U, then the following conclusion is true (see [1]):
In 1933, a classical Fekete-Szegö problem for h(z)=z+∞∑n=2anzn∈S was introduced by Fekete and Szegö [3] as follows,
The result is sharp.
Using the subordination, the classes S∗(ϕ) and K(ϕ) of starlike and convex functions were defined by Ma and Minda [4] in 1994. The function h(z)∈S∗(ϕ) iff zh′(z)h(z)≺ϕ(z) and zh″(z)h′(z)≺ϕ(z), where h∈A and ϕ∈P. Moreover, Fekete-Szegö problems of the classes were obtained by Ma and Minda [4]. The problem of Fekete-Szegö has always been a hot topic in geometry function theory. Many authors studied and obtained many results (see [5,6,7]).
Let ϕ(z)=1+Az1+Bz and −1≤B<A≤1. The classes S∗(ϕ) and K(ϕ) reduce to S∗(1+Az1+Bz) and K(1+Az1+Bz), which are the classes of Janowski starlike and convex functions respectively (see [8]).
Without loss of generality, both S∗(1+z1−z)=S∗ and K(1+z1−z)=K represent the well-known classes of starlike and convex function respectively.
In 2015, Mediratta et al. [9] introduced the family of exponential starlike functions S∗(ez), that is
or, equivalently
According to the properties of the exponential function ez and the subordination relationship, the class S∗(ez) maps the unit disc U onto a region, which is symmetric with respect to the real axis and 1.
In 1959, the class S∗s of starlike functions with respect to symmetric points was introduced by Sakaguchi [10]. The function h∈S∗s if and only if
In 1987, the classes S∗c and S∗cs of starlike functions with respect to conjugate points and symmetric conjugate points were introduced by El-Ashwa and Thomas [11] as follows,
For analytic functions h(z) and g(z)(z∈U). Let SH define the class of harmonic mappings with the following form (see [12,13])
where
In particular, h is called the analytic part and g is called the co-analytic part of f.
It is well known that the function f=h+¯g is locally univalent and sense preserving in U if and only if |h′(z)|>|g′(z)|(z∈U)([14]).
According to the above conclusion, the coefficient estimations, distortion theorems, integral expressions, Jacobi estimates and growth condition in geometric properties of covering theorem of the co-analytic part can be obtained by using the analytic part of harmonic functions. In the recent years, various subclasses of SH were researched by many authors as follows.
In 2007, the subclass of SH with h∈K was studied by Klimek and Michalski [15].
In 2014, the subclass of SH with h∈S was studied by Hotta and Michalski [16].
In 2015, the subclasses of SH with h∈S∗(1+(1−2β)z1−z) and h∈K(1+(1−2β)z1−z) were studied by Zhu and Huang [17].
In this paper, by using subordination relationship, we studied the subclasses of SH with h(z)−¯h(−¯z)2∈S∗(ez) and h(z)−¯h(−¯z)2∈K(ez).
Definition 1. Suppose f=h+¯g∈SH of the form (1.3). Let HS∗,αsc(e) denote the class of harmonic univalent exponential starlike functions with symmetric conjecture point consisting of f with h∈S∗sc(e). That is, the function f=h+¯g∈HS∗,αsc(e) if and only if
Also, let HKαsc(e) denote the class of harmonic univalent convex exponential functions with symmetric conjecture point consisting of f with h∈Ksc(e), that is, f=h+¯g∈HKαsc(e) if and only if
We know that h(z)∈Ksc(e)⟺zh′(z)∈S∗sc(e).
2.
Preliminary preparation
In order to obtain our results, we need Lemmas as follows.
Lemma 1. ([18]). Let ω(z)=c0+c1z+…+cnzn+… be analytic satisfying |ω(z)|≤1 in U. Then
and
Lemma 2. Let
we have
Lemma 3. If h(z)=z+∞∑n=2anzn∈S∗sc(e), then
The estimate is sharp for h given by
If h(z)=z+∞∑n=2anzn∈K∗sc(e), then
The estimate is sharp for h given by
Proof. Let h(z)=z+∞∑n=2anzn∈S∗sc(e). According to Definition 1, we have
There exists a function p(z)=1+∞∑k=1pkzk satisfying
that is,
Using the results of Rogosinski [19], we have |pk|≤1 for k≥1.
By means of comparing the coefficients of the both sides of (2.5), we get
and
Let ϕ(n)=1+|a3|+⋯+|a2n−1|. It is easy to verify that
and
From (2.7), we have
According to (2.6), (2.7) and (2.8), we can obtain (2.3).
If h(z)=z+∞∑n=2anzn∈Ksc(e), then zh′(z)∈S∗sc(e). Using the results in (2.3), we can obtain (2.4) easily.
Lemma 4. Let μ∈C.
(1) If h(z)=z+∞∑n=2anzn∈S∗sc(e), then
(2) If h(z)=z+∞∑n=2anzn∈Ksc(e), then
The estimates are sharp.
Proof. Let h(z)=z+∞∑n=2anzn∈S∗sc(e). According to the subordination relationship and Definition 1, we get
that is,
where ν(z)=c1z+c2z2+⋯ is an analytic function with ν(0)=0 and |ν(z)|<1(z∈U).
By means of comparing the coefficients of two sides of (2.11), we get
Therefore, we have
Using the fact that (2.2) in Lemma 1, we obtain
The bound is sharp for h given as follows,
Taking h(z)=z+∞∑n=2anzn∈Ksc(e)⟺zh′(z)=z+∞∑n=2nanzn∈S∗sc(e) into consideration, it is easy to obtain (2.10). The bound is sharp for h given as follows,
Lemma 5. Suppose h(z)∈A and |z|=r∈[0,1).
(1) Let h(z)∈S∗(e). Then
and
(2) Let h(z)∈K(e). Then
and
Proof. Let h(z)∈S∗(e) and |z|=r∈[0,1). According to the subordination relationship and Definition 1, there exists an analytic function ν(z)=c1z+c2z2+⋯ satisfying ν(0)=0 and |ν(z)|<|z|, such that
Thus, it is concluded that
that is,
Since
By (2.17) and (2.18), we get
From (2.16) and (2.19), we have
Similar to the previous proof. We let h(z)∈K(e) and |z|=r∈[0,1), then
After simple calculation, we have
By (2.18) and (2.20), we get
Using the conclusion in [19], for h(z)∈K(e), we have 2zh′(z)h(z)−1≺ez. According to the subordination relationship, we have
After simple calculation, we have
By (2.18) and (2.21), we get
Therefore, we complete the proof of Lemma 5.
Lemma 6. ([20]). If h(z)∈S∗sc(e), then h(z)−¯h(−¯z)2∈S∗(e).
Lemma 7. If h(z)∈Ksc(e), then h(z)−¯h(−¯z)2∈K(e).
Lemma 8. Suppose h(z)∈A and |z|=r∈[0.1).
(1) Let h∈S∗sc(e). Then
where
(2) Let h∈Ksc(e). Then
where
Proof. Suppose h(z)∈S∗sc(e). It is quite similar to the proof of Lemma 5, we have
According to Lemma 6 and (2.13) of Lemma 5, we have
By (2.24) and (2.25), we can obtain (2.22).
If h(z)∈Ksc(e), then
According to Lemmas 7 and (2.14) of Lemma 5, we have
By (2.26) and (2.27), we get
By (2.28), integrating along a radial line ξ=teiθ, we obtained immediately,
The verification for the remainder of (2.23) is given as follows. Let H(z):=zh′(z), which is univalent. Suppose that ξ1∈Γ=H({z:|z|=r}) is the nearest point to the origin. By means of rotation, we suppose that ξ1>0 and z1=H−1(ξ1). Let γ={ξ:0≤ξ≤ξ1} and L=H−1(γ). If ς=H−1(ξ), then dξ=H′(ς)dς. Hence
Thus the proof of Lemma 8 is completed.
3.
Main results
Next, the integral expressions for functions of the classes defined in Definition 1 are obtained.
Theorem 1. Let ω and ν be analytic in U with |ω(0)|=α,ν(0)=0,|ω(z)|<1 and |ν(z)|<1. If f=h+¯g∈HS∗,αsc(e). Then
where
Proof. Let f=h+¯g∈HS∗,αsc(e). Using Definition 1 and the subordination relationship, there exist analytic functions ω and ν satisfying ω(0)=b1,ν(0)=0,|ω(z)|<1 and |ν(z)|<1(z∈U), such that
and
If we substitute z by −¯z in (3.4), we obtain
It follows from (3.4) and (3.5) that
A routine computation for the equality (3.6) gives rise to the following equation,
Plugging (3.7) back into (3.3), we have
If the equality (3.8) is integrated from the both sides of it, then
Inserting (3.8) into (3.4), it is easy to show that
Thus, the proof of Theorem 1 is completed.
Taking Theorem 1 and h∈Ksc(e)⟺zh′(z)∈S∗sc(e) into consideration, we get the following result.
Theorem 2. Let ω and ν be analytic in U satisfying |ω(0)|=α,ν(0)=0,|ω(z)|<1 and |ν(z)|<1. If f∈HKαsc(e), then
where φ(ξ) is defined by (3.2).
In the following, the coefficient estimates of the class HS∗,αsc(e) will be obtained.
Theorem 3. Let h and g be given by (1.3). If f=h+¯g∈HS∗,αsc(e), then
and
The estimates are sharp and the extremal function is
Specially, if f∈HS∗,0sc(e), then
and
The estimates are sharp and the extremal function is
Proof. Let h and g be given by (1.3). Using the fact that g′=ωh′ satisfying ω(z)=c0+c1z+c2z2+⋯ analytic in U, we obtain
and
It is easy to show that
and
Since g′=ωh′, it follows that c0=b1. By (2.1), it is obvious that |ck|≤1−α2 for k∈N. Therefore,
and
According to Lemma 3, (3.13) and (3.14), after the simple calculation, (3.9) and (3.10) can be obtained easily. We also obtain the extreme function.
By using the same methods in Theorem 3, the following results are obtained.
Theorem 4. Let h and g of the form (1.3). If f=h+¯g∈HKαsc(e), then
and
For functions of the classes defined in the paper, Fekete-Szegö inequality of which are listed below.
Theorem 5. Let f=h+¯g with h and g given by (1.3) and μ∈C.
(1) If f∈HS∗,αsc(e), then
and
(2) If f∈HKαsc(e), then
and
Proof. From the relation (3.11) and (3.12), we have
and
By (2.1), we have
and
According to Lemma 3 and Lemma 4, we can compete the proof of Theorem 5. The estimates above are sharp.
Paralleling the results of Zhu et al.[17], the corresponding results for functions of the classes defined in the paper can be obtained. For example, the estimates of distortion, growth of g and Jacobian of f and so on.
Theorem 6. Let |z|=r∈[0,1).
(1) If f=h+¯g∈HS∗,αsc(e), then
where ϕ1(r) and ϕ2(r) are given by (2.22).
Especially, let α=0, we have
(2) If f=h+¯g∈HKαsc(e), then
where ψ1(r) and ψ2(r) are given by (2.23).
Especially, let α=0, we have
Proof. According to the relation g′=ωh′, it is easy to see ω(z) satisfying |ω(0)|=|g′(0)|=|b1|=α such that ([21]):
It is easy to show
A tedious calculation gives
Applying (3.17) and (2.22), we get (3.15). Similarly, applying (3.17) and (2.23), we get (3.16). Thus we complete the proof of Theorem 6.
Using the method analogous to that in proof of Lemma 8, we can obtain the following results.
Theorem 7. Let |z|=r∈[0,1).
(1) If f=h+¯g∈HS∗,αsc(e), then
where ϕ1(ξ) and ϕ2(ξ) are given by (2.22).
Especially, let α=0, we have
(2) If f=h+¯g∈HKαsc(e), then
where ψ1(ξ) and ψ2(ξ) are given by (2.23).
Especially, let α=0, we have
Next, the Jacobian estimates and growth estimates of f are obtained.
Theorem 8. Let |z|=r∈[0,1).
(1) If f=h+¯g∈HS∗,αsc(e), then
where ϕ1(r) and ϕ2(r) are given by (2.22).
(2) If f=h+¯g∈HKαsc(e), then
where ψ1(r) and ψ2(r) are given by (2.23).
Proof. It is well known that Jacobian of f=h+¯g is
where ω satisfying g′=ωh′ with ω(0)=0 and |ω(z)|<1 for z∈U.
Let f∈HS∗,αsc(e), plugging (3.17) and (2.22) back into (3.18), we get
and
Thus this completes the proof of (1). Plugging (3.17) and (2.23) back into (3.18), (2) of Theorem 8 can be proved by the same method as employed before.
Theorem 9. Let |z|=r,0≤r<1.
(1) If f=h+¯g∈HS∗,αsc(e), then
where ϕ1(ξ) and ϕ2(ξ) are given by (2.22).
(2) If f=h+¯g∈HKαsc(e), then
where ψ1(ξ) and ψ2(ξ) are given by (2.23).
Proof. For any point z=reiθ∈U, let Ur={z∈U:|z|<r} and denote
It is easy to see that U(0,d)⊆f(Ur)⊆f(U). Thus, there is zr∈∂Ur satisfying d=|f(zr)|. Let L(t)=tf(zr) for t∈[0,1], then ℓ(t)=f−1(L(t)) is a well-defined Jordan arc. For f=h+¯g∈HS∗,αsc(β), by (2.22) and (3.17), we get
Using (2.22) and (3.17), the right side of (3.19) is obtained. The remainder of proofs is similar to that in (3.20) and so we omit.
According to (3.19) and (3.20), it follows that the covering theorems of f.
Theorem 10. Let f=h+¯g∈SH.
(1) If f∈HS∗,αsc(e), then UR1⊂f(U), where
(2) If f∈HKαsc(e), then UR2⊂f(U), where
4.
Conclusion
In this paper, with the help of the analytic part h satisfying certain conditions, we obtain the coefficients estimates of the co-analytic part g and the geometric properties of harmonic functions. Applying the methods in the paper, the geometric properties of the co-analytic part and harmonic function with the analytic part satisfying other conditions can be obtained, which can enrich the research field of univalent harmonic mapping.
Acknowledgments
This work was supported by Research Program of Science and Technology at Universities of Inner Mongolia Autonomous Region(Grant No. NJZY20198; Grant No. NJZZ19209), Natural Science Foundation of Inner Mongolia Autonomous Region of China (Grant No. 2020MS01011; Grant No. 2019MS01023; Grant No. 2018MS01026) and the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region Under Grant (Grant No. NJYT-18-A14).
Conflict of interest
The authors agree with the contents of the manuscript, and there is no conflict of interest among the authors.













 DownLoad:
DownLoad: