Surface modification of materials to encourage beneficial biofilm formation

1.   Introduction

In their celebrated paper ^[10], Brezis, Coron and Lieb showed, in the context of harmonic maps and liquid crystals theory, the existence of a close relation between sphere-valued harmonic maps having prescribed topological singularities at given points in $ \mathbb{R}^3 $ and minimal connections between those points, i.e., optimal mass transportation networks (in the sense of Monge-Kantorovich) having those points as marginals. This relation was further enlightened by Almgren, Browder and Lieb in ^[4], who recovered the results in ^[10] by interpreting the (minimal connection) optimal transportation problem as a suitable Plateau problem for rectifiable currents having the given marginals as prescribed boundary.

Our aim is to consider minimizing configurations for maps valued into manifolds and with prescribed topological singularities when the energy is possibly more general than the Dirichlet energy, and investigate the connection with Plateau problems for currents (or flat chains) with coefficients in suitable groups. The choice of these groups is linked to the topology of the involved target manifolds.

In this paper we will consider the particular case where the manifold is a product of spheres and the maps have assigned point singularities, and we will show, in Theorem 1 below, that energy minimizing configurations are related with Steiner-type optimal networks connecting the given points, i.e., solutions of the Steiner problem or solutions of the Gilbert-Steiner irrigation problem. The investigation of maps with values into product of spheres arises in several physical problems, such as the study of the structure of minimizers of two-component Ginzburg-Landau functionals, where the reference (ground state) manifold is a torus ($ \mathbb{S}^{1}\times \mathbb{S}^{1} $) (see ^[1]), or the case of Dipole-Free $ ^3 $He-A, where the order parameter takes values into $ (\mathbb{S}^{2}\times $ SO(3))$ / \mathbb{Z}_{2} $, whose covering space is $ \mathbb{S}^{2}\times \mathbb{S}^{3} $ (see ^[18,24]). In a companion paper in preparation we will discuss and state the results which correspond to more general situations. Let us also stress that the generalization of the results to a broader class of energies (and thus different norms) is not moot, this being the case, for instance, for dislocations in crystals (see ^[15]).

Steiner tree problems and Gilbert-Steiner (single sink) problems can be formulated as follows: given $ n $ distinct points $ P_{1}, \ldots, P_{n} $ in $ \mathbb{R}^{d} $, where $ d, n \geq 2 $, we are looking for an optimal connected transportation network, $ L = \cup_{i = 1}^{n-1}\lambda_i $, along which the unit masses initially located at $ P_{1}, \ldots, P_{n-1} $ are transported to the target point $ P_n $ (single sink); here $ \lambda_i $ can be seen as the path of the $ i^{\rm th} $ mass flowing from $ P_{i} $ to $ P_{n} $, and the cost of moving a mass $ m $ along a segment with length $ l $ is proportional to $ lm^{\alpha} $, $ \alpha\in[0, 1] $. Therefore, we are led to consider the problem

where the energy $ I_\alpha $ is computed as $ I_\alpha(L) = \int_L |\theta(x)|^\alpha d{\mathcal H}^1(x) $, with $ \theta(x) = \sum_{i = 1}^{n-1} \textbf{1}_{\lambda_i}(x) $. Let us notice that $ \theta $ stands for the mass density along the network. In particular, we consider the range $ \alpha\in[0, 1] $:

● when $ \alpha = 0 $ the problem is equivalent to optimize the total length of the graph $ L $, as in the Steiner Tree Problem (STP);

● when $ \alpha = 1 $ the problem $ (I) $ becomes the well-known Monge-Kantorovich problem;

● and when $ 0 < \alpha < 1 $ the problem is known as the Gilbert-Steiner problem, or, more generally, as a branched optimal transport problem, due to the fact that the cost is proportional to a concave function $ \theta^{\alpha} $, which favours the clustering of the mass during the transportation, thus giving rise to the branched structures which characterize the solutions (we refer the reader to ^[5] for an overview on the topic).

In the last decade, the communities of Calculus of Variations and Geometric Measure Theory made some efforts to study (Gilbert-)Steiner problems in many aspects, such as existence, regularity, stability and numerical feasibility (see for example ^{[6,7,8,9,13,14,20,21,23,25,26,27]} and references therein). Among all the significant results, we would like to mention recent works in ^[20,21] and ^[6,7], which are closely related to the present paper. To be more precise, in ^[20,21] the authors turn the problem $ (I) $ into the problem of mass-minimization of integral currents with multiplicities in a suitable group. For the sake of readability we postpone proper definitions about currents to Section 2, in this introduction we only recall that a $ 1 $-dimensional integral current with coefficients in a group can be thought as a formal sum of finitely many curves and countably many loops with coefficients in a given normed abelian group. For instance, considering the group $ \mathbb{Z}^{n-1} $ and assigning to the boundary datum $ P_{1}, P_{2}, \ldots, P_{n-1}, P_{n} $ the multiplicities $ e_{1}, e_{2}, \ldots, e_{n-1}, -(e_{1}+\ldots+ e_{n-1}) $, respectively (where $ \lbrace e_{i} \rbrace_{1 \leq i \leq n-1} $ is the basis of $ \mathbb{R}^{n-1} $), we recover the standard model in ^[20,21].

In fact we can interpret the network $ L = \bigcup_{i = 1}^{n-1}\lambda_i $ as the superposition of $ n-1 $ paths $ \lambda_i $ connecting $ P_{i} $ to $ P_{n} $ labelled with multiplicity $ e_{i} $. This point of view requires a density function with values in $ \mathbb{Z}^{n-1} $, which corresponds to the so-called $ 1 $-dimensional current with coefficients in the group $ \mathbb{Z}^{n-1} $. Furthermore, by equipping $ \mathbb{Z}^{n-1} $ with a certain norm (depending on the cost of the problem), we may define the notion of mass of those currents, and problem $ (I) $ turns out to be equivalent to the Plateau problem.

where $ T $ is a 1-dimensional current with coefficients in the group $ \mathbb{Z}^{n-1} $ (again, we refer the reader to the Section $ 2 $ for rigorous definitions). For mass minimization, there is the very useful notion of calibration (see section 3), that is, a tool to prove minimality when dealing with concrete configurations (see Example $ 3.2 $). To be precise, a calibration is a sufficient condition for minimality, see Definition 11 and the following remarks.

In ^[6,7], by using ^[20,21], a variational approximation of the problem $ (I) $ was provided through Modica-Mortola type energies in the planar case, and through Ginzburg-Landau type energies (see ^[3]) in higher dimensional ambient spaces via $ \Gamma $-convergence. The corresponding numerical treatment is also shown there.

Following ^[6,7,20,21], and the strategy outlined in ^[4] (relating the energy of harmonic maps with prescribed point singularities to the mass of $ 1 $-dimensional classical integral currents) we provide here a connection between an energy functional with its energy comparable with $ k $-harmonic map problem with prescribed point singularities and (Gilbert-)Steiner problems $ (I) $. More precisely, let $ P_{1}, \ldots, P_{n-1}, P_{n} $ in $ \mathbb{R}^{d} $ be given, and consider the spaces $ H_{i} $ defined as the subsets of $ W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{S}^{d-1}) $ where the functions are constant outside a neighbourhood of the segment joining $ P_i, P_n $ and have distributional Jacobian $ \frac{\alpha_{d-1}}{d}(\delta_{P_i}-\delta_{P_n}) $, respectively. Here $ \alpha_{d-1} $ is the surface area of the unit ball in $ \mathbb{R}^{d} $.

Let $ \mathbb{\psi} $ be a norm on $ \mathbb{R}^{n-1} $ which will be specified in Section $ 3 $ (see $ (3.1) $), and set

where $ {\textbf u} = (u_{1}, \ldots, u_{n-1})\in H_{1}\times H_{2} \times \ldots \times H_{n-1} $ is a $ 2 $-tensor. The functional $ \mathbb{H} $ is the so-called $ k $-harmonic energy, it is modeled on the $ (d-1) $-Dirichlet energy. We will consider here a class of energies $ \mathbb E $ for maps in $ H_{1}\times H_{2} \times \ldots \times H_{n-1} $ which are suitably related to $ \mathbb M $ and $ \mathbb H $, according to Definition 13 below. In this case, we investigate the problem of characterizing

The main contribution of this paper is the following equivalence result in the minimization problem for the mass $ \mathbb M $ and an energy $ \mathbb E $ which is suitably related to $ \mathbb M $ and $ \mathbb H $.

Theorem 1. Assume that a minimizer of the problem $ (M) $ admits a calibration (see Definition 11). Consider an energy functional $ \mathbb{E} $ which is suitably related to $ \mathbb M $ and $ \mathbb H $, in the sense of Definition 13. Then, we have

or equivalently, in view of paper ^[20,21],

Currently, we cannot evade the assumption on the existence of a calibration, because it is still not known if a calibration, or even a weak version of it, is not only sufficient but also a necessary condition for minimality (see Section 2). Nonetheless, dropping this assumption we can still state some partial result as follows.

Remark 2. (ⅰ) If $ \alpha = 1 $, $ \psi = \|\cdot \|_{1} $, $ \mathbb{E} = \frac{1}{(d-1)^{\frac{d-1}{2}}}\mathbb{H} $, then we are able to prove that $ (1.2) $ still holds true, as a variant of the main result in ^[10].

(ⅱ) In case $ 0\leq \alpha < 1 $, we obtain the following inequality

The investigation of equality in $ (1.4) $ when $ 0\leq \alpha < 1 $ is delicate and will be considered in forthcoming works.

Remark 3. We believe that the assumption of the existence of a calibration is not too restrictive. We actually conjecture that minimizing configurations for the problem $ (M) $ admit a calibration in case of uniqueness, which is somehow a generic property (see ^[11]). We carry out in Example $ 3.2 $ the construction of configurations of $ n $ points in $ \mathbb{R}^{n-1} $ with $ n-2 $ branching points which are generic in character and these configurations admit a calibration.

The organization of the paper is as follows: in Section $ 2 $, we briefly review some basic notions of Geometric Measure Theory which will be used in the paper, in Section $ 3 $ we recall (Gilbert-) Steiner problems and briefly describe their connection with Plateau's problem for currents with coefficients in a group. Finally, in Section $ 4 $ we prove the Theorem 1.

2.   Preliminaries and notations

2.1.   Rectifiable currents with coefficients in a group G

In this section, we present the notion $ 1 $-dimensional currents with coefficients in the group $ \mathbb{R}^{n-1} $ in the ambient space $ \mathbb{R}^{d} $ with $ n, d\geq 2 $. We refer to ^[22] for a more detailed exposition of the subject.

Consider $ \mathbb{R}^{n-1} $ equipped with a norm $ \psi $ and its dual norm $ \psi^{*} $. Denote by $ \Lambda_{1}(\mathbb{R}^{d}) $ the space of $ 1 $-dimensional vectors and by $ \Lambda^{1}(\mathbb{R}^{d}) $ the space of $ 1 $-dimensional covectors in $ \mathbb{R}^{d} $.

Definition 4. An $ (\mathbb{R}^{n-1})^{*} $-valued $ 1 $-covector on $ \mathbb{R}^{d} $ is a bilinear map

Let $ \lbrace e_{1}, e_{2}, \ldots, e_{n-1} \rbrace $ be an orthonormal basis of $ \mathbb{R}^{n-1} $, and let $ \lbrace e^{*}_{1}, e^{*}_{2}, \ldots, e^{*}_{n-1} \rbrace $ be its dual. Then, each $ (\mathbb{R}^{n-1})^{*} $-valued $ 1 $-covector on $ \mathbb{R}^{d} $ can be represented as $ w = w_{1} e^{*}_{1}+\ldots+w_{n-1}e^{*}_{n-1}\, , $ where $ w_{i} $ is a "classical" $ 1 $-dimensional covector in $ \mathbb{R}^{d} $ for each $ i = 1, \ldots, n-1 $. To be precise, the action of $ w $ on a pair $ (\tau, \theta)\in\Lambda_1(\mathbb{R}^d)\times \mathbb{R}^{n-1} $ can be computed as

where the scalar product on the right hand side is the standard Euclidean scalar product in $ \mathbb{R}^d $. We denote by $ \Lambda^{1}_{(\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d}) $ the space of $ (\mathbb{R}^{n-1})^{*} $-valued $ 1 $-covectors in $ \mathbb{R}^{d} $, endowed with the (comass) norm:

Similarly, we can define the notion of space $ (\mathbb{R}^{n-1}) $-valued $ 1 $-vectors in $ \mathbb{R}^{d} $, $ \Lambda_{1, (\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d}) $, endowed with pre-dual (mass) norm: for any $ v\in \Lambda_{1, (\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d}) $ we define:

Definition 5. An $ (\mathbb{R}^{n-1})^{*} $-valued $ 1 $-dimensional differential form defined on $ \mathbb{R}^{d} $ is a map

Let us remark that the regularity of $ \omega $ is inherited from the components $ \omega_{i} $, $ i = 1, \ldots, n-1 $. Let $ \varphi = (\varphi_1, \ldots, \varphi_{n-1}) $ be a function of class $ C^{1}(\mathbb{R}^d; \mathbb{R}^{n-1}) $. We denote

where $ {\rm d} \varphi_{i} $ is the differential of $ \varphi_{i} $. Thus $ {\rm d} \varphi \in C(\mathbb{R}^{d}; \Lambda^{1}_{(\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d})) $. $

Definition 6. A $ 1 $-dimensional current $ T $ with coefficients in $ (\mathbb{R}^{n-1}, \psi) $ is a linear and continuous map

Here the continuity is meant with respect to the (locally convex) topology on $ C^\infty_c(\mathbb{R}^d; \Lambda^1_{(\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^d)) $ defined in analogy with the topology on $ C^\infty_c(\mathbb{R}^d; \mathbb{R}) $ which allows the definition of distributions. The mass of $ T $ is defined as

Moreover, if $ T $ is a $ 1 $-dimensional current with coefficients in $ (\mathbb{R}^{n-1}, \psi) $, we define the boundary $ \partial T $ of $ T $ as a distribution with coefficients in $ (\mathbb{R}^{n-1}, \psi) $, $ \partial T: C^{\infty}_{c}(\mathbb{R}^{d}; (\mathbb{R}^{n-1}, \psi)) \longrightarrow \mathbb{R} $, such that

The mass of $ \partial T $ is the supremum norm

A current $ T $ is said to be normal if $ \mathbb{M}(T)+\mathbb{M}(\partial T) < \infty $. $

Definition 7. A $ 1 $-dimensional rectifiable current with coefficients in the normed (abelian) group $ (\mathbb{Z}^{n-1}, \psi) $ is a ($ 1 $-dimensional) normal current (with coefficients in $ (\mathbb{R}^{n-1}, \psi) $) such that there exists a $ 1 $-dimensional rectifiable set $ \Sigma\subset \mathbb{R}^d $, an approximate tangent vectorfield $ \tau \, : \, \Sigma \longrightarrow \Lambda_{1}(\mathbb{R}^{d}) $, and a density function $ \theta : \Sigma \longrightarrow \mathbb{Z}^{n-1} $ such that

for every $ \omega \in C^{\infty}_{c}\left(\mathbb{R}^{d}; \Lambda^{1}_{(\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d}) \right) $. We denote such a current $ T $ by the triple $ \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $. $

Remark 8. The mass of a rectifiable current $ T = \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $ with coefficients in $ (\mathbb{Z}^{n-1}, \psi) $ can be computed as

Moreover, $ \partial T: C^{\infty}_{c}(\mathbb{R}^{d}; (\mathbb{R}^{n-1}, \psi)) \longrightarrow \mathbb{R} $ is a measure and there exist $ x_{1}, \ldots, x_{m} \in \mathbb{R}^{d} $, $ p_{1}, \ldots, p_{m} \in \mathbb{Z}^{n-1} $ such that

Finally the mass of the boundary $ \mathbb{M}(\partial T) $ coincides with $ \sum_{j = 1}^{m}\psi(p_{j}) $. $

Remark 9. In the trivial case $ n = 2 $, we consider rectifiable currents with coefficients in the discrete group $ \mathbb{Z} $ and we recover the classical definition of integral currents (see, for instance, ^[16]). $

Finally, it is useful to define the components $ T $ with respect to the index $ i\in\{1, \ldots, n-1\} $: for every $ 1 $-dimensional test form $ \tilde\omega\in C^\infty_c(\mathbb{R}^d; \Lambda^1(\mathbb{R}^d)) $ we set

Notice that $ T^{i} $ is a classical integral current (with coefficients in $ \mathbb{Z} $). Roughly speaking, in some situations we are allowed to see a current with coefficients in $ \mathbb{R}^{n-1} $ through its components $ (T^{1}, \ldots, T^{n-1}) $.

For future convenience we adopt the notation

where $ S = e_{1}\delta_{P_1}+\ldots+e_{n-1}\delta_{P_{n-1}}-(e_1+e_2+\ldots+e_{n-1})\delta_{P_{n}} $ is a given boundary (and $ \lbrace e_i \rbrace_{i = 1}^n $ is the canonical basis of $ \mathbb{R}^{n-1} $).

When dealing with the Plateau problem in the setting of currents, it is important to remark a couple of critical features. For the sake of understandability, we recall them here for the particular case of $ 1 $-dimensional currents, but the matter does not depend on the dimension.

Remark 10. If a boundary $ \{P_1, \ldots, P_n\}\subset \mathbb{R}^d $ is given, then the problem of the minimization of mass is well posed in the framework of rectifiable currents and in the framework of normal currents as well. In both cases the existence of minimizers is due to a direct method and, in particular, to the closure of both classes of currents. Obviously

but whether the inequality is actually an identity is not known for currents with coefficients in groups. The same question about the occurence of a Lavrentiev gap between normal and integral currents holds for classical currents of dimension bigger than $ 1 $ and it is closely related to the problem of the decomposition of a normal current in rectifiable ones (see ^[22] for a proper overview of this issue). $

A formidable tool for proving the minimality of a certain current is to show the existence of a calibration.

Definition 11. Consider a rectifiable current $ T = \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $ with coefficients in $ \mathbb{Z}^n $, in the ambient space $ \mathbb{R}^{d} $. A smooth $ (\mathbb{R}^{n})^{*} $-valued differential form $ \omega $ in $ \mathbb{R}^{d} $ is a calibration for $ T $ if the following conditions hold:

(ⅰ) for a.e. $ x\in \Sigma $ we have that $ \langle \omega(x); \tau(x), \theta (x)\rangle = \psi (\theta(x)); $

(ⅱ) the form is closed, i.e., $ {\rm d}\omega = 0; $

(ⅲ) for every $ x\in \mathbb{R}^{d} $, for every unit vector $ t \in \mathbb{R}^{d} $ and for every $ h\in \mathbb{Z}^{n} $, we have that

It is straightforward to prove that the existence of a calibration associated to a current implies the minimality of the current itself. Indeed, with the notation in Definition 11, if $ T' = \left[\!\left[\Sigma', \tau', \theta'\right]\!\right] $ is a competitor, i.e., $ T' $ is a rectifiable current with coefficients in $ \mathbb{Z}^n $ and $ \partial T' = \partial T $, then

We stress that fact that the existence of a calibration is a sufficient condition for the minimality of a current, so it is always a wise attempt when a current is a good candidate for mass minimization. Nonetheless, it is also natural to wonder if every mass minimizing current has its own calibration and this problem can be tackled in two ways: for specific currents or classes of currents (such as holomorphic subvarieties) one has to face an extension problem with the (competing) constraints (ⅱ) and (ⅲ), since condition (ⅰ) already prescribes the behaviour of the form on the support of the current. In general, one may attempt to prove the existence of a calibration as a result of a functional argument, picking it in the dual space of normal currents, but this approach has two still unsolved problems:

● the calibration is merely an element of the dual space of normal currents, thus it is far to be smooth;

● this argument works in the space of normal currents and it is not known whether a minimizer in this class is rectifiable as well (see Remark 10).

Anyway, in this specific case of currents with coefficients in $ \mathbb{Z}^n $ which match the energy minimizing networks of a branched optimal transport problem (with a subadditive cost), we think that the Lavrentiev phenomenon cannot occur, as explained in Remark 3.

2.2.   Distributional Jacobian

We recall the definition of distributional Jacobian of a function $ u\in W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{R}^{d})\cap L^{\infty}_{\rm loc}(\mathbb{R}^{d}; \mathbb{R}^{d}) $, see also ^[2,19].

Definition 12. Let $ u $ be in $ W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{R}^{d})\cap L^{\infty}_{\rm loc}(\mathbb{R}^{d}; \mathbb{R}^{d}) $, we define the pre-jacobian $ ju \in L^1_{\rm loc}(\mathbb{R}^d; \mathbb{R}^d) $ as

where $ u_{x_j} $ is a $ L^{d-1}_{\rm loc}(\mathbb{R}^d; \mathbb{R}^d) $ representative of the partial derivative of $ u $ with respect to the $ j^{\rm th} $ direction. Thus we define the Jacobian $ Ju $ of $ u $ as $ \frac{1}{d}{\rm d}(ju) $ in the sense of distributions. More explicitly, if $ \varphi \in C^{\infty}_{c}(\mathbb{R}^{d}; \mathbb{R}) $ is a test function, then one has

The identity required in (2.3) is clearer if one notices that $ ju $ has been chosen in such a way that $ {\rm div}(\varphi\tilde u) = \nabla\varphi\cdot j\tilde u+d\varphi\det D\tilde u $ whenever $ \tilde u $ is smooth enough to allow the differential computation.

Once the singularities of the problem $ {P_1, \ldots, P_n} $ have been prescribed, we can also introduce the energy spaces $ H_{i} $, for each $ i = 1, \ldots, n-1 $. By definition a map $ u\in W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{S}^{d-1}) $ belongs to $ H_i $ if $ Ju = \frac{\alpha_{d-1}}{d}(\delta_{P_i}-\delta_{P_n}) $, and there exists a radius $ r = r(u) > 0 $ such that $ u $ is constant outside $ B(0, r(u))\ni P_{i}, P_{n} $, where $ B(0, r) $ is the open ball of radius $ r $ centered at $ 0 $.

For any $ \textbf{u}\in H_1\times \ldots \times H_{n-1} $, we define the (matrix-valued) pre-jacobian of $ \textbf{u} $ by

and its Jacobian by

We observe that $ \textbf{ju} $ is actually a $ 1 $-dimensional normal currents with coefficients in $ \mathbb{R}^{n-1} $. Moreover

Definition 13. Given $ P_1, \ldots, P_n\in \mathbb{R}^d $ and a norm $ \psi $ on $ \mathbb{R}^{n-1} $, a functional $ \mathbb{E} $ defined on $ H_{1}\times \ldots \times H_{n-1} $ is said to be suitably related to $ \mathbb{M} $ and $ \mathbb{H} $ (see (1.1) for its definition) if the following properties hold.

(i) $ \mathbb{M}(\textbf{ ju})\leq \mathbb{E}({\textbf u}) $, where $ \textbf{ ju} $ is the normal current defined by the pre-jacobian.

(ii) If there exist an open set $ U\subset \mathbb{R}^d $ and a subset $ I $ of the set of labels $ {1, \ldots, n-1} $ such that $ u_i = u_l $ for every pair $ i, l\in I $ and $ u_i = 0 $ otherwise, we have

where $ \mathcal{X}_U $ is the characteristic function of $ U $.

(iii) When $ k = 1 $, the functional $ \mathbb{E} $ coincides with the harmonic energy considered in ^[10].

Let us point out that requirement (ii) is taylored on the dipole construction maps $ {\textbf u} = (u_{1}, \ldots, u_{n-1}) $ in the Step $ 1 $ of the proof of Theorem 1.

We consider the following problem:

As indicated in the introduction, the inspiration for considering the problem $ (H) $ and comparing it with the irrigation problem $ (I) $ is coming from the works ^[20,21] and ^[4]. More precisely, ^[20,21] provided a new framework for the problem $ (I) $ by proving it to be equivalent to the problem of mass-minimizing currents with coefficients in the group $ \mathbb{Z}^{n-1} $ with a suitable norm. The point is to look at each irrigation network $ L = \bigcup_{i = 1}^{n-1}\lambda_i $ encoded in the current $ T = (T^{1}, \ldots, T^{n-1}) $ where $ T^{i} $ is a classical current supported by $ \lambda_{i} $, and the irrigation cost of $ L $ is the mass of the current $ T $. Then, combining this point of view with ^[4] (see also ^[10]), where the energy of harmonic maps with prescribed point singularities was related to $ 1 $-dimensional classical currents, we are led to investigate the problem $ (H) $ in connection with problem $ (I) $.

Before moving to the next section, we provide a candidate for the functional $ \mathbb{E} $ satisfying the properties in Definition 13. Let $ \textbf{u} = (u_1, \ldots, u_{n-1}) \in H_1\times \ldots \times H_{n-1} $. Let $ e_1, \ldots, e_{n-1} $ be the canonical basis of $ \mathbb{R}^{n-1} $, and let $ I $ be a subset of $ \lbrace 1, \ldots, n-1 \rbrace $, then we denote by $ e_{I} $ the sum $ \sum_{i\in I}e_{i} $. We define the energy density $ \textbf{e}(\textbf{u}) $ at a point $ x\in \mathbb{R}^d $ as

To be precise, here the matrix $ \textbf{ju} (x) $ is decomposed according to a partition $ {\mathcal I} $ of the set $ \{1, \ldots, n-1\} $ in such a way that $ ju_i(x) = ju_l(x) $ for every pair $ i, l\in I $.

As an example, take $ {\textbf u} = (u_1, u_2)\in H_1\times H_2 $ for some choice of the points $ P_1, P_2, P_3\in \mathbb{R}^d $. Then, at some point $ x\in \mathbb{R}^d $, either $ ju_1(x)\neq ju_2(x) $ or $ ju_1(x) = ju_2(x) $.

● If $ ju_1(x)\neq ju_2(x) $, then the unique decomposition that we are allowing is $ {\textbf j}({\textbf u})(x) = ju_1(x)e_1+ju_2(x)e_2 $ and $ \textbf{e}(\textbf{u})(x) = c_d(|\nabla u_1(x)|^{d-1}+|\nabla u_2(x)|^{d-1}) $, where we abbreviated $ c_d = (d-1)^{-\frac{d-1}{2}} $.

● If $ ju_1(x) = ju_2(x) $, then, thanks to the subadditivity of $ \|\cdot\|_\alpha $, the most convenient decomposition is $ {\textbf j}({\textbf u})(x) = ju_1(x)(e_1+e_2) $ and $ \textbf{e}(\textbf{u})(x) = c_d\|e_1+e_2\|_\alpha|\nabla u_1(x)|^{d-1} $.

Finally, we consider the functional

Proposition 14. Let $ \psi $ be the norm defined as

Let $ \mathbb{E} $ be the functional defined above, in (2.9). If $ \alpha = 1 $, i.e., $ \psi = \|\cdot \|_{1} $, we choose $ \mathbb{E} = \frac{1}{(d-1)^{\frac{d-1}{2}}}\mathbb{H} $. Then $ \mathbb{E} $ is suitably related to $ \mathbb{M} $ and $ \mathbb{H} $ in the sense of Definition 13.

Proof. We start with property (i). Let $ \omega \in C^{\infty}_{c}\left(\mathbb{R}^{d}; \Lambda^{1}_{(\mathbb{R}^{n-1}, \psi)}(\mathbb{R}^{d})\right) $ be a test form with comass norm $ \sup_{x\in \mathbb{R}^d} |\omega \, |_{c, \psi} \leq 1 $. By using the very definition of $ |\cdot |_{m, \psi} $, see (2.1), we obtain

On the other hand, as already observed, for a.e. $ x\in \mathbb{R}^d $ we have

Observe that for any $ v\in H_{l} $, $ l = 1, \ldots, n-1 $, one has for a.e. $ x\in \mathbb{R}^d $

see also [10,Page 64], [4,A.1.3]. Therefore, we obtain that for a.e. $ x\in \mathbb{R}^d $

This in turn implies that

So, by the arbitrariness of $ \omega $, we conclude that

Concerning property (ii), assume that, in some open set $ U $, each $ u_{i} $ is equal to either $ 0 $ or a given function $ v\in W^{1, d-1}_{\rm loc}(\mathbb{R}^d, \mathbb{S}^{d-1}) $, thus in $ U $ the jacobian $ \textbf{ju} $ can be written as $ \textbf{ju} = jv {e}_{I} $, for some $ I\subset \lbrace 1, \ldots, n \rbrace $. This implies that

for a.e. $ x $ in the dipole, so we can conclude that

Finally, if $ k = 1 $ (i.e., we have just one component $ \textbf{u} = u $), it is obvious that

To conclude the proof, we observe that, in case $ \alpha = 1 $, that is, $ \psi = \| \cdot \|_{1} $, $ \mathbb{E} = \frac{1}{(d-1)^{\frac{d-1}{2}}}\mathbb{H} $ and this functional obviously satisfies the three properties.

3.   (Gilbert-)Steiner problems and currents with coefficients in a group

Let us briefly recall the Gilbert-Steiner problem and the Steiner tree problem and see how it can be turned into a mass-minimization problem for integral currents in a suitable group.

Let $ n $ distinct points $ P_{1}, \ldots, P_{n} $ in $ \mathbb{R}^{d} $ be given. Denote by $ G(A) $ the set of all acyclic graphs $ L = \bigcup_{i = 1}^{n-1}\lambda_i $, along which the unit masses located at $ P_{1}, \ldots, P_{n-1} $ are transported to the target point $ P_n $ (single sink). Here $ \lambda_i $ is a simple rectifiable curve and represents the path of the mass at $ P_{i} $ flowing from $ P_{i} $ to $ P_{n} $. In ^[20,21], the occurrence of cycles in minimizers is ruled out, thus the problem $ (I) $ is proved to be equivalent to

where $ \theta $ is the mass density along the network $ L $. Moreover, in ^[20,21] the problem $ (I) $ can be turned into a mass-minimization problem for integral currents with coefficients in the group $ \mathbb{Z}^{n-1} $: the idea is to label differently the masses located at $ P_{1}, P_{2} \ldots, P_{n-1} $ (source points) and to associate the source points $ P_{1}, \ldots, P_{n-1} $ to the single sink $ P_{n} $. Formally, we produce a $ 0 $-dimensional rectifiable current (a.k.a. a measure) with coefficients in $ \mathbb{Z}^{n-1} $, given by the difference between

We recall that $ \lbrace e_{1}, e_{2}, \ldots, e_{n} \rbrace $ is the canonical basis of $ \mathbb{R}^{n-1} $. The measures $ \mu^{-}, \mu^{+} $ are the marginals of the problem $ (I) $. To any acyclic graph $ L = \bigcup_{i = 1}^{n-1}\lambda_i $ we associate a current $ T $ with coefficients in the group $ \mathbb{Z}^{n-1} $ as follows: to each $ \lambda_{i} $ associate the current $ T_{i} = \left[\!\left[\lambda_{i}, \tau_{i}, e_{i}\right]\!\right] $, where $ \tau_{i} $ is the tangent vector of $ \lambda_{i} $. We associate to the graph $ L = \bigcup_{i = 1}^{n-1}\lambda_i $ the current $ T = (T_{1}, \ldots, T_{n-1}) $ with coefficients in $ \mathbb{Z}^{n-1} $. By construction we obtain

Choosing the norm $ \psi $ on $ \mathbb{Z}^{n-1} $ as

in view of Remark 8, the problem $ (I) $ is equivalent to

We refer the reader to ^[20,21] for more details. From now on we restrict our attention to the coefficients group $ (\mathbb{Z}^{n-1}, ||\cdot||_{\alpha}) $, $ 0\leq \alpha \leq 1 $.

Remark 15. Let $ \textbf{u} = (u_1, \ldots, u_{n-1})\in H_1\times \ldots \times H_{n-1} $. One has

We remark that turning the problem $ (I) $ into a mass-minimization problem allows to rely on the (dual) notion of calibration, which is a useful tool to prove minimality, especially when dealing with concrete configurations. We also recall that the existence of a calibration (see Definition 11) associated with a current $ T $ implies that $ T $ is a mass-minimizing current for the boundary $ \partial T $.

Example 16. Let us consider an irrigation problem with $ \alpha = \frac{1}{2} $. We will consider a minimal network joining $ n+1 $ points in $ \mathbb{R}^{n} $, the construction of the network is explained below. Let us stress that in this example the coincidence of the dimension of the ambient space with the dimension of the space of coefficients is needed.

Adopting the point of view of ^[17], we propose a calibration first, and only a posteriori we construct a current which fulfills the requirement (i) in Definition 11. We briefly remind that the problem $ (I) $ can be seen as the mass-minimization problem for currents with coefficients in $ \mathbb{Z}^{n} $ with the norm $ \Vert \cdot \Vert_{\frac{1}{2}} $.

Let $ \{{\rm d}x_1, \ldots, {\rm d}x_n\} $ be the (dual) basis of covectors of $ \mathbb{R}^n = {\rm span}(e_1, \ldots, e_n) $. We now prove that the differential form

satisfies conditions (ⅱ) and (ⅲ) in Definition 11. Obviously $ {\rm d}\omega = 0 $. Moreover, let $ \tau = (\tau_{1}, \tau_{2}, \ldots, \tau_{n})\in \mathbb{R}^{n} $ be a unit vector (with respect to the Euclidean norm). Thus, for our choice of the norm $ \psi = \|\cdot\|_{\frac 12} $ we can compute $ \Vert \langle \omega; \tau, \cdot \rangle \Vert^{\frac{1}{2}} = (\tau_{1}^{2}+\tau_{2}^{2}+\tau_{3}^{2}+\ldots+\tau_{n}^{2})^{\frac{1}{2}} = 1 $.

We will build now a configuration of $ n+1 $ points $ P_{1}, P_{2}, \ldots, P_{n+1} $ in $ \mathbb{R}^{n} $ calibrated by $ \omega $. Notice that the network has $ n-1 $ branching points and is somehow generic in character. More precisely, our strategy in building such a configuration is to choose end points, and branching points following the directions parallel to $ e_{1}, e_{2}, e_{3}, \ldots, e_{n}, e_{1}+e_{2}, e_{1}+e_{2}+e_{3}, \ldots, e_{1}+e_{2}+\ldots+e_{n-1}, e_{1}+e_{2}+\ldots+e_{n} $. We illustrate the construction in $ \mathbb{R}^{3}, \mathbb{R}^{4} $. This process can be extended to any dimension.

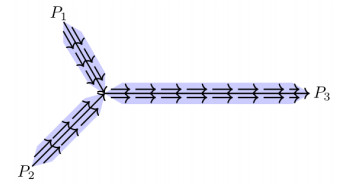
● In $ \mathbb{R}^{3} $, let us consider $ P_{1} = (-1, 0, 0) $, $ P_{2} = (0, -1, 0) $, $ P_{3} = (1, 1, -1) $, $ P_{4} = (2, 2, 1) $, as in Figure 1. Take, as branching points, $ G_{1} = (0, 0, 0) $, $ G_{2} = (1, 1, 0) $. Now consider the current $ T = \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $ with support $ \Sigma $ obtained by the union of the segments $ \overline{P_1G_1}, \overline{P_2G_1}, \overline{G_1G_2}, \overline{P_3G_2}, \overline{G_2P_4} $.

The multiplicity $ \theta $ is set as

We observe that $ T $ is calibrated by $ \omega $, thus $ T $ is a minimal network for the irrigation problem with sources $ P_1, P_2 $ and $ P_3 $ and sink $ P_4 $. Notice that edges of the network meet at the branching points with the $ 90 $ degrees angles, as known for branched optimal structures with cost determined by $ \alpha = 1/2 $.

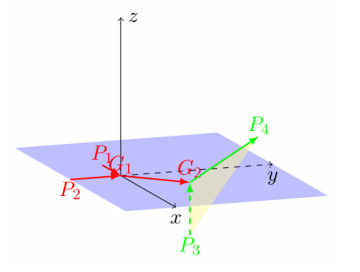
● In $ \mathbb{R}^{4} $, we keep points $ P_{1} = (-1, 0, 0, 0) $, $ P_{2} = (0, -1, 0, 0) $, $ P_{3} = (1, 1, -1, 0) $ and, in general, the whole network of the example above as embedded in $ \mathbb{R}^{4} $. We relabel $ G_{3}: = (2, 2, 1, 0) $. We now pick $ P_{4} $ and $ P_{5} $ in such a way that $ \overrightarrow{P_4G_{3}} = e_{4} $ and $ \overrightarrow{G_{3}P_{5}} = e_{1}+e_{2}+e_{3}+e_{4} $. For instance, we choose $ P_{4} = (2, 2, 1, -1) $ and $ P_{5} = (3, 3, 2, 1) $. As before, the marginals of the irrigation problem are $ P_1, P_2, P_3, P_4 $ as sources and $ P_5 $ as sink, while $ G_1, G_2, G_3 $ are branching points.

Let us now consider the current $ T = \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $ supported on the union of segments $ \overline{P_1, G_1}, \overline{P_2G_1}, \overline{G_1G_2}, \overline{P_3G_2}, \overline{G_2G_3}, \overline{P_4G_3}, \overline{G_3P_5} $ and multiplicity $ \theta $ given by

It is easy to check that the orientation of each segment coincides with the multiplicity, therefore $ T $ is calibrated by $ \omega $.

● This procedure can be replicated to construct a configuration of $ n+1 $ points $ P_{1}, P_{2}, \ldots, P_{n+1} $ in $ \mathbb{R}^{n} $ calibrated by $ \omega $, always in the case $ \alpha = 1/2 $.

Example 17. We now consider a Steiner tree problem. As in the previous example, we aim to construct calibrated configurations joining $ n+1 $ points in $ \mathbb{R}^{n} $ (with $ n-1 $ branching points). Consider the following differential form:

It is easy to check that the differential form $ \omega $ is a calibration only among those currents having multiplicities $ e_{1}, e_{2}, e_{3}, \ldots, e_{n}, e_{1}+e_{2}, e_{1}+e_{2}+e_{3}, \ldots, e_{1}+e_{2}+\ldots+e_{n-1}, e_{1}+e_{2}+\ldots+e_{n} $ and hence it will allow to prove the minimality of configurations in the class of currents with those multiplicities (cf.^[12] for the notion calibrations in families). Nevertheless, it is enough to prove the minimality of global minimizers in some configurations.

● Consider $ n = 3 $ and $ P_{1} = \left(\frac{-1}{2}, \frac{\sqrt{3}}{2}, 0\right) $, $ P_{2} = \left(\frac{-1}{2}, \frac{-\sqrt{3}}{2}, 0\right) $, $ P_{3} = \left(\frac{\sqrt{6}}{2}-\frac{1}{2}, 0, \frac{\sqrt{3}}{2}\right) $, $ P_{4} = \left(\frac{\sqrt{6}}{2}-\frac{1}{2}, 0, -\frac{\sqrt{3}}{2}\right) $ (see also the example in [7,Section $ 3 $]). Indeed, we observe that the lengths $ |\overline{P_{1}P_{2}}| = |\overline{P_{1}P_{3}}| = |\overline{P_{1}P_{4}}| = |\overline{P_{2}P_{3}}| = |\overline{P_{2}P_{4}}| = |\overline{P_{3}P_{4}}| = \sqrt{3} $, meaning that the convex envelope of points $ P_{1}, P_{2}, P_{3}, P_{4} $ is a tetrahedron: this observation allows us to restrict our investigation among all currents having multiplicities $ e_{1}, e_{2}, e_{3}, e_{1}+e_{2}, e_{1}+e_{2}+e_{3} $. More precisely, given any $ 1 $-dimensional integral current $ T $ with $ \partial T = (e_{1}+e_{2}+e_{3})\delta_{P_{4}}-e_{1}\delta_{P_{1}}-e_{2}\delta_{P_{2}}-\ldots -e_{3}\delta_{P_{3}} $ whose support is an acyclic graph with two additional Steiner points, we can always construct a corresponding current $ L $ with multiplicities $ e_{1}, e_{2} $, $ e_{1}+e_{2} $, $ e_{1}+e_{2}+e_{3} $ having the same boundary with $ T $ such that $ \mathbb{M}(T) = \mathbb{M}(L) $ thanks to the symmetric configuration $ P_{1}, P_{2}, P_{3}, P_{4} $ combined with the fact that any minimal configuration cannot have less than two Steiner points. Indeed, by contradiction, if a minimal configuration for the vertices of a tetrahedron had $ 1 $ Steiner point, then this configuration would violate the well-known property of the $ 120 $ degrees angles at Steiner points. Therefore, $ \omega $ calibrates the current $ T = \left[\!\left[\Sigma, \tau, \theta\right]\!\right] $, where $ S_{1} = (0, 0, 0), S_{2} = \left(\frac{\sqrt{6}}{2}-1, 0, 0\right) $ are the Steiner points, $ \Sigma = \overline{P_{1}S_{1}}\cup \overline{P_{2}S_{1}} \cup \overline{S_{1}S_{2}} \cup \overline{P_{3}S_{2}} \cup \overline{S_{2}P_{4}} $ and the multiplicity is given by

● Using the same strategy of Example 3.2, we can build a configuration $ P_{1}, P_{2}, P_{3}, P_{4}, P_{5} $ in $ \mathbb{R}^{4} $ starting from the points $ P_{1}, P_{2}, P_{3}, P_{4} $ above, in such a way that the new configuration is calibrated by $ \omega $ among all currents with multiplicities $ e_{1}, e_{2}, e_{3}, e_{4}, e_{1}+e_{2}, e_{1}+e_{2}+e_{3}, e_{1}+e_{2}+e_{3}+e_{4} $. This construction can be extended to any dimension.

4.   Proof of the main results

The proof of Theorem 1 is much in the spirit of the dipole construction of ^[4,10] (in the version of ^[2]), the properties of the functional $ \mathbb{E} $, and making use of the existence of calibration.

Proof. Let $ \mathbb{E} $ be the functional which fulfills the requirements of Definition 13. In the first steps we prove the inequality

We briefly recall the dipole construction (see, for instance, [10,Theorem 3.1,Theorem 8.1]). Given a segment $ \overline{AB}\subset \mathbb{R}^d $ and a pair of parameters $ \beta, \gamma > 0 $, we define

to be a pencil-shaped neighbourhood with core $ \overline{AB} $ and parameters $ \beta, \gamma $. For any fixed $ \varepsilon > 0 $, the dipole construction produces a function $ u\in W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{S}^{d-1}) $ with the following properties:

● $ u\equiv (0, \ldots, 0, 1) $ in $ \mathbb{R}^d\setminus U $;

● $ Ju = \frac{\alpha_{d-1}}{d}(\delta_{A}-\delta_{B}) $;

● moreover the map $ u $ satisfies the following inequality

Step 1. Let $ L = \bigcup_{i = 1}^{n-1}\lambda_i $ be an acyclic connected polyhedral graph, and $ T $ be the associated current with coefficients in $ \mathbb{Z}^{n-1} $ corresponding to $ L $. Since $ L $ is polyhedral, it can also be written as $ L = \bigcup_{j = 1}^{k} I_{j} $, where $ I_j $ are weighted segments. For each segment $ I_{j} $ we can find parameters $ \delta_j, \gamma_j > 0 $ such that the pencil-shaped neighbourhood $ U_j = \left\{ x \in \mathbb{R}^d:\, \text{dist}(x, I_{j}) \leq \min \left\{ \beta_{j}, \gamma_j\text{dist}(x, \partial I_{j}) \right\} \right\} $ (modelled after (4.1), see also Figure 2) is essentially disjoint from $ U_\ell $ for every $ \ell\neq j $. Then, for every $ i = 1, \ldots, n-1 $, let $ V_{i} = \bigcup_{j\in K_i} U_j $ be a sharp covering of the path $ \lambda_{i} $. To be precise, we choose $ K_i\subset\{1, \ldots, k\} $ such that $ V_i\cap U_\ell $ is at most an endpoint of the segment $ I_\ell $, if $ \ell\notin K_i $.

For each path $ \lambda_i $, $ i = 1, \ldots, n-1 $, we build the map $ u_{i}\in H_{i} $ in such a way that it coincides with a dipole associated to the segment $ I_j $ in the neighbourhood $ U_j $ for each $ j\in K_i $. We put $ u_i\equiv (0, \ldots, 0, 1) $ in $ \mathbb{R}^d\setminus V_i $.

We obtain that $ u_{i}\in W^{1, d-1}_{\rm loc}(\mathbb{R}^{d}; \mathbb{S}^{d-1}) $ and satisfies $ Ju_{i} = \frac{\alpha_{d-1}}{d}(\delta_{P_{i}}-\delta_{P_{n}}) $. Moreover, summing up inequality (4.2) repeated for each segment $ I_j $ with $ j\in K_i $, the following inequality holds

where $ T_{i} $ is the (classical) integral current corresponding to the $ i^{\rm th} $ component of $ T $.

In particular, let us stress that the maps $ u_1, \ldots, u_{n-1} $ have the following further property: if some paths $ \lambda_{i_1}, \lambda_{i_2}, \ldots, \lambda_{i_m} $ have a common segment $ I_j $ for some $ j\in K_{i_1}\cap K_{i_2}\cap\ldots\cap K_{i_m} $, then $ u_{i_1}, \ldots, u_{i_m} $ agree in $ U_j $. Furthermore, setting $ h_{i_{1}, i_{2}, \ldots, i_{m}} = (0, \ldots, |\nabla u_{i_{1}}|^{d-1}, \ldots, |\nabla u_{i_{m}}|^{d-1}, \ldots, 0) $, we obtain

where $ h_{i_{1}, i_{2}, \ldots, i_{m}} = (0, \ldots, |\nabla u_{i_{1}}|^{d-1}, \ldots, |\nabla u_{i_{m}}|^{d-1}, \ldots, 0) $. This holds for every $ \alpha\in[0, 1] $.

Combining all the previous observations, we can conclude that, given any $ \tilde \varepsilon > 0 $, there exist $ u_{i}\in H_{i} $, $ i = 1, \ldots, n-1 $ such that

where $ \theta(x) = \sum_{i = 1}^{n-1} \textbf{1}_{\lambda_i}(x) $. Thus, by the properties of $ \mathbb{E} $, one obtain that

Step 2. Considering an arbitrary acyclic graph $ L = \bigcup_{i = 1}^{n-1}\lambda_i $, there is a sequence of acyclic polyhedral graphs $ \left(L_{m} \right)_{m\ge 1} $, $ L_{m} = \bigcup_{i = 1}^{n-1}\lambda^{m}_i $ such that the Hausdorff distance $ d_{H}(\lambda^m_i, \lambda_i) \leq \frac{1}{m} $, moreover (see [6,Lemma $ 3.10 $]) denoting by $ T $ and $ T_{m} $ the associated currents with coefficients in $ \mathbb{Z}^{n-1} $ we also have that

here $ \theta_{m}(x) = \sum_{i = 1}^{n-1} \textbf{1}_{\lambda_i^{m}}(x) $. On the other hand, by previous construction there exists a sequence $ \lbrace {\textbf u}_{m} \rbrace_{m} $, $ {\textbf u}_{m} = (u_{1, m}, \ldots, u_{n-1, m})\in H_{1}\times \ldots \times H_{n-1} $ such that

This implies that

On the other hand, by the properties $ (i) $ of Definition 13, we also have that for any $ \textbf{u} = (u_1, \ldots, u_{n-1})\in H_{1}\times \ldots \times H_{n-1} $

(see Remark 15 to see why the constant $ \alpha_{d-1} $ appears in front of $ \inf \mathbb{N} $ and also see $ (2.2) $ for the definition of $ \inf \mathbb{N} $). This allows us to conclude that

Therefore we obtain the following inequality:

By assumption, a minimizer of the problem $ (M) $ admits a calibration, we have

this also means that

which is the sought conclusion.

Remark 18. In the proof of Theorem 1, step 3, we must assume the existence of a calibration $ \omega $. Observe that, without this assumption, we still can deduce from that

where $ \inf{\mathbb{N}} $ is the infimum of the problem obtained measuring the mass among $ 1 $-dimensional normal currents with coefficients in $ \mathbb{R}^{n-1} $ (see (2.2)).

Moreover, in case $ \alpha = 1 $, $ \psi = \| \cdot \|_{1} $, $ \mathbb{E} = \mathbb{H} $. First, $ (I) $ turns out to coincide with the Monge-Kantorovich problem. Then,

To see this is to use the results of Brezis-Coron-Lieb ^[10] separately for each map $ u_{i} $, $ i = 1, \ldots, n-1 $, for the energy

where, again, $ {\textbf u} = (u_{1}, \ldots, u_{n-1})\in H_{1}\times \ldots \times H_{n-1} $. The investigation of equality cases in $ (4.10) $, when $ 0\leq \alpha < 1 $, will be considered in forthcoming works.

Acknowledgements

The authors are partially supported by GNAMPA-INdAM. The research of the third author has been supported by European Union's Horizon 2020 programme through project 752018 and by STARS@unipd project "QuASAR – Questions About Structure And Regularity of currents" (MASS_STARS_MUR22_01).

The authors wish to warmly thank Giacomo Canevari for extremely fruitful and enlightening discussions.

Conflict of interest

The authors declare no conflict of interest.