1.
Introduction
The study of predator-prey systems is increasingly becoming an important topic in biology and mathematics because it helps us to better understand the connections between populations. Turing pointed out in 1952 that stable homogeneous states in reaction-diffusion systems can destabilize under certain conditions and spontaneously generate a wide variety of ordered and disordered patterns [1]. Populations do not remain in a fixed space for a variety of reasons, so it is relevant to introduce diffusion into the predator-prey systems. Many scholars have begun to study the effect of diffusion terms on system patterns (see [2,3,4,5,6]).
Among many ecological systems, the Leslie-Gower system has the following form
where v and u denote the densities of predators and prey, respectively; Q(u) denotes the functional response; K stands for the environmental capacity; h measures the translation of prey food quality into predator birth rates; and s and r represent the intrinsic growth rate of predator and prey populations, respectively. This system has been studied by many researchers, such as the simplified Holling IV Q(u)=αuu2+b [7]. Meanwhile, the generalized Holling IV functional response can describe an ecological phenomenon: When the density of the prey population exceeds a critical value, the group defense capability of the prey population can increase, which not only does not promote the increase of the predator population, but also inhibits its increase [8,9]. Thus, we use the generalized Holling IV functional response function Q(u)=αuu2+cu+b to describe the interaction between predators and prey, where α, c, b are biologically meaningful positive numbers.
At the same time, according to experiments [10], it is known that the fear effect in prey cannot be ignored. The fear effect can have an important impact on the dynamical behavior of the system (see [11,12,13,14,15]). Also the harvesting of predators is often of great practical importance (see [16,17]). Thus, we can continue to add these factors to the system (1.1), and a new system can be represented as follows
where a, q, m(0<m<1), and E are biologically meaningful positive numbers. Due to the inevitability of the diffusion effect, by adding the diffusion to the system (1.2), we can obtain the system (1.3)
where Δ indicates the Laplacian operator, and d1 and d2 represent the diffusion rates of the prey and predators, respectively.
For simplicity, by taking the following transformations:
One can attain a new diffusive predator-prey system as follows
where Ω⊂RN(N≥1) denotes a smooth bounded domain and ∂Ω is its boundary; n and ∂n denote outward unit normal vector and directional derivative, respectively; and u0(x) and v0(x) stand for non-negative smooth initial conditions.
Its ODE system is as follows:
whose dynamic behaviors have been studied by us [18]. It is obvious that the positive equilibrium points of the system (1.5) are the intersection of two intersecting curves 1−u1+kv−vu2+du+e=0 and the straight line δ(β−vu)=λ in the first quadrant. That is, they are the positive roots of the following cubic equation:
Let Γ=p2−4qr, q=m2−3n, p=mn+9e, r=n2+3em, where m=(β−λδ)2k+d−1, n=β−λδ−d+e.
The conditions for the number of positive equilibrium points have been obtained in detail in [18], so they are not given here, but they are the basis for subsequent numerical simulations in this paper.
The Jacobi matrix of the system (1.5) at the internal equilibrium point is not difficult to obtain
It is easy to find that the equilibrium point E∗5 is always a saddle for the reason that Det(JE∗5)<0. However, Det(JE∗i)>0 at the other equilibrium point E∗i. Therefore, the equilibrium point E∗i is locally asymptotically stable if the condition a11+a22<0 is satisfied, where
and F(u,v)=u(1−u)1+kv−uvu2+du+e, G(u,v)=δv(β−vu)−λv.
The framework of the article is organized as follows. In Section 2, the boundedness and existence conditions for solutions of the system (1.4) are given. Then, we analyze the existence and non-existence of non-constant steady states of the elliptic system corresponding to the system (1.4) in Section 3, which facilitates the determination of the existence of Turing patterns. In Section 4, we give the conditions for Turing instability and the amplitude equations at the neighborhood of the threshold of Turing instability. The existence and direction of the Hopf bifurcation are explored in Section 5. Finally, numerical simulations and short conclusions are presented in Sections 6 and 7, respectively.
2.
Boundedness and existence of solutions
In this section, the existence and boundedness conditions for solutions of the system (1.4) will be given.
Theorem 2.1. Suppose that k,d,e,δ,β,λ,u0(x)≥0,v0(x)≥0, and d1>0,d2>0 in Ω⊂RN(N≥1), then solutions of the system (1.4) are unique and positive, i.e., u>0 and v>0 for (u,v)∈Λ,t≥0 and x∈ˉΩ, where Λ={(u,v):k(1−u)(u2+du+e)+(1+kv)2≥0}. Also, if kc2+c−e<0 holds, where c=β−λδ, we have
(i) limt→∞supmaxx∈ˉΩu(⋅,t)≤1, limt→∞supmaxx∈ˉΩv(⋅,t)≤c,
(ii) limt→∞infminx∈ˉΩu(⋅,t)≥1−ce(1+kc), limt→∞infminx∈ˉΩv(⋅,t)≥c[1−ce(1+kc)].
Proof. Let (ˉu,ˉv)=(˜u(t),˜v(t)) and (u_,v_)=(0,0), where (˜u(t),˜v(t)) is the unique solution to the following system
Then
and
This shows that (ˉu,ˉv)=(˜u(t),˜v(t)) and (u_,v_)=(0,0) are the upper and lower solutions of the system (1.4), respectively. Furthermore, we have 0≤u0(x)≤˜u and 0≤v0(x)≤˜v. By a simple calculation, we can easily find Fv(u,v)=−uk(1−u)(u2+du+e)+(1+kv)2(1+kv)2(u2+du+e)≤0, Gu(u,v)=δv2u2 for (u,v)∈Λ, where Λ is written as Λ={(u,v):k(1−u)(u2+du+e)+(1+kv)2≥0}. By the well-known conclusion in [19], we find that the system (1.4) is a mixed quasi-monotone system, which owns a globally defined unique solution (u,v) that satisfies 0≤u(x,t)≤˜u(t) and 0≤v(x,t)≤˜v(t). Furthermore, we have u(x,t)>0 and v(x,t)>0 for t≥0 and x∈ˉΩ by the strong maximum principle.
Next, we begin to explore the boundedness of the solutions u(x,t) and v(x,t). We find that (i) is easily obtained by comparison principle. However, (ii) is the one that needs to be worked out. Observing the first equation of the system (1.4), we have
where c=β−λδ. Using the comparison principle again, there exists T1>0 and ε1>0 such that u(x,t)≥1−ce(1+kc)+ε1 holds for t>T1 and x∈ˉΩ. Similarly, we still have
where c=β−λδ. Thus, the comparison principle helps us to obtain that there exists T2>0 and ε2>0 such that v(x,t)≥c[1−ce(1+kc)+ε1]+ε2 holds for t>T2 and x∈ˉΩ. By the arbitrariness of ε1 and ε2, we complete the proof.□
3.
Non-existence and existence of non-constant steady states
In this section, we will focus on the elliptic equations of the system (1.4):
Next, the conditions for the existence and non-existence of the steady states of the system (3.1) will be given.
3.1. A priori estimates
Theorem 3.1. Assume that k,d,e,δ,β,λ,d1,d2>0 and λ>−δ(−1+√1+4ke2k−β) holds, we have
1−ce(1+kc)≤u(x)≤1, c[1−ce(1+kc)]≤v(x)≤c, where c=β−λδ.
Proof. Let (u(x),v(x)) be a non-negative solution of the system (3.1), and
By maximum principle [20], the system (3.1) follows
and
Thus, we obtain a set of upper bounds for u,v
Similarly, using maximum principle again, we can derive
and
The above two inequalities indicate that
Next, we would like to explore whether an unrestricted positive lower bound exists in the priori estimates for positive solutions.
Theorem 3.2. Let ˇd be a given positive constant; then, there exists a positive constant ˆC, which depends on k,d,e,δ,β,λ,ˇd, such that the solution (u,v) of the system (3.1) for d1,d2≥ˇd satisfies
Proof. It is clear that 0<u(x)≤1,0<v(x)≤β−λδ with the help of the maximum principle.
Denote
We have
Then
where c=β−λδ and D1 is a positive constant.
Define
then, u satisfies the condition
Using Harnack inequality [21], it can be easily pointed out that
where D∗ depends on |z|∞.
Therefore, we can get
which means u(x1)≥ˆC.
Furthermore,
which means v(y1)≥ˆC(β−λδ).□
Next, we will prove the non-existence of non-constant steady states of the system (3.1). We assume that all eigenvalues of the operator −Δ with zero-flux boundary conditions in Ω are 0=μ0<μ1≤μ2≤⋯≤μj<∞ and limj→∞μj=∞.
3.2. The non-existence
Now, we set ˉu=1|Ω|∫Ωu(x)dx,ˉv=1|Ω|∫Ωv(x)dx, where (u(x),v(x)) is a solution of the system (3.1), and if ϕ=u−ˉu,ψ=v−ˉv, then we have ∫Ωϕdx=∫Ωψdx=0. Thus, we have Theorems 3.3 and 3.4.
Theorem 3.3. Assume λ>−δ(−1+√1+4ke2k−β), for ϕ and ψ, the following inequalities hold
(i) ∫Ωϕ2dx+∫Ω|▽ϕ|2dx≤(1+μ1)e2|Ω|16d21(1+kc)2(e−kc2)2μ21,
(ii) ∫Ωψ2dx+∫Ω|▽ψ|2dx≤(1+μ1)δ2c4|Ω|d22μ21,
where μ1 denotes the first positive eigenvalue of the operator −Δ and c=β−λδ.
Proof. Using the first equation of the system (3.1) and Cauchy-Schwarz inequality, there holds
and
Through Poincaré's inequality, we have
This means
Again with the help of Poincaré's inequality, we have
∫Ωϕ2dx+∫Ω|▽ϕ|2dx≤(1+μ1)e2|Ω|16d21(1+kc)2(e−kc2)2μ21,
∫Ωψ2dx+∫Ω|▽ψ|2dx≤(1+μ1)δ2c4|Ω|d22μ21.□
Theorem 3.4. Assume that k,d,e,δ,β,λ,d1,d2>0, then the system (3.1) has no non-constant steady states if d1>¯d1,d2>¯d2, where
Proof. Multiplying the first equation for the system (3.1) by ϕ and integrating it by parts
where W1:=∫Ωϕu(1−u)1+kvdx,W2:=−∫Ωϕuvu2+du+edx.
Through Theorem 3.2, we get
and
Therefore,
Similarly, multiplying the last equation of the system (3.1) by ψ and integrating it by parts
With the help of Poincaré's inequality, we finally have
where ¯d1=1μ1(δc22ˆC2+(k+24)e2+4e(1+2c)+4d+4+8c8e2), ¯d2=1μ1(δc+δc22ˆC2+ke2+4e+4d+48e2) and c=β−λδ.
Clearly, as soon as d1>¯d1 and d2>¯d2 are satisfied, there is ▽ϕ=▽ψ=0, which means that all solutions of the system (3.1) are constant steady states.□
3.3. The existence
To simplify the calculation process, we set z=(u,v) and
where τi=−u∗i3u∗2i+(2d−2)u∗i+e−d(1+kv∗i)(u∗2i+du∗i+e),ρi=u∗i1+2kv∗i(1+kv∗i)(u∗2i+du∗i+e) and c=β−λδ.
Let T(μj) be the eigensubspace generated by eigenfunctions corresponding to the eigenvalue μj, j=0,1,2.... Set
(i) X:={z∈[C1(ˉΩ)]×[C1(ˉΩ)]|∂u∂n=∂v∂n=0on∂Ω},
(ii) Xjs:={hϕjs|h∈R2}, where {ϕjs:s=1,...,n(μj)} is an orthonormal basis of T(μj), and n(μj)=dimT(μj).
Then, X=⨁∞j=1Xj and Xj=⨁n(μj)s=1Xjs.
In addition, the system (3.1) can be re-represented as
Therefore, finding a positive solution to the above system if and only if z satisfies
where (I−Δ)−1 is the inverse of I−Δ. Obviously, simple calculations show that
Furthermore, it is easy to know that ζ is an eigenvalue of Dzg(d1,d2;E∗i) on Xj, which is equivalent to ζ(1+μj), which is an eigenvalue of the following matrix
If we set
then we can get the following equation
where n(μj) denotes the multiplicity of μj.
Therefore, we only need to discuss the sign of Mi(d1,d2;μj) to obtain the index of g(d1,d2;⋅) at the internal equilibrium point E∗i. Suppose that
then, Mi(d1,d2;μj) has two real roots,
Next, we will discuss the existence of non-constant steady states of the system (3.1) based on the number of internal equilibrium points.
First, we consider the case when the number of internal equilibrium points is one.
Theorem 3.5. Suppose that Γ>0 and 3u∗21+(2d−2)u∗1+e−d>0, then the unique equilibrium point E∗1(u∗1,v∗1) is locally asymptotically stable, which implies that no non-constant steady states exist near the neighborhood of E∗1.
Proof. Let
ζ being an eigenvalue of J in Xj is equivalent to ζ being an eigenvalue of the following matrix
Thus, the characteristic equation of the above matrix is given as follows
Since 3u∗21+(2d−2)u∗1+e−d>0, then τ1<0, which means M1(d1,d2;μj)>0 and d1μj+d2μj−τ1+δc>0. By the Routh-Hurwitz criterion, both roots ζj1,ζj2 of the characteristic equation have negative real parts and Reζj1,Reζj2<−γ, where γ is a positive constant. This assertion is valid.□
Clearly, for a sufficiently large d2, we define limd2→∞μ(1)+(d1,d2)=τ1d1:=μ1∗ and limd2→∞μ(1)−(d1,d2)=0.
Theorem 3.6. Suppose that Γ>0 and 3u∗21+(2d−2)u∗1+e−d<0. If μ1∗∈(μq,μq+1) for some q≥1, and σq=∑qj=1n(μj) is odd, then there is a positive constant ˜d such that the system (3.1) has at least one non-constant positive steady state solution when d2>˜d.
Proof. It is easily found that there exists a sufficiently large ˜d′ such that τ1d2−δcd1>0 holds for d2>˜d′. Thus, we get μ(1)+(d1,d2)>0,μ(1)−(d1,d2)>0. By μ(1)+(d1,d2)→μ1∗,μ(1)−(d1,d2)→0, then there exist two positive constants ˜d>˜d′ and q≥1, and we have
when d2>˜d. In addition, there exists d⋆2>˜d, which can satisfy
Therefore, it is valid that there exists d⋆1>d⋆2 such that τ1d⋆1<μ1; we get
Next, we will assume that the assertion is not valid and introduce the contradiction by means of a homotopy argument.
We define
for t∈[0,1], and consider the problem
Therefore, z is a solution to the above problem if and only if z needs to satisfy the following equation
By Theorem 3.2, we set
Then, we can get f(z;t)≠0 when z∈∂Θ and 0≤t≤1. Homotopy invariance of the Leray-Schauder degree indicates
So we have
This gets the contradiction, which shows that the assertion is correct.□
We now proceed to explore the existence of non-constant steady state solutions for the system (3.1) when the number of internal equilibrium points is three. Therefore, it is always guaranteed that Γ<0,(β−λδ)2k+d−1<0,β−λδ−d+e>0. Next, we give different conditions to prove it. At the same time, assume that e<d is valid, in order to better distinguish the sign of τi.
There are three cases that need to be considered: (1)u⋆<u∗4,(2)u∗4<u⋆<u∗6,(3)u⋆>u∗6 where u⋆=1−d+√(d−1)2−3(e−d)3.
Theorem 3.7. Suppose that u⋆<u∗4 holds, if μ5+(d1,d2)∈(μm,μm+1) and σm=∑mj=0n(μj) is even for m≥1, then the system (3.1) has at least one non-constant positive steady state solution.
Proof. Since u⋆<u∗4, we get τ4,τ5,τ6<0. In addition, since ρ4δc2−τ4δc>0,ρ6δc2−τ6δc>0,ρ5δc2−τ5δc<0, we have
Next, assume that the assertion is not valid. We still use the homotopy argument to introduce a contradiction. For 0≤t≤1, we set
and think about the problem
Therefore, z is a solution to the above problem if and only if z needs to satisfy the following equation
Similarly to Theorem 3.6, we set
Then, we get p(z;t)≠0 when z∈∂Ξ and t∈[0,1]. Homotopy invariance of the Leray-Schauder degree shows
Therefore,
Moreover, if t=0, p(z;0)=0 only owns a positive solution z∗(1,β−λδ), by repeating the previous work, we get
This gets the contradiction, which shows that the assertion is correct.□
Theorem 3.8. Suppose that u⋆>u∗6 holds, if μ5+(d1,d2)∈(μm,μm+1),μ4−(d1,d2)∈(μp,μp+1),μ4+(d1,d2)∈(μq,μq+1),μ6−(d1,d2)∈(μs,μs+1),μ6+(d1,d2)∈(μg,μg+1) and σm=∑mj=0n(μj),σq=∑qj=p+1n(μj), σg=∑gj=s+1n(μj) as long as there are at least two odd numbers or all even numbers, then there exists a positive constant d∗ such that the system (3.1) has at least one non-constant positive steady state solution for d2>d∗.
Proof. Since u⋆>u∗6, we get τ4,τ5,τ6>0. In addition, since ρ4δc2−τ4δc>0,ρ6δc2−τ6δc>0,ρ5δc2−τ5δc<0, we have that there exists a positive constant d∗ such that there is μi−(d1,d2)>0,μi+(d1,d2)>0(i=4,6) when d2>d∗.
In addition, we have
Repeating the proof of Theorem 3.7, we have
Obviously,
Our assertion is ultimately proven correct.□
Theorem 3.9. Suppose that u∗4<u⋆<u∗6 holds, if μ5+(d1,d2)∈(μm,μm+1),μ4−(d1,d2)∈(μp,μp+1), μ4+(d1,d2)∈(μq,μq+1) and σm=∑mj=0n(μj),σq=∑qj=p+1n(μj), then when σm+σq is even, there exists a positive constant d∗ such that the system (3.1) has at least one non-constant positive steady state solution for d2>d∗.
Proof. Since u∗4<u⋆<u∗6, we get τ4>0,τ6<0. Regardless of whether the sign of τ5 is positive or negative, we have
Moreover, there exists a positive constant d∗ such that there is μ4−(d1,d2)>0,μ4+(d1,d2)>0 when d2>d∗. Then, we get
Repeating the proof of Theorem 3.7, we have
Obviously,
The assertion is valid. □
4.
Turing instability and weakly nonlinear analysis
In this section, we derive the conditions for Turing instability. At the same time, the amplitude equation derived from the weak linear analysis [22,23,24,25,26] facilitates the differentiation of different patterns. For simplicity, we first set the spatial region Ω as a one-dimensional interval (0,π), then the system (1.4) becomes the following system
Now we can consider the following eigenvalue problem
which has eigenvalue μj=j2 and eigenfunction ωj(x)=cos(jx) for j∈{0,1,2…}.
Suppose that (ση)=∑∞j=0(AjBj)cos(jx) is the eigenfunction corresponding to the eigenvalue ξj of the matrix Jj, thus we have
where I is the identity matrix and Jj=(τi−j2d1−ρiδc2−δc−j2d2), τi=−u∗i3u∗2i+(2d−2)u∗i+e−d(1+kv∗i)(u∗2i+du∗i+e),ρi=u∗i1+2kv∗i(1+kv∗i)(u∗2i+du∗i+e),c=β−λδ.
Clearly, the characteristic equation has the form
where
The roots of the above equation are
Based on the characteristic equation, we quickly have the following theorem.
Theorem 4.1. If 3u∗2i+(2d−2)u∗i+e−d>0, then the positive equilibrium point E∗i(u∗i,v∗i) is locally asymptotically stable, expect for E∗5.
Proof. Since 3u∗2i+(2d−2)u∗i+e−d>0, then τi<0 holds. In addition, we have ρic−τi>0, expect for i=5, thus it is easy to find that Tj<0 and Dj>0 hold, which means E∗i is locally asymptotically stable.□
4.1. Existence of Turing instability
Theorem 4.2. Suppose that 3u∗2i+(2d−2)u∗i+e−d<0, τi−δc<0 and d2>σ1d1 are valid, where σ1=δc−τi+2ρic+2√ρic(ρic−τi)τ2i, then E∗i is unstable for the reaction-diffusion system apart from E∗5, which implies that the system suffers Turing instability at λ=λT with the wave number j2=j2T=√δc(ρic−τi)d1d2, where λT is a root that can satisfy the equation (−δ2d21+4d1d2δρi)(β−λδ)2−2d1d2τi(βδ−λ)−d22τ2i=0.
Proof. Since ρiδc2−τiδc>0, expect for i=5, we can get that the internal equilibrium point E∗i of the ODE system is locally asymptotically stable if τi−δc<0, i.e., a11+a22<0. Next, we will explore the conditions for Turing instability under the assumption that 3u∗2i+(2d−2)u∗i+e−d<0 and τi−δc<0, i.e., a11>0 and a11+a22<0. It is well known that we only need to ensure that there exists j≥1 such that Dj<0, which causes the equation χ(ξ) to have a positive real root and a negative real root.
Obviously, if
then Dj will reach a minimum value
where j∗2=τid2−δcd12d1d2>0.
Let σ=d2d1 and
we have the following equivalent condition
It is not difficult to find that
because ρic−τi>0 and ρi>0.
Therefore, G(σ) has two positive real roots, which are
In addition, we have G(δcτi)<0, which means σ2<δcτi<σ1. So, from the above analysis, d2>σ1d1 can be obtained.□
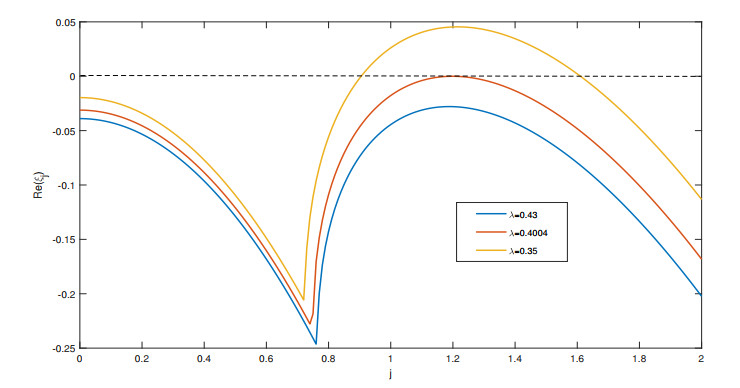
Remark 4.1. To verify the validity of the Theorem 4.2, the relation between Re(ξj) and wave number j is described in Figure 1. It is easy to find that there exists a threshold λ=λT=0.4004 for Turing instability when k=0.63,d=9,e=0.01,δ=0.1,β=9,d1=0.118,d2=0.6. This means that we should control λ<λT to induce the Turing instability.
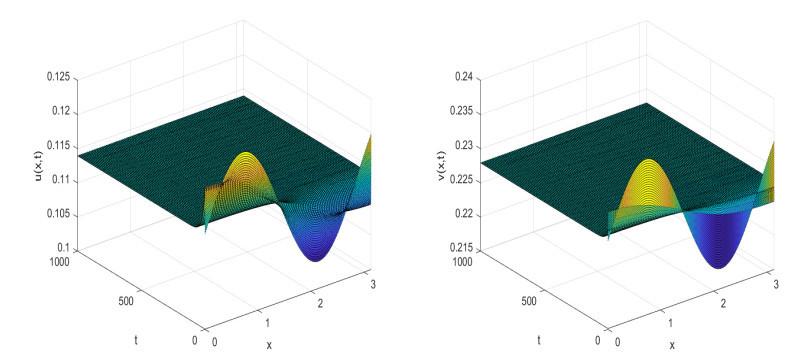
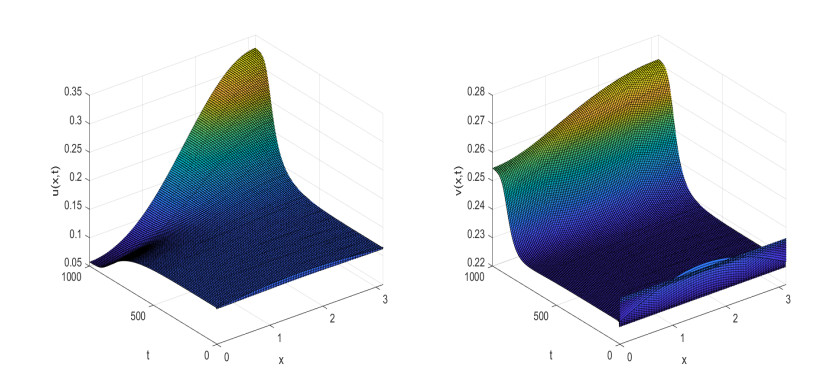
Remark 4.2. We fix the parameters k=0.8,d=0.8,e=0.2,δ=0.4,β=6,λ=1.6,d1=0.15 to explore the effect of the diffusion coefficient d2 on Turing instability; then, we can obtain 3u∗2i+(2d−2)u∗i+e−d=−0.6066<0 and τi−δc=−0.6078<0, which means that the positive equilibrium point E∗i is locally asymptotically stable in ODE system (1.5). Furthermore, if d2=7 is valid, then σ1=66.3106 and d2−σ1d1=−2.9466<0, so the positive equilibrium point E∗i remains locallyasymptotically stable in PDE system (see Figure 2). If d2 increases to 20, then σ1=66.3106 and d2−σ1d1=10.0534>0, so the positive equilibrium point E∗i will become unstable in PDE system (see Figure 3).
4.2. Weakly nonlinear analysis for Turing pattern
In this subsection, in order to distinguish the different patterns, multiple-scale analysis will be used to obtain the amplitude equation near λ=λT.
Since the weak linear analysis method will be used next, we need to rewrite the system at the positive equilibrium point E∗i(u∗i,v∗i) and still use (u,v)T to represent the perturbation solution (u−u∗i,v−v∗i)T of the system (1.4)
where
Let U=(uv), then the above system can be equivalently written as
where P and Q are linear and nonlinear operators, respectively,
with n11=−dτidλ|λ=λT and n12=dρidλ|λ=λT.
Then, the variables are expanded using the small parameter ε:
where
Substituting the variables from the above expansion into the equation and combining the terms about ε, for the order ε, ε2 and ε3, we have
By solving the equation, we obtain that: (u1v1)=(ϕ1)(∑3j=1Wjexp(ikj⋅r)+c.c) where ϕ=ρi(λT)d1j2T−τi(λT), Wj denotes the amplitude of exp(ikj⋅r) under first-order perturbation, and its form is controlled by the higher-order perturbation term.
According to the Fredholm solvability condition, the vector function at the right end of the equation needs to be orthogonal to the zero eigenvectors of the operator L+T, which can guarantee the existence of nontrivial solutions. A simple calculation gives the zero eigenvector of L+T as
where φ=d1j2T−τi(λT)δc2(λT). Applying again the Fredholm solvability condition, one has
with s1=Fuu2ϕ2+Fuvϕ+Fvv2,s2=Guu2ϕ2+Guvϕ+Gvv2, and
where
Substituting (u2v2) into the equation, the Freudian solvability condition shows
where
and the other two equations can be obtained by transforming the subscripts of V and W.
Since the amplitude can be expressed as follows
we obtain the amplitude equation by combining the variables
with
Next, we can decompose the amplitude into Dj=ϱjexp(iθj)(j=1,2,3), where ϱj and θj denote the mode length and phase angle, respectively. Then, we will substitute it into the amplitude equation, and separate the real and imaginary parts of the equation; thus, we can yield the following result
with θ=θ1+θ2+θ3. Meanwhile, we are only interested in the stable solutions of equations, then we get the following equations
On the basis of the theory of [23], the above amplitude equations have four solutions, which will imply four different patterns.
(i) Spotted pattern:
It always exists and is stable if ξ<ξ2=0 and unstable if ξ>ξ2=0.
(ii) Stripe pattern:
It exists when ξ>0 and is stable if ξ>ξ3=s2I1(I2−I1)2 and unstable if ξ<ξ3=s2I1(I2−I1)2.
(iii) Hexagonal pattern (H0,Hπ):
It exists when ξ>ξ1=−s24(I1+2I2). Furthermore, solution ϱ+=|s|+√s2+4ξ(I1+2I2)2(I1+2I2) is stable if ξ<ξ4=s2(2I1+I2)(I2−I1)2 and solution ϱ−=|s|−√s2+4ξ(I1+2I2)2(I1+2I2) is always unstable.
(iv) Mixed pattern:
It exists when I2>I1,ξ>ξ3=s2I1(I2−I1)2 and is always unstable.
5.
Existence, direction, and stability of the Hopf bifurcation
In this section, we will explore the existence of spatial Hopf bifurcation of the system (1.4) with Ω∈(0,π) and further derive the stability and direction of the Hopf bifurcation.
5.1. The existence
In the previous discussion of Turing instability, we have obtained the characteristic equation of the PDE system as
where
In order to find the Hopf bifurcation value λH and verify the transversality conditions, we need to explore whether the PDE system satisfies the following conditions [27], i.e., there exists j≥0 such that:
and η′(λH)≠0 for complex eigenvalues η(λ)±iγ(λ).
For the existence of Tj(λH)=0, it is only necessary to satisfy τi(λH)−δc(λH)−j2(d1+d2)=0, i.e., λH=λjH=τi(λH)−j2(d1+d2)δ>0. Obviously, we must make it valid so that τi>0, i.e., 3u∗2i+(2d−2)u∗i+e−d<0.
Therefore, there exists a positive integer j∗≥1 such that
and it is clear that there is Tl(λH)≠0. Furthermore, η′(λH)=τ′i(λH)+12≠0 can be verified by numerical simulations. With the expression for Dj(λH), we can easily find out that
where E∗5 is not considered.
Thus, if the following inequality holds
then Dj(λH)>0. Similarly, we have Dl(λH)>0.
Therefore, assuming 3u∗2i+(2d−2)u∗i+e−d<0 and d1d2−(τid2−δcd1)>0, we know that all roots of the characteristic equation for λ=λ0H=λ0 have negative real parts except for the imaginary roots ±i√D0(λ0H). However, at least one of the roots of the equation for λ=λlH(l=1,…,j∗−1) has a positive real part.
Theorem 5.1. Assuming that 3u∗2i+(2d−2)u∗i+e−d<0 and d1d2−(τid2−δcd1)>0 are valid, then the system (1.4) undergoes Hopf bifurcation at E∗i except E∗5 with λ=λjH(j=0,…j∗−1). Furthermore, for λ=λjH(j=1,…j∗−1), the bifurcating periodic solutions are non-homogeneous, and for λ=λ0H=λ0, the bifurcating periodic solutions are homogeneous, which means that it can coincide with the periodic solution of the ODE system.
5.2. The direction and stability
First, make the following definition: Ut=RU, where U=(u,v)T,R=DΔ+J(E∗i),J(E∗i)=(τi−ρiδc2−δc),D=diag(d1,d2). Meanwhile, we set R∗ as the conjugate operator of R, which is defined as
We let ϖ(λ) be the imaginary part of the roots of the characteristic equation
which has the following form
Meanwhile, we set
where ϖ0=ϖ(λ0),ζ=δ2c20+ϖ20,c0=β−λ0δ.
It is easy to get that ⟨R∗ν,μ⟩=⟨ν,Rμ⟩,R(λ0)q=iϖ0q,R∗(λ0)q∗=−iϖ0q∗,⟨q∗,ˉq⟩=0,⟨q∗,q⟩=1, where ⟨ν,μ⟩=∫π0ˉνTμdx indicates the inner product. From [28], the complex space is decomposed into X=Xc⊕Xs, where Xc={zq+ˉzˉq|z∈C} and Xs={w∈X|⟨q∗,w⟩=0}.
For any U=(u0,v0)T, we have that there exist z∈C and w∈(w0,w1) such that
Apparently,
Thus, the system (1.4) is represented as
where
From [28], ˜g can be written as
where H,P have a complex symmetrical form, and direct calculations show that
Thus,
where
Meanwhile, we get G20=G11=G02=(0,0)T and G(z,ˉz,w)=O(|z|3,|z|⋅|w|,|w|2). From [28], it is clear that the system has a center manifold, and we can write it as
Then, we have
Thus, the system that is confined to the center manifold can be represented as
where
and
A straightforward calculation demonstrates
Therefore,
Based on the above analysis, we have the following conclusion.
Theorem 5.2. Assuming that 3u∗2i+(2d−2)u∗i+e−d<0 and d1d2−(τid2−δcd1)>0 are valid, then the system (1.4) undergoes Hopf bifurcation at λ=λ0H=λ0 for E∗i except E∗5.
(i) The direction of the Hopf bifurcation is supercritical (resp. subcritical) if
(ii) The bifurcating periodic solutions are unstable (resp. stable) if Re(c1(λ0H))>0 (resp.<0).
6.
Numerical simulations
In this section, in order to verify the correctness of the previous theoretical derivations and explore the impact characteristics of harvest on the ecological relationship of predator populations, we will perform numerical experiments.
6.1. Turing pattern
In this subsection, we set the bounded region Ω=[0,200]×[0,200], while the time step is limited to △t=0.01 and the spatial step is determined to be △h=0.8. The initial condition is set as a random perturbation at the positive equilibrium point E∗i. Moreover, we only give different spatiotemporal pattern formations for prey u, since the spatiotemporal patterns of v are similar to u. Now we will fix the following parameters
then, we have
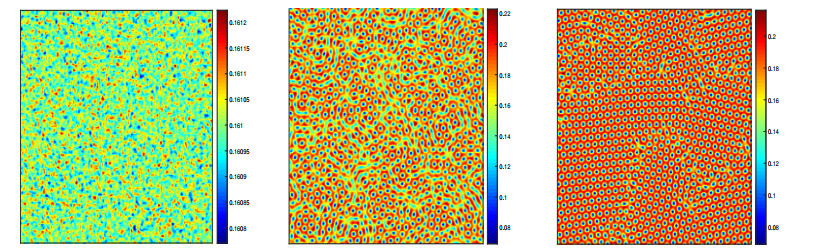
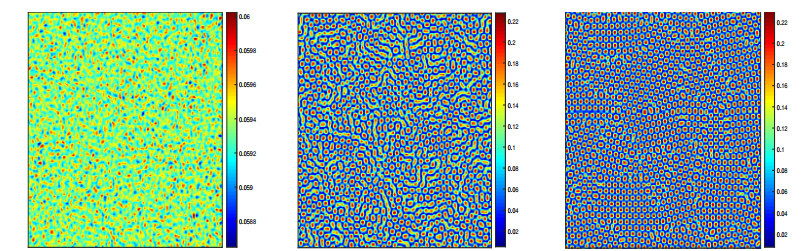
Now it is not very difficult to get λ=0.39<λT and ξ=0.02588∈(ξ2,ξ3). Thus, it is easy to find from Figure 4 that the pattern formation of prey u is spot patterns and stripe patterns coexisting with each other when time is short. As time continues to increase, the spot patterns dominate until the stripe patterns disappear; the spot patterns are the final form and no other structures appear. This result suggests that the prey populations ultimately form a high-density interconnected spatial distribution trend, while the predator populations have its own capture space and are not interconnected, which means that they have a separate capture space.
If we choose the parameter λ=0.35 and ξ=0.12579∈(ξ3,ξ4), it is obvious from Figure 5 that the whole region appears as an irregular patterns, in which the spot and stripe patterns are in competition with each other. Thereafter, as time grows, the spot and stripe patterns have a stable distribution until both coexist; finally, mixed patterns are presented in Figure 5.
Furthermore, we similarly give the formation of spot patterns of prey u with the parameter λ=0.21 and ξ=0.4755>ξ4 in Figure 6. As the number of iterations increases, we can clearly observe that eventually, only spot patterns exist, which is not consistent with the theoretical analysis. This phenomenon occurs for the following reasons. In the relationship of ξ>ξ4>ξ3>ξ2>ξ1, the value of λ is far away from the threshold λT, which means that some active modes will dominate compared with the primary slave modes. Consequently, they are very difficult to be adiabatically eliminated in the derivation of the amplitude equation. In addition, during the transition from uniform state modes to active modes, the amplitude equation of D1 has an extra third-order term D0¯D2⋅¯D3. Similarly, the amplitude equations of D2 and D3 have extra terms D0¯D1⋅¯D3 and D0¯D1⋅¯D2. The inclusion of these terms leads to the re-stabilization of the spot patterns, which is why the numerical simulations do not match the theoretical analysis. Similar numerical simulation results can be found in [29,30]. More details of the theory can be found in [23].
By comparing and analyzing the results of Figures 4–6, it can be concluded that the spatial distribution of prey and predator populations undergoes essential changes as the predator harvesting parameter values decrease, and the spatial distribution density of the prey populations gradually decreases. Furthermore, the final spatial pattern transitions from a spot pattern to stripe and spot mixed patterns, which means that, as the spatial distribution density of the prey populations decreases, the predator populations must spread to the predation domain in order to survive. Therefore, it is worth emphasizing that the size of the predator harvesting not only affects the predation dynamics between predatory populations, but also affects the density spatial distribution characteristics of the populations.
6.2. Hopf bifurcation
In this subsection, we will fix the following parameters
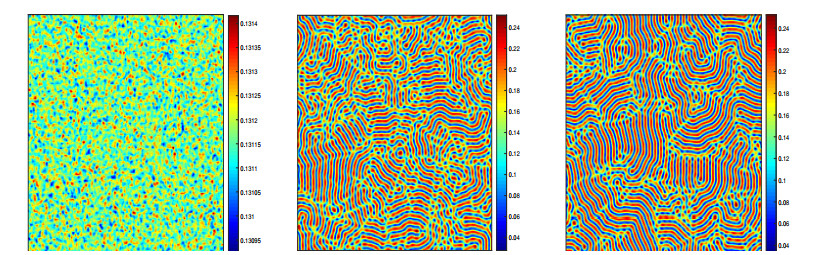
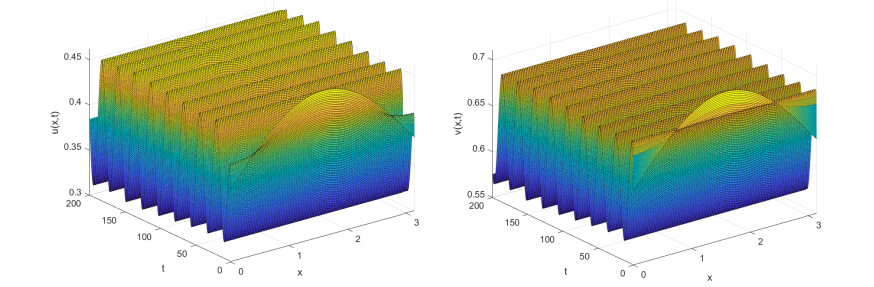
By a simple calculation, we can get λ0H=0.1346, and the parameters can satisfy the conditions in Theorem 5.2. In addition, we can get Re(c1(λ0H))≈−1.3526<0 and η′(λ0H)>0, thus it is worth pointing out that the PDE system undergoes a supercritical Hopf bifurcation at λ=λ0H and produces stable bifurcated periodic solutions (see Figure 7). This result means that appropriate predator harvesting behavior can promote the formation of a stable periodic growth coexistence mode between prey and predator populations, which is beneficial for their sustainable survival.
7.
Conclusions
This paper mainly proposed a predator-prey system with harvesting and diffusion to explore how harvesting affects predatory ecological relationships. Within the framework of theoretical analysis, we first give the existence of solutions of the system (1.4) by using the methods in [19] and boundedness by using the comparison principle, and prove that the solutions of the elliptic system (3.1) are upper and lower bounded. Second, with the help of Poincaré's inequality, the non-existence conditions for the non-constant steady states of the elliptic system (3.1) are investigated. At the same time, the existence of the non-constant steady states is analyzed by homotopy invariance of the Leray-Schauder degree. Moreover, we obtain the condition for Turing instability, and derive the amplitude equation at the threshold of Turing instability by weak linear analysis, which gives different patterns such as spot patterns, mixed patterns, and so on. Finally, the existence, direction, and stability of Hopf bifurcation are analyzed through theories like central manifolds. Under the framework of numerical simulation, we first validate the effectiveness and feasibility of the theoretical analysis results and dynamically display the trend of spatial distribution changes in population density. Second, through comparative analysis of numerical simulation results, the impact characteristics of harvesting behavior on predatory ecological relationships and spatial changes in population density are pointed out. Finally, based on the numerical simulation results, it is clear that appropriate harvesting behavior can promote the formation of a stable periodic growth coexistence mode between the predator and prey populations. Based on the above results, it can be clearly emphasized that harvesting has a significant impact on predatory ecological relationships.
One innovation of this paper is the introduction of the generalized Holling IV functional response to describe the interaction between predator and prey, which can not only enrich the dynamic properties of the system (1.4) but also make it more suitable for exploring the spatial distribution trends of prey and predator in natural ecosystems. Another innovation of this paper is to reveal the spatial coexistence mode of prey and predator during the gradual enhancement of group defense in the prey populations from the perspective of the dynamic evolution process of Turing patterns. Furthermore, it is also worth emphasizing that prey and predator populations have a stable periodic oscillation growth coexistence mode, which can indicate that appropriate harvesting behavior can not only effectively control the growth of prey populations but also maintain sustainable survival between prey and predator. This research result can be applied to the control of Microcystis aeruginosa bloom outbreaks by monitoring the its population density and of filter-feeding fish. If the dynamic change law of Microcystis aeruginosa population density is a stable periodic oscillation mode under low density, and the dynamic change law of filter-feeding fish population density is a stable periodic oscillation mode, this can indicate that filter-feeding fish can effectively control the outbreak of Microcystis aeruginosa blooms.
To emphasize the feasibility of the theoretical and numerical results in this paper, we conducted comparative analysis on the published papers separately. The paper [18] has thoroughly explored the bifurcation dynamics behaviors of the system (1.5), and we have compared and analyzed the research results of this paper with those of [18]. It is worth pointing out that the systems (1.4) and (1.5) have stable periodic solutions, which means that the predator and prey populations can eventually form a stable periodic oscillation growth coexistence mode with time. This indicates that the system (1.4) continues some of the dynamic characteristics of the system (1.5) in the time state. Furthermore, these papers [2,31,32,33] have obtained some excellent research results on steady states and spatiotemporal patterns of predator-prey system with generalized Holling IV functional response, Holling type I functional, and Beddington-DeAngelis functional response. Under the same theoretical analysis and numerical simulation framework, we have investigated all possible stationary distributions of prey and predator in two dimension habitats (for example, spots and mixture of spots and stripes). These research results are similar to those presented in the papers [2,31,32,33]. Based on the above, it is necessary to demonstrate that the theoretical and numerical results of this paper are reliable.
In summary, although this paper obtained some theoretical and numerical results in steady states and spatiotemporal patterns, there is still much to be explored in subsequent work, such as using laboratory or field monitoring data to calibrate the values of system parameters, investigating the impact of population migration behavior on the dynamic relationship between prey and predator, etc. Finally, we hope that the research results of this paper can provide some theoretical support for the control of Microcystis aeruginosa blooms.
Author contributions
Rongjie Yu, Hengguo Yu and Min Zhao: Conceptualization, Methodology, Validation, Software, Writing-original draft, Writing-review & editing. All authors contributed equally to the manuscript. All authors have read and approved the final version of the manuscript for publication.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grants No.61871293 and No.61901303), the National Key Research and Development Program of China (Grant No. 2018YFE0103700), by the Zhejiang Province College Student Science and Technology Innovation Activity Plan (New Talent Plan) (Grant No: 2024R429A010).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: