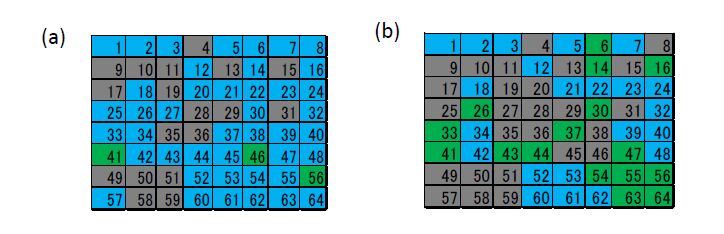
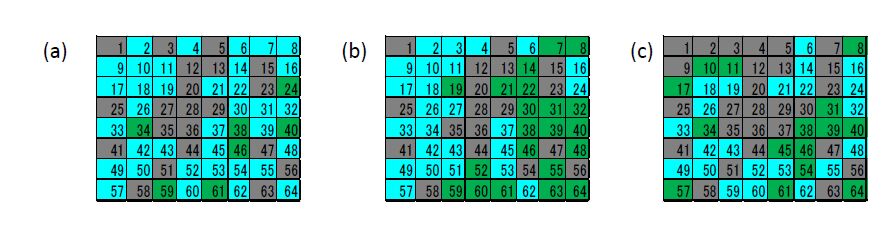
In brain information science, it is still unclear how multiple data can be stored and transmitted in ambiguously behaving neuronal networks. In the present study, we analyze the spatiotemporal propagation of spike trains in neuronal networks. Recently, spike propagation was observed functioning as a cluster of excitation waves (spike wave propagation) in cultured neuronal networks. We now assume that spike wave propagations are just events of communications in the brain. However, in reality, various spike wave propagations are generated in neuronal networks. Thus, there should be some mechanism to classify these spike wave propagations so that multiple communications in brain can be distinguished. To prove this assumption, we attempt to classify various spike wave propagations generated from different stimulated neurons using our original spatiotemporal pattern matching method for spike temporal patterns at each neuron in spike wave propagation in the cultured neuronal network. Based on the experimental results, it became clear that spike wave propagations have various temporal patterns from stimulated neurons. Therefore these stimulated neurons could be classified at several neurons away from the stimulated neurons. These are the classifiable neurons. Moreover, distribution of classifiable neurons in a network is also different when stimulated neurons generating spike wave propagations are different. These results suggest that distinct communications occur via multiple communication links and that classifiable neurons serve this function.
1.
Introduction
The applications of the generalized inverse of matrices or operators are of interest in numerical mathematics. Indeed, when a matrix is singular or rectangular, many computational and theoretical problems require different forms of generalized inverses. In the finite-dimensional case, an important application of the Moore-Penrose inverse is to minimize a Hermitian positive definite quadratic form xtx where t denotes the transpose, under linear constraints. Precisely, weighted Moore-Penrose inverse plays a prominent role in the indefinite linear least-square problems [1,2].
Let Cm×n denotes the set of all matrices of order m×n, having complex entries. Further, assume that for an arbitrary matrix A∈Cm×n, and two Hermitian positive definite matrices M∈Cm×m, and N∈Cn×n, there exist a unique matrix S∈Cn×m such that satisfying the following properties:
Then, S is said to be a weighted Moore-Penrose inverse (WMPI) of A with respect to matrices M and N; generally, it is denoted by A†MN. In particular, when the matrix M and N are the identity matrix of order m and n, respectively, then S is known as Moore-Penrose inverse, denoted by A†. Moreover, the above relation is reduced to well-known Penrose equations [3,4] as follows:
The elementary technique for computing the WMPI of the matrix is entirely based on the weighted singular value decomposition [5], in accordance with the following form. Let A∈Cm×nr, where Cm×nr be a set of complex matrices of order m×n with rank r, there exist matrices P∈Cm×m and Q∈Cn×n satisfying the conditions P∗MP=Im and Q∗N−1Q=In, such that
where D=diag(σ1,σ2,…,σr), σ2i is the nonzero eigenvalue of matrix N−1A∗MA, and it satisfies the relation: σ1≥σ2≥…σr>0. Then, the WMPI (A†MN) of matrix A could be expressed as:
Note that, in this manuscript weighted conjugate transpose of matrix A is denoted by A# and is equal to N−1A∗M, whereas A∗ denotes the conjugate transpose of the matrix A∈Cm×n. Consequently, (A†MN)#=M−1(A†MN)∗N=M−1(A∗)†N−1M−1N and (AA†MN)#=P(Ir000)P−1 [6, pp. 41]. Moreover, the following properties hold:
A diverse range of other methodologies has presented in the literature to determine the WMPI of a matrix. For calculating the generalized inverse numerically, Greville's partitioning method was introduced in [7]. A new proof of Greville's method was illustrated by Wang [8] for WMPI. But, such methods involve more operations and therefore more rounding errors are accumulated. Often numerical techniques for finding the Moore-Penrose inverse lack in numerical stability [9]. Besides it, Wang [10] obtained a comprehensive proof for the WMPI of a partition matrix in a recursive form. Also, WMPI method was introduced in [9] for the multi-variable polynomial. Moreover, new determinantal representations for weighted generalized inverse were presented in [11]. Whereas, a representation of the WMPI of a quaternion matrix was discussed by Ivan Kyrchei [12,13]. Further, its explicit representation for the two-sided restricted quaternionic matrix equations was investigated in [14].
The hyperpower iterative method was given by Altman [15] for inverting a linear bounded operator in the Hilbert space, whereas it's applicability for generating the Moore-Penrose inverse of a matrix was shown by Ben-Israel [16]. Several iterative methods fall in this category of hyperpower matrix iterations and the general pth order iterative method is written as follows:
where Rk=I−ASk, I is identity matrix of order m and S0 is the initial approximation to input matrix A−1. This scheme is attractive as it is entirely based on matrix-matrix products, which is implemented fruitfully in parallel machines. By this approach, each pth- order iterative method brought forward in terms of hyperpower series, which require p times matrix-matrix multiplications. If p=2, iterative method (1.5) yields well known Newton-Schulz method (derived in [17,18]):
Although it is a quadratically convergent method, and its complexity is poly-logarithmic and numerically stable (discussed in [19]). But, scheme (1.6) often shows slow convergence behavior during the initial process, thus would lead to an increment in computational workload while calculating matrix inverse.
In 2017, H. Esmaeili and A. Pirnia [20] constructed a quadratic convergence iterative scheme as follows:
If p=3, the hyperpower iterative method (1.5) turns into a cubically convergent method and can also be derived from Chebyshev scheme [21]:
and investigated by Li et al. [21] in 2001. Along with this, they developed two other third-order iterative methods, from the mid-point rule method [22] and Homeier's method [22], given as:
and
respectively. In 2017, a fourth-order scheme has been presented by Esmaeili et al. [23] and demonstrated below:
Toutounian and Soleymani [24] have proposed the following fourth-order method:
As a general way of extracting can be done by using equation (1.5). Thus, for p=4 the fourth-order iterative scheme:
that uses four matrix-matrix multiplications. In 2013, Soleymani [25] demonstrated the fifth-order iterative method with the use of six times matrix multiplications at each step and scheme is presented below:
In this paper, we have been investigated the fifth-order convergent iterative method for computing the weighted Moore-Penrose inverse. We focused on one of the major factors of computational cost which is paying close attention to reduce the time of computations. In addition, the theoretical study was carried out to justify the ability to finding the weighted Moore-Penrose inverse of any matrix. Also, the aim of the presented work have been supported by the numerical performance.
2.
Iterative method
Our aim is to derive a fifth-order iterative method with the help of Eq. (1.5) to find the weighted Moore-Penrose inverse of a matrix A, that uses minimum number of matrix multiplications than the required ones in (1.5). The hyperpower series for p=5 can be written as:
where Φ(ASk)=5I−10ASk+10(ASk)2−5(ASk)3+(ASk)4. The count of matrix multiplications in the iterative method (2.1) is five. The computational time used by the iterative method (2.1) can be minimized by reducing the count of matrix-matrix multiplications at each step. For this, we re-formulate the above scheme (2.1) as follows:
This is a new iterative method (2.2) for computing the generalized inverse of any matrix. It can be seen easily that it uses four matrix-matrix multiplications at every step.
In the next section, we will prove theoretically that the order of convergence of the above scheme is five and is applicable for generating the weighted Moore-Penrose inverse.
3.
Weighted Moore-Penrose inverse (WMPI):
Lemma 3.1. For the approximate sequence {Sk}∞k=0 generated by the iterative method (2.2) with the initial matrix
the following Penrose equations hold:
(a) SkAA†MN=Sk, (b) A†MNASk=Sk, (c) (MASk)∗=MASk, (d) (NSkA)∗=NSkA.
Proof. This lemma could be proved via mathematical induction on k. For k=0, the Eq. (a) is true. That is,
Further, we assume that the result holds for k, i.e.,
Now, we will prove that the Eq. (a) continues to hold for k+1, i.e., Sk+1AA†M,N=Sk+1. Thus, considering its left-hand side expression and using the iterative scheme (2.2), we get
Substituting Eq. (3.2) in the above equation, one can obtain
Hence, by the principle of mathematical induction, the Eq. (a) holds for k∈W, where W={0,1,2, 3,…}. Now, third Eq. (c) of this lemma can easily be verified for k=0. Let the result is true for k i.e., (MASk)∗=MASk. Next, we will show that the result holds for k+1. Using the iterative scheme (2.2),
Using the fact (MASk)∗=MASk, and also for q>0,
Thus, the Eq. (3.3) becomes:
Thus, third equality holds for k+1. The second and the fourth equations (i.e., (c) & (d)) can be proved analogously. Hence, the proof is completed.
Let A be a complex matrix of order m×n having rank r. Assume that the matrices P∈Cm×m, Q∈Cn×n, M and N are the Hermitian positive definite matrices satisfy P∗MP=Im and Q∗N−1Q=In. Then, the weighted singular value decomposition of matrix A can be expressed by Eq. (1.4).
Lemma 3.2. Considering the conditions of Lemma 3.1, for each approximate inverse produced by the iterative scheme (2.2), the following expression holds:
where Tk is a diagonal matrix and it is given by
Here, D denotes the diagonal matrix of order r.
Proof. We prove this lemma by using the mathematical induction on k. For k=0, we have
Further, we assume that the result holds for k. Now, we will prove that the result (3.5) is valid for k+1. For this, it is sufficient to prove that
Thus,
Theorem 3.1. For a complex matrix A∈Cm×n, the sequence {Sk}∞k=0 generated by (2.2) with initial matrix S0=δA#, for any k>0 converges to A†MN with at least fifth-order of convergence.
Proof. In view of iterative scheme (2.2) and to establish this result, we must show that
It follows from Lemma 3.2, that
and
The sequence generated by Eq. (3.11) gives rise to the result of applying the iterative scheme (2.2) for computing the zero ξ−1 of the function f(t)=ξ−t−1 with the initial guess t(0)i. It could be seen that the iteration converges to ξ−1i, provided 0<t(0)i<2ξi, which leads to the condition on δ (so the choice of initial guess is proved). Thus, Tk→D−1 and relation (3.9) is satisfied. It proves that the iterative method (2.2) converges to its weighted matrix inversion A†MN. Now, we will show that the obtained sequence {Sk}∞k=0 converges with the fifth-order. For this, assume that
Since P∗MP=Im, and Q∗N−1Q=In, we have (Q∗)−1=N−1Q. Consequently,
where Ek=TkD=diag(β(k)1,β(k)2,…,β(k)3). This yields to
therefore
Eqs. (3.13) and (3.15) implies Ek+1=Ekp(Ek). Now by simplifying, we obtain
and thus for all j, 1≤j≤r, we have (1−β(k+1)j)≤(1−β(k)j)5. That shows at least the fifth-order of convergence of the method (2.2) for finding the WMPI. This completes the proof.
4.
Numerical results and discussions
The purpose of this section is to confirm the theoretical aspects through numerical testing. For this, an attempt is made to illustrate the comparison of the proposed strategy with the existing schemes on practical and academic models. The outcomes are estimated by using the Mathematica software, as numerical calculations are accomplished with high accuracy. Moreover, its programming language posses the symbolic calculations and exact arithmetics. The software Mathematica 11 with the specification of a processor is Intel(R) Core(TM) i7-8565U CPU @ 1.89GHz (64-bit operating system) Window 10 Pro @ 2019 Microsoft Corporation was used. The comparisons have been done by considering the total number of matrix multiplications (TMM), actual running time (T) in seconds, and the computational order of convergence (ρ). For calculating the ρ,
the last three approximations Sk−1,Sk,Sk+1 are used and here, ‖⋅‖∗ denotes the generic matrix norm. For comparison purposes, the proposed scheme PM5 (2.2) is compared with methods proposed by Schulz (1.6), Esmaeili et al. (1.7), Li. et al. {(1.8), (1.9) and (1.10)}, Esmaeili et al. (1.11), Toutounian and Soleymani (1.12), Li et al. (1.13), and Soleymani (1.14) and denoted by SM2, EM2, CM3, MP3, HM3, EM4, TM4, LM4, and SO5, respectively.
Example 1. (Academic problem) Consider the rank-deficiency matrix
The comparison of this test problem is calculated by using initial guess S0=1σ2min+σ2maxA [26], where σmin and σmax are the bounds of singular values of A. Moreover, the stopping criteria ‖Sk+1−Sk‖<10−100 is used for finding a better approximation. From Table 1, we can observe that the presented method attains the desired result with the lesser number of multiplications of the matrix than the existing schemes, in minimum time. The presented scheme is, therefore, more efficient for this rank-deficient matrix because it shows better outcomes in each component, whereas some of the techniques are not able to determine the solution for this test problem.
Example 2. Consider the following elliptic partial differential equation:
where ϕ is a function of x and y. It is satisfied at every point inside the square formed by x=±1, y=±1 and subject to the following the boundary conditions:
(ⅰ) ϕ(x,y)=0 on y=1, −1≤x≤1,
(ⅱ)ϕ(x,y)=1 on y=−1, −1≤x≤1,
(ⅲ)
∂ϕ∂x=−12ϕ(x,y) on x=1, −1≤y≤1,
(ⅳ)
∂ϕ∂x=12ϕ(x,y) on x=−1, −1≤y≤1.
By using the central difference formulae on Eq. (4.3), one can obtain
here ϕi,j=ϕ(xi,yj). Consider square mesh size h=14 which yields seventy finite difference equations to find the approximate solution ϕ(xi,yj). By observing the boundary conditions, one can easily see that the function ϕ is symmetric about the y-axis. Finally, implementing the boundary conditions on (4.4), we obtain the linear system Aϕ=u, of thirty-five unknown parameters, where A=(YIIYIIYIIYIIYIIYIIY) is a tri-diagonal matrix, I is the identity matrix of order 5×5, Y=(−620001−610001−610001−610002−254), ϕ and u are the column vector whose transpose is equal to (ϕ1,ϕ2,…,ϕ34,ϕ35), and (0,0,…,0,−1,−1,−1,−1,−1), respectively. To tackle the large sparse array, the SparseArray and Band function are applied for saving the memory space and reduce the computational burden of matrix multiplication as follows:
The initial guess for this test problem is considered as S0=1‖A‖1‖A‖∞A∗ [26], where ‖A‖1=maxj(∑mi=1|ai,j|), and ||A||∞=maxi(∑nj=1|ai,j|). The results of comparisons are shown in Table 2. The methods LM4 and PM5 are better for this example than other methods, as uses minimum computational cost (i.e., matrix products), despite it PM5 yields the result faster. Thus, overall it demonstrates that the presented method converges faster than its competitors.
Example 3. In this test, we compute the weighted Moore-Penrose inverse of random dense matrix Am×n as follows:
where the M and N are the Hermitian positive definite matrices and considered as:
The results are drawn by using initial guess and stopping criteria as 1σ2min+σ2maxA# [26] and ‖Sk+1−Sk‖<10−12, respectively. The comparisons of this problem are listed in Table 3, which manifests that the PM5 is much efficient than other existing methods, in each aspect.
Example 4. Consider the following different order of ill-conditioned Hilbert matrix for computing the Moore-Penrose inverse
The comparison is obtained with the initial approximation 1σ2min+σ2maxAT [26], with stopping criteria ‖Sk+1−Sk‖≤10−20. The results are listed in Table 4 for various order of matrices. It can be concluded that the PM5 method gives the desired result faster than other methods, while in this test problem some methods are failed. Moreover, PM5 over-performs using a minimum number of matrix multiplications in each different order matrices. Hence, this justifies the aim of this paper.
5.
Conclusion
In this manuscript, we have established new formulations of the fifth-order hyperpower method to compute the weighted Moore-Penrose inverse. Compared to standard hyperpower method from a theoretical perspective, this new formulation has improved efficiency indices. Such approximations A†MN are found to be robust and effective when implemented as a preconditioned matrix to solve the linear systems. Further, a wide range of the practical and academical test is performed to test our proposed iterative scheme consistency and effectiveness. The outcomes in each test problems show that the presented method gives the desired result with the least number of matrix multiplications in minimum computational time. Hence, it supports our attempt for new transformations of the hyperpower iterative scheme of order five.
Acknowledgments
The authors wish to thank anonymous reviewers for careful reading and valuable comments which improved the quality of the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: