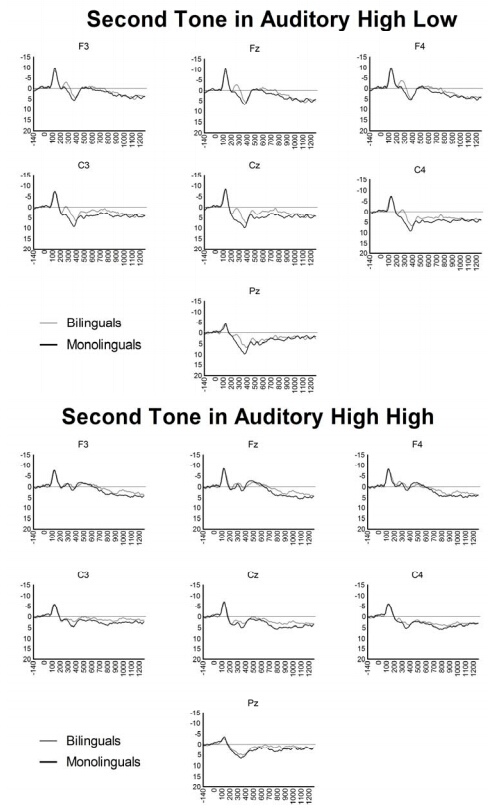
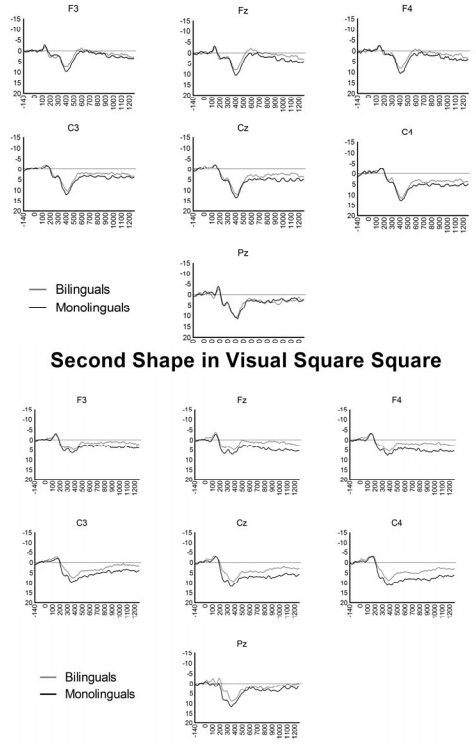
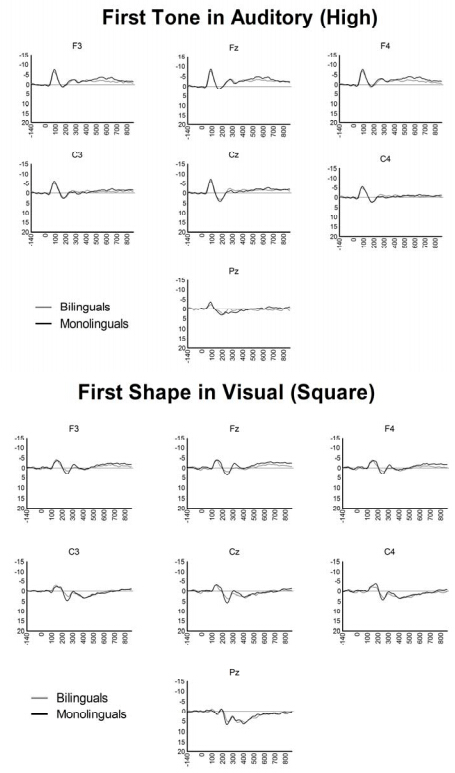
The purpose of the present study was to replicate and extend our original findings of enhanced neural inhibitory control in bilinguals. We compared English monolinguals to Spanish/English bilinguals on a non-linguistic, auditory Go/NoGo task while recording event-related brain potentials. New to this study was the visual Go/NoGo task, which we included to investigate whether enhanced neural inhibition in bilinguals extends from the auditory to the visual modality. Results confirmed our original findings and revealed greater inhibition in bilinguals compared to monolinguals. As predicted, compared to monolinguals, bilinguals showed increased N2 amplitude during the auditory NoGo trials, which required inhibitory control, but no differences during the Go trials, which required a behavioral response and no inhibition. Interestingly, during the visual Go/NoGo task, event related brain potentials did not distinguish the two groups, and behavioral responses were similar between the groups regardless of task modality. Thus, only auditory trials that required inhibitory control revealed between-group differences indicative of greater neural inhibition in bilinguals. These results show that experience-dependent neural changes associated with bilingualism are specific to the auditory modality and that the N2 event-related brain potential is a sensitive marker of this plasticity.
1.
Introduction
The stability problem of functional equations originated from a question of Ulam [43] concerning the stability of group homomorphisms and it was affirmatively answered for Banach spaces by Hyers [17]. Hyers' theorem was generalized by Aoki [1] for approximate additive mappings and by Rassias [37] for approximate linear mappings by considering an unbounded Cauchy difference. Furthermore, a generalization of the Rassias' theorem was obtained by Găvruţă [12] by replacing the unbounded Cauchy difference by a general control function. The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem (see [2,3,4,8,18,20,21,38,41] and references therein). The stability problems in non-Archimedean Banach spaces were studied in [13,14,28,30,31,32].
The functional equation
is called quadratic functional equation. In particular, every solution of the quadratic functional equation is said to be a quadratic mapping. The Hyers-Ulam stability problem for the quadratic functional Eq (1.1) was proved by Skof [42] for mappings from a normed space to a Banach space. Cholewa [5] noticed that Skof's theorem remains true if the domain is replaced by an Abelian group. In $ 1992 $, Czerwik [7] gave a generalization of the Skof–Cholewa's result. Later, Lee et al. [26] proved Hyers-Ulam-Rassias stability of quadratic functional Eq (1.1) in fuzzy Banach spaces.
In 2008, Ravi et al. [39] introduced the following quadratic functional equation
and solved the generalized Hyers-Ulam stability of this Eq (1.2). Jun and Kim [19] considered the following functional equation
and they established the general solution and the generalized Hyers-Ulam stability of the functional Eq (1.3) in Banach spaces. The functional Eq (1.3) and its pexiderized version
were studied by Sahoo [40] on commutative groups using an elementary method quite different from Jun and Kim [19]. The function $ f(x) = cx^{3} $ satisfies the functional Eq (1.3), which is thus called a cubic functional equation and every solution of the cubic functional equation is said to be a cubic function.
In 2010, Wang and Liu [44] considered the following mixed type functional equation
It is easy to show that the function $ f(x) = ax^{2}+bx^{3} $ is a solution of the functional Eq (1.4), where $ a, b $ are arbitrary constants. They established the general solution of the functional Eq (1.4), and then proved the generalized Hyers-Ulam stability of the Eq (1.4) in quasi-$ \beta $-normed spaces.
In 2011, Park [34] investigated the approximate additive mappings, approximate Jensen mappings and approximate quadratic mappings in $ 2 $-Banach spaces. This is the first result for the stability problem of functional equations in $ 2 $-Banach spaces. Later, the stability problems of additive functional inequalities, approximate multi-Jensen and multi-quadratic mappings in $ 2 $-Banach spaces were also studied [6,36], respectively. In 2012, Xu and Rassias [48] determined the generalized Hyers-Ulam stability of the mixed additive-cubic functional equation in $ n $-Banach spaces. In 2013, Xu [47] investigated approximate multi-Jensen, multi-Euler-Lagrange additive and quadratic mappings in $ n $-Banach spaces.
Kim and Park [24] proved the generalized Hyers-Ulam stability of additive functional inequalities in non-Archimedean $ 2 $-normed spaces. Park et al. [35] proved the generalized Hyers-Ulam stability of the system of additive-cubic-quartic functional equations with constant coefficients in non-Archimedean $ 2 $-normed spaces. In 2015, Yang et al. [49] proved the generalized Hyers-Ulam stability of the Cauchy functional equation and the Jensen functional equation in non-Archimedean $ (n, \beta) $-normed spaces and that of the Pexiderized Cauchy functional equation in $ (n, \beta) $-normed spaces.
The main purpose of this paper is to establish the generalized Hyers-Ulam stability of the mixed type quadratic-cubic functional Eq (1.4) in non-Archimedean $ (n, \beta) $-normed spaces.
Throughout this paper, let $ {\mathbb{N}} $ denote the set of positive integers and $ i, j, m, n\in {\mathbb{N}} $, and let $ n\geq 2 $ be fixed.
2.
Preliminaries
The concept of $ 2 $-normed spaces was initially developed by Gähler [9,10] in the middle of the 1960s. Then the concept of $ 2 $-Banach spaces was introduced by Gähler [11] and White [45,46]. A systematic development of linear $ n $-normed spaces is due to Kim and Cho [25], Malceski [27], Misiak [29] and Gunawan and Mashadi [15]. Following [48,49], we recall some basic facts concerning $ (n, \beta) $-normed space and some preliminary results.
Definition 2.1. (cf. [49]) Let $ n\in {\mathbb{N}} $, and let $ X $ be a real linear space with $ \dim X\geq n $ and $ 0 < \beta \leq 1 $, let $ \|\cdot, \ldots, \cdot\|_{\beta}: X^{n}\to {\mathbb{R}} $ be a function satisfying the following properties:
(N1) $ \|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} = 0 $ if and only if $ x_{1}, x_{2}, \ldots, x_{n} $ are linearly dependent;
(N2) $ \|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} $ is invariant under permutation of $ x_{1}, x_{2}, \ldots, x_{n} $;
(N3) $ \|\alpha x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} = |\alpha|^{\beta}\|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} $;
(N4) $ \|x+y, x_{2}, \ldots, x_{n}\|_{\beta}\leq \|x, x_{2}, \ldots, x_{n}\|_{\beta}+\|y, x_{2}, \ldots, x_{n}\|_{\beta} $ for all $ x, y, x_{1}, x_{2}, \ldots, x_{n}\in X $ and $ \alpha\in {\mathbb{R}} $.
Then the function $ \|\cdot, \ldots, \cdot\|_{\beta} $ is called an $ (n, \beta) $-norm on $ X $ and the pair $ (X, \|\cdot, \ldots, \cdot\|_{\beta}) $ is called a linear $ (n, \beta) $-normed space or an $ (n, \beta) $-normed space.
Note that the concept of an $ (n, \beta) $-normed space is a generalization of an $ n $-normed space $ (\beta = 1) $ and of a $ \beta $-normed space $ (n = 1) $. For some examples of $ n $-normed space, we can refer to [48,49].
Definition 2.2. (cf. [49]) A sequence $ \{x_{k}\} $ in an $ (n, \beta) $-normed space $ X $ is called a convergent sequence if there exists $ x\in X $ such that
for all $ y_{2}, \ldots, y_{n}\in X $. In this case, we call that $ \{x_{k}\} $ converges to $ x $ or that $ x $ is the limit of $ \{x_{k}\} $, write $ x_{k}\to x $ as $ k\to \infty $ or $ \lim\limits_{k\to \infty}x_{k} = x $.
Definition 2.3. (cf. [49]) A sequence $ \{x_{k}\} $ in an $ (n, \beta) $-normed space $ X $ is called a Cauchy sequence if
for all $ y_{2}, \ldots, y_{n}\in X $. A linear $ (n, \beta) $-normed space in which every Cauchy sequence is convergent is called a complete $ (n, \beta) $-normed space.
Remark 2.1. (cf. [49]) Let $ (X, \|\cdot, \ldots, \cdot\|_{\beta}) $ be a linear $ (n, \beta) $-normed space, $ 0 < \beta\leq 1 $. One can show that conditions $ {\rm{(N2)}} $ and $ {\rm{(N4)}} $ in Definition 2.1 imply that
for all $ x, y, y_{2}, \ldots, y_{n}\in X $.
Lemma 2.1. (cf. [49]). Let $ (X, \|\cdot, \ldots, \cdot\|_{\beta}) $ be a linear $ (n, \beta) $-normed space, $ n\geq 2 $, $ 0 < \beta\leq 1 $. If $ x\in X $ and $ \|x, y_{2}, \ldots, y_{n}\|_{\beta} = 0 $ for all $ y_{2}, \ldots, y_{n}\in X $, then $ x = 0 $.
Lemma 2.2. (cf. [48,49]). Let $ (X, \|\cdot, \ldots, \cdot\|_{\beta}) $ be a linear $ (n, \beta) $-normed space, $ n\geq 2 $, $ 0 < \beta\leq 1 $. For a convergent sequence $ \{x_{k}\} $ in a linear $ (n, \beta) $-normed space $ X $,
for all $ y_{2}, \ldots, y_{n}\in X $.
In 1897, Hensel [16] has introduced a normed space which does not have the Archimedean property. It turned out that non-Archimedean spaces have many nice applications [22,23,33].
Definition 2.4. (cf. [30]) By a non-Archimedean field we mean a field $ {\mathbb{K}} $ equipped with a function (valuation) $ |\cdot|:{\mathbb{K}}\to [0, \infty) $ such that for $ r, s \in {\mathbb{K}} $, the following conditions hold:
(1) $ |r| = 0 $ if and only if $ r = 0 $;
(2) $ |rs| = |r||s| $;
(3) $ |r+s|\leq \max\{|r|, |s|\} $.
Clearly $ |1| = |-1| = 1 $ and $ |n|\leq 1 $ for all $ n\in {\mathbb{N}} $. By the trivial valuation we mean the function $ |\cdot| $ taking everything but $ 0 $ into $ 1 $ and $ |0| = 0 $ (i.e., the function $ |\cdot| $ is called the trivial valuation if $ |r| = 1, \forall r\in {\mathbb{K}}, r\neq 0 $, and $ |0| = 0 $).
Definition 2.5. (cf. [30]) Let $ X $ be a vector space over a scalar field $ {\mathbb{K}} $ with a non-Archimedean non-trivial valuation $ |\cdot| $. A function $ \|\cdot\|:X\to {\mathbb{R}} $ is called a non-Archimedean norm (valuation) if it satisfies the following conditions:
(ⅰ) $ \|x\| = 0 $ if and only if $ x = 0 $;
(ⅱ) For any $ r\in {\mathbb{K}} $ and $ x\in X $, $ \|rx\| = |r|\|x\| $;
(ⅲ) For all $ x, y\in X $, $ \|x+y\|\leq \max \{\|x\|, \|y\|\} $ (the strong triangle inequality).
Then $ (X, \|\cdot\|) $ is called a non-Archimedean normed space.
Now, we give the definition of a non-Archimedean $ (n, \beta) $-normed space which has been introduced in [49].
Definition 2.6. (cf. [49]) Let $ X $ be a real vector space with $ \dim X\geq n $ over a scalar field $ {\mathbb{K}} $ with a non-Archimedean non-trivial valuation $ |\cdot| $, where $ n $ is a positive integer and $ \beta $ is a constant with $ 0 < \beta\leq 1 $. A real-valued function $ \|\cdot, \ldots, \cdot\|_{\beta}: X^{n}\to {\mathbb{R}} $ is called a non-Archimedean $ (n, \beta) $-norm on $ X $ if the following conditions hold:
$ \rm{(N1^{\prime})} $ $ \|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} = 0 $ if and only if $ x_{1}, x_{2}, \ldots, x_{n} $ are linearly dependent;
$ \rm{(N2^{\prime})} $ $ \|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} $ is invariant under permutation of $ x_{1}, x_{2}, \ldots, x_{n} $;
$ \rm{(N3^{\prime})} $ $ \|\alpha x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} = |\alpha|^{\beta}\|x_{1}, x_{2}, \ldots, x_{n}\|_{\beta} $;
$ \rm{(N4^{\prime})} $ $ \|x+y, x_{2}, \ldots, x_{n}\|_{\beta}\leq \max\{\|x, x_{2}, \ldots, x_{n}\|_{\beta}, \|y, x_{2}, \ldots, x_{n}\|_{\beta}\} $ for all $ x, y, x_{1}, x_{2}, \ldots, x_{n}\in X $ and $ \alpha\in {\mathbb{K}} $. Then $ (X, \|\cdot, \ldots, \cdot\|_{\beta}) $ is called a non-Archimedean $ (n, \beta) $-normed space.
It follows from the preceding definition that the non-Archimedean $ (n, \beta) $-normed space is a non-Archimedean $ n $-normed space if $ \beta = 1 $, and a non-Archimedean $ \beta $-normed space if $ n = 1 $, respectively.
Remark 2.2. (cf. [49]) A sequence $ \{x_{k}\} $ in a non-Archimedean $ (n, \beta) $-normed space $ X $ is a Cauchy sequence if and only if $ \{x_{k+1}-x_{k}\} $ converges to zero.
3.
Main results
In this section, we will assume that $ X $ is an $ n $-normed space vector space and $ Y $ is a complete non-Archimedean $ (n, \beta) $-normed space, where $ n\geq 2 $ and $ 0 < \beta \leq 1 $. We prove the generalized Hyers-Ulam stability of the mixed type quadratic-cubic functional Eq (1.4) in non-Archimedean $ (n, \beta) $-normed spaces. For the sake of convenience, given mapping $ f:X\to Y $, we define the difference operator $ D_{f}(x, y):X\to Y $ of the functional Eq (1.4) by
for all $ x, y\in X $.
Before proceeding to the proof of the main results, we first introduce the following lemmas which will be used in this paper.
Lemma 3.1. (cf. [44]). Let $ V $ and $ W $ be real vector spaces. If an even mapping $ f:V\to W $ satisfies (1.4), then $ f $ is quadratic.
Lemma 3.2. (cf. [44]). Let $ V $ and $ W $ be real vector spaces. If an odd mapping $ f:V\to W $ satisfies (1.4), then $ f $ is cubic.
Theorem 3.1. Let $ \varphi:X^{n+1}\to [0, \infty) $ be a function such that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. The limit
denoted by $ \tilde{\varphi}_{Q}(x, u_{2}, \ldots, u_{n}) $, exists for all $ x, u_{2}, \ldots, u_{n}\in X $. Suppose that $ f: X\to Y $ is an even function satisfying $ f(0) = 0 $ and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a quadratic function $ Q:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $, and if, in addition,
then $ Q $ is the unique quadratic function satisfying (3.4).
Proof. Putting $ x = 0 $ in (3.3), and by the evenness of $ f $, we get
for all $ y, u_{2}, \ldots, u_{n}\in X $. If we replace $ y $ by $ x $ in (3.5) and divide both sides of (3.5) by $ |4|^{\beta} $, then we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. Replacing $ x $ by $ 2^{m}x $ in (3.6) and dividing both sides of (3.6) by $ |4|^{m\beta} $, we obtain
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. Taking the limit as $ m\to \infty $ and using (3.1), we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. By Remark 2, we know that the sequence $ \{\frac{f(2^{m}x)}{4^{m}}\} $ is Cauchy. Since $ Y $ is a complete space, we conclude that $ \{\frac{f(2^{m}x)}{4^{m}}\} $ is convergent. So we can define the function $ Q: X\to Y $ by
for all $ x\in X $. It follows from (3.1) and (3.3) that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. By Lemma 2.1, we get $ D_{Q}(x, y) = 0 $ for all $ x, y\in X $. Therefore the function $ Q:X\to Y $ satisfies (1.4). Since $ f $ is an even function, $ Q $ is an even function. By Lemma 3.1 (see also [44, Corollary 2.2]), $ Q $ is quadratic. Then $ Q $ satisfies
for all $ x, y\in X $. Letting $ x = 0 $ in (3.9), and by the evenness of $ Q $, we get $ Q(2x) = 4Q(x) $, so $ Q(2^{m}x) = 4^{m}Q(x) $.
Replacing $ x $ by $ 2x $ in (3.6) and dividing both sides by $ |4|^{\beta} $, we obtain
for all $ x, u_{2}, \ldots, u_{n}\in X $. It follows from (3.6) and (3.10) that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
By induction on $ m $, we get
for all $ x, u_{2}, \ldots, u_{n}\in X $. Replacing $ x $ by $ 2x $ in (3.11) and dividing both sides by $ |4|^{\beta} $, we get
for all $ x, u_{2}, \ldots, u_{n}\in X $. By (3.6) and (3.12), we obtain
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. This completes the proof of (3.11). By taking the limit as $ m\to \infty $ in (3.11) and using (3.2), one obtains (3.4).
Now we proceed to prove the uniqueness property of $ Q $. Let $ Q^{\prime} $ be another quadratic function satisfying (3.4). Since
for all $ x, u_{2}, \ldots, u_{n}\in X $. So we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. If
then $ \|Q(x)-Q^{\prime}(x), u_{2}, \ldots, u_{n}\|_{\beta} = 0 $. By Lemma 2.1, $ Q = Q^{\prime} $, and the proof is complete.
Corollary 3.1. Let $ \rho:[0, \infty)\to [0, \infty) $ be a function satisfying
(ⅰ) $ \rho(|2|t)\leq \rho(|2|)\, \rho(t) $ for all $ t\geq 0 $,
(ⅱ) $ \rho(|2|)\leq |2|^{r\beta} $, where $ r $ is a fixed real number in $ r\in [2, \infty) $.
Let $ \delta > 0 $, $ X $ be an $ n $-normed space with norm $ \|\cdot, \ldots, \cdot\| $, let $ f:X\to Y $ be an even function with $ f(0) = 0 $ and satisfying the inequality
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a unique quadratic function $ Q:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Proof. Define $ \varphi:X^{n+1}\to [0, \infty) $ by
Since $ |4|^{-\beta}\rho(|2|) < |2|^{(r-2)\beta}\leq 1 $, we have
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Also
and
for all $ x, u_{2}, \ldots, u_{n}\in X $. Hence the result follows by Theorem 3.1.
Theorem 3.2. Let $ \varphi:X^{n+1}\to [0, \infty) $ be a function such that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. The limit
denoted by $ \tilde{\varphi}_{C}(x, u_{2}, \ldots, u_{n}) $, exists for all $ x, u_{2}, \ldots, u_{n}\in X $. Suppose that $ f: X\to Y $ is an odd function satisfying
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a cubic function $ C:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $. And if, in addition,
then $ C $ is the unique cubic function satisfying (3.19).
Proof. Putting $ x = 0 $ in (3.18), and by the oddness of $ f $, we get
for all $ y, u_{2}, \ldots, u_{n}\in X $. If we replace $ y $ by $ x $ in (3.20) and divide both sides of (3.20) by $ |8|^{\beta} $, then we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. Replacing $ x $ by $ 2^{j}x $ in (3.21) and dividing both sides of (3.21) by $ |8|^{m\beta} $, we obtain
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. Taking the limit as $ m\to \infty $ and using (3.16), we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. By Remark 2, we know that the sequence $ \{\frac{f(2^{m}x)}{8^{m}}\} $ is Cauchy. Since $ Y $ is a complete space, we conclude that $ \{\frac{f(2^{m}x)}{8^{m}}\} $ is convergent. So we can define the function $ C: X\to Y $ by
for all $ x\in X $.
Similar to the proof of Theorem 3.1, using induction one can show that
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. By taking $ m $ to approach infinity in (3.24) and using (3.17), one obtains (3.19). It follows from (3.16) and (3.18) that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. By Lemma 2.1, we get $ D_{C}(x, y) = 0 $ for all $ x, y\in X $. Therefore the function $ C:X\to Y $ satisfies (1.4). Since $ f $ is an odd function, $ C $ is an odd function. By Lemma 3.2 (see also [44, Corollary 2.2]), $ C $ is cubic. Then $ C $ satisfies
for all $ x, y\in X $. Letting $ x = 0 $ in (3.25), and by the oddness of $ C $, we get $ C(2x) = 8C(x) $, so $ C(2^{m}x) = 8^{m}C(x) $. Let
for all $ x, u_{2}, \ldots, u_{n}\in X $ and let $ C^{\prime} $ be another cubic function satisfying (3.19). Then
for all $ x, u_{2}, \ldots, u_{n}\in X $. Therefore $ \|C(x)-C^{\prime}(x), u_{2}, \ldots, u_{n}\|_{\beta} = 0 $. By Lemma 2.1, we have $ C = C^{\prime} $. This completes the proof of the uniqueness of $ C $.
Corollary 3.2. Let $ \rho:[0, \infty)\to [0, \infty) $ be a function satisfying
(ⅰ) $ \rho(|2|t)\leq \rho(|2|)\, \rho(t) $ for all $ t\geq 0 $,
(ⅱ) $ \rho(|2|)\leq |2|^{\lambda\beta} $, where $ \lambda $ a fixed real number in $ \lambda\in [3, \infty) $.
Let $ \delta > 0 $, $ X $ be an $ n $-normed space with norm $ \|\cdot, \ldots, \cdot\| $, let $ f:X\to Y $ be an odd function satisfying the inequality
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a unique cubic function $ C:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Proof. The proof is similar to the proof of Corollary 3.1 and the result follows from Theorem 3.2.
Combining Theorems 3.1 and 3.2, we obtain the following theorem.
Theorem 3.3. Let $ \varphi:X^{n+1}\to [0, \infty) $ be a function such that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. The limit
denoted by $ \tilde{\varphi}_{Q}(x, u_{2}, \ldots, u_{n}) $, and
denoted by $ \tilde{\varphi}_{C}(x, u_{2}, \ldots, u_{n}) $, exists for all $ x, u_{2}, \ldots, u_{n}\in X $. Suppose that $ f:X\to Y $ is a function satisfying $ f(0) = 0 $ and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exist a quadratic function $ Q:X\to Y $ and a cubic function $ C:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $, and if, in addition,
then $ Q $ is the unique quadratic function and $ C $ is the unique cubic function.
Proof. Let $ f_{e}(x) = \frac{1}{2}[f(x)+f(-x)] $ for all $ x\in X $. Then $ f_{e}(0) = 0 $, $ f_{e}(-x) = f_{e}(x) $ for all $ x \in X $, and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. By Theorem 3.1, then there exists a unique quadratic function $ Q:X\to Y $ satisfying
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Let $ f_{o}(x) = \frac{1}{2}[f(x)-f(-x)] $ for all $ x\in X $. Then $ f_{o}(0) = 0 $, $ f_{o}(-x) = -f_{o}(x) $, and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. By Theorem 3.2, then there exists a unique cubic function $ C:X\to Y $ satisfying
for all $ x, u_{2}, \ldots, u_{n}\in X $. Hence, (3.32) follows from (3.33) and (3.34). This completes the proof of the theorem.
From now on, assume that $ |2|\neq 1 $, $ X $ is a non-Archimedean $ (n, \beta_{1}) $-normed space and $ Y $ is a complete non-Archimedean $ (n, \beta) $-normed space, where $ n\geq 2 $ and $ 0 < \beta, \beta_{1}\leq 1 $. We can formulate our results as follows.
Theorem 3.4. Let $ \theta\in [0, \infty) $, $ p, q\in (0, \infty) $ with $ (p+q)\beta_{1} > 2\beta $. Suppose that $ f: X\to Y $ is an even function satisfying $ f(0) = 0 $ and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a unique quadratic function $ Q:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Proof. Putting $ x = 0 $ in (3.35), and by the evenness of $ f $, we get
for all $ y, u_{2}, \ldots, u_{n}\in X $. If we replace $ y $ by $ x $ in (3.37) and divide both sides of (3.37) by $ |4|^{\beta} $, then we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. Replacing $ x $ by $ 2^{m}x $ in (3.38) and dividing both sides of (3.38) by $ |4|^{m\beta} $, we obtain
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. Since $ (p+q)\beta_{1} > 2\beta $ and $ |2|\neq 1 $, we have
for all $ x, u_{2}, \ldots, u_{n}\in X $. By Remark 2, we know that the sequence $ \{\frac{f(2^{m}x)}{4^{m}}\} $ is Cauchy. Since $ Y $ is a complete space, we conclude that $ \{\frac{f(2^{m}x)}{4^{m}}\} $ is convergent. So we can define the function $ Q: X\to Y $ by
for all $ x\in X $. Similar to the proof of Theorem 3.2, using induction one can show that
for all $ x, u_{2}, \ldots, u_{n}\in X $ and $ m\in {\mathbb{N}} $. By taking the limit as $ m\to \infty $ in (3.41), we obtain (3.36).
It follows from (3.35) and Lemma 2.2 that
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Since $ (p+q)\beta_{1} > 2\beta $ and $ |2|\neq 1 $, we get
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. By Lemma 2.1, we get $ D_{Q}(x, y) = 0 $ for all $ x, y\in X $. Therefore the function $ Q:X\to Y $ satisfies (1.4). Since $ f $ is an even function, $ Q $ is an even function. By Lemma 3.1 (see also [44, Corollary 2.2]), $ Q $ is quadratic. Then, we get $ Q(2x) = 4Q(x) $ and $ Q(2^{m}x) = 4^{m}Q(x) $.
To prove the uniqueness property of $ Q $. Let $ Q^{\prime} $ be another quadratic function satisfying (3.36). Then
for all $ x, u_{2}, \ldots, u_{n}\in X $. By Lemma 2.1, we get $ Q = Q^{\prime} $ for all $ x\in X $. So $ Q $ is the unique quadratic function satisfying (3.36).
Theorem 3.5. Let $ \theta\in [0, \infty) $, $ p, q\in (0, \infty) $ with $ (p+q)\beta_{1} > 3\beta $. Suppose that $ f: X\to Y $ is an odd function satisfying
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exists a unique cubic function $ C:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Proof. The proof is similar to the proof of Theorem 3.4.
Next, combining Theorems 3.4 and 3.5, we obtain the following result.
Theorem 3.6. Let $ \theta\in [0, \infty) $, $ p, q\in (0, \infty) $ with $ (p+q)\beta_{1} > 3\beta $. Suppose that $ f:X\to Y $ is a function satisfying $ f(0) = 0 $ and
for all $ x, y, u_{2}, \ldots, u_{n}\in X $. Then there exist a unique quadratic function $ Q:X\to Y $ and a unique cubic function $ C:X\to Y $ such that
for all $ x, u_{2}, \ldots, u_{n}\in X $.
Proof. The proof is similar to the proof of Theorem 3.3 and the result follows from Theorems 3.4 and 3.5.
Acknowledgments
The author is grateful to the referees for their helpful comments and suggestions that help to improve the quality of the manuscript.
Conflict of interest
The author declares no conflict of interest in this paper.













 DownLoad:
DownLoad: