Time and frequency responses of non-integer order RLC circuits

1.   Introduction

Many of the physical systems show intrinsic fractional order behavior ^{[1,2,3,4,5,6]}. Therefore, fractional calculus provides more accurate models than classical calculus for such systems ^[7,8]. A significant benefit of fractional modelling appears for systems where hereditary and memory behaviors are involved since fractional derivative takes into account the past history as well ^[3,9,10]. Another beneficial use appears for the analysis of porous and/or self-similar structures where theory of fractals are involved ^[10,11].

Like many of the physical systems, some electrical systems are also better modelled by fractional calculus either due to their structures (such as tree structures, domino ladders, etc.) or element behaviors (coils, capacitors, memristors) ^{[9,12,13,14,15]}.

A systematic way of constructing fractional differential equation for physical systems consists in to analyze the dimensionality and to bring the fractional derivative operator in consistency ^[16]. As the generalization of this work, F. Gomez, J. Rosales, and M. Guia have obtained an analytical time domain solution in terms of the Mittag-Leffler function for the fractional $RLC$ circuit ^[17]. This circuit is not externally excited but it is forced by the initial charge on the capacitor. They have not studied the forced solution of the circuit when it is excited by an external source but commented about the use of the circuit as fractional filters analogical to ordinary second order electrical $RLC$ filters; the element behavior equations are also missing.

The purpose of this contribution is to investigate the time and frequency domain responses of the $RLC$ circuit proposed by F. Gomez at al. under the excitement by an external voltage source; the frequency responses obtained show that the circuit can be used as fractional low-pass, high-pass and band-pass filters. Section Ⅱ is devoted to the introduction of the fractional $RLC$ circuit and its natural response. Section Ⅲ covers its frequency response characteristics and its usage as three basic types of electrical filters. The sinusoidal responses of the obtained filters are studied in Section Ⅳ. Finally, Section Ⅴ covers the conclusions.

2.   Fractional $RLC$ circuit; Natural response

It is well known that a series $RLC$ circuit is described by the homogenous differential equation

where $R, L, C$ are the resistance, inductance, and capacitance in ohms $(\Omega ),$ henries $(H),$ and farads $(F),$ respectively; $q(t)$ is the charge circulating in the circuit and accumulated on the capacitor. Each term in the above formula represents the potential across the associated component so that the total potential in the circuit sums to zero ^[18].

A systematic way to construct the fractional differential equation from Eq. (2.1) is to replace the derivative operator by fractional operator as follows:

where the parameter $\sigma$ has the dimension of seconds and $0<\gamma \leq 1$ represents the order of Caputo fractional time derivative ^[16,17] defined by

where $\tau \in R, n-1<\gamma \leq n\in N = \{1, 2, \ldots \}, f^{n}$ represents the ordinary derivative of order $n,$ and $\Gamma$ is the Gamma function. For $\Gamma = 1,$ Eq. (2.2) gives the usual derivative. Result of application of Eq. (2.2) to Eq. (2.1) yields the fractional differential equation

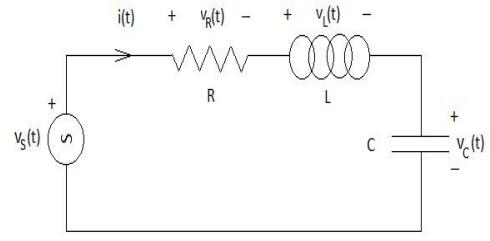
where $v_{s}(t)$ is the added voltage source excitation in the circuit as shown in Figure 1. The voltage across each component and hence the element behavior equations in the circuit are represented by the following equations:

The homogeneous solution of the fractional differential equation in (2.3) with the initial condition $q(t) = q_{0}$ is obtained by F. Gomez et al. ^[17]. But there are some conflicts in their solutions and plots. To be sure, the correct solution is derived for the underdamped case $R<2\sqrt{L/C},$ the result is

where

In these formulas, $w_{0}$ is the undamped natural frequency, $\xi$ is the damping ratio, $\lambda _{1}$ is a zero of the characteristic polynomial in powers of $s^{\gamma },$ and $E_{\alpha , \beta }(\bullet )$ is the $2-$parameter Mittag-Leffler function.

The solutions show that the oscillatory damping occurs for values of $\gamma$ near to $1$. For values of $\gamma$ near to zero, the solutions monotonically damp to $0$ as $t\rightarrow \infty .$

3.   Fractional $RLC$ circuit; Forced response

Although analytical and explicit solutions are given for the natural response in ^[17] and corrected in (2.7-2.11), these results do not give direct information about the behavior of the $RLC$ circuit of non-integer order in respect to its time and frequency domain characteristics, that is they do not give information about the input-output relation of the circuit since it is unexcited by an external forcing source. In this section, the frequency domain characteristics (gain and phase) and the time domain characteristics for step responses are obtained, and the relevant filtering property of the circuit excited by a voltage source is investigated.

Taking the Laplace transform of the equations in (2.3) and (2.4-2.6), and solving them for $V_{R}(s), V_{L}(s), V_{C}(s),$ where the uppercase lettered signals represent the Laplace transform of the lowercase lettered signals, we obtain the following transfer functions in the complex frequency variable $s = \sigma +j\omega :$

Obviously, these are the fractional transfer functions resulting with the band pass, high pass and low pass filter characteristics, respectively. Gain $(M)$ and phase $(\emptyset )$ characteristics are obtained by substituting $s = j\omega$ and taking the magnitude and phase angle of the transfer functions. The results are:

where

As the numerical example for the underdamped case, consider $R = 0.3922327$ $\mathbb U{2126} ,$ $L = 1$ $H,$ $C = 1$ $F,$ which corresponds to the case $R/2L\sqrt{w_{0}^{2}-\xi ^{2}} = 1/5$ as in ^[17], and $\omega _{0} = 1$ $r/s,$ $\xi = 0.196116,$ $\gamma = 0.980581$ $\sigma$. The frequency response curves (magnitude and phase) and the step responses are obtained and plotted in Figures 2-7, for the band pass, high pass and low pass cases. The plots are carried for values of $\gamma = 1.00, 0.92, 0.75, 0.25$. The overdamped case is not considered as the numerical example since all the three types of basic filter characteristics valid for underdamped case do not occur for the overdamped case.

The band pass characteristics plotted in Figure 2 show that the peak value of the magnitude, the center frequency, and the quality factor decrease with decreasing $\gamma$. The data including the cutoff frequencies are shown in Table 1 where $w_{p}$: Center frequency, $M_{p}$: Peak magnitude, $w_{1}, w_{2}$: Cut off frequencies, $BW$: Band width, $Q = \omega _{p}/BW$: Quality factor.

For $\gamma = 0.25,$ it is hard to say that the characteristic is of band-pass type since $Q$ is very small. The phase responses in the same figure is seen to change from $90^{o}$ to $-90^{o}$ but flatter with decreasing $\gamma$.

The step responses of the filters are obtained by multiplying the transfer functions in Eqs. (3.7), (3.8), (3.9) by $1/s$ and taking their inverse Laplace transforms. The results for $BP,$ $HP,$ $LP$ filters are obtained, respectively, as

The step response of the band pass filter is plotted in Figure 3 for values of $\gamma = 1.00, 0.92, 0.75, 0.25$. It is observed that all step responses start from $0$ and after several peaks damp to $0$. Number of peaks and their magnitudes $\left( M_{p1}, M_{p2}, \cdots \right)$ decrease as $\gamma$ decreases from $1$ to $0.25$. The data including characteristic time values are shown in Table 2. Note that the rise time and the settling time are not defined for reference value is not defined for $BP$ characteristics. It is important to remark also that although the element values of $R, L, C$ correspond to an underdamped second order dynamics, the fractional $RLC$ circuit do not show the oscillatory time response characteristics of an ordinary underdamped $RLC$ circuit for small values of $\gamma$ (see the plot for $\gamma = 0.25$ in Figure 3, see also the natural responses for $\gamma = 0.25, 0.50$ in Figure 1 of ^[17]). In fact, number of peaks (and hence oscillations) decreases with decreasing $\gamma$.

The high pass characteristics plotted in Figure 4 show that the $0$ frequency and $\infty$ frequency gains are $0$ and $1$, respectively. But the peak value of the magnitude decreases with decreasing $\gamma$ whilst the peak frequency is increasing. The relevant data are shown in Table 3 in detail. There is no peak value and stop bandwidth is very narrow for $\gamma = 0.25$. So, it is hard to say that the characteristic is of high pass type. The characteristic is like that of a band pass type (with higher peak gains$>0$) around the center frequency for $\gamma = 1.00$ and $0.92$. For $\gamma = 0.25$, there is no peak in the gain. The phase responses in the same figure is seen to change from $180^{o}$ to $0^{o},$ but flatter with decreasing $\gamma$ as in the band pass case.

The step response of the high pass filter is plotted in Figure 5 for values of $\gamma = 1.00, 0.92, 0.75, 0.25$; all the responses start from $1$ at $t = 0$ and approach to zero with increasing time as expected due to high pass characteristics. It is observed that the magnitude and number of the oscillations reduces with decreasing $\gamma$. And the circuit step response gets away from the typical underdamped oscillatory characteristics of an underdamped second order $RLC$ circuit as $\gamma$ approaches to $0$. In fact, the step response monotonically decays to zero for $\gamma = 0.25$. The relevant data are shown in Table 4.

The low pass characteristics plotted in Figure 6 show that the $0$ frequency and $\infty$ frequency gains are $1$ and $0$, respectively. The peak value of the magnitude decreases and disappears with decreasing Ue30d. For $\gamma = 1.00$ and $\gamma = 0.92$, the characteristics is like that of band pass due to high peak values of the magnitudes. The relevant data are shown in Table 5. For $\gamma = 0.25$, the characteristic is of low-pass type with a very narrow band width. The phase responses in Figure 6 are seen to change from $0^{o}$ to $-180^{o}$, but flatter with decreasing $\gamma$ as in the band pass case.

The step response of the low pass filter is shown in Figure 7 for values of $\gamma = 1.00, 0.92, 0.75, 0.25$. All the responses start from $0$ at $t = 0$ and increase to unity as $t\rightarrow \infty$. It is observed that the magnitude of the oscillations and the number of oscillations reduce with decreasing $\gamma$. Again, the plots get away from the typical underdamped oscillatory characteristics of an underdamped second order $RLC$ circuit as $\gamma$ approaches to $0$. In fact, the step response monotonically increases to $1$ for $\gamma = 0.25$. The relevant data is shown in shown in Table 6. The rise time and the settling time could not be detected be for the case $\gamma = 0.25$ since the data is taken up to $t = 50s$.

4.   Sinosoidal responses

When a sine wave voltage is applied at the input, the resulting sinusoidal responses of the filters are discussed in this section. A sine wave input voltage of magnitude $1$ and phase $0$ is used as the voltage excitation in all the simulations.

The band pass filter sinusoidal response is checked by applying a sine wave of frequency $f = 0.125$ $Hz,$ $\omega = 0.25\pi$ $r/s$ which is smaller than the center frequencies in Table 1 (except $\gamma = 0.25$). The sinusoidal responses are shown in Figure 8, where the peaks and phases of the sine waves as approaching to steady-state are consistent with the frequency response curves in Figure 2. All the responses are leading the input by a phase decreasing with $\gamma$. All the magnitudes decrease with decreasing $\gamma$ as well. Note that the consistency holds after a few periods of time when the steady state sinusoidal response has been reached. When the input frequency is increased to $\omega = 1$ and $0.4\pi$ $r/s$, the sinusoidal responses are shown in Figures 11, 12 and 13 respectively. The consistency with the frequency response curves in Figure 2 still holds. For example, for $\omega = 0.4\pi$, all the responses are lagging due to the negative phase characteristics at this frequency. Note that all the responses have almost in phase with the input for $\omega = 1$ as seen in Figures 11 and 12, which is expected due to the small phases in Figure 2 at this frequency for all $\gamma .$

The sinusoidal response of the high pass filter is obtained at two frequencies $\omega = 0.5$ and $1.5$. The results are shown in Figures 11 and 12. It is observed that the sinusoidal responses at the steady state conditions show the gain and phase characteristics implied by Figure 4.

Finally, the sinusoidal response of the low pass filter is obtained for a single frequency $\omega = 0.5$ $r/s$ in the pass band. It is seen in Figure 13 that all the responses are lagging the input in accordance to the phase response seen in Figure 6. Further, the gain is decreasing with decreasing $\gamma$ as implied by the magnitude characteristic of the same figure.

The steady state variations of the sinusoidal responses in Figures 8-13, that is their variations for large time, are seen to be in coherence with the following formulas giving the steady state sinusoidal responses

where the gains $M_{i}$'s and the phases $\theta _{i}$' are as defined in Eqs. (3.4), (3.5), (3.6), respectively.

5.   Conclusion

The frequency and time response characteristics of an $RLC$ electrical circuit of non-integer order are examined in this paper. The circuit is shown to be used as band pass, high pass and low pass filters. The original $RLC$ values are chosen for a second order ordinary $RLC$ circuit of an underdamped type. The overdamped case is not considered since not all the considered three types of filter characteristics occur for this case. FOMCON Toolbox integrated with MATLAB R2017a is used to evaluate the fractional operations and Bode plots ^[19]. Fractional order RLC circuit is derived by applying the fractional derivative operator in consistency with the dimensionality ^[16] to the Kirchhoff's voltage low equation of the ordinary series $RLC$ circuit excited by a voltage source ^[18]. The results stand as the answer to the future work indicated by F. Gomez at al. who obtained analytical solutions for time domain natural responses in terms of the Mittag-Leffler function for the treated fractional unexcited $RLC$ circuit ^[17].

As the future work, the underdamped forced responses can be studied and the associated analytical results for the step responses can be searched. Similar research could also be conducted for higher order fractional $RLC$ circuits.

Conflict of Interest

Authors declare that there is no conflict of interest.