Citation: Oanh Chau. A class of thermal sub-differential contact problems[J]. AIMS Mathematics, 2017, 2(4): 658-681. doi: 10.3934/Math.2017.4.658
Phenomena of contact between deformable bodies abound since the dawn of time. In order to understand their inherent complexity, considerable efforts have been achieved in modeling, mathematical analysis and numerical simulations, within the weak distributional formulation framework, expressed in terms of evolutional variational inequalities and hemivariational inequalities. The literature dedicated to this field is increasing day by day. The state of the art can be found in the masterpieces [4], [6], [7], [8].
This work is a continuation of the paper in [1], where the authors studied a dynamic frictional sub-differential contact for a short memory visco-elastic body, which was supposed to be fixed in some part on its boundary. There were no thermal effects and no numerical studies.
Here we investigate the extension of this work to thermal contact with friction, for time depending long memory visco-elastic materials, with or without the clamped condition. Moreover, we propose a fully discrete scheme for numerical approximations of the different solutions, and elaborate a general numerical analysis of error estimates. Finally various corresponding numerical computations in dimension two will be given.
The paper is organized as follows. In Section 2 we describe the mechanical problem, its corresponding variational formulation, and then we claim the main existence and uniqueness result under specific assumptions, that we prove in Section 3. In Section 4, we introduce a fully discrete approximation scheme, derive and prove an optimal order error estimate under certain solution regularity assumptions. Finally in Section 5, we present several numerical simulations, showing then the evolution of the displacement field and temperature, as well as of the Von Mise's stress norm.
In this section we study a class of thermal contact problems with sub-differential conditions, for long memory visco-elastic materials. We describe the mechanical problem, list the assumptions on the data and derive the corresponding variational formulation. Then we state an existence and uniqueness result on displacement field and temperature, which we will prove in the next section.
The physical setting is as follows. A visco-elastic body occupies a domain $\Omega$ in $\mathbb{R}^d$ ($d=1$, $d=2$ or $d=3$) with a Lipschitz boundary $\Gamma$ that is partionned into three disjoint measurable parts, $\Gamma_1$, $\Gamma_2$ and $\Gamma_3$. We denote by $ \mathit{\boldsymbol{\nu}}$ the unit outward normal on $\Gamma$. Let $[0, T]$ be the time interval of interest, where $T > 0$. The body is clamped on $\Gamma_{1} \times (0, T)$ and therefore the displacement field vanishes there. Here we suppose that meas$(\Gamma_1) = 0 $ or meas$(\Gamma_1) > 0 $, which means that $\Gamma_1$ may be an empty set or reduced to a finite set of points. We assume that a volume force of density $\mathit{\boldsymbol{f}}_0$ acts in $\Omega \times (0, T)$ and that surface tractions of density $\mathit{\boldsymbol{f}}_2$ act on $\Gamma_2 \times (0, T)$. The body may come in contact with an obstacle, the foundation, over the potential contact surface $\Gamma_3$. The model of the contact is specified by a general sub-differential boundary condition, where thermal effects may occur in the frictional contact with the basis. We are interested in the dynamic evolution of the body.
Let us recall now some classical notations, see e.g. [4] for further details. We denote by $S_{d}$ the space of second order symmetric tensors on $ \mathbb{R}^{d}$, while `` $\cdot$ " and $|\cdot|$ will represent the inner product and the Euclidean norm on $S_{d}$ and $\mathbb{R}^d$. Everywhere in the sequel the indices $i$ and $j$ run from $1$ to $d$, summation over repeated indices is implied and the index that follows a comma represents the partial derivative with respect to the corresponding component of the independent variable. We also use the following notation:
| $ H= \Big(L^{2}(\Omega)\Big)^d, \qquad {\mathcal H}=\{\, \mathit{\boldsymbol{\sigma }}=(\sigma_{ij})\, \, |\, \, \sigma_{ij}=\sigma_{ji} \in L^{2}(\Omega), \ 1\leq i, j \leq d \}, $ |
| $ H_{1}=\{\, {\mathit{\boldsymbol{u}}} \in H\, \, |\, \, \mathit{\boldsymbol{\varepsilon }}({\mathit{\boldsymbol{u}}}) \in {\mathcal H}\, \}, \qquad {\mathcal H}_{1} = \{\, \mathit{\boldsymbol{\sigma }} \in {\mathcal H} \, \, |\, \, {\rm{Div}}\, \mathit{\boldsymbol{\sigma }} \in H\, \}. $ |
Here $ \mathit{\boldsymbol{\varepsilon }} : H_{1} \longrightarrow {\mathcal H}$ and $ {\rm {\rm{Div}}} : {\mathcal H}_{1} \longrightarrow H $ are the deformation and the divergence operators, respectively, defined by :
| $ \mathit{\boldsymbol{\varepsilon }}({\mathit{\boldsymbol{u}}}) = (\varepsilon_{ij}({\mathit{\boldsymbol{u}}})), \quad \varepsilon_{ij}({\mathit{\boldsymbol{u}}}) = \frac{1}{2}( u_{i, j} + u_{j, i} ), \quad {\rm{Div}}\, \mathit{\boldsymbol{\sigma }} = (\sigma_{ij, j} ). $ |
The spaces $H$, ${\mathcal H}$, $H_{1}$ and ${\mathcal H}_{1}$ are real Hilbert spaces endowed with the canonical inner products given by :
| $ ( {\mathit{\boldsymbol{u}}}, \mathit{\boldsymbol{v}} )_H = \int_{\Omega}{u_{i}v_{i}\, dx}, \qquad ( \mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\tau }} )_{\mathcal H} = \int_{\Omega}{\sigma_{ij}\tau_{ij}\, dx }, $ |
| $ ( {\mathit{\boldsymbol{u}}}, \mathit{\boldsymbol{v}} )_{H_{1}}= ( {\mathit{\boldsymbol{u}}}, \mathit{\boldsymbol{v}} )_H + ( \mathit{\boldsymbol{\varepsilon }}({\mathit{\boldsymbol{u}}}), \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}}) )_{\mathcal{H}}, \qquad ( \mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\tau }} )_{{\mathcal H}_1} = (\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\tau }} )_{\mathcal H} + ( {\rm{Div}}\, \mathit{\boldsymbol{\sigma }}, {\rm{Div}}\, \mathit{\boldsymbol{\tau }} )_{H}. $ |
Recall that $ \mathcal{D}(\Omega)$ denotes the set of infinitely differentiable real functions with compact support in $\Omega$; and $ W^{m, p}(\Omega) $, $H^m(\Omega) := W^{m, 2}(\Omega)$, $m\in \mathbb{N}$, $1 \leq p \leq +\infty$ for the classical real Sobolev spaces; $L^p(U; X)$ the classical $L^p$ spaces defined on $U$ with values in $X$.
To continue, the mechanical problem is then formulated as follows.
Problem $Q$: Find a displacement field $\mathit{\boldsymbol{u}} :(0, T) \times \Omega \longrightarrow \mathbb{R}^{d}$ and a stress field $\, \mathit{\boldsymbol{\sigma }} :\, (0, T) \times \Omega\longrightarrow S_d$ and a temperature field $\xi:\, (0, T) \times \Omega\longrightarrow \mathbb{R}_+$ such that for a.e. $t \in (0, T)$:
| $ \mathit{\boldsymbol{\sigma }}(t) = {\mathcal A}(t) \mathit{\boldsymbol{\varepsilon }}(\dot{\mathit{\boldsymbol{u}}}(t))+ {\mathcal G}(t) \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(t)) \\ \qquad + \int_0^t\, {\mathcal B}(t-s)\, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds + \, C_e(t, \xi(t)) \quad \mbox{in} \quad \Omega $ | (2.1) |
| $ \ddot{\mathit{\boldsymbol{u}}}(t) = {\rm Div}\, \mathit{\boldsymbol{\sigma }}(t) + \mathit{\boldsymbol{f}}_0(t) \quad \mbox{in} \quad \Omega $ | (2.2) |
| $ \mathit{\boldsymbol{u}}(t) = 0 \quad \mbox{on} \quad \Gamma_{1} $ | (2.3) |
| $ \mathit{\boldsymbol{\sigma }}(t) \mathit{\boldsymbol{\nu}} = \mathit{\boldsymbol{f}}_2(t) \quad \mbox{on} \quad \Gamma_2 $ | (2.4) |
| $ \mathit{\boldsymbol{u}}(t) \in U, \quad {\varphi_u}(t, \mathit{\boldsymbol{w}}) - \varphi_u(t, \dot {\mathit{\boldsymbol{u}}}(t)) \geq -\mathit{\boldsymbol{\sigma }}(t)\mathit{\boldsymbol{\nu}}\cdot(\mathit{\boldsymbol{w}}-\dot {\mathit{\boldsymbol{u}}}(t))\quad \forall \mathit{\boldsymbol{w}} \in U \quad \mbox{ on } \ \Gamma_3 $ | (2.5) |
| $ \dot{\xi}(t) - {\rm div}({\cal K}_{c}(t, \nabla \xi(t))) = {\cal C}_e(t, \dot{\mathit{\boldsymbol{u}}}(t) ) + q(t) \quad \mbox{in}\quad \Omega, $ | (2.6) |
| $ -{\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \nabla \xi(t, \mathit{\boldsymbol{x}})) \, \nu := \Xi(t, \mathit{\boldsymbol{x}}, \xi(t, \mathit{\boldsymbol{x}})) \in \partial \varphi(t, \mathit{\boldsymbol{x}}, \xi(t, \mathit{\boldsymbol{x}})) \quad \mbox{a.e.}\quad \mathit{\boldsymbol{x}} \in \Gamma_3, $ | (2.7) |
| $ \xi(t) = \theta_a(t) \quad \mbox{on} \quad \Gamma_1 \cup \Gamma_2 $ | (2.8) |
| $ \xi(0) = \xi_0 \quad \mbox{in} \quad \Omega $ | (2.9) |
| $ \mathit{\boldsymbol{u}}(0) = \mathit{\boldsymbol{u}}_0, \quad \dot{\mathit{\boldsymbol{u}}}(0)=\mathit{\boldsymbol{v}}_0 \quad \mbox{in} \quad \Omega $ | (2.10) |
Here, (2.1) is the Kelving Voigt's time-dependent long memory thermo-visco-elastic constitutive law of the body, where $ \mathit{\boldsymbol{\sigma }}$ represents the stress tensor; ${\cal A}$ denotes the viscosity operator depending on the velocity of infinitesimal deformations $\mathit{\boldsymbol{\varepsilon }}(\dot{\mathit{\boldsymbol{u}}})$, with the notation : for $\mathit{\boldsymbol{\tau }} \in S_d$, $ {\cal A}(t)\mathit{\boldsymbol{\tau }} = {\cal A}(t, \cdot, \mathit{\boldsymbol{\tau }}) $ some function defined on $\Omega$; here a dot above a quantity represents the derivative of the quantity with respect to the time variable; ${\cal G}$ is the elastic operator depending on the linearized strain tensor $\mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}})$ of infinitesimal deformations, with $ {\cal G}(t)\mathit{\boldsymbol{\tau }} = {\cal G}(t, \cdot, \mathit{\boldsymbol{\tau }}) $ which is defined on $\Omega$. The term $ {\cal B}(t)\mathit{\boldsymbol{\tau }} = {\cal B}(t, \cdot, \mathit{\boldsymbol{\tau }}) $ represents the so called relaxation tensor which is time-depending on the linearized strain tensor and is defined on $\Omega$. Recall that the visco-elastic short memory corresponds to the case ${\cal B} \equiv 0$. The last tensor $ C_e(t, \theta) := C_e(t, \cdot, \theta)$ denotes the thermal expansion tensor depending on time and on the temperature, defined on $\Omega$. For example,
| $ {C}_e(t, \theta) := - \theta\, C_{exp}(t) \quad \mbox{in} \ \Omega, $ |
where
| $ C_{exp}(t) := (c_{ij}(t, \cdot)) $ |
is some time-depending expansion tensor, defined on $\Omega$.
In (2.2) is the dynamic equation of motion where the mass density $\varrho \equiv 1$. The equation in (2.3) is the clamped condition and in (2.4) is the traction condition. On the contact surface, the general relation (2.5) is a sub-differential boundary condition such that
| $ \mathcal{D}(\Omega)^d \subset U, $ |
where $U$ represents the set of contact admissible test functions and $ \mathcal{D}(\Omega)^d $ is the distribution space. Here $\mathit{\boldsymbol{\sigma }}\mathit{\boldsymbol{\nu}}$ denotes the Cauchy stress vector on the contact boundary and $\varphi_u\, :\, (0, T)\times \Gamma_3\times \mathbb{R}^d \longrightarrow \mathbb{R}$ is a given function. Various situations may be modelled by such a condition, see e.g. the monograph [6] or the Habilitation thesis [2] p. 117. The differential equation (2.6) describes the evolution of the temperature field, where $ {\cal K}_{c}(t, \nabla \xi) := {\cal K}_{c}(t, \cdot, \nabla \xi)$ is some nonlinear thermal conductivity function defined on $\Omega$, depending on time and on the temperature gradient $ \nabla \xi $. For axample, denote by
| $ K_c(t, \cdot) := (k_{ij}(t, \cdot)) $ |
the thermal conductivity tensor defined on $\Omega$, we could consider
| $ {\cal K}_{c}(t, \cdot, \nabla \xi) = K_c(t, \cdot)\, \nabla \xi. $ |
In the second member, $ {\cal C}_e(t, \dot{\mathit{\boldsymbol{u}}}(t)) := {\cal C}_e(t, \cdot, \dot{\mathit{\boldsymbol{u}}}(t)) $ is some nonlinear function defied on $\Omega$, depending on the displacement velocity, and $q(t)$ represents the density of volume heat sources. For example,
| $ {\cal C}_e(t, \dot{\mathit{\boldsymbol{u}}}(t) )= -C_{exp}(t):\bigtriangledown \dot{\mathit{\boldsymbol{u}}}(t) = -c_{ij}(t, \cdot)\, \frac{\partial\, \dot{u}_i}{\partial\, x_j} (t). $ |
The associated temperature boundary condition is given by (2.7) and (2.8), where $\Xi $ and $ \varphi$ are some functions defined on $ (0, T) \times \Gamma_3 \times \mathbb{R}$ and $\theta_a(t)$ represents the ambient temperature. Here
| $ \partial \varphi(t, \mathit{\boldsymbol{x}}, r) := \partial \varphi(t, \mathit{\boldsymbol{x}}, \cdot) (r), \ \forall (t, \mathit{\boldsymbol{x}}, r) \in (0, T) \times \Gamma_3 \times \mathbb{R} $ |
denotes the sub-differential on the third variable of $ \varphi$ in the convex or maybe locally Lipschitz framework.
We recall that for a locally Lipschitz function $ G\, :\, \mathbb{R} \longrightarrow \mathbb{R}$, at any point $a \in \mathbb{R}$ and for any vector $d \in \mathbb{R}$, we can define the following directional derivative with respect to $d$ :
| $ \overline{\lim}_{\tau\rightarrow 0+} \frac{G(a+\tau d)-G(a)}{\tau}:= G^0(a;d). $ | (2.11) |
We have for all $a, \, d \in \mathbb{R}$, for all $ \xi \in \partial G(a)$:
| $ G^0(a;d) \geq \xi\, d $ |
and
| $ |G^0(a;d) | \leq |G^0(a)|\times |d|, \quad |\xi | \leq |G^0(a)| $ |
where
| $ \overline{\lim}_{h\rightarrow 0, \, h\neq 0} \frac{G(a+ h)-G(a)}{h}:= G^0(a). $ |
In the case where $G$ is convex on $ \mathbb{R}$, we have
| $ G^0(a;d) = \left\{ \begin{array}{ll} G'_r(a) d \quad \mbox{if} \quad d > 0 \\ G'_l(a) d \quad \mbox{if} \quad d < 0 \\ 0 \qquad \quad \ \mbox{if} \quad d = 0, \end{array} \ \right. $ |
and
| $ G^0(a) = \max\{ G'_r(a), G'_l(a) \}, $ |
where $ G'_r$ and $G'_l$ denotes the right side and left side derivatives respectively.
In the sequel, for a.e. $ (t, \mathit{\boldsymbol{x}})\in (0, T)\times {\Gamma}_c$, for all $ (r, s)\in \mathbb{R}^2$, we use the notation
| $ \varphi^0(t, \mathit{\boldsymbol{x}}, r;s) := [\varphi(t, \mathit{\boldsymbol{x}}, \cdot)]^0(r;s), $ |
and
| $ \varphi^0(t, \mathit{\boldsymbol{x}}, r) := [\varphi(t, \mathit{\boldsymbol{x}}, \cdot)]^0(r). $ |
Taking the previous example for $ {\cal K}_{c}$, we have
| $ {\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \nabla \xi) \, \nu = k_{ij}(t, \mathit{\boldsymbol{x}})\, \frac{\partial\, \xi}{\partial\, x_j}\, \nu_i. $ |
Let consider the following standard example
| $ \varphi(t, \mathit{\boldsymbol{x}}, r) := \frac{1}{2} k_e(t, \mathit{\boldsymbol{x}}) (r- \theta_R(t, \mathit{\boldsymbol{x}}))^2, \ \forall (t, \mathit{\boldsymbol{x}}, r) \in (0, T) \times \Gamma_3 \times \mathbb{R}, $ | (2.12) |
where $\theta_R$ is the temperature of the foundation, and $k_e$ is the heat exchange coefficient between the body and the obstacle. We obtain
| $ \Xi(t, \mathit{\boldsymbol{x}}, r) = \partial \varphi(t, \mathit{\boldsymbol{x}}, r) = k_e(t, \mathit{\boldsymbol{x}})\, (r -\theta_R(t, \mathit{\boldsymbol{x}})), \ (t, \mathit{\boldsymbol{x}}, r) \in (0, T) \times \Gamma_3 \times \mathbb{R}. $ |
Finally in (2.9) and (2.10), $\xi_0, \, \mathit{\boldsymbol{u}}_0, \, \mathit{\boldsymbol{v}}_0$ represent the initial temperature, displacement and velocity respectively.
One may remark that since $\varphi_u$ is assumed real-valued, then unilateral contact, defined by indicator functions taking infinite values, is excluded. So the body is in fixed contact with the foundation of the body according to a friction law. This is consistent with the linear heat conduction modeled in (2.6). We insist that the new feature here is that we may have the absence of the usual claimed condition in the case where meas$(\Gamma_1) = 0$. However, there is coerciveness with regard to the temperature by (2.7). To derive the variational formulation of the mechanical problems (2.1)–(2.10) we need additional notations. Thus, let consider $V$ the closed subspace of $H_1$ defined by
| $ V = \{\, \mathit{\boldsymbol{v}} \in H_{1}\ |\ \mathit{\boldsymbol{v}} = {\bf{0}} \quad \mbox{on } \quad \Gamma_{1} \, \} \cap U. $ |
We remark that the subspace $V$ may be different or not to the whole space $ H_{1} $, depending on the set $U$ of admissible contact conditions.
On $V$ we consider the inner product given by
| $ ( \mathit{\boldsymbol{u}}, \mathit{\boldsymbol{v}} )_{V} = ( \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}), \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}}) )_{\mathcal H} + (\mathit{\boldsymbol{u}}, \mathit{\boldsymbol{v}})_H \qquad \forall\, \mathit{\boldsymbol{u}}, \, \mathit{\boldsymbol{v}}\, \in V, $ |
and let $\|\cdot\|_{V}$ be the associated norm, i.e.
| $ \|\mathit{\boldsymbol{v}}\|_{V}^2 = \|\mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}})\|_{\mathcal H}^2 + \|\mathit{\boldsymbol{v}}\|_H^2 \qquad \forall\, \mathit{\boldsymbol{v}} \in V. $ |
It follows that $\|\cdot\|_{H_{1}}$ and $\|\cdot\|_{V}$ are equivalent norms on $V$ and therefore $(V, \|\cdot\|_{V})$ is a real Hilbert space. Moreover, by the Sobolev's trace theorem, we have a constant $C_0\, >\, 0$ depending only on $\Omega$, and $\Gamma_3$ such that
| $ \|\mathit{\boldsymbol{v}}\|_{L^{2}(\Gamma_3)}\ \leq\ C_0\, \|\mathit{\boldsymbol{v}}\|_{V} \qquad \forall\, \mathit{\boldsymbol{v}} \in V. $ |
For functional reason, it is convenient to shift the ambient temperature to zero on $\Gamma_1 \cup \Gamma_2$. We introduce for this propose $ \theta = \xi -\theta_a$, by assuming $ \theta_a \in H^1(0, T; H^1(\Omega))$. Thus we have $\forall t\in [0, T]$:
| $ \xi(t) = \theta_a(t) \Longrightarrow \theta(t) = 0 \quad \mbox{on} \quad \Gamma_1 \cup \Gamma_2. $ |
In what follows, we use the following change of variables:
| $ \xi = \theta + \theta_a, \quad \xi_0 = \theta_0 + \theta_a(0). $ |
Consider then the following spaces for the temperature field:
| $ E=\{\eta\in H^{1}(\Omega), \ \eta = 0 \quad \mbox{on } \quad \Gamma_1 \cup\Gamma_2\}; \quad F=L^2(\Omega). $ |
The spaces $E$ and $F$, endowed with their respective canonical inner product, are Hilbert spaces.
Identifying then $H$ and $F$ with their own duals, we obtain two Gelfand evolution triples (see e.g. [9] Ⅱ/A p. 416):
| $ V\subset H \equiv H' \subset V', \quad E\subset F \equiv F' \subset E' $ |
where the inclusions are continuous and dense.
In the study of the mechanical problem (2.1)-(2.10), we assume that the viscosity operator $ {\mathcal A} \, :\, (0, T)\times \Omega\times S_d\longrightarrow S_d$, $(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }}) \longmapsto {\mathcal A}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }})$ satisfies
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \; {\mathcal A}(\cdot, \cdot, \mathit{\boldsymbol{\tau }}) \mbox{ is measurable on } (0, T)\times \Omega, \ \forall \mathit{\boldsymbol{\tau }} \in S_d;\\ {\rm (ii)} \; {\mathcal A}(t, \mathit{\boldsymbol{x}}, \cdot) \mbox{ is continuous on } S_d \mbox{ for a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Omega;\\ {\rm (iii)} \; \mbox{there exists } m_{\mathcal A} > 0\ \mbox{ such that } \\ \qquad ({\mathcal A}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }}_1) - {\mathcal A}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }}_2) ) \cdot (\mathit{\boldsymbol{\tau }}_1 - \mathit{\boldsymbol{\tau }}_2) \geq m_{\mathcal A}\, |\mathit{\boldsymbol{\tau }}_1-\mathit{\boldsymbol{\tau }}_2|^2, \\ \qquad \qquad \forall \mathit{\boldsymbol{\tau }}_1, \, \mathit{\boldsymbol{\tau }}_2 \in S_d, \mbox{ for a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Omega; \\ {\rm (iv)} \; \mbox{there exists } c_0^{\mathcal A} \in L^2((0, T)\times \Omega; \mathbb{R}^+), \ c_1^{\mathcal A} > 0 \mbox{ such that } \\ \qquad |{\mathcal A}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }}) | \leq c_0^{\mathcal A}(t, \mathit{\boldsymbol{x}}) + c_1^{\mathcal A}\, |\mathit{\boldsymbol{\tau }}|, \\ \quad \qquad \forall \mathit{\boldsymbol{\tau }} \in S_d, \mbox{ for a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Omega. \end{array} \right. \end{equation} $ | (2.13) |
In this paper for every $t\in (0, T)$, $\mathit{\boldsymbol{\tau }} \in S_d$ we denote by ${\mathcal A}(t) = {\mathcal A}(t, \cdot, \cdot)$ a functional which is defined on $\Omega \times S_d$ and ${\mathcal A}(t) \, \mathit{\boldsymbol{\tau }} = {\mathcal A}(t, \cdot, \mathit{\boldsymbol{\tau }})$ some function defined on $\Omega$.
The elasticity operator ${\mathcal G} : (0, T)\times \Omega \times S_d \longrightarrow S_d $ satisfies :
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \quad \mbox{there exists}\ L_{\mathcal G} > 0\ \mbox{such that}\\ \qquad | {\mathcal G}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\varepsilon }}_1) - {\mathcal G}(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\varepsilon }}_2)| \leq L_{\mathcal G} |\mathit{\boldsymbol{\varepsilon }}_1 - \mathit{\boldsymbol{\varepsilon }}_2|\\ \qquad \forall \mathit{\boldsymbol{\varepsilon }}_1, \, \mathit{\boldsymbol{\varepsilon }}_2\in S_d, \, \, a.e.\, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Omega\, ;\\ {\rm (ii)} \quad {\mathcal G}(\cdot, \cdot, \mathit{\boldsymbol{\varepsilon }})\ \mbox{is Lebesgue measurable on}\ (0, T)\times\Omega, \forall \mathit{\boldsymbol{\varepsilon }} \in S_d\, ;\\ {\rm (iii)} \quad \mbox{the mapping}\ {\mathcal G}(\cdot, \cdot, {\bf{0}}) \in {\mathcal H}. \end{array} \right. \end{equation} $ | (2.14) |
We put again ${\mathcal G}(t)\mathit{\boldsymbol{\tau }} = {\mathcal G}(t, \cdot, \mathit{\boldsymbol{\tau }})$ some function defined on $\Omega$ for every $t\in (0, T)$, $\mathit{\boldsymbol{\tau }} \in S_d$.
The relaxation tensor ${\mathcal B}\, :\, (0, T) \times \Omega \times S_d \longrightarrow S_d$, $(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tau }}) \longmapsto (B_{ijkh}(t, \mathit{\boldsymbol{x}})\, \tau_{kh})$ satisfies
| $ \begin{equation} \label{h3} \left\{ \begin{array}{l} {\rm (i)}\ B_{ijkh}\in L^{\infty}((0, T)\times \Omega);\\ {\rm (ii)}\ {\mathcal B}(t)\mathit{\boldsymbol{\sigma }}\cdot\mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{\sigma }}\cdot{\mathcal B}(t)\mathit{\boldsymbol{\tau }} \\ \qquad \forall \mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\tau }} \in S_d, ~ \mbox{a.e.}~ t\in(0, T), ~ \mbox{a.e. in}~ \Omega \end{array}\right. \end{equation} $ | (2.15) |
where we denote by $ {\mathcal B}(t)\mathit{\boldsymbol{\tau }} = {\mathcal B}(t, \cdot, \mathit{\boldsymbol{\tau }}) $ which is defined on $\Omega$ for every $t\in (0, T)$, $\mathit{\boldsymbol{\tau }} \in S_d$.
We suppose the body forces and surface tractions satisfy
| $ \mathit{\boldsymbol{f}}_0\in L^{2}(0, T;H), \qquad \mathit{\boldsymbol{f}}_2\in L^{2}(0, T;L^{2}(\Gamma_2)^d) $ | (2.16) |
On the contact surface, the following frictional contact function
| $ \psi_u(t, \mathit{\boldsymbol{w}}) := \int_{\Gamma_3} \varphi_u(t, \mathit{\boldsymbol{w}})\, da $ |
verifies
| $ \begin{equation} \left\{ \begin{array}l \mbox{ (i) }\quad \psi_u\, :\, (0, T)\times V \longrightarrow \mathbb{R} \quad \mbox{is well defined};\\ \mbox{ (ii) }\quad t \in (0, T)\longmapsto \psi_u(t, \mathit{\boldsymbol{w}})\ \mbox{is Lebesgue measurable}\ \forall \mathit{\boldsymbol{w}} \in V;\\ \mbox{(iii)} \quad |\psi_u(t, \mathit{\boldsymbol{w}}) | \leq c(t) + d\, \|\mathit{\boldsymbol{w}} \|_V, \ \forall \mathit{\boldsymbol{w}} \in V, \ \mbox{a.e.}\ t \in (0, T); \\ \mbox{(iv)} \quad \psi_u(t, \cdot) \ \mbox{is convex on} \ V\ \mbox{a.e.}\ t \in (0, T), \end{array} \right. \end{equation} $ | (2.17) |
where $d>0$ is some constante and $c \in L^2(0, T; \mathbb{R}^+)$.
The thermal expansion tensor $C_e \, :\, (0, T) \times \Omega \times \mathbb{R} \longrightarrow S_d$ verifies
| $ \begin{equation} \left\{ \begin{array}{ll} {\rm (i)} \; C_e(\cdot, \cdot, \vartheta) \mbox{ is measurable on } (0, T)\times \Omega, \ \forall \vartheta \in \mathbb{R};\\ {\rm (ii)} \quad \mbox{there exists}\ L_{e} > 0\ \mbox{such that}\\[1mm] \qquad | {C_e}(t, \mathit{\boldsymbol{x}}, \vartheta_1) - {C_e}(t, \mathit{\boldsymbol{x}}, \vartheta_2)| \leq L_{e}\, |\vartheta_1 - \vartheta_2| \\[1mm] \qquad \, \, \forall \vartheta_1, \, \vartheta_2 \in \mathbb{R}, \, \, a.e.\, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Omega; \\ {\rm (iii)} \; \mbox{there exists } c_0^{C_e} \in L^\infty((0, T)\times \Omega; \mathbb{R}^+), \ c_1^{C_e} \geq 0 \mbox{ such that } \\[1mm] \qquad |{C_e}(t, \mathit{\boldsymbol{x}}, \vartheta) | \leq c_0^{C_e}(t, \mathit{\boldsymbol{x}}) + c_1^{C_e}\, |\vartheta|, \quad \forall \vartheta \in \mathbb{R}, \mbox{ for a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Omega. \end{array}\right. \end{equation} $ | (2.18) |
Here we recall the notation $ C_e(t, \vartheta) = C_e(t, \cdot, \vartheta)$ some function defined on $\Omega$, for all $ t\in (0, T)$ and $ \vartheta \in \mathbb{R} $.
The nonlinear function ${\cal K}_{c} : (0, T)\times \Omega \times \mathbb{R}^d \longrightarrow \mathbb{R} $ satisfies :
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \; {\cal K}_{c}(\cdot, \cdot, \xi) \mbox{ is measurable on } (0, T)\times \Omega, \ \forall \xi \in \mathbb{R}^d;\\ {\rm (ii)} \; {\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \cdot) \mbox{ is continuous on } \mathbb{R}^d, \mbox{ a.e. } (t, \mathit{\boldsymbol{x}})\in (0, T)\times \Omega;\\ {\rm (iii)} \; \mbox{there exists } c_0^{{\cal K}_{c}} \in L^2((0, T)\times \Omega; \mathbb{R}^+), \, c_1^{{\cal K}_{c}} \geq 0, \ \mbox{ such that } \\ \qquad |{\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \xi) | \leq c_0^{{\cal K}_{c}}(t, \mathit{\boldsymbol{x}}) + c_1^{{\cal K}_{c}}\, |\xi|, \quad \forall \xi \in \mathbb{R}^d, \, \mbox{ a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Omega;\\ {\rm (iv)} \mbox{ there exists}\ m_{{\cal K}_{c}} > 0\ \mbox{such that}\\ \qquad ({\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \xi_1) - {\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \xi_2) ) \cdot (\xi_1 - \xi_2) \geq m_{{\cal K}_{c}}\, |\xi_1 - \xi_2|^2, \\ \qquad \forall \xi_1, \, \xi_2 \in \mathbb{R}^d, \, \, a.e.\, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Omega\, ;\\ {\rm (v)} \mbox{ there exists}\ n_{{\cal K}_{c}} > 0\ \mbox{such that} \quad {\cal K}_{c}(t, \mathit{\boldsymbol{x}}, \xi) \cdot \xi \geq n_{{\cal K}_{c}}\, |\xi|^2, \\ \qquad \forall \xi \in \mathbb{R}^d, \, \, a.e.\, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Omega. \end{array} \right. \end{equation} $ | (2.19) |
We suppose that the nonlinear function ${\cal C}_e : (0, T)\times \Omega \times \mathbb{R}^d \longrightarrow \mathbb{R} $ satisfies :
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \; {\cal C}_e(\cdot, \cdot, \mathit{\boldsymbol{v}}) \mbox{ is measurable on } (0, T)\times \Omega, \ \forall \mathit{\boldsymbol{v}} \in \mathbb{R}^d;\\ {\rm (ii)} \quad \mbox{there exists}\ L_{{\cal C}_e} > 0\ \mbox{such that}\\[1mm] \qquad | {\cal C}_e(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{v}}_1) - {\cal C}_e(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{v}}_2)| \leq L_{{\cal C}_e}\, |\mathit{\boldsymbol{v}}_1 - \mathit{\boldsymbol{v}}_2|, \\[1mm] \qquad \quad \forall \mathit{\boldsymbol{v}}_1, \, \mathit{\boldsymbol{v}}_2\in \mathbb{R}^d, \, \, a.e.\, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Omega. \end{array} \right. \end{equation} $ | (2.20) |
We assume for the heat sources density, that
| $ q \in L^{2}(0, T;L^{2}(\Omega)) $ | (2.21) |
The nonlinear function $\Xi, \, \varphi : (0, T)\times \Gamma_c \times \mathbb{R} \longrightarrow \mathbb{R} $ verifies :
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \; \Xi(\cdot, \cdot, r), \, \varphi(\cdot, \cdot, r) \mbox{ are measurable on } (0, T)\times \Gamma_c, \ \forall r \in \mathbb{R};\\ {\rm (ii)} \; \varphi(t, \mathit{\boldsymbol{x}}, \cdot) \mbox{ is locally Lipschitz on on } \mathbb{R} \mbox{ for a.e. } \, \, (t, \mathit{\boldsymbol{x}}) \in (0, T)\times \Gamma_c;\\ {\rm (iii)} \; \mbox{there exists } c_0^{\varphi} \in L^2((0, T)\times \Gamma_c; \mathbb{R}^+), \, c_1^{\varphi} \geq 0, \ \mbox{ such that } \\[1mm] \qquad |\varphi^0(t, \mathit{\boldsymbol{x}}, r) | \leq c_0^{\varphi}(t, \mathit{\boldsymbol{x}}) + c_1^{\varphi}\, |r|, \\[1mm] \qquad \quad \forall r \in \mathbb{R}, \, \mbox{ a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Gamma_c; \\ {\rm (iv)} \; (\Xi(t, \mathit{\boldsymbol{x}}, r_1)-\Xi(t, \mathit{\boldsymbol{x}}, r_2))\, (r_1-r_2) \geq 0, \\[1mm] \qquad \quad \forall r_1, \, r_2 \in \mathbb{R}, \, \mbox{ a.e. } (t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Gamma_c. \end{array} \right. \end{equation} $ | (2.22) |
We notice that these assumptions are verified for the example (2.12).
Finally we assume that the initial data satisfy the conditions
| $ \mathit{\boldsymbol{u}}_0 \ \in \ H, \quad \mathit{\boldsymbol{v}}_0 ~ \in ~ V, \quad \theta_0\in E. $ | (2.23) |
To continue, using Green's formula, we obtain the variational formulation of the mechanical problem $Q$ in abstract form as follows.
Problem $QV$ : Find $\mathit{\boldsymbol{u}} : [0, T]\to V$, $\theta : [0, T]\to E$ satisfying a.e. $ t\in (0, T)$:
| $ \begin{equation}\label{QVdispla} \left\{ \begin{array}l \left\langle {\ddot{\mathit{\boldsymbol{u}}}(t)+ A(t)\, \dot{\mathit{\boldsymbol{u}}}(t)+ B(t)\, \mathit{\boldsymbol{u}}(t) + C(t)\, \theta(t), \, \mathit{\boldsymbol{w}} - \dot{\mathit{\boldsymbol{u}}}(t)} \right\rangle_{V'\times V} \\ + (\int_0^t\, \mathcal{B}(t-s)\, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{w}})- \mathit{\boldsymbol{\varepsilon }}(\dot{\mathit{\boldsymbol{u}}}(t)))_{\mathcal H} + \psi_u(t, \mathit{\boldsymbol{w}}) - \psi_u(t, \dot{\mathit{\boldsymbol{u}}}(t)) \\ \qquad \geq \left\langle {\mathit{\boldsymbol{f}}(t), \, \mathit{\boldsymbol{w}} - \dot{\mathit{\boldsymbol{u}}}(t)} \right\rangle_{V'\times V} \quad \forall \mathit{\boldsymbol{w}} \in V. \end{array} \right. \end{equation} $ | (2.24) |
| $ \begin{equation}\label{QVtheta} \left\{ \begin{array}{l} <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\, \theta(t), \eta>_{E'\times E} + \psi(t, \theta(t);\eta) \\[1mm] \qquad \geq \, <R(t) \dot{\mathit{\boldsymbol{u}}}(t), \eta>_{E'\times E} + <Q(t), \eta>_{E'\times E}, \ \forall\, \eta\, \in E. \end{array} \right. \end{equation} $ | (2.25) |
| $ \mathit{\boldsymbol{u}}(0)=\mathit{\boldsymbol{u}}_0, \quad \dot{\mathit{\boldsymbol{u}}}(0)=\mathit{\boldsymbol{v}}_0, \quad \theta(0)=\theta_0. $ | (2.26) |
Here, the operators and functions $A(t), \, B(t)\, : \, V \longrightarrow V'$, $ C(t)\, : \, E \longrightarrow V'$, $\mathit{\boldsymbol{f}}\, :\, [0, T] \longrightarrow V'$, $K(t)\, :\, E \longrightarrow E'$, $\psi(t, \cdot; \cdot)\, :\, E\times E \longrightarrow \mathbb{R}$, $R(t)\, :\, V \longrightarrow E'$ and $Q:[0, T] \longrightarrow E'$ are defined by $\forall \mathit{\boldsymbol{v}}\, \in V$, $\forall \mathit{\boldsymbol{w}}\, \in V$, $\forall \tau \, \in E$, $\forall \eta \, \in E$, a.e. $ t\in (0, T)$:
| $ \left\langle {A(t)\, \mathit{\boldsymbol{v}}, \mathit{\boldsymbol{w}}} \right\rangle_{V'\times V} = ({\mathcal A}(t)\, \mathit{\boldsymbol{\varepsilon }} \mathit{\boldsymbol{v}}, \mathit{\boldsymbol{\varepsilon }} \mathit{\boldsymbol{w}})_{\mathcal H}; $ | (2.27) |
| $ \left\langle {B(t)\, \mathit{\boldsymbol{v}}, \mathit{\boldsymbol{w}}} \right\rangle_{V'\times V}=({\mathcal G}(t)\, \mathit{\boldsymbol{\varepsilon }} \mathit{\boldsymbol{v}}, \mathit{\boldsymbol{\varepsilon }} \mathit{\boldsymbol{w}})_{\mathcal H}; $ | (2.28) |
| $ \left\langle {C(t) \zeta, \mathit{\boldsymbol{w}}} \right\rangle_{V'\times V} = (C_e(t, \zeta(\cdot) + \theta_a(t)), \, \mathit{\boldsymbol{\varepsilon }} \mathit{\boldsymbol{w}})_{\cal H}; $ | (2.29) |
| $ \left\langle {{\mathit{\boldsymbol{f}}}(t), \mathit{\boldsymbol{w}}} \right\rangle_{V'\times V} = ({\mathit{\boldsymbol{f}}}_0(t), \mathit{\boldsymbol{w}} )_H \, + ({\mathit{\boldsymbol{f}}}_F(t), \mathit{\boldsymbol{w}})_{(L^2(\Gamma_2))^d}; $ | (2.30) |
| $ \left\langle {K(t)\, \zeta, \eta} \right\rangle_{E'\times E} = \int_{\Omega}\, {\cal K}_c(t, \nabla\zeta + \nabla\theta_a(t) )\cdot \nabla \eta \, dx ; $ | (2.31) |
| $ \psi(t, \zeta; \eta) = \int_{\Gamma_3} \varphi^0(t, x, \zeta(x)+ \theta_a(t);\eta(x))\, da(x); $ | (2.32) |
| $ \left\langle {R(t)\, \mathit{\boldsymbol{v}}, \eta} \right\rangle_{E'\times E} = \int_{\Omega} \, {\cal C}_e(t, \mathit{\boldsymbol{v}}) \, \eta\, dx; $ | (2.33) |
| $ \left\langle {Q(t), \eta} \right\rangle_{E'\times E} = \int_\Omega (q(t) - \dot{\theta}_a(t) )\, \eta\, dx. $ | (2.34) |
We verify that from (2.22) then the term $ \psi(t, \zeta; \eta)$ is well defined for all $ \zeta \, \in E$, $ \eta \, \in E$, for a.e. $ t\in (0, T)$.
The inequality (2.25) is a consequence of the equation below,
| $ \begin{equation}\label{QVthetabis} \left\{ \begin{array}{l} <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\, \theta(t), \eta>_{E'\times E} + \int_{\Gamma_3}\, \Xi(t, \theta(t) + \theta_a(t)) \eta \, da \\[1mm] \qquad = \, <R(t) \dot{\mathit{\boldsymbol{u}}}(t), \eta>_{E'\times E} + <Q(t), \eta>_{E'\times E}, \ \forall\, \eta\, \in E, \end{array} \right. \end{equation} $ | (2.35) |
where recall that $ \Xi(t, r):= \Xi(t, \cdot, r) $ defined on $\Gamma_3$, for $ (t, r)\in (0, T)\times \mathbb{R}$.
Our main existence and uniqueness result is stated as follows, that we prove in the next Section.
Theorem 2.1. Assume that t (2.13)–(2.23) hold, then there exists an unique solution $\{\mathit{\boldsymbol{u}}, \theta\}$ to problem $QV$ with the regularity :
| $ \begin{equation} \label{reg} \left\{ \begin{array}l \mathit{\boldsymbol{u}}\in W^{1, 2}(0, T;V)\cap W^{2, 2}(0, T;V') \cap C^1(0, T;H) \\ \theta\in L^{2}(0, T;E)\cap W^{1, 2}(0, T;E') \cap C(0, T;F). \end{array} \right. \end{equation} $ | (2.36) |
The idea is to bring the second order inequality to a first order inequality, using monotone operator, convexity and fixed point arguments, and will be carried out in several steps.
Lvelocity variable
| $ \mathit{\boldsymbol{v}} = \dot{\mathit{\boldsymbol{u}}}. $ |
The system in Problem $QV$ is then written for a.e. $ t\in (0, T)$:
| $ \left\{ \begin{array}l {\mathit{\boldsymbol{u}}}(t) = \mathit{\boldsymbol{u}}_0 + \int_0^t\, {\mathit{\boldsymbol{v}}}(s)\, ds; \\ \left\langle {\dot{\mathit{\boldsymbol{v}}}(t)+ A(t)\, {\mathit{\boldsymbol{v}}}(t) + B(t)\, \mathit{\boldsymbol{u}}(t) + C(t)\, \theta(t), \, \mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{v}}}(t)} \right\rangle_{V'\times V} \\ + (\int_0^t\, \mathcal{B}(t-s)\, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{w}})- \mathit{\boldsymbol{\varepsilon }}({\mathit{\boldsymbol{v}}}(t)))_{\mathcal H} + \psi_u(t, \mathit{\boldsymbol{w}}) - \psi_u(t, {\mathit{\boldsymbol{v}}}(t)) \\ \qquad \geq \left\langle {\mathit{\boldsymbol{f}}(t), \, \mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{v}}}(t)} \right\rangle_{V'\times V} \quad \forall \mathit{\boldsymbol{w}} \in V; \\ <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\, \theta(t), \eta>_{E'\times E} + \psi(t, \theta(t);\eta) \\[1mm] \qquad \geq \, <R(t) \dot{\mathit{\boldsymbol{u}}}(t), \eta>_{E'\times E} + <Q(t), \eta>_{E'\times E}, \ \forall\, \eta\, \in E;\\ \mathit{\boldsymbol{v}}(0)=\mathit{\boldsymbol{v}}_0, \quad \theta(0)=\theta_0, \end{array} \right. $ |
with the regularity
| $ \left\{ \begin{array}l \mathit{\boldsymbol{v}} \in \mathit{\boldsymbol{v}} \in L^{2}(0, T;V) \cap W^{1, 2}(0, T;V')\cap C(0, T;H)\\ \theta \in L^{2}(0, T;E) \cap W^{1, 2}(0, T;E')\cap C(0, T;F). \end{array} \right. $ |
To continue, we assume in the sequel that the conditions (2.13)–(2.17) of the Theorem 1 are satisfied. Let define
| $ \mathcal{W} := L^{2}(0, T;\mathcal{H}). $ |
We begin by
Lemma 1. For all $\eta\in \mathcal{W}$, there exists an unique
| $ \mathit{\boldsymbol{v}}_\eta \in L^{2}(0, T;V) \cap W^{1, 2}(0, T;V')\cap C(0, T;H) $ |
satisfying
| $ \begin{equation} \label{3.1} \left\{ \begin{array}l \left\langle {\dot{\mathit{\boldsymbol{v}}}_\eta(t) + A(t)\, \mathit{\boldsymbol{v}}_\eta(t), \, \mathit{\boldsymbol{w}} - \mathit{\boldsymbol{v}}_\eta(t) } \right\rangle_{V'\times V} + ( \eta(t), \mathit{\boldsymbol{\varepsilon }} (\mathit{\boldsymbol{w}}) - \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}}_\eta(t)) )_{\mathcal{H}} \\ \quad + \psi_u(t, \mathit{\boldsymbol{w}}) - \psi_u(t, \mathit{\boldsymbol{v}}_\eta(t)) \geq \left\langle {\mathit{\boldsymbol{f}}(t), \mathit{\boldsymbol{w}}-\mathit{\boldsymbol{v}}_\eta(t)} \right\rangle_{V'\times V}, \\ \qquad \qquad \quad \forall\, \mathit{\boldsymbol{w}} \in V, \quad \mbox{ a.e.}\ t \in (0, T); \\ \mathit{\boldsymbol{v}}_\eta(0)=\mathit{\boldsymbol{v}}_0. \end{array} \right. \end{equation} $ | (3.1) |
Moreover, $\exists c >0$ such that $\forall \eta_1, \, \eta_2 \in \mathcal{W}$:
| $ \| {\mathit{\boldsymbol{v}}}_{\eta_2}(t) - {\mathit{\boldsymbol{v}}}_{\eta_1}(t) \|_H^2 + \int_0^t\, \| \mathit{\boldsymbol{v}}_{\eta_1}-\mathit{\boldsymbol{v}}_{\eta_2} \|_V^2 \leq c\, \int_0^t\, \| \eta_1-\eta_2 \|_{\mathcal{H}}^2, \quad \forall t\in [0, T]. $ | (3.2) |
Proof. Let $\eta\in \mathcal{W}$. Using [9] Ⅱ/B p. 893, we deduce the existence and uniqueness of $\mathit{\boldsymbol{v}}_\eta$.
Now let $\eta_1, \, \eta_2 \in \mathcal{W}$. In (3.1) we take $(\eta = \eta_1, \, \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{v}}_{\eta_2}(t))$, then $(\eta = \eta_2, \, \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{v}}_{\eta_1}(t))$. Adding the two inequalities, we deduce that for a.e. $t\in (0;T)$:
| $ \begin{array}l \left\langle { \dot{\mathit{\boldsymbol{v}}}_{\eta_2}(t)-\dot{\mathit{\boldsymbol{v}}}_{\eta_1}(t), {\mathit{\boldsymbol{v}}}_{\eta_2}(t)-{\mathit{\boldsymbol{v}}}_{\eta_1}(t)} \right\rangle_{V'\times V} + \left\langle { A(t)\, {\mathit{\boldsymbol{v}}}_{\eta_2}(t)- A(t)\, {\mathit{\boldsymbol{v}}}_{\eta_1}(t), {\mathit{\boldsymbol{v}}}_{\eta_2}(t)-{\mathit{\boldsymbol{v}}}_{\eta_1}(t) } \right\rangle _{V'\times V} \\ \leq - ( \eta_2(t)-\eta_1(t), \mathit{\boldsymbol{\varepsilon }}( {\mathit{\boldsymbol{v}}}_{\eta_2}(t))- \mathit{\boldsymbol{\varepsilon }}( {\mathit{\boldsymbol{v}}}_{\eta_1}(t)) )_{\mathcal{H}}. \end{array} $ |
Then integrating over $(0, t)$, from (2.13)(ⅲ) and from the initial condition on the velocity, we obtain:
| $ \begin{array}l \forall t\in [0, T], \quad \| {\mathit{\boldsymbol{v}}}_{\eta_2}(t) - {\mathit{\boldsymbol{v}}}_{\eta_1}(t) \|_H^2 + m_A\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_2}(s)-{\mathit{\boldsymbol{v}}}_{\eta_1}(s)\|_V^2 \, ds \\ \leq - \int_0^t\, ( \eta_2(s)-\eta_1(s), \mathit{\boldsymbol{\varepsilon }}( {\mathit{\boldsymbol{v}}}_{\eta_2}(s))- \mathit{\boldsymbol{\varepsilon }}({\mathit{\boldsymbol{v}}}_{\eta_1}(s)) )_{\mathcal{H}}\, ds + m_A\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_2}(s)-{\mathit{\boldsymbol{v}}}_{\eta_1}(s)\|_H^2 \, ds. \end{array} $ |
We conclude that $\exists c >0$ such that $\forall \eta_1, \, \eta_2 \in \mathcal{W}$, $\forall t\in [0, T]$:
| $ \| {\mathit{\boldsymbol{v}}}_{\eta_2}(t) - {\mathit{\boldsymbol{v}}}_{\eta_1}(t) \|_H^2 + \int_0^t\, \| \mathit{\boldsymbol{v}}_{\eta_1}(s) -\mathit{\boldsymbol{v}}_{\eta_2}(s) \|_V^2 ds \\ \leq c\, \int_0^t\, \| \eta_1(s)-\eta_2(s) \|_{\mathcal{H}}^2 ds + c\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_2}(s)-{\mathit{\boldsymbol{v}}}_{\eta_1}(s)\|_H^2 \, ds. $ | (3.3) |
Now let fix $ \tau\in [0, T]$. We have $\forall t\in [0, \tau]$:
| $ \| {\mathit{\boldsymbol{v}}}_{\eta_2}(t) - {\mathit{\boldsymbol{v}}}_{\eta_1}(t) \|_H^2 \leq c\, \int_0^\tau\, \| \eta_1(s) -\eta_2(s) \|_{\mathcal{H}}^2 + c\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_2}(s)-{\mathit{\boldsymbol{v}}}_{\eta_1}(s)\|_H^2 \, ds. $ |
Using then Gronwall's inequality, we obtain $ \forall \tau\in [0, T]$:
| $ \| {\mathit{\boldsymbol{v}}}_{\eta_2}(\tau) - {\mathit{\boldsymbol{v}}}_{\eta_1}(\tau) \|_H^2 \leq \Big(c\, \int_0^\tau\, \| \eta_1(s) -\eta_2(s) \|_{\mathcal{H}}^2 \Big)\, e^{cT}. $ |
Finally, integrating the last inequality and reporting the result in (3.3), we get (3.2).
Here and below, we denote by $c>0$ a generic constant, which value may change from lines to lines.
Lemma 2. For all $\eta \in \mathcal{W}$, thereexists an unique
| $ \theta_\eta \in L^{2}(0, T;E) \cap W^{1, 2}(0, T;E')\cap C(0, T;F) $ |
satisfying
| $\left\{ \begin{array}{l} <\dot{\theta}_\eta(t), \eta>_{E'\times E} + <K(t)\, \theta_\eta(t), \eta>_{E'\times E} + \int_{\Gamma_c}\, \Xi(t, \theta_\eta(t)) \eta \, da \\[1mm] \qquad = \, <R(t) {\mathit{\boldsymbol{v}}}_\eta(t), \eta>_{E'\times E} + <Q(t), \eta>_{E'\times E}, \ \forall\, \eta\, \in E, \ \mbox{ a.e.} \ t \in (0, T); \\ \theta_\eta(0)=\theta_0. \end{array} \right. $ | (3.4) |
Moreover, $\exists c >0$ such that $\forall \eta_1, \, \eta_2 \in \mathcal{W}$:
| $ \| \theta_{\eta_1}(t) - \theta_{\eta_2}(t) \|_F^2 \leq c\, \int_0^t\, \| \mathit{\boldsymbol{v}}_{\eta_1} -\mathit{\boldsymbol{v}}_{\eta_2} \|_{V}^2, \quad \forall t\in [0, T]. $ | (3.5) |
Proof. The existence and uniqueness result verifying (3.3) follows from standard result on first order evolution equation (see e.g. [5]). Indeed we verify that from the expression of the operator $R$, we have
| $ \mathit{\boldsymbol{v}}_\eta \in L^{2}(0, T;V) \Longrightarrow R\, \mathit{\boldsymbol{v}}_\eta \in L^{2}(0, T;E'), $ |
as $ Q \in L^{2}(0, T; E')$ then $ R\, \mathit{\boldsymbol{v}}_\eta + Q \in L^{2}(0, T; E')$.
Using the assumptions (2.19) and (2.22), the operator $ \Psi(t)\, :\, E \longrightarrow E'$ for a.e. $t\in (0, T)$ defined by
| $ <\Psi(t)\, \xi, \eta>_{E'\times E} := <K(t)\, \xi, \eta>_{E'\times E} + \int_{\Gamma_3}\, \Xi(t, \xi) \eta \, da, \quad \forall\, \xi, \, \eta\, \in E $ |
is strongly monotone.
Now for $\eta_1, \, \eta_2 \in \mathcal{W}$, we have for a.e. $t\in (0;T)$:
| $ \begin{array}l \left\langle { \dot{\theta}_{\eta_1}(t)-\dot{\theta}_{\eta_2}(t), {\theta}_{\eta_1}(t) - {\theta}_{\eta_2}(t)} \right\rangle_{E'\times E} + \left\langle { K(t)\, {\theta}_{\eta_1}(t)- K(t)\, {\theta}_{\eta_2}(t), \, {\theta}_{\eta_1}(t)-{\theta}_{\eta_2}(t) } \right\rangle _{E'\times E} \\ = \left\langle {R(t)\, {\mathit{\boldsymbol{v}}}_{\eta_1}(t) - R(t)\, {\mathit{\boldsymbol{v}}}_{\eta_2}(t), \, {\theta}_{\eta_1}(t)-{\theta}_{\eta_2}(t) } \right\rangle _{E'\times E}. \end{array} $ |
Then integrating the last property over $(0, t)$, using the strong monotonicity of $K(t)$ and the Lipschitz continuity of $R(t)\, :\, V \longrightarrow E'$, we deduce (3.5).
Proof of Theorem 1.
We have now all the ingredients to prove the Theorem 1.
Consider the operator $\Lambda\, :\, \mathcal{W} \to \mathcal{W}$ defined by for all $\eta \in \mathcal{W}$:
| $ \Lambda\, \eta\, (t) = {\mathcal G}(\mathit{\boldsymbol{\varepsilon }} (\mathit{\boldsymbol{u}}_{\eta}(t)) ) + \int_0^t\, B(t-s)\, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}_{\eta}(s))\, ds + C_e(t, {\theta}_{\eta}(t)), \quad \forall t \in [0, T], $ |
where
| $ \mathit{\boldsymbol{u}}_{\eta}(t) = \mathit{\boldsymbol{u}}_0+ \int_0^t\, {\mathit{\boldsymbol{v}}}_{\eta}(s)\, ds, \ \forall t \in [0, T]; \quad \mathit{\boldsymbol{u}}_{\eta} \in W^{1, 2}(0, T;V) \cap W^{2, 2}(0, T;V') \cap C^1(0, T;H). $ |
Then from (2.14), (2.15), and Lemma 2, we deduce that for all $\eta_1, \, \eta_2 \in \mathcal{W}$, for all $t\in [0, T]$:
| $ \label{ea1} \begin{array}l \| \Lambda\, \eta_1\, (t)-\Lambda\, \eta_2\, (t) \|_{\mathcal{H}}^2 \leq c\, \| {\theta}_{\eta_1}(t) - {\theta}_{\eta_2}(t) \|_F^2 + c\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_1}(s)-{\mathit{\boldsymbol{v}}}_{\eta_2}(s)\|_V^2 \, ds \\ \leq c\, \int_0^t\, \|{\mathit{\boldsymbol{v}}}_{\eta_1}(s)-{\mathit{\boldsymbol{v}}}_{\eta_2}(s)\|_V^2 \, ds. \end{array} $ | (3.6) |
Now using (3.6), after some algebraic manipulations, we have for any $\beta >0$:
| $ \int_0^T\, e^{-\beta \tau}\, \| \Lambda\, \eta_1\, (\tau)-\Lambda\, \eta_2\, (\tau) \|_{\mathcal{H}}^2 \leq \frac{c}{\beta}\, \int_0^T\, e^{-\beta \tau}\, \| \eta_1(\tau)- \eta_2(\tau) \|_{\mathcal{H}}^2 \, d\tau. $ |
We conclude from the last inequality by contracting principle that the operator $\Lambda$ has a unique fixed point $\eta^* \in \mathcal{W}$. We verify then that the functions
| $ {\mathit{\boldsymbol{u}}}(t) := \mathit{\boldsymbol{u}}_0 + \int_0^t\, {\mathit{\boldsymbol{v}}}_{\eta^*}, \ \forall t\in [0, T], \quad \theta := \theta_{\eta^*} $ |
are solutions to problem $QV$ with the regularity (2.36), the uniqueness follows from the uniqueness in Lemma 1 and Lemma 2.
In this section, we study a fully-discrete numerical approximation scheme of the variational problem $QV$. For this purpose, let $\{ \mathit{\boldsymbol{u}}, \theta \}$ be the unique solution of the problem $QV$, and introduce the velocity variable
| $ \mathit{\boldsymbol{v}}(t)=\dot{\mathit{\boldsymbol{u}}}(t), \quad \forall t\in [0, T]. $ |
Then
| $ \mathit{\boldsymbol{u}}(t)= \mathit{\boldsymbol{u}}_0 + \int_0^t \mathit{\boldsymbol{v}}(s)\, ds, \quad \forall t\in [0, T]. $ |
Here we make the following additional assumptions on the different data, operators and solution fields:
| $ A \in C([0, T]; \mathcal{L}(V, V')), \\ B \in C([0, T]; C(V, V')), \\ C \in C([0, T]; \mathcal{L}(V, V')), \\ \mathcal{B} \in C([0, T]; \mathcal{L}( \mathcal{H}, \mathcal{H})), \\ \psi_u \in C([0, T]; C(V, \mathbb{R})), \\ \psi \in C([0, T]; C(E\times E, \mathbb{R})), \\ \mathit{\boldsymbol{f}} \in C([0, T];V'), \\ K \in C([0, T]; \mathcal{L}(E, E')), \\ R \in C([0, T]; \mathcal{L}(E, E')), \\ Q \in C([0, T];E'), \\ \mathit{\boldsymbol{v}} \in C([0, T];V)\cap C^1([0, T];H), \\ \theta \in C([0, T];E)\cap C^1([0, T];F). $ | (4.1) |
Moreover we assume that for all $r, r_1, r_2 \in \mathbb{R}$, a.e. $(t, \mathit{\boldsymbol{x}}) \in(0, T)\times \Gamma_c$ :
| $ \begin{equation} \left\{ \begin{array}{l} {\rm (i)} \; \varphi'(t, \mathit{\boldsymbol{x}}, r; r_1+r_2) \leq \varphi'(t, \mathit{\boldsymbol{x}}, r; r_1) + \varphi'(t, \mathit{\boldsymbol{x}}, r; r_2);\\ {\rm (ii)} \; \varphi'(t, \mathit{\boldsymbol{x}}, r_2; r_1-r_2) + \varphi'(t, \mathit{\boldsymbol{x}}, r_1; r_2-r_1) \leq 0;\\ {\rm (iii)} \; \mbox{there exists } c^{\varphi} \geq 0 \ \mbox{ such that } \\[1mm] \qquad \varphi'(t, \mathit{\boldsymbol{x}}, r_1; r) + \varphi'(t, \mathit{\boldsymbol{x}}, r_2; -r) \leq c^{\varphi}\, |(r_1 - r_2)\, r|. \end{array} \right. \end{equation} $ | (4.2) |
We remark that the example of $ \varphi$ given in (2.12) satisfies the hypotheses (4.2).
From Theorem 1, $\{ \mathit{\boldsymbol{v}}, \theta \}$ verify for all $t\in [0, T]$:
| $ \begin{equation} \label{4.1} \left\{ \begin{array}l \left\langle {\dot{\mathit{\boldsymbol{v}}}(t)+ A(t)\, {\mathit{\boldsymbol{v}}}(t)+ B(t)\, \mathit{\boldsymbol{u}}(t) + C(t)\, \theta(t), \mathit{\boldsymbol{w}} - \mathit{\boldsymbol{v}}(t) } \right\rangle_{V'\times V} \\ + (\int_0^t\, \mathcal{B}(t-s)\, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{w}})- \mathit{\boldsymbol{\varepsilon }}(\dot{\mathit{\boldsymbol{u}}}(t)))_{\mathcal H} + \psi_u(t, \mathit{\boldsymbol{w}}) - \psi_u(t, \mathit{\boldsymbol{v}}(t)) \\ \qquad \geq \left\langle {\mathit{\boldsymbol{f}}(t), \, \mathit{\boldsymbol{w}} - \mathit{\boldsymbol{v}}(t)} \right\rangle_{V'\times V}, \quad \forall\, \mathit{\boldsymbol{w}}\in V. \end{array} \right. \end{equation} $ | (4.3) |
| $ \begin{equation} \label{4.2} \begin{array}l <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\, \theta(t), \eta>_{E'\times E} +\psi(t, \theta(t);\eta) \\[1mm] \qquad \geq <R(t) \dot{\mathit{\boldsymbol{u}}}(t), \eta>_{E'\times E} + <Q(t), \eta>_{E'\times E}, \ \forall\, \eta\, \in E. \end{array} \end{equation} $ | (4.4) |
| $ \mathit{\boldsymbol{u}}(0)=\mathit{\boldsymbol{u}}_0, \quad \mathit{\boldsymbol{v}}(0) = \mathit{\boldsymbol{v}}_0, \quad \theta(0)=\theta_0, $ | (4.5) |
Now let $V^h\subset V$ and $E^h\subset E$ be a family of finite dimensional subspaces, with $h>0$ a discretization parameter. We divide the time interval $[0, T]$ into $N$ equal parts: $t_n=n\, k$, $n=0, 1, \dots, N$, with the time step $k=T/N$.
For a continuous operator or function $U \in C([0, T]; X)$ with values in a space $X$, we use the notation $U_n = U(t_n)\in X$.
Then from (4.3) and (4.4) we introduce the following fully discrete scheme.
Problem $P^{hk}$. Find $\mathit{\boldsymbol{v}}^{hk}=\{\mathit{\boldsymbol{v}}^{hk}_n\}_{n=0}^N \subset V^h$, $\theta^{hk}=\{\theta^{hk}_n\}_{n=0}^N \subset E^h$ such that
| $ \mathit{\boldsymbol{v}}^{hk}_0=\mathit{\boldsymbol{v}}_0^h, \quad \theta^{hk}_0=\theta_0^h $ | (4.6) |
and for $n=1, \cdots, N$,
| $ \begin{equation} \label{4.4} \left\{ \begin{array}l \Big( \frac{\mathit{\boldsymbol{v}}^{hk}_n-\mathit{\boldsymbol{v}}^{hk}_{n-1}}{k}, \, \mathit{\boldsymbol{w}}^h - \mathit{\boldsymbol{v}}^{hk}_n \Big)_H + \left\langle {A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \mathit{\boldsymbol{w}}^h - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} +\left\langle {B_n\, \mathit{\boldsymbol{u}}_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} \\ + \left\langle {C_n\, \theta_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} + \psi_u(t_n, \mathit{\boldsymbol{w}}^h) - \psi_u(t_n, \mathit{\boldsymbol{v}}^{hk}_n) \\ + ( k\, \sum\limits_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}^{hk}_m), \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{w}}^h) - \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}}^{hk}_n) )_{\mathcal{H}} \\ \qquad \geq \left\langle { \mathit{\boldsymbol{f}}_n, \, \mathit{\boldsymbol{w}}^h - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{V^\prime\times V}, \quad \forall\, \mathit{\boldsymbol{w}}^h\in V^h. \end{array} \right. \end{equation} $ | (4.7) |
| $ \begin{equation} \label{4.5} \left\{ \begin{array}{l} \Big(\frac{\theta^{hk}_n-\theta^{hk}_{n-1}}{k}, \, \eta^h \Big)_{L^2(\Omega)} + \left\langle {K_n\, \theta^{hk}_n, \, \eta^h} \right\rangle_{ E^\prime\times E} +\psi(t_n, \theta^{hk}_n;\eta^h) \\ \qquad \geq \left\langle {R_n \, \mathit{\boldsymbol{v}}^{hk}_n, \, \eta^h} \right\rangle_{ E^\prime\times E} + \left\langle {Q_n, \eta^h} \right\rangle_{ E^\prime\times E}, \quad \forall\, \eta^h\in E^h. \end{array} \right. \end{equation} $ | (4.8) |
where
| $ \mathit{\boldsymbol{u}}_{n}^{hk} = \mathit{\boldsymbol{u}}_{n-1}^{hk} + k\, \mathit{\boldsymbol{v}}^{hk}_n, \quad \mathit{\boldsymbol{u}}^{hk}_0 = \mathit{\boldsymbol{u}}_0^h. $ | (4.9) |
Here $ \mathit{\boldsymbol{u}}^h_0 \in V^h $, $ \mathit{\boldsymbol{v}}^h_0 \in V^h $, $\theta^{h}_0 \in E^h$ are suitable approximations of the initial values $\mathit{\boldsymbol{u}}_0$, $\mathit{\boldsymbol{v}}_0$, $\theta_0$.
For $n=1, \dots, N$, suppose that $\mathit{\boldsymbol{u}}^{hk}_{n-1}$, $\mathit{\boldsymbol{v}}^{hk}_{n-1}$, $\theta^{hk}_{n-1}$ are known, then by using standard result on elliptic variational inequalities of the second kind (see e.g. [9] p. 892), we calculate $\mathit{\boldsymbol{v}}^{hk}_{n}$ by (4.7), $\theta^{hk}_{n}$ by (4.8) and $\mathit{\boldsymbol{u}}^{hk}_{n}$ by (4.9). Hence the discrete solution $\mathit{\boldsymbol{v}}^{hk}\subset V^h$, $\theta^{hk}\subset E^h$ exists and is unique.
We now turn to an error analysis of the numerical solution. The main result of this section is the following.
Theorem 2. We keep the assumptions of Theorem 1. Under the additional assumptions (4.1), then for the unique solution $\mathit{\boldsymbol{v}}^{hk}\subset V^h$, $\theta^{hk} \subset E^h$ of the discrete problem $P^{hk}$, we have the following error estimate
| $ \begin{equation} \label{est} \begin{array}l \max\limits_{1\le n\le N}{\|}\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}{\|}_H^2 +\Big(k\sum\limits_{n=1}^N \|\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}\|_V^2\Big) \\ \quad + \max\limits_{1\le n\le N}{\|}\theta_n-\theta_n^{hk}{\|}_{F}^2 +\Big(k\sum\limits_{n=1}^N \|\theta_n-\theta_n^{hk}\|_E^2\Big) \\ \le \ c\, \|\mathit{\boldsymbol{u}}_0-\mathit{\boldsymbol{u}}_0^{h}\|_V^2 + c\, {\|}\mathit{\boldsymbol{v}}_0-\mathit{\boldsymbol{v}}_0^{hk}{\|}_H^2 + c\, \|\theta_0-\theta_0^{h}\|_{F}^2 \\ \quad + c\, \max\limits_{1\le n\le N} \| \mathit{\boldsymbol{v}}_n - \mathit{\boldsymbol{w}}_n^{h} \|_{H} + c\, \max\limits_{1\le n\le N}{\|}\theta_n-\eta_n^{h}{\|}_{F}^2 \\ \quad +c\, k\sum\limits_{j=1}^N \|\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j \|_V^2 + c\, k\, \sum\limits_{j=1}^N{\|}\theta_j-\eta_j^{h}{\|}_{E}^2 \\ \quad + c\, \Big( \sum\limits_{j=1}^{N-1}{\|}(\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j) -(\mathit{\boldsymbol{v}}_{j+1}-\mathit{\boldsymbol{w}}^h_{j+1}){\|}_H \Big)^2 \\ \quad + c\, \Big( \sum\limits_{j=1}^{N-1} \| \theta_j-\eta_j^{h} - ( \theta_{j+1}-\eta_{j+1}^{h}) \|_{F} \Big)^2 \\ \quad + c\, k^2 + c\, k\, \sum\limits_{j=1}^N \, \| \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j \|_V, \end{array} \end{equation} $ | (4.10) |
where for $j=1, \dots, N$, $\mathit{\boldsymbol{w}}^h_j\in V^h$, $\eta^h_j\in E^h$ are arbitrary.
Proof. The method takes again and generalize classical techniques used in [2], where we refer for details. Here we mention only the main steps of the proof.
Denote
| $ \mathit{\boldsymbol{e }}_n=\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}^{hk}_n, \quad \varepsilon_n=\theta_n-\theta^{hk}_n, \quad 0\le n\le N, $ |
the numerical solution errors.
We begin by the estimate of $(\varepsilon_n)$.
Let fix $n = 1, \cdots, N$. From (4.4) where we put $t=t_n$ and $ \eta = -\eta^h $, $\eta^h\in E^h$, then add to (4.8), we obtain
| $ \begin{array}l \Big( \dot{\theta}_n - \frac{\theta^{hk}_n-\theta^{hk}_{n-1}}{k}, \, \eta^h \Big)_{L^2(\Omega)} + \left\langle {K_n\, \theta_n - K_n\, \theta^{hk}_n, \, \eta^h} \right\rangle_{ E^\prime\times E}\\ \quad \leq \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ) + \left\langle {R_n\, \mathit{\boldsymbol{v}}_n - R_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \eta^h} \right\rangle_{E^\prime\times E}. \end{array} $ |
Writing then
| $ \dot{\theta}_n - \frac{\theta^{hk}_n-\theta^{hk}_{n-1}}{k} = \dot{\theta}_n - \frac{\theta_n - \theta_{n-1}}{k} + \frac{ \varepsilon_n - \varepsilon_{n-1}}{k}, $ |
and replacing $\eta^h$ by $\eta^h_n -\theta_n + \varepsilon_n$ we obtain
| $ \begin{array}l \Big( \frac{ \varepsilon_n - \varepsilon_{n-1}}{k}, \, \varepsilon_n \Big)_{L^2(\Omega)} + \left\langle {K_n\, \theta_n - K_n\, \theta^{hk}_n, \, \varepsilon_n} \right\rangle_{ E^\prime\times E} \\ \qquad \leq \left\langle {K_n\, \theta_n - K_n\, \theta^{hk}_n, \, \theta_n - \eta^h_n} \right\rangle_{ E^\prime\times E} \\ \qquad \quad + \left\langle {R_n\, \mathit{\boldsymbol{v}}_n - R_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \varepsilon_n } \right\rangle_{ E^\prime\times E} + \left\langle {R_n\, \mathit{\boldsymbol{v}}_n -\mathit{\boldsymbol{v}}^{hk}_n, \, \theta_n -\eta^h_n } \right\rangle_{ E^\prime\times E} \\ \qquad \quad + \Big( \dot{\theta}_n - \frac{\theta_n-\theta_{n-1}}{k} +\frac{\varepsilon_n- \varepsilon_{n-1}}{k}, \, \theta_n - \eta^h_n \Big)_{L^2(\Omega)} - \Big( \dot{\theta}_n - \frac{\theta_n-\theta_{n-1}}{k}, \, \varepsilon_n \Big)_{L^2(\Omega)} \\ \qquad \quad + \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ). \end{array} $ |
From (2.19) we have
| $ | \left\langle {K_n\, \theta_n - K_n\, \theta^{hk}_n, \, \theta_n - \eta^h_n} \right\rangle_{ E^\prime\times E} | \leq c\, \| \theta_n - \theta^{hk}_n\|_E \times \| \theta_n - \eta^h_n\|_E. $ |
From (2.20) we have
| $ | \left\langle {R_n\, \mathit{\boldsymbol{v}}_n - R_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \eta^h} \right\rangle_{E^\prime\times E} | \leq c\, \| \mathit{\boldsymbol{v}}_n - \mathit{\boldsymbol{v}}^{hk}_n \|_{L^2(\Omega)} \times \| \eta^h \|_{L^2(\Omega)}. $ |
Then using (4.2) we obtain
| $ \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ) \leq c\, \| \theta_n - \theta^{hk}_n \|_E\, \times \| \theta_n - \eta^h_n \|_E. $ |
Consider the quantity for $ n = 1, \cdots, N $,
| $ \Xi_n := \Big( \frac{ \varepsilon_n - \varepsilon_{n-1}}{k}, \, \varepsilon_n \Big)_{F} + \left\langle {K_n\, \theta_n - K_n\, \theta^{hk}_n, \, \varepsilon_n} \right\rangle_{ E^\prime\times E}. $ |
We have for some $c_K > 0$,
| $ \Xi_n \geq \frac{1}{2k}\, \Big( \| \varepsilon_n \|_F^2 - \| \varepsilon_{n-1} \|_F^2 \Big) + c_K\, \| \varepsilon_n \|_E^2. $ |
Summing then $\Xi_j$ from $j=1$ to $j=n $, and after some manipulation, we obtain
| $ \begin{array}l \frac{1}{2k}\, \Big( \| \varepsilon_n \|_F^2 - \| \varepsilon_0 \|_F^2 \Big) + \sum\limits_{j=1}^n\, \| \varepsilon_j \|_E^2\\ \qquad \leq c\, \sum\limits_{j=1}^n\, \Big\| \dot{\theta}_j - \frac{\theta_j-\theta_{j-1}}{k} \Big\|_F^2 + c\, \sum\limits_{j=1}^n\, \| \theta_j -\eta^h_j \|_E^2 \\ \qquad \quad + c\, \sum\limits_{j=1}^n\, \| \mathit{\boldsymbol{e }}_j \|_V^2 + c\, \sum\limits_{j=1}^n\, \Big( \frac{\varepsilon_j-\varepsilon_{j-1}}{k}, \, \theta_j -\eta^h_j \Big)_{F}. \end{array} $ |
Denote now by
| $ \begin{array}l M_\varepsilon := \max\limits_{1\le n\le N} {\|}\varepsilon_n{\|}_{F}, \\ AT_0 := \max\limits_{1\le n\le N}{\|}\theta_n-\eta_n^{h}{\|}_{F}, \\ AT_1 := \sum\limits_{j=1}^N {\Big\|} \dot{\theta}_j - \frac{\theta_j-\theta_{j-1}}{k} {\Big\|}_{F}^2, \\ AT_2 := \sum\limits_{j=1}^N{\|}\theta_j-\eta_j^{h}{\|}_{E}^2, \\ AT_3 := \sum\limits_{j=1}^N{\|}\theta_j-\eta_j^{h} - ( \theta_{j+1}-\eta_{j+1}^{h}) {\|}_{F}. \end{array} $ |
We deduce from the last inequality that for some constant $c>0$ and for $n=1, \cdots, N$,
| $ \begin{equation} \label{estep} \begin{array}l \| \varepsilon_n {\|}_{F}^2+ k\sum\limits_{j=1}^n \|\varepsilon_j \|_E^2 \leq \ c\, {\|}\varepsilon_0{\|}_{F}^2 + c\, AT_0^2 + c\, k\, (AT_1 + AT_2) \\ + c\, AT_3\, M_\varepsilon + c\, k\, \sum\limits_{j=1}^n \, \| \mathit{\boldsymbol{e }}_{j} \|_{V}^2. \end{array} \end{equation} $ | (4.11) |
We now turn to the estimate of $(\mathit{\boldsymbol{e }}_n)$.
Let fix $n = 1, \cdots, N$. Using (4.3) where we put $t=t_n$ and $\mathit{\boldsymbol{w}} = \mathit{\boldsymbol{v}}_n^{hk}$, and adding to (4.7) where $\mathit{\boldsymbol{w}}^h = \mathit{\boldsymbol{w}}_n^h$, we have
| $ \begin{array}l ( \dot{\mathit{\boldsymbol{v}}}_n, \, \mathit{\boldsymbol{v}}^{hk}_n - \mathit{\boldsymbol{v}}_n )_H + \Big( \frac{\mathit{\boldsymbol{v}}^{hk}_n-\mathit{\boldsymbol{v}}^{hk}_{n-1}}{k}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}^{hk}_n \Big)_H \\ + \left\langle {A_n\, \mathit{\boldsymbol{v}}_n, \, \mathit{\boldsymbol{v}}^{hk}_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} + \left\langle {A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} \\ + \left\langle {B_n\, \mathit{\boldsymbol{u}}_n^{hk}, \, \mathit{\boldsymbol{v}}^{hk}_n -\mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} + \left\langle {B_n\, \mathit{\boldsymbol{u}}_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} \\ + \left\langle {C_n\, \theta_n, \, \mathit{\boldsymbol{v}}^{hk}_n -\mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} + \left\langle {C_n\, \theta_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}^{hk}_n} \right\rangle_{ V^\prime\times V} \\ + \mathcal{R}_n^{hk} + \psi_u(t_n, \mathit{\boldsymbol{w}}^h_n) - \psi_u(t_n, \mathit{\boldsymbol{v}}_n) \geq \left\langle {\mathit{\boldsymbol{f}}_n, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{V^\prime\times V}, \quad \forall\, \mathit{\boldsymbol{w}}^h_n\in V^h, \end{array} $ |
where for $n = 1, \cdots, N$:
| $ \begin{array}l \mathcal{R}_n^{hk} = \Big( \int_0^{t_n}\, \mathcal{B}(t_n-s) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds - k\, \sum\limits_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}^{hk}_m), \, - \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{e }}_n) \Big)_{\mathcal{H}} \\ \qquad \quad + \Big( k\, \sum\limits_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}^{hk}_m), \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{w}}^h_n) - \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{v}}_n) \Big)_{\mathcal{H}}. \end{array} $ |
Writing then
| $ \left\{ \begin{array}l \dot{\mathit{\boldsymbol{v}}}_n = \dot{\mathit{\boldsymbol{v}}}_n - \frac{\mathit{\boldsymbol{v}}^{hk}_n-\mathit{\boldsymbol{v}}^{hk}_{n-1}}{k} + \frac{\mathit{\boldsymbol{v}}^{hk}_n-\mathit{\boldsymbol{v}}^{hk}_{n-1}}{k};\\ A_n\, \mathit{\boldsymbol{v}}_n = A_n\, \mathit{\boldsymbol{v}}_n - A_n\, \mathit{\boldsymbol{v}}^{hk}_n + A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \end{array} \right. $ |
we obtain
| $ \begin{array}l \Big( \frac{\mathit{\boldsymbol{e }}_n-\mathit{\boldsymbol{e }}_{n-1}}{k}, \, \mathit{\boldsymbol{e }}_n \Big)_H + \left\langle {A_n\, \mathit{\boldsymbol{v}}_n - A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \mathit{\boldsymbol{e }}_n} \right\rangle_{ V^\prime\times V} \\ \leq \left\langle {A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} \\ \quad + \Big( \dot{\mathit{\boldsymbol{v}}}_n - \frac{\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_{n-1}}{k}, \, - \mathit{\boldsymbol{e }}_n \Big)_H + \Big( \frac{\mathit{\boldsymbol{v}}^{hk}_n-\mathit{\boldsymbol{v}}^{hk}_{n-1}}{k}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n \Big)_H \\ \quad + \left\langle {B_n\, \mathit{\boldsymbol{u}}_n - B_n\, \mathit{\boldsymbol{u}}_{n-1}^{hk}, \, -\mathit{\boldsymbol{e }}_n} \right\rangle_{ V^\prime\times V} + \left\langle {B_n\, \mathit{\boldsymbol{u}}_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} \\ \quad + \left\langle {C_n\, \theta_n - C_n\, \theta_{n-1}^{hk}, \, -\mathit{\boldsymbol{e }}_n} \right\rangle_{ V^\prime\times V} + \left\langle {C_n\, \theta_{n-1}^{hk}, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{ V^\prime\times V} \\ \quad + \mathcal{R}_n^{hk} + \psi(t_n, \mathit{\boldsymbol{w}}^h_n) - \psi_u(t_n, \mathit{\boldsymbol{v}}_n) - \left\langle {\mathit{\boldsymbol{f}}_n, \, \mathit{\boldsymbol{w}}^h_n - \mathit{\boldsymbol{v}}_n} \right\rangle_{V^\prime\times V} \end{array} $ |
Consider the quantity for $ n = 1, \cdots, N $,
| $ E_n=\Big(\frac{\mathit{\boldsymbol{e }}_n-\mathit{\boldsymbol{e }}_{n-1}}{k}, \mathit{\boldsymbol{e }}_n \Big)_H + \left\langle {A_n\, \mathit{\boldsymbol{v}}_n -A_n\, \mathit{\boldsymbol{v}}^{hk}_n, \mathit{\boldsymbol{e }}_n} \right\rangle_{ V^\prime\times V}. $ |
We have
| $ E_n \geq \frac{1}{2\, k}\, \big({\|}\mathit{\boldsymbol{e }}_n{\|}_H^2-{\|}\mathit{\boldsymbol{e }}_{n-1}{\|}_H^2\big) +m_{\mathcal{A}}\, (\|\mathit{\boldsymbol{e }}_n\|_V^2 - \|\mathit{\boldsymbol{e }}_n\|_H^2 ). $ |
For $N$ large enough (recall that $k= \frac{T}{N} $), we have $ \frac{1}{2\, k} -m_{\mathcal{A}} \geq 1$, then
| $ E_n\ge \frac{1}{2\, k}\, \big({\|}\mathit{\boldsymbol{e }}_n{\|}_H^2-{\|}\mathit{\boldsymbol{e }}_{n-1}{\|}_H^2\big) +m_{\mathcal{A}}\, \|\mathit{\boldsymbol{e }}_n\|_V^2. $ |
To continue, we denote in the sequel by
| $ \begin{array}l M_e := \max\limits_{1\le n\le N} {\|}\mathit{\boldsymbol{e }}_n{\|}_H, \\ BV_0 := \max\limits_{1\le n\le N}{\|}\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{w}}_n^{h}{\|}_{H}, \\ BV_1 := \sum\limits_{j=1}^N {\Big\|}\frac{\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{v}}_{j-1}}{k} -\dot{\mathit{\boldsymbol{v}}}_j{\Big\|}_H^2, \\ BV_2 := \sum\limits_{j=1}^N \|\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j\|_V^2; \quad \widehat{BV}_2 := \sum\limits_{j=1}^N \|\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j\|_V, \\ BV_3 := \sum\limits_{j=1}^{N-1}{\|}(\mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j) -(\mathit{\boldsymbol{v}}_{j+1}-\mathit{\boldsymbol{w}}^h_{j+1}){\|}_H, \\ I := \sum\limits_{j=1}^{N-1}\, \Big\| \int_0^{t_j}\, \mathit{\boldsymbol{v}} - k\, \sum\limits_{i=1}^{j} \mathit{\boldsymbol{v}}_i \Big\|_V^2, \\ BV_4 := \sum\limits_{j=1}^N\, {\|}\mathit{\boldsymbol{u}}_j - \mathit{\boldsymbol{u}}_{j-1} {\|}_{V}^2, \quad AT_4 := \sum\limits_{j=1}^N\, {\|}\theta_j - \theta_{j-1} {\|}_F^2, \\ BV_5 := \sum\limits_{j=1}^N | \left\langle {B_j\, \mathit{\boldsymbol{u}}_{j-1}, \, \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j} \right\rangle_{V'\times V} |, \quad AT_5 := \sum\limits_{j=1}^N | \left\langle {C_j\, \theta_{j-1}, \, \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j} \right\rangle_{V'\times V} |, \\ F := \sum\limits_{j=1}^N | \left\langle {A_j\, \mathit{\boldsymbol{v}}_j, \, \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j } \right\rangle _{V'\times V} + \psi_u(t_j, \mathit{\boldsymbol{v}}_j) - \psi_u(t_j, \mathit{\boldsymbol{w}}^h_j) - \left\langle {\mathit{\boldsymbol{f}}_j, \, \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j} \right\rangle_{V'\times V} |, \end{array} $ |
Then we sum $E_j$ from $j=1$ to $ j=n $. After some algebraic manipulations, we obtain for $N$ large enough, for any small $\varepsilon >0$, for some constant $c>0$, for $n=1, \cdots, N$,
| $ \begin{array}l {\|}\mathit{\boldsymbol{e }}_n{\|}_H^2+ k\sum\limits_{j=1}^n \, \|\mathit{\boldsymbol{e }}_j\|_V^2 \leq \ c\, {\|}\mathit{\boldsymbol{e }}_0{\|}_H^2 + c\, \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^h \|_V^2 \\ + c\, BV_0 + c\, k\, ( BV_1 + BV_2 + BV_4 + BV_5 + I ) + c\, BV_3\, M_e \\ + c\, k\, ( AT_4 + AT_5 ) + c\, k\, F \\ + c\, k\sum\limits_{j=1}^{n} \, (\alpha^{hk}_j)^2 + c\, k\sum\limits_{j=1}^{n} \, \beta^{hk}_j\, \| \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j \|_V \\ + \varepsilon\, k\, \sum\limits_{j=0}^{n-1} \, \| \varepsilon_j \|_F^2 + c\, k\sum\limits_{j=1}^{n-1} \, \Big( k\sum\limits_{i=1}^{j} \, \|\mathit{\boldsymbol{e }}_i\|_V^2 \Big), \end{array} $ |
where for $n = 1, \cdots, N$:
| $ \begin{array}l \alpha^{hk}_n := \Big\| \int_0^{t_n}\, \mathcal{B}(t_n-s) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}(s))\, ds - k\, \sum\limits_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}^{hk}_m) \Big\|_{\mathcal{H}} \\ \beta^{hk}_n = \Big\| k\, \sum\limits_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \, \mathit{\boldsymbol{\varepsilon }}(\mathit{\boldsymbol{u}}^{hk}_m) \Big\|_{\mathcal{H}}. \end{array} $ |
From (4.1) and after some upper bound computations, we obtain for $n=1, \cdots, N$:
| $ \begin{array}l k\sum\limits_{j=1}^{n} \, (\alpha^{hk}_j)^2 \leq c\, k^2 + c\, k\, \sum\limits_{m=0}^{n-1}\, \| \mathit{\boldsymbol{u}}^{hk}_m- \mathit{\boldsymbol{u}}_m\|_V^2 \\ \leq c\, k^2 + c\, \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^h \|_V^2 + c\, k\, I + c\, k\sum\limits_{j=1}^{n-1} \, \Big( k\sum\limits_{i=1}^{j} \, \|\mathit{\boldsymbol{e }}_i\|_V^2 \Big); \end{array} $ |
and
| $ \begin{array}l \, k\sum\limits_{j=1}^{n} \, \beta^{hk}_j\, \| \mathit{\boldsymbol{v}}_j-\mathit{\boldsymbol{w}}^h_j \|_V \leq c\, k\, \sum\limits_{m=0}^{n-1}\, \| \mathit{\boldsymbol{u}}^{hk}_m- \mathit{\boldsymbol{u}}_m\|_V^2 + c\, k\, (BV_2 + \widehat{BV}_2) \\ \leq c\, \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^h \|_V^2 + c\, k\, I + c\, k\sum\limits_{j=1}^{n-1} \, \Big( k\sum\limits_{i=1}^{j} \, \|\mathit{\boldsymbol{e }}_i\|_V^2 \Big) + c\, k\, (BV_2 + \widehat{BV}_2); \end{array} $ |
and
| $ \begin{array}l k\, I \leq c\, k^2; \\ k\, AT_1 \leq c\, k^2; \\ k\, BV_1 \leq c\, k^2; \\ k\, AT_4 \leq c\, k^2; \\ k\, BV_4 \leq c\, k^2; \\ AT_5 + BV_5 + F \leq c\, \widehat{BV}_2. \end{array} $ |
Using then (4.11), we deduce for some constant $c>0$, for $n=1, \cdots, N$,
| $ \begin{array}l \| \mathit{\boldsymbol{e }}_n{\|}_H^2 + k\sum\limits_{j=1}^n \|\mathit{\boldsymbol{e }}_j\|_V^2 \\ \ \leq c\, \| \mathit{\boldsymbol{e }}_0 \|_H^2 + c\, \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^h \|_V^2 + c\, \| \varepsilon_0 \|_{F}^2 + c\, BV_0 + c\, AT_0^2 \\ \quad + c\, k\, ( BV_2 + \widehat{BV}_2 ) + c\, k\, AT_2 + c\, k^2 \\ \quad + c\, BV_3\, M_e + c\, AT_3\, M_\varepsilon \\ \quad + c\, k\sum\limits_{j=1}^{n-1} \, \Big( k\, \sum\limits_{i=1}^{j} \, \|\mathit{\boldsymbol{e }}_i\|_V^2 \Big). \end{array} $ |
Using then Gronwall's inequality, and again the estimation (4.11), we conclude that for some constant $c>0$, and for $n=1, \cdots, N$,
| $ \begin{array}l \max\Big( \| \mathit{\boldsymbol{e }}_n{\|}_H^2 + k\sum\limits_{j=1}^n \|\mathit{\boldsymbol{e }}_j\|_V^2;\, \| \varepsilon_n {\|}_{F}^2+ k\sum\limits_{j=1}^n \|\varepsilon_j\|_E^2 \Big) \\ \ \leq c\, \| \mathit{\boldsymbol{e }}_0 \|_H^2 + c\, \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^h \|_V^2 + c\, \| \varepsilon_0 \|_{F}^2 + c\, BV_0 + c\, AT_0^2 \\ \quad + c\, k\, ( BV_2 + \widehat{BV}_2 ) + c\, k\, AT_2 \\ \quad + c\, k^2 + c\, BV_3^2 + c\, AT_3^2. \end{array} $ |
This gives the estimation (4.10) stated in Theorem 2.
The inequality (4.10) is a basis for error estimates for particular choice of the finite-dimensional subspace $V^h$ and under additional data and solution regularities.
As a typical example, let us consider $\Omega \subset \mathbb{R}^d$, $d\in \mathbb{N}^*$, a polygonal domain. Let ${\mathcal T}^h$ be a regular finite element partition of $\Omega$. Let $V^h\subset V$ and $E^h\subset E$ be the finite element space consisting of piecewise polynomials of degree $\leq m-1$, with $m \geq 2$, according to the partition ${\mathcal T}^h$. Denote by $\Pi^h_V\, :\, H^m(\Omega)^d \to V^h$ and $\Pi^h_E\, :\, H^m(\Omega)\to E^h$ the corresponding finite element interpolation operator. Recall (see e.g. [3]) that:
| $ \left\{ \begin{array}l \| \mathit{\boldsymbol{w}} - \Pi_V^h \mathit{\boldsymbol{w}} \|_{H^l(\Omega)^d} \leq c\, h^{m-l}\, |\mathit{\boldsymbol{w}}|_{H^m(\Omega)^d}, \quad \forall\, \mathit{\boldsymbol{w}} \in H^m(\Omega)^d; \\ \| \eta -\Pi_E^h \eta \|_{H^l(\Omega)} \leq c\, h^{m-l}\, |\eta|_{H^m(\Omega)}, \quad \forall\, \eta \in H^m(\Omega). \end{array} \right. $ |
where $l=0$ (for which $H^0=L^2$) or $l=1$.
We assume more generally the following additional data and solution regularities for some $\alpha \geq 1$:
| $ \begin{equation} \label{addss} \left\{ \begin{array}l \mathit{\boldsymbol{u}}_0 \in H^{\alpha + 1}(\Omega)^d ; \\ \mathit{\boldsymbol{v}}\in C([0, T];H^{2\alpha +1}(\Omega)^d), \quad \dot{\mathit{\boldsymbol{v}}} \in L^1(0, T; H^{\alpha}(\Omega)^d); \\ \theta \in C([0, T];H^{\alpha +1}(\Omega)), \quad \dot{\theta} \in L^1(0, T;H^{\alpha}(\Omega)). \end{array} \right. \end{equation} $ | (4.12) |
Then we choose in (4.10) the elements
| $ \mathit{\boldsymbol{u}}_0^{h}=\Pi^h_V\, \mathit{\boldsymbol{u}}_0, \quad \mathit{\boldsymbol{v}}_0^{h}=\Pi^h_V\, \mathit{\boldsymbol{v}}_0, \quad \theta_0^{h}=\Pi^h_E\, \theta_0, $ |
and
| $ \mathit{\boldsymbol{w}}_j^{h}=\Pi^h_V\, \mathit{\boldsymbol{v}}_j, \quad \eta_j^{h}=\Pi^h_E\, \theta_j, \quad j=1\cdots N. $ |
From the assumptions (4.12), we have:
| $ \| \mathit{\boldsymbol{u}}_0 - \mathit{\boldsymbol{u}}_0^{h} \|_V \leq c\, h^\alpha, \quad \| \mathit{\boldsymbol{e }}_0 \|_H \leq c\, h^\alpha, \quad \| \varepsilon_0 \|_F \leq c\, h^\alpha; \\ AT_0 \leq c\, h^\alpha, \quad BV_0 \leq c\, h^{2\alpha};\\ AT_3 \leq c\, h^\alpha, \quad BV_3 \leq c\, h^\alpha;\\ k\, AT_2 \leq c\, h^{2\alpha}, \quad k\, BV_2 \leq c\, h^{2\alpha}, \quad k\, \widehat{BV}_2 \leq c\, h^{2\alpha}. $ |
Using these estimates in (4.10), we conclude to the following error estimate result.
Theorem 3. We keep the assumptions of Theorem 2. Under the additional assumptions (4.12), we obtain the error estimate for the corresponding discrete solution $\mathit{\boldsymbol{v}}_n^{hk}$, $\theta_n^{hk}$, $n=1, \dots, N$.
| $ \begin{array}l \max\limits_{0\le n\le N}{\|}\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}{\|}_H +\Big(k\sum\limits_{n=0}^N \|\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}\|_V^2\Big)^{1/2} \\ + \max\limits_{0\le n\le N}{\|}\theta_n-\theta_n^{hk}{\|}_{F} +\Big(k\sum\limits_{n=0}^N \|\theta_n-\theta_n^{hk}\|_E^2\Big)^{1/2} \le c\, (h^{\alpha} + k). \end{array} $ |
In particular, for $ \alpha = 1$, we have
| $ \begin{array}l \max\limits_{0\le n\le N}{\|}\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}{\|}_H +\Big(k\sum\limits_{n=0}^N \|\mathit{\boldsymbol{v}}_n-\mathit{\boldsymbol{v}}_n^{hk}\|_V^2\Big)^{1/2} \\ + \max\limits_{0\le n\le N}{\|}\theta_n-\theta_n^{hk}{\|}_{F} +\Big(k\sum\limits_{n=0}^N \|\theta_n-\theta_n^{hk}\|_E^2\Big)^{1/2} \le c\, (h + k). \end{array} $ |
Here we provide numerical simulations derived from the previous discrete schemes, by using Matlab computation codes, in the case of bilateral contact with Tresca's friction law. Here the following classical examples are taken :
| $ \begin{array}l {C}_e(t, \theta) := - \theta\, (c_{ij}(t) ) \quad \mbox{in} \quad \Omega; \\ {\cal K}_c(t, \nabla \theta) = (k_{ij}(t))\, \nabla \theta \quad \mbox{in} \quad \Omega; \\ {\cal C}_e(t, \mathit{\boldsymbol{v}} ) = -c_{ij}(t)\, \frac{\partial\, v_i}{\partial\, x_j} \quad \mbox{in} \quad \Omega;\\ \varphi(t, r) = \frac{1}{2} k_e(t)\, (r -\theta_R(t) )^2 \quad \mbox{on} \quad \Gamma_3. \end{array} $ |
On the contact surface $\Gamma_3$, we consider a bilateral condition and satisfies (see e.g. [4], [6]):
| $ \left\{ \begin{array}{l} u_\nu=0, \quad |{\mathit{\boldsymbol{\sigma }}}_{\tau}|\leq g(t), \\ |{\mathit{\boldsymbol{\sigma }}}_{\tau}|<g(t)\, \Longrightarrow \, \dot {\mathit{\boldsymbol{u}}}_{\tau}={\bf{0}}, \\ |{\mathit{\boldsymbol{\sigma }}}_{\tau}|=g(t)\, \Longrightarrow\, \dot {\mathit{\boldsymbol{u}}}_{\tau}=-\lambda{\mathit{\boldsymbol{\sigma }}}_{\tau}, \mbox{ for some } \lambda\geq 0, \end{array} \right.\quad \mbox{ on } (0, T) \times \Gamma_3. $ |
Here $g(t)$ represents the friction bound, i.e., the magnitude of the limiting frictional traction at which slip begins, with $g\in L^{\infty}((0, T) \times \Gamma_3)$, $g(t) \geq 0$ a.e. on $\Gamma_3$. We deduce the admissible displacement space:
| $ V := \{ \mathit{\boldsymbol{w}} \in H_1; \ w_\nu = 0 \ \mbox{on} \ \Gamma_3 \}, $ |
and the sub-differential contact function independent on time:
| $ \varphi_u(t, \mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y }}) = g(t, \mathit{\boldsymbol{x}})|\mathit{\boldsymbol{y }}_{\tau(x)}|\quad\forall \mathit{\boldsymbol{x}}\in \Gamma_3, \ \mathit{\boldsymbol{y }}\in \mathbb{R}^d, $ |
where $\mathit{\boldsymbol{y }}_{\tau(x)} := \mathit{\boldsymbol{y }} -y_{\nu(x)}\mathit{\boldsymbol{\nu}}(\mathit{\boldsymbol{x}})$, $y_{\nu(x)} := \mathit{\boldsymbol{y }} \cdot \mathit{\boldsymbol{\nu}}(\mathit{\boldsymbol{x}})$, with $\mathit{\boldsymbol{\nu}}(\mathit{\boldsymbol{x}})$ the unit normal at $\mathit{\boldsymbol{x}}\in\Gamma_3$. We have then
| $ \psi_u(t, \mathit{\boldsymbol{v}}) := \int_{\Gamma_3} g(t)\, | \mathit{\boldsymbol{v}}_\tau |\, da, \quad \forall \mathit{\boldsymbol{v}} \in V $ |
is well defined on $V$ and independent on time with the property: for some $c>0$,
| $ | \psi_u(t, \mathit{\boldsymbol{w}}) -\psi_u(t, \mathit{\boldsymbol{v}})| \leq c\, \| \mathit{\boldsymbol{v}}-\mathit{\boldsymbol{w}} \|_{ L^2(\Gamma_3)^d}, \quad \forall \mathit{\boldsymbol{v}}, \, \mathit{\boldsymbol{w}} \in V. $ |
Thus from the definition it is clear that $\psi_u(t, \cdot)\, :\, V \longrightarrow \mathbb{R}$ is convex. By using the continuous embedding from $V$ into $ L^2(\Gamma_3)^d$ and the last inequality, we find that
| $ \psi_u(t, \cdot)\ \mbox{is Lipschitz continuous on} \ V. $ |
Then the assumptions in (2.17) are verified.
We consider for simulations a rectangular open set, linear elastic and long memory viscoelastic operators, with non clamped condition.
| $ \begin{array}l \Omega = (0, L_1) \times (0, L_2);\quad \Gamma_1 = \emptyset; \\ \Gamma_2 = (\{0\}\times [0, L_2]) \cup ([0, L_1] \times \{L_2\} ) \cup (\{L_1\}\times [0, L_2]); \quad \Gamma_3 = [0, L_1] \times \{0\};\\ ({\mathcal G}(t)\, \mathit{\boldsymbol{\tau }})_{ij}= \frac{E(t)\, \kappa(t)}{1-\kappa(t)^2}(\tau_{11}+\tau_{22})\, \delta_{ij}+\frac{E(t)}{1+\kappa(t)}\tau_{ij}, \quad 1\leq i, \, j\leq 2, \ \mathit{\boldsymbol{\tau }} \in S_2;\\ ({\mathcal A}(t)\, \mathit{\boldsymbol{\tau }})(t)_{ij}= \mu(t)\, (\tau_{11}+\tau_{22})\, \delta_{ij}+ \eta(t)\, \tau_{ij}, \quad 1\leq i, \, j\leq 2, \ \mathit{\boldsymbol{\tau }} \in S_2;\\ ({\mathcal B}(t)\, \mathit{\boldsymbol{\tau }})_{ij}= B_1(t)\, (\tau_{11}+\tau_{22})\, \delta_{ij}+ B_2(t)\, \tau_{ij}, \quad 1\leq i, \, j\leq 2, \ \mathit{\boldsymbol{\tau }} \in S_2, \ t\in [0, T] \end{array} $ |
Here $E(t)$ is the Young's modulus, $\kappa(t)$ the Poisson's ratio of the material, $\delta_{i j}$ denotes the Kronecker symbol, $\mu(t)$ and $\eta(t)$ are viscosity constants, at each time $t \in [0, T]$.
We refer to the previous numerical scheme, and use spaces of continuous piecewise affine functions $V^h\subset V$ and $E^h\subset E$ as families of approximating subspaces. %, with the time and space steps $k=h=1/8$. For computations we considered the following data (IS unity), $\forall t\in [0, T]$:
| $\begin{array}{l} L_1 = L_2 = 1, \quad T = 1\\ \displaystyle \mu(t) = 8\, e^{t}, \quad \eta(t) = \frac{20}{1+ t^2}, \quad E(t) = \frac{4}{1+ t}, \quad \kappa(t) = \frac{0, 2}{1+ t^2}, \quad \mathit{\boldsymbol{f}}_0(\mathit{\boldsymbol{x}}, t) = (0, \, -5 t) \\ \mathit{\boldsymbol{f}}_2(t, \mathit{\boldsymbol{x}})=(0, \, 0), \quad \forall \mathit{\boldsymbol{x}} \in \{0\}\times [0, L_2] \\ \mathit{\boldsymbol{f}}_2(t, \mathit{\boldsymbol{x}})=(1+t, \, 0), \quad \forall \mathit{\boldsymbol{x}} \in ([0, L_1] \times \{L_2\}) \cup (\{L_1\}\times [0, L_2]) \\ c_{11}(t) = c_{12}(t) = c_{21}(t) = t, \quad c_{22}(t)=t^2 \\ k_{11}(t) = k_{22}(t) = 1+t, \quad k_{12}(t) = k_{21}(t) = t \\ k_e(t) = 1+t, \quad q(t)=e^t \\ B_1(t)=B_2(t)= 10^{-2}\, e^{-t} \\ \mathit{\boldsymbol{u}}_0=(0, 0), \quad \mathit{\boldsymbol{v}}_0=(0, 0), \quad \theta_0 = 0 \end{array}$ |
In Figure 1 (see figures below) is representing the initial configuration.
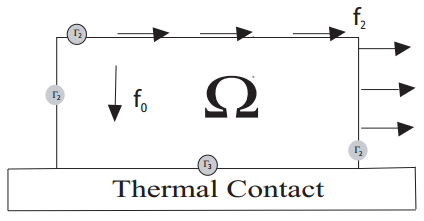 Figure 1. Initial configuration.
Figure 1. Initial configuration.In Figure 2 we have the deformed configuration at final time, where $\theta_R(t) = 0$, $ \theta_a(t) = 5\, e^{-t}$, $0\leq t\leq 1$, for two different types of Tresca's friction bounds. For smaller friction bound with respect to the surface fraction on $\Gamma_2$, where $ g(t, x)= \frac{t+x}{4}$, $0\leq t \leq 1$, $0\leq x \leq 1$, we observe on the contact surface a slip phenomena in the direction of the fraction: which means that the friction bound has been obtained. Whereas for large friction bound, e.g. for $g(t, x)= 9\, (t+x)$, $0\leq t \leq 1$, $0\leq x \leq 1$, then slip in the direction of the traction could be less easy, friction in this case appears more important as well as for the deformation.
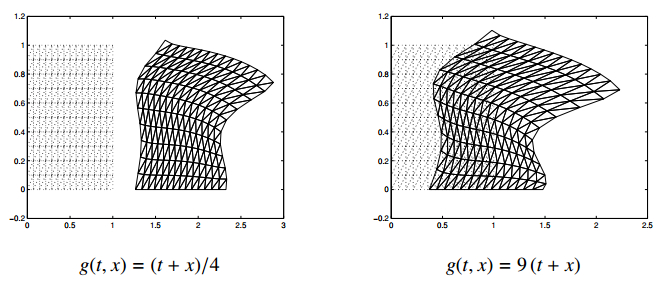 Figure 2. Deformed configurations at final time, $\theta_R(t) = 0$, $ \theta_a(t) = 5\, e^{-t}$, $ 0\leq t\leq 1$.
Figure 2. Deformed configurations at final time, $\theta_R(t) = 0$, $ \theta_a(t) = 5\, e^{-t}$, $ 0\leq t\leq 1$.In Figures 3, we compute the Von Mises' norm which gives a global measure of the stress in the body. We observe that stress is more important for larger friction bounds, at the contact surface or at the traction surface.
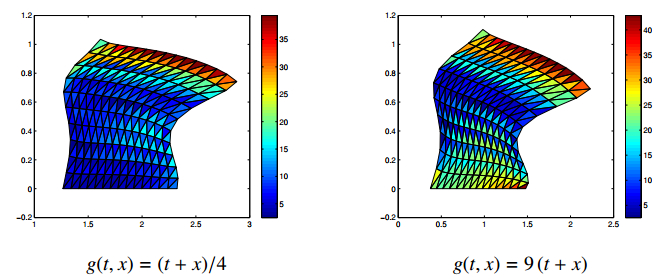 Figure 3. Von Mises' norm in long memory deformed configurations,
$\theta_R(t) = 0$, $\theta_a(t) = 5\, e^{-t}$.
Figure 3. Von Mises' norm in long memory deformed configurations,
$\theta_R(t) = 0$, $\theta_a(t) = 5\, e^{-t}$.In Figures 4, we show the influence of the different temperatures of the foundation ($\theta_R(t) = 0$ or $\theta_R(t) = 30$) on the temperature field $\xi$ of the body.
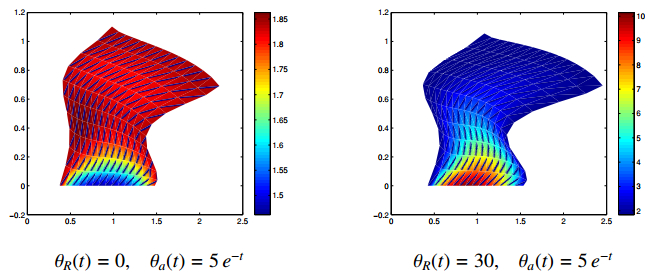 Figure 4. Temperature $\xi$ at final time in long memory, $g(t, x)= 9\, (t+x)$.
Figure 4. Temperature $\xi$ at final time in long memory, $g(t, x)= 9\, (t+x)$.I am immensely grateful for the reviewer to have read this work and for the AIMS Mathematics to publish the paper.
The author declares no conflicts of interest in this paper.
| [1] | O. Chau, V. V. Motreanu, Dynamic contact problems with velocity conditions, Int. J. Ap. Mat. Com-Pol, 12 (2002): 17-26. |
| [2] | O. Chau, Quelques problèmes d'évolution en mécanique de contact et en biochimie, Habilitation thesis, Saint Denis La Réunion: University Press, 2010. |
| [3] | P. G. Ciarlet, The Finite Element Method for Elliptic Problems, Contributions to Nonlinear Functional Analysis, Amsterdam: North Holland, 1978. |
| [4] | G. Duvaut, J. L. Lions, Les Inéquations en Mécanique et en Physique, Paris: Dunod, 1972. |
| [5] | J. L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires, Contributions to Nonlinear Functional Analysis, Dunod et Gauthier-Villars, 1969. |
| [6] | P. D. Panagiotopoulos, Inequality Problems in Mechanics and Applications, Contributions to Nonlinear Functional Analysis, Basel: Birkhäuser, 1985. |
| [7] | P. D. Panagiotopoulos, Hemivariational Inequalities, applications in Mechanics and Engineering, Contributions to Nonlinear Functional Analysis, Springer-Verlag, 1993. |
| [8] | N. Costea, V. Radulescu, Hartman-Stampacchia results for stably pseudomonotone operators and non-linear hemivariational inequalities, Appl. Anal., 89 (2010): 175-88. |
| [9] | E. Zeidler, Nonlinear Functional Analysis and its Applications, Contributions to Nonlinear Functional Analysis, Springer Verlag, 1997. |
| 1. | Lamia Chouchane, Lynda Selmani, A HISTORY-DEPENDENT FRICTIONAL CONTACT PROBLEM WITH WEAR FOR THERMOVISCOELASTIC MATERIALS, 2019, 24, 1392-6292, 351, 10.3846/mma.2019.022 |